Abstract
Explaining macroevolutionary divergence in light of population genetics requires understanding the extent to which the patterns of mutational input contribute to long-term trends. In the context of quantitative traits, mutational input is typically described by the mutational variance–covariance matrix, the -matrix, which summarizes phenotypic variances and covariances introduced by new mutations per generation. However, as a summary statistic, the -matrix does not fully capture all the relevant information from the underlying mutational architecture, and there exist a myriad of possible underlying mutational architectures that give rise to the same -matrix. Using individual-based simulations, we demonstrate mutational architectures that produce the same -matrix can lead to different levels of constraint on evolution and result in difference in within-population genetic variance, between-population divergence, and rate of adaptation. In particular, the rate of adaptation and that of neutral evolution are both reduced when a greater proportion of loci are pleiotropic. Our results reveal that aspects of mutational input not reflected by the -matrix can have a profound impact on long-term evolution and suggest it is important to take them into account in order to connect patterns of long-term phenotypic evolution to underlying microevolutionary mechanisms.
Keywords: M-matrix, phenotypic evolution, pleiotropy, adaptation
Significance.
Mutational input for quantitative traits is typically quantified in terms of phenotypic (co)variances caused by mutations, and it has been unclear how hidden mutational parameters that are not captured by the (co)variances could shape evolution. In this study, we used population genetic simulations to explore how genotype–phenotype (G–P) maps that give rise to identical mutational (co)variances shape the course of evolution differently. We found G–P maps where pleiotropy is prevalent reduce the amount of within-population phenotypic variance and constrain both neutral and adaptive evolution despite mutational (co)variances are the same. Together, we show classic quantitative genetic statistics to describe mutational input is insufficient for understanding mechanisms of evolution.
Introduction
How the structure of mutational input constrains the availability of standing genetic variation and ultimately shapes the course of long-term phenotypic evolution has been a question of great interest (Gould 1980; Nei 2013; Stoltzfus 2021), and addressing this problem requires understanding the quantity and pattern of mutational input. In studies of quantitative traits, abundance of mutational input is usually quantified using the mutational variance, defined as phenotypic variance introduced by new mutations per unit time, typically on a per-generation basis. For multidimensional traits, the mutational variance–covariance matrix (the -matrix, hereafter ) is used to summarize the amount and correlational structure of mutational input simultaneously. Each diagonal element of represents a trait’s mutational variance, and each off-diagonal element represents the mutational covariance (phenotypic covariance introduced by new mutations per generation) between two traits. To estimate , one can use mutagenesis or mutation accumulation (MA) experiments to generate a large number of mutant genotypes and compute phenotypic (co)variances among them (e.g. Camara and Pigliucci 1999; Houle and Fierst 2013).
Often underappreciated is that is only an insufficient summary statistic for the mutational architecture (i.e. the number of genomic loci affecting each trait, the mutation rate and spectrum at each locus, and the phenotypic effects of mutations). By definition, the mutational variance is a product of the mutation rate and variance of mutations’ effect on the trait; similarly, the mutational covariance of a given pair of traits is a product of the rate of pleiotropic mutations affecting both traits and the covariance of the mutations’ effects on two traits (Lynch and Hill 1986; Hansen 2006). With each (co)variance being a product of different parameters, the same can potentially result from different combination of parameter values. For instance, the lack of mutational covariance between two traits may result from the lack of pleiotropic mutations, or the lack of correlation between pleiotropic mutations’ effects on two traits.
With details of the pleiotropic structure underappreciated and unknown, studies concerning the effect of mutational constraints on evolution often make implicit assumptions about pleiotropy. In particular, models for the evolution of multivariate traits often assume universal pleiotropy—that is, every mutation affects every trait, which can have substantial impact on their conclusions and implications. For instance, Fisher’s Geometric Model (FGM) makes this assumption, which leads to the prediction that mutations with smaller effect sizes are more likely to be adaptive and that there is a “cost of complexity” as adaptation is slower when there are a greater number of phenotypic dimensions (Fisher 1930; Orr 2000; Welch and Waxman 2003; Tenaillon 2014). The degree to which the assumption of universal pleiotropy is reasonable remains an open question (Wagner and Zhang 2011; Hill and Zhang 2012a, 2012b; Paaby and Rockman 2013; Boyle et al. 2017; Zhang 2023). Some studies have found that each gene or mutation typically affects only a small subset of traits and suggested that adaptation is not necessarily more constrained in complex organisms as FGM would indicate (Wagner et al. 2008; Wang et al. 2010; Ho and Zhang 2014). Others argue that pleiotropy is more pervasive and that many empirical studies underestimate the prevalence of pleiotropy due to technical issues (Hill and Zhang 2012b). Furthermore, the “omnigenic” model (Boyle et al. 2017; Liu et al. 2019) argues that, because of properties of the regulatory network, each individual gene or mutation can affect a large number of traits while having major effects on a small number of traits. No matter how the debate is resolved, it is clear we cannot take the universal pleiotropy assumption for granted, and it is essential for future studies to be cautious when modeling the evolution multivariate traits and interpreting observed phenotypic variations.
Also underappreciated and yet poorly understood is how different combinations of parameters values that produce the same could affect the evolutionary dynamics differently. It is known that mutations that affect more traits under stabilizing selection tend to be more deleterious, which is the basis of the “cost of complexity” prediction of FGM. This could be true even given the pleiotropic mutations produce the same amount of mutational (co)variances as nonpleiotropic mutations with the same per-trait effect. For example, when traits under concern are all under stabilizing selection, a pleiotropic mutation whose effect is equivalent to their combined effect of multiple nonpleiotropic mutations will be more deleterious than the nonpleiotropic mutations (Fig. 1a, left); if mutational variances mainly result from pleiotropic mutations, the rate of evolution would be lower. If a trait under concern is not under selection, nonpleiotropic mutations affecting this trait will be neutral, whereas pleiotropic mutations that affect traits under stabilizing selection will be deleterious (Fig. 1a, right); if some or all mutations affecting the neutral trait are pleiotropic, the neutral trait’s evolutionary rate will be lower than the neutral expectation.
Fig. 1.
a) A comparison of pleiotropic and nonpleiotropic mutations with the same phenotypic effect on focal trait(s) but different fitness effects. The origin point denotes the optimal phenotype, and fitness decrease with the distance to the optimum. Grey area in each graph represents a zone of effective neutrality determined by the effective population size; mutations that do not cause the phenotype to move outside this zone are effectively neutral. Left: Both traits under concern are under stabilizing selection. Nonpleiotropic mutations and are within the zone of effective neutrality, where as the pleiotropic mutation , which as the same effects on each traits, moves the phenotype outside the zone. Right: Only trait 2 is under stabilizing selection. A nonpleiotropic mutation is neutral, whereas a pleiotropic mutation , which has the same effect on trait 1 is deleterious. b–d) Schematic illustration of alternative genotype–phenotype maps that produce the same -matrix. A locus’s effect on a trait is indicated by a line connecting the trait and the locus. In all three scenarios, each trait is affected by five loci, the distribution of mutations’ per-trait effect is the same for all loci, and pleiotropic mutation’s effect on two traits are uncorrelated. Thus, the two traits have the same mutational variance and zero genetic covariance in all scenarios. b) Each trait affected by five nonpleiotropic loci. c) Each trait is affected by three nonpleiotropic loci and two pleiotropic loci. d) Both traits are affected by the same five loci.
In this study, we use population genetic simulations to explore dynamics of phenotypic evolution in the face of the same but different underlying mutational architectures. Specifically, we examined series of scenarios where the fraction of loci that are pleiotropic varied and show that both neutral evolution and adaptation are more constrained when the fraction is higher.
Results
One-to-Many Mapping Between the -Matrix and Underlying Mutational Architectures
As an illustration of the one-to-many mapping between and the underlying mutational architectures, let us consider two quantitative traits, and hereafter, and derive the mutational (co)variances from population genetic first principles (see supplementary table S1, Supplementary Material online for a summarization of notations). Genomic loci affecting these traits fall into three groups: there are loci that exclusively affect , loci that exclusively affect , and loci that pleiotropically affect and simultaneously (, , and are all nonnegative integers). Let us assume each loci has two possible alleles, and all loci’s phenotypic effects are additive. Mutational variance resulting from loci that exclusively affect is then given by Lynch and Hill (1986)
where is mutation rate of the ith locus and is the phenotypic effect of a mutation at the ith locus. Similarly, mutational variance resulting from is given by
where is the phenotypic effect of a mutation at the ith locus.
Let us denote the effect of a mutation at the ith pleiotropic locus as a vector . The total mutational (co)variance contributed by pleiotropic locus is then given by
The mutational covariance matrix, or -matrix for and is a sum of contribution from three types of loci:
| (1) |
If all loci have the same mutation rate μ, the above equation becomes
| (2) |
and if we also assume that mutation’s effect on a trait is normally distributed across loci, there is
| (3) |
In the above equation, and are the standard deviations of phenotypic effects of mutations at loci that exclusively affect and those at loci that exclusively affect , respectively. Standard deviations of pleiotropic mutations’ effects on and are and , respectively. At last, ρ is the correlation coefficient between pleiotropic mutations’ effects on two traits. It can be seen that every element of is a product of multiple quantities, and it is plausible that different combinations of them give rise to the same . Below we will demonstrate how can remain unchanged with multiple parameters in Equation 3 are altered. We denote to a particular set of values , where hereafter for convenience.
To see how we can manipulate the parameters while holding constant, let , ρ, , and each be multiplied by a rescaling coefficient, such that they become , , , and , respectively, where and . Let us multiply and by rescaling coefficients and , respectively, to keep the mutational variances unchanged:
Solving the above equations gives
| (4) |
and must be nonnegative as no mutation rate or standard deviation can be negative. Therefore, and can only be solved if
Solving the above system of inequalities gives
| (5) |
Hence, given , certain combinations of , , , and are guaranteed to alter the mutational variances. Biologically, if the portion of mutational variance attributable to pleiotropic mutations gets too high, it would be impossible to keep the total mutational variance unchanged by reducing the portion contributed by nonpleiotropic mutations. Given that can be solved, the change to can be done by altering , , or both. Thus, for any given combination of , , , and , there exists a myriad of ways to adjust to keep unchanged. Similarly, there are also alternative ways to adjust . Hence, there exists many unique that give rise to the same .
To demonstrate how mutational architectures that produce identical -matrices can lead to different evolutionary dynamics, we performed evolutionary simulations in SLiM (Haller and Messer 2023) and examined phenotypic variation within and between populations at the end of the simulations. We considered genotype–phenotype (G–P) maps where each trait is affected by 50 genomic loci with equal effect size. Some loci are nonpleiotropic, whereas others are pleiotropic loci that affect all the traits. Different G–P maps being compared have different numbers of pleiotropic and nonpleiotropic loci, but the number of loci affecting each trait is constant (see Fig. 1 for a schematic illustration). Pleiotropic mutation’s effects on different traits are uncorrelated. Together, all these G–P maps produce the same mutational variances and zero mutational covariance (i.e. the -matrices are identical).
G–P Maps Producing the Same can Lead to Different Neutral Evolutionary Rates
We first examined scenarios where traits under concern are all under stabilizing selection. For each G–P map, we simulated 50 replicate populations, and genetic variance (within-population phenotypic variance due to standing genetic variation; denoted ) and evolutionary variance (between-population phenotypic variance; denoted ) over time. Under most of the simulation settings, and first underwent relatively fast increase and saturated (supplementary fig. S1, Supplementary Material online). Notably, G–P maps producing the same -matrix led to different equilibrium values of and . G–P maps that produce the same 2D -matrix showed little difference (Fig. 2, supplementary fig. S1a and b, Supplementary Material online). In contrast, the G–P map where every loci affects five traits resulted in stronger constraint than other maps that produce the same 5D -matrix, leading to lower and (Fig. 2, supplementary fig. S1c and d, Supplementary Material online). Similarly, the G–P map where every loci affects ten traits caused stronger constraint than maps producing the 10D , to the extent that and did not increase over time (Fig. 2, supplementary fig. S1e and f, Supplementary Material online). Interestingly, mutational architectures with strong pleiotropy also led to apparent evolutionary correlation between traits. While mutational covariances are zero in our simulations and the expected evolutionary covariance (and correlation) between any pair of traits is zero, it is plausible that traits end up correlated with each other among lineages by chance. We found that, when all loci are pleiotropic, evolutionary correlations between traits are generally stronger (supplementary table S2, Supplementary Material online), indicating hidden aspects of mutational architectures can not only affect the evolutionary rate, but also observed correlation among traits.
Fig. 2.
Phenotypic variance within and between populations when all traits are under stabilizing selection. Colors correspond to the dimensionality of -matrices being compared. a) Within-population genetic variance (), which is averaged across populations for each trait and then averaged across traits. Error bars reflect standard error, which is first calculated for each trait and then averaged across traits. b) Between-population variance (), which is first calculated for each trait and then averaged across traits. Error bars reflect sampling standard deviation of sample variance at sample size of 50. Y-axes are in log10 scale.
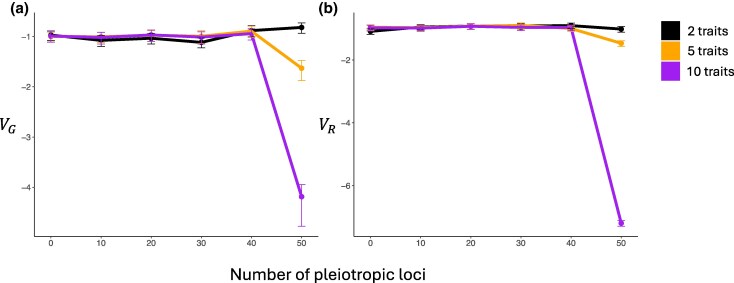
We also examined the evolution of a neutral trait () that does not affect fitness directly and asked how its evolution would be constrained by the indirect effect of other traits being under stabilizing selection. We predicted that, as the proportion of underlying loci of increases, and of will decrease. Indeed, the G–P map where every locus pleiotropically affects five traits led to lower equilibrium than those producing the same 5D -matrix (Fig. 3, supplementary fig. S2c, Supplementary Material online), and the G–P map where every locus pleiotropically affects ten traits prevented from growing over time (Fig. 3, supplementary fig. S2e, Supplementary Material online), which are similar to observations where all traits are under stabilizing selection. The between-population variance underwent faster initial increase and kept increasing, albeit slowly, over time, displaying different dynamics as that observed when all traits are under stabilizing selection (supplementary fig. S2b, d, and f, Supplementary Material online). Among G–P maps producing the same , those with more pleiotropic loci generally correspond to lower , which held for all three -matrices examined (Fig. 3, supplementary fig. S2b, d, and f, Supplementary Material online). Note that even in the absence of pleiotropy, of is lower than the neutral expectation and lower when more traits are under stabilizing selection (Fig. 3b), indicating the rate of fixation of neutral mutations, namely nonpleiotropic mutations that affect only, was reduced by unlinked background selection (Charlesworth 2012; Matheson and Masel 2024). Together, our results show that prevalent pleiotropy can constrain the rate of neutral evolution as captured by phenotypic variance among lineages.
Fig. 3.
Variance of a neutral trait () within and between populations when all other traits are under stabilizing selection. Colors correspond to the dimensionality of -matrices being compared. a) Within-population genetic variance () of , which is averaged across populations. Error bars reflect standard error, which is first calculated for each trait and then averaged across traits. b) Between-population variance () of . Error bars reflect sampling standard deviation of sample variance at sample size of 50. Y-axes are in log10 scale.
G–P Maps Producing the Same Impose Different Levels of Constraint on Adaptation
We asked how these different G–P maps could constrain adaptation when a focal trait () is under directional selection and other traits are under stabilizing selection. Under such selective regimes, selection on different traits can interfere, and pleiotropy can have a profound impact on a trait’s response to directional selection (Hansen and Houle 2008). We let the simulation run for generations, and examined the mean of across population at the end of the simulation. As pleiotropic loci are more likely to have detrimental effects on traits under stabilizing selection, the supply of adaptive mutations will be more limited when a greater fraction of loci are pleiotropic (supplementary fig. S3, Supplementary Material online), which could result in lower rate of adaptation, and a higher probability that the population does not reaching the optimum by the end of the simulation. We simulated evolution in both Wright–Fisher (WF) populations, whose sizes are constant through time, and non-WF populations, whose size can change through time. In the non-WF populations, each individual’s phenotype affects its viability while fecundity is invariable among individuals. As the population undergoes adaptive evolution, it will be able to reach and maintain a greater size as death rate is lower; when the population is well adapted (all individuals have the optimal phenotype), its size will stay close to the carrying capacity K, which is an upper limit imposed by the environmental condition.
As predicted, the rate adaptation generally decreased with the proportion of loci that are pleiotropic. As the number of pleiotropic loci increased, the mean across populations () at the end generally became farther away from the optimum, which held for both WF (Fig. 4a) and non-WF (Fig. 4b) populations. Given that the optimum is reached, the time taken to reach the optimum generally increased with the degree of pleiotropy among mutational architectures producing the same (supplementary figs. S4 and S5, Supplementary Material online). In cases where is far away from the optimum, many populations underwent no adaptive evolutionary change at all within time of simulation (supplementary tables S3 and S4, Supplementary Material online). The average size of non-WF populations () over time showed trends that are consistent with those of : at the end of the simulation was close to K when the number of pleiotropic loci is no more than 20 but decreased when the number of pleiotropic loci increased (Fig. 4c); change of over time displayed consistent patterns (supplementary fig. S6, Supplementary Material online). Under some conditions, populations were not only maladapted over the course of our simulations, but also underwent not noticeable change in and/or N (curves corresponding to G–P maps with 50 pleiotropic loci, supplementary figs. S4c, S5b and c, and S6b and c, Supplementary Material online), indicating they are unlikely to show significant response even given more abundant time.
Fig. 4.
Adaptive evolution when one trait is under directional selection and others are under stabilizing selection. Colors correspond to the dimensionality of -matrices being compared. a) Mean value of trait under directional selection () at the end of simulation in Wright–Fisher (WF) populations. b) Mean at the end of simulation in non-WF populations. Mean was first calculated for each population, then the population means were averaged to obtain a cross-population mean. c) Mean population size () at the end of simulation in non-WF populations (no population went extinct during the simulations). Dashed lines in (a) and (b) represent the optimal phenotype. The dark red dashed line in (c) represents the carrying capacity (K). Error bars in both panels reflect standard error.
Together, our simulation results show mutational architectures that produce the same -matrix but have distinct “hidden” properties can have drastically different effects on dynamics of neutral phenotypic evolution and adaptation.
Discussion
In this study, we compared the evolutionary consequences of mutational architectures that produce the same -matrix showed that these alternative mutational architectures can have different dispositional effects on phenotypic evolution. We found that pleiotropic mutations are generally more deleterious, less likely to be adaptive, and less likely to fix, resulting in constraints on both neutral and adaptive evolution. Our findings regarding the effect of pleiotropy on evolution agree with those of earlier studies (Orr 2000; McGuigan 2006; Chevin et al. 2010; Martin 2014; Jiang and Zhang 2020; Battlay et al. 2024), but further show that this effect persists even given the same -matrix. It is also worth noting that pleiotropy makes a difference even when mutations’ effects on different traits are uncorrelated. Correlated pleiotropic effects, which manifest as mutational covariances, are known to shape the structure of genetic covariances and eventually patterns of correlated evolution (Lande 1979, 1980; Wagner 1989), whereas the effect of unstructured pleiotropy on evolution is less appreciated. Nevertheless, unstructured pleiotropy can indeed alter the distribution of effects of new mutations, potentially constraining the course of evolution. Together, we suggest that, with only the -matrix along with regime of selection, robust predictions about the course of evolution cannot be made without further information, and more detailed understanding of the mutational architecture would be essential for understanding mechanisms of phenotypic evolution. If the effect of details of pleiotropy is overlooked and assumed to make little difference to evolution, conclusions about phenotypic evolution that are contingent on strong assumptions about pleiotropy could be mis-interpreted as general.
Our simulations of evolution under directional selection ran for a fixed amount of time, so results at the end may or may not reflect equilibrium behaviors. While the equilibrium if often of interest, transient behaviors are also highly relevant in many contexts. While it is not impossible for a population with very low rate of adaptation to reach the optimum in the end if it is given unlimited time (Sella 2009), actual populations do not evolve in constant environments indefinitely, and it is often the dynamics of adaptation during a transient period rather than the long-term equilibrium in a static environment that is most relevant (e.g. in the context of evolutionary rescue Orr and Unckless 2014; Anciaux et al. 2018 or fluctuating selection Holstad et al. 2024). Upon examining the temporal dynamics, it turns out that some populations were still approaching the optimum at the end of the simulation, indicating mutational constraints reduced the rate of adaptation but would not necessarily affect the equilibrium mean phenotype (supplementary fig. S5b and c, Supplementary Material online); however, there were also populations that showed no noticeable adaptive response during the simulation (supplementary fig. S5c, Supplementary Material online, yellow curve), indicating alternative mutational architectures that impose strong enough constraints can potentially render the population virtually unable to adapt.
The effect of hidden aspects of the mutational architecture on phenotypic evolution has important implications for understanding mechanisms of phenotypic evolution in nature. A subject to which the one-to-many mapping problem is highly relevant to is the relationship between patterns of mutational input, additive genetic variance, and long-term phenotypic evolution. In principle, one can compare to patterns of within-species additive genetic (co)variances (as encapsulated by the genetic variance–covariance matrix, ) and evolutionary (co)variance among species (as encapsulated by the evolutionary variance–covariance matrix, ) (e.g. Houle et al. 2017); strong similarity between and the other two matrices would be consistent with the patterns of mutational input driving long-term evolution. However, this test faces conceptual difficulties and is not as straightforward as it appears to be: as the dispositional effect of mutational input on evolution cannot be learned from the -matrix alone, a comparison of matrices alone is also not sufficient to tell whether and how mutational constraints have shaped observed phenotypic divergence. It is worth noting that, the existence of one-to-many mapping alone does not make specific predictions about how similar should be to or , nor does it support or contradict observed patterns of similarity (e.g. Houle et al. 2017; Jiang and Zhang 2020; Rohner and Berger 2023; Saito et al. 2024; Rohner and Berger. 2025), as the exact effect of mutational constraints will depend on the specific mutational architecture and its interaction with selection. It should also be noted that studies that compare covariances matrices like , , and have been using different methods and their summary statistics may not be readily comparable (see also Houle et al. 2020; Jiang and Zhang 2020). The debate over methods to quantify degree of similarity between matrices is beyond the scope of this study, but caution should be advised when making cross-study comparisons and assessing of the generality of specific findings.
Like one-to-many mapping between and the underlying mutational architectures, there also exists one-to-one mapping between the -matrix and the underlying genetic architectures (i.e. frequencies and distribution of effects of standing genetic variations). Unlike , however, is a result of both mutation and selection on the phenotype (Barton 1990; Houle et al. 1996; Jones et al. 2003, 2004; McGuigan 2006; Arnold et al. 2008). Thus, alternative genetic architectures that produce the same are presumably not equally likely to be observed. For instance, genetic variations with less pleiotropic effects on traits under strong selection are more likely to contribute to standing phenotypic variation. Consequently, aligns more strongly with than does. This prediction is consistent with our results, which shows concordant effect of pleiotropy on within- and between-population phenotypic variances, as well as previously reported correlations between additive genetic variances and evolutionary rates (Schluter 1996; Ackermann and Cheverud 2004; Bolstad et al. 2014; Porto et al. 2015; McGlothlin et al. 2018; Opedal et al. 2023; Voje et al. 2023; Holstad et al. 2024; Saito et al. 2024; Tsuboi et al. 2024).
In this study, the mutational architecture is assumed to be constant over time, but in theory, the mutational architecture itself can also evolve due to second-order selection for mutational robustness as well as evolvability. Such selection can contribute to the observed alignment between and or : second-order selection can reduce mutational variances in phenotypic dimensions subject to strong stabilizing selection, making aligned with the adaptive landscape (Jones et al. 2007, 2014). However, previous theoretical studies of second-order selection focused on effect sizes of pleiotropic mutations ( and in Equation (2)) and correlation between their effects on different traits (ρ in Equation (2)), assuming other aspects of the mutational architecture unchanging. Principles of evolution of other mutational parameters as well as the coevolution of different mutational parameters, in contrast, are less well understood. For example, selection may act to reduce the mutation rate of highly pleiotropic loci or reduce their degree of pleiotropy by decoupling some loci and traits. In a case where an ancestrally pleiotropic gene undergoes duplication and subfunctionalization such that each duplicate affects only some of the traits affected by the ancestral gene, mutational variances can stay unchanged. It is also plausible that second-order selection on these parameters can make all alternative mutational architectures producing the same not equally likely to be observed, which could also contribute to alignment between and or . It would be of great interest to future studies to model the coevolution of different mutational parameters and to investigate the impact of their evolution on observed phenotypic variations.
Another important implication of the many-to-one mapping, which is also highly related to the topic of second-order selection discussed above, is about modularity. Researchers have hypothesized that the underlying genetic architecture of multivariate traits can evolve to be modular such that mutations tend not to affect traits belong to different functional modules simultaneously; this leads to enhanced mutational robustness and/or evolvability (Wagner 1996; Wagner and Altenberg 1996; De Visser et al. 2003; Wagner et al. 2007; Wagner and Zhang 2011; Goswami et al. 2014; Melo and Marroig 2015). A widely used method to quantify modularity is the covariance ratio, a statistic that summarizes the overall amount of covariance between traits of different predefined modules relative to the overall amount of within-module covariance (Adams 2016; Adams and Collyer 2019). However, as covariances do not fully capture properties the mutational architecture, tests based on the covariance ratio may not capture modularity of the G–P map—if pleiotropy is indeed restricted within functional modules, yet mutations’ effects on traits are not well correlated, there may not be signal of modularity in covariance-based tests, despite such a scenario shall still be considered a case of modularity. As such hidden modularity can also have significant evolutionary consequences, relying solely on covariance-based tests could also hinder our effort to understand of the evolution of modularity and the influence of modularity on phenotypic evolution.
For the purpose of this study, we focused on many-to-one mapping between underlying mutational architectures and due to variation in the number of pleiotropic and nonpleiotropic loci. In addition to these aspects of the mutational architecture, there are others that are also not captured by mutational (co)variances yet can potentially affect the pattern of evolutionary divergence at least under some conditions, such as normality of the distribution of phenotypic effects of mutations (Schraiber and Landis 2015), the number of loci affecting the trait (Lynch and Hagner 2015; Schraiber and Landis 2015; Lynch 2020; Jiang et al. 2025; Lynch and Menor 2025), mutational bias (Svensson and Berger 2019), and structure of gene regulatory networks (Hether and Hohenlohe 2014). We would encourage theorists and empiricists to pay close attention to the (often implicit) assumptions about underlying architecture of traits embedded in both models and statistical tests. Furthermore, recent studies have suggested that developmental constraints, by channeling the effect of mutations and genetic variations on the phenotype, can shape the structure of and , and are key to connecting evolutionary patterns across timescales (Milocco and Salazar-Ciudad 2022; Mongle et al. 2022; Machado et al. 2023; Rohner and Berger 2023; Saito et al. 2024; Jiang et al. 2025; Rohner and Berger. 2025). As developmental processes mediate the relationship between genotypes and phenotypes, understanding development can help us understand the origin of hidden properties of the mutational architecture and plausibility of different potential mutational architectures.
Conclusion
In this study, we show that the -matrix, a summary statistic commonly used to describe mutational input for quantitative traits, does not fully capture key features of the mutational architecture even when mutations’ effects are all additive. Using simulations, we show difference in properties of these mutational architectures can result in different evolutionary dynamics. Specifically, when a greater fraction of loci affecting a given trait are pleiotropic, the trait under concern will have lower rates of neutral evolution and adaptation. We suggest that hidden aspects of mutational architectures that are not reflected by -matrices poses significant challenge to attempts to understand mechanisms of phenotypic evolution and requires more explicit consideration in future studies.
Materials and Methods
G–P Maps
We considered a set of quantitative traits, each affected by a set of underlying loci (each loci being a genes or genomic region). We considered an infinite sites model where mutations at any given locus are all distinct from each other and recurrent mutations never occur. Therefore, in our simulations, each mutation’s phenotypic effect is sampled independently from the locus-specific distribution.
Two types of loci were considered in our simulations: nonpleiotropic loci that each affects a single trait, and pleiotropic loci that each affects all traits. When a mutation occurs at a nonpleiotropic locus, its effect on the trait to be affected was sampled from a normal distribution . If a mutation occurs at a pleiotropic locus, its effect is sampled from a multivariate normal distribution characterized by a covariance matrix whose diagonal elements are equal to and off-diagonal elements are all equal to zero. We assumed no bias in mutation’s phenotypic effect; that is, the mean effect of mutations at any given locus on any given trait was zero. The contribution of any given locus to the mutational variance of any given trait it affects is thus equal to , where μ is the per-locus mutation rate; accordingly, the total mutational variance of any given trait is
where L is the total number of loci affecting the trait. The total mutational covariance between two traits, on the other hand, is given by
where is the number of pleiotropic loci and ρ is the correlation between mutations’ effects on two traits. Under our simulations’ setting, , so there is for all trait pairs regardless of . Alternative G–P maps being compared differ in but have the same L for all traits, so mutational variances are constant across G–P maps. Together, by varying the proportion of L and , a series of alternative G–P maps producing the same -matrix were obtained.
In our simulations, all traits had underlying loci, and σ was equal to one for all traits. We considered three -matrices, which have 2, 5, and 10 dimensions, respectively; diagonal elements of all these matrices were equal to . or each -matrix, and compared G–P maps where was equal to 0, 10, 20, 30, 40, and 50. For simplicity, phenotypic effects of mutations were assumed to be additive and heritability was assumed to be for all traits.
Selection on Phenotypic Traits
We considered a multivariate Gaussian fitness function, which is described by a covariance matrix . Each diagonal element of is the width of an individual trait’s Gaussian fitness function, and off-diagonal elements represent correlational selection for relationships between traits (Arnold et al. 2001, 2008).
To calculate fitness given the n-dimensional phenotype , we first calculate its distance to the optimal phenotype :
We then calculate the projection of on eigenvectors of :
where is the eigenvector matrix of . Fitness is then calculated as
| (1) |
where is the ith element of and is the nth eigenvalue of . If an eigenvalue of (e.g. ) is zero, the corresponding term in Equation (1) () would be dropped. The biological interpretation of such a situation is the lack of selection on a specific phenotypic dimension, in which case the phenotypic dimension with no selection should not be considered when calculating fitness.
In our simulations, we only considered scenarios without correlational selection, so -matrices being considered were all diagonal. Equation (1) thus becomes
| (2) |
where is the ith element of and is the ith diagonal element of , characterizing strength of selection on the ith trait.
We had all traits start from a value of 0 in our simulations. All traits’ optimal values are equal to 0, unless noted otherwise. Diagonal elements of are all equal to 1, unless noted otherwise. In simulations where one trait () is neutral, the corresponding diagonal element of , is equal to 0 and the trait is not counted when calculating fitness. In simulations where one trait () is under directional selection, we set trait’s optimal value to be 20 and . Under such a setting, it requires multiple substitutions for the phenotype to be optimized and the initial fitness is not too low to cause quick extinction such that it is easy to quantify and visualize rate of adaptation using the population mean phenotype.
SLiM Simulations
We simulated the evolution of orthogonal traits with zero mutational covariance in diploid, hermaphrodite, and free-mating populations in SLiM 4 (Haller and Messer 2023). Each locus that affect trait(s) was represented as a single genomic element object in SLiM. Loci affecting a given trait is represented as a type of genomic element, whereas pleiotropic loci are represented as another type. Each locus’s mutation rate was set to be per generation. We also assumed free recombination between loci and no recombination within each locus; this interprets as that causal loci are sparsely distributed along the chromosome. Fitness with respect to traits under consideration is calculated following Equation (2).
We simulated evolution of both Wright–Fisher (WF) and non-WF diploid populations. All WF populations had population size , and simulation for each population lasted for ticks (generations). In the WF simulation, each individual’s fitness value is equal to fitness with respect to traits of concern. Simulation for each non-WF population started with , where K is the carrying capacity, and ran for ticks. Reproduction takes place at the beginning of each tick, and the expected number of offspring produced by each individual each time was set to be 1, which was set to be the same for all individuals. Variation in fitness between individuals is mediated by death probability. The fitness value of the ith individual at a given time t is calculated as , where is its fitness with respect to the traits under concern and is the population size at the moment. If, after reproduction, an individual’s fitness is equal to or greater than 1, it will survive at the end of the tick; if all individuals’ fitness values are equal to or greater than 1, the population will grow.
For each evolutionary scenario, we simulated 50 replicate populations, which correspond to 50 subpopulation objects in SLiM with zero gene flow in SLiM. Genetic variance () of each trait was computed as phenotypic variance among individuals in a population at the end of the simulation. For each trait, genetic variances from the 50 replicate populations were averaged to represent the expected genetic variance. For scenarios where traits were either under stabilizing selection or no selection, we quantified the degree of evolutionary divergence among population using variance of mean phenotypes among replicate populations (). Because all traits under consideration had the same mutational variance, we averaged different traits’ and for simulation setting to represent the overall degree of constraint in the corresponding scenario. When a trait is under directional selection, we examined its mean across populations at the end; for non-WF simulations, population that had zero population sizes in the end where excluded calculating this mean phenotype.
Strength of Evolutionary Correlations
For each simulation setting where all traits are under stabilizing selection, we examined the evolutionary correlation matrix, where each off-diagonal element is the correlation between two traits among populations. To quantify the overall strength of correlation, we calculated the variance of eigenvalues of the evolutionary correlation matrix (denoted ); a high means strong overall correlation (Pavlicev et al. 2009). As a control, we sampled 50 vectors from the distribution of , obtained a correlation matrix from the samples, and computed ; this was repeated for 200 times, yielding a null distribution. For each simulation setting, we compared the observed to the corresponding null distribution. If the observed value is greater than more than of those in the null distribution, the difference is considered as significant (Jiang and Zhang 2023).
Supplementary Material
Acknowledgments
We thank Alex Cope, Joshua Schraiber, Arlin Stoltzfus, David McCandlish, Joanna Masel, Masahito Tsuboi, and an anonymous reviewer for their thoughtful comments on this work. This study was supported by NIH grant R35GM151348 to M.P. D.J. is supported by Okinawa Institute of Science and Technology Graduate University.
Contributor Information
Daohan Jiang, Department of Quantitative and Computational Biology, University of Southern California, Los Angeles, CA 90089, USA; Macroevolution Unit, Okinawa Institute of Science and Technology Graduate University, Onna-son, Okinawa 904-0497, Japan.
Matt Pennell, Department of Quantitative and Computational Biology, University of Southern California, Los Angeles, CA 90089, USA; Department of Biological Sciences, University of Southern California, Los Angeles, CA 90089, USA; Department of Computational Biology, Cornell University, Ithaca, NY 14853, USA.
Data Availability
The code and data underlying this article are available GitHub at https://github.com/applied-phylo-lab/m-matrix.
Supplementary Material
Supplementary material is available at Genome Biology and Evolution online.
Literature cited
- Ackermann RR, Cheverud JM. Detecting genetic drift versus selection in human evolution. Proc Natl Acad Sci U S A. 2004:101(52):17946–17951. 10.1073/pnas.0405919102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams DC. Evaluating modularity in morphometric data: challenges with the RV coefficient and a new test measure. Methods Ecol Evol. 2016:7(5):565–572. 10.1111/mee3.2016.7.issue-5. [DOI] [Google Scholar]
- Adams DC, Collyer ML. Comparing the strength of modular signal, and evaluating alternative modular hypotheses, using covariance ratio effect sizes with morphometric data. Evolution. 2019:73(12):2352–2367. 10.1111/evo.v73.12. [DOI] [PubMed] [Google Scholar]
- Anciaux Y, Chevin L-M, Ronce O, Martin G. Evolutionary rescue over a fitness landscape. Genetics. 2018:209(1):265–279. 10.1534/genetics.118.300908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold SJ, Bürger R, Hohenlohe PA, Ajie BC, Jones AG. Understanding the evolution and stability of the g-matrix. Evolution. 2008:62(10):2451–2461. 10.1111/evo.2008.62.issue-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold SJ, Pfrender ME, Jones AG. The adaptive landscape as a conceptual bridge between micro-and macroevolution. Genetica. 2001:112:9–32. 10.1007/978-94-010-0585-2. [DOI] [PubMed] [Google Scholar]
- Barton NH. Pleiotropic models of quantitative variation. Genetics. 1990:124(3):773–782. 10.1093/genetics/124.3.773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battlay P, Yeaman S, Hodgins KA. Impacts of pleiotropy and migration on repeated genetic adaptation. Genetics. 2024:228(1):iyae111. 10.1093/genetics/iyae111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolstad GH, Hansen TF, Pélabon C, Falahati-Anbaran M, Pérez-Barrales R, Armbruster WS. Genetic constraints predict evolutionary divergence in Dalechampia blossoms. Philos Trans R Soc B Biol Sci. 2014:369(1649):20130255. 10.1098/rstb.2013.0255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyle EA, Li YI, Pritchard JK. An expanded view of complex traits: from polygenic to omnigenic. Cell. 2017:169(7):1177–1186. 10.1016/j.cell.2017.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camara MD, Pigliucci M. Mutational contributions to genetic variance-covariance matrices: an experimental approach using induced mutations in Arabidopsis thaliana. Evolution. 1999:53:1692–1703. 10.1111/j.1558-5646.1999.tb04554.x. [DOI] [PubMed] [Google Scholar]
- Charlesworth B. The effects of deleterious mutations on evolution at linked sites. Genetics. 2012:190(1):5–22. 10.1534/genetics.111.134288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevin L-M, Martin G, Lenormand T. Fisher’s model and the genomics of adaptation: restricted pleiotropy, heterogenous mutation, and parallel evolution. Evolution. 2010:64(11):3213–3231. 10.1111/evo.2010.64.issue-11. [DOI] [PubMed] [Google Scholar]
- De Visser JAG, Hermisson J, Wagner GP, Meyers LA, Bagheri-Chaichian H, Blanchard JL, Chao L, Cheverud JM, Elena SF, Fontana W, et al. Perspective: evolution and detection of genetic robustness. Evolution. 2003:57:1959–1972. 10.1111/j.0014-3820.2003.tb00377.x. [DOI] [PubMed] [Google Scholar]
- Fisher RA. The genetical theory of natural selection. Oxford, UK: Oxford University Press; 1930. [Google Scholar]
- Goswami A, Smaers JB, Soligo C, Polly PD. The macroevolutionary consequences of phenotypic integration: from development to deep time. Philos Trans R Soc B Biol Sci. 2014:369(1649):20130254. 10.1098/rstb.2013.0254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gould SJ. Is a new and general theory of evolution emerging? Paleobiology. 1980:6(1):119–130. 10.1017/S0094837300012549. [DOI] [Google Scholar]
- Haller BC, Messer PW. Slim 4: multispecies eco-evolutionary modeling. Am Nat. 2023:201(5):E127–E139. 10.1086/723601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen TF. The evolution of genetic architecture. Annu Rev Ecol Evol Syst. 2006:37(1):123–157. 10.1146/ecolsys.2006.37.issue-1. [DOI] [Google Scholar]
- Hansen TF, Houle D. Measuring and comparing evolvability and constraint in multivariate characters. J Evol Biol. 2008:21(5):1201–1219. 10.1111/jeb.2008.21.issue-5. [DOI] [PubMed] [Google Scholar]
- Hether TD, Hohenlohe PA. Genetic regulatory network motifs constrain adaptation through curvature in the landscape of mutational (co) variance. Evolution. 2014:68(4):950–964. 10.1111/evo.2014.68.issue-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Zhang X-S. Assessing pleiotropy and its evolutionary consequences: pleiotropy is not necessarily limited, nor need it hinder the evolution of complexity. Nat Rev Genet. 2012a:13(4):296–296. 10.1038/nrg2949-c1. [DOI] [PubMed] [Google Scholar]
- Hill WG, Zhang X-S. On the pleiotropic structure of the genotype–phenotype map and the evolvability of complex organisms. Genetics. 2012b:190(3):1131–1137. 10.1534/genetics.111.135681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho W-C, Zhang J. The genotype–phenotype map of yeast complex traits: basic parameters and the role of natural selection. Mol Biol Evol. 2014:31(6):1568–1580. 10.1093/molbev/msu131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holstad A, Voje KL, Opedal ØH, Bolstad GH, Bourg S, Hansen TF, Pélabon C. Evolvability predicts macroevolution under fluctuating selection. Science. 2024:384(6696):688–693. 10.1126/science.adi8722. [DOI] [PubMed] [Google Scholar]
- Houle D, Bolstad GH, Hansen TF. Fly wing evolutionary rate is a near-isometric function of mutational variation. bioRxiv 268938. 10.1101/2020.08.27.268938, Pages 2020–08, preprint: not peer reviewed. [DOI]
- Houle D, Bolstad GH, van der Linde K, Hansen TF. Mutation predicts 40 million years of fly wing evolution. Nature. 2017:548(7668):447–450. 10.1038/nature23473. [DOI] [PubMed] [Google Scholar]
- Houle D, Fierst J. Properties of spontaneous mutational variance and covariance for wing size and shape in Drosophila melanogaster. Evolution. 2013:67(4):1116–1130. 10.1111/evo.2013.67.issue-4. [DOI] [PubMed] [Google Scholar]
- Houle D, Morikawa B, Lynch M. Comparing mutational variabilities. Genetics. 1996:143(3):1467–1483. 10.1093/genetics/143.3.1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang D, Kejiou N, Qiu Y, Palazzo AF, Pennell M. Mol Syst Biol. 2025:21:472–491. 10.1038/s44320-025-00095-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang D, Pennell M, Sallan L. A general evolutionary model for the emergence of novel characters from serial homologs. bioRxiv 645690. 10.1101/2025.03.27.645690, Pages 2025–03, preprint: not peer reviewed. [DOI]
- Jiang D, Zhang J. Fly wing evolution explained by a neutral model with mutational pleiotropy. Evolution. 2020:74(9):2158–2167. 10.1111/evo.v74.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang D, Zhang J. Detecting natural selection in trait-trait coevolution. BMC Ecol Evol. 2023:23(1):50. 10.1186/s12862-023-02164-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones AG, Arnold SJ, Bürger R. Stability of the g-matrix in a population experiencing pleiotropic mutation, stabilizing selection, and genetic drift. Evolution. 2003:57:1747–1760. 10.1111/j.0014-3820.2003.tb00583.x. [DOI] [PubMed] [Google Scholar]
- Jones AG, Arnold SJ, Burger R. Evolution and stability of the g-matrix on a landscape with a moving optimum. Evolution. 2004:58:1639–1654. 10.1111/j.0014-3820.2004.tb00450.x. [DOI] [PubMed] [Google Scholar]
- Jones AG, Arnold SJ, Bürger R. The mutation matrix and the evolution of evolvability. Evolution. 2007:61(4):727–745. 10.1111/evo.2007.61.issue-4. [DOI] [PubMed] [Google Scholar]
- Jones AG, Bürger R, Arnold SJ. Epistasis and natural selection shape the mutational architecture of complex traits. Nat Commun. 2014:5(1):3709. 10.1038/ncomms4709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lande R. Quantitative genetic analysis of multivariate evolution, applied to brain: body size allometry. Evolution. 1979:33:402–416. [DOI] [PubMed] [Google Scholar]
- Lande R. The genetic covariance between characters maintained by pleiotropic mutations. Genetics. 1980:94(1):203–215. 10.1093/genetics/94.1.203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Li YI, Pritchard JK. Trans effects on gene expression can drive omnigenic inheritance. Cell. 2019:177(4):1022–1034. 10.1016/j.cell.2019.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M. The evolutionary scaling of cellular traits imposed by the drift barrier. Proc Natl Acad Sci U S A. 2020:117(19):10435–10444. 10.1073/pnas.2000446117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Hagner K. Evolutionary meandering of intermolecular interactions along the drift barrier. Proc Natl Acad Sci U S A. 2015:112:E30–E38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Hill WG. Phenotypic evolution by neutral mutation. Evolution. 1986:40(5):915–935. 10.2307/2408753. [DOI] [PubMed] [Google Scholar]
- Lynch M, Menor S. The divergence of mean phenotypes under persistent Gaussian selection. Genetics. 2025:229:iyaf031. 10.1093/genetics/iyaf031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado FA, Mongle CS, Slater G, Penna A, Wisniewski A, Soffin A, Dutra V, Uyeda JC. Rules of teeth development align microevolution with macroevolution in extant and extinct primates. Nat Ecol Evol. 2023:7(10):1729–1739. [DOI] [PubMed] [Google Scholar]
- Martin G. Fisher’s geometrical model emerges as a property of complex integrated phenotypic networks. Genetics. 2014:197(1):237–255. 10.1534/genetics.113.160325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matheson J, Masel J. Background selection from unlinked sites causes nonindependent evolution of deleterious mutations. Genome Biol Evol. 2024:16(3):evae050. 10.1093/gbe/evae050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGlothlin JW, Kobiela ME, Wright HV, Mahler DL, Kolbe JJ, Losos JB, Brodie III ED. Adaptive radiation along a deeply conserved genetic line of least resistance in Anolis lizards. Evol Lett. 2018:2(4):310–322. 10.1002/evl3.72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuigan K. Studying phenotypic evolution using multivariate quantitative genetics. Mol Ecol. 2006:15(4):883–896. 10.1111/mec.2006.15.issue-4. [DOI] [PubMed] [Google Scholar]
- Melo D, Marroig G. Directional selection can drive the evolution of modularity in complex traits. Proc Natl Acad Sci U S A. 2015:112(2):470–475. 10.1073/pnas.1322632112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milocco L, Salazar-Ciudad I. Evolution of the G matrix under nonlinear genotype-phenotype maps. Am Nat. 2022:199(3):420–435. 10.1086/717814. [DOI] [PubMed] [Google Scholar]
- Mongle CS, Nesbitt A, Machado FA, Smaers JB, Turner AH, Grine FE, Uyeda JC. A common mechanism drives the alignment between the micro-and macroevolution of primate molars. Evolution. 2022:76:2975–2985. 10.1111/evo.14600. [DOI] [PubMed] [Google Scholar]
- Nei M. Mutation-driven evolution. Oxford, UK: Oxford University Press; 2013. [Google Scholar]
- Opedal ØH, Armbruster WS, Hansen TF, Holstad A, Pélabon C, Andersson S, Campbell DR, Caruso CM, Delph LF, Eckert CG, et al. Evolvability and trait function predict phenotypic divergence of plant populations. Proc Natl Acad Sci U S A. 2023:120(1):e2203228120. 10.1073/pnas.2203228120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr HA. Adaptation and the cost of complexity. Evolution. 2000:54(1):13–20. 10.1111/evo.2000.54.issue-1. [DOI] [PubMed] [Google Scholar]
- Orr HA, Unckless RL. The population genetics of evolutionary rescue. PLoS Genet. 2014:10(8):e1004551. 10.1371/journal.pgen.1004551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paaby AB, Rockman MV. The many faces of pleiotropy. Trends Genet. 2013:29(2):66–73. 10.1016/j.tig.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlicev M, Cheverud JM, Wagner GP. Measuring morphological integration using eigenvalue variance. Evol Biol. 2009:36(1):157–170. 10.1007/s11692-008-9042-7. [DOI] [Google Scholar]
- Porto A, Sebastião H, Pavan SE, VandeBerg JL, Marroig G, Cheverud JM. Rate of evolutionary change in cranial morphology of the marsupial genus Monodelphis is constrained by the availability of additive genetic variation. J Evol Biol. 2015:28(4):973–985. 10.1111/jeb.2015.28.issue-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohner PT, Berger D. Developmental bias predicts 60 million years of wing shape evolution. Proc Natl Acad Sci U S A. 2023:120(19):e2211210120. 10.1073/pnas.2211210120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohner PT, Berger D. Macroevolution along developmental lines of least resistance in fly wings. Nat Ecol Evol. 2025:9:639–651. 10.1038/s41559-025-02639-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito K, Tsuboi M, Takahashi Y. Conserved variation across scales unveils dialectical relationships of micro-and macroevolution. bioRxiv 610914, 10.1101/2024.09.02.610914, Pages 2024–09, preprint: not peer reviewed. [DOI]
- Schluter D. Adaptive radiation along genetic lines of least resistance. Evolution. 1996:50(5):1766–1774. 10.2307/2410734. [DOI] [PubMed] [Google Scholar]
- Schraiber JG, Landis MJ. Sensitivity of quantitative traits to mutational effects and number of loci. Theor Popul Biol. 2015:102(3):85–93. 10.1016/j.tpb.2015.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sella G. An exact steady state solution of fisher’s geometric model and other models. Theor Popul Biol. 2009:75(1):30–34. 10.1016/j.tpb.2008.10.001. [DOI] [PubMed] [Google Scholar]
- Stoltzfus A. Mutation, randomness, and evolution. Oxford, UK: Oxford University Press; 2021. [Google Scholar]
- Svensson EI, Berger D. The role of mutation bias in adaptive evolution. Trends Ecol Evol. 2019:34(5):422–434. 10.1016/j.tree.2019.01.015. [DOI] [PubMed] [Google Scholar]
- Tenaillon O. The utility of fisher’s geometric model in evolutionary genetics. Annu Rev Ecol Evol Syst. 2014:45(1):179–201. 10.1146/ecolsys.2014.45.issue-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsuboi M, Sztepanacz J, De Lisle S, Voje KL, Grabowski M, Hopkins MJ, Porto A, Balk M, Pontarp M, Rossoni D, et al. The paradox of predictability provides a bridge between micro-and macroevolution. J Evol Biol. 2024:37(12):1413–1432. 10.1093/jeb/voae103. [DOI] [PubMed] [Google Scholar]
- Voje KL, Grabowski M, Holstad A, Porto A, Tsuboi M, Bolstad GH. Does lack of evolvability constrain adaptation? If so, on what time scales? Evolvability: a unifying concept in evolutionary biology? p. 289–306. 2023.
- Wagner G. Multivariate mutation-selection balance with constrained pleiotropic effects. Genetics. 1989:122(1):223–234. 10.1093/genetics/122.1.223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner GP. Homologues, natural kinds and the evolution of modularity. Am Zool. 1996:36(1):36–43. 10.1093/icb/36.1.36. [DOI] [Google Scholar]
- Wagner GP, Altenberg L. Perspective: complex adaptations and the evolution of evolvability. Evolution. 1996:50(3):967–976. 10.2307/2410639. [DOI] [PubMed] [Google Scholar]
- Wagner GP, Kenney-Hunt JP, Pavlicev M, Peck JR, Waxman D, Cheverud JM. Pleiotropic scaling of gene effects and the ‘cost of complexity’. Nature. 2008:452(7186):470–472. 10.1038/nature06756. [DOI] [PubMed] [Google Scholar]
- Wagner GP, Pavlicev M, Cheverud JM. The road to modularity. Nat Rev Genet. 2007:8(12):921–931. 10.1038/nrg2267. [DOI] [PubMed] [Google Scholar]
- Wagner GP, Zhang J. The pleiotropic structure of the genotype–phenotype map: the evolvability of complex organisms. Nat Rev Genet. 2011:12(3):204–213. 10.1038/nrg2949. [DOI] [PubMed] [Google Scholar]
- Wang Z, Liao B-Y, Zhang J. Genomic patterns of pleiotropy and the evolution of complexity. Proc Natl Acad Sci U S A. 2010:107(42):18034–18039. 10.1073/pnas.1004666107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch JJ, Waxman D. Modularity and the cost of complexity. Evolution. 2003:57:1723–1734. 10.1111/j.0014-3820.2003.tb00581.x. [DOI] [PubMed] [Google Scholar]
- Zhang J. Patterns and evolutionary consequences of pleiotropy. Annu Rev Ecol Evol Syst. 2023:54(1):1–19. 10.1146/ecolsys.2023.54.issue-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code and data underlying this article are available GitHub at https://github.com/applied-phylo-lab/m-matrix.