3D printed near-infrared high-numerical aperture achromatic metalens

Summary

Traditional optical Fresnel microlenses have limitations such as large size, limited optical quality for imaging, and low focusing efficiency in achromatic lenses with high NA. In contrast, metalenses rely on their subwavelength structure to modulate the phase distribution, resulting in smaller volumes and superior focusing performance. In this work, we inverse designed and fabricated an achromatic metalens with high-NA and broad wavelength range through direct laser writing using the two-photon polymerization technique. With a focal length of 19 μm, a thickness of 3.6 μm, and a numerical aperture of 0.8, the metalens exhibits an average focusing efficiency of 53.6% and an average half maximum width of 1.27 μm at the working wavelength. The measured average focusing efficiency is 50.4% within the bandwidth range of 1510 nm–1610 nm. The presented work demonstrates the great potential of 3D printing and inverse design for realizing functional meta-devices for aerospace sector.

Graphical abstract

Highlights

• •A high-performance achromatic metalens is inverse-designed
• •Metalens with high NA and focusing efficiency were 3D printed
• •A regularized approximation method with a penalty function is proposed

Optics; Optical materials; Photonics; Metamaterials

Introduction

In the past decade, there has been a consistent surge in interest and effort toward the development of optical metamaterials that display great electromagnetic properties.^1,2 Since the introduction of optical metasurfaces, researchers have been exploring their potential in integrated optics and optical communications.^3,4,5,6 The physical properties of these metamaterials primarily depend on their unique structures. Optical metasurfaces are artificial patterned optical films and generally exploit the interaction of subwavelength structures with light to adjust properties such as amplitude, phase, and polarization. Furthermore, metasurfaces are gradually replacing traditional optical components in planar and integrated applications: beam deflectors,⁷ vortex phase plates,^8,9 holograms,^10,11 and gratings.^12,13 With extraordinary electromagnetic response characteristics and high design freedom degree,^14,15 metalenses have shown remarkable potential for sub-resolution imaging,¹⁶ optical cloaking,¹⁷ and correcting monochromatic aberrations.¹⁸

Lightweight, miniaturized optical imaging systems are massively used in these fields of aerospace exploration, consumer electronics, industrial vision, or medical imaging.^19,20 Traditional refractive optical elements, such as lenses, rely on continuous phase shifting of light and are usually much larger compared to the operating wavelength. This limitation greatly affects the performance of micro-nanophotonic systems. It means, conventional optical techniques are intricate to downscale as refractive lenses mostly rely on phase accumulation. Metalens, composed of subwavelength nanostructures that locally control light waves, offers a disruptive path for small-scale imaging systems. Metalenses, on the other hand, are lighter and thinner compared to traditional refractive lenses and can be fabricated at the micro-nano scale using 3D printing techniques^21,22 and other lithography techniques.^{23,24,25,26,27,28} When light propagates with a specific range of wavelengths in conventional diffractive optics, it causes chromatic aberration by phase accumulation. Conventional diffractive optics suffer from significant chromatic aberration and have low broadband focusing efficiency, making them unsuitable for imaging photonic systems. In contrast, metalens owns the ability to fully control and modulate the phase, amplitude, and polarization at the nanoscale, which can achieve wavefront shaping with a high degree of freedom through its sub-wavelength structure.²⁹ This enables a single metalens to perform multiple functions, leading to further miniaturization and improved efficiency of the lens.

How to find the optimal structure for a given response represents a new paradigm in designing electromagnetic metasurfaces. This problem is difficult to solve in a forward design method where one structure corresponds to one response. The inverse design method can achieve the transformation from response to structure with iterative optimization.^30,31 It is in stark contrast to traditional forward design methods, which heavily rely on intuition and experience. Metasurface design methods, such as the genetic algorithm^32,33 and particle swarm algorithm,^34,35 involve performing numerous calculations using optimization algorithms in order to obtain optimal solutions. In recent studies, Wang et al.³⁶ and Dou et al.³⁷ have designed achromatic metalens in the visible light range, using the particle swarm optimization method. The latter also has aberration correction properties. Additionally, based on the inverse design method, Ou et al.³⁸ and Zhang et al.³⁹ use the filtering strategy method and the linear programming method to optimize the metasurface structure, respectively, and demonstrate high efficiency achromatic metalens in the mid-infrared wavelength range. Although they can achieve high focusing effects, metalenses suffer from the disadvantage of relatively low numerical aperture (NA). Increasing the design space’s degree of freedom is a direct approach to enhance the performance of metasurfaces. One way to design achromatic lenses is by combining multiple metalenses, where each layer of the metalens operates independently within different wavelength ranges. In order to ensure the phase dispersion and diffraction efficiency, Wang et al.⁴⁰ use a double-layer structure to increase the degree of design freedom and design a large-bandwidth near-infrared achromatic metalens. On the other hand, employing a metalens with a “freeform” topology instead of a “constant-z” metalens can significantly improve focusing efficiency.^29,41 By increasing the design freedom of a single metalens, it is possible to both reduce chromatic aberration and improve focusing efficiency. Even though this method poses a challenge for fabrication, additive manufacturing is a great solution.

Additive manufacturing has emerged as a viable option for manufacturing high-performance micro-nano optical components. Specifically, two-photon polymerization (2PP) technology, based on the two-photon absorption process, is a three-dimensional printing process at micro-nano dimensions, which can fabricate any three-dimensional structure with high precision.^{42,43,44,45,46} The high degree of design freedom provides the possibility for low refractive index materials to achieve high performance. For multi-layer metalens, 2PP can complete multi-layer processing and combine the various parts together and ensuring both performance and compactness of the overall optical system.^47,48 In addition, 2PP does not have many constraints on the design surface of the device.⁴⁹ This ensures that free-form metalenses’ nonintuitive structures optimized in inverse design can be fabricated.

In this article, a metalens with high NA and achromatic properties in the infrared band is proposed and studied. It is designed with a 2D profile and manufactured with a simple 3D structure by the inverse design method and 2PP technique, respectively. Intuitively, having a greater number of degrees of freedom implies increased computational complexity. The objective-first inverse design method can quickly obtain an optimal design by decomposing the objective function into two subproblems.^50,51,52,53 Another advantage of this method is that it can avoid inefficient local optimal solutions by enforcing high-performance boundary condition constraints. Recently, we reported the development of an inverse-designed monochromatic metalens with high NA operating at 980 nm.⁵⁴ To further extend the functions of the metalens, we employ the objective-first inverse design method to demonstrate the average efficiency of 53.6% of broadband achromatic metalens with 0.79 NA operating from 1360 nm to 1740 nm. Moreover, this method could accommodate a certain degree of random initial values without specifying regular or uniform initial values. By utilizing the penalty function approximation method,⁵⁵ the metalens can be transformed from a “grayscale” pattern to a “binary” pattern without requiring additional optimization stages. This approach helps to minimize the deterioration of lens performance during the conversion process. Metalens-based optical devices for imaging and sensing are an important key for micro/nano-robots, micro air vehicles, and intelligent sensing devices in the future. For future smart cities, smart homes, and Industry 5.0, metalens assisted unmanned aerial vehicles will be a key factor in the development of artificial intelligence.

Results

Metalens inverse design framework

In an inverse problem, a reasonable objective function needs to be specified based on the geometric degrees of freedom within the design area. In our work, a two-dimensional plane serves as the design area of the metalens. For geometric degrees of freedom, the value of a uniform mesh divided into planes is allowed to vary between 0 and 1. As shown in Figure 1A, the design area is treated as a black box with perfectly corresponding input and output responses. For a metalens, once an input of the plane wave phase is provided on the right, the metalens can generate enough phase change to produce a spherical wavefront output on the left side:

$$\varphi \left(r,\lambda \right)=\frac{2\pi }{\lambda }\left(\sqrt{r^2+f^2}-f\right)\text{,}$$ (Equation 1)

where f and λ are the working focal length and specific wavelength of the metalens, respectively. Obviously, the output phase of the metalens exhibits a hyperbolic characteristic. As the numerical aperture of the lens increases, the phase change at the edge will become steeper. At this point, a more refined meshing is required to guarantee the accuracy of the optimization. The minimum mesh grid needs to satisfy the Nyquist sampling criterion: P < λ/2NA. The fine grid selected in this article satisfies this condition.

Figure 1.

Principles of Inverse-designed metalens

(A) Schematic diagram of the objective-first inverse design method. The input and output serve as constraints and the Maxwell equation serves as the objective function.

(B) Design principles of achromatic metalens. The parallel wavefront is considered as input, and the metalens is required to phase compensate the output spherical wavefront.

(C) Design and manufacturing process of metalens. The initial value is a random distribution. Rotate the optimized metalens along the symmetry axis. Finally, the 2PP technology is used for manufacturing.

There are several methods available for reducing chromatic aberration in the output phase of a metalens.⁵⁶ In our case, we opt to design achromatic lenses by implementing phase compensation for various wavelengths. The input electromagnetic field is selected as the transverse electromagnetic wave (TE) with the polarization direction perpendicular to the design area. Similarly, the output electromagnetic field is also selected as a spherical transverse electromagnetic wave. The output is given by:

$${\varphi }_{lens}\left(r,\lambda \right)=\varphi \left(r,{\lambda }_0\right)+2\pi \left(\sqrt{r^2+f^2}-f\right)\left(\frac{1}{{\lambda }_0}-\frac{1}{\lambda }\right)\text{,}$$ (Equation 2)

where the first term Φ contains the optical wavefront information of the metalens and is independent of the working wavelength.

For the objective-first inverse design method, all input and output boundary conditions must be provided and serve as constraints. Furthermore, the Maxwell wave eq. in the design space is considered a function of the magnetic field H and the material permittivity ε. The objective function is given by:

$$\underset{\epsilon ,H}{\min }\underset{{\omega }_i}{\max }\Vert \nabla \times \frac{1}{\epsilon }\nabla \times H-{{\omega }_i}^{2}H\Vert$$ (Equation 3)

where ω_i represents the different operating frequencies of the metalens. Equation 3 can be divided into two sub-problems by assigning ε and H as variables, respectively. It is evident that these sub-problems are linear minimization problems. This division results in a significant relationship where changes in the two variables are independent. For instance, one variable is held constant while the other is optimized in each iteration. Both variables are alternately optimized until an optimal solution is achieved. The value of the objective function is referred to as the physical residual. In general, a smaller residual value signifies a more effective optimization for broadband focusing across all frequencies. It is worthwhile to mention that utilizing the average optimization method, not minimax optimization such as Equation 3, will result in the device converging to a solution where the lens performs well only at a single frequency, but poorly within the desired bandwidth. This contradicts our goal of achromatism throughout the entire bandwidth. In contrast, the minimax optimization method aims to enhance the performance of frequencies with the poorest outcome within the bandwidth of interest. This ensures that all frequencies within the bandwidth attain at least a moderate focusing efficiency.

In order to ensure the convenience of additive manufacturing for the final optimized metalens structure, it is necessary to restrict the variability of the structural variable during the optimization process. Therefore, we initially allow the structural variable ε to continuously vary within the design area. A lens structure with intermediate values of structural variables is referred to as a continuous structure, whereas a lens structure without intermediate values is known as a binary structure. Interpolation is used to ensure continuity of the structural variable in Equation 3 between the background material (ε_air) and the material composing the designed structure (ε_mat):

$${\epsilon }_{design}={\epsilon }_{mat}+p\left({\epsilon }_{mat}-{\epsilon }_{air}\right)\text{,}$$ (Equation 4)

where p is the relaxation parameter and 0 < p < 1. The refractive index of the polymer material used in this article is 1.52@1550 nm, so the value of ε can only vary between 1 and 2.31. Compared to optimizing on a discretized design space, the advantage of this approach is that the algorithm has a larger searchable optimization space. This ensures that the relaxation parameters can reach extreme values and prevents falling into inefficient local optimal solutions. The initial value of the permittivity distribution in the design area is determined based on a random distribution of the relaxation parameter p, ranging from 0.37 to 0.47, as shown in Figure 1C. In our approach, the random distribution of initial structures does not result in poor structures with numerous small features. Continuous structures often exhibit excellent performance, but they are non-physical and cannot be manufactured. The optimized lenses can be fabricated using 3D printing, with materials consisting solely of air and selected materials. Accordingly, a binarization process is required for the continuous structure. This process involves applying a threshold to the permittivity distribution within the design area. Any values above the threshold are converted to the material’s permittivity, while values below the threshold are converted to the air’s permittivity. This results in the generation of a binarized permittivity distribution (ε_bin). However, the obtained device structure through this direct method is usually inefficient and has poor performance. To address this, we opt for the penalty approximation method to solve the binarization constraint (see the method details). To achieve a fully fledged 3D metalens, it is necessary to rotate the 2D plane metalens along its central symmetry axis, as depicted in Figure 1C. After rotation, the 3D lens we fabricated is polarization insensitive.

Inverse design of achromatic metalens

The optimization process primarily focuses on reducing the physical residual and binarizing structure variable, ε. The metalens is defined by a focal length of 12.4λ, a thickness of approximately 2.3λ, and a diameter of around 32.5λ, where λ indicates the central wavelength. Consequently, the numerical aperture calculated was approximately 0.79. Theoretically, the metalens can be scaled to meet different wavelength bands' focusing conditions. Given our selected materials' relative non-dispersiveness, we scaled the lens for operation at 1536 nm. Therefore, the metalens' focal length at 1536 nm is 19 μm, thickness is 3.6 μm, and diameter is 50 μm, as shown in Figure 2A. Taking the device’s performance and manufacturing complexity into account, the geometric pixel size in the design area was set at 100 nm × 100 nm. The design area is discretized into 500 × 36 pixels.

Figure 2.

Optimization process of the metalens

(A) Metalens dimensions.

(B) Physics residual.

(C) Binary value.

(D) The focusing efficiency of the selected three wavelengths of 1400 nm, 1536 nm, and 1700 nm varies with the number of iterations.

(E) Continuous and binary structures at the 300th iteration.

(F) Unmanufacturable and manufacturable structures for free-form metalens.

All data are from numerical simulations.

Figure 2 illustrates the optimization process of the designed achromatic metalens and highlights the differences between various optimization results. We evaluate the performance of metalens from three perspectives: physical residual, binary coefficient, and focusing efficiency. In the initial stage of optimization, the focusing performance of the continuous structure improves rapidly, but the focusing performance of the binary structure remains at a low level. As the weight of the penalty approximation increases, the focusing efficiency of the binary structure is significantly improved. Correspondingly, there is a reasonable degradation in the performance of continuous structures. The physical residual refers to the value of Equation 3, which serves as the figure of merit in optimization. The size of the residual directly indicates the quality of the lens performance. As depicted in Figure 2B, the residual of the binary structure consistently exhibits a decreasing trend. In contrast, the residual of the continuous structure first decreases, then increases, followed by oscillations, and finally stabilizes. Figure 2C demonstrates that although the residual change of the binary structure slowly decreases after 100 iterations, the binarization coefficient continues to improve. This indicates the success of the penalty function approximation method. The structure variable finally reaches its extreme value, and the optimal solution is attained under binary constraints.

Based on phase compensation for different wavelengths, three wavelengths of 1400 nm, 1536 nm, and 1700 nm were selected as optimization wavelengths to ensure the metalens' achromatic properties. Given the initial random permittivity distribution, the three field variables (H1, H2, H3) were calculated for each of the three different wavelengths. Then, convex optimization was performed using Equation 3 to obtain the corresponding structural variables and complete one iteration. In each iteration, the variable in our design space is the continuous structure, while our desired result is the binary structure. Figure 2D shows that the focusing efficiency reached convergence at 53%, 50%, and 55% for the three optimized wavelengths, respectively. The focusing efficiency is determined by the integrated intensity of the full width at half maximum on the focal plane. In the initial stage of optimization, the continuous structure exhibits better-focusing efficiency than the binary structure. Under penalty function approximation, the focusing efficiencies of the two structures eventually converge to the same value. Generally, increasing the number of wavelengths for phase compensation is a convenient choice to improve the average focusing performance of the metalens over the working bandwidth. However, due to the low refractive index of polymer, the ability to confine electromagnetic fields is relatively weak. Adding more optimized wavelengths will not only fail to enhance the average focusing performance of the lens but will also result in a monochromatic lens. The final optimization results of the lens are shown in Figure 2E. The difference between the final continuous structure and the binary structure is minimal, indicating only a slight performance loss in converting between the two.

Optimized metalens structures, despite their several benefits in terms of focusing performance and bandwidth, still pose challenges in terms of fabrication via the 2PP process. One of the main difficulties lies in the irregular and nonintuitive nature of freeform-topology metalenses. Unlike those composed of meta-atoms, these lenses often incorporate small features and suspended structures that are challenging to achieve using additive manufacturing techniques. Therefore, it becomes imperative to ensure that the lens design avoids such intricate elements, even if it means compromising on performance. For instance, in Figure 2F, we can observe two different lens structures derived from the objective-first inverse design method. The top structure appears more discreet, with numerous disconnected characteristic features that cannot be manufactured using 3D printing technology. To address this issue, we utilize a regularized approximation method to smooth the lens profile and combine the penalty function approximation to guarantee the binarization of the lens. By employing this approach, we can ensure that the optimized lens structure meets the requirements for 3D printing, ultimately enabling us to obtain the desired bottom lens. Note that it features a thin grating-like structure.

After obtaining the metalens, we performed 2D simulations using a commercial finite-difference time-domain (FDTD) Maxwell’s equation solver (Lumerical Inc.). Figure 3 shows the light intensity profile and focusing performance of the metalens at different wavelengths. Figure 3A demonstrates the normalized intensity profiles at the focal plane and transmission plane for six different wavelengths. The focal length of the metalens shows a noticeable shift (3 microns) around 1588 nm. However, this shift falls within the acceptable range of the focal depth, which is typically measured by the full width at half maximum. In Figure 3B, the focusing efficiency ranges from 38% to 56%, and the maximum and minimum values correspond to 1370 nm and 1700 nm respectively. Because of the limited number of wavelengths for phase compensation (only three), the metalens demonstrates high focusing efficiency specifically around the optimized wavelength. However, at other wavelengths, the focusing efficiency tends to be relatively low. The average focusing efficiency over the working bandwidth is 53.6%. In addition, the focal length of the metalens varies within a range of 16–22 μm across the operational wavelength range. This variation is attributed to the chromatic dispersion inherent in the metalens design. Despite this fluctuation, the metalens maintains effective focusing performance, as evidenced by the consistent formation of a high-quality focal spot within this range. In Figure 3C, the average full-width at half-maximum (FWHM) of the optimized metalens was found to be 1.27 μm, which was slightly larger than the diffraction-limited FWHM (λ/2NA). The FWHM of the focus at 1600 nm reaches a maximum value of 2.2 μm.

Figure 3.

Simulation results of an achromatic metalens

(A) Focusing properties of the metalens at different wavelengths. The intensity distribution at the transmission plane (top), and the normalized intensity profile (|E|2) at the focal plane of the metalens (bottom).

(B) The focusing efficiency and the focal length of the metalens in the 1360 nm–1740 nm bandwidth.

(C) FWHM of the spot at the focal plane compared to the diffraction-limited FWHM.

All data are from numerical simulations.

Experiments

To experimentally verify the performance of the lens, we fabricated it on a glass slide using two-photon 3D printing. Due to the fabrication tolerance, the lens model was further optimized to eliminate the difference between the simulation and experiment (see the method details). Figure 1C displays a cross-section of a 3D-printed lens with a substrate made of the same material below it. The substrate underneath the lens is of the same material as the lens structure. We set its thickness to 3 microns to facilitate 3D printing for manufacturing. The details of the fabrication process for the 3D printing and the construction of the experimental setup are provided in the method details. Figure 4A shows the fabricated lens, with grooves on its edge to allow any accumulated liquid in the lens cavity to flow out. We constructed our own optical system to measure the light field information transmitted by the lens along the axial direction. The lens exhibits a distinct focusing effect and a prominent achromatic effect at the focal plane within the wavelength range of 1510 nm–1610 nm, which corresponds to our experimental light source.

Figure 4.

Experimental characterization of an achromatic metalens

(A) SEM image of the lens.

(B and C) depict a comparison between the simulated and experimentally measured focusing efficiency and FWHM, respectively.

(D) The normalized intensity distribution at the focal plane (top), and the normalized intensity distribution of the lens measured in the experiment (bottom). The focal length is indicated by a white dotted line at 19 μm.

(E) A comparison between the measured intensity (red line) and the simulated intensity (blue line) at the focal plane is illustrated. The measured data is depicted in red circles.

Experimental data are from single measurements; data are shown as measured without averaging.

The wavelength was swept from 1510 nm to 1610 nm, and we measured the intensity profile of the lens at every 10 nm wavelength interval. Figure 4B illustrates that the measured focusing efficiencies range between 48% and 54%, with an average of 50.2%. Within the experimentally measured 100 nm bandwidth range, the experimental effects of the lens are consistent with the simulation results. Furthermore, the measured Full Width at Half Maximum (FWHM) ranges from 1.35 μm to 1.71 μm, as shown in Figure 4C, with an average FWHM of 1.56 μm. Interestingly, the simulated average focusing efficiency and average FWHM within this bandwidth is 50.4% and 1.53 microns, respectively, which are both very close to the experimental results. However, due to the limitations of our experimental equipment, the number of data points obtained from the experimental measurement is relatively small. To address this, we performed cubic spline interpolation on the experimental data before comparing it with the simulated data. Figure 4D displays the normalized intensity cross-section for each wavelength at both the focal plane and the plane containing the optical axis. From 1510 nm to 1610 nm, the length of the focus increases slightly. In Figure 4E, we plotted the measured and simulated intensity profiles at the focal plane. When comparing the simulated and measured intensity profiles of the focal plane of the lens, there are slight variances. These differences can be attributed to factors such as the size of the incident light source being larger in comparison to the size of the lens. This size discrepancy can lead to increased errors caused by scattering.

Discussion

In order to address the issues of large volume, small numerical aperture, and insufficient focusing efficiency associated with traditional refractive lenses, this article utilizes the objective-first inverse design method to optimize the structure of low refractive index polymer lenses. As a result, an achromatic metalens structure with a small volume, high numerical aperture is achieved. In the optimization process, we observed that the field variable H and the structure variable ε of the objective-first algorithm we utilized are independent. The device is successfully converged into a binary structure through penalty function approximation, and the regularized approximation method ensures the manufacturability of the device and its smoothness.

Additionally, the lens structure can more effectively cater to our specific requirements, ensuring its compatibility with two-photon 3D printing technology. To prevent the lens from converging into a monochromatic lens due to low refractive of material constraints, we decided to track information at only three wavelengths. It is worth noting that the experimentally measured focusing efficiency of the lens slightly differs from the simulation results. It is important to consider experimental errors due to the metalens manufacturing tolerances as shown in Figure 5 (see the method details), and the fact that the lens is fabricated on a glass substrate. In conclusion, we have successfully demonstrated the creation of a metalens with an achromatic bandwidth of 380 nm in the near-infrared band through optimized design and experiments. The metalens has a focal length of 19 μm, a thickness of 3.2 μm, a diameter of 50 μm, and a numerical aperture (NA) of 0.79. It is manufactured using two-photon 3D printing technology. Experimental measurements have indicated an average focusing efficiency of 50.4% within the wavelength range of 1510 nm–1610 nm. This article paves the way to explore metalens as a technology for sensing and imaging in unmanned vehicles in aero sector, augmented-reality displays, and consumer electronics. By replacing traditional refractive lenses of bulky size, researchers have successfully demonstrated not only novel metalens designs but also advanced metalens-based optical systems with ultra-compact size.

Figure 5.

Simulation results of metalens manufacturing tolerances

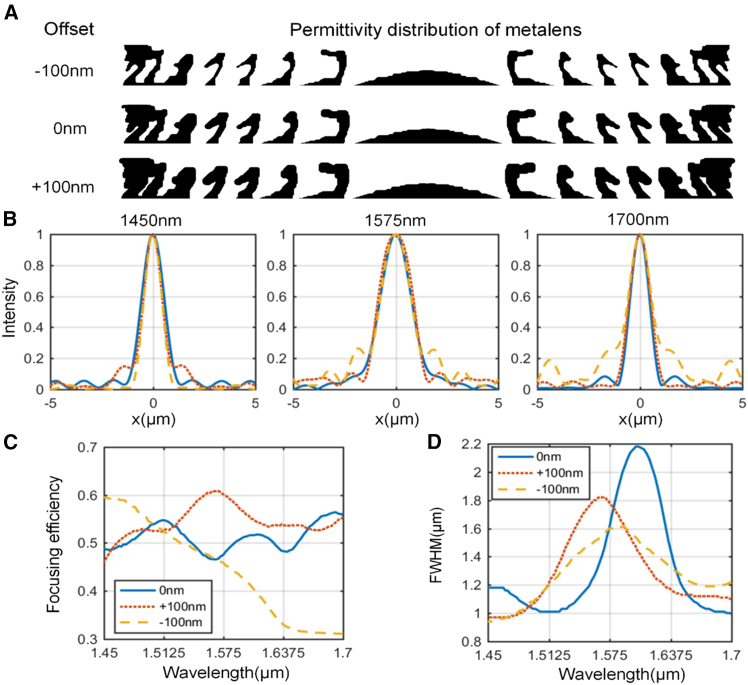
(A) The metalens profile is offset by −100 nm, 0 nm, and +100 nm, respectively.

(B) Normalized field distribution at the focal plane for three different metalens at 1450 nm, 1575 nm, and 1700 nm. The red dotted line, blue line, and yellow dashed line represent offsets of +100 nm, 0 nm, and −100 nm, respectively.

(C) The FWHM of the three lenses in the range of 1450 nm–1700 nm.

All data are from numerical simulations.

Limitations of the study

This study has certain limitations. The algorithm is not suitable for multi-materials as this increases the complexity, and the fabrication efficiency is low, which is not suitable for large-scale structures. Further study is necessary to explore multi-materials and multi-scale optical elements design and fabrication.

Resource availability

Lead contact

For further information and resource requests, please direct your requests to the lead contact, Heming Wei (hmwei@shu.edu.cn).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• •All data reported in this article will be shared by the lead contact upon request.
• •This article does not report original code.
• •Any additional information required to reanalyze the data reported in this article is available from the lead contact upon request.

Acknowledgments

H.W. and F.P. acknowledge the financially support by the National Natural Science Foundation of China (62005153, U2241237). This study was developed within the scope of the projects CICECO (LA/P/0006/2020, UIDB/50011/2020 and UIDP/50011/2020), DigiAqua (PTDC/EEI-EEE/0415/2021), financed by national funds through the (Portuguese Science and Technology Foundation/MCTES (FCT I.P.)). The research was co-funded by the financial support of the European Union under the REFRESH – Research Excellence For REgion Sustainability and High-tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Program Just Transition. This work was also supported by the Ministry of Education, Youth, and Sports of the Czech Republic conducted by the VSB-Technical University of Ostrava, under grants no. SP2025/039.

Author contributions

H.W. supervised and conceived the project. W. Hu conducted the simulation and design. H. W. and W. H conducted the experiments. J.H., G.H., F.P., S.K., J.N., and C.M. assisted in the methodology, analysis, and discussions of the results. All authors contributed to the writing of the article and gave approval to the final version of the article.

Declaration of interests

The authors declare no competing interests.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
IP-DIP	Nanoscribe	N/A
Propylene glycol monomethyl ether acetate	Sigma-Aldrich	CAS: 484431
isopropanol	Sigma-Aldrich	CAS: W292907
Software and algorithms
MATLAB R2016a	MathWorks	https://www.mathworks.com/
Spins-b	Github	https://github.com/stanfordnqp
Scipy 1.8.0	Scipy	https://scipy.org/
AutoCAD	Autodesk	https://www.autodesk.com/products/autocad
DeScribe	Nanoscribe	https://www.nanoscribe.com/en/products/software/

Method details

Materials

The photoresist used, IP-DIP, was supplied by Nanoscribe. Propylene glycol monomethyl ether acetate (PGMEA, purity > 99.5%) and isopropanol (purity > 99.5%) supplied by Sigma-Aldrich were used as developer.

Penalty approximation method

In order to describe the proximity of the calculated continuous structure to the binary structure, the binary coefficient is defined as:

$$B=\frac{2{\sum }_{i=1}^m\left|p_i-0.5\right|}{m}$$ (Equation 5)

where p denotes the relaxation parameter and m represents the number of grids in the design area. The binary coefficient of B = 1 implies that the structure is purely binary, while the value of B = 0 suggests that all mesh relaxation parameters are halved. For the binarization of metalens structure, the penalty function is defined as the discrepancy between the permittivity to be optimized in the next iteration and the binarized permittivity from the last iteration. The Equation 3 is transformed into:

$$\underset{{\epsilon }^{\left(n\right)},H}{\min }\underset{{\omega }_i}{\max }\Vert \nabla \times \frac{1}{{\epsilon }^{\left(n\right)}}\nabla \times H-{{\omega }_i}^{2}H\Vert +{\lambda }_{bin}\Vert {\epsilon }^{\left(n\right)}-{\epsilon }_{bin}^{\left(n-1\right)}\Vert \text{,}$$ (Equation 6)

where n represents the number of iterations, λ_bin is a hyperparameter, which can be changed to adjust the strength of binarization. As the number of iterations increases, the lens structure tends to be stable. The value of λ_bin may not satisfy further binarization of the structure. Therefore, the value of lambda is required to increase together with the number of iterations, which is specifically defined as: λ_bin=λ₀/(1-B). Compared with the violent discretization of structural variables, optimizing through penalty function approximation is more reasonable and in line with expectations.

When the design area has a random initial distribution, the final optimization results often consist of many small features. For instance, there may be two or three isolated pixels with the refractive index of the material, while being surrounded by air. However, even with an average initial distribution, there might still be dangling and unmanufacturable structural features. Hence, to ensure smooth device contours and reduce manufacturing difficulty, we employ a regularized approximation method incorporating a penalty function into the objective function. The objective function, following the regularization approximation, is given as follows:

$$\underset{\epsilon ,H}{\min }\underset{{\omega }_i}{\max }\Vert \nabla \times \frac{1}{\epsilon }\nabla \times H-{{\omega }_i}^{2}H\Vert +{\lambda }_{reg}\left(\Vert D_x\epsilon \Vert +\Vert D_y\epsilon \Vert \right)\text{,}$$ (Equation 7)

where the matrix D represents a second-order differential operator, and $\Vert D_x\epsilon \Vert$ represents the change or smoothness of the permittivity distribution ε in the x direction. For instance,

$$D_x\epsilon =\sum _{i=1}^{n-1}{\epsilon }_{i+1,y_0}-{\epsilon }_{i,y_0}$$ (Equation 8)

and so,

$$D_y\epsilon =\sum _{j=1}^{m-1}{\epsilon }_{x_0,j+1}-{\epsilon }_{x_0,j}$$ (Equation 9)

where n and m represent the number of grids in the x and y directions, respectively. The parameter λreg in Equation 7 is a hyperparameter that controls the strength of the regularized approximation. When the value of λreg is large, the device will exhibit clear straight boundaries. Conversely, when the value of λ_reg is small, suspended and intricate feature structures will be visible, as shown in the structure depicted at the top of Figure 2F. Additionally, since ε and H are independent of each other in the objective-first inverse design method, there is no need for any extra calculation of gradient information. The approximation method in the objective function will not result in excessive optimization calculations. The optimization problem necessitates approximately 300 simulations, and the total simulation time on a single 16-core Intel Core i9 machine is approximately k hours, where k represents the number of optimized wavelengths.

Effect of contour offset on the focusing

In the actual two-photon polymerization process, the profile of the final manufactured metalens may deviate from our simulation expectations due to the intensity of the optical power and value in stage velocity. If the laser power is too high and the stage velocity is too slow, the device outline will expand. Conversely, if the laser power is too low and the stage velocity is too fast, the photoresist polymerization will be insufficient, resulting in shrinkage of the device outline, and rendering the printed device unusable. To account for these potential deviations, we shifted the outline of the metalens inward and outward by 100 nm respectively, as shown in Figure 5A. It is important to note that both shrinkage and expansion will cause the lens to lose some details, but this does not necessarily mean that the lens performance is reduced.

The different characteristics of the three structures are demonstrated through simulation, particularly in their focusing characteristics within a bandwidth of 250 nm. Figure 5B presents the normalized field profiles of the three lenses at focal lengths of 1400 nm, 1575 nm, and 1700 nm. Notably, as the wavelength increases, the side lobes of the contracted lens’s focal point become larger, while the expanded lens does not exhibit this phenomenon. The changes in focusing efficiency and FWHM of the three lenses are shown in Figures 5C and 5D respectively. The shrinking lens shows a significant decline in focusing performance, with the decline becoming more pronounced at longer wavelengths. On the contrary, the expanded lens demonstrates better focusing characteristics within the range of 1450 nm-1700 nm and has a smaller average full width at half maximum (FWHM) compared to the original lens. Before engaging in two-photon 3D printing, we implemented a strategy of shrinking the outline of the lens model by 50 nm to compensate for the slight expansion that may be caused by high optical power and slow table speed during actual manufacturing.

Details of metalens fabrication

The metalens in this article was fabricated using the two-photon lithography system of Nanoscribe Photonic Professional GT (Nanoscribe GmbH, Germany), which utilizes a femtosecond laser with a central wavelength of 780 nm and a repetition rate of 80MHz. We created the cross-sectional structure of the metalens in AutoCAD, performed a three-dimensional rotation on its central axis of symmetry, and added four symmetrical grooves on the edge of the metalens. Then we exported it as an STL file. The hatching and slicing distances of the metalens were set to 100 nm in the DeScribe software, which matched the feature size set in the simulation. During the 3D printing process, we used quartz glass as a substrate and maintained the 63x objective lens immersed in the IP-Dip photoresist to print the device layer by layer in the opposite z-axis direction as shown in Figure S1. Here, a galvo-scanning system and a microscope z stage were used for writing where the laser power and the scanning speed were set as 10 mW and 1000 μm/s, respectively. It looks about one hour for fabrication. After the sample was exposed, we developed it in propylene glycol monomethyl ether acetate (PGMEA) solution for 30 minutes to ensure the removal of unpolymerized IP-Dip photoresist. Subsequently, we soaked it in isopropyl alcohol (IPA) solution for 5 minutes to eliminate the PGMEA solution present in the sample.

Apparatus for measuring field intensity

A simple optical measurement setup was constructed to characterize the intensity profile of the metalens. As depicted in Figure S2, the laser’s output wavelength can vary between 1510 nm and 1610 nm, with the collimator connected to the laser via an optical fiber. Due to the large light spot emitted by the collimator, the light is focused onto the metalens through a 2x objective lens. Moreover, the metalens, which is printed on a glass substrate, is securely held in place by an upright sample holder. The 50x objective lens is utilized in conjunction with the nanopositioner to facilitate movement, and subsequently, a tube lens is employed to concentrate the light onto the charge coupled device (CCD) camera. The piezoelectric nanopositioner moves incrementally along the optical axis in 100 nm intervals, while the camera captures the intensity profile image of the metalens for each movement.

Quantification and statistical analysis

The inverse design method was implemented via MATLAB R2016a with single 16-core Intel Core i9 CPU. The objective-first algorithm and analysis of average running time were realized in MATLAB R2016a.

Published: May 11, 2025