Brain sources composing irregular field potentials have unique temporal signatures

Abstract

The prevailing irregular pattern of field potentials is little used due to the uncertain origin and identity of the source populations. After recovering clean source-specific dynamics (field potential-generators) in multiple brain areas of anesthetized rats we explored if they contain temporal identity features and to what extent they remain upon blending in the volume (raw field potentials). Relevant factors and mechanisms were further explored through a feed-forward model of field potentials. Signals were characterized with a multivariate set of statistical, spectral and nonlinear measures and explored with machine-learning classifiers. Despite the strong variability of electrographic patterns, field potential generators exhibit unique temporal signatures that allow their discrimination. Signatures are contained in 1 to 5 s segments in any given brain region and are robust across groups of animals. In contrast, the spatial overlap of sources and the contribution by remote potentials cause indeterminacy of raw field potentials, making them approach a noisy behavior. The so revealed source-specific signatures contain spectral and nonlinear features, thus overcoming the traditional notion of waves and frequency bands. We propose that besides upstream dynamics cytoarchitectural factors of the source population contribute to these unique signatures. These findings pave the way to utilize the vast reserve of information contained in irregular field potentials.

Introduction

Physical stimuli that influence animal behavior occur over different time scales and they are largely stochastic and non-stationary in nature (e.g. sounds, vision, odors). During their coding and processing in sensory nuclei, or even later in higher order structures, the correlated activation of groups of neurons (cell assemblies) occurs that implies population coding (Wilson and McNaughton 1993; Panzeri et al. 2022), and yet the resulting electric field activity is still largely non-stationary and unpredictable, with strong variations at nearby positions and over time (Eckhorn 1994; Bullock et al. 1995, 2003; Logothetis 2002; Monto et al. 2008; Thivierge and Cisek 2008; Freeman and Zhai 2009; He et al. 2010). While connectivity and electrogenic properties of individual neurons determine the emergence of population and circuit dynamics (Tesler et al. 2024), massive cancellation of unitary currents and volume conduction of field potentials (FPs) are major handicaps to understand how the microscopic elements shape the extraordinarily varied field dynamics (Lorente de Nó 1947; Woodbury 1960; Nunez and Srinivasan 2006; Srinivasan et al. 2006; Ahlfors et al. 2010; Herreras et al. 2022, 2023; Pang et al. 2023).

Apart from a few cases where a single source has strong spatial dominance, such as in some oscillatory FPs, several sources have a significant contribution in most situations although in highly variable degree and proportion, making their sum present extremely variable fluctuations with irregular noise-like appearance (Pijn et al. 1991; Bullock et al. 2003; Herreras 2016; Makarova et al. 2024). Interlaced waves of different amplitudes, duration, and spatial extensions occur in unpredictable sequences that make their anatomical assignation an arduous and often impossible task. Consequently, and despite being the largest reservoir of dynamic information in neural networks, irregular FPs are little used in physiology and somewhat more as biomarkers of dysfunction in humans, with spectral estimates, and more recently complexity measures, the most commonly approaches adopted (Niedermeyer 1997; Sigurdsson et al. 2010; Şeker et al. 2021; Pardo-Valencia et al. 2024; Li et al. 2025).

In recent years source-demixing techniques have provided reliable separate dynamics of co-active sources, so called FP generators (Makarov et al. 2010; Fernández-Ruiz et al. 2012, 2021; Schomburg et al. 2014; Whitmore and Lin 2016; Torres et al. 2019; López-Madrona et al. 2020, 2024; Orellana et al. 2023). These are spatially coherent potentials that are pathway-specific in some structures, and their main advantage over raw FPs is that their uncontaminated dynamics allow quantitative use in the time domain, while bolstering precision in frequency-based studies (Martín-Vázquez et al. 2013; Herreras et al. 2015). Here we explored if de-mixed sources have temporal identity properties that could support quantitative use of irregular FPs. Our goal was to identify temporal signatures of separated generators beyond the nominal presence of waves, transient motifs, and frequency bands that may fail to identify or discriminate neural pathways or populations sufficiently well (Herreras 2016). We rely on the classification ability of supervised machine learning (ML) methods over a multidimensional space in which signals are characterized by combining statistical, spectral and nonlinear features measured on short segments (Hastie et al. 2009; Tahernezhad-Javazm et al. 2018; Makarov et al. 2023).

We used a number of ML techniques to analyze multisite FPs recorded in various brain structures of anesthetized rats, comparatively with their FP generators disentangled through an independent component analysis (ICA) (Makarov et al. 2010). Mechanistic insight was obtained by (i) off-line shuffling of generators; (ii) exploring the spatial pattern of misidentified segments; (iii) exploring the effects of added noise; and (iv) through feed-forward FP models with known sources. We found source-specific signatures contained in < 5 s segments that are robust across animals. Signatures are optimally discriminated in multiple brain structures, whether tested alone or in combination. However, raw FPs are poorly classified due to blurring of temporal features inherent to volume averaging of sources. These findings open path to quantitative use of predominant irregular FP activities through the signatures of their disentangled sources.

Materials and methods

Ethics Approval disclosure. The experiments were performed in accordance with EU directive (2010/63/UE), and Spanish (RD 53/2013) and local (Autonomous Community of Madrid, Order 1988 August 4 guidelines regarding the use of laboratory animals, and the experimental protocols were approved by the Research Committee of the Cajal Institute (I.D. Proex 367.5/21). All participants gave informed consent before taking part in the study.

Study rationale

We use the term source (of current) to refer to an anatomical region that produces coherent potentials, (i.e. FP generators: Lorente de Nó 1947; Herreras et al. 2015). It was previously demonstrated that the disentangled FP generators display some stereotyped waves or oscillatory patterns, although for the most part they show predominantly irregular activity and present little if any cross-correlation (Lopes da Silva et al. 1989; Benito et al. 2014; Hernández-Recio et al. 2023). Thus, it remains almost impossible to distinguish FP generators through standard statistical or spectral cues of their temporal activity, and particularly when the segments considered are short. Yet, some traits in the fine temporal structure or measures of signal complexity could still be recognizable by more efficient methods. Since multiple sources underlie raw FPs, should a hypothetical temporal signature exist for FP segments in a given recording site it would only provide information regarding the particular blend of sources therein. It should be noted that these would still be insufficient to locate and identify the sources, not least as they may be many, extensive and/or remote (Herreras 2016). In contrast, since ICA-derived FP generators are spatially coherent (same dynamics anywhere), if segments of such activities have a common temporal signature, we will have established a generator-specific signature that can be used as a proxy for recognition. Besides, they can be assigned an identity, since generators have unique spatial profiles (Herreras et al. 2015).

Analysis design

A pipeline was set up to classify signals through an ICA and for ML processing (Fig. 1a). The coactivation of (unknown) sources in the brain (S1–S5) makes their associated potentials spread in the volume and mix, giving rise to raw FPs that have variable dynamics in space. That is so because any recording site is contributed by every one of the sources albeit in different proportions (see detailed analysis and discussion in Herreras 2016; Herreras et al. 2022, 2023). Such space-dependent blending was recorded using linear arrays, and the set of multiple recordings was then subjected to an ICA (top row) that separates in different threads a small number of significant components, which happen to be the spatially coherent activities of the original sources, i.e. the FP generators (Makarov et al. 2010; Herreras et al. 2015). For comparison, a subset of FP recordings (as many as there are FP generators) was also selected (Fig. 1a, bottom), and both the generators and the raw FPs underwent parallel processing up to ML classification. This includes: (i) the windowing of signals into short segments; (ii) a thorough characterization of each segment by evaluating multiple statistical measures; and (iii) tagging of segments with either the site of recording for raw FP segments or the generator’s name. The classification results are examined by building confusion matrices (Fig. 1b) that indicate the number of correctly classified segments along the diagonal (accuracy), and incorrectly classified segments in the off-diagonal elements. In the present context, incorrectly classified segments are so because their temporal characteristics differ from those expected to define a true class (as predetermined by the ICA). This may happen because the class has no signature (classification has chance level) or has a signature but only some segments adhere to it (thus the others are misclassified).

Fig. 1.

Methodological issues relevant to the application of ML to classify FPs and FP generators. a) The data analysis of experimental recordings. From left to right: The dipolar neuron sources (S1–S5) add their potentials in the volume, where they undergo strong cancellation, and they are recorded as raw FPs using linear arrays. The activities of the FP sources (FP generators) are retrieved through an ICA. These (upper row), or the equivalent number of selected FPs (lower row), are windowed in 5 s segments, each characterized by 12 different measurements (compounded as a time signature), pre-labeled by the generator identity (or the FP site), and then all signatures are pooled together into a 12D space. b) After ML classification, the correct and incorrect assignment of pre-labeled segments to the original signals is examined in confusion matrices (blue diagonal and brown-colored boxes, respectively). Misallocated segments are to be found in the respective row (exemplary horizontal box for G3). c) No single measurement type was sufficient to achieve optimal ML accuracy. A set of power spectral parameters performed generally better than an equivalent number of nonlinear measurements (n = 4, in both cases). Data obtained for 5 specimens (colored) using the SVM technique in epochs of 1 min with non-overlapped segments of 1 s (solid lines) or 5 s duration (overlapped, Δt = 1 s). d) Estimation of the minimum duration of the segment required to achieve optimal accuracy of ML techniques when classifying FP-generators. The data are presented as the mean ± s.e.m. (black trace) for the 33 different techniques evaluated (one per line plot).

To better explore the relevant mechanisms that could define a source signature and to understand how the volume mixing of potentials from different sources influences the performance of ML, we adapted a formerly deployed 3D volume conductor model generated by the finite element method (FEM). The model simulates brain sources of known geometry and activities, and reproduces model FPs resembling experimental recordings (see below and Supplementary Fig. 1). Experimentally obtained complex activation patterns were fed into anatomically corresponding model sources to keep fluctuations as realistic as possible and whatever temporal signatures these may have. Synthetic FPs were then reconstructed in a 3D mesh by distance weighted addition of the FPs elicited by all the sources according to a solution of Poisson’s equation (Video 1). Using the simulated FPs, we issued recording tracks matching experimental linear FPs (Torres et al. 2019). The activities fed into the model sources and the model FPs obtained are equivalent to the activity of the FP-generators and the raw FP recordings in experiments, respectively.

Experimental procedures

The recordings analyzed in this study were taken from the database held in our laboratory, all obtained from experiments that followed identical preparatory procedures and only using epochs of spontaneous activity prior to any treatment. Female Wistar rats (250 to 300 g) were used, aged 3 to 4 months old. The rats were all maintained on a 12-hour light/dark cycle, at stable temperature (20 to 22°C), with food and water were given ad libitum.

The rats were anesthetized with urethane (1.2 to 1.5 g/kg, i.p.) and placed in a stereotaxic device. The long-lasting anesthetic bupivacaine (0.75%) was applied to the surgical wounds. In different experiments, concentric stimulating electrodes were placed in different areas to enable the evoked potentials recorded to be assigned to spatial landmarks: the soma layer of the CA3b region to activate the Schaffer input to the CA1; the lateral posterolateral thalamic nucleus (LPL) to activate thalamo-cortical inputs to the V2 cortex; the olfactory tract to (di-synaptically) activate the lateral perforant path (LPP) input to the dentate gyrus (DG); or the angular bundle to activate the medial perforant path (MPP) input to the DG. Evoked potentials were also used to prime specific pathways and help identify FP generators (Korovaichuk et al. 2010). One or 2 linear silicon probes, each with 16 or 32 sites each and 50, 65 or 100 μm intersite distance (Atlas Neuroengineering, Leuven, Belgium or Neuronexus, Ann Arbor, MI) were placed stereotaxically in different areas (in mm): the forelimb somatosensory (S1) cortex (AP: –0.7; L: 3.9); the M1 motor cortex (AP: 2.9; L: 2.6), which included deeper regions like the striatum; the dorsal hippocampus across the CA1 region, also spanning the DG/CA3 (AP: –4.5; L: 2.6–3), and parts of the regions above and below (the V2 cortex or the thalamus). In some experiments the probes were soaked in DiI before insertion (Molecular Probes, Invitrogen, Carlsbad, CA) to assess their location post-mortem in histological sections. A silver chloride wire implanted under the skin of the neck served as a reference for recordings. Signals were amplified and acquired using a MultiChannel System (Reutlingen, Germany), or Open Ephys hardware and software, at a 20 kHz sampling rate. At the end of each experiment selected animals were perfused with PBS followed by paraformaldehyde (4%) through the abdominal aorta, and sagittal brain sections (100 μm) were then stained with bis-benzimide to assess the electrode position by fluorescence microscopy.

Signal treatment and analysis

The selected signals were wideband FPs (0.1 to 5 kHz) from prior studies (Benito et al. 2014; Torres et al. 2019; Hernández-Recio et al. 2023; Montero-Atalaya et al. 2023). Only epochs recorded in control conditions were used (i.e. prior to any treatment, drug or manipulation), and they lasted for periods between 1 and 20 minutes. A high-pass digital filter was set at 0.5 Hz to remove slow transient artifacts, and the signals were resampled at 4 kHz to speed up analyses.

Only epochs displaying persistent oscillations were left out of the study, such as theta rhythm in the hippocampus or highly regular cortical delta (slow wave activity, SWA). The anesthetic plane achieved in all experimental series was similar, permitting a wide variety of short-lived electrographic patterns between these 2 conditions. Occasional bouts of theta were admitted as was less regular SWA. Stereotyped events known to be associated to specific FP generators such as CA1 sharp-waves or dentate spikes were also maintained (Bragin et al. 1995; Fernández-Ruiz et al. 2012; Santiago et al. 2024), as their short duration and occasional occurrence made no impact on the overall performance of ML classification that uses large numbers of short segments over minute-long epochs.

Short rhythmic oscillations at different frequencies may appear in certain structures. As some frequency bands could still be considered cues for regional or pathway identification, we set un upper limit for a rhythmicity index (RI) to exclude excessively rhythmic epochs. The RI was calculated in band-pass filtered signals at selected positions through the decline of the first peaks in the autocorrelation function (ACF) as follows:

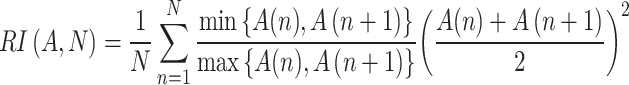(1)

where A(n) is the peak of the ACF (n = 5). RI is bounded so that RI = 1 corresponds to sine waves, whereas 0 is for noise. RI was quantified for each of the bands most commonly acknowledged: delta (0.5 to 2 Hz), theta (3 to 5 Hz); alpha (9 to 11 Hz), beta (15 to 20 Hz), and gamma (30 to 80 Hz). For a reference, persistent theta in the stratum lacunosum-moleculare (Lac-Mol) of CA1 has RI ~ 0.8. We chose FP epochs for analysis if none of the frequency bands had RI > 0.4. Most values of RI in segments of signals ​​remained between 0.15 and 0.3. This cannot be strictly considered an aperiodic signal; hence we adopted the less stringent term of irregular. Although the power of discrete frequency bands was not used for ML classification, global spectral estimates were used (see below), and their relative impact on ML performance explored.

Separation of mixed sources in the recorded and simulated FPs

The performance of an ICA largely depends on the nature and characteristics of the signals (Bell and Sejnowski 1995; Stone et al. 2002). The application of ICA to intracranial FPs obtained with linear multi-electrode arrays can be optimized by placing the probes in the space occupied by the FP sources. It greatly facilitates resolving the different voltage gradients produced by distinct synaptic inputs even if they reach the same cell population (Makarov et al. 2010; Benito et al. 2014).

The ICA algorithm renders the activity time course of the separated sources, and it also provides their relative power at the recorded sites. This information together with anatomical data can be used to establish the location, polarity and additional geometrical features of the source, albeit with certain restrictions (Herreras et al. 2015). We employed the kernel density ICA algorithm (KDICA) (Chen 2006) customarily implemented in Matlab (the package is available at: http://blogs.mat.ucm.es/vmakarov/downloads). Recorded FP signals u_m(t) were considered as the weighted sum of the activities of N neuronal sources or FP-generators:

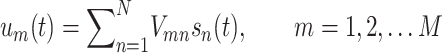(2)

where (V_mn) is the mixing matrix composed of the so-called voltage loadings—or spatial weights—of N FP-generators on M electrodes, and s_n(t) is the time course of the n-th FP-generator. Thus, the raw FP observed at the m-th electrode is a linear mixture of the electrical activity of several independent FP-generators. Using {um(t)}, the ICA finds both the matrix (V_mn) and s_n(t). The joint group of spatial weights (V_mn) is ordered into instant depth profiles of the voltage according to electrode position and reflects a linear sample of the 3D voltage shell generated by a given source. Such profiles can be compared to the spatial profiles of the standard evoked potentials of specific pathways when available. In fact, both spontaneous and evoked potentials are captured in the temporal envelope of an FP generator (Korovaichuk et al. 2010; Benito et al. 2014).

Although a single linear profile is insufficient to infer the full 3D voltage field, it provides critical information on gradients in a given direction that reflect whether electrode arrays are within or close to the source (accelerating curved spatial gradients) or far out (non-zero flat profile) (Torres et al. 2019; Nasretinov et al. 2023). The time-course of an FP-generator s_n(t) can be considered as a postsynaptic temporal convolution of spike output in an afferent population (i.e. afferent spike trains), as shown experimentally for the CA3–CA1 pathway (Fernández-Ruiz et al. 2012) and numerically for a variety of inputs (Makarova et al. 2011; Martín-Vázquez et al. 2013, 2016). The mathematical validation and practical limitations of this approach, as well as the possible causes leading to faulty separation and some of the possible workarounds have been thoroughly investigated using feed-forward models of FPs with realistic geometry (Makarova et al. 2011; Martín-Vázquez et al. 2016; Torres et al. 2019). Such profiles are accurate to the subcellular level in monolayered structures, while they are less precise in glomerular structures where they reproduce the joint field distribution of the activated populations where volume cancellation is heaviest (Lorente de Nó 1947). For additional information on the choice and robustness of ICA components see Supplementary Material.

In experiments were the FP generators from multiple animals were pooled together it was still necessary to correctly identify the identity of corresponding ones for labeling purposes (see below). This was achieved through hierarchical clustering of the spatial profiles (Hernández-Recio et al. 2023). A distance measure between curves was obtained using Icasso software (http://www.cis.hut.fi/jhimberg/icasso/). The dissimilarities among components were calculated as the sum of the squared differences between 2 spatial profiles. The function hcluster.m was then used to determine each cluster.

ML approach and variables used to represent signals in a multidimensional space

Earlier, ML classifiers using FPs have reported reasonable success in determining the phases of a motor task (DePass et al. 2022) or in predicting seizure occurrence (Maimaiti et al. 2022) based on the presence of specific temporal motifs. Here we could not use the strategy of searching for specific motifs to characterize irregular epochs as their very nature means they may be innumerable in multisource signals like FPs. Instead, we seek to provide a low-dimensional description of the temporal structure of voltage fluctuations and we use a classification framework driven by supervised ML techniques.

The signals are segmented into small partially overlapping segments (usually 5 s long, Δt = 1 s) and labeled with the FP generator they belong to (Fig. 1a, upper row). The shortest epoch of analysis used was 1-minute long (i.e. 56 segments). Epoch durations for all experiments is in Supplementary Table 1). Each segment is characterized by 12 measures (described below), jointly called temporal signature, and hence is represented as a point in 12D space . The 12D points for all segments and generators (or FPs) are then used for ML analysis. Thus, for a customary set of 5 generators per array, we generate 280 (5 × 56) segments of irregular activity or points in .Different ML methods (see below) attempted to classify the cloud of 12D points into an ICA-predefined number of classes (as many as there are significant generators) or FP channels. This classification is effectuated after training with 90% of randomly chosen samples. The remaining 10% is used for validating the model. Then, the confusion matrix is built (Fig. 1b). We defined the method accuracy as the ratio of the total number of correctly classified segments (i.e. those whose predicted labels matches the actual ones) to the total number of segments. If the accuracy is over 90%, the signatures are deemed as generator specific (or FP-channel specific), i.e. the vast majority of segments of irregular activity can be assigned to the sources of origin and therefore they inherit whatever additional information we may have on them, particularly their spatial profile, even pathway identity. When the accuracy is below the threshold, we check misclassified segments and classes they have been assigned using the confusion matrix. In some trials, we pooled together the generators obtained from 2 or more different arrays to check ML performance with more abundant and complex data.

To compose the 12D representation space, initially, we tested a large set of different variables. Then, the number has been reduced by discarding those that (i) are contained in others, (ii) show linear correlations with others, and (iii) do not increase ML-accuracy. This preliminary procedure selected 12 variables: statistical (mean, standard deviation, kurtosis and skewness); spectral (mean, variance, kurtosis and skewness of the spectral domain); nonlinear (dimension correlation, negentropy and Shannon and Renyi entropies). In the Supplementary Material we describe the less common and provide their interpretation in physiological terms whenever possible.

Since optimal ML classification of FP generators is an important goal toward automated analysis, we performed a preliminary verification on a limited sample of animals to compare the accuracy of ML using only nonlinear or only spectral features to characterize the signals. Figure 1c shows the data obtained for the supervector machine technique (SVM-1) in 2 exemplary animals. It was clear that no one type of measurement was sufficient on its own and the best strategy was to combine them all.

ML methods and techniques

Since there are no prior studies using ML approaches on ICA-derived FP generators, we tested different approaches on the same data sets in order to better define the ML methods and their variants (here termed as techniques) that best fit these signals, assessing their relative performance. We used the Classification Lerner tool in MATLAB®. The methods were: Decision Trees, Discriminant, Efficient Logistic Regression, Naïve Bayes, Support Vector Machine (SVM), Efficient Linear SVM, Neural Network, Logistic Regression, and Ensemble Lerner of previous methods, which were employed with different hyperparameters to give a total of 33 different techniques (Supplementary Table 2: for additional information on these approaches see Hastie et al. (2009) and Tahernezhad-Javazm et al. (2018).

To determine the classification accuracy, we used a test portion of data points and compared the method’s prediction to the predefined classes. The same accuracy was found for test and training data. To estimate the error of the models, we used the binomial distribution for a sequence of n independent experiments, each providing either right or wrong response. Then, the error and the confidence interval of a technique are:

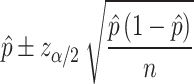(3)

where 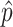is the estimated probability value, n is the sample size and 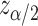is the value corresponding to a certain signification level α, which was set to α = 0,05.

Selecting optimal segment length for ML

Since different ML techniques handle the specific set of measurements differently, we searched for the shortest length that led to stable classification performance. To this end, we tested all techniques and parameters (n = 33) on 5 selected animals from different experimental series. The accuracy was evaluated over segments of increasing duration (from 0.5 s to 20 s, Fig. 1d) while maintaining the same total number of segments (i.e. size of the cloud of data points). Segments as short as 1 s already led to > 80% correct classification, and a plateau was reached for epochs ≥3 s-long (mean accuracies 0.9 ± 0.02 and 0.94 ± 0.01 for 3 s and 20s-long segments, respectively; P = 0.004, Kruskal–Wallis). The plateau level was highly constant across animals and generators (>94%), with only 4 out of 33 techniques remaining slightly below 80%. Thus, in further studies, we routinely used 5 s-long segments. This length is a compromise between stable operation and temporal precision of the methods, and indicates the minimum temporal module that contains the signature when optimality is achieved.

Forward model of FPs

To better examine the spatiotemporal characteristics of the sources and potential inaccuracies inherited from the source separation process (ICA) that influence ML performance, we used a computational model of multiple sources of known geometry in a volume conductor to obtain simulated multisource FPs. We used a modified feed-forward 3D model of the main structures in a rat brain hemisphere obtained through the FEM using COMSOL Multiphysics software (COMSOL, Inc. Burlington, MA) (Torres et al. 2019) (Supplementary Fig. 1). For information on model construction, parameters, and other details see Supplementary Material. The main FP-generating structures were reproduced in a hemisphere as rectangular slabs spatially assembled to match the curvatures. The structures were the cortical mantle, the CA1 and the DG, each represented by experimentally reported FP generators (Benito et al. 2014; Torres et al. 2019). Here we choose non-experimental (user-guided) extensions of different modules to better challenge ML classification in relation to the role of previously reported geometric factors on volume conduction (Herreras et al. 2015, 2023).

Thus, the cortical and CA1 Schaffer generators were arbitrarily regionalized into 3 antero-posterior and septotemporal regions, respectively, each with different dynamics, whereas the DG was activated synchronously all over (Video 1 and Supplementary Fig. 1). Model FP generators were obtained following the same ICA procedure as for real FPs, and it was assessed that their activity matched that entered to the sources (otherwise the ICA process would not be reliable, as it may happen for highly regular mixes: Makarova et al. 2011). Importantly, activation of different modules in the same structure implies distinct current sources, which are readily separated by the ICA as independent generators. Hence, the 3 synaptic pathways simulated here provide a total of 7 different generators, 3 cortical, 3 Schaffer and 1 DG.

The dynamics for each generator were obtained from actual experiments and epochs were selected in which irregular activity was dominant. The estimated pairwise CC was negligible in all cases (max CC < 0.015). For the cortex, we used epochs with the 2 main electrographic patterns, the SWA and the activated states. The current density of positive and negative stacked slabs was balanced, and it was manually adjusted to achieve 0.6 to 1 mV delta waves or 60 to 120 μV irregular series of waves in the center of the active sink layer (Chauvette et al. 2010; Torres et al. 2019). Schaffer activation was mostly composed of irregular waves with short strings of gamma waves interspersed that reached 80 to 120 μV in the active sink layer (Fernández-Ruiz et al. 2012). The inhibitory generator in the DG, with an active source layer facing the hilar side (equivalent to somatic inhibition), was composed of irregular activity with interspersed 100 to 200 ms-long waves and superimposed bursts of alpha waves, jointly reaching 0.8 to 1 mV in the hilus (Benito et al. 2014).

The simulated FPs could be represented as dynamic 3D video displays or as linear profiles mimicking experimental array recordings (Video1). The spatial resolution was 50 μm in dorso-ventral tracts. Different simulated tracks were examined to challenge ML techniques on different blends of FPs elicited by the same generators as well as to test the ICA capability of separating remote generators.

Measurements and statistics

Data are given as the mean ± s.e.m, except for the accuracy obtained through ML that is given in percent ± binomial error using Eq. (3). To estimate a range of performance across different ML techniques we performed statistical comparisons between the same pair of techniques chosen among the best and worst performing (SVM-1 and KNN-3, respectively), regardless of whether in different tests others could perform better or worse. We used customary box plots to describe the data distribution in individuals and non-parametric Kruskal–Wallis tests (α < 0.01) were used to compare between original and shuffled data, or groups of animals.

Results

Temporal signatures of FP-generators can be optimally discriminated during irregular epochs but less so in raw FPs

We applied a battery of 33 ML techniques (Supplementary Table 2) to classify epochs of irregular FPs obtained with a single electrode array in different brain regions (Fig. 2a) and, separately, to the most stable FP sources disentangled with ICA from such recordings (referred to as FP generators). In individual experiments, recordings were segmented and prelabeled with either the FP channel or the generator identity to which they belong, regardless of the specific brain region recorded in each case. The target variable was the correct classification of the segments with their pre-labeled identities. Generator’s identity for labeling was based on their unique spatial profile (see Methods). We first describe general temporal features and measurements taken to characterize the activity segments (jointly termed as a signature) for subsequent ML assessment.

Fig. 2.

Breakdown and global analysis of the ML classification of FP recordings and their FP generators in multiple brain areas. a) Sagittal drawing of the rat brain showing the location and coverage of the multisite linear electrodes (vertical lines) implanted into multiple brain regions in different experiments. b) ICA analysis of irregular FP epochs to obtain the FP generators in a representative animal. A 1 s segment is illustrated as an example. The 5 main generators (amplitude normalized) and their respective spatial power profiles (Vprof) are shown in matching colors. The FP samples at the peak site of the main generators are shown to the left (Raw FPs). Note the different time course of the FPs and their FP generators. c) A collection of 5 s FP generator segments (colored) from a 1 min epoch analyzed. Most segments/generators display irregular activity that is hardly distinguishable to the eye. d) The distribution of all the segments for each of the 12 variables used to characterize them in each generator (colored dots). Note the varying degree of overlap across generators. e) Partial plot of the 12D space for a selected pair of variables in a representative animal shows the stronger overall clustering of data points for FP generators (color-coded) relative to the raw FPs. It must be born in mind that any FP segment is a blend of all the generators. f) Additional plots for pairs of variables in the same set of FP generators. Note that some variables produced a better class segregation than others. g) Complete 12D data cloud for 2 1 min epochs from 2 different experiments. The values are line-bound to better appreciate of signatures (1 per segment). Each FP generator (color-coded) exhibits a visible signature with overlapping and discriminant values of different variables. h) Full analysis with a representative ML technique (SVM-2) of a large set of experiments (n = 58 animals). Optimal classification was achieved for the majority of the FP-generators (black circles), whereas the accuracy for a corresponding set of raw FPs was only moderate (blue circles; values reflect the accuracy ± binomial error; all pairs are significantly different; P < 0.001, Kruskal–Wallis test).

Figure 2b shows typical examples of raw FPs from 5 selected electrodes (left) and time series and voltage profiles of 5 FP generators (right) obtained by ICA from the entire linear series of raw FPs. The number of persistent FP-generators contributing to raw FPs in the region scanned by an array varied with the specific structure (Supplementary Table 1). There were typically 3 to 5 generators in the cortex, 5 to 6 in the hippocampus (Benito et al. 2016; Torres et al. 2019), 2 to 3 in the striatum or thalamus, and 4 to 5 in the subiculum. Since the arrays may cover 1 or more brain structures, the set of FP generators can include local (in-source) and remote (out-of-source) potentials, which were distinguished by the shape and steepness of the associated spatial voltage gradients (voltage profiles, Fig. 2b), reconstructed through the relative power at the recording sites (Herreras et al. 2023). As expected, the dynamics of the FPs varied at nearby sites according to the local power of the sources (Fig. 2a).

The temporal dynamics of the ICA-derived FP generators diverged from each other (Fig. 2b; Hernández-Recio et al. 2023). For this analysis we focus on intrinsic temporal properties rather than waveforms, frequency bands or EEG states. We assessed that 1 to 5 s long segments of activity each evaluated by a comprehensive set of twelve descriptive, spectral and nonlinear variables making up the epoch signature were already optimal for the present purposes (Fig. 1d). Although some recognizable transients could be visually identified in a few 5 s segments, most had a largely irregular appearance with a multiplicity of waveforms and with no outstanding visual cues that could anticipate a correspondence to any particular FP generator (Fig. 2c).

To help assess the challenge faced by ML we present the values of all 12 variables in segments within a 1 min long epoch for each FP-generator (color-coded), and from a representative animal (Fig. 2d). There was a large dispersion of these values/segment and ranges differed between generators, anticipating their potential usefulness as discriminant features. If a partial plot of the 12D space from raw FPs and their FP generators is considered for the same pair of selected variables (see Fig. 2e), such plots always showed a stronger overall clustering of data points for FP generators relative to raw FPs. Further visualizing different pairs of 2D plots indicated that some variables led to better class segregation than others (Fig. 2f), anticipating the need to combine multiple variables to achieve an optimal classification. Indeed, the choice of variables for characterizing segments of activity was critical (see below). For example, in the entire 12D data cloud of 2 1-minute epochs from 2 different experiments (Fig. 2g), each and every generator (color-coded) exhibited a visible signature with both overlapping and discriminant values.

The capability of an ML technique that performed among the best (SVM-2) in classifying these segments through multivariate signatures in a large group of animals (n = 58) is shown in Fig. 2h. In different animals the recordings were from different brain regions (see Supplementary Table 2, for the number of FP-generators, the type and spatial coverage of the recording arrays, and additional data). For FP generators, the classification was very successful (98.5 ± 0.3% accuracy for the SVM-2 technique), i.e. the signatures of very few segments failed to be classified in their actual pre-labeled generator. Hence, despite being quite variable and visually unrecognizable, the dynamics of individual segments retain identifiable features of the generator to which they belong, regardless of the brain region of origin. By contrast, classification accuracy of the same raw FP segments from which generators had been derived by ICA was markedly lower (71.9 ± 1.9%; comparison of FPs vs generators: P = 0, Kruskal–Wallis test, n = 58). Since only a few of these FP channels were selected at sites where the generators reach their maximum power, the reduced ML performance may indicate partial blurring of temporal features by contamination with other generators contributing at the selected sites. In addition, FP generators usually have a different mean variance at each recording site, which might be sufficiently discriminatory per se. Hence, we repeated this analysis with only 10 variables composing the signature leaving out the mean and deviation (all other variables are normalized). These results again offered optimal classification (98.2 ± 0.2%, Kruskal–Wallis test comparison between 10 vs 12 variables: P = 0.8339, n = 58), indicating that the other 10 chosen variables were sufficient to discriminate fully the temporal signature of each FP generator.

Since only a few FP channels at sites where the FP-generators peaked were selected for the above comparison, we extended the analysis to all sites in the electrode array to obtain a more representative estimate of the similitude or difference in raw FPs at any recording location using short-epoch signatures. We chose a subset of twelve animals from 2 groups of experiments in which arrays of 32 contacts spanned the cortico-striatal or cortico-hippocampal regions, and we increased the epoch analyzed to 5 min to augment the data-cloud size and strengthen the robustness of ML. The accuracy of SVM1 ML to classify a cloud of FP segments dropped from 64.9 ± 2.8% with selected 5 channels to 28.5 ± 5.38% with all 32 channels (P = 0.0015) and that of KNN-3 ML from 58.7 ± 3.04% to 18.5 ± 1.94% (P = 0.0002, Kruskal–Wallis, n = 10). This result demonstrates that the selected channels indeed had temporal features enriched in specific generators that favor successful ML classification, while the inclusion of sites in which FPs with more balanced generator mixes (i.e. their temporal features are averaged further), is less favorable for ML classification. This reduction in sensitivity should not be interpreted in a rigid manner as the relationship between the spatial frequency of FP generators and the inter-electrode distance determines the degree of similarity between contiguous recordings across an array and hence, the proportion of similar segments in the data cloud.

Since there was a notable scatter in the performance of ML on raw FPs in different animals (Fig. 2h), we set out to gain insight into the robustness of the results obtained with different techniques (Supplementary Fig. 2). Most of the ML techniques used here (Supplementary Table 2) had a similar optimal success in classifying irregular segments of FP generators, yet only moderate success was achieved for raw FPs, although there was wide scatter among the animals tested (see below).

Internal consistency of source-specific signatures

Before exploring the factors that promote the source specificity of signatures we wanted to ensure their consistency over time and robustness. On this purpose we subjected the time course of the separated FP generators to transformations that should maintain or destroy the homogeneity of features over time. To do this, we shuffle 5 s long segments “horizontally” (a moved segment does not change the generator) or in a “mosaic” form, i.e. horizontally and vertically (a moved segment jumps between generators and also in time, Fig. 3a). The first type of shuffling should maintain the features of each FP generator (Fig. 3a, middle panel), whereas the mosaic shuffling must destroy the generator specific features homogeneity (Fig. 3a, right).

Fig. 3.

Assessing the generator specificity resulting from optimal ML performance through data shuffling. a) Left panel, G1–G5 represent the original FP generators (color-coded); middle panel, G1s–G5s are shuffled generators formed by internal shuffling of 5 s segments (boxes); right panel, G1m–G5m are mosaic (fake) generators constructed through the random recombination of 5 s segments across generators. The arrows indicate the start and end sites of some segments for tracking. FPs signals were manipulated in the same way. b) The accuracy calculated for a subset of 10 animals using 2 different (the best and worst) ML-techniques (SVM-1 and KNN-3) with FP generators or raw FPs. Note the similar accuracy for original and internal shuffling, whereas mosaic shuffling reduced accuracy to the level of chance. c) ML accuracy calculated for mosaic FP generators and raw FPs randomized 100 times for 3 different animals. In all cases the accuracy was at the level of chance. d) Confusion matrices for intact and mosaic generators in a representative animal and technique (rat#12, SVM-1). e) The precision for mosaic generators is inversely proportional to the number of predefined generators. The data are represented as box/whisker plots and statistical comparisons were made with the Kruskal–Wallis test.

For a subset of 10 different animals using 2 different (best and worst) techniques (SVM-1 and KNN-3), internally shuffled generators were still optimally classified (SVM-1: 98.1 ± 0.74%), whereas the efficiency dropped drastically for mosaic generators (SVM-1: 20.4 ± 1.29%: Fig. 3b). The same protocol yielded similar results when applied to raw FPs, except for a lower mean accuracy (SVM-1 original: 70.2 ± 3.38%; surrogate: 71.6 ± 4.36%) and a larger dispersion across individuals. Mosaic FP generators and mosaic raw FPs both drastically reduced ML accuracy to levels expected by chance (SVM-1: 20.4 ± 1.29% and 20.4 ± 1.19%, respectively, for data-clouds with 5 generators).

To check for possible randomization bias, we repeated the process 100 times with as many different shuffles of segments in 3 animals, each with 5 generators. The accuracy obtained was that expected by chance (20%) in all cases (Fig. 3c), as also evident in the respective confusion matrices for intact and mosaic generators (see Fig. 3d for an example of SVM-1 applied to rat#12). It was also assessed that chance levels, equal to 1 over the number of pre-defined classes, were reproduced in experiments by changing the number of generators (Fig. 3e) (accuracy: 35.1 ± 0.49, 20.9 ± 0.31 and 15.2 ± 0.23% for a representative animal with 3, 5 or 7 generators, respectively, n = 100). These findings support a true source-specific nature of the signatures and their robustness over time despite notable differences of the gross visual appearance.

The proportion of local and remote contributions to irregular FPs determines their identifiability

We found that the animal variability of ML performance for classifying FP epochs was related to the brain structure recorded. Thus, the lowest performing third belong to animals whose recordings spanned large portions of the striatum or the thalamus (Supplementary Fig. 2 and Supplementary Table 1). Since these regions are not considered major producers of FP (Herreras et al. 2023) we considered the local and/or remote origin of the potentials as a source of successful or failed classification of FP segments. The volume spread of 3 main FP generators formerly studied (1 each in the cortex, CA1 and DG regions) (Torres et al. 2019; Herreras et al. 2023) is graphically illustrated in Fig. 4a to visualize spatial blending and facilitate comprehension of ML results displayed in confusion matrices (Figs. 4b–d). The spatial power gradients of the component FP generators (middle panels in Figs. 4b–d) served to determine the local (strong spatial gradients) or remote origin of the sources (flat spatial profiles: blue and brown asterisks). And additional visual cue also indicating the presence of local or remote contributions to FPs is the divergent or stable time course of FPs examined at contiguous recording sites across the array (black traces in right panels). In turn, the confusion matrices spanning all FP channels provide the spatial reference for successful or erroneously classified FP segments (to be found as bluish squares along the diagonal and brownish squares off the diagonal, respectively).

Fig. 4.

The local/remote location of sources contributing to FPs in a linear series determines the accuracy of ML. a) Diagram of the linear electrode location (vertical rectangles) for each of the 3 prototypic cases marking the structures covered. Ctx, cortex; St, striatum; Th, thalamus. The efficiency of ML to classify recordings in arrays 1 (cortico-striatal, b), 2 (cortico-hippocampal, c), and 3 (striatal, d) was examined. The colored arrows and curved traces depict the direction of declining voltage gradients in the volume from fixed FP generating sources, indicating the expected sites of remote potentials and mixing. b–d) Three representative experiments that illustrate the performance of ML with FPs recorded in structures containing strong, weak, or mixed FP generating sources. Purple, black, and blue squares in (b) and (c) indicate the recording sites within the cortex, hippocampus, and DG hilus, respectively. From left to right: Confusion matrices for raw FPs, spatial profiles of FP generators, and linear samples of raw FPs. The tone of the squares reflects the percentage of successful (blue) and failed classification (brown) of segments by SVM-1. Gray background denotes that no segments were assigned. Note the triple spatial matching for sites with higher rate of successful ML classification, sites where FP generators peaked, and sites where contiguous FP recordings show stronger spatial gradients. The cyan and purple ovals and arrows in (c) mark the sources location in the st. radiatum and Lac-Mol of the CA1, and the blue arrows mark the DG (granule cell) sources. A cortical generator (marked by the brown asterisk) is present in all 3 cases with different spatial gradients according to the position of the array. The sites of misclassified segments form spatial domains (brown ovals) with volume-conducted cortical FPs, which are discontinued (2 asterisks) at sites whose segments were correctly classified by the presence of local sources and hence, with different time signature. An extreme case of all-remote FP composition is shown in the striatum (d), where most recordings have similar temporal characteristics due to fairly stable mixtures of 2 remote sources (note opposite maximum in 2 main FP generators with flat profiles, the arrows in FP traces mark the FP decay from the remote sources (outside recordings) that matched large domains where ML perform worse (lighter blue squares in the diagonal). N.a.u, p.a.u. normalized and proportional arbitrary units. Similar spatial patterns for additional experiments are shown in Supplementary Fig. 3.

Segments of FPs recorded at sites hosting local generators were better classified (darker blue tone) and only a few were misallocated to nearby sites. By contrast, segments of FPs recorded at sites where the contribution is mostly from remote generators (colored asterisks) were very poorly classified. Indeed, numerous segments were erroneously assigned to other sites, and they were therefore assumed to have temporal signature closer to that of the “landing” site. In particular, the sites where the misclassified segments landed formed discrete spatial domains that were repeated for recordings in similar positions in different animals (see the main patterns illustrated in Figs 4b and c for cortico-striatal and cortico-hippocampal arrays, respectively, and the additional experiments in Supplementary Fig. 3).

Sites hosting local generators also appeared to act as exclusion zones where misclassified FP segments originally recorded in other sites were not assigned (double asterisks), consistent with the stringent, characteristic values that define the temporal signature at sites with a high success rate. An extreme case of poor ML accuracy was evident in the striatum (Fig. 4d), corresponding to the dominance of flat generators there that shaped FPs with very similar dynamics over large areas. Together, these findings indicate that successful ML classification of raw FP segments to their recording sites depends on the fraction of them in the data cloud that were recorded at sites with richer blends, i.e. they are influenced by multiple generators bearing strong spatial gradients that varied rapidly across the space. Meanwhile, the areas that produced weak or no local FP activity display volume-conducted potentials from sources at distances and sites where they show little spatial decay. In these cases, the blends at contiguous sites varied little and misclassified segments scattered widely. It should be noted that these spatial domains were more or less conspicuous depending on the overall efficiency of each ML technique (Supplementary Fig. 3), the choice of which can be used to select the sensitivity needed for different objectives.

Signatures are source-specific, not structure-specific

Given the optimal efficiency of ML on classifying irregular segments from a few FP generators obtained from the same or nearby regions, we expanded the essay to experiments with simultaneous recordings from 2 arrays recording in different brain structures. This allows us to explore whether the specificity is due to the recorded structure or is unique to the generator, i.e. with combined information from the afferent population determining the temporal dynamics (Herreras et al. 2015). Furthermore, it increases the total number of generators and informs the robustness of the chosen measurements and ML techniques in signals resulting from more complex mixtures. The analysis was performed on a group of 10 animals with 2 linear arrays placed at M1-Striatum and V2-Hpc (n = 7), CA1/DG and subiculum (n = 2), and S1 and V2-Hpc (n = 1), a sum of 10 to 12 generators per animal.

Note that for 10 generators, by chance classification gives a 10% performance (compared to 20% for 5 generators). Yet, the ML classification still showed similar results. The mean accuracy was 98.6 ± 0.28% and 87.2 ± 2.69% for the SVM-1 and KNN-3 techniques, respectively. The less efficient techniques misclassified a number of segments that nevertheless landed on specific generators (i.e. they were not randomly distributed), indicating similar signatures. Preferred landings were observed within and between brain structures (e.g. between the main cortical generators in M1 and V2, and between a remote generator in M1 and a DG generator in the hippocampal array).

Modeling of FPs supports the blurring of temporal features in the mixing

In order to explore the importance of the mixing of potentials from different sources and the subsequent fading of their original temporal characteristics as a factor determining the success or failure of ML-segment classification, we turned to synthetic multi-source FP models in brain-like volume conductors (Martín-Vázquez et al. 2016; Torres et al. 2019). Such models allow to gain insight into the joint FP dynamics elicited by independent co-active sources and assessed the similarity or difference of the signatures of model FPs respect to their ICA-extracted FP generators, whose activity should equal that of the sources that we now know a priori. Multilayer sources of current for cortical and hippocampal FP generators were used that accounted for extracellular domains of net inward and outward currents (Fig. 5a), as formerly described upon activation of afferent pathways onto target populations (Fernández-Ruiz et al. 2013). We co-activated them in several combinations and regional configurations. Each source was fed with FP generator dynamics extracted from experiments with an ICA (Fig. 5b) in order to preserve the original temporal signatures. We then computed the 3D FPs (see 2 snapshots in Fig. 5c, and Video 1), and extracted linear samples to simulate recording tracks (Fig. 5d).

Fig. 5.

A multi-source FEM model to explore the blurring of temporal signatures when mixing in the volume: relation to ML sensitivity. (a–f) and (g–k) Different simulations involving 5 or 7 dipolar sources, respectively, and the corresponding analyses. (a and g) Diagrams of the multilayer source blocks representing 3 brain structures in 1 hemisphere, the cortex, CA1 and DG. Orientation, a, d, l, anterior, lateral and dorsal. Dipolar sources are co-activated in various combinations and regional configurations. R1–3 represent linear tracks of FP recording. (b and h) Each current source is fed with an FP generator the dynamics of which are extracted from experiments with an ICA (colors match the source blocks in a or g). (c) Instant 3D potentials recorded at t1 and t2 (marked in b) in a 2D sagittal plane depicted in the left-hand diagram (zenith view). Pseudo 3-D expansions are shown dynamically in Video 1. d) Estimates of model FPs across R1 and R3, 50 recording sites stretching from the top to the site marked by the arrow in (a). The corresponding confusion matrices obtained for best ML technique (SVM-1) are very accurate (darker blue diagonal squares) at sites where model FPs produce strong spatial gradients (i.e. rapid variations at contiguous sites). Purple, black, and red squares mark the cortical, hippocampal, and DG boundaries. Note the discrete spatial domains formed by failed assignations are similar to the experiments in Fig. 4, yet these never land in channels whose FPs were well assigned (yellow asterisk). e and i) FP generator profiles. In each simulation the same generators maintain their color across recording sites. Note the distinct absolute and relative power, and their spatial variations, which are critical to define temporal dynamics of composed FPs. In model FPs, even remote tiny potentials are well separated by the ICA due to the absence of background noise [amplification of the normalized profiles in the box in (e)]. (f, j, k) ML confusion matrices for model FPs (similar to (d) but the number of sites is limited by the number of generators) and FP generators. The less efficient ML techniques began to yield some misallocated segments (KNN-3 in the case of 7 FP generators). Note a reduction of ML performance on model FPs compared to FP-generators (k). The horizontal colored arrows in (j) mark the preferred generators where misallocated segments landed.

The discrimination of signatures on model FP segments from different sites along linear tracks was weak and the misclassified segments formed spatial patterns, as seen in experiments (compare Fig. 5d with Figs. 4b and d). Accuracy was 41.6% and 25.1% for SVM-1 and KNN-3 techniques, respectively) for recordings along a track passing a source at R1, and it dropped further (27.2% and 10.2%) for remote recordings (R2), matching experimental results. This accuracy was not homogeneous along the track as it was greater in spatial domains that hosted strong potential gradients (dark blue sites in R1), while it approached random values at remote sites, consistent with the spatial equalization of the FP waveforms (R3).

The ICA of these model-FPs (Fig. 5e) returned FP generators whose relative power decreased as the simulated recordings were taken further away from the sources, yet they could still be well resolved (box in Fig. 5e). The time courses all matched those of the original sources (CC > 99.9% in all cases) as expected from the instantaneous spread of FPs. We estimated a voltage drop for potentials in the CA1 Lac-Mol generator of 1:0.017 at a distance of 5.2 mm (green trace in Fig. 5e), which means that a gamma wave 50 μV at the source site would measure < 1 μV at R3 (below the noise of standard recording equipment). Such resolution for remote sources cannot be achieved experimentally, where low voltages become buried in the noise, yet this is avoided in noise-free models. Since this could affect the performance of an ICA and of ML distinctly, we investigated this issue further (see below). Indeed, the most efficient ML technique (SVM-2) classified the segments of model FP-generators optimally (accuracy > 99.5%), regardless of the distance of simulated recording from the sources (Fig. 5f).

In large, functionally regionalized structures, such as the cortex and hippocampus, activity varies regionally, and regional sources also combine their potentials within the volume (Torres et al. 2019). Therefore, mixing may be influenced by different input topologies (defining spatially coherent modules: Benito et al. 2014) or by different microstructural features (Martín-Vázquez et al. 2016). To maintain focus on temporal features, the experimental activities used to feed model regional sources were from the same recording sites. The regional cortical activities were obtained from different recording periods in the same site and animal (purple traces in Fig. 5h), whereas hippocampal model CA1 subregions were fed with Schaffer activity from different animals recorded at identical positions (dorsal CA1). We set arbitrary dimensions to the sub-regions for exploratory purposes (see color-coded geometries in Fig. 5g). The FP generators extracted with an ICA from model FP blends again matched each of the time courses of the original sources, showing the expected distance-dependent loss of power that was more pronounced for quadrupolar (Schaffer) than dipolar sources (cortex and DG: Fig. 5i). The best performing ML technique (SVM-2) optimally classified all 7 FP generators irrespective of whether they were derived from FPs computed at sites near or far from the sources (R1 and R2, respectively: Fig. 5j). Nor did this performance depend on the origin of the temporal signature given to each (from the same or different animal). Less efficient ML techniques began to misclassify some segments (e.g. KNN-3: Fig. 5j), and they were generally assigned to homologous generators with similar dynamics (horizontal purple and blue arrows). As in the experiments, the less sensitive ML techniques were confused by specific regions with a similar temporal signature. When applied to data clouds of assorted segments from a few model FPs at selected sites, ML still performed worse than for FP generators, replicating experimental results, and the misallocated segments were assigned to sites whose FPs were contributed largely by a homologous generator (R1, KNN-3: Fig. 5k), indicating a similar temporal signature. This spatial specificity began to decline when simulated recordings were farther away from the sources (R2). Taken together, these findings support that the degradation of temporal features by mixing them in the volume reduces their usefulness as identity features or for locating sources.

Drop of signal-to-noise ratio hampers FP discrimination when sources are remote

Several aspects related to the presence of noise in recorded signals (electronic or biological, whether generator-specific or not, or resulting from a mixture of signals) can affect both the separation of generators by ICA and the performance of ML. We tested the effect of increasing levels of white noise added to model-FPs generated by 5 independent sources (CC < 0.1; the same model as in Fig. 5a). The ML performance on noised FPs dropped notably (range: 39.13% and 27.09% for SVM-2 and KNN-3, respectively, with noise −30 dB at R1 position; and 5.06% and 7.96% with −10 dB noise at R3). As the noise amplitude augmented, misclassified segments scattered at increasing distances from the “recording” site and formed spatial patterns akin to those observed in experimental recordings (panels from top to bottom in Fig. 6a), indicating that larger areas displayed FPs with similar temporal signature (and closer to that of noise). Notably, the same trend was found for a given noise level when the model FPs were collected further away from the sources (from left to right in Fig. 6a). That is, since distant sources produce FPs with little spatial decay, their blending keeps same proportions over large areas away from sources, and the joint dynamics also equalizes. We inferred that in presence of noise the increasing distance to the sources acts as a signal-to-noise reduction, which in real experiments would mean that generators extracted from FPs remote to the sources are noisier and their source-specific FP temporal signature become degraded. This was further supported by attempting to disentangle the FP generators with the ICA from such noised model FPs distant to the sources (Fig. 6b). Unlike noise-free models, fewer if any of the ICA components could be identified through either the time course or the spatial profile, both of which differed increasingly from the activations originally fed into the sources. That is, they either remained buried in the noise or their relative contribution to recording sites was reduced so much that ICA could not adequately separate them.

Fig. 6.

Background noise determines the ICA separation of FP generators and ML performance. (a, b) Increasing levels of white noise were added to model-FPs synthesized from five independent sources (values are given as signal-to-noise ratio, SNR). ML was essayed on linear tracks at different positions (as in Fig. 6a). a) Note increasing abundance and spatial scattering of misclassified segments as both noise and distance to the sources increase, matching the reduction of ML performance on experimental FPs dominated by local or remote sources. b) ICA extraction of FP generators from noised FPs rendered fewer recognizable components compared to the original source activations, both in the time course and the spatial profiles. c–e) A different approach was essayed by prior adding of noise to source activations, then model FPs were generated and the generators retrieved by the ICA at different distances from the sources. The generators obtained differed increasingly from the injected sources (c), and only the stronger and closer ones had a recognizable time course matching the original activations. Correspondingly, ML achieved decreasing levels of accuracy as the distance from the sources augmented (d). The orange, brown and cyan traces correspond to a SNR of (in decibels) +10, 0 and − 10. Accuracy was heterogeneously distributed among generators, with only the stronger ones achieving moderate success. (e) The colored rectangles in the top center matrix indicate the identity of the generator.

To further confirm that the specific temporal signature of the FP generators is the subject where ML found its path to discrimination, we constructed data clouds with the same sets of FP generators obtained from FPs at increasing distances from the sources used after adding increasing levels of noise (+10, 0 and − 10 db) (i.e. the same dynamics but with different S/N ratios: R1 to R3 in Fig. 6c). Note this is an artificial (post-hoc) noising of source’s activities since in actual experimental recordings, the dynamics of the main FP generators disentangled by the ICA are devoid of any noise that is not intrinsic to the source, with any other noise assigned to separated ICA components. The added noise blurred the temporal signature and in turn, provoked a reduction in the accuracy of ML to classify the pooled segments. This blurring also accentuated as the power decreased at increasing distance to recordings (Figs. 6d and e). Together, these simulations indicate a similar effect of the noise present in the recordings and the distance from the sources, which synergistically reduce the efficiency of the ICA to separate the sources, and the capacity of ML to identify (classify) FP generators through their specific temporal signatures.

Generator-specific signatures are robust across individuals

Given the extreme variability in the voltage fluctuations of FP recordings, we explored whether individual FP generators maintain a temporal signature across animals. As such, ML was used to analyze data clouds grouping several animals from the same experimental series, and also by pooling animals from different series. We selected 2 series of 5 animals each, recorded years apart using arrays with different interelectrode distances, but in both cases recording across the CA1/DG (Benito et al. 2016; Hernández-Recio et al. 2023). Up to 6 different homologous FP generators were matched between individuals based on their spatial profiles, allowing all segments from the same generator to be tagged as a single class across animals.

Despite addressing similar anesthetic planes, visual inspection could identify heterogeneous temporal patterns in any given FP generator, within and across animals (Fig. 7a). By inspecting the distributions of datapoints per measure across animals (exemplary bidimensional plots in Supplementary Fig. 4) it was appreciated that the population range of datapoints for a given generator and measure could largely exceed that for individual animals, whose ranges may partially overlap or not. Even with such notable signature variability across segments, those for a given generator still showed visually recognizable patterns, which repeated across animals (Fig. 7b).

Fig. 7.

FP generators maintain their temporal signature across animals. a) The same FP generator can present different patterns in an animal and also between animals. The 2 epochs of the Lac-Mol generator are from 2 different animals. b) Time signatures of 3 main generators (colored) for 3 different animals (1–3). Each line corresponds to the signatures of individual 5 s segments from which visual similarity of the same generator can be recognized across animals. Some but not all variables have very repeatable ranges. c) ML (SVM-2) on a series of animals (n = 5). Generators, Sch, Schaffer; L-M, Lac-Mol; DG1-DG3, dentate gyrus 1–3; rem, remote. d) Complete test of all the ML techniques on 2 assembled experimental series with common FP generators (n = 10 animals). The horizontal blue line is the 90% degree of accuracy. e) Confusion matrix for the ML technique marked by the red arrow in d. f) Decreasing the number of variables used to characterize the segments reduces the accuracy of ML. The data belong to 4 different ML techniques (colored plots, see Supplementary Table 2).

Likewise, ML techniques yielded remarkable within-series accuracy (for SVM-1 and KNN-3, respectively); series 1: 93.9 ± 1.27% and 79.6 ± 2.14% (n = 1466 segments); series 2: 99.6 ± 0.31% and 95.1 ± 1.06% (n = 1600 segments) (Fig. 7c). After mixing the 2 series (n = 10 animals), ML accuracy still was notable, with 14 out of 33 ML techniques tested achieving > 90% success for a total of 3066 segments (Fig. 7d). Hence, the temporal signature of individual generators appears to be very robust across animals. We did not test whether increasing the segment length or adding more characterizing variables may recover the small proportion of misclassified segments. The SVM-2 technique performed best (Fig. 7e: 95.1 ± 0.78% accuracy). We also found that techniques regarded as unfit differ in the individual or population analyses (compare Supplementary Fig. 2 and Fig. 7d). Hence, some ML techniques may better fit the population’s variability than others.

As it is important to achieve optimal ML classification of FP generators in order to advance toward automated analysis, we explored the performance of ML for a decreasing number of variables used to make up the multidimensional space in the same pooled group of animals (Fig. 7f). The variables dropped were chosen arbitrarily from the initial group of twelve. As expected, ML accuracy decreased as did the number of variables used, most markedly below 6 variables, an observation that was constant for all ML techniques. Thus, it was concluded that no single variable is sufficient, at least when analyzing the short fragments assessed here.

Discussion

Long-known issues with the quantitative analysis of ongoing FP activity are its propagative and multi-source nature, as well as the irregular time course. Here we show that decomposing irregular FPs into their generators not only recovers the uncontaminated dynamics of the original sources but also, it enables ML techniques to optimally discriminate them using very short segments. Despite the variable mesoscopic dynamics, the multivariate characterization revealed temporal signatures that are source-specific and robust across animals, and they transcend waveforms and frequency bands. The mixing of the potentials from co-active sources in the volume partially blurs these signatures in raw FPs. Thus, a door is opened to the quantitative use of irregular brain FPs and the automated identification of their anatomical sources.

Technical and biological issues

Different strategies have been employed to characterize heterogeneous rapidly varying time courses of FPs as well as of their FP generators, such as statistic distribution of time-point values (Hernández-Recio et al. 2023), spectral features (Leung et al. 1982; Donoghue et al. 2020), and nonlinear properties (Makarov et al. 2023). However, no single one alone is sufficient to identify the source composition of an FP epoch. Even for highly prototypic transient FP events or patterns, source identification is an arduous task requiring the use of pharmacological or molecular tools in conjugation with evoked responses or unit firing (Fernández-Ruiz et al. 2021). The low dimension characterization of signals and ML approach used here represents a stand-alone method, since the source identity is inherent to the uniqueness of the FP generators voltage profiles, and many were formerly identified. In addition, since segments pooled from different structures are also optimally classified, one can infer that signatures are generator-specific rather than structure-specific.

Notably, some of the variables measured may have non-overlapping ranges in different animals. Yet the overall multivariate signature for each generator can be recognized across them, and thus optimal ML classification comes of no surprise. Only a few ML techniques appear unsuited, while optimal ones had a mild bias for the signal type, either the raw FPs or their generators. Presumably, internal data handling may fit different features of the signals. Indeed, some ML-sensitive signal properties were found, for example with the local or remote location of the active sources determining the accuracy. This was revealed by the spatial domains formed by misclassified segments, which relates to the increased blurring of the temporal characteristics of a source at a distance. The same mechanism also accounts for the deterioration of ML performance on multisource raw FPs relative to their FP generators. This conclusion is supported by computer simulations on which ML behaves similarly in modeled FPs relative to their component sources, and further confirmed by adding white noise to the sources to simulate the reduced signal-to-noise ratio when the source is weak or distant.

On the nature of the generator-specific temporal signatures

The physiological grounds of source signatures are not yet known, and cannot be deduced from the ML techniques since many yield optimal classifications. Relevant elements/mechanisms should be in the minimal period in which optimal ML classification is achieved, i.e. the 1 to 5 s. Such duration may already encompass individual FP waves and short oscillatory episodes, both of which emerge from synchronous synaptic currents elicited by incoming spikes from upstream populations and they may indeed carry information on their origins (Fernández-Ruiz et al. 2012; Santiago et al. 2024). Yet all FP generators so far described can display variety of waves (e.g. gamma, theta, or delta), either in isolation or forming motifs that range from stereotypic to noise-like (Torres et al. 2019; Hernández-Recio et al. 2023). Thus, though spectral properties may have been decisive to correctly classify a fraction of segments, additional factors are at play in correctly classifying another fraction of highly aperiodic segments.

We show that including nonlinear variables optimizes ML performance, as when they were removed from the multidimensional space the accuracy dropped below 50%. This is consistent with an earlier study in which we found that the correlation dimension (a fractal measurement) provides predictable values of activity changes in FP generators (Makarov et al. 2023) but not in multisource signals (Hernández et al. 1995; Harrison et al. 2005).

The structural basis provided by the very notion of FP generators (stable spatial current modules: Herreras et al. 2015, 2022, 2023), reduces the possible candidate elements to give individual entity to signatures. We consider 3 main likely contributors. An obvious candidate is the collective dynamics of the upstream population, which may be reasonably assumed to differ for different afferent populations and it shall be constrained by the properties of individual cells. These can determine a limited range of grouped discharges that will give rise to postsynaptic waveforms with equally limited temporal characteristics and which are globally captured in the spectral properties used in the signatures.

A role may also be considered for asynchronous synaptic bombardment, thought to underlie the 1/f structure of the aperiodic component in power spectra and to also vary in different behavioral states/transitions (Miskovic et al. 2019). Noisy networks have been proposed to favor responsiveness and network propagation of activity (Destexhe 2022), although the mechanism is unknown (Bédard and Destexhe 2009; Salvatore et al. 2024). While this asynchronous firing barely contributes to measurable FP waves when recorded in AC-coupled mode, it may determine nonlinear characteristics implicit in the “background noise,” and these may well be specific to FP generators (Makarov et al. 2023).

Last but not least, cytoarchitectonic factors of the target (source) population can also play an important role, as these are critical to translate coherent inputs into measurable signals that survive volume cancellation (Lorente de Nó 1947; Herreras et al. 2022). Indeed, computer simulations show that a particular incoming series of spikes into pyramidal-like or multipolar cells, either ordered or in glomerular-like arrangements results in remarkably different extracellular waveforms and strong changes in the power spectrum when these are scaled to FPs in the population (Martín-Vazquez et al. 2016).

Some of the variables used here were entropy-based measurements, widely used to characterize functional states within a scale of hundreds of milliseconds to a few seconds. These so called “microstates” (von Wegner et al. 2024) are thought to have a physical substrate in the spatial topography of networks, and the very concept relies on the temporal stability of co-active nodes. For their part, FP generators reflect activity in only 1 node and though their disentangling is also based on the spatial coherence of potentials, they have no temporal limits to stability. Rather they are tremendously fluctuating. Therefore, the generator-specific factors detected by ML are different from those defining microstates, possibly more akin to those defining baseline activity in default networks (Raichle et al. 2001).

Irregular activity versus stereotyped FP events: always the sources!

Irregular FP activity is dominant in the brain. Although stereotyped patterns have shown value as biomarkers in tasks or pathologies, the exploration of their sources is problematic since more often than not these are multiple and of variable extension (Dehghani et al. 2010; Mak-McCully et al. 2015; López-Madrona et al. 2020). Furthermore, their association with behavioral tasks or states is mostly based on probability of occurrence (Swanson et al. 2025) rather than true causality. It is often overlooked that source populations display different temporal patterns. For example, the CA3–CA1 Schaffer excitatory input is known to display occasional sharp waves, strings of gamma oscillations and irregular activity, while these have been assigned various behavioral tasks, such as episodic memory, the representation of potential threats, metabolic alarm signaling, the exchange/conjugation of interhemispheric information or as a switch for signal-poor/rich spatial navigation, among others (Benito et al. 2016; Zheng et al. 2016; Sharif et al. 2021; Tingley et al. 2021; Calvin et al. 2025; Chang et al. 2025). While a population’s participation in all of these is guaranteed by their belonging to a specific generator, the emerging view is that FP patterns will simply reflect modes of computation or communication between populations (Fernández-Ruiz et al. 2023).

Expanding capabilities for simultaneous reading of multiple populations and circuits is the goal, which happens to be the achievement of source decomposition techniques. It turns out that these operate more efficiently on irregular FP activity than on transient events or rhythmic oscillations (Herreras et al. 2015, 2023), which typically involve significant levels of synchronization of several types of cells and circuits whose spatial overlap burdens separability (Makarova et al. 2011). Therefore, we consider that the source-specific signatures discovered here and their ML optimal classification outweigh the advantages of the easy recognition of transient FPs. Some benefits of FP generator signatures are: (i) source selectivity: they identify a single source, whereas most FP transients do not; (ii) full time resolution: in contrast to transient events, signatures allow access to all population’s activity regardless of its different patterns; (iii) increased biomarker capabilities: temporal accuracy signatures are recognized by ML in segments that are only seconds long, omitting probabilistic search and circumstantial association to tasks; (iv) given the structural nature of FP generators, signatures provide structural and functional support for multiple modern estimates of EEG complexity measures currently used in human and animal research (Castro et al. 2024; Makarova et al. 2024; Wan et al. 2024).

Clearly the bulk of information contained in irregular FPs needs to be surfaced. FP generators and leveraging the extraordinary classification capabilities of ML provides a safer path toward this goal. While the suboptimal performance of ML on raw FPs discourages the use of these signals for studies requiring high temporal precision, the optimal performance they achieve on the separated sources makes possible large-scale automated readout of the activity of multiple neural networks under any condition. To this end, it would also be important to be able to associate each generator with a specific synaptic pathway. This would have a significant impact on describing the many rapid changes in the varying constellation of circuits that are activated in a coordinated manner in the multiple phases of any behavioral or cognitive task, something that is only at the reach of methods with full temporal resolution. Identifying these pathways with FP generators is not trivial (Herreras et al. 2015), as they can take on different spatial profiles when the recordings do not sample the same section of the volume or when, as in humans, the functional regions can vary significantly due to experience. We believe that if FP generators can be uniquely and unambiguously characterized by temporal, albeit subliminal, characteristics, as suggested by the present findings, we will be able to advance more quickly and with greater precision toward these objectives.

Author contributions

Ricardo Muñoz-Arnaiz (Conceptualization, Formal analysis, Investigation, Methodology, Software, Visualization, Writing—review & editing), Julia Makarova (Data curation, Formal analysis, Investigation, Methodology, Software, Visualization, Writing—review & editing), Valeri A. Makarov (Methodology, Software, Supervision, Validation, Writing—review & editing), and Oscar Herreras (Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Verification, Visualization, Writing—original draft).

Funding

This work was supported by the Spanish Ministerio de Ciencia e Innovación (MICIN) under grants PID2022-137801NB-I00 (OH) and PID2021-124047NB-I00 (VAM), and the European Commission Next Generation EU under grants PDC2021-121103-I00 (Agencia Estatal de Evaluación) and EU 2020/2094-IASOMM24006 (CSIC's excellence programs) (OH). RMA is financed by a PhD fellowship PIPF-2023/SAL-GL-30443 from the Comunidad Autónoma de Madrid.

Conflict of interest statement: The authors declare no conflict of interests.