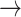Heart rate transition patterns reveal autonomic dysfunction in heart failure with renal function decline: a symbolic and Markov model approach

Abstract

Around half of heart failure (HF) patients develop chronic kidney disease (CKD) and early detection of renal impairment in HF remains a clinical challenge. Both HF and CKD are characterized by autonomic dysfunction, suggesting that early identification of autonomic dysregulation may assist in early diagnosis and intervention. Conventional heart rate variability (HRV) metrics serve as non-invasive markers of autonomic nervous system (ANS) function; however, they are limited in their ability to capture directional and nonlinear dynamics associated with autonomic impairment during renal function decline. In this study, we digitized heart rate (HR) changes from 5-minute electrocardiogram (ECG) recordings in 358 patients with chronic HF (CHF). We applied a first-order Markov model and motif pattern analyses to compare HR transition dynamics between patients with normal and reduced estimated glomerular filtration rate (eGFR). The results revealed decreased monotonic HR transitions and increased tonic fluctuations in patients with reduced eGFR. Building on these findings, we introduced a transition stability index (TSI), which was significantly lower in patients with reduced eGFR compared to those with normal eGFR (p < 0.05). These results suggest that TSI may serve as a novel indicator of autonomic dysfunction associated with renal decline. Motif analysis further supported these findings by identifying distinctive HR transition patterns in patients with low eGFR.

Supplementary Information

The online version contains supplementary material available at 10.1186/s13040-025-00460-x.

Introduction

Heart failure (HF) and chronic kidney disease (CKD) frequently occur together, and they share common physiological processes that can lead to a complex clinical condition known as the cardiorenal syndrome. The interplay between the heart and kidneys is critical, as a dysfunction in one can affect the other, leading to a cycle of progressive autonomic dysfunction associated with increased morbidity and mortality [1, 2]. It is estimated that around 50% of HF patients exhibit some level of renal impairment. On the other hand, around 17–50% of individuals with CKD have HF [1]. Patients with chronic HF are at an increased risk of developing CKD due to different factors such as long-term use of diuretics and beta blocker medications. Over time, this can lead to a gradual decline in glomerular filtration rate (GFR), even in patients with initially preserved renal function [1].

To slow the progression of CKD symptoms in HF patients, it is essential to thoroughly understand the connection between declined renal function or CKD in HF. This can be achieved by unveiling the CKD-related alterations in HF patients as early as possible. However, despite advances in the management of HF and CKD, identifying early physiological changes that indicate impaired renal function in HF patients, such as autonomic dysregulation or hemodynamic stress, remains a challenge [3, 4].

Heart rate variability (HRV) is a non-invasive measure of the autonomic nervous system (ANS) and it was used to assess autonomic dysfunction in cardiovascular disorders, such as in HF [5, 6]. However, conventional HRV measurements frequently lack sensitivity to transient, nonlinear, and distinctive patterns of HR regulation, particularly in the detection of early autonomic dysfunction [7, 8]. These limitations reduce their utility for early diagnosis of CKD-related alterations in HF patients.

Symbolic HR analysis offers a more robust approach to analyse HRV. In previous studies, RR interval (RRI) was symbolized into 3-beat symbolic patterns representing: 0 V (no variation), 1 V (one variation), and 2 V (2 variations) [9, 10]. In some other studies, the symbols were further converted into alphabets [11]. Analysing symbolic HRs may provide richer information than conventional HRV metrics and can be further enhanced if combined with probabilistic models such as Markov Chains [12]. Symbolic RRI analysis remains unpopular and underutilized, and further research is needed to fully exploit its analytical potential, especially in a clinical context. Currently, with the advancement of artificial intelligence (AI) technologies, especially interpretable models, the scope of using symbolic RRI is increasingly feasible. Also, it offers the advantage of being non-invasive.

In this study, we propose a novel approach to analyze HR through transition dynamics and symbolic pattern analysis. We aim to extract interpretable features that may serve as early digital biomarkers of autonomic dysfunction associated with renal function decline by applying first-order Markov model and motif-based analysis to beat-to-beat HR transitions. Although not the primary aim of this study, we also calculated frequency-based HRV metrics to bridge them with our transition features and gain additional physiological insights into the ANS function.

Methodology

Dataset description

In this study, we used data from the publicly available MUSIC (MUerte Subita en Insuficiencia Cardiaca) cohort, a prospective, multicenter, longitudinal study aimed at identifying predictors of cardiac mortality and sudden cardiac death (SCD) in ambulatory patients with chronic heart failure (CHF) [13, 14]. The detail of the study is explained in detail in [14]. Briefly, between April 2003 and December 2004, 992 chronic HF (CHF) patients were enrolled consecutively from eight specialized HF clinics located in Spanish university hospitals. The cohort was followed for a median duration of 44 months, with follow-up completed by November 2008. At baseline, all participants underwent a comprehensive clinical and physiological assessment. At baseline, information related to age, body mass index (BMI), and medication use (e.g., beta blockers, calcium channel blockers, anticoagulants, ACE inhibitors, statins) were collected. In addition, blood laboratory parameters, a 3-lead high-resolution 20-min ECG, chest X-ray, and were collected. High resolution ECG was recorded at a 1000 Hz sampling rate for 20 min.

All patients had symptomatic CHF (New York Heart Association (NYHA) class II-III) and were treated per institutional standards. The dataset covers participants with either reduced (< 45%) or preserved LVEF (> 45%). The latter were included if they had HF symptoms and had previously been hospitalized for HF, or if they showed objective evidence of HF confirmed by chest X-ray (pulmonary congestion) and/or ECG. The collection of this dataset was approved by Institutional investigator’s committees and all patients gave written informed consent [14].

Electrocardiogram (ECG) R peak detection

From MUSIC dataset, we could download a total of 687 dat files that contained the high-resolution ECG signals [13]. In this study, ECG analysis was conducted using 5-minute segments per participant. We selected a 5-minute duration as it is the minimum recommended length for reliable assessment of the very-low-frequency (VLF) power [5]. The quality of ECG signals was confirmed visually for each participant before inclusion. Only ECG recordings with clearly identifiable R peaks, detectable by our MATLAB script, were considered. We chose the beginning of ECG records to choose the 5-min segment; however, if the beginning of the recording contained noise, we shifted the window to identify a clearer ECG signal. The code uses the “findpeaks” function in MATLAB to detect R peaks. Before R peak detection or applying the “findpeaks”, a high-pass filter was used to filter baseline wandering for easier identification of R peaks. Ectopic beats or extreme RRI values were corrected manually by replacing them with mean RRI values based on previous or succeeding beats. ECG recordings with excessive ectopic beats/extreme RRI values (defined as more than 20% of the detected beats) were excluded. After exclusion, a total of 358 ECG recordings were included in the final analysis.

Estimated glomerular filtration rate (eGFR) calculation and grouping

The estimated glomerular filtration rate (eGFR) was calculated by using the CKD- Epidemiology Collaboration (EPI) equation [15]:

1

K = 0.7 (female), K = 0.9 (male), 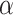= -0.329 (female), -0.411 (male)

This equation was chosen for its improved accuracy in distinguishing between CKD stages and because it does not require racial adjustment [15]. Based on the calculated eGFR, participants were categorized into three groups according to the Kidney Disease Improving Global Outcomes (KDIGO) guidelines [16]:

• Normal: eGFR ≥ 90 mL/min/1.73m².

• Stage 2 (S2): 60 ≤ eGFR < 90 mL/min/1.73m².

• Stage 3 (S3): 30 ≤ eGFR < 60 mL/min/1.73m².

Participants classified as CKD Stage 4 and Stage 5 based on the KDIGD guidelines were excluded due to the small number of available cases in each category (8 and 1, respectively).

Heart rate variability (HRV) analysis

Frequency based analysis of HRV was conducted by considering the following bands (identified by the Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology) [5, 17]: VLF: (0.0033–0.4) Hz, LF: (0.04–0.15) Hz, HF: (0.15–0.4) Hz. The “Plomb” function in MATLAB was used for spectral HRV analysis. Plomb is robust to non-uniform sampling.

First-order Markov model and transition matrix probability calculation

Here, we used a first-order Markov model because we are analyzing short-term directional transitions between consecutive heartbeats, represented as symbolic trends. In a first-order Markov model, it is assumed that the current state depends on the previous state, based on this, we identified three states based on consecutive RR interval (RRI) differences as follows (the subscript x indicates beat count):

State − 1

HR deceleration (RRI_x+1 - RRI_x > 0).

State 0

no change in HR (RRI_x+1 - RRI_x = 0).

State 1

HR acceleration (RRI_x+1 - RRI_x < 0).

Using these states, a 3 × 3 Markov transition matrix was constructed for each participant. In the transition matrix, P (i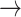j) represents the probability of transitioning from state i to state j. The sum of transition probabilities across each row equals 1, as each row represents all possible transitions from a given state.

Table 1 provides a conceptual illustration of the transition matrix that was used in this study. For example, P (-1 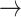-1) indicates the probability of remaining in the deceleration state across two consecutive beats, representing a monotonic deceleration run.

Table 1.

Demonstration of the transition matrix for heart rate (HR) acceleration and deceleration

State	-1	0	1
-1	P (-1 -1) Monotonic HR deceleration run	P (-1 0) No change in HR value/direction from a deceleration state	P (-1 1) Transition to HR acceleration from deceleration
0	P (0 -1) Transition from no change to HR deceleration	P (0 0) No change in HR value/direction	P (0 1) Transition from no change to HR acceleration
1	P (1 -1) Transition to HR deceleration from acceleration	P (1 0) No change in HR value from an acceleration state	P (1 1) Monotonic HR acceleration run

-1: heart rate (HR) deceleration, 0: no change, 1: HR acceleration

Transition stability index (TSI)

From the transition probabilities, we calculated the transition score index (TSI) as follows:

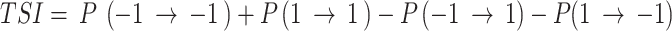Eq. 2.  

Positive TSI values represent a tendency to maintain the current direction (monotonic runs or stability), whereas negative values indicate a tendency to switch directions (tonic changes or instability). The TSI focused on transition probabilities that did not involve the 0 state, as it was significantly uncommon in the dataset. We investigated the association of TSI with Porta’s index [18, 19], and the percentage of inflection points (PIPs) [20]. In addition, we investigated TSI association with the symbolic RRI analysis described earlier [18, 21], 0 V, 1 V, 2LV and 2UV. The same symbols were identified for 3 consecutive beats, where 0 V: denotes no variation. 1 V: one variation or two consecutive equal symbols with one different direction. 2LV: two similar variations. 2UV: two unlike variations. The results of the correlation analysis are provided in Supplementary Table 1.

Motif analysis

In MATLAB, we calculated the number of occurrences of motifs of length 3. Mathematically, a sequence of three states yields 27 possible motifs; however, we focused our analysis on the following four: (-1, -1, -1), (1, 1, 1), (1, -1, 1), and (-1, 1, -1). This decision was based on two main reasons. First, the state 0 (no change) was uncommon in our dataset. Second, we were primarily interested in motifs that reflect clear directional dynamics rather than stability. Although motifs such as (-1, 1, 1) and (1, 1, -1) contain elements of directional change, they also include monotonic runs, which were not the focus of this specific analysis.

Statistical analysis and linear regression model

Correlation analysis was performed using Spearman’s rank correlation. Comparisons of group means were conducted using the Wilcoxon rank-sum test. To adjust for co-factors, we applied the linear regression model to examine the relationship between frequency-based HRV metrics with eGFR. We performed three regression models to avoid the collinearity that can result from combining HF, LF and VLF together since they are highly correlated (r > 0.6). In Model 1, we adjusted for HF, in Model 2 we adjusted for LF and in Model 3 we adjusted for VLF. Before feeding the variables to the regression model, we normalized the variables by using Z-score normalization in MATLAB. Figure 1 provides a summary of the methods of this study.

Fig. 1.

Graphical summary of the methodology. In this study, we calculated heart rates (HR) from 5-minute electrocardiogram (ECG) records of 358 chronic heart failure patients (CHF). The patients were divided based on estimated glomerular filtration rate into three groups to compare HR transition dynamics across different renal function. The dynamics were investigated after digitizing HR based on their acceleration/deceleration patterns

Results

Summary of the features

Table 2 summarizes the clinical, demographic, and HRV features of the study population (N = 358), categorized by kidney function stages. Participants with S3 were significantly older (69 ± 8.8) years compared to those in the normal kidney function group (51 ± 12) years. The proportion of male participants was highest in the normal group (83%), although overall, the cohort was predominantly male (94%). BMI was highest in S2 (30 ± 4.6) kg/m² and lowest in the normal group (28 ± 4.4) kg/m².

Table 2.

Summary of the features

Feature	All (n = 358)	Normal (n = 56)	S2 (n = 159)	S3 (n = 133)
Demographics
Age (years)	62 ± 12	51 ± 12	60 ± 10	69 ± 8.8
Sex (Male, %)	264 (73%)	49 (83%)	125 (79%)	83 (62%)
BMI (kg/m2)	29 ± 4.5	28 ± 4.4	30 ± 4.6	29 ± 4.3
Medication
Calcium Channel Blocker	53 (15%)	21 (8.9%)	21 (14%)	21 (16%)
Diabetes Medication	111 (31%)	8 (14%)	51 (32%)	48 (36%)
Amiodarone	33 (9.2%)	2 (3.6%)	11 (6.9%)	19 (14%)
Angiotensin II Receptor Blocker	59 (16%)	5 (8.9%)	26 (16%)	20 (14%)
Anticoagulants Antitrombotics	293 (82%)	41 (73%)	130 (82%)	113 (85%)
Beta Blockers	250 (70%)	47 (84%)	119 (75%)	77 (58%)
Digoxin	76 (21%)	15 (27%)	31 (20%)	28 (21%)
Loop Diuretics	244 (68%)	30 (54%)	95 (60%)	111 (83%)
Spironolactone	117 (33%)	16 (29%)	48 (30%)	50 (38%)
Statins	193 (54%)	27 (48%)	90 (57%)	74 (56%)
Hidralazine	5 (1.4%)	0	1 (0.6%)	3 (2.2%)
ACE Inhibitor	274 (77%)	46 (82%)	120 (75%)	101 (76%)
Nitrovasodilato	116 (32%)	11 (20%)	51 (32%)	46 (35%)
HR & Frequency-based HRV
HR (bpm)	68 ± 12	68 ± 12	69 ± 13	67 ± 12
HF (Ln)	4.5 ± 1.4	5.0 ± 1.5	4.6 ± 1.3	4.2 ± 1.4
LF (Ln)	4.8 ± 1.4	5.6 ± 1.3	5.1 ± 1.2	4.4 ± 1.4
VLF (Ln)	6.0 ± 1.3	6.5 ± 1.2	6.2 ± 1.2	5.6 ± 1.4

BMI: body mass index, HR: heart rate, HRV: HR variability (HRV), bpm: beats per minute, HF: high frequency, LF: low frequency (LF), VLF: very LF

Medication usage differed between groups. Beta-blocker use was highest in the normal group (84%) but decreased with renal function decline (75% in S2, 58% in S3). ACE inhibitor and anticoagulant/antithrombotic usage remained high across all stages, while use of amiodarone and diabetes medications increased with CKD severity. The number of participants consuming loop diuretic was highest in S3 (111 participants). This is consistent with increased fluid management needs in advanced kidney disease.

In terms of HR and HRV metrics, participants with normal kidney function had higher LF (5.6 ± 1.3), HF (5.0 ± 1.5), and VLF (6.5 ± 1.2), compared to those in S3 (LF: 4.4 ± 1.4, HF: 4.2 ± 1.4, VLF: 5.6 ± 1.4). HR was lowest in S3 (67 ± 12) beats per minute (bpm) and highest in S2 (69 ± 13) bpm. The results concerning HRV indicate a progressive decline in HRV components with worsening kidney function.

After adjusting for clinical covariates, frequency-based HRV parameters are associated with renal function

We assessed the relationship between frequency-based HRV metrics and renal function, as measured by eGFR, across three regression models adjusting for age, sex, BMI, and medications (Table 3).

Table 3.

Parameters of multiple linear regression model to predict estimated glomerular filtration rate (eGFR):

Feature	Model 1 (β)	Model 2 (β)	Model 3 (β)
Demographics
Age	-9.4*	-8.89*	-9.1*
Sex	6.3*	6.2*	6.0*
BMI	-0.35	-0.43	-0.49
Medications
Calcium Channel Blocker	-2.4	-2.6	-2.5
Diabetes Medication	-1.3	-0.79	-1.3
Amiodarone	-3.1	-3.1	-3.1
Angiotensin II Receptor Blocker	-1.3	-1.6	-1.1
Anticoagulants Antitrombotics	-2.2	-2.2	-2.1
Beta Blockers	1.13	1.4	1.5
Digoxin	3.8	3.4	3.8
Loop Diuretics	-8.0*	-7.6*	-7.8*
Spironolactone	-1.4	-0.88	-1.5
Statins	1.4	1.3	1.04
Hidralazine	-15	-15*	-16*
ACE Inhibitor	0.77	0.053	0.49
Nitrovasodilato	0.39	0.55	0.51
Heart rate Variability
HF	2.5*	-	-
LF	-	3.1*	-
VLF	-	-	2.4*
Model parameters
Adjusted R-Squared	0.36	0.37	0.36
P-value	P < 0.05	P < 0.05	P < 0.05

* P < 0.05. Rows 3–21 show Beta coefficients. The table shows standardized beta coefficients for multilinear regressiong models. Model 1, which was adjusted for demographics and Medication & high frequency (HF). Model 2 was adjusted for demographics and Medication & low frequency (LF). Model 3 was adjusted for demographics, medication & very LF (VLF). BMI: body mass index

• - In Model 1 (Table 3), HF was significantly associated with eGFR (β = 2.5, p < 0.05), alongside negative effects of age (β = − 9.4, p < 0.05) and loop diuretic use (β = − 8.0, p < 0.05).

• - In Model 2 (Table 3), LF power demonstrated the strongest association with eGFR (β = 3.1, p < 0.05). Similar covariate effects are observed as in Model 1; however, Hydralazine uptake was additionally associated with a significant negative effect on eGFR (β = − 15, p < 0.05).

• - In Model 3 (Table 3), VLF power was also significantly correlated with eGFR (β = 2.4, p < 0.05), though with a slightly lower effect size than LF. Similar covariate effects are observed as in Model 2.

Across all models, loop diuretic use and increasing age were consistently associated with lower eGFR, while female sex was associated with higher eGFR. In models 2 and 3, Hydralazine uptake was associated with lower eGFR. LF power yielded the highest beta coefficient among HRV metrics, implying its sensitivity to changes in renal function.

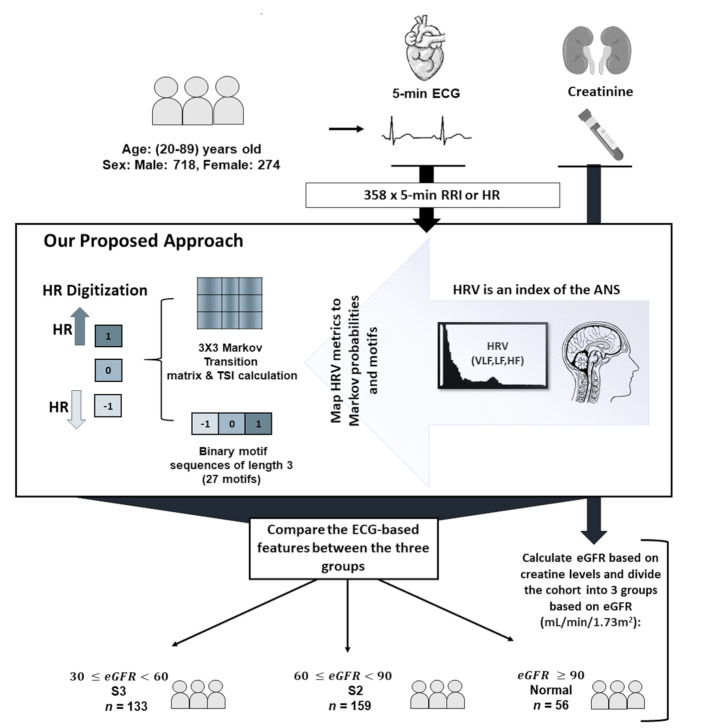
Transition probabilities differentiate between normal and stage (S3)

We compared the transition probabilities of HR direction across three kidney function groups: normal function, S2, and S3 (Fig. 2). Transitions were classified into eight possible states: monotonic runs (-1 -1, 1 1), tonic changes (-1 1, 1 -1), and transitions involving a zero state (-1 0, 0 -1, 0 0, 1 0, 0 1). Significant differences in HR transition dynamics were observed across different renal function stages per transition state. The probability of monotonic runs (-1 -1, 1 1) declined with worsening kidney function, with S3 showing the lowest probabilities: [(-1 -1): normal: 0.44 ± 0.11, S2: 0.43 ± 0.11, S3: 0.36 ± 0.11, (p < 0.05)], [(1 1): normal: 0.45 ± 0.10, S2: 0.42 ± 0.11, S3: 0.36 ± 0.10, p < 0.05].

Fig. 2.

Comparison of transition probabilities for heart rate (HR) dynamics/transitions across different renal function stages. Transitions were derived using a first-order Markov model with three states: -1 (HR deceleration), 0 (no change), and 1 (HR acceleration). Significant differences between groups are indicated by red asterisks (*). The figure shows monotonic runs (-1 -1, 1 1) declined, while tonic changes (-1 1, 1 -1) increased with renal function decline, highlighting altered autonomic regulation

In contrast, tonic changes (-1 1, 1 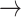-1) increased significantly in S3, [(-1 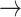1): normal: 0.53 ± 0.10, S2: 0.54 ± 0.11, S3: 0.60 ± 0.11] (p < 0.05), [(1 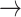-1): normal: 0.47 ± 0.24, S2: 0.49 ± 0.21, S3: 0.47 ± 0.21] (p < 0.05). Minor but significant increases were observed between normal and S3 in the transition [(-1 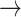0): normal: 0.03 ± 0.03, S3: 0.04 ± 0.04, p < 0.05] and the transition [(1 0): normal: 0.52 ± 0.10, S2: 0.55 ± 0.11, S3: 0.60 ± 0.10, p < 0.05].

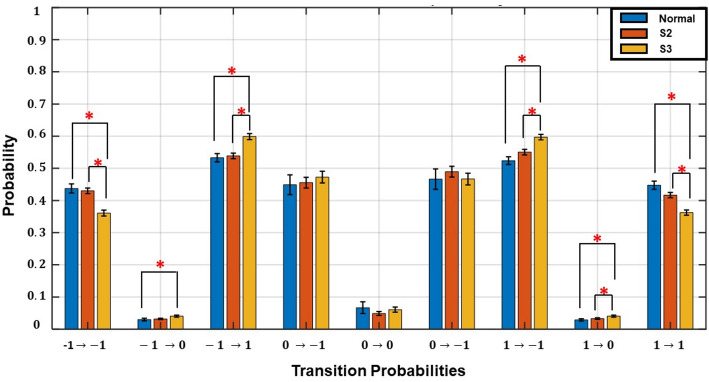
Directional stability and low frequency (LF) power

We assessed the relationship between LF power and the TSI across kidney function stages (Fig. 3). Each point represents an individual subject, with color-coded groups: normal kidney function (blue), S2 (orange), and S3 (yellow). A significant positive correlation was observed between LF and TSI (r = 0.36, p < 0.05), indicating that higher LF is associated with greater directional stability in HR transitions. A negative trend in TSI and LF was observed with advancing CKD stage, particularly in S3.

Fig. 3.

Transition Stability Index (TSI) vs. Low Frequency (LF) by Renal Function Stage. Scatter plot showing the relationship between log-transformed LF power and the TSI across kidney function stages. Each dot represents an individual subject, coloured by group: normal kidney function (blue), Stage 2 (S2) (orange), and Stage 3 (S3) (yellow). Ellipses indicate ± 1 standard deviation around the mean of each group, highlighting the variability in TSI and LF. The downward trend in TSI with renal function decline suggests reduced directional stability of heart rate (HR)

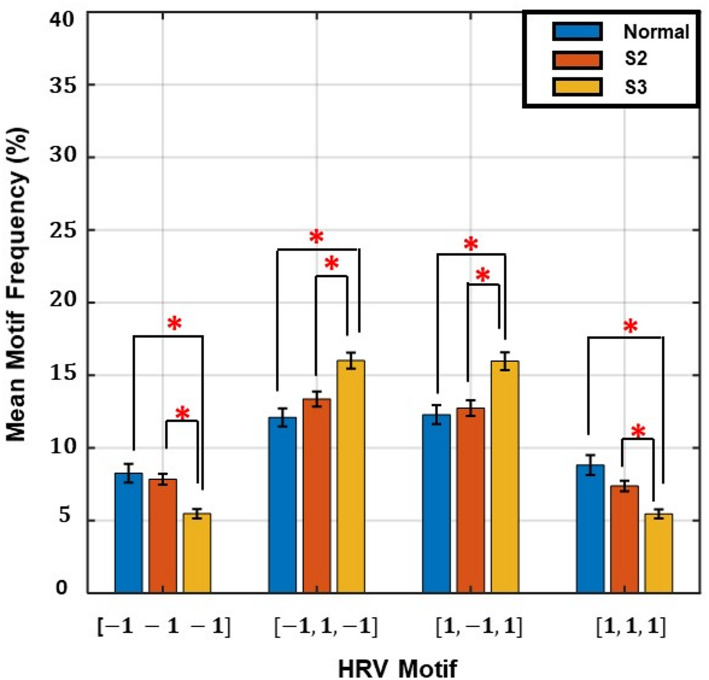
Motif analysis bar graph

The plot shows the mean frequency percentage of four representative motifs of length 3, categorized based on HR direction: monotonic patterns (-1 -1 -1, 1 1 1) and alternating patterns (-1 1 -1, 1 -1 1). Participants with normal kidney function exhibited a higher prevalence of monotonic motifs, indicating greater beat-to-beat directional stability. In contrast, S3 participants showed increased frequency of alternating motifs, reflecting greater variability and reduced autonomic regulation of heart rate dynamics.

We performed motif analysis using HR transition sequences of length three to capture short-term HRV patterns. Figure 4 shows the frequency distribution of key motifs across kidney function groups. Monotonic motifs (-1 -1 -1 and 1 1 1) were more common in the normal kidney function group and declined progressively with renal function. In contrast, tonic fluctuation motifs such as (-1 1 -1) and (1 -1 1) were more frequent in S3, suggesting increased directional alternation. This shift in motif pattern further supports the notion that directional stability of HR transitions deteriorates with advancing CKD, consistent with findings from TSI and transition probability analyses.

Fig. 4.

Motif frequency distribution of heart rate (HR) transition sequences across kidney function stages

Discussion

In this study, we investigated the association of HR transition dynamics with renal function, measured by eGFR. Our results demonstrate that frequency-based HRV metrics, specifically the LF power, are significantly and positively associated with eGFR. This association persisted even after adjusting for age, sex, BMI, and medication intake. While the association between reduced HRV and worsening kidney function has been previously reported [22–24], to our knowledge, the relationship between the HR transition dynamics (acceleration/deceleration) and renal function has not been explored yet.

In our study, the application of a first-order Markov model distinguished patterns in HR transition between those with normal eGFR and declined eGFR (S3). Monotonic runs (-1 -1, 1 1) decreased, while tonic changes (-1 1, 1 -1) increased significantly with declining renal function (Fig. 2). The increased tonic transitions observed in patients with reduced eGFR likely reflect underlying autonomic instability. Physiologically, these abrupt transitions in HR may arise from competing sympathetic and parasympathetic influences on the sinoatrial node. Impaired baroreflex sensitivity and disordered central autonomic integration, both known to worsen with CKD [23].

The HR transition patterns were not only associated with eGFR, but also physiologically meaningful. Our TSI, an index that measures monotonic runs versus tonic transitions, was positively correlated with LF power (r = 0.36, p < 0.05; Fig. 3), suggesting that higher LF oscillations reflect greater stability in HR transition dynamics. A motif analysis of HR transition sequences further reinforced this interpretation (Fig. 4). Participants with normal kidney function exhibited a higher frequency of stable, monotonic triplet patterns (-1 -1 -1 or 1 1 1), whereas alternating or unstable motifs (-1 1 -1, or 1 -1 1) were more prevalent in S3. The disruption in HRV patterns may reflect a growing autonomic stress that accelerates renal function deterioration.

Correlation analysis between the TSI and PIP (Supplementary Table 1) revealed a strong negative association (r = – 0.97, p < 0.05). This inverse relationship suggests that higher PIP values reflect frequent directional changes in HR. Previous studies [20, 25] have linked PIP to intrinsic pacemaker activity rather than purely autonomic nervous system (ANS) modulation. Therefore, the strong correlation between TSI and PIP implies that some HR transition dynamics captured by TSI may reflect intrinsic cardiac properties beyond ANS control. It is important to note that TSI, as currently defined, excludes transitions involving no change (i.e., 0 → 0), whereas PIP explicitly includes them.

In Supplementary Table 1, TSI showed minimal correlation with Porta’s Index (r = – 0.08), but weak associations with: 0 V% (r = 0.20), 1 V% (r = – 0.22), 2LV% (r = 0.23), and a modest negative correlation with 2UV% (r = – 0.34), all statistically significant (p < 0.05). Among (0 V%, 1 V%, and 2LV%), TSI was most strongly, though moderately, associated with 2UV% (r = – 0.34). This is expected, as 2UV patterns reflect alternating changes in HR, indicative of instability or directional reversals. In contrast, 0 V% and 2LV% represent stable or monotonic behavior, and 1 V% captures partial variation; these patterns showed only weak associations with TSI.

Clinically, our results have several implications. First, measures such as TSI and motif frequency could serve as non-invasive early indicators of renal impairment in HF patients, potentially enabling timely intervention. Second, our results lend further support to monitoring autonomic markers in HF patients for better health management, particularly in individuals with declining renal function. These findings can further broaden our understanding of the mechanisms involved in the cardiorenal syndrome, in which chronic cardiac dysfunction leads to progressive renal impairment [26].

Our work may pave the way for transforming HRs into interpretable digital features that can be readily utilized in AI models to better understand how cardiac electrical activity and ANS dynamics influence overall health. Also, HR digitization can be integrated into wearable devices and a remote monitoring system. HR transition motifs can be converted into tokens that can be further integrated into linear language models (LLMs). It is worth noting that our significant results may be characteristic of HF patients specifically; therefore, further investigation is needed in cohorts without HF to determine the generalizability of these findings.

This study has several limitations that should be acknowledged. First, the analysis was conducted in a cohort of patients with HF, which may limit the generalizability of our findings to broader patients with impaired renal function without cardiac comorbidities. Our derived directional stability and motif could have been influenced by the underlying autonomic alterations commonly present in HF [27]. Second, the correlations between HRV and eGFR, although adjusted for key clinical covariates including age, sex, BMI, and medication use, residual confounding, particularly from unmeasured variables such as physical activity, cannot be ruled out. Third, our HRV analysis was based on short-term (5-minute) ECG recordings, which, while clinically practical, may lack physiological inferences related to the circadian fluctuations. Also, our symbols of [-1,0,1], which are based on beat-to-beat differences, are prone to inaccuracy due to R-peak morphology. Creating symbols based on a threshold may reduce errors related to R-peak detection.

Conclusion

In this study, we demonstrated HR transition probabilities and motif-based analysis revealed significant differences between individuals with normal kidney function and those with declined renal function in a CHF cohort. These findings suggest that autonomic dysfunction in patients with impaired heart and renal function can be captured through temporal and directional analyses of beat-to-beat HR transition. Incorporating such measures into routine risk assessment may enhance CKD monitoring and management in patients with HF.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

Author Contribution: NW: Conceptualized the study, performed the analysis, and prepared and revised the manuscript. SA: Prepared the manuscript, assisted with study conceptualization and reviewed the manuscript. AK: Provided funding, supervised the study and reviewed the manuscript.

Funding

The work in this study is supported by 8474000376 (KU-KAU project), 8474000132 (HEIC) and CIRA grant (8474000408) awarded to Ahsan Habib Khandoker by Khalifa University, Abu Dhabi, UAE.

Data availability

Data is publicly available online in PhysioNet: https://physionet.org/content/music-sudden-cardiac-death/1.0.0/.

Declarations

Competing interests

The authors declare no competing interests.