Parental mixed-gender preferences revealed by IVF twin births

Significance

This paper shows that IVF significantly impacts the occurrence of twin births and their gender composition, hence the importance of parental gender preferences. Our results indicate that In vitro fertilization (IVF) has risen markedly among older and wealthier mothers, also affecting the overall gender composition of twins. These findings imply that in wealthier populations that can afford IVF, major changes can be made in the direction of strategically shaping family gender composition, therefore underscoring the greater influence of economic factors on reproductive decision-making and ultimately on future sibship trends. These insights signify the importance of socioeconomic factors in evaluating assisted reproductive technologies, particularly in countries where parental gender preferences are prevalent.

Abstract

In vitro fertilization (IVF) affects human fertility by 1) increasing the probability of multiple births through the transfer of multiple embryos, 2) raising the proportion of dizygotic twins, which leads to a higher occurrence of one-boy-one-girl twins, and 3) enabling gender selection through preimplantation genetic screening (PGS) when parents have specific gender preferences. While the above-mentioned increase in multiple births is well documented, the impact on the twins’ gender composition remains under-explored, partly because 2) and 3) are intertwined. This study uses millions of administrative observations from Taiwan to disentangle the effects of IVF on twin birth rates, gender composition, and parental preferences. Families are grouped by maternal age and family wealth across different periods, enabling a comparative analysis of socioeconomic and temporal factors. By examining the gender composition of first-born twins within these age-wealth-time groups, we can identify and test whether parents have gender preferences for one-boy-one-girl twins. Our empirical evidence reveals a significant increase in IVF adoption, particularly among older and wealthier mothers. The proportion of one-boy-one-girl twins among first-birth twins has risen from 20.42 to 41.86% over the past 30 y, and this proportion increases with wealth ranking, significantly exceeding expected ratios in the absence of gender preference. Parental gender preference contributed to approximately 10.95% of one-boy-one-girl twins among the wealthiest group, revealing a significant impact of parental preference on twin gender composition. These trends raise ethical and social concerns regarding reproductive technologies.

Advances in assisted reproductive technology, especially in vitro fertilization (IVF), have reshaped modern fertility patterns by impacting human reproduction in three ways: first, by increasing the probability of multiple births due to the transfer of multiple embryos; second, by raising the likelihood of dizygotic twins, which elevates the percentage of one-boy-one-girl twins among twin births, and third, by enabling gender selection through preimplantation genetic screening (PGS) when parents have gender preferences (1). While the first effect on multiple births is thoroughly researched (2, 3), the second and third effects remain less explored, particularly in regard to socioeconomic influences.

IVF’s high costs and moderate success rates make it more accessible to affluent families, granting them greater chances of having dizygotic twins and, thus, having both a boy and a girl. Gender selection is also available through Preimplantation Genetic Diagnosis (PGD) and PGS, allowing parents to select their child’s gender without incurring additional costs. Although gender selection is illegal in many countries, it may occur covertly through implicit agreements. This access brings up questions about whether IVF adopters remain neutral regarding child gender, as wealthier parents’ gender preferences may subtly influence the gender composition of their multiple births.

Leaving aside the rare cases of gender-based abortions, prior studies on gender preferences either primarily use surveys to measure parental preferences (1, 4, 5) or analyze reproductive decisions based on sibling gender composition (6, 7). As for the first approach, some people believe that survey respondents tend to provide answers that conform to social norms, and hence questionnaires may induce a “social desirability bias” (8). In the case of the second approach, since reproductive decisions are complex, the research focus often hinges upon effectively controlling other family factors, so as to identify the pure impact of gender preferences on fertility decisions.

Several studies have examined the impact of assisted reproduction technologies on the sex ratio at birth (SRB) (9–13), while primarily focusing on objective fertilization methods. Our study, however, suggests that parental subjective gender preferences may also influence results. There have also been discussions regarding the factors contributing to the use of IVF/PGD for sex selection (14, 15), but this is not our paper’s focus.

In this paper, we will explain why the administrative data for Taiwan allow us to adopt a different approach to study gender preferences. First, parents who adopt IVF often choose to implant multiple embryos, thereby increasing the likelihood of success. According to the International Committee for Monitoring Assisted Reproductive Technologies (ICMART), Taiwan has the highest twin and multifetal rates in the world, with over 35% in 2011 compared to less than 10% in Japan and Sweden (3). This high multifetal birth rate generates abundant multifetal birth data for us to analyze gender compositions.

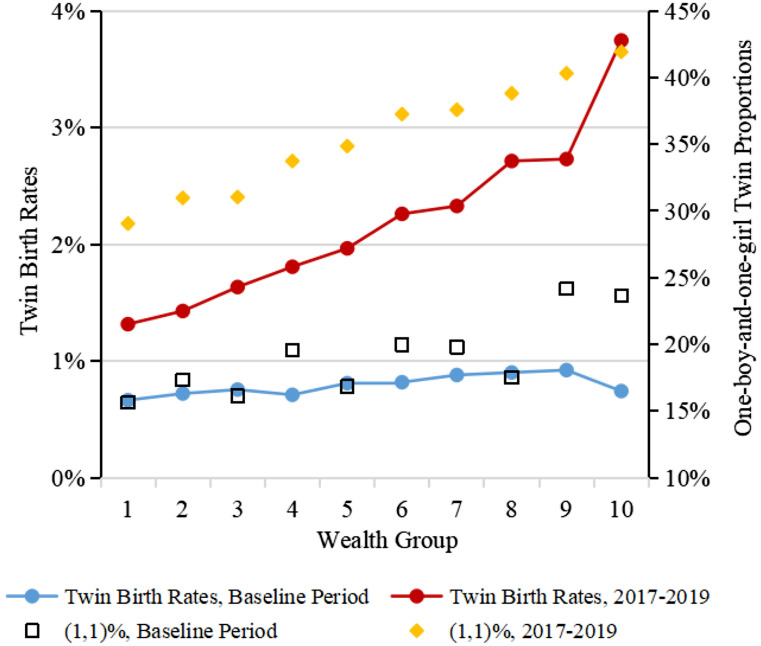
Second, Taiwan’s administrative data include the mother’s age and family wealth, which help us to identify and estimate the possible gender preferences statistically. Historically, twin rates in East Asia around 1989–1991 were generally low: Japan’s rates ranged from 6 to 8 per 1,000 births (16), South Korea’s were about 9 to 10 per 1,000 births (17), Hong Kong’s rate varied between 7 and 8 per 1000 births, and the twin rate for Singapore during this period was also less than 8 per 1,000 births (18). Taiwan’s twin rate from 1989 to 1991 was approximately 8.1 per 1,000 births—comparable to neighboring regions.^* In Fig. 1, we show the twin rates for different wealth-ranking groups (labeled 1 to 10 from low to high) during the 1989 to 1991 baseline period and the more recent 2017–2019 period.^† The twin rate across wealth groups was similar and low during the baseline period when IVF was not prevalent. In 2017–2019, however, the twin rate was significantly higher and exhibited a clear upward trend as the parents’ wealth increased.

Fig. 1.

Twin Birth Rates and One-Boy-One-Girl Twin Proportions by Wealth Ranking. Twin birth rates and proportions of one-boy-one-girl twins are shown for household wealth ranking groups (labeled 1 to 10, from low to high) in Taiwan during the baseline period (1989–1991) and 2017–2019. The blue and red solid lines show twin birth rates per delivery for the baseline period and 2017–2019, respectively, on the left vertical axis. Black squares and yellow diamonds depict the actual proportions of one-boy-one-girl twins (1,1) among first-birth twins for the baseline period and 2017–2019, respectively, on the right vertical axis. Twin rates were low and similar across wealth groups during the baseline period. By 2017–2019, the twin rate rose significantly, increasing with parental wealth. The one-boy-one-girl twin proportion was around 17.60% in the baseline period but rose substantially with wealth ranking in 2017–2019.

Similarly, the proportion of one-boy-one-girl twins among all first-born twins has also increased significantly in recent years. Note that the natural monozygotic-to-dizygotic (MZ/DZ) ratio largely determines the baseline proportion of these mixed-gender twins. Historical data indicate that Taiwan’s MZ/DZ ratios—2.36 in 1975–1979, 2.52 in 1980–1984 (19), 1.91 in 1985–1989 (20), and 1.63 in 2001–2008 (21)—are considerably higher than those in neighboring regions [e.g., 1.16 in Hong Kong (22) and 1.60 in Japan (23)], resulting in a naturally lower baseline for mixed-gender twins.^‡ Moreover, the gap compared to that of the baseline period tends to widen with the increase in family wealth. The family wealth variable, therefore, may help us identify the cause of gender composition differences.

Third, the large number of observations in the dataset allows us to focus on the mothers’ first births. Mothers’ first births, by definition, are not dependent upon the siblings of previous births. Analyzing first births helps us avoid the complex control factors associated with mothers’ second and third births, which are their “conditional” decisions. Since the choice of gender through IVF can be exercised accurately and costlessly, we refer to the possible parental gender preferences revealed in their first-birth twins as “intrinsic” preferences.

This study investigates how wealth influences IVF birth rates, one-boy-one-girl twins proportions, and parental gender preferences. Using Taiwan’s administrative data, we explore the interplay between economic standing and reproductive technologies, shedding light on their broader demographic and social implications.

Results

Wealth Impact on IVF Birth Proportion.

The estimated proportions of births via IVF corresponding to different periods, age groups, and wealth-ranking categories are shown in Fig. 2. The blue (red) color denotes percentages smaller (larger) than the overall average of two periods. As one can see, the average adoption rate of IVF tends to increase with the wealth ranking and the mother’s age. For example, during 2008–2010 (the earliest of our observations), the overall average was 2.00%. Across all age groups, it rises from 0.92% in the lowest wealth-ranking group to 3.73% in the highest wealth-ranking group. Across all wealth-ranking groups, it rises from 0.86% for the youngest group (aged 29 or below) to 4.89% for the oldest group (aged 37 or above). We also find that the IVF adoption rate generally rises with increasing wealth, regardless of the age group or time period.

Fig. 2.

Estimated IVF Birth Proportions by Period, Age, and Wealth. The estimated proportion of births via IVF is shown across different periods, age groups, and wealth categories (labeled 1 to 10, from low to high). Blue indicates that the group average is below the overall average for both periods, while red shows values above it, with darker shades representing greater deviation from the overall average. IVF_at refers to the group-(a-t) percentage of mothers adopting IVF, as Taiwan’s Ministry of Health and Welfare reported. IVF_wt represents the weighted average IVF adoption percentage for each wealth decile in period t.

The proportion of births attributable to IVF has increased over time. Between 2017 and 2019 (more recently, and our latest observation period), the average IVF rate increased to 5.73%. The average rates for the youngest and oldest age groups were 2.17 and 10.24%, respectively. The magnitude of the increase is observed to gradually rise with age. While the youngest cohort (16 to 29 y) experienced a modest 1.31% (=2.17% – 0.86%) increase, the 35 to 36 age group had a 3.66% (=7.42% – 3.76%) increase, with the 37 and above age group exhibiting the most substantial increase of 5.35% (=10.24% – 4.89%), this increase being the highest among all age cohorts.

The IVF rates across different age groups also generally increased with the wealth ranking during the 2017–2019 period. This rate among the lowest and highest wealth groups ranged from 3.80 to 8.33%, marking a significant increase of 2.88 to 4.60% compared to the 2008–2010 average. Among delivered women aged 37 and above, the rates for the lowest, median, second-highest, and highest-wealth ranking groups increased to 7.54%, 9.10 to 9.62%, 10.73%, and 12.59%, respectively. Finally, within the same wealth ranking group, IVF adoption also increased with age. The gap between 2017–2019 and 2008–2010 also widens with age. Among the sixth-richest group in 2017–2019, the rate for women aged 33 to 34 was 5.44%, compared to 9.10% for women aged 37 and above. For the oldest and highest-wealth group, the rate rose significantly to 12.59%.^§

Parental Mixed-gender Preferences among IVF Adopters?

When the utilization of IVF increases with age and wealth and the number of fertilized eggs tends to exceed one per implantation, the birth rate of twins also increases with age and wealth. Suppose that parents do have gender preferences for the twins. In that case, the proportion of twin pairs with particular gender combinations should not only increase with wealth (and age) but should also exceed the theoretical gender-neutral values in dizygotic twins. Conversely, if there is no gender preference, the proportions of certain gender compositions among IVF twins should be the same as in naturally occurring dizygotic twins, regardless of parental characteristics. Fig. 3 shows that the proportion of one-male-and-one-female fraternal twins [denoted as (1,1) for convenience] among all first-born twins increases with wealth ranking. This seems to be consistent with mixed-gender parental preference documented in the literature (24). In addition, in Fig. 4, we find that the proportion of two-boy twins [denoted as (2,0)] decreases with wealth ranking between 2017–2019. Is this sufficient to suggest the presence of gender preferences? Not quite, yet.

Fig. 3.

Proportions of One-boy-one-girl Twins by Wealth Rankings. The actual, estimated, and theoretical gender-neutral proportions for one-boy-one-girl twins [denoted as (1,1)] are shown across wealth rankings. The red dashed lines show the 2017–2019 estimates, with shaded areas indicating the gap from theoretical gender-neutral proportions. One-boy-one-girl twin proportions in 2017–2019 exceed theoretical and baseline values.

Fig. 4.

Proportions of Two-boy Twins by Wealth Rankings. The actual, estimated, and theoretical gender-neutral proportions for two-boy twins [denoted as (2,0)] are shown across wealth rankings. The red dashed lines show the 2017-2019 estimates, with shaded areas indicating the gap from theoretical gender-neutral proportions. Two-boy twin proportions in 2017–2019 fall below gender-neutral and baseline values. A minor irregularity appears in the highest wealth group’s baseline two-boy proportion but does not impact estimation or testing.

In order to ascertain the existence of gender preferences, it is critical to examine whether the desired gender proportions exceed the theoretical values in a gender-neutral situation. Since IVF twins are all dizygotic, if the two fertilized eggs implanted are chosen at random, the proportion of twins that produce one-boy-one-girl twins should not differ significantly from that of the natural occurrence. Of all newborns in Taiwan, 51.62% are males. Based on this ratio and the known probability of twinning (0.995) among all multiple births, the probability of randomly selecting two fertilized eggs resulting in one boy and one girl is $49.70\%=0.5162\times (1-0.5162)\times 0.995\times 100\%$. Likewise, the probability of randomly selecting two fertilized eggs resulting in two boys is $26.51\%=(0.5162{)}^2\times 0.995\times 100\%$ and that of two girls is 23.29%.

We then use these theoretical probabilities along with the IVF adoption rate for different wealth rankings to calculate the theoretical values in the absence of gender preferences. The empirically projected proportions of one-boy-one-girl (two-boy) twins is higher (lower) than the gender-neutral values across wealth rankings, as shown in Figs. 3 and 4. The figure for the complementary case of two-girl twins is skipped here, but it can be similarly drawn. For IVF adopters who experienced their first twin births, we hypothesize that their achieved gender compositions of {(2,0), (0,2), and (1,1)} do not deviate far from the gender-neutral case. We then implement statistical tests and find that this gender-neutral hypothesis is rejected at the 1% level, implying that IVF adopters tend to prefer one-boy-one-girl twins, and try to avoid two-boy or two-girl twins. We further analyze the increase in the proportion of one-boy-one-girl twins (the estimated proportion minus the baseline period proportion) by separating it into two parts: neutral gender and parental gender preferences (as divided by the yellow line in Figs. 3 and 4). On average, 9.56% of the increase in one-boy-one-girl twins is attributed to parental gender preferences; this figure is 10.95% for the wealthiest group.^¶

Discussion

Our empirical findings reveal that the adoption of IVF has increased among older and wealthier mothers, and this trend is magnified over time. By relating the gender composition of first-born twins to their mothers in different age-wealth-time groups, we can identify and test whether parents have specific gender preferences.

Our estimates indeed suggest that IVF has changed the gender composition of first-born twins over the past two decades. The ratio of one-boy-one-girl twins has increased from 20.42 to 41.86%, with a more pronounced increase among wealthier groups. This ratio for each wealth group also surpasses theoretical values in the absence of gender preferences. Overall, mothers in Taiwan adopting IVF for their first-born twins indeed exhibit a preference for a gender combination of one boy and one girl. It is possible that having at least one male offspring is considered significant in Asian families. Still, there is also a desire for gender balance when given the opportunity (25). However, the difference in magnitude is not significant, which is consistent with the finding that Taiwanese son preferences have become milder in recent years (5).

Our results go beyond traditional notions of son preference to reveal a clear preference for specific sex combinations, particularly one-boy-one-girl twins. This implies that if parents can choose, they may prioritize sex balance over a strict promale bias. This pattern is particularly pronounced among wealthier IVF users, implying that assisted reproductive technologies can subtly present gender preferences.

The aforementioned gender preferences were estimated using the gender ratio for the first-born twins and the proportion of IVF adoption. We understand that most first births are still singletons and that parents may exercise their gender preferences in their second births. If a mother uses IVF for her second birth, does the gender of the first birth affect the gender preferences in relation to the second birth? This question is related to the conditional gender preference that we referred to in our previous discussion. Some studies have explored this aspect using surveys of infertility patients (26–29), but such attitude surveys may still be partially affected by “social desirability bias.” Analysis of conditional gender preferences based on our data demands more complicated modeling and will be an essential avenue for future research.

Methods

Data.

We used two datasets from Taiwan’s Ministry of Finance (MOF) to link birth and parental wealth: A) the Family Member database and B) the Nationwide Personal Property database. The Family Member database provides anonymized information on birth dates, marriage status, and family relations, enabling us to identify twins and multifetal births by matching birth dates within families. Twin percentages calculated from this dataset align precisely with official Ministry of Interior (MOI) statistics, ensuring data reliability.

The Nationwide Personal Property database contains individual savings, stocks, real estate, land, and car ownership, with cars valued by brand and engine size, real estate prices assessed locally, and stocks valued annually. We used the total asset value to calculate wealth: For single mothers, individual wealth serves as parental wealth; for couples, combined wealth is used. Families were divided into ten wealth ranks per period, with roughly equal numbers in each rank. Wealth rankings, rather than monetary values, are used in the analysis to avoid inflation complexities.

Our study focuses on mothers who gave birth between 2008 and 2019.^# For each age a, wealth w, and time group t, we analyze multifetal birth gender compositions. While individual IVF usage is unobservable, the Ministry of Health and Welfare publishes age-specific IVF adoption rates ${\left(IVF\%\right)}_{\mathit{at}}$ for each year. Assuming wealth does not impact IVF adoption, ${\left(IVF\%\right)}_{\mathit{at}}$ would be uniform across wealth groups, resulting in similar multiple birth proportions. However, if wealth affects IVF adoption, then for each (a-w-t) cell, age-wealth factors ${\alpha }_{\mathit{aw}}$ can reveal statistically significant associations, indicating that wealth rank influences IVF’s impact on multiple births.

For the analysis, we grouped mothers by age (5 categories, 16 to 29 y, 30 to 32 y, 33 to 34 y, 35 to 36 y, and 37 to 50 y), wealth rank (10 groups), and time (4 periods: 2008–2010, 2011–2013, 2014–2016, and 2017–2019).^‖ In the SI Appendix, Table S1 provides birth counts, multiple births, and twin gender proportions across these periods.

Estimation Procedure.

Reliable estimation of IVF adoption, wealth, and gender preferences requires rigorous methods. We use nonlinear least squares and maximum likelihood to capture these complex relationships. While technical, these details are essential for robust inference and accurate conclusions.

The estimation procedure employed in this article can be separated into two sequential steps. First, we utilize the occurrence of multiple births to examine the impact of parental wealth on the adoption of IVFs. The rationale underlying this step is based on the observed tendency of IVFs to elevate the likelihood of multiple births (15). In the second step, we estimate the gender preference parameters of first-birth mothers who adopt IVFs. In each step, the research hypotheses of interest are statistically tested.

Step 1: Let ${\left(IVF\%\right)}_{\mathit{awt}}$ denote the proportion of delivering mothers who adopt IVF in the mother group indexed by age $a$ in year $t$ and family wealth-rank $w$ in year t−1:

$${\left(IVF\%\right)}_{\mathit{awt}}=\frac{\#[\mathrm{\text{births}}\mathrm{through}\mathrm{IVF}\mathrm{by}\mathrm{group}(awt)]}{\#[\mathrm{all}\mathrm{births}\mathrm{by}\mathrm{group}(awt)]}.$$

More precisely, this ratio represents the percentage of mothers who give birth after assisted reproductive technology (ART) procedures. Among the mothers adopting ART procedures, 99.01% used IVF during our study period (2008–2019). Between 2017 and 2019, this proportion was even higher at 99.96%. (30)

Notice that the total number of multiple births comes from natural birth and IVF. We therefore have

$$(2^{+}\%{)}_{\mathit{awt}}=\left[1-{\left(IVF\%\right)}_{\mathit{awt}}\right]C_a+{\beta }_w\left[{\left(IVF\%\right)}_{\mathit{awt}}\right],$$ [1]

where ${{(2}^{+}\%)}_{\mathit{awt}}$ denotes the time-t percentage of multiple births for the mother group indexed by age a and wealth rank w, the $C_a$’s are the constant multiple birth proportions for mothers aged-a in the baseline period (when IVF technology was not available or not prevalent), and the parameter ${\beta }_w\ge 0$ captures the marginal contribution of IVF to multiple births for wealth rank w. In the early period of economic development, the term $C_a$ may also depend on the nutrition of mothers when they are pregnant. However, the Taiwan economy had already passed that poor stage in the late 1980s. Our calculation of $C_a$ is based on the period from 1989 to 1991, and nutrition is unlikely to be a determinant here. Moreover, we choose the period of 1989–1991 as the baseline for two reasons: A) the occurrence of Black Monday in 1987, a significant global stock market crash that disrupted economic stability, potentially influencing childbirth decisions at the time; and B) although the first two cases of IVF in Taiwan were recorded in 1985 and 1987 respectively, the adoption of IVF among infertile parents was not yet widespread during the years 1989–1991. Since IVF expenses are measured by cycles, it is expected that wealthier parents will be more likely to implant multiple fertilized eggs.

Note that ${\left(IVF\%\right)}_{\mathit{awt}}$ is not directly observed from our data, but we do observe the average ${\left(IVF\%\right)}_{\mathit{at}}$. We then adopt the following assumption:

$${\left(IVF\%\right)}_{\mathit{awt}}={\left(IVF\%\right)}_{\mathit{at}}+{\alpha }_{\mathit{aw}},$$

where ${\left(IVF\%\right)}_{\mathit{at}}$ is the group-(a-t) percentage of mothers who adopted IVF (for which the data were published by the Ministry of Health and Welfare), and the parameter ${\alpha }_{\mathit{aw}}$ captures the possible influence of wealth on IVF adoption, relative to the (a-t) group average.^** Because ${\alpha }_{\mathit{aw}}$ captures the discrepancy relative to the (a-t) group mean, we should have an additional constraint ${{\mathrm{\Sigma }}_w\alpha }_{\mathit{aw}}{(N}_{\mathit{aw}}/N_a)=0 \forall a$, where $N_{\mathit{aw}}$ denotes the number of mothers in the group (a-w) over periods and ${\sum }_w{N}_{\mathit{aw}}=N_a$. To estimate ${\alpha }_{\mathit{aw}}$ and ${\beta }_w$, we consider the following linear probability regression:

$$y_{\mathit{iawt}}=\left[1-\left({\left(IVF\%\right)}_{\mathit{at}}+{\alpha }_{\mathit{aw}}\right)\right]C_a+{\beta }_w\left[{\left(IVF\%\right)}_{\mathit{at}}+{\alpha }_{\mathit{aw}}\right]+u_{\mathit{iawt}},$$

where $y_{\mathit{iawt}}=1$ if observation i in the (a-w-t) group is a multiple birth and = 0 if it is a single birth, and $u_{\mathit{iawt}}$ is the error term fulfilling the regularity assumptions. We directly apply the nonlinear least squares method to obtain the estimates for ${\widehat{\beta }}_w$ and ${\widehat{\alpha }}_{\mathit{aw}}$.^†† This in turn gives us the predicted percentage value of IVF% for the (a-w-t) group, denoted by ${\left(\widehat{IVF\%}\right)}_{awt}$:

$${\left(\widehat{IVF\%}\right)}_{\mathit{awt}}=\left[{\left(IVF\%\right)}_{\mathit{at}}+{\widehat{\alpha }}_{\mathit{aw}}\right].$$ [2]

Fig. 5 plots the estimated values of ${\widehat{\beta }}_w$ and ${\widehat{\alpha }}_{\mathit{aw}}$ along with their 95% confidence intervals. It can be seen that ${\widehat{\beta }}_w$ and ${\widehat{\alpha }}_{\mathit{aw}}$ tend to increase with the wealth ranking w, and the ${\widehat{\beta }}_w^{\text{'}}\text{s}$ are all significantly different from zero. For the age groups 33 and above, the ${\widehat{\alpha }}_{\mathit{aw}}$’s are significantly different from zero for the highest wealth group. The estimates for ${\widehat{\alpha }}_{\mathit{aw}}$ show greater dispersion as the age increases as well, indicating that older mothers are more flexible in adopting IVF. The standard error of ${\alpha }_{\mathit{aw}}$ depends on the sample size and twin rate in group (a-w). Among the youngest mothers (a = 16 to 29, w = 10), the confidence interval of ${\alpha }_{\mathit{aw}}$ for the wealthiest group is larger than that of other wealth groups, primarily because this group has a smaller sample size compared to other groups but a relatively high rate of twins. The small sample size of the young wealthiest mothers does constitute a unique demographic group. We also reject the null hypothesis that the ${\beta }_w$ are the same across w (F = 93.27, P = 0.000). Finally, we substitute the value of ${\widehat{\alpha }}_{\mathit{aw}}$ for each (a-w-t) group into Eq. 2 to obtain the values of ${\left(\widehat{IVF\%}\right)}_{\mathit{awt}}$, which are the numbers shown in Fig. 2.

Fig. 5.

Estimates of ${\alpha }_{\mathit{aw}}$ and ${\beta }_w$ with Confidence Intervals. The nonlinear least squares estimates of ${\alpha }_{\mathit{aw}}$ (Left panel) and ${\beta }_w$ (Right panel) are shown with their 95% confidence intervals. The Left panel is divided into 5 age groups, and each age group is arranged in ascending order from Bottom to Top according to the wealth ranking w. Similarly, the Right panel is arranged in ascending order from Bottom to Top according to w. (N = 1,598,003).

Step 2: Our second-stage regression is performed to investigate whether there exist gender preferences for first-birth twins. Note that ${\left(\widehat{IVF\%}\right)}_{\mathit{awt}}$ is the estimated IVF proportion of all births (first and subsequent births). To implement the estimation for the case of first-birth twins, we should adjust ${\left(\widehat{IVF\%}\right)}_{\mathit{awt}}$ to the IVF proportion for the first birth, denoted by ${\left(\widehat{IVF\%}\right)}_{\mathit{awt}}^I$ , with a superscript $I$ indicating the first birth. The adjustment formula is

$${\left(\widehat{IVF\%}\right)}_{\mathit{awt}}^I\left(r_t\right)={\left(\widehat{IVF\%}\right)}_{\mathit{awt}}·\frac{\#[\mathrm{all}\mathrm{births}\mathrm{by}\mathrm{group}(awt)]}{\#[\mathrm{all}\mathrm{multibirths}\mathrm{by}\mathrm{group}(awt),\mathrm{I}]}·{\widehat{\beta }}_w{r}_t,$$ [3]

where $r_t$ is the proportion of all IVF births that are from the first births in period t, which is a parameter to be estimated. Note that both $\#[\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{b}\mathrm{i}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{s}\mathrm{b}\mathrm{y}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}(awt)]$ and $\#[\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{b}\mathrm{i}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{s}\mathrm{b}\mathrm{y}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}(awt),\mathrm{I}]$ are numbers and can be calculated from our data.

Let $j\in \{\left(2,0\right),\left(0,2\right),\left(1,1\right),\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{s}\}\equiv \mathrm{\Omega }$ be the gender composition of multiple births, where the first three terms denote two-boys, two-girls, and one-boy-and-one-girl, respectively, and the last term denotes higher-order multifetal births. In the case of natural births, the probability of event $j$ (among all multiple births) occurring is a constant and is denoted by $\overline{{\delta }^j}$. In the case of IVF births, the probability of event $j$ occurring is denoted by ${\theta }^j$. These ${\theta }^j$’s are parameters to be estimated and are possibly related to parental gender preferences.

According to our data from the MOF, the gender ratio for first-birth newborns in Taiwan from 2008 to 2019 was 51.62% male to 48.38% female. Here, we assume that IVF does not significantly affect the gender ratio at birth. Through records of IVF and ICSI cycles, the United Kingdom exhibits a gender ratio of approximately 104.0 male newborns for every 100 female newborns. This ratio is similar to the gender ratio observed in England and Wales from 1991 to 2016, as obtained from the national statistics database (31). Based on this ratio and the fact that the probability of having twins is 0.995 among multiple births, if IVF adopters do not have any gender preferences, then $\left({\theta }^{\left(2,0\right)},{\theta }^{\left(0,2\right)},{\theta }^{\left(1,1\right)}\right)$ should not deviate much from (0.2651, 0.2329, 0.4970).

Given ${\left(\widehat{IVF\%}\right)}_{\mathit{awt}}^I\left(r_t\right)$, the overall probability of event $j$ for the $\left(a,w,t\right)$ group can be expressed as a combination of two sources, the first being natural births and the second being IVF:

$${\delta }_{\mathit{awt}}^j=\overline{{\delta }^j}·\left[1-{\left(\widehat{IVF\%}\right)}_{\mathit{awt}}^I\left(r_t\right)\right]+{\theta }^j·{\left(\widehat{IVF\%}\right)}_{\mathit{awt}}^I\left(r_t\right),j\in \mathrm{\Omega }.$$ [4]

Moreover, ${\delta }_{\mathit{awt}}^{\mathit{others}}\equiv 1-{\delta }_{\mathit{awt}}^{\left(2,0\right)}-{\delta }_{\mathit{awt}}^{\left(0,2\right)}-{\delta }_{\mathit{awt}}^{\left(1,1\right)}$ > 0 and ${{\theta }^{\mathit{others}}=1-\theta }^{\left(2,0\right)}-{\theta }^{\left(0,2\right)}$ $-{\theta }^{\left(1,1\right)}>\; >0$, because events in $\mathrm{\Omega }$ are mutually exclusive. Since we have already obtained consistent estimators $\left({\widehat{\alpha }}_{aw},{\widehat{\beta }}_w\right)$ and ${\left(\widehat{IVF\%}\right)}_{\mathit{awt}}$ in the first step, together with Eqs. 3 and 4, the log-likelihood function can be written as

$$L\left(r_t,{\theta }^j\right)\equiv \sum _{a,w,t,j}N\left(a,w,t,j\right)·\text{ln}({\delta }_{\mathit{awt}}^j)$$ [5]

where $N\left(a,w,t,j\right)$ is the number of event j, given that the observations are from the group $\left(a,w,t\right)$. We apply the maximum likelihood method to estimate $\left(r_t,{\theta }^j\right).$ Intuitively, the ${\theta }^j$’s (the gender composition of twins through IVF) together with the $\overline{{\delta }^j}$’s (the gender composition of twins through natural birth) determine the values of the ${\delta }_{\mathit{awt}}^j$’s (the gender composition of twins of all births) in Eq. 4, which in turn determine the likelihood value in Eq. 5. We try to find the ${\theta }^j$’s that maximize this likelihood value.

Table 1 shows the estimated values of the parameters. We then jointly test whether $\left({\theta }^{\left(2,0\right)},{\theta }^{\left(0,2\right)},{\theta }^{\left(1,1\right)}\right)=(0.2651, 0.2329, 0.4970)$. The likelihood ratio test is 16.18 > ${\chi }_{\left(3,0.99\right)}^2=11.35,$ which indicates that the hypothesis that IVF adopters do not have gender preferences can be rejected. Gender preferences may potentially occur in IVF with a single birth and can bias the calculation of the 51.62% male newborn rate. For our robustness check, we conducted sensitivity analyses to address this by changing the assumed threshold value of the natural male birth ratio and recalculating the test statistics. It turns out that our statistical test fails only when the male birth rate drops to 48.1%. However, this contradicts the natural fertility pattern, where male births consistently outnumber those of females.^‡‡ We also conducted tests for different gender combination parameters. The chi-squared statistics corresponding to (2,0), (0,2), and (1,1) are 51.44, 59.66, and 28.28, respectively, all significant at the 1% level (${\chi }_{\left(1,0.99\right)}^2=6.635$). These findings suggest that, compared to the probability of gender-neutral outcomes, IVF adopters tend to express a preference for one-boy-and-one-girl twins while trying to avoid same-gender twins. We then test the null that ${\gamma }_1={\gamma }_2={\gamma }_3={\gamma }_4$. The likelihood ratio test is 76.80 > ${\chi }_{\left(3,0.99\right)}^2=11.35$, which implies that the proportions of all IVF births that are from the first births are not the same in different periods. The decreasing trend of the $\gamma$’s indicates that, as time goes by, second-birth mothers are also more willing to adopt IVF.

Table 1.

Maximum likelihood estimated parameters

${\theta }^j$	coeff.	SE	${\theta }^j$ under gender-neutral	${\gamma }_t$	coeff.	SE
${\theta }^{\left(2,0\right)}$	0.2436***	(0.0121)	0.2651	${\gamma }_1$	0.9418***	(0.0514)
${\theta }^{\left(0,2\right)}$	0.2180***	(0.0121)	0.2329	${\gamma }_2$	0.9111***	(0.0497)
${\theta }^{\left(1,1\right)}$	0.5332***	(0.0112)	0.4970	${\gamma }_3$	0.6967***	(0.0380)
${\theta }^{\mathit{other}}$	0.0052		0.0050	${\gamma }_4$	0.6965***	(0.0394)

Note: In the case of IVF births, the probability of event $j$ occurring is denoted by ${\theta }^j$, $j\in \{\left(2,0\right),\left(0,2\right),\left(1,1\right),others\}$. By definition, ${\theta }^{\mathit{other}}=1-{\theta }^{\left(2,0\right)}-{\theta }^{\left(0,2\right)}-{\theta }^{\left(1,1\right)}$. $r_t$ denotes the proportion of all IVF births from the first births during period t. The periods are denoted by t=1,2,3,4 and correspond to 2008–2010, 2011–2013, 2014–2016, and 2017–2019. The number of observations is 905,630. Standard errors are calculated based on the assumption of homoskedasticity. *, **, and *** represent 10%, 5%, and 1% significance levels, respectively.

Based on Eq. 4, we can further calculate the predicted and theoretical values of ${\delta }_{\mathit{awt}}^j$ when we replace ${\theta }^j$ with the estimated values and theoretical values, as shown in Figs. 3 and 4. To obtain the estimated proportion of type j multiple births for the (a-w-t) group, ${\widehat{\delta }}_{\mathit{awt}}^j$, we replace $({\theta }^j,r_t)$ with $({\widehat{\theta }}^j,{\widehat{r}}_t)$ in Eq. 4. For given (w-t), we calculate ${\widehat{\delta }}_{\mathit{wt}}^j$, the average of ${\widehat{\delta }}_{\mathit{awt}}^j$ across age groups, weighted by the number of multiple births in each age group. Then, we fit the line of ${\widehat{\delta }}_{\mathit{wt}}^j$’s, w=1, ...,10, to generate the red dashed lines in Figs. 3 and 4. Similarly, we compute the gender-neutral proportions by replacing $({\theta }^j,r_t)$ with $({\theta }^{j0},{\widehat{r}}_t)$ in Eq. 4, where ${\theta }^{j0}$ denotes the theoretical gender-neutral value ${\widehat{\delta }}_{\mathit{awt}}^{j0}$ for type j and calculate the weighted average ${\widehat{\delta }}_{\mathit{wt}}^{j0}$.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Anonymized dta, xls, csv data have been deposited in github (https://github.com/Chingyuan123/Parental-mixed-gender-preferences-revealed-by-IVF-twin-births.git) (32). Some study data available (Our empirical analyses are based on publicly accessible income/property tax datasets from the Ministry of Finance (MOF), Taiwan. These datasets and labs are indeed open to the public, as long as the operation complies with the administrative rules of the Fiscal Information Agency of MOF. The summarized data for estimation and estimated parameter values for graphs and tables are available on GitHub. The codes for compiling raw data, estimation, and inference with explanations used in this article are also available on GitHub at the above link.).