A comprehensive analysis of 40 blind protein structure predictions

Abstract

Background

We thoroughly analyse the results of 40 blind predictions for which an experimental answer was made available at the fourth meeting on the critical assessment of protein structure methods (CASP4). Using our comparative modelling and fold recognition methodologies, we made 29 predictions for targets that had sequence identities ranging from 50% to 10% to the nearest related protein with known structure. Using our ab initio methodologies, we made eleven predictions for targets that had no detectable sequence relationships.

Results

For 23 of these proteins, we produced models ranging from 1.0 to 6.0 Å root mean square deviation (RMSD) for the C_α atoms between the model and the corresponding experimental structure for all or large parts of the protein, with model accuracies scaling fairly linearly with respect to sequence identity (i.e., the higher the sequence identity, the better the prediction). We produced nine models with accuracies ranging from 4.0 to 6.0 Å C_α RMSD for 60–100 residue proteins (or large fragments of a protein), with a prediction accuracy of 4.0 Å C_α RMSD for residues 1–80 for T110/rbfa.

Conclusions

The areas of protein structure prediction that work well, and areas that need improvement, are discernable by examining how our methods have performed over the past four CASP experiments. These results have implications for modelling the structure of all tractable proteins encoded by the genome of an organism.

Background

The state of blind protein structure prediction

The community-wide experiment on methods to test protein structure prediction (CASP) was first initiated in 1994, as a means of evaluating structure prediction methods in a blind and rigourous manner [1]. This was motivated in part by claims in the literature of the protein folding problem being "solved" without producing tangible benefits, since most of the "solutions" included a strong dependence on the test set. These experiments evaluate prediction techniques by asking modellers to construct models for a number of protein sequences before the experimental result is known, over a period of 3–4 months. We have taken part in all four CASP experiments, including the most recent one (CASP4) that finished in December 2000 http://predictioncenter.llnl.gov. The CASP4 results provide a benchmark as to what level of model accuracy we can currently expect from our approaches.

There are three primary categories of methods for predicting protein structure from sequence: comparative modelling, fold recognition, and ab initio prediction. In the comparative modelling and fold recognition categories, the methodologies rely on the presence of one or more evolutionarily related template protein structures that are used to construct a model; the evolutionary relationship can be deduced from sequence similarity [2-5] or by "threading" a sequence against a library of structures and selecting the best match [6-8]. For both of these approaches, a sequence alignment between the target protein to be modelled and the evolutionarily related protein with known structure is used to create the initial or seed model. In the ab initio category, there is no strong dependence on database information and prediction methods are based on general principles that govern protein structure and energetics [9-13]. The categories vary in difficulty, and consequently methods in each of these categories produce models with different levels of accuracy relative to the experimental structures.

Since the inception of CASP, predictors all over the world have built models for 128 proteins using the methodologies described above. Before the first CASP experiment, published results in comparative modelling in the literature usually were obtained by applying structure prediction methods in the context of the exact experimental structure; for example, re-building side chains on the native main chain, or re-building regions of main chain keeping the rest of the experimental structure fixed. (This practice continues to this day.) Ab initio methodologies, parameterised extensively on small test sets, failed when given novel types of sequences.

CASP1 was an eye-opener in terms of understanding the difficulty of making accurate predictions on approximate templates in comparative modelling [14]. The main problems in creating a good comparative or fold recognition model were related to alignment between the template and target sequences, and building of non-conserved variable regions (side chains, and main chain loops). In the ab initio category, it appeared that methods could not sample conformational space accurately, and select native-like conformations, for all but very small fragments. The highlight of CASP1 was the recognition of threading as viable method for predicting folds [15], and the success of neural-network based secondary structure prediction methods [16].

The second CASP showed some improvement in two areas: In comparative modelling, loops were being built better, and the use of hand-inspected alignments greatly increased model accuracy [17]. In the fold recognition category, alignments as well as prediction of folds improved [18]. The results in the ab initio category remained virtually unchanged except for one model of the alpha-helical protein NK-Lysin predicted to within 6.0 Å C_α RMSD, capturing the correct topology [19].

The third CASP saw consistent but little progress relative to CASP2 in both comparative modelling and fold recognition categories [20,21], but the most dramatic results were observed in the ab initio category. Here multiple groups predicted large parts of a few protein sequences at a crude topological level (within 6.0 Å C_α RMSD for ≈ 60 residues) [22].

Performance of our methods at CASP1-3: Comparative modelling

Table 1 shows a general estimate of how well our comparative modelling prediction methods have performed at different CASP experiments [23,24].

Table 1.

Qualitative assessment of our comparative modelling methods at CASP experiments.

Category	CASP1	CASP2	CASP3	CASP4
Alignment quality	poor	fair	fair	fair
Side chains	~50%	~75%	~75%	~75%
Short loops (≤ 6 aa)	~3.0 Å	~1.0 Å	~1.0 Å	~1.0 Å
Longer loops (> 6 aa)	> 5.0 Å	~3.0 Å	~2.5 Å	~2.0 Å

The results given are for predictions for which there was little or no alignment error (since we relied on publicly available webservers for alignments). For evaluating side chain predictions, the percentage of χ₁ torsion angles predicted within 30° on average is given. For evaluating variable main chain (loop) predictions, the average of the C_α root mean square deviation (RMSDs) (calculated using a global superposition of the target and the model) is shown. The major improvement in our methods from CASP1 to CASP2 is from the use of manually-curated alignments and the development of a graph-theory approach to handle the interconnectedness problem in protein structures [35].

Even though our methods produced mediocre results at CASP1, we realised that a major problem with accurate comparative modelling had to do with the interconnected nature of protein structures [23]: If a certain region of the protein varied with respect to the homologue, then it was likely that a structurally interacting region would also vary, even if that region was conserved in sequence. We therefore developed a graph-theory based approach to address this problem which demonstrated significant progress in loop building at CASP2 (Table 1) [24]. The CASP3 and CASP4 results are minor improvements over the CASP2 results since the enhancements made to the graph theory method have been minimal.

Performance of methods at CASP1-3: Ab initio prediction

In the ab initio category, as with comparative modelling, the first CASP experiments did not live up to the results previously published in the literature [16,19]. It was not until CASP3 (the first time where we took part in this category) that the first consistent positive results were seen: several groups were able to predict the correct topologies for small proteins, or large fragments of a protein (~60–80 residues to about 6.0 Å C_α RMSD relative to the experimental conformation) [22,25].

CASP4

The fourth CASP was held in December 2000. CASP4 demonstrated further improvement in our methodologies in both comparative modelling and ab initio prediction [26]. Our approaches combine a Monte Carlo procedure, simulated annealing, genetic algorithms, graph theory, and semi-exhaustive searches with move sets consisting of fragments and discrete state models, and scoring functions consisting of all atom-based pairwise functions, hydrophobicity indices, secondary structure preferences, and hydrogen bonding. The goal was to develop components that form a structure prediction engine, combining and innovating upon previously developed approaches by observing what methods work well at the previous CASP experiments, and adding new components of our own.

We focus here on the results of our prediction methodologies on all of the 40 sequences, for which an experimental answer was later available. Unlike the assessors' evaluations at CASP (which has recently appeared in the special issue (S5) of Proteins: Structure, Function, and Genetics), which focus on how well a particular group performs, we treat CASP as a test-bed for how well an individual method performs. Using the lessons learnt from CASP successes and failures, we suggest a unified approach that mixes and matches between the best predictions to produce the best results. The aim of this work is to illustrate when our prediction methods work, when they fail, and what this means in the context of building models for all proteins encoded by the genome of an organism at the present time.

Results and Discussion

We present a comprehensive analysis of all 40 blind predictions, for which an experimental answer was later available, that were made for CASP4 using a barrage of different but related techniques. We discuss what went right, what went wrong, what further improvements can be made to the methodologies, and the implications of these results for modelling the structure of all tractable proteins encoded by the genome of an organism.

What went right; what went wrong

The CASP4 results show that within each of the general structure prediction categories, some methods, including ours, are able to produce models with a fair amount of accuracy (quantified in the sections below). Further improvements are necessary to overcome the limits of current approaches.

Comparative modelling and fold recognition

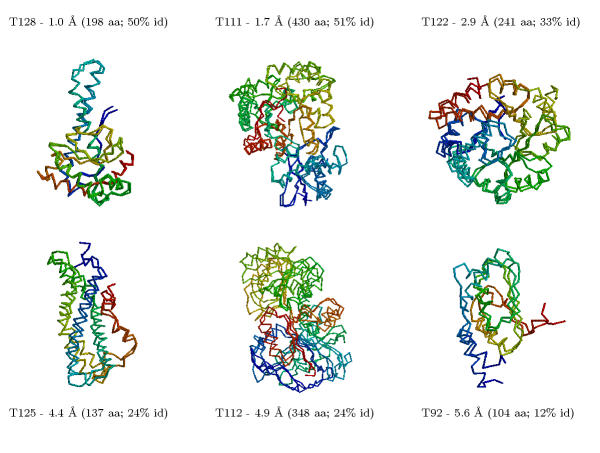
Table 2 compares all the predictions we made for CASP4 using comparative modelling and fold recognition methods. The results are qualitatively assessed as being one of "excellent", "good", "useful", and "failure". In the comparative modelling category, we made 29 predictions for targets that had sequence identities ranging from 50% to 10% to the nearest related protein with known structure. For 23 of these proteins, we produced models ranging from 1.0 to 6.0 Å root mean square deviation (RMSD) for the C_α atoms between the model and the corresponding experimental structure for all or large parts of the protein, with model accuracies scaling fairly linearly with respect to sequence identity (i.e., the higher the sequence identity, the better the prediction). These 23 proteins ranged in accuracy from "excellent" to "useful". Figure 1 shows some examples of the comparative modelling predictions with different difficulties made at CASP4.

Table 2.

Results of our comparative modelling and fold recognition predictions made at CASP4.

Rating	Difficulty	Target	Fraction of Residues1	% of Residues1	RMSD1 (Å)	Number of Residues2	RMSD2 (Å)	Models considered	% sequence identity
E	1	T0128/sodm	202/211	96	1.4	198	1.0	1–5/5	50
E	1	T0122/trpa	235/241	98	2.1	241	2.9	1–5/5	33
E	1	T0123/lacp	145/160	91	3.0	160	4.0	1–5/5	60
E	1	T0099/xxxx	49/56	88	3.0	56	4.7	1–4/4	53
E	1	T0111/eno	425/430	99	1.3	430	1.7	1–5/5	51
E	2	T0125/sp18	125/137	91	3.7	137	4.4	1–4/5	24
E	2	T0113/hcd2	231/251	92	2.0	251	4.4	1–5/5	33
E	3	T0121/malk	228/372	61	3.0	245	3.9	1–5/5	27
G	3	T0112/dhso	290/348	83	3.1	348	4.9	1–5/5	24
G	3	T0103/picp	162/368	44	3.6	156	6.0	1–3/5	26
G	3	T0092/yeco	108/227	48	3.5	104	5.6	1–5/5	12
U	3	T0117/dnk	124/250	63	3.9			1–5/5	21
U	4	T0109/orn	82/182	45	4.3	67	6.3	4–5/5	16
U	4	T0100/pmea	98/342	29	4.0	65	6.0	1/5	10
F	4	T0095/ctn1	33/244	14	4.5			1–5/5	20
U	4	T0127/bchi	95/332	29	3.6	60	5.8	1,3/5	23
U	4	T0101/pell	72/400	18	3.3	74	6.0	1–5/5	22
U	5	T0090/yqie	96/209	48	3.6	107	6.0	1–5/5	19
G	5	T0089/ftsa	124/378	33	3.6	81	5.9	1–5/5	20
F	5	T0108/cbd17	26/179	15	3.4	25	6.1	1–5/5	22
F	5	T0107/cbd9	27/188	14	4.8	28	6.0	1–5/5	19
F	5	T0115/khse	46/296	16	4.5	40	6.0	4–5/5	20
G	6	T0096/fadr	70/222	30	3.6	83	6.0	1–3/5	21
U	6	T0104/yjee	55/158	55	4.0			1–5/5	21
U	6	T0087/ppx1	50/309	16	4.3	54	6.0	1–5/5	17
F	6	T0094/cpdas	35/177	20	3.4	29	6.0	1–5/5	20
U	6	T0120/xrcc4	82/203	40	3.0	96	5.2	5/5	12
F	6	T0116/muts	46/811	6	4.2	50	6.3	1–5/5	11
U	8	T0124/plcb	54/120	22	3.1	60	3.6	2/5	19

The targets (column 3) are sorted by their difficulty (column 2) as provided by the CASP4 assessors (determined by the degree of similarity of the target protein to proteins with known structures). Shown also is a subjective evaluation of the quality of the model (column 1; E – excellent, G – good, U – useful, F – failure), the number of residues (over the total) evaluated using the criterion¹ provided by the CASP4 assessors which considers non-consecutive C_α atoms in the calculation of the RMSD, the percentage of residues evaluated by criterion¹, and the corresponding RMSD¹; the number of residues evaluated using our criterion² which considers only consecutive regions and the corresponding C_α RMSD² (some values are missing using this criteria since the experimental result was not provided to the predictors); the models (out of a total of five) for which the evaluation/result applies; and the percent sequence identity for the alignment between the target and the closest template structure used to construct the model. The data indicate that the modelling performs best on targets with alignments that have > 25% sequence identity to the closest template structure, resulting in 23/29 useful, good, or excellent predictions.

Figure 1.

Six examples of our comparative modelling predictions at CASP4 for targets with different difficulties. The superposition of the model and the experimental structures is shown, along with the C_α RMSD relative to the experimental structure and the percentage identity of the alignment between the target and template sequences. We made useful predictions for 23 out of 29 targets: sequences with high percentage identity to the template structures (≥ 50%) were modelled well (1–2 Å C_α RMSD) with model accuracy decreasing (4–6 Å C_α RMSD) fairly linearly as the relationship becomes more tenuous (10–25% sequence identity). Models considered are listed in Table 2.

The comparative modelling and fold recognition targets are in Table 2 are sorted by the difficulty index. The percentage identities for alignments between several comparative modelling targets and their corresponding templates fall in the twilight zone or below (alignments with percentage identities <= 30%). In fact, such targets belong more in the category of fold recognition since it is clear that even a 20% identity alignment can easily result in a wrong fold assignment. (The percentage identity is used for illustration purposes only–BLAST e-values follow a similar trend but are most robust.)

Our comparative modelling methods produce excellent models when the percentage identity between the target and corresponding template sequence is high (usually within 2.0 Å C_α RMSD for > 30% identity). In several cases where the alignment falls into the twilight zone (20–30% sequence identity), models around 4.0 Å C_α RMSD are produced (T0122/trpa, T0112/dhso, T0125/spl8, T0121/malk).

In one case, T0092/yeco, the percentage identity between the target and template proteins in the alignment we used was 12%, but we predict 107 residues to within 6.0 Å C_α RMSD. However, not all cases where we assumed a homology relationship provided similar results, and the failures are indicated as "F" in Table 2.

While the graph-theory methods have been fairly successful at handling the interconnectedness problem to build non-conserved side chains and main chains [24], other major problems preventing the construction of accurate comparative models have to do with inaccurate alignments and using the template structure as a static model upon which to build variable main chains. In the former case, if a region of the alignment is incorrect but is assumed to be correct, then no amount of further model building will fix this error. In the latter case, the loop and side chain construction methods, even if interconnectedness is taken into account, are limited by the approximate nature of the template framework. In other words, alignment errors are irrecoverable. Even though 50–70% of the regions (of up to 15 residues) we thought would vary with respect to the parent homologue structure were predicted to within 3.0 Å C_α RMSD, this is mostly in cases where the approximate template is well-predicted (within 2.0 Å C_α RMSD).

Ab initio prediction

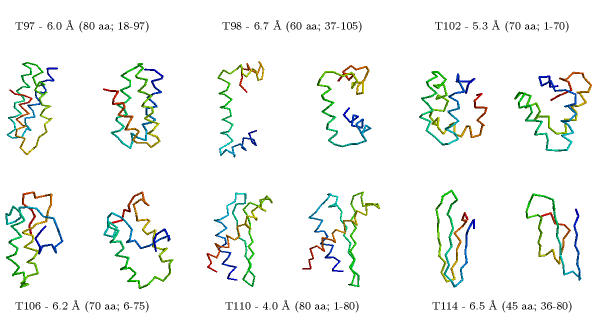
Table 2 compares all the predictions we made for CASP4 using our ab initio methods. We made eleven predictions for targets that had no detectable sequence relationships when we began the modelling process. We produced nine models with accuracies ranging from 4.0 to 6.0 Å C_α RMSD for 60–100 residue proteins (or large fragments of a protein). Figure 2 illustrates some of our more successful predictions.

Figure 2.

Examples of our ab initio predictions. Five of the examples were predictions submitted for CASP4; the sixth (T102/as48) is a "postdiction" using the actual secondary structure assignment that was available to all CASP4 predictors (our CASP4 submission for this target used predicted secondary structure that was only 60% accurate). The experimental structure is on the left and the model is on the right. We were able to make topologically accurate predictions (≈ 6.0 Å C_α RMSD) for 9 out of 11 targets modelled. Targets with largely helical content are modelled well, with predictions as accurate as 4.0 Å C_α RMSD for 80 residues between the model and the experimental result. Models considered are given in Table 3.

Table 3.

Results of our ab initio predictions made at CASP4.

Rating	Difficulty	Target	Fraction of Residues1	% of Residues1	RMSD1 (Å)	Number of Residues2	RMSD2 (Å)	RMSD2 range (Å)	Models considered
E	4	T0110/rbfa	77/95	85	3.9	80	4.0	4.0–16.5	3
G	5	T0126/omp	44/163	27	4.3	60	6.9	5.5–13.0	1,3
G	5	T0105/sp100	39/94	41	4.3	55	6.4	5.8–12.5	4,5
G	5	T0114/afp1	34/87	39	3.9	45	6.5	5.6–12.1	1
F	5	T0102/as48	33/70	47	4.3	70	8.9	7.3–12.5	1–5
-	5	T0102/as48	70/70	99	5.6	70	5.6	3.7–12.0	2
F	5	T0118/enrn	28/149	22	4.5	40	6.7	4.2–10.5	2–5
E	6	T0097/er29	58/105	55	3.7	80	6.2	3.6–13.0	4
E	7	T0091/ybab	50/109	56	3.0				1–5
E	7	T0106/sfrp3	49/125	39	4.0	70	6.2	5.2–13.6	3,5
G	8	T0098/sp0a	47/119	40	3.5	60	6.0	3.6–11.7	2
G	8	T0086/ubic	44/164	27	4.3	50	6.7	5.3–10.8	1–5

The targets (column 3) are sorted by their difficulty (column 2) as provided by the CASP4 assessors (determined by the degree of similarity of the target protein to proteins with known structures). Shown also is a subjective evaluation of the quality of the model (column 1; E – excellent, G – good, U – useful, F – failure), the number of residues (over the total) evaluated using the criterion¹ provided by the CASP4 assessors which considers non-consecutive C_α atoms in the calculation of the RMSD, the percentage of residues evaluated by criterion¹, and the corresponding RMSD¹; the number of residues evaluated using our criterion² which considers only consecutive regions, the corresponding RMSD², and the RMSD² ranges for the regions of the same length in all the sampled conformations (some values are missing using this criteria since the experimental result was not provided to the predictors); and the models (out of a total of five) for which the evaluation/result applies. The second row/result given for T102/as48 is actually a "post-diction" made using the NMR secondary structure assignments available to all CASP4 predictors (we used predicted secondary structure with a three-state accuracy of 60% in the original prediction, resulting in a signi cantly worse model). Nine out of eleven predictions are good or excellent.

At CASP4, we were consistently able to predict 60–80 residue consecutive fragments to within 6.0 Å, and, at times, to within 4.0 Å C_α RMSD. These results are much more consistent than at CASP3, and are also of better quality.

While these predictions are a significant improvement compared to the previous CASP results, we still have to make much progress before we can produce models rivalling that of experiment in accuracy. Given the range of RMSDs for the population of conformations sampled (i.e., "decoys") for each of the proteins (average range for the eleven predictions was 9.3 – 17.6 Å C_α RMSD for the entire protein; and 5.0 – 12.6 Å C_α RMSD when only the best fragments are considered), it is clear that devising representations that will allow us to explore protein conformational space such that near-native conformations are encountered is a major bottleneck. Our filter-based scoring function approach generally picks conformations from the lower end of the RMSD distribution (usually within the top 1%, and no worse than the 10%, of the conformations sampled), but further improvements can be made.

Caveats regarding the use of results from CASP experiments

Averaging over different methods and contexts

The results provided by the CASP organisers and assessors show how well a particular group did, but do not measure performance of individual methods in separate contexts. This makes it harder to determine which methods work well and places an inherent penalty on trying different non-conservative approaches. For example, even successful loop and side chain building methods will fail on comparative models based on incorrect alignments (in our case, we tried six different approaches in the three categories combined, the results for only two of which are listed in Figures 1 and 2). This problem has been alleviated to some degree by the CAFASP experiment [47], which provides a strict method-by-method automatic evaluation, but it requires that models be prepared by the means of an automated server in a relatively short time-frame. Ranking results by methods used (based on keywords provided when the model is submitted, which could be standardised), and considering subsets of the target relevant to particular methods, would help significantly in identifying the methods that work best.

Subjective quality of evaluations

Once a certain evaluation measure is chosen, then evaluating all models submitted by that measure is objective. However, particular methods appear to perform better depending on the choice of evaluation criteria used (for example, C_α RMSD over a contiguous set of residues, which we prefer, vs. C_α RMSD over non-contiguous residues). This illustrates the need for more than one measure, but even with that taken into account, there exists an inherent subjectivity in measurement, especially given the assessor's visual evaluation of the models during the CASP experiment (one of the authors of the paper, M.L., was an assessor at CASP2). The reason there is a problem is because the results are not entirely clear (i.e., the problem has not been solved). Until predictions with accuracies rivalling that of experiment are made, assessment of predictions must be done automatically using limited and stringent criteria, most relevant to biologists interested in function. Such a criteria could include, for example, how well the model picks out structurally similar proteins from the database of known structures, relative to the experimental result.

What can be done

Promising future areas

While the CASP experiments provide for an environment where rapid testing of ideas is possible in a rigourous manner, a lot of the development is ad hoc, guided by intuition, and not all parameter choices are explored thoroughly.

The CASP experiments also show that there is not one single algorithm that can "solve" the protein structure prediction problem. The most successful methods are those that combine and build upon the techniques developed by several researchers in the last thirty years (special issues of Proteins: Structure, Function, Genetics, 1995, 1997, 1999, and 2002). Generally the methods have incorporated different sampling techniques and a variety of scoring functions each of which aids prediction of structure only to a limited degree when used individually, but are producing models useful for further biological study when combined together in a coherent manner.

To provide a guidance for future work, we analysed some of the more promising paths that we discovered to assess their viability in improving our methods and making better predictions, focusing on four major areas: alignment, refinement, sampling, and selection. An analysis of the results generated by our methods at the next CASP (evaluated in December 2002) will provide a measure of the effectiveness of these improvements.

Comparative modelling and fold recognition: Alignment and template selection using all-atom scoring functions

A major reason for alignment methods failing at CASP has to do with using sequence information only and not incorporating structural information. For example, while modelling T24/ubc9, sequence alignments generated by several methods have an alignment error relative to the structural alignment [24]. The sequence identity/similarity scores would have been lower with the new alignment since the number of identical residues decreases by six in a region of fourteen residues. This phenomenon has been observed time and again at CASP, illustrated in Figure 3 by three examples, including T24/ucb9. We were later able to readily distinguish between the correct and incorrect alignments when an all-atom scoring function was applied to the models constructed using both alignments, and justify the changes by detailed environment analysis. The score for the models based on the correct alignments were better by ~10% on average relative to the model with the original alignment. This would indicate that a sequence alignment algorithm that incorporates structural information in a rigourous manner is useful and necessary to handle the alignment problem.

Figure 3.

Comparison of sequence-based and structure-based alignments for T24/ubc9, T9/csc, and T28/egi. For each target, the percentage identity to the template is given based on an alignment after structure comparison, and the sequence alignment we used at CASP. Identities are indicated by "*". For all cases, the structure-based alignment, generated using the ALIGN [66] or CE programs [67], results in a lower similarity/percentage identity score between the target and template proteins. An all-atom conditional probability discriminatory function is able to readily distinguish a model constructed using the accurate structure-based alignment from one that is constructed using the sequence-based alignment.

Historically, in comparative modelling, the template with the highest sequence identity or similarity to the target sequence being modelled has been used for further analysis. However, a comparison of members of a family with known structures shows that sequence only measures do not correlate absolutely with the structural similarity [48] even in cases where the evolutionary relationships are obvious.

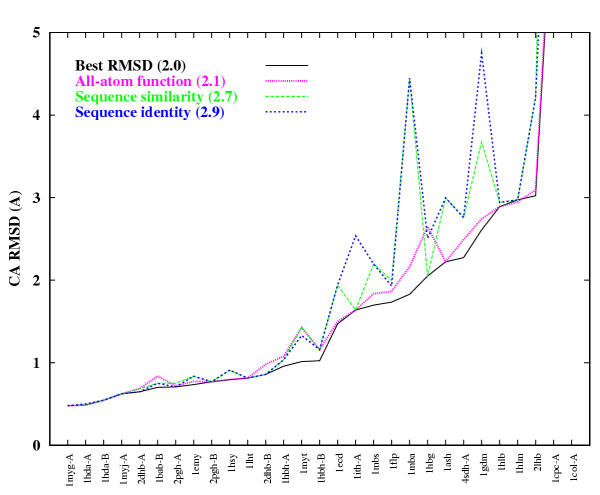
We thus devised an experiment where we constructed models for protein families with large numbers of known structures (specifically the globin and the immunoglobulin families). We then conducted an all-against-all homology modelling exercise where every member of the family was modelled on every other template (resulting in 29 and 60 models for each member of the globin and immunoglobulin families respectively). We compared the performance of the all-atom scoring function to two sequence only metrics. The results for the globin family are given in Figure 4. On average, using the all-atom function improves model quality by 0.8 Å C_α RMSD compared to only using sequence identity. The theoretical best improvement that could have been achieved on average is 0.9 Å C_α RMSD. Similar improvements are observed for the immunoglobulin family.

Figure 4.

Performance of different metrics for selecting the best model for the globin protein family. The C_α RMSD selected by a particular metric is shown by a line connecting each member of the family. The different metrics are sequence identity, sequence similarity based on several different scoring matrices (the best results are shown, based on using the BLOSUM62 matrix), and the all-atom scoring function. The best model that could have been selected is shown by a solid line. On average, using the all-atom function improves model quality by 0.8 Å C_α RMSD compared to only using sequence identity to select the template structure. The best improvement that could have been achieved on average is 0.9 Å C_α RMSD.

Taken together with previously published results [32,49], these results strongly indicate that the all-atom scoring function is a powerful method to handle the alignment problem, the template selection problem, the construction of side chains and main chains, and potentially helpful in refining models when continuous forms of the function are used.

Ab initio prediction: Sampling conformational space

At CASP4, we mixed and matched different move sets and search methods for sampling protein conformational space. Since we did not have the time to test the performance of each move set or search method, we assumed they would work equally well on average and combined them sequentially which generally resulted in improvements.

Table 4 shows the average results of different combinations of move sets and search methods for a set of six proteins (PDB codes: 1ctf, 1e68, 1eh2, 1nkl, 1pgb, 1sro; four of these were CASP targets). The results shown are for 10,000 trajectories with different starting random seeds. While some of the combinations do not necessarily enhance the simple approach of using only 3-residue fragments with a straight-forward monte carlo procedure, the combination of using fragments and the 14-state model for making moves, with MC and GA search techniques for the sampling, shows a significant improvement, which we hope to demonstrate at CASP5 by further extending the preliminary studies described here. Since these combinations were tried with equal weighting, further improvement may be obtained by parameterising how the different move sets and search techniques are applied depending on the trajectory landscape.

Table 4.

Performance of different move sets and search techniques on a set of six proteins.

Method	RMSD range (Å)(average)	Percentage ≤ 6.0 Å (average %)
3-residue fragments + MC	4.5 – 14.9	4.1
14-state φ/ψ model + MC	4.6 – 15.1	4.2
3-residue fragments + MC + GA	4.2 – 14.2	4.6
14-state φ/ψ model + MC + GA	4.1 – 13.8	4.8
fragments + 14-state model + MC + GA	3.8 – 14.4	9.3

For each combination of methods, the C_α RMSD range and the percentage of conformations within 6.0 Å C_α RMSD are given. The results are over six proteins and 10,000 decoys each, and each trajectory to produce a single decoy consisted of 50,000 steps. The combination of the two move sets and the two search techniques performs the best.

Ab initio prediction: Selecting native-like conformations

Even though our all-atom function is readily able to distinguish native-like conformations in certain scenarios, it is not adequate for large sets of decoys where the closest conformation generated is represented at the topological level (≈ 6.0 Å C_α RMSD relative to the experimental result). Using the all-atom function alone to select native-like conformations is not likely to suffice when it is also used in the actual minimisation/search process, since all conformations generated in such searches represent local minima of this function. Thus, our method has incorporates multiple functions and uses hierarchical filtering to reduce the number of conformations from a large sample to a tiny fraction to enhance the signal and eliminate false positives.

At CASP4, we used our expertise to manually devise a single hierarchical filtering scheme where we successively eliminated 10% of the conformations with each filter until we were left with one conformation. In the experiment in Table 5, we compare the average performance of each of the individual filters to our final hierarchical combination when reducing the 10,000 conformations generated for each protein by our search method (corresponding to the last entry in Table 4) to 1000 conformations. The hierarchical combination first reduces the 10,000 conformations to 8000 by applying the density function, which is then reduced to 6000 by applying the hydrophobic compactness function, which is then reduced to 4000, 3000, 2000, and 1000 in the same order as presented in Table 5.

Table 5.

Performance of individual and combination scoring functions on six decoy sets.

Scoring function	RMSD range (Å) (average)	Percentage ≤ 6.0 Å (average)
Initial	3.8 – 14.4	9.3
Density	3.9 – 12.1	12.3
Hydrophobic compactness	4.1 – 13.8	10.1
All-atom pairwise	4.1 – 14.1	11.0
Electrostatics	5.2 – 14.4	4.2
Van der Waals	5.6 – 13.1	3.9
Secondary structure match	4.5 – 10.1	10.2
Combined	3.9 – 13.2	14.1
Random	6.6 – 12.1	0.5

Each function reduces a sample of 10,000 conformations to 1000 for which the C_α RMSD range and the percentage of conformations within 6.0 Å C_α RMSD are given. The "Initial" row represents the initial distribution (generated by the method corresponding to the last entry in Table 4). The "Random" function simply selects an arbitrary 1000 conformations from the pool of 10,000 for each protein. The best results are achieved using the combined function.

Table 5 shows that particularly promising filters include the use of density-based scoring functions, hydrophobic compactness, all-atom pairwise preferences and match of the final conformation to the predicted secondary structure. Physics-based functions based on electrostatics and van der Waals interactions do not discriminate well on their own, and only do so when an explicit solvation term is added to the functions.

Table 5 also shows that even though some of the individual functions perform well, the combination of all the functions applied in a hierarchical manner performs the best. As mentioned earlier, this combination was developed through intuition under pressure from the CASP experiment (though here the goal was to reduce the total number of conformations to five). This suggests that there exists more optimal (linear and non-linear) combinations of these functions.

Computational issues

Table 6 lists the times taken for the computational tasks outlined in this paper. Times are given per 1000 MHz Pentium III processor and for a cluster of 64 such processors when the algorithm can run in parallel. For CASP4, predictions were made with computing power 1/4th of the capability shown.

Table 6.

Approximate computation times.

Task	~ Time per CPU	~ Time for cluster
Comparison of two protein sequences	< 1 sec	-
Clustering of sequence families for 3000 proteins	3 days	1 day
Initial model building by minimum perturbation	< 1 sec	-
Graph-theory search with 30,000 nodes	24 hours	-
Re nement of single model using ENCAD for 200 steps	< 1 sec	-
Evaluation by all-atom function for one conformation	< 1 sec	-
Generating a three-dimensional conformation	< 1 sec	-
Trajectory of 10,000 steps to generate one decoy	1 minute	-
Generating 10,000 decoys	10000 minutes	3 hours

Times are shown for a single 1000 MHz processor, and for a cluster of 64 such processors if the algorithms used can run in parallel. ^* indicates times can vary based on the quality of the results desired.

Application of structure prediction methods to whole genomes

The qualitative assessment of our methods, considered independently of the difficulty of the prediction, ranks 32/40 models as useful, good, or excellent. Similar results are likely to be observed when these methods are applied to large numbers of sequences if we assume that the sample of 40 proteins roughly reflects the distribution of proteins seen in a genome. In practice, it is likely that we will encounter more homologous proteins in a genome since experimentalists are not as likely to solve a structure for which there clearly exists a homolog.

This is a long way from our predictions at CASP1 [23], and our initial implementations of these methodologies [12,24]. Yet there is much room for further improvement. Besides improving the existing methodologies, and developing new ones, we can also integrate other existing algorithms such that consensus predictions can be used to assign confidence levels, as well as having multiple choices for an outcome that can be tested experimentally.

Analyses of small genomes show that about 30–40% of the proteins within the genome can be modelled by comparative modelling and fold recognition methods [27,50,52]. An additional 20–30% of the sequences are (or contain) small domains with simple secondary structures that are viable candidates for ab initio structure prediction [53]. The remaining proteins are usually not amenable to structure prediction and sometimes even structure determination (a significant fraction of the latter are membrane proteins).

It is thus possible to construct a "genome prediction engine" using the computational resources available where we can take the protein sequences encoded by an organism's genome and attempt to predict their structures, and use the modelled structures to predict functions. The goal of this endeavour is to improve existing methods and develop new ones to perform various facets of the genome/proteome modelling task in an automated fashion. To this end, our predictions for the next CASP are almost entirely focused on the fully-automated (CAFASP) aspect via the use of a prediction server http://protinfo.compbio.washington.edu

Using predicted structures to annotate function

The reason for obtaining structures for proteins encoded by a genome is that they can be used to understand function and further our knowledge about the organism's biology. Even though structure prediction methods need further development, it is possible to produce models where functional hypotheses can be tested in a rational manner (for example, with mutagenesis experiments) through detailed analysis [54]. Additionally, structure comparisons can be used to detect functional relationships that cannot be detected by sequence information alone [52], and micro-environment analyses that parse models for particular three-dimensional motifs [55] can be used to discern molecular function. Both of these structure-based approaches, used complementarily in conjunction with sequence-only motif-finding approaches [56-58] and experimental data, will enable to us better assign function to all or large parts of a proteome.

Conclusions

Why is protein/proteome modelling important?

Even given the ongoing structural genomics projects, the continually increasing amount of DNA and protein sequence data from genome projects makes it infeasible for NMR and x-ray crystallography techniques to rapidly provide information about the 3D structures of the sequences determined [59]. Thus there is an urgent need for reliably predicting structure from amino acid sequence.

Proteins in a cell do not work in isolation of one another. Thus to understand the function of multi-protein complexes, or whole proteomes, from a structural viewpoint, it is necessary to have a model for many proteins encoded by the genome of an organism. The CASP results indicate that structure prediction methods have matured to a point where they can be applied on a genome-wide scale, and that these structures can be used with novel but straight-forward approaches to annotate and understand function [54,55,60,61]. The resulting models and annotations, when combined with other genomic/proteomic data, including that from gene expression arrays [62], genome-wide two-hybrid experiments [63], and other proteomics studies [64], will provide us with a dynamic picture of organismal structure, function, and evolution [65].

Methods

In this section, we describe the procedures we used for making predictions at CASP4. The techniques described are divided based on the major structure prediction categories, but methods developed for application in one category are useful in the other.

Comparative modelling and fold recognition

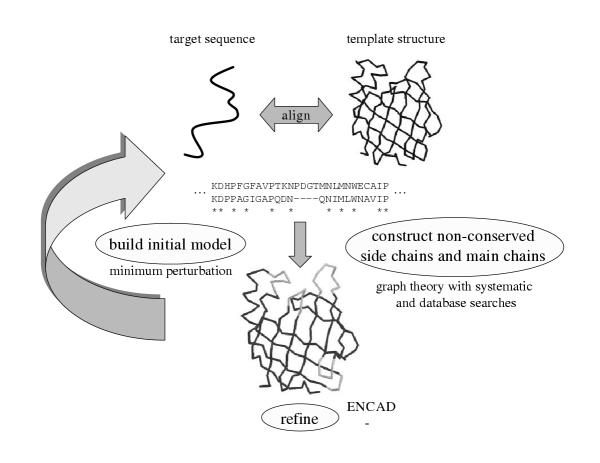
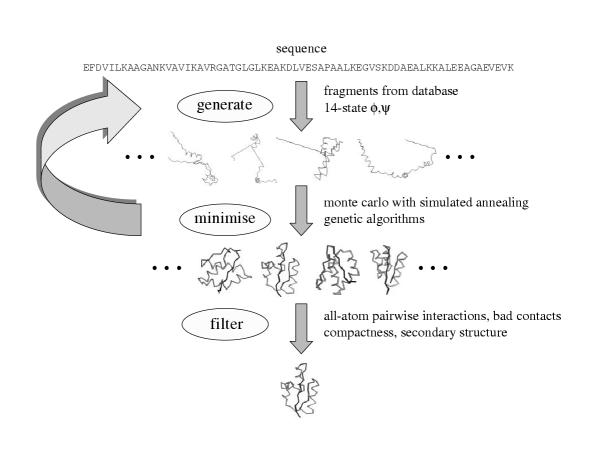
The same procedure was used for comparative modelling and fold recognition targets. Protein sequences determined to be evolutionarily related to sequences with known structure were modelled using comparative modelling techniques developed by us. We used a combination of methodologies grouped together as shown in Figure 5. Our primary focus was on improving alignment and template selection techniques, and developing methods for moving an approximate conformation closer to the native structure. Additionally, the lessons we learnt from application of our ab initio methodologies were incorporated to better construct non-conserved side chains and main chains.

Figure 5.

Methodology for comparative modelling. Target sequences related to the sequences with conformations determined by experiment were candidates for comparative modelling. Generally alignments were obtained from the various servers available as part of the CAFASP meta-server [29]. Initial models were then be constructed and structure-based alignments were used in an iterative manner to refine alignments manually. Non-conserved side chains and main chains were constructed using a graph-theoretic approach with sampling provided by exhaustive and database searches. The final conformations were minimised by ENCAD [36].

Template selection and alignment

Target sequences related to proteins that have conformations determined by experiment (X-ray crystallography or NMR) were candidates for comparative modelling. If the sequence relationship between the template and target proteins was unambiguous (usually when the sequence identity is > 40%), or if there was only one protein with known structure in the family, the template structure was used to construct the sole initial model. If there were many possible template structures, models were constructed using all available templates.

PSIBLAST alignments and other publicly available servers such as GenTHREADER [27] and SAM-T99 [28], available as part of the CAFASP meta-server [29], were also used to generate a variety of choices for alignments. These alternate alignments were used to construct initial models. Thus, for a given protein in a family with at least one known representative structure, there could be many template and alignment choices for constructing the initial models.

Constructing initial models

Following the sequence alignment, an initial model was generated for each template structure and corresponding alignment by copying atomic coordinates for the main chain (excluding any insertions/loops) and for the side chains of identical residues in the target and template proteins. Residues that differed in side chain type were constructed using a minimum perturbation (MP) technique [24]. The MP method changes a given amino acid to the target amino acid preserving the values of equivalent torsion angles between the two side chains, where available. The other angles were constructed for each residue type using internally developed library based on the most frequently observed χ values in a database of known structures [30].

Manual inspection to improve alignments

An all-against-all structure comparison between all the initial models was used to produce a multiple sequence alignment based on structural similarity for a given family. This alignment was used in conjunction with sequence information and interactive graphics to create new sequence alignments.

Constructing variable side chains and main chains

Multiple side chain conformations for residue positions that differ in type between the template and target proteins were generated by exploring all the possibilities in a rotamer library [31]. The most probable conformations based on the interactions of a given conformation with the local main chain were selected using an all-atom distance dependent conditional probability discriminatory function [32].

A set of possible conformations were generated for main chain regions (loops) considered to vary in the target with respect to the template structures, including insertions and deletions. Main chain sampling was performed using an exhaustive enumeration technique based on 14 discrete torsion angle states [33]. For longer main chain regions (> 15 residues), fragments from a database of protein structures are used to generate the torsion angle values. Developments in our ab initio sampling protocol were incorporated into our loop sampling technique.

In CASP experiments, main chain regions and side chains selected for sampling were determined visually using interactive computer graphics. We partially automated this procedure by developing programs to identify side chains with implausible packing, clashes, and unfavorable electrostatic interactions with other side chains and/or main chain.

All-atom conditional probability scoring function

The all-atom scoring function is the core of many aspects of this project where identification of native-like conformations is required. The function calculates the probability of a conformation being native-like given a set of inter-atomic distances [32]. The conditional probabilities are compiled by counting frequencies of distances between pairs of atom types in a database of protein structures. All non-hydrogen atoms are considered, and a residue-specific description of the atoms is used, i.e., the C_α of an alanine is different from the C_α of a giycine. This results in a total of 167 atom types. The distances observed are divided into 1.0 Å bins ranging from 3.0 Å to 20.0 Å. Contacts between atom types in the 0–3 Å range are placed in a separate bin, resulting in a total of 18 distance bins. Distances between atoms within a single residue are not included in the counts.

We then compile tables of scores proportional to the negative log conditional probability that one is observing a native conformation given an interatomic distance for all possible pairs of the 167 atom types for the 18 distance ranges. Given a set of distances in a conformation, the probability that the conformation represents a "correct" fold is evaluated by summing the scores for all distances and the corresponding atom pairs.

Using graph theory to generate consistent conformations

We use a graph-theoretic approach to assemble the sampled side chain and main chain conformations together in a consistent and optimal manner: Each possible conformation of a residue is represented using the notion of a node in a graph. Each node is given a weight based on the degree of the interaction between its side chain atoms and the local main chain atoms. The weight is computed using the all-atom scoring function [32]. Edges are then drawn between pairs of residues/nodes that are consistent with each other (i.e., clash-free and satisfying geometrical constraints). The edges are also weighted according to the probability of the interaction between atoms in the two residues. Once the entire graph is constructed, all the maximal sets of completely connected nodes (cliques) are found using a clique-finding algorithm [34]. The cliques with the best total weights represent the optimal combinations of mixing and matching among the various possibilities, taking the respective environments into account [35]. The clique-finding approach for generating conformations is fast, since it pre-calculates all the scores. In its present implementation, it can sample up to 10¹¹ conformations in a 24-hour period on a 1000 MHz Intel processor.

Selecting the most native-like conformations

All models produced are refined using the Energy Calculation and Dynamics (ENCAD) package [36]. For a given protein sequence, there could be more than one all-atom model produced. For such cases, all models were ranked using the all-atom pairwise scoring function [32] and the best scoring models are considered to be the most native-like ones.

Ab initio prediction

Target sequences without known homologues or analogues that were small in size and/or predicted to have largely helical content were modelled by our ab initio protocol. Such sequences can be subsequences of larger proteins, in which case they most likely represent domain boundaries [37].

Our general paradigm for predicting structure involves sampling the conformational space (or generating "decoys") such that native-like conformations are observed, and then selecting them using a hierarchical filtering technique with many different scoring functions (Figure 6). The two parts to our method are designed to be completely automated and readily extendable to application for hundreds or thousands of sequences. Generally, we explore combinations of different representations/move sets with two search methods for exploring protein conformational space, and combinations of a variety of scoring function "filters" to identify biologically relevant conformations.

Figure 6.

Methodology for ab initio prediction. We start with a sequence and generate conformations using two different move sets: fragments from a database with identical sequence and a 14-state φ/ψ model. Many trajectories are generated and minimised using two different protocols: Monte Carlo with simulated annealing and a genetic algorithm search. The minimisation function is primarily an all-atom conditional probability discriminatory function, a hydrophobic compactness function, and a bad contacts function. Once a set of conformations is generated, a hierarchical filtering technique is applied using many different filters/scoring functions to produce one or a few final conformations.

Sampling protein conformational space

We initially start with an all-atom conformation where the torsion values for residues predicted to be in helix/sheet by PSIPRED secondary structure prediction [38] are set to idealised values [33]. The remaining φ/ψ values are set in an extended conformation. Side chain conformations are predicted by simply using the most frequently observed rotamer in a database of protein structures [30]. New conformations are generated by perturbing the existing conformation at an arbitrary residue by one of two methods: (i) the torsion values for three residues with identical sequence from a known structure are used to modify the current conformation, similar in spirit to that of Baker and colleagues [39]; (ii) one of possible 14 torsion (φ/ψ) values derived based on the most frequently occurring torsion values for a given residue in a database of known structures. The move sets were combined sequentially (i.e., where a certain number of iterations consisted of copying torsion values for 3-residue fragments and the next few iterations would use torsion values from the 14-state φ/ψ model).

The scoring function for minimisation is primarily a combination of the all-atom function, a hydrophobic compactness function, and a bad contacts function [40]. The primary search technique we used was a Metropolis Monte Carlo (MC) procedure where conformations are accepted or rejected based on the Boltzmann's equation [41]. Each trajectory was allowed 50,000 iterations, starting with a high temperature such that 99% of the moves were accepted for the first 1000 steps and "cooled" linearly until only 1% of the moves were accepted for the last 100 steps.

At particular points in the trajectory (every 1000 steps), a fragment from another trajectory was copied at random, similar in spirit to genetic algorithms (GA) strategies [42,43]. The standard Metropolis criterion would then apply: i.e., if the selected fragment enhanced the score of the conformation relative to the previous conformation, it would be accepted. If not, its probability of acceptance would be determined by the difference in score between the current conformation and the previous conformation. The probability is calculated by the Boltzmann-like equation 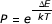where ΔE is the difference in scores and kT, representing the product of Boltzmann's constant and temperature, is set to a value calculated using the standard deviation of the scores of the first 1000 steps in a given trajectory.

Selecting biologically relevant conformations

The conformations generated were minimised using ENCAD [36] and scored using a combination of scoring functions that hierarchically reduces the total number of conformations produced to one final conformation. The scoring functions used for the final filtering include the all-atom function [32], hydrophobic compactness [40], a simple residue-residue contact function [44], a density-scoring function that is based on the distance of a conformation to all its relatives in the conformation pool, contact order [45], a secondary structure based scoring function that evaluates the match between the predicted structure and the secondary structure of a final energy-minimised conformation, and standard physics-based electrostatics and Van der Waals terms [46].

Internal testing and comparison of models to the experimental result

We initially ran our algorithms on test sets consisting of 10–20 proteins. To minimise bias of a particular algorithm to a fixed test set, new proteins were added to the test sets regularly. In all cases where a three-dimensional model must be compared to an experimental structure, we use the root mean square deviation (RMSD) between corresponding atoms of the prediction and the experimental answer (usually calculated using the C_α atoms).

Availability of software and decoys

The ensembles of structures that were generated and much of the software used to generate them are available at http://compbio.washington.edu

Authors' contributions

RS performed the algorithm development, carried out the computations, evaluated the results, and drafted the manuscript. ML helped with the algorithm development and evaluation of the results produced, and provided intellectual guidance and mentorship. All authors read and approved the final manuscript.