Self-adaptive evolutionary neural networks for high-precision short-term electric load forecasting

Abstract

Reliable short-term electric load forecasting (STLF) is essential for enhancing grid stability, optimizing energy distribution, and minimizing operational costs in modern power systems. However, existing forecasting models, including statistical approaches and deep learning architectures such as multi-layer perceptron (MLP), struggle to capture complex nonlinear load variations while maintaining computational efficiency. To overcome these limitations, a self-adaptive Kolmogorov–Arnold network (SADE-KAN), an optimized forecasting framework that combines the power of Kolmogorov–Arnold networks (KAN) with self-adaptive differential evolution (SADE) is introduced to enhance both predictive accuracy and computational efficiency. Unlike conventional MLP models, KAN replaces fixed activation functions with spline-based learnable functions that offers greater flexibility in capturing temporal dependencies. However, these learnable activation functions introduce a new set of hyperparameters that require careful optimization to ensure efficient training and manage network complexity. To address this, SADE dynamically tunes these hyperparameters, ensuring an optimal balance between accuracy, complexity, and training efficiency. The proposed SADE-KAN model is validated on ISO-NE hourly load data (2019–2023, ~ 1 million observations) across multiple forecasting horizons (24, 48, 96, and 168 h). Experimental results demonstrate that SADE-KAN reduces mean absolute percentage error (MAPE) by up to 35% and root mean squared error (RMSE) by 38% compared to MLP models, while requiring 35% fewer learnable parameters. Despite a slightly higher training time, SADE-KAN significantly enhances generalization and robustness, capturing rapid load fluctuations more effectively than MLP, conventional KAN and other recently published advanced models. These findings establish SADE-KAN as a computationally efficient and highly accurate forecasting framework, offering a robust solution for real-time power system applications, demand response strategies, and energy market operations.

Introduction

Modern power systems aim to reduce peak load and maintain a balance between power generation and consumption to ensure safe, reliable, and cost-effective operations¹. Utilities engaged in generation, transmission, and distribution rely on load forecasting to facilitate effective resource allocation, generation planning, integration of renewable energy sources, and stability of the grid². Given its critical role, load forecasting has been a long-standing area of research. Despite numerous advancements, the demand for highly accurate models continues to rise as forecast precision directly influences system efficiency and financial outcomes. For instance, Hobbs et al.³ showed that even a 1% improvement in forecast accuracy could translate into substantial economic savings for utilities.

Recent advancements in energy forecasting have seen a growing reliance on artificial intelligence and hybrid machine learning models to improve prediction accuracy across various energy domains. Al-Suod et al.⁴ employed artificial neural networks to forecast energy consumption in mining plants, showcasing the adaptability of ANNs to industrial loads with high nonlinearity. Building upon the potential of machine learning in complex systems, Singh et al.⁵ explored energy management and power forecasting in grid-connected microgrids comprising multiple distributed energy resources, integrating multiple data sources to support real-time decision-making. Extending the use of neural models, Alharbi et al.⁶ combined multilayer perceptrons with a waterwheel plant algorithm for hyperparameter tuning to forecast energy efficiency in buildings, highlighting the role of hybrid optimization in enhancing model performance. Guermoui et al.⁷ advanced photovoltaic (PV) power forecasting by employing multi-scale fusion techniques across diverse case studies, emphasizing the value of spatio-temporal data integration. Similarly, Sharma et al.⁸ addressed the challenges of solar forecasting under varying weather conditions by utilizing gradient descent and Levenberg–Marquardt-based ANN models, demonstrating the benefit of adaptive training algorithms. Focusing on regional applications, Mfetoum et al.⁹ designed a multilayer perceptron for solar irradiance forecasting in Central Africa, incorporating meteorological insights to account for climatic variability. In the hydrological forecasting domain, Reihanifar et al.¹⁰ developed a multi-objective genetic programming model for drought prediction using meteorological data, illustrating the versatility of evolutionary algorithms in time series forecasting. Forecasting irradiance with hybrid deep learning, Mouloud et al.¹¹ assessed bidirectional architectures for short-term global horizontal irradiance (GHI), demonstrating improved accuracy via deep temporal modeling. Pushing the boundary of renewable energy forecasting, Alhussan et al.¹² targeted green hydrogen production with a hybrid dynamic optimization ensemble, reflecting growing interest in clean fuel systems. Al-qaness et al.¹³ proposed ResInformer, a residual transformer-based architecture for PM2.5 forecasting, bringing attention to the potential of transformer models in high-dimensional environmental time series. Wind power forecasting was explored by Saeed et al.¹⁴ using an enhanced Al-Biruni Earth radius metaheuristic algorithm, showing notable improvements in prediction quality through metaheuristic-tuned models. Similarly, Molu et al.¹⁵ utilized a hybrid deep learning framework with Bayesian optimization for short-term solar irradiance forecasting, underlining the effectiveness of probabilistic search in hyperparameter tuning. Seasonal forecasting of GHI was tackled by Kheldoun et al.¹⁶ using a combined CNN-BiGRU model, indicating the benefits of combining spatial and temporal neural networks for grid-connected PV applications. Finally, Khelifi et al.¹⁷ introduced a hybrid TVF-EMD-ELM model for short-term PV power forecasting, integrating signal decomposition and extreme learning machines to effectively capture non-stationary features in solar data. Collectively, these studies illustrate a clear trend toward hybrid, adaptive, and domain-specific forecasting models, often merging deep learning, signal processing, and evolutionary optimization techniques to address the growing complexity of energy systems.

Generally, load forecasting processes are categorized into two primary groups: short-term load forecasting (STLF) and long-term load forecasting (LTLF). Further, these processes can be subdivided into very short-term load forecasting (VSTLF) and medium-term load forecasting (MTLF) based on their time horizons¹⁸. Among these, STLF is crucial for making effective real-time decisions and managing system operations such as day-ahead and hour-ahead scheduling, energy trading and demand response management¹⁹. To perform STLF, both machine learning (ML) techniques and non-ML or statistical techniques have been adopted. The non-ML techniques include auto-regressive integrated moving average (ARIMA)²⁰, exponential smoothing (ES)²¹, linear regression (LR)²² and Kalman filtering (KF)²³. These techniques traditionally address the time series forecasting problem, utilizing statistical methods to forecast future load based on the historical data. ARIMA is particularly known among the non-ML techniques, as it combines auto-regression, integration, and moving averages to predict future load. Its variants, such as seasonal ARIMA (SARIMA), have been developed to accommodate seasonality in data series²⁴. ES are another widely used set of non-ML forecasting techniques, known for their simplicity and efficiency in dealing with data that exhibit trends and seasonality²⁵. While these models are widely used for their efficiency and interpretability, they have limitations in capturing the dynamics of nonlinear systems, complicated seasonal patterns, and long-term dependencies²⁶.

On the other hand, ML techniques, particularly neural networks (NNs) offer greater flexibility in modeling nonlinearity, handling large data volumes, and learning from historical patterns²⁷. The simple multi-layer perceptron (MLP) was one of the earliest NNs used for STLF, showing considerable promise in modeling the nonlinear data²⁷. Based on the foundation of MLP, more complex architectures have been developed to enhance the capabilities of NNs. Wide and deep NNs stand out for their ability to capture both linear and non-linear relationships within large datasets, handling multiple input features and learning hierarchical patterns effectively²⁸. Advanced architectures like convolutional neural networks (CNNs)²⁹, recurrent neural networks (RNNs)³⁰, long short-term memory (LSTM) networks³¹, and gated recurrent units (GRUs)³² have evolved from the simple MLP and are widely used in STLF. These models effectively handle temporal sequences, retaining information over longer periods while mitigating the vanishing gradient problem, making them highly suitable for load forecasting tasks³³.

Researchers have leveraged these advanced NN techniques in various innovative ways to improve load forecasting accuracy and efficiency. For example, Kong et al.³⁴ developed an LSTM-based model for short-term residential load forecasting, demonstrating its superiority over traditional methods in capturing complex temporal patterns. However, the model’s training time is significantly longer due to its complexity and requires substantial computational resources. Smyl et al.³⁵ introduced a hybrid method combining ES with RNNs for forecasting electricity demand, showing improved accuracy and robustness. Despite its effectiveness, its interpretability is limited, making it difficult for stakeholders to understand the model’s decision-making process. Wu et al.³⁶ proposed a CNN-LSTM hybrid model, utilizing CNNs for feature extraction and LSTMs for sequence prediction. This model outperformed standalone models in accuracy and computational efficiency. However, the model’s performance heavily depends on the quality of the input features, and it may require extensive hyperparameter tuning. Yang et al.³⁷ applied a dilated CNN (DCNN) for day-ahead electricity price forecasting, capturing long-term dependencies more effectively than conventional RNN-based models. The primary limitation is the need for large datasets to train the DCNN effectively, which may not always be available. Marino et al.³⁸ utilized deep NNs with stacked LSTM layers for multi-step ahead forecasting, significantly improving performance over shallow networks. However, the deep architecture increases the risk of overfitting, especially when the training dataset is not sufficiently large. Hong et al.³⁹ demonstrated that LSTM models incorporating weather forecasts outperformed those using only historical load data. However, the reliance on accurate weather data can be a limitation, as errors in weather forecasting can directly impact the accuracy of electricity demand forecasts. Unfortunately, most of the techniques, being primarily based on the MLP architecture, often suffer from limitations such as lack of interpretability, reduced accuracy in complex scenarios, high computational complexity, and significant data dependency. These shortcomings raise the need for further research and innovation in developing more efficient and accurate forecasting models^{19,24,26,27,33}.

Surprisingly, in a recent study⁴⁰, Kolmogorov–Arnold Network (KAN) is introduced as a novel NN architecture potentially supplanting the traditional MLP. Inspired by the Kolmogorov–Arnold representation theorem (KART), KAN leverages this theorem to create a unique architecture. They revolutionize by replacing the linear weights with spline-based univariate functions as learnable activation functions along the network edges. This unique architecture improves both accuracy and interpretability of the networks while significantly reducing the number of parameters needed (138000 in KAN compared to 394,000 in MLP)⁴¹. Several studies have explored the theoretical and practical aspects of KAN. For instance, the authors in⁴¹ examined KAN in time-series forecasting and highlighted that KAN consistently outperformed MLP, achieving lower error metrics while using fewer computational resources. However, the study also highlighted the importance of optimizing parameters such as node count and grid size to improve performance. Similarly, the authors in⁴² examined the use of KAN for time-series forecasting highlighted that, although KAN provided improved accuracy over MLP, the training time was significantly longer due to the need to learn coefficients for the spline functions. Further, in⁴³ the Graph KAN variant faced the same challenge of slow training speed, and optimizing training time was left as a goal for future work. Moreover, a comprehensive survey in⁴⁴ explored the use of various polynomial functions as basis functions in KAN, the study pointed out the need for further research into model complexity, parameter tuning, and training time, particularly on more complex datasets. In⁴⁵, KAN models were found to be more effective than MLP models in federated learning tasks, but the high computational cost of spline-based functions was noted as an area for future optimization. Table 1 presents summary of the recent works, their contributions and limitations. These findings emphasize the importance of careful optimization of spline-based KAN parameters to balance model complexity, efficiency, and computational demands. To obtain accurate load forecasts, the following challenges in KAN need to be addressed:

• The increased training time due to the complexity of learning spline-based coefficients, particularly in complex architectures.

• The need to optimize model architecture and spline grid settings as KAN introduce new hyperparameters.

• A trade-off between complexity, training time, and the risk of overfitting when selecting these hyperparameters.

Table 1.

Summary of the recent works, their contributions and limitations.

References	Forecasting model	Ke contributions	Identified limitations
24,26,27,33	MLP-based techniques	Provided foundational frameworks for STLF using standard neural networks	Suffer from interpretability issues, reduced accuracy in complex scenarios, and high data/computational demands
Kong et al.34	LSTM-based model	Demonstrated superiority over traditional methods in capturing complex temporal patterns for residential load forecasting	Long training time and high computational resource requirements
Smyl et al.35	Hybrid Exponential Smoothing and RNN	Improved forecasting accuracy and robustness for electricity demand	Limited interpretability of the model, challenging stakeholder understanding
Wu et al.36	CNN-LSTM hybrid model	Combined CNNs for feature extraction and LSTMs for sequence prediction, outperforming standalone models	Performance is heavily dependent on feature quality and requires extensive hyperparameter tuning
Yang et al.37	Dilated CNN (DCNN)	Effectively captures long-term dependencies in day-ahead electricity price forecasting	Requires large datasets for effective training, which may not always be available
Marino et al.38	Deep LSTM network	Achieved better multi-step ahead forecasting accuracy using stacked LSTM layers	Increased risk of overfitting with deep architecture, especially on small datasets
Hong et al.39	LSTM with weather forecasts	Showed enhanced performance using weather data alongside historical load	Accuracy heavily depends on the reliability of external weather forecasts
Liu et al.40	Kolmogorov–Arnold Network (KAN)	Novel architecture replacing linear weights with spline-based univariate functions, improving interpretability and parameter efficiency	Requires careful optimization of node count and grid size
Abbas et al.41	KAN for short term load forecasting	Outperformed MLP in accuracy and resource efficiency	The need to optimize model architecture and spline grid settings
VacaRubio et al.42	KAN	Achieved higher accuracy than MLP for time-series data	Noted longer training time due to learning spline coefficients
Kiamari et al.43	Graph-KAN	Extended KAN for graph-based data with consistent performance	Training speed was slow, with optimization deferred to future work
Seydi et al.44	KAN with polynomial basis functions	Surveyed basis function choices and emphasized model complexity challenges	Called for more research into parameter tuning and efficient training
Zeydan et al.45	KAN in federated learning	Demonstrated effectiveness over MLP in distributed learning	High computational cost of spline-based functions remained a challenge

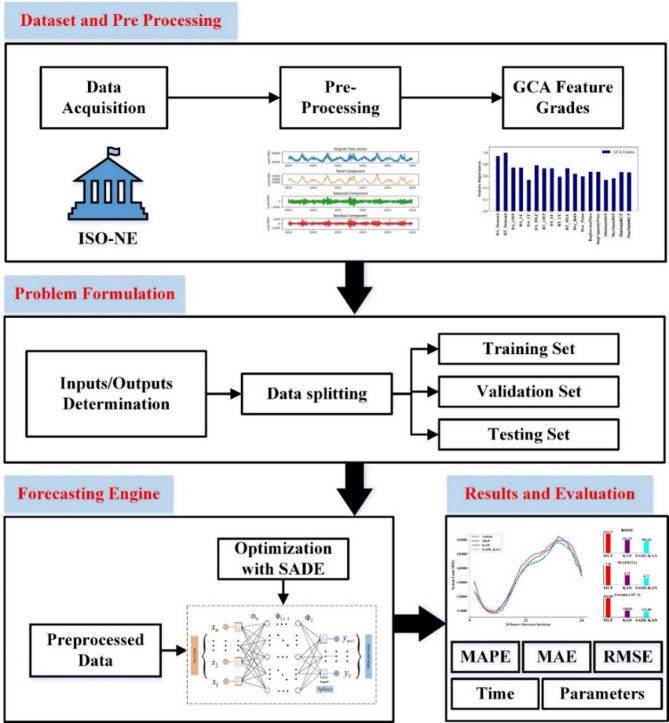
To address the above challenges, this study introduces KAN optimized with self-adaptive differential evolution (SADE) as a novel approach for STLF, a method not previously explored in the existing literature. The adaptive spline-based activation functions of KAN enable the capture of complex and nonlinear patterns in load data, while SADE optimization enhances efficiency, mitigates overfitting and reduce training time. By auto-tuning the crucial hyperparameters, our approach addresses the challenge of model architecture and spline grid settings without compromising predictive accuracy. The primary objective is to asses the practical applicability of our proposed model by examining its accuracy and efficacy with respect to their trainable parameters, training time, data dependency, and capability to capture temporal dependencies. We validate the efficacy of our proposed model on the latest real-world ISO-NE-CA load data from Jan 2019 to Dec 2023, using performance metrics such as root mean squared error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE) across various prediction horizons. Moreover, a detailed comparative analyses are conducted against the conventional models and advanced frameworks to assess its competitiveness in the field of STLF. Conceptual diagram of the proposed SADE-KAN model is presented in Fig. 1.

Fig. 1.

Conceptual diagram of the proposed SADE-KAN model for STLF.

Contributions of this work are summarized as follows:

• This paper introduces the KAN optimized with SADE as a novel approach for multi-horizon STLF, aiming to achieve higher accuracy by leveraging its adaptive spline-based activation functions.

• KAN have recently emerged and its application for short term electric load forecasting remains unexplored, particularly on large datasets with high dimensionality and numerous dependent variables. This study fills that gap by evaluating KAN on a real-world large-scale dataset having significant variability.

• By optimizing the hyperparameters introduced by the spline-based activation functions using SADE, this study overcomes training and complexity challenges of KAN.

• Performance of the proposed SADE-KAN is comprehensively evaluated in terms of accuracy, parameters count, several error metrics, training time, and is compared against the conventional models and advanced frameworks.

The rest of the paper is organized as follows:

Section "Problem formulation" provides the problem formulation, KAN’s fundamental background and the proposed SADE-KAN. Section "Dataset and preprocessing" presents the dataset and preprocessing steps used in this study. Section "Experimental setup and results" details the experimental setup and presents the simulation results, analyzing the performance of SADE-KAN. Finally, Section "Conclusion" offers concluding remarks, followed by references.

Problem formulation

We aim to predict future electricity load values based on historical time-series data. Given a historical observation window of length 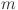, the goal is to forecast the load sequence over a specified horizon 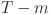, represented as:

1

where 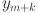corresponds to the load value at the 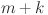th timestamp for 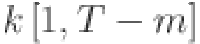. The input data for forecasting is represented by a multivariate time series matrix X of historical load and its associated features, where each row corresponds to a specific time step, and each column represents a feature, expressed as:

2

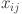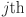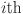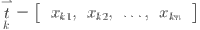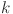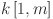where represents the value of the feature at the timestamp. The vector represents the feature vector at time step for , and 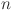is the number of features, which may include variables such as system load, temperature, electricity pricing, and other relevant factors. The problem is framed as a supervised learning task, where the objective is to map the historical feature matrix 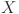to the future load sequence 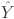, thereby enabling accurate prediction of load values at future timestamps.

Kolmogorov Arnold network background

Contrary to MLP, which are deeply rooted in the universal approximation theorem stating that “a feed-forward network (FFN) with a single hidden layer and a finite number of neurons can approximate any continuous function on compact subsets of 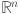”, KAN derive their foundation from the KART theorem. KART states that any continuous function 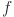dependent on multiple variables, such as 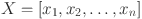within a bounded domain, can be decomposed into a finite set of simpler continuous functions²³. In more formal terms, a real and smooth multivariate continuous function 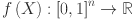can be expressed as a composition of univariate functions and the addition operations as

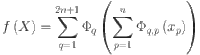3

where are the univariate functions that map each input variable 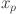, specifically 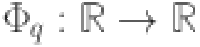are the outer functions and 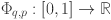are the inner functions.

This implies that instead of directly approximating a complex multivariate function 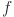, we can decompose it into a combination of one-dimensional simpler functions. This decomposition approach initially seems highly beneficial for machine learning, as it simplifies the challenge of learning a high-dimensional function into learning a smaller number of one-dimensional functions. Theoretically, this could enhance the learning process and make it more efficient and manageable. However, in practice, these one-dimensional functions can be very complicated and exhibit non-smooth characteristics hence making them difficult to learn using traditional machine learning techniques. Consequently, despite its theoretical advantages, the KART has seen limited application in the field of machine learning.

Interestingly, recent theoretical developments as presented in⁴⁰ suggest that the KART could inspire new types of neural network architectures. These architectures have the potential to leverage this theorem in a way that is practical and effective for machine learning tasks. The authors in ⁴¹ propose a two-layer neural network model described by Eq. (3) having two layers of non-linearities, with 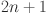terms in the middle layer. Thus, the key task is to identify appropriate functions and 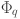that map the input variable 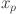effectively.

Kolmogorov Arnold Network

In MLP, a layer includes a linear transformation followed by nonlinear operations, and the network can be made deeper by adding more layers ⁴⁶. Let us define an MLP network as a sequence of linear transformations and non-linear activations applied to the input 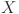as

4

where 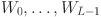are the learnable weights on the edges and 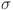is the fixed activation function such as ReLu applied at each node. The KAN replace these fixed activation functions and express 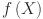as a composition of inner and outer function matrices applied to the input vector.

Mathematically, the output of a KAN model is a composition of layers, where each layer applies an activation function to its inputs. These layers, build on each other, transform the output progressively. The input to the KAN is passed through successive layers, where the activation value of a neuron in the layer is computed as the sum of all incoming post-activations from the layer :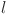

5

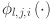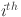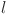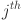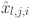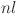Here, denotes the activation function for the connection between the neuron of layer and the neuron in layer . Similarly, and are the post activation value and number of neurons in the 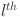layer respectively. It can be presented in the matrix form as:

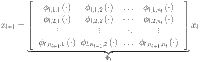6

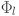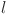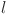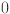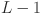Here is the function matrix representing a set of transformation applied by the layer in the network, with ranging from to . The composition of these transformations across all layers results in the output as:

7

The input data 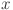is transformed by each function matrix 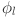in the 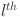layer. This architecture includes B-splines as the core activation function for these transformations, where each is parameterized as a B-spline such that:

8

where 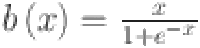is a basis function, 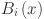is the B-spline function of order 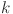with trainable coefficients 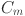that determines the shape of the B-spline and refers to the number of intervals. The B-splines are used to approximate the non-linear relationship between features in the data. The KAN is particularly suited for this task due to its ability to capture complex relationships within the data through a series of nonlinear transformations ⁴⁰. KANs are visualized similarly to fully connected layers in traditional neural networks, with the distinction that each edge represents a one-dimensional function. This design simplifies the interpretation of complex networks by directly representing function layers ⁴⁰. Consequently, KAN offers a more interpretable connection between input features and output, showcasing its potential for improved transparency.

We have framed the load forecasting problem as a supervised learning framework, using a training dataset having input–output pairs and represented as 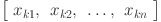. We aim to find 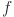that approximates 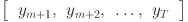. More formally:

9

Our model employs KAN structured as 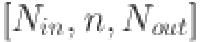with 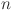as the count of neurons in the hidden layer. The relevant features are selected by grey correlation analysis (GCA) and flattened to serve as input to the KAN. This architecture is designed to produce forecasts for various time horizons: the next day (24 h), the next two days (48 h), the next four days (72 h) and the next week (168 h). A 24-step window is utilized, and the number of outputs 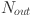are comprised of nodes corresponding to the total amount of time steps in Eq. (1). Our KAN is represented by composition of these layers as

10

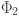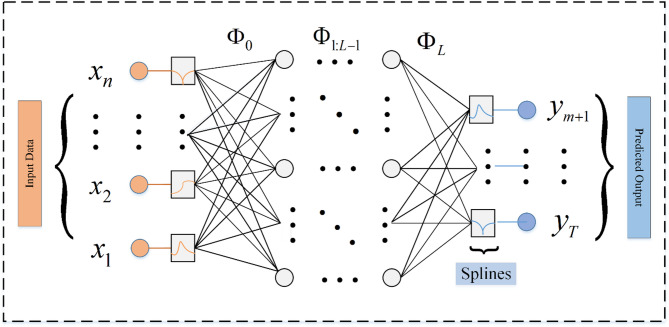
where transforms the outputs from the hidden layer into final predictions (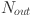). Figure 2 illustrates a generic representation of a KAN network for any arbitrary number of layers 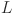. The number of inputs 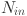and number of outputs 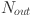are comprised of nodes corresponding to the total amount of time steps in Eq. (2) and (1) respectively. A detailed configuration and parameter settings of KAN and MLP models are provided in Table 2.

Fig. 2.

Kolmogorov–Arnold Network representation with L number of layers.

Table 2.

Hyperparameters and configuration of the conventional models.

Model	Forecast horizon	Configuration	Other parameters	Selected value
MLP	24 h	[RFx24, 300, 300, 24]	Epochs	200
	48 h	[RFx48, 300, 300, 48]	Optimizer	Adam
	96 h	[RFx96, 300, 300, 96]	Batch Size	32
	168 h	[RFx168, 300, 300, 168]	Activation	Fixed Relu
KAN	24 h	[RFx24, 30, 24]	Epochs	200
	48 h	[RFx48, 30, 48]	Optimizer	Adam
	96 h	[RFx96, 30, 96]	Batch Size	32
	168 h	[RFx168, 30, 168]	Activation	B-Spline, k = 3, G = 5

Optimization of KAN with SADE

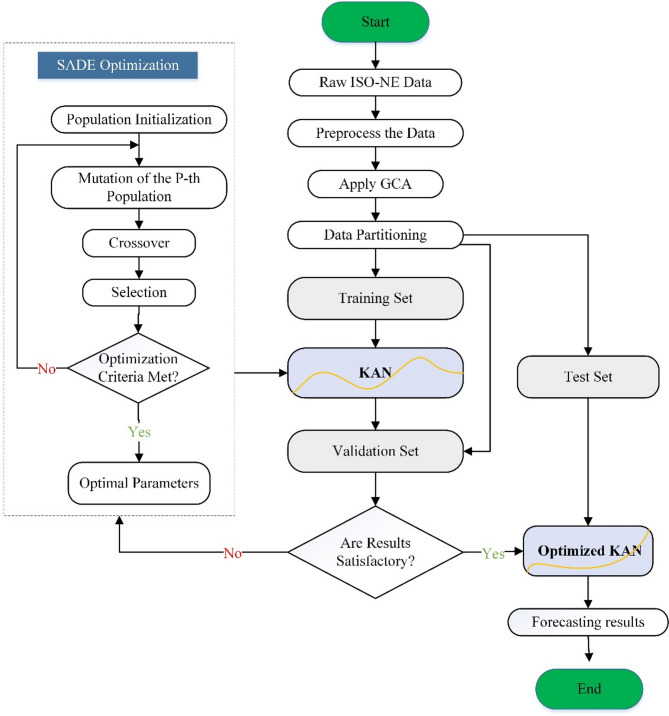
The performance of KAN is highly sensitive to the choice of several key hyperparameters, particularly the grid size of the B-spline (G), the number of hidden layers (D), and the number of neurons per layer (W). Optimizing these parameters is essential to balancing model expressiveness with computational efficiency, especially in the context of STLF, where overfitting and poor generalization are common challenges. To simplify the optimization process, we fix certain settings to reduce the complexity of the search and focus on the most impactful parameters. These parameters control the expressive power and computational complexity of the model. Traditional methods such as gradient descent or cross-validation, often carry computational complexity and may not converge efficiently ⁴⁷. Therefore, a more robust SADE algorithm is used to optimize these parameters.

SADE extends the classical Differential Evolution (DE) framework by enabling the control parameters such as the mutation factor F and crossover rate C to adapt dynamically during the optimization process. This self-adaptive mechanism reduces the need for manual parameter calibration and allows the optimizer to adjust its behavior based on the historical success of mutations and recombinations, thereby improving convergence and robustness. The optimization objective is to minimize the mean squared error (MSE) on the validation set by identifying the most effective configuration for the KAN model. The parameter search space was defined according to Table 3, where the grid size G was constrained to integer values between 4 and 12, the network depth D could take values in the discrete set ^1–3, and the network width W was allowed to vary over [30,40,50,60]. To reduce complexity, other settings such as the spline type (fixed as cubic), the number of epochs (200), and knot positioning (uniform) were held constant to reduce the dimensionality of the search space and enhance convergence reliability.

Table 3.

Implementation steps of SADE.

The SADE algorithm was initialized with a population size of 30. For each individual 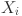, the associated control parameters such as the mutation factor 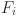and crossover rate 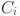were independently initialized by sampling from the ranges  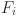∈ [0.4,0.9] and  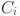∈ [0.1,0.9]. Unlike classical DE, where F and C are typically fixed for all individuals, SADE treats these as self-adaptive parameters. During the evolutionary process, successful values of 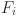and 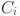are tracked, and their distributions are updated using Gaussian perturbations centered around their historically successful means. This allows the algorithm to adaptively fine-tune its exploration and exploitation strategies across generations without external parameter tuning.

At each generation, SADE applies mutation and crossover operators to produce new candidate solutions. For each individual in the population, a mutant solution is created by combining information from multiple randomly selected individuals in the current population. This mutant is then combined with the original solution to produce a trial solution through a crossover operation. The trial solution is evaluated using the same validation MSE metric. If it demonstrates better performance than the original solution, it replaces it in the next generation. This selection mechanism ensures that only equal or superior solutions are retained, guiding the population toward optimal hyperparameter configurations over successive iterations ⁴⁸. The process iterates until a stopping criterion is met, either a maximum number of generations or no improvement over several consecutive generations. The full SADE implementation for KAN optimization is summarized in Table 3.

The final optimized KAN configuration selected by SADE consisted of a grid size of 10, network depth of 2 hidden layers, and 50 neurons per layer. These settings, summarized in Table 4, were used for all subsequent forecasting experiments reported in this study. By leveraging the adaptive mechanisms of SADE, the optimization achieved a favorable trade-off between model accuracy and computational overhead of KAN. Figure 3 shows the flow chart of the SADE-KAN model for STLF.

Table 4.

Optimized hyperparameters of KAN with SADE.

Model	Hyperparameters	Tuning range/value	Selected value
SADE-KAN	Grid size—G	[3–12]	10
	Hidden layer (Depth)	[1,2,3]	2
	Neurons/hidden layer (Width)	[30,40,50,60]	50
	Epochs	Fixed	200
	Optimizer	Fixed	Adam
	Batch Size	Fixed	32
	Activation	B-Spline	k = 3, G = 10

Fig. 3.

Flowchart of the proposed SADE-KAN STLF method.

Dataset and preprocessing

The dataset utilized in this study is collected from the ISO New England Control Area (ISO-NE-CA) publicly available data. It comprises hourly samples of weather data, system load, and other relevant information for all the wholesale load zones of ISO-NE-CA. The dataset is sampled every hour and covers a period of five years from Jan 2019 to Dec 2023, resulting in approximately one million samples. The data is arranged month wise, i.e. the data is structured in a month wise sequence, where observations are grouped by calendar month across all years. Such data arrangement facilitates temporal analysis, allowing for the examination of seasonal variations and trends within individual months. The data attributes are detailed in Table 5.

Table 5.

Description of the data attributes.

Feature	Description
Date	The calendar date of data
Hr_End	Observation at hour ending
DA_Demand	Day-ahead cleared demand in MW
RT_Demand	Real-time demand in MW
DA_LMP	Day-ahead locational marginal price (LMP) in $/MWh
DA_EC	Energy component of day-ahead LMP in $/MWh
DA_CC	Congestion component of day-ahead LMP in $/MWh
DA_MLC	Marginal loss component of day-ahead LMP in $/MWh
RT_LMP	Real-time locational marginal price (LMP) in $/MWh
RT_EC	Energy component of real-time LMP in $/MWh
RT_CC	Congestion component of real-time LMP in $/MWh
RT_MLC	Marginal loss component of real-time LMP in $/MWh
Dry_Bulb	The dry-bulb temperature in °F for the weather stations
Dew_Point	The dewpoint temperature in °F for the weather stations
System_Load	The actual New England system load in MW
Reg_SP	Regulation market service clearing price in $/MWh
Reg_CP	Regulation market capacity clearing price in $/MWh
Min_5min_RSP	The lowest pool level 5-min regulation service price in $/MWh
Max_5min_RSP	The highest pool level 5-min regulation service price in $/MWh
Min_5min_RCP	The lowest pool level 5-min regulation capacity price in $/MWh
Max_5min_RCP	The highest pool level 5-min regulation capacity price in $/MWh

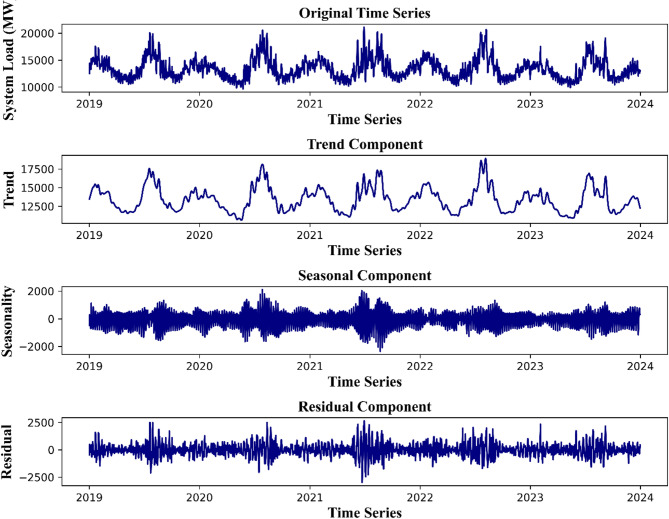
To broadly understand the system load which is our target variable, we decomposed it into trend, seasonal, and residual components, as shown in Fig. 4. The trend component represents the long-term behavior of the load, capturing underlying changes. Meanwhile, the seasonal component shows recurring patterns that repeat over shorter periods, often daily or weekly and the residual component highlights deviations from the trend and seasonal patterns, indicating irregularities. This decomposition helps in identifying the underlying patterns and variations in our target variable.

Fig. 4.

The original load sequence and its components from Jan 2019 to Dec 2023.

Input data preparation

To efficiently implement our proposed model, proper data preparation is essential. Data preparation plays a critical role in the performance of both ML and non-ML models. This is particularly crucial when employing the proposed SADE-KAN model that incorporates unique learnable activation functions and are sensitive to the scale of input data. Due to the sensitivity of the model to the scale of the data and the varying degrees of influence that different features exert on the final predicted load, we applied two standard preprocessing steps to our dataset.

First, we normalize our data by implementing MinMax scaling technique. This scaler transforms data to lie within a specified range, typically [0, 1], ensuring that each feature is scaled uniformly. This approach is particularly advantageous for neural networks, which are sensitive to variations in the magnitude of input data. Unlike standard normalization, which adjusts data to have a mean of zero, MinMax scaling retains the original zero reference point of the series. This is commonly achieved by dividing each value by the maximum observed value in the training dataset, as:

11

where 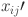is the normalized value of the 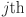feature at the 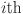timestamp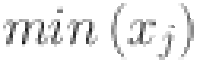, and and 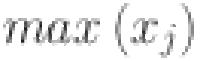are the minimum and maximum values of the 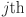feature respectively. This method maintains consistent scaling across input features, preventing problems such as activation function saturation and numerical instability during computations.

Second, the GCA technique is applied to compute the grey correlation coefficients for each feature. These coefficients quantify the similarity between the feature sequences and the target load sequence, even amidst noise or complex interactions. The grey coefficient is calculated as ¹

12

where, 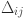is the absolute difference between the target sequence and the 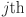feature at timestamp , 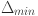and 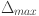are the minimum and maximum differences across all time points, and 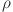is the distinguishing coefficient usually set to 0.5 ¹. Finally, the grey correlation grades for each feature can be computed by averaging the grey correlation coefficients across all time points as

13

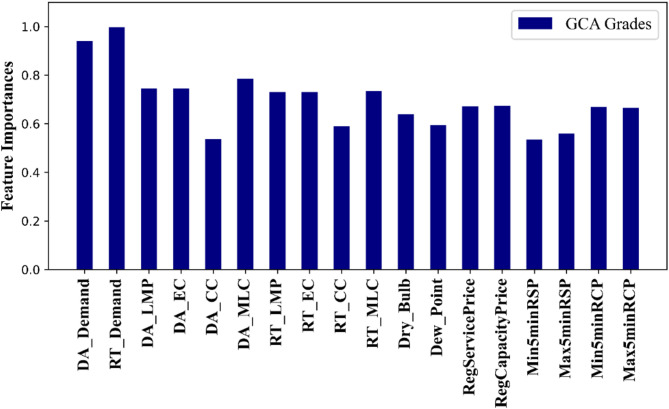
GCA helps in focusing on the most relevant features by assessing the similarity degree between the feature sequences and the target variable, thereby reducing data dimensionality and eliminating irrelevant features. The grey correlation grades for each feature are calculated and visualized in Fig. 5. This visualization underscores the importance of each feature and its direct relationship with the system load, providing a clear rationale for their inclusion in the model. Features with higher grey correlation grades are considered more relevant to the target variable, while those with lower grades are deemed less important and are dropped from the analysis. After filtering out the irrelevant features, the selected features are fed into our KAN model for further processing. We evaluated the performance of our KAN model using different sets of features selected based on varying grey correlation grade thresholds. The optimal results were achieved with a grey correlation grade of 0.7. This threshold guarantees that only the most significant features are retained, resulting in improved accuracy and efficiency of the proposed SADE-KAN model.

Fig. 5.

Grey correlation grades given to each feature.

Experimental setup and results

To evaluate the effectiveness of the proposed SADE-KAN model, a simulation environment was developed in Python, following the architectural specifications outlined in Sections “Kolmogorov arnold network” and “Optimization of KAN with SADE”. All experiments were executed using Python version 3.12.0 on a Windows 11 platform, running on a 2.60 GHz 64-bit Intel Core i5-4210U processor with 12 GB RAM and a 500 GB hard drive. The hourly load data from ISO-NE, preprocessed as described in Section "Dataset and preprocessing", served as the input to the forecasting model. Data partitioning details are provided in Table 6. The performance of SADE-KAN was benchmarked against conventional MLP, the original KAN, and several recently proposed state-of-the-art models. Evaluation was based on key performance indicators, including mean absolute error (MAE), root mean squared error (RMSE), mean absolute percentage error (MAPE), training time, and model complexity (measured by the number of parameters), across multiple forecasting horizons.

Table 6.

Division of training, validation and testing sets of the data.

Dataset	Training set	Validation set	Testing set
From	01/01/2019 01:00	01/01/2023 01:00	01/07/2023 01:00
To	31/12/2022 00:00	30/06/2023 00:00	31/12/2023 00:00

The experiments were structured to systematically compare the performance of these models with differing architectures, in order to comprehensively assess their impact on forecasting accuracy, training efficiency, and model complexity. Each model is trained for 200 epochs using the Adam optimizer with a learning rate of 0.001 and mean squared error (MSE) as the training and validation loss function calculated as ⁴⁹

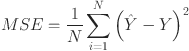14

The evaluation metrics used in this experiment to assess the performance of these networks are MAE, RMSE, and MAPE, which are calculated as ⁴⁹

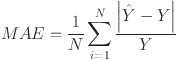15

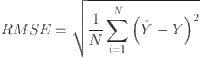16

17

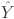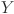where N denotes number of samples, and represents the predicted and corresponding actual load respectively. By averaging the squared differences between observed and predicted values, the MSE offers a precise evaluation of model performance. The squaring step penalizes larger errors more heavily, making the metric suitable for addressing outliers and significant deviations. The MAPE quantifies the average deviation between the predicted values and the actual values, expressed as a percentage. The MAE, on the other hand, calculates the average of the absolute differences between predicted and actual values, providing a direct and interpretable measure of the average forecasting error. In contrast, the RMSE measures the standard deviation of the differences between the predicted and actual values, providing insight into the magnitude of prediction errors. Lower values of MAE, MAPE and RMSE indicate superior model performance, showing more accurate and reliable forecasts.

Results and comparative assessment

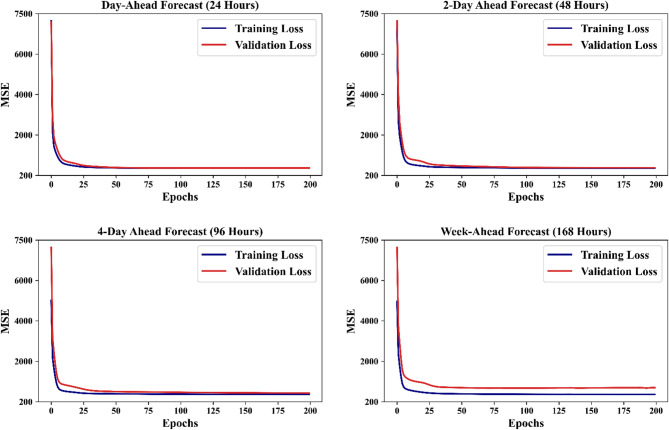
The evaluation results of the SADE-KAN model reveal significant insights into its performance in comparison to the traditional MLP, the original KAN and recently published advanced models. The results indicate that the predictions obtained using our proposed model better approximate the actual system load across all forecasting horizons, demonstrating robust generalization to unseen data. This is particularly evident in Fig. 6 which depicts the training and validation loss curves across all forecast horizons. The curves reveal a rapid convergence and robust learning of the underlying data patterns without overfitting. The training loss demonstrates a steady decrease with each epoch, while the validation loss follows a similar trajectory which shows robust generalization to unseen data. This stability in the learning process proves the robustness and reliability of the proposed SADE-KAN.

Fig. 6.

KANs learning evaluation on ISO-NE-CA hourly data.

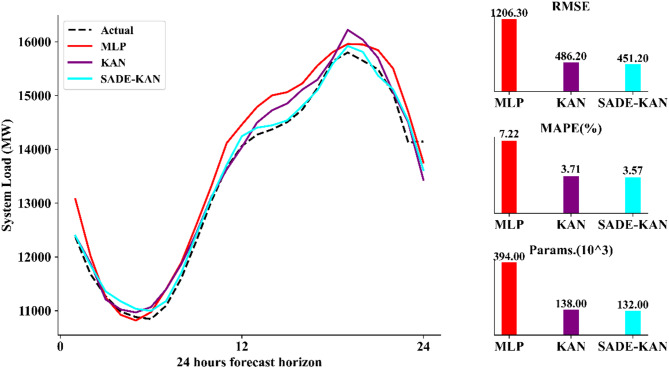
Additionally, Fig. 7 illustrates the 24-h forecasting performance, where SADE-KAN captures rapid changes in system load more effectively than both the KAN and MLP models. While the original KAN and MLP show occasional over-prediction or under-predictions, especially in the middle hours of the forecast horizon, SADE-KAN adapts more quickly to sudden shifts in load demand. This enhanced adaptability demonstrates suitability of the SADE-KAN for dynamic load forecasting, which is a critical aspect of effective load management.

Fig. 7.

One day ahead forecasted load with hour resolution using MLP, KAN and SADE-KAN.

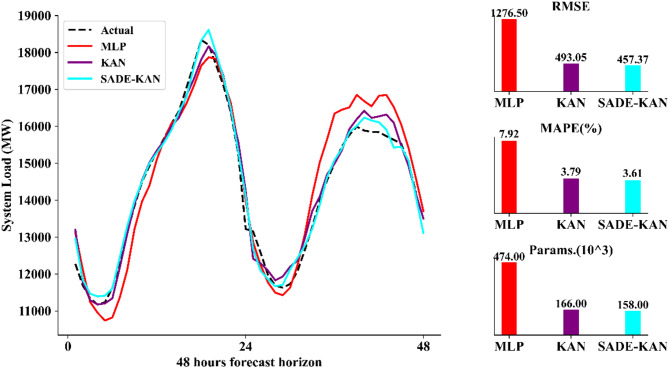
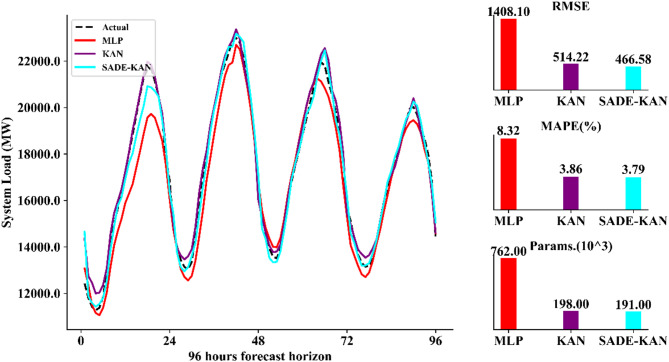
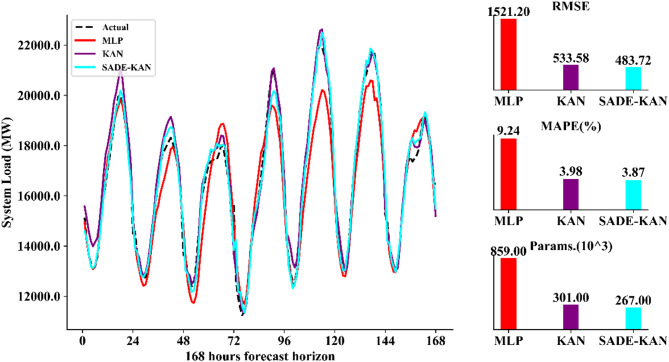
Further, the capability of SADE-KAN to capture dynamic load variations is evident in the load forecasts for the next 48 h, 96 h and 168 h as illustrated in Figs. 8, 9, and 10 respectively. SADE-KAN consistently outperforms both the original KAN and MLP models in capturing rapid load fluctuations, especially at longer forecast horizons. While KAN demonstrates a robust capacity to model load variations, it shows some limitations in tracking abrupt changes compared to the enhanced adaptability of SADE-KAN. In contrast, the MLP model exhibits a noticeable lag in responding to these variations, particularly over the longer horizons, where it struggles to capture immediate shifts in load. The ability of SADE-KAN to adjust quickly and accurately to these dynamic changes across longer forecasting horizons not only demonstrates its robustness but also makes it a more reliable and effective model for STLF.

Fig. 8.

Two days ahead forecasted load with hour resolution using MLP, KAN and SADE-KAN.

Fig. 9.

Four days ahead forecasted load with hour resolution using MLP, KAN and SADE-KAN.

Fig. 10.

Week ahead forecasted load with hour resolution using MLP, KAN and SADE-KAN.

To comprehensively quantify the performance of our proposed model, a thorough comparison with MLP and KAN is presented in Table 7. The table displays several key performance metrics including, MAPE, MAE, RMSE, training time, and the count of trainable parameters across four forecasting horizons, 24, 48, 96, and 168 h. Across all horizons, SADE-KAN consistently achieves the lowest error values, with a MAPE ranging from 3.57% (24-h horizon) to 3.87% (168-h horizon), compared to 3.71–3.98% for KAN and a significantly higher 7.22–9.24% for MLP. Similarly, MAE and RMSE values follow the same trend. For instance, at the 168-h horizon, SADE-KAN achieves an RMSE of 483.72 MW and an MAE of 397.16 MW, outperforming KAN (533.58 MW RMSE, 435.75 MW MAE) and substantially surpassing MLP (1521.2 MW RMSE, 1176.2 MW MAE). This consistent accuracy across increasing horizons underlines robustness and generalization capability of the SADE-KAN. Particularly, while MLP suffers a sharp degradation in performance as the horizon lengthens, SADE-KAN maintains stable accuracy with only marginal increases in error metrics.

Table 7.

SADE-KAN evaluation results on the testing set compared to MLP and Conventional KAN.

Model	Horizon	MAPE	MAE	RMSE	Training time (Sec)	Parameters (103)
MLP	24 h	7.22	957.58	1206.3	147.8	394
	48 h	7.92	986.24	1276.5	176.9	474
	96 h	8.32	1055.7	1408.1	224.7	762
	168 h	9.24	1176.2	1521.2	382.2	859
KAN	24 h	3.71	393.25	486.21	1113.7	138
	48 h	3.79	402.12	493.05	1590.2	166
	96 h	3.86	416.27	514.22	1862.6	198
	168 h	3.98	435.75	533.58	2697.2	301
SADE-KAN	24 h	3.57	353.69	451.22	1519.9	132
	48 h	3.61	366.37	457.37	1712.4	158
	96 h	3.79	379.29	466.58	1819.9	191
	168 h	3.87	397.16	483.72	2307.2	267

In terms of computational cost, SADE-KAN incurs higher training times than MLP but remains comparable to or slightly more efficient than the original KAN. For example, at the 96-h horizon, SADE-KAN completes training in 1819.9 s, whereas KAN requires 1862.6 s. Moreover, SADE-KAN achieves this improved performance with a slightly reduced number of trainable parameters compared to KAN, further highlighting the efficiency of the proposed model.

A significant advantage of SADE-KAN is its performance in both accuracy and parameter efficiency. With only 132,000 trainable parameters for the 24-h forecasting horizon, SADE-KAN significantly reduces model complexity compared to the MLP, which requires 394,000 parameters for the same task. Across all forecasting horizons, SADE-KAN utilizes, on average, approximately 35% of the parameters used by the MLP, while also improving upon parameter count of the original KAN. This substantial reduction in model size indicates that SADE-KAN can deliver superior forecasting performance with lower computational overhead which is a critical attribute for deployment in resource-constrained environments.

In terms of performance, SADE-KAN outperforms MLP significantly across all forecast horizons, delivering lower error metrics. Moreover, SADE-KAN enhances the original KAN by refining its training process and boosting its ability to capture complex load dynamics. These improvements ensure that our proposed model provides more reliable and precise forecasts.

In terms of accuracy, SADE-KAN consistently outperforms the MLP across all forecast horizons, achieving significantly lower MAPE, MAE, and RMSE values. Furthermore, it enhances the original KAN by optimizing its training process and improving its capacity to model complex load patterns. These enhancements result in more precise and reliable forecasts, particularly for extended horizons where traditional models often degrade in performance.

While the proposed model achieves these gains, it still requires longer training time than MLP. This remains the only area where MLP holds an advantage. However, compared to the original KAN, SADE-KAN slightly reduces the training time, offering improvement in computational efficiency. Despite the longer training duration relative to MLP, the substantial improvements in forecast accuracy and reduced error rates make SADE-KAN a much more effective model for STLF practices.

Input features sensitivity analysis

The performance of the SADE-KAN model varies significantly with the number of input features used, as illustrated in Table 8. In this table, the GCA grade represents the proportion of features retained, and its effect on model performance is analyzed across all forecasting horizons. Initially, with 18 input features with GCA grade 0.5, the model exhibits relatively high error metrics, with an RMSE of 1296.78 MW, MAE of 989.65 MW, and MAPE of 6.9%. However, as the number of features is reduced, its performance improves, reaching optimal accuracy at GCA grade 0.7 with 8 features. At this level, the RMSE drops to 451.22 MW, MAE to 353.69 MW, and MAPE to 3.57%, indicating that a moderate reduction in input features enhances its ability to forecast load with greater precision.

Table 8.

Performance of the SADE-KAN in varying input features.

GCA Grade	0.5	0.6	0.7	0.74	0.9	1.0
RMSE (MW)	1296.78	755.23	451.22	492.18	583.29	N/A
MAE (MW)	989.65	523.96	353.69	386.92	421.84	N/A
MAPE (%)	6.9	4.02	3.57	3.87	6.52	N/A
No. of input features	18	13	8	5	2	0

Further reduction in the number of features, as seen at GCA grades 0.74 and 0.9, leads to a slight deterioration in performance. The RMSE increases to 492.18 MW and 583.29 MW, respectively, while MAPE rises to 3.87% and 6.52%. These results suggest that while reducing input features can improve model performance up to a point, there is a threshold beyond which accuracy declines due to the loss of critical information that is necessary for effective forecasting.

Performance in longer forecast horizons

The forecasting capability of SADE-KAN across extended time horizons is presented in Table 9. This evaluation aims to assess its temporal generalization ability and its capacity to maintain predictive accuracy as the forecast window is stretched from 24 to 168 h.

Table 9.

Performance of the SADE-KAN in extended horizons.

Forecast Horizon	MAPE (%)	MAE (MW)	RMSE (MW)	Run. Time (Sec)
24 Hours	3.57	353.69	451.22	1519.9
48 Hours	3.61	366.37	457.37	1712.4
96 Hours	3.79	379.29	466.58	1819.9
168 Hours	3.87	397.16	483.72	2307.2

At the 24-h horizon, SADE-KAN achieves a MAPE of 3.57%, MAE of 353.69 MW, and RMSE of 451.22 MW, establishing a strong baseline performance. As the forecasting horizon extends to 48, 96, and 168 h, the model exhibits a gradual increase in error, which is expected due to the cumulative uncertainty associated with longer temporal predictions. However, the degradation is minimal and consistent, indicating its robustness. Specifically, at 168 h, the MAPE increases only to 3.87%, with MAE and RMSE rising moderately to 397.16 MW and 483.72 MW, respectively. This marginal increase in forecasting error over a 7-day horizon is a noteworthy result. It suggests that SADE-KAN is capable of learning complex temporal dependencies and preserving stability over extended prediction intervals. Additionally, while the runtime increases with the horizon, growing from 1519.9 s for 24 h to 2307.2 s for 168 h, the computational cost remains within practical limits.

Importantly, the model avoids the steep performance degradation typically seen in conventional architectures such as MLP when extrapolated to multi-day forecasts. These results affirm that SADE-KAN not only delivers high accuracy for immediate forecasts but also sustains performance across longer-term horizons, making it suitable for diverse STLF applications with varying planning requirements.

Performance compared to advanced models

To further establish the efficacy and competitiveness of the proposed SADE-KAN model, its forecasting performance was benchmarked against several recently published advanced machine learning and deep learning approaches. The comparison, summarized in Table 10, includes state-of-the-art models such as Bi-directional LSTM (Bi-LSTM) ⁵⁰, CNN-LSTM hybrid ⁵⁰, extreme gradient boosting (XGBoost) ⁵¹, light gradient boosting machine (LightGBM) ⁵¹, and an ensemble of XGB, gradient boosting regressor (GBR), support vector regressor (SVR) and K nearest neighbors (KNN) reported in ⁵².

Table 10.

Performance of the SADE-KAN compared to recently published advanced models.

Algorithm	RMSE (MW)	MAE (MW)	MAPE (%)	Run. Time (Sec)
Bi-LSTM 50	562.25	408.14	4.62	N/A
CNN-LSTM 50	483.21	370.51	4.24	N/A
XGBoost 51	943.98	668.32	12.7	3643.24
LGBM 51	700.67	495.06	3.85	3664.78
XGB + GBR + SVR + KNN 52	2920.7	2282.1	3.69	1234.12
SADE-KAN	451.22	353.69	3.57	1519.9

SADE-KAN consistently outperforms all compared models across key accuracy metrics. It achieves the lowest MAPE of 3.57%, indicating superior relative error performance. In terms of absolute metrics, SADE-KAN attains an RMSE of 451.22 MW and an MAE of 353.69 MW, both of which are the lowest among all models presented. While the ensemble method reports a comparable MAPE of 3.69%, its extremely high RMSE of 2920.7 MW and MAE of 2282.1 MW expose significant absolute deviation, suggesting poor generalization despite a favorable percentage error.

Compared to Bi-LSTM and CNN-LSTM, SADE-KAN offers clear gains in accuracy. It reduces MAPE by 22.7% and 15.8% relative to Bi-LSTM and CNN-LSTM, respectively, while also improving RMSE and MAE. Particularly, SADE-KAN also demonstrates a more efficient runtime profile than gradient boosting models such as XGBoost and LGBM, which require over 3600 s for training. SADE-KAN completes training in 1519.9 s, offering a practical balance between accuracy and computational cost.

In summary, SADE-KAN surpasses the accuracy of deep learning and ensemble-based models, while maintaining computational feasibility. These results underscore its effectiveness and suitability for real-world STLF applications where both precision and efficiency are critical.

Conclusion

In summary, this study proposed the Kolmogorov–Arnold network optimized with Self-Adaptive Differential Evolution (SADE-KAN) for short-term load forecasting (STLF). By substituting the static linear weights of conventional MLP with adaptive spline-based activation functions, the KAN architecture effectively captures nonlinear dependencies in power system load data. Its optimization using SADE further enhances learning efficiency, mitigates overfitting through dynamic parameter tuning, and reduces complexity.

The experimental results revealed that SADE-KAN consistently delivered superior accuracy across all tested forecasting horizons (24, 48, 96, and 168 h), significantly outperforming both MLP and the original KAN in terms of RMSE, MAE, and MAPE. Particularly, SADE-KAN achieves the lowest MAPE values, ranging from 3.57% at the 24-h horizon to 3.87% at the 168-h horizon, compared to 3.71–3.98% for KAN and 7.22–9.24% for MLP. The same trend is evident in MAE and RMSE values. This consistent performance across increasingly long horizons demonstrates robustness and superior generalization ability of the proposed model, particularly where traditional models like MLP show noticeable performance degradation. In addition to accuracy, the model demonstrates remarkable parameter efficiency. For example, SADE-KAN requires only 132 k trainable parameters at the 24-h horizon, substantially fewer than the 394 k used by MLP, which implies reduced computational complexity and resource demand. Furthermore, the proposed model was benchmarked against several recently published advanced methods, including Bi-LSTM, CNN-LSTM, XGBoost, and ensemble hybrid models. SADE-KAN outperformed all of them in accuracy, achieving a MAPE of 3.57%, MAE of 353.69 MW, and RMSE of 451.22 MW, while also demonstrating more favorable computational efficiency than many of the ensemble and gradient boosting approaches.

While SADE-KAN demonstrates strong forecasting accuracy and parameter efficiency, several limitations remain. First, the model exhibits sensitivity to input feature, this implies that feature selection is crucial as excessive input dimensionality introduces redundancy that impairs learning. Second, SADE-KAN incurs higher training times compared to simpler models like MLP due to its spline-based activation functions. Lastly, the current evaluation of SADE-KAN is limited to ISO-NE load data, broader validation across diverse geographic regions, varying weather conditions, and different load patterns is essential to confirm its generalizability and robustness in real-world applications.

To address the limitations identified in this study, several technical enhancements can be pursued. Given its sensitivity to input dimensionality, advanced feature selection methods could be employed to retain only the most informative inputs. Alternatively, attention-based mechanisms or dimensionality reduction techniques may help reduce redundancy. To mitigate the relatively high training time, future work could explore simplifying the spline functions by reducing the number of knots or opting for less computationally intensive spline types such as linear or quadratic splines. This would reduce the number of trainable parameters and result in faster training times. To improve generalizability across regions and datasets, future research should focus on evaluating SADE-KAN across diverse datasets from different regions and power systems.

Abbreviations

ARIMA

Auto-regressive integrated moving average

Bi-LSTM

Bi-directional long short-term memory

CNN

Convolutional neural network

DCNN

Dilated convolutional neural network

DE

Differential evolution

ES

Exponential smoothing

FFN

Feed-forward network

GRU

Gated recurrent unit

ISO-NE

Independent system operator—New England

KAN

Kolmogorov–Arnold network

KART

Kolmogorov–Arnold representation theorem

KF

Kalman filtering

KNN

K nearest neighbors

LGBM

Light gradient boosting machine

LR

Linear regression

LSTM

Long short-term memory

LTLF

Long-term load forecasting

MAE

Mean absolute error

MAPE

Mean absolute percentage error

ML

Machine learning

MLP

Multi-layer perceptron

MTLF

Medium-term load forecasting

NNs

Neural networks

RMSE

Root mean squared error

RNNs

Recurrent neural networks

SADE

Self-adaptive differential evolution

STLF

Short-term load forecasting

SVR

Support vector regressor

VSTLF

Very short-term load forecasting

XGB

Extreme gradient boosting

Indices and parameters

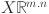
Input feature matrix where m is the number of time steps and n is features

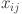
Value of the 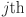feature at the 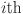timestamp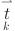

Feature vector at the time step ,

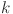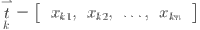
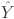
Predicted output load sequence

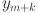
Load value at the 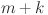th timestamp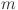

Length of historical observation window

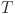
Forecast horizon (total number of prediction steps)

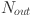
Number of output nodes in KAN

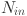
Number of input nodes (flattened features passed to KAN)

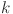
Order of the B-spline basis function

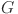
Number of grid intervals of B-spline

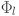
Function matrix applied at layer

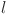
Univariate function on the edge from neuron in layer 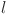to neuron 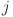in layer

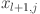
Activation of the 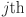neuron in layer

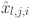
Post-activation output from neuron in layer 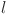to neuron 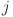in layer

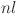
Number of neurons in layer

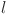
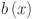
Basis function

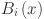
B-spline basis function of order

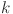
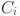
Trainable coefficients for the B-spline basis functions

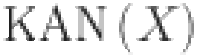
Output of the Kolmogorov–Arnold Network model

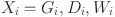
Solution vector comprising KAN hyperparameters

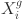
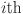Individual (solution) in generation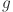

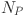
Population size in SADE

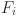
Mutation factor for individual ,  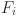∈ [0.4,0.9]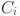

Crossover rate for individual ,  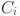∈ [0.1,0.9]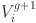

Mutant vector for individual at generation

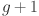
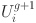
Trial vector after crossover

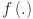
Fitness function evaluating solution quality

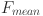
Mean of successful mutation factors

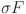
Standard deviation used in sampling mutation factor

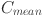
Mean of successful crossover rates

Standard deviation used in sampling crossover rate

Author contributions

Muhammad Abbas, Yanbo Che, Sarmad Maqsood, Muhammad Zain Yousaf: Conceptualization, Methodology, Software, Visualization, Investigation, Writing—Original draft preparation. Saqib Khalid, Wajid Khan: Data curation, Validation, Supervision, Resources, Writing—Review & Editing. Mustafa Abdullah, Mohammad Shabaz, Mohit Bajaj: Project administration, Supervision, Resources, Writing—Review & Editing.

Data availability

The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.