Role of backbone solvation in determining thermodynamic β propensities of the amino acids

Abstract

There is a paradox concerning the β propensities of the amino acids: the amino acids with the highest β propensities such as valine and isoleucine have the highest tendency to desolvate the peptide backbone, which should result in a loss of stability. Nevertheless, backbone solvation, calculated as electrostatic solvation free energy (ESF), is highly correlated with mutant stability in the zinc-finger system studied by Kim and Berg [Kim, C. A. & Berg, J. M. (1993) Nature (London) 362, 267–270], and valine and isoleucine are among the most stabilizing amino acids. This inverse correlation between stability and ESF can be explained, because the mutant ESF differences in the unfolded protein are larger than in the native protein. Consequently, mutations such as Ala to Val destabilize the unfolded form more than the native protein. By comparing mutant ΔESF values in isolated β-strands versus β-sheets, we conclude that amino acids with high β propensities should exert their stabilizing effects at early stages in folding. This deduction agrees with the studies by Clarke and coworkers [Lorch, M., Mason, J. M., Clarke, A. R. & Parker, M. J. (1999) Biochemistry 38, 1377–1385, and Lorch, M., Mason, J. M., Sessions, R. B. & Clarke, A. R. (2000) Biochemistry 39, 3480–3485] of the thermodynamics of folding of the β-sheet protein CD2.d1.

There are large differences among the statistical preferences of the amino acids for β structure (β-sheets or β-hairpins; ref. 1), but the origins of β preferences are ill-defined. Thermodynamic experiments in which protein stability has been measured for variants produced by substituting 20 different amino acids at a single site give conflicting results for β propensities in four systems studied (2–5). This outcome suggests that either more than one effect contributes strongly to β propensities or, if there is one dominant effect, the β propensities must depend strongly on neighboring residues. Some, but not all, of the mutant studies yield good correlations between thermodynamic stability and statistical β preference (2–5).

We reported earlier that solvation of the peptide backbone is a major factor determining thermodynamic helix propensities (6–8, 9, 10), and Makhatadze and coworkers (11) found recently that backbone solvation likewise is important in determining thermodynamic stability when mutants are made at a solvent-exposed position in ubiquitin. We ask here whether peptide backbone solvation is expected to be a major factor determining thermodynamic β propensities.

Calculations (6, 7, 9, 10) and also some experiments (12) show that peptide backbone solvation depends strongly on how side chains affect the access of water to the peptide backbone. The effect of a mutation on backbone solvation can be estimated straightforwardly provided the mutation does not change either the geometry of the peptide backbone or the peptide H bonds. Then, provided also that the side chain rotamers are known, one can use a standard electrostatic algorithm without introducing any adjustable parameters to compute the change in backbone solvation caused by a mutation. The electrostatic solvation free energy (ESF) can be calculated by two alternative approaches (13, 14), the results of which have been compared for tripeptides (7) and found to agree satisfactorily. We use here the DelPhi algorithm and a modified PARSE parameter set in which the side chain atomic charges are set to zero. The PARSE parameter set (13) has been calibrated against an experimental database of solvation free energies measured for polar small molecules. The resulting ΔESF value for a mutation can be compared directly with experiment without using any scaling factor. Because the parameters used in calculating ESF values have been calibrated against solvation free energies, the mutation-induced ΔESF values should be reliable.

Our procedure is to compute the predicted ESF values of the mutants in the experiments of Kim and Berg (2), Minor and Kim (3, 4), and Smith et al. (5) and then to ask whether ESF is correlated with thermodynamic stability in these experiments. We find that there is a strong correlation (correlation coefficient, 0.94) between stability and ESF for the zinc-finger mutants studied by Kim and Berg (2), and our main objective is to understand this result. The correlations in the other systems studied are not as good, and we briefly consider additional factors that may affect thermodynamic stability in these studies (3–5).

ESF Values of Mutants in the Zinc-Finger System Studied by Kim and Berg

Kim and Berg used the metal-dependent folding of a zinc-finger protein to measure spectrophotometrically the free energy change for its unfolding reaction by varying the free Co(II) concentration, for which there is a competition between the protein and a chromophoric indicator (2). In this way they were able to measure differences in unfolding free energy between mutants with excellent precision even though the free-energy differences are small. They studied a solvent-exposed nonhydrogen-bonded position (residue 3) in the β-hairpin moiety of a 26-residue zinc finger, CP-1. In the absence of metal ion, CP-1 is unfolded completely.

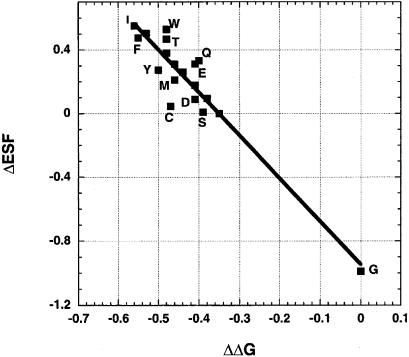
Fig. 1 shows the plot of the change in backbone solvation (ΔESF) versus the change in thermodynamic stability (ΔΔG of unfolding) for variants with 19 different amino acids at position 3 of CP-1; proline is excluded. To find ΔESF for a mutant, the total ESF of all peptide groups in the sequence is calculated, and then the ESF of the alanine variant is subtracted from that of the mutant. ESF calculations require accurate coordinates. The X-ray structure of a designed zinc finger (PDB code 1mey) is available that is highly homologous to CP-1. Although the X-ray structure shows 1mey bound to DNA, several NMR structures of free zinc-finger proteins are available that are very similar to the structure of 1mey, suggesting that DNA binding does not change the structure especially of the β-hairpin moiety, which is not bound to DNA. Consequently, the X-ray structure of 1mey can be used for ESF calculations after making adjustments for sequence differences. Details of the structures used for ESF calculations are given in the legend to Fig. 1.

Figure 1.

Linear relation between the mutant ΔESF values in the native state and mutant ΔΔG values in the zinc-finger system studied by Kim and Berg (2). Amino acid outliers are labeled. The correlation coefficient is −0.94, and the units (both axes) are kcal/mol. On the y axis, ΔESF is the difference between the mutant ESF and that of the alanine variant, both in the native form; on the x axis, ΔΔG is the difference in free energy of unfolding between the mutant and the glycine variant. The x-ray coordinates of the segment c32–c57 of 1mey in the Protein Data Bank are used for the zinc-finger protein studied by Kim and Berg (2). To obtain the same sequence studied by Kim and Berg, residues c45 and c49 are replaced by Lys and Val. Residue c34 is the mutated site (residue 3 in the notation of Kim and Berg), and standard χ1 torsion angles are used for all residues substituted at this position. For all residues except Val, the standard torsion angle is −60°, but for some residues this choice causes a steric clash with c41 Ser, the χ1 torsion angle of which was therefore changed to +60°.

The strong correlation between ΔESF and ΔΔG for the mutants shown in Fig. 1 indicates that ESF should be a main determinant of thermodynamic stability for these mutants. However, if the difference between the ESF value of a mutant and the alanine variant is the only contributor to ΔΔG, then ΔESF should have the same sign as ΔΔG and should be numerically equal to ΔΔG, whereas in Fig. 1 the ΔESF values are numerically larger than the ΔΔG values, and they have opposite signs. The explanation may reside in the mutant ESF values in the unfolded form; although ΔΔG includes both a difference in free energy between the native and unfolded forms and a difference in stability between the mutant and the alanine variant, ΔESF in Fig. 1 includes only the difference in ESF between the native forms of the mutant and the alanine variant, and the ΔESF difference in the unfolded form must be subtracted to complete the analysis.

ESF Values of Mutants in the Unfolded State

It is straightforward to calculate mutation-induced ΔESF values in a known structure such as the native form of the zinc finger CP-1, provided the backbone geometry and side chain torsional angles are known accurately. The mutation-induced difference in ESF arises only from the mutant side chain, which alters the ESF, because it affects the access of water to the backbone. The problem of calculating a mutation-induced difference in ESF in the unfolded state is more difficult, because information is lacking about the conformation of the unfolded state. A commonly used model for an unfolded protein is the COIL model of Smith et al. (15), in which the backbone conformation of any residue, say a leucine residue, is chosen at random from the conformations of leucine residues in 85 protein structures taken from the Protein Data Bank, excluding those leucine residues that appear in secondary structure. The backbone conformations of each amino acid are divided into three major categories: “core α,” “core β,” and “other.” The backbone conformations of leucine in the COIL model are 25% core α, 63% core β, and 12% other (15), meaning that (according to this model) every leucine residue in an unfolded protein exists 25% of its time in core α, 63% in core β, and 12% in other backbone conformations such as polyproline II. The major backbone conformation in the COIL model is core β for every amino acid except Gly and Asp. The COIL model for the unfolded state is only one of several models being tested currently by various workers, and it is used here only for illustration.

Our approach to the problem of estimating ΔESF values for mutants in the unfolded state is as follows. Because the β conformation is the major backbone conformation according to the COIL model, and because mutations made in an all-alanine background are the simplest to interpret, we begin with a 15-residue all-alanine extended β-strand (φ = −120°, ψ = 120°) and mutate a single residue (residue 9) either in the α or β conformation. To give the β conformation, residue 9 remains β; to give the α conformation, residue 9 is α (φ = −65°, ψ = −40°), and all other residues are β. Because the peptide NH and CO dipoles are parallel in the α conformation but antiparallel in the β conformation (9, 16), the ESF of a given peptide group depends strongly on its own backbone conformation (β, α, or other) and to a lesser extent on those of neighboring residues.

Mutation-induced ΔESF values in the α and β conformations, in an extended β-strand background, are given in Table 1. The ΔESF value is numerically larger when residue 9 is in the α conformation than in the β conformation for all amino acids except Thr. In the COIL model of the unfolded state (15), all amino acids except Asp, Glu, Ser, and Thr have values for core α-backbone conformations between 20 and 34%. A possible model for calculating mutant ΔESF values in the unfolded state then is to make ΔESF a composite of the α and β values given in Table 1 by using the proportions given in the COIL model. Because this model is very approximate, and for simplicity, the proportions are taken to be 25% α and 75% β for all amino acids. A typical residue in an unfolded protein has neighboring residues in the β conformation according to the COIL model, and this is true of the mutated residues in Table 1. A basic result from Table 1 is that mutant ΔESF values are numerically larger in the unfolded state than in an extended β-strand for all amino acids except Ser and Thr. This property is a consequence of the striking difference in the NH–CO dipole-dipole interactions between the β- and α-backbone conformations (9, 16).

Table 1.

Mutation-induced changes in ESF in the β- and α-backbone conformations and in a simplified model for the unfolded state and in the native form of a zinc-finger protein^*

Amino acid	ΔESF(β)†	ΔESF(α)†	ΔESF(U)†	ΔESF(N)†
Gly	−0.49	−1.02	−0.62	−0.99
Ala	0.00	0.00	0.00	0.00
Val	0.71	1.14	0.82	0.51
Ile	0.72	1.12	0.82	0.55
Leu	0.73	0.89	0.77	0.38
Phe	0.71	1.67	0.95	0.48
Met	0.35	0.82	0.47	0.21
Trp	0.68	1.57	0.90	0.53
Cys	0.29	0.77	0.41	0.04
Ser	0.14	0.15	0.14	0.01
Thr	0.47	0.44	0.46	0.47
Asn	0.36	0.76	0.46	0.09
Gln	0.34	0.80	0.46	0.33
Tyr	0.67	1.52	0.88	0.27
His	0.56	1.34	0.75	0.31
Asp	0.40	0.80	0.50	0.09
Glu	0.35	0.81	0.47	0.31
Lys	0.36	0.84	0.48	0.18
Arg	0.38	0.78	0.48	0.26

^*The units are kcal/mol. ΔESF refers to the total ESF of the mutant peptide or protein (the sum of the ESF values of all peptide groups) minus the total ESF of the alanine variant. The ΔESF values of all mutants except Gly have positive signs, meaning that the mutant is less solvated than the alanine variant. 

^† ΔESF(α) and ΔESF(β) are the mutant ΔESF values in the α-(−65°, −40°) and β-(−120°, 120°) backbone conformations in an extended β-strand background. The host peptide is a 15-residue alanine peptide, the ends of which are blocked by acetyl and N-methyl groups. The mutated residue, number 9, is present in either the α- or β-backbone conformation. ΔESF(U) gives values for the simplified model of the unfolded state (see text) obtained by adding 75% β and 25% α, where the β and α values are given in the preceding two columns. ΔESF(N) is the value calculated for the native form of the zinc-finger protein studied by Kim and Berg (2). 

Moreover, Table 1 shows that the mutant ΔESF values are numerically larger in the unfolded state than in the native state of the zinc-finger protein except for Gly and Thr. This result explains the inverse correlation between mutant ΔΔG and mutant ΔESF values in the zinc-finger system studied by Kim and Berg (Fig. 1). Although decreasing solvation implies decreasing stability, the native zinc finger is stabilized by an indirect mechanism in which desolvating mutations destabilize the unfolded state more than the native state. The native-state mutant ΔESF values are numerically smaller than those in the model for the unfolded state except for Gly and Thr. In fact, the native-state ΔESF values are smaller than those in an extended β-strand except for Gly and Thr (Table 1).

Thus, the results in Table 1 provide plausible answers to both questions arising from Fig. 1. Why is there an inverse correlation between ESF and stability? It is because mutant ΔESF values are larger in the unfolded state than in the native state. Why are the mutant ΔESF values in Fig. 1 numerically larger than the ΔΔG values? It is because the appropriate ΔESF values include differences between the native and unfolded states, and only the native-state ΔESF values are shown in Fig. 1. Unfortunately, reliable mutant ΔESF values for the unfolded state cannot be supplied at this time because of the lack of knowledge about the conformation of the unfolded state. The native-state ΔESF values for the zinc-finger protein are correlated closely with those in the model of the unfolded state given in Table 1 (correlation coefficient 0.994) and also in the extended β-strand (correlation coefficient 0.996), which helps to explain the good correlation shown in Fig. 1 between ΔΔG values, which include differences between the native and unfolded states, and ΔESF values, which are given only for the native protein.

Comparison with Other β-Propensity Studies

For comparison with the later work of Minor and Kim (3, 4) and Smith et al. (5), ESF values were calculated for the β-sheet protein GB1 by using the exact sequences they studied, and mutant ΔESF values then were computed at the sites that they studied. Minor and Kim studied first mutants made at residue 53 of GB1 (3); this site is a surface-exposed position inside a center strand. Later they studied residue 44 of GB1, which is inside an edge strand. They replaced certain neighboring residues of the mutated site with the aim of simplifying interpretation of the mutant results. Smith et al. (5) likewise studied position 53 of GB1 but without replacing neighboring residues.

Although the β propensities obtained from ΔΔG values in these three studies are not uniform either in rank order or numerical value, nevertheless the three studies have in common the following features when compared with the results of Kim and Berg (2). First, the ΔΔG values in the studies by Minor and Kim (3, 4) and Smith et al. (5) are larger than those of Kim and Berg (2). The difference in ΔΔG for unfolding between the Ala variant and the most stable mutant is only 0.21 kcal/mol for Kim and Berg (2), whereas it is 1.1 kcal/mol for the first system of Minor and Kim (3), site 53, 0.83 kcal/mol for the second system of Minor and Kim (4), site 44, and 1.63 kcal/mol for Smith et al. (5), site 53. Second, Kim and Berg (2) found a good correlation between stability and statistical β preference (correlation coefficient, 0.83 excluding Gly and Pro), whereas Minor and Kim (3, 4) and Smith et al. (5) do not report correlation coefficients from their studies. We find that when Gly and Pro are excluded, the correlation coefficient between stability and statistical β preference at site 53 is 0.79 for the first system of Minor and Kim (3) and 0.74 for Smith et al. (5), although it is only 0.25 at site 44 for the second system of Minor and Kim (4).

The mutant ΔESF values in the studies by Minor and Kim (3, 4) give only weak correlations between ΔESF and ΔΔG: the correlation coefficient was 0.57 for the first system of Minor and Kim (3), site 53, and the correlation coefficient was 0.47 for the second system of Minor and Kim (4), site 44. The correlation is given for 19 amino acids, with proline excluded, and the ΔESF values are computed for the altered sequences studied by Minor and Kim. There are some evident reasons for the weak correlations between ΔΔG and ΔESF values. First, other energetic factors besides ESF, particularly burial of nonpolar surface area, contribute more to the ΔΔG values in the β-sheet protein GB1 than in the solvent-exposed β-hairpin studied by Kim and Berg [ref. 2; see the discussion by Minor and Kim (4)]. Second, the mutant ΔESF values are more difficult to interpret in a β-sheet protein than in a solvent-exposed β-hairpin, because the protein structure is more complex. In GB1 the side chain of a mutant amino acid may hinder the access of solvent to peptide groups not only in the same peptide strand but also in a neighboring strand, away from the site of mutation. Finally, NMR data (17) indicate the presence of important residual structure in residues 42–51, which include mutated site 44 of GB1. The presence of residual structure in a segment of the denatured protein makes the COIL model (15) an unsatisfactory representation for this segment.

Backbone Solvation at Later Stages in Folding of a β-Sheet

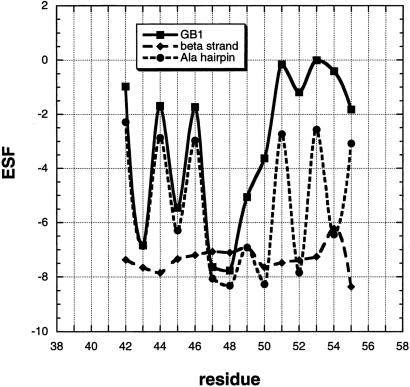
Backbone solvation is affected chiefly by two factors in addition to backbone geometry: the access of solvent to the peptide group and the presence or absence of hydrogen bonds, either peptide or side chain–main chain H bonds. These two effects are illustrated in Fig. 2 with plots of ESF versus residue position for a 14-residue segment (residues 42–55) of protein GB1. Two related plots are shown in addition to the one showing GB1 itself. In the first plot, the backbone structure of GB1 is retained, but all amino acids are replaced by alanine, giving an alanine β-hairpin. Comparison between this plot and that for GB1 shows how side chains in GB1 reduce the accessibility of water to the backbone. The second plot shows the ESF values of peptide groups in an extended β-strand that has the sequence of GB1 studied by Minor and Kim (3). This second plot shows how side chains reduce the accessibility of water to the peptide backbone when the conformation is an extended β-strand and no H bonds are present.

Figure 2.

ESF plotted against residue number for a 15-residue segment of protein GB1 with the sequence studied by Minor and Kim (3). The units of ESF are kcal/mol. ESF values are calculated by DelPhi (13) with the probe radius = 1.4, a protein dielectric constant of 2.0, with the salt concentration and ion radius set to zero, and the side chain point atomic charges set to zero. The ESF values of the native protein are shown and compared with those of the same sequence in an extended β-strand conformation. The third plot shows the ESF values of an alanine hairpin β-peptide, the backbone conformation and peptide H bonds of which are the same as those of native GB1. The GB1 sequence is EWAYDDATKSFTVS (residues 42–55), and the PDB entry for GB1 is 2gb1.ent.

Some important properties of backbone solvation in β-structure can be seen in Fig. 2. First, the effects of backbone geometry and peptide H bonds are large; they can be seen in the alanine β-hairpin plot as well as in the plot for GB1 itself. The residues whose peptide groups are H-bonded (residues 42, 44, 46, 51, 53, and 55) are picked out easily by their low ESF values. Note that these H-bonded peptide groups still interact strongly with water; they have nonzero ESF values between −2.6 and −3.0 kcal/mol, close to the −2.5 kcal/mol found earlier (6) for H-bonded peptide groups in the interior of an alanine helix. Residues 47–50 form a reverse turn that is well solvated, and these residues have high numerical ESF values. The loss in stability resulting from desolvation when a peptide H bond is formed is approximately compensated by the energy of the H bond itself if the gas phase value of −6.6 kcal/mol (18) is used for the peptide H bond.

The second conclusion is that side chains in GB1 reduce the backbone solvation substantially; this can be seen by comparing GB1 itself with the simplified all-alanine version, which has the same backbone geometry. Indeed, the mutant site 53 studied both by Minor and Kim (3) and Smith et al. (5) has an ESF value of only −0.005 kcal/mol in GB1, although this site in the corresponding alanine hairpin has a negative ESF value numerically greater than 2, similar to all other sites in the alanine hairpin (Fig. 2). Thus, mutations made at site 53 in GB1 cannot reduce appreciably its numerical ESF value, which is already close to zero. In this case, the mutant ΔESF value has little meaning. Residue 44, the mutant site in an edge position of GB1 (4), is H-bonded and has an ESF value of −1.7 kcal/mol. In contrast, the mutant edge site (residue 3) studied by Kim and Berg (2) is not H-bonded and has the more substantial ESF value of −5.5 kcal/mol with Gly at residue 3.

The third general conclusion from Fig. 2 is that side chains, when examined in a uniform β-strand background without peptide H bonds, have relatively small effects on ESF compared with the larger effects of backbone geometry and peptide H bonds. Nevertheless, the mutant ΔESF values caused by side chains in this background are highly significant, as illustrated in Table 1 (see also ref. 6).

The β-Sheet Mutants of CD2 Studied by Clarke and Coworkers

The folding of domain 1 of the cell surface protein CD2 (CD2.d1) has been analyzed in detail by Lorch et al. (19, 20). This 98-residue protein, the structure of which is a β sandwich, or two β-sheets arranged in the Ig fold, shows a well populated transient folding intermediate. In a remarkable series of experiments, the free energy, enthalpy, entropy, and heat capacity changes produced in forming the intermediate, the transition state, and the native state from the unfolded protein all have been determined, both for wild type and a set of core mutants. The basic assumption is that both the transient intermediate and the transition state are formed in two-state reactions. The mutations studied are made by truncation of aliphatic amino acids such as the mutation Val to Ala, in which two-CH₂ groups are deleted. The authors provide their own quantitative β-propensity scale for these nonpolar amino acids (19) based on frequencies of residues in the β region of the φ,ψ map of backbone angles by using structures in the Protein Data Bank. Their rank order of β propensities is Val, Ile, Leu, Ala, and Gly.

The first of their conclusions germane to our study is that most mutations with favorable β propensities stabilize the molten globule intermediate even though they destabilize the folded protein (19). Thus, β-propensity mutations are most effective at an early stage in folding, as we argue here from comparing the mutation-induced changes in ESF in isolated β-strands with those in a β-sheet. Second, the mutants with favorable changes in β propensity show favorable changes in enthalpy when the intermediate is formed (20). The authors conclude that β propensities probably are enthalpic in origin and arise from changes in backbone solvation as proposed by Avbelj and Moult (9). Their conclusion agrees with work on the origin of helix propensities, which have been shown to be largely enthalpic for the aliphatic amino acids (8). Finally, Lorch et al. (20) observe that formation of the folding transition state from the unfolded protein is opposed by a large unfavorable enthalpy change, contrary to popular models for the folding process. They propose that the unfavorable enthalpy change is caused by the presence of isolated water molecules in the transition state. We propose instead that the unfavorable enthalpy change is caused by stripping water molecules from H-bonded peptide CO groups in the folding intermediate. The interaction of water with H-bonded peptide groups is shown here in Fig. 2, especially in the plot for the alanine β-hairpin.

Concluding Comments

Avbelj and Moult (9) proposed that both helix and β propensities should arise from the screening by water dipoles of electrostatic interactions among CO and NH dipoles in the peptide backbone, because these interactions are large and can be screened substantially by water, and amino acid side chains strongly affect the access of water to the peptide backbone. A later study (6) based on ESF calculations showed that water interacts strongly (−2.5 kcal/mol) with a peptide group in the interior of an alanine helix, and it is this residual backbone solvation that is affected by mutation (6). This conclusion contradicts the common assumption that there is no interaction between a peptide group and water after the peptide H bond is formed. According to the ESF calculations, most of the interaction between water and an H-bonded peptide group in a helix occurs with the peptide CO group [−2.0 kcal/mol (6)]. The mutant ΔESF values for some aliphatic amino acids in an alanine helix are comparable in size to observed helix-propensity differences (6). Experiments on thermal unfolding of peptide helices monitored by circular dichroism show that helix-propensity differences among aliphatic amino acids arise chiefly from differences in their enthalpies of unfolding (8). The enthalpy differences probably result from backbone solvation, because experimental transfer data for amides show that their ESF values are almost entirely enthalpic (6).

The situation is different with β propensities. Amino acids with high β propensities such as Val and Ile are highly desolvating, as shown in Table 1 by ΔESF values. Nevertheless, there is an excellent correlation between mutant ΔΔG values for unfolding and mutant ΔESF values in the native state of the zinc-finger system of Kim and Berg (2). Moreover, Val and Ile are among the most stabilizing amino acids in this system. The probable explanation, as we show here, is that mutations such as Ala to Val destabilize the unfolded form more than the native form such that the native form is stabilized indirectly. For this explanation to be valid, it is necessary that β-propensity mutations exert their effects at early stages in folding, for which mutation-induced changes in ESF are modest in size. This deduction agrees with the observation by Clarke and coworkers (19) that most β-propensity mutations stabilize an early folding intermediate of CD2.d1 but destabilize the native form. Interior positions in a folded β-sheet protein tend to have low native-state ESF values (see Fig. 2), because the access of solvent to interior peptide groups is severely limited; mutant ΔESF values are complex and not interpreted easily in this case, as discussed above for GB1.

Street and Mayo (21) use simulations to compute the conformational entropy cost of occupying the β region of the φ,ψ-backbone map for the various amino acids by using three-residue peptides of sequence AXA, fixed bond lengths and angles, and uniform distribution of dihedral angles (φ, ψ, and χ) in their simulations. They conclude that steric interaction of an amino acid side chain with the peptide backbone is a significant factor contributing to thermodynamic β propensities. The entropy differences that they find correspond to rather small free-energy differences (the range is ≈0.15 kcal/mol, see ref. 7), and the experimental free-energy differences between the mutants of Kim and Berg (2) are also small (see Fig. 1 here). The correlation between their entropy differences and the ΔΔG values of Kim and Berg, however, is weak; we find a correlation coefficient of 0.70, with Pro and Gly excluded.

In studies of mutations in proteins, it is rare to find backbone solvation considered as a significant contributing factor. Nevertheless, the numbers given here (Figs. 1 and 2 and Table 1) indicate that solvation is important. The question then arises of how reliable these numbers are for backbone solvation. A recent theoretical analysis of salt bridges in barnase by Vijayakumar and Zhou (22) argues that salt-bridge energetics have been misinterpreted as a result of using the water-accessible, or solvent exclusion, surface as contrasted with the molecular (or joined van der Waals) surface. These authors point out that the solvation free energy is a central factor in their analysis. It will be informative to apply an approach based on the molecular surface (23) to the problem considered here. The point of using the molecular surface (23) rather than assigning a probe radius of zero in the DelPhi algorithm is that solvent then is not assigned erroneously to the interstitial space in which water cannot in fact penetrate. The large free-energy values assigned to peptide solvation when the peptide backbone is exposed to solvent are a direct result of the experimentally determined solvation free energies of amides, as Wolfenden emphasized in his pioneering study of N-methylacetamide (24). The polar contribution to the solvation free energy of N-methylacetamide is −12.2 kcal/mol, and the polar contribution to the solvation enthalpy, which is determined from an independent experimental approach, is nearly as large at −11.5 kcal/mol (6).

Abbreviations

ESF

electrostatic solvation free energy

ΔESF

difference in ESF between a mutant and the reference type (usually the alanine variant)

ΔΔG

difference in unfolding free energy between a mutant and the reference type