Techno-economic optimization of hybrid renewable systems for sustainable energy solutions

Abstract

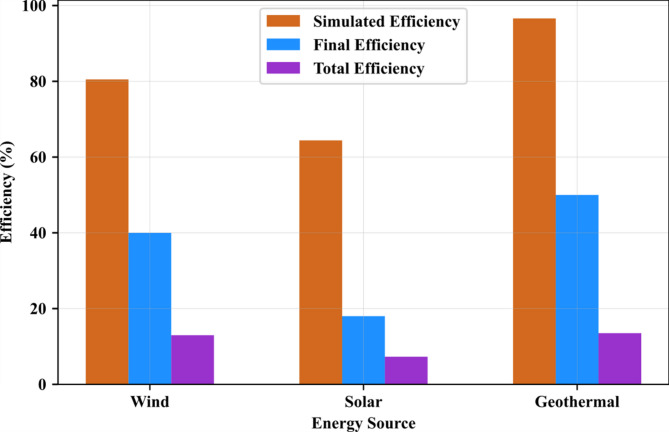
This study is focusing on the techno-economic optimization of hybrid renewable energy systems and the energy. The system integrates geothermal, wind, and solar sources for sustainable hydrogen production its important. The objective is to maximize energy efficiency, reduce operational costs, and ensure stable energy delivering. A simulation-based framework is used for analyse system behaviour under various environmental conditions it helps. The scope includes defining parameter, sensitivity analysis, and optimization using iterative algorithms which are complex. Time-step simulations evaluating energy dynamics help to and performance trade-offs, which is necessary for understanding. The proposed hybrid system achieves 78.5% energy efficiency and 64.3% exergy efficiency, and this is good. It produces 500 kg of hydrogen daily with an LCOE of $0.085 per kWh, which is quite low. Sensitivity results show that a 15% increase in wind speed improves output by 10%, and this is significant. A 20% drop in solar irradiance reduces output by 8%, which is not good. Geothermal contributes 40% of the total energy share, with wind and solar supplying 35% and 25%, respectively, and this shows balance. Optimization improves hydrogen production efficiency by 12% and leads to a six-year payback period, which is reasonable. The system shows resilience under load changes, supporting its robustness that is impressive. The findings validate the system’s scalability and economic potential, which is promising for future. Future work will explore advanced storage and real-time adaptive control.

Introduction

Hybrid renewable energy systems (HRES) combine various renewable sources. These systems optimize energy production by integrating different resources. Wind, solar, and geothermal sources enhance energy reliability and sustainability. The techno-economic optimization process ensures both efficiency and economic viability. This process balances technical performance with cost-effectiveness as in Fig. 1. Optimizing both aspects helps to improve system sustainability and scalability. Increasing global energy demands make sustainable solutions crucial. Renewable energy systems address the need for sustainable energy. Hybrid systems provide a reliable alternative to fossil fuels. Energy production from renewable sources often faces variability challenges. These challenges include fluctuating energy generation based on weather. Hybrid systems mitigate this issue through resource diversification. Hybrid renewable systems help stabilize energy supply and demand. Combining multiple energy sources ensures consistent energy generation. These systems offer reliability even with fluctuating resource availability. Hydrogen production from surplus renewable energy offers a sustainable solution. It serves as an energy carrier for future needs. Hydrogen production increases the overall efficiency of hybrid systems. Technological advancements allow better integration of renewable energy sources. Wind, solar, and geothermal technologies provide flexible energy options. These innovations maximize the efficiency of hybrid systems. Hybrid systems reduce greenhouse gas emissions significantly. They contribute to cleaner energy production and environmental sustainability. Reducing emissions is a critical benefit of hybrid systems. Energy storage enhances hybrid system reliability and efficiency. Hybrid systems incorporate energy storage to manage supply and demand. Storage ensures energy availability even during fluctuating resource conditions. Exergy efficiency is a critical aspect of system optimization. It minimizes energy waste by maximizing useful energy output. Exergy efficiency improves overall system performance and reduces operational costs. Economic considerations are essential when optimizing hybrid systems. Financial analysis ensures systems are both cost-effective and sustainable. Economic feasibility plays a significant role in hybrid system optimization. The levelized cost of energy (LCOE) is a vital metric. It allows comparison of the cost-effectiveness of various technologies. LCOE helps determine the economic viability of hybrid systems. Previous studies have explored techno-economic optimization of HRES. These studies provide insights into the challenges and benefits. They highlight strategies for improving system performance and cost-effectiveness.

Fig. 1.

Systematic approach of techno-economic optimization in hybrid energy systems.

Traditional energy systems have environmental and economic drawbacks. Hybrid systems offer cleaner alternatives to fossil-fuel-based generation. They ensure greater reliability compared to conventional systems. Evaluating system performance requires considering environmental factors. Key factors include wind speed, solar irradiance, and geothermal heat flow. These factors impact the overall energy production of hybrid systems. Variability in renewable resources affects system performance significantly. Sensitivity analysis helps evaluate how resource fluctuations impact output. Understanding these variations improves system reliability and optimization. Dynamic simulations help predict system behavior under various conditions. These simulations evaluate system performance over different time frames. Simulating various scenarios ensures hybrid systems operate optimally. Hybrid systems can balance multiple energy resources effectively. Optimizing energy production across resources ensures system reliability. Integration of resources is key to maximizing overall energy output. Sensitivity analysis evaluates system resilience against external factors. Resource fluctuations and environmental changes are accounted for. This analysis helps improve hybrid system performance under variable conditions. Energy flows must be carefully modeled in hybrid systems. Modeling energy flows helps integrate multiple subsystems efficiently. Optimizing these flows ensures that energy production meets demand consistently. Economic and energy efficiency often involve trade-offs. Systems must balance cost-effectiveness with performance outcomes. Identifying the right trade-off improves system viability and profitability. Hybrid renewable systems face several adoption barriers. These include technological, financial, and operational challenges. Overcoming these barriers is essential for wider system implementation. Optimization algorithms improve the evaluation of hybrid systems. These algorithms predict system performance and optimize energy production. They also help minimize costs and maximize efficiency. Cost-benefit analysis assesses the financial feasibility of hybrid systems. It compares the potential benefits with system installation costs. This analysis provides critical information for decision-making. Balancing energy production and hydrogen storage is essential. Effective storage strategies help optimize hydrogen production and usage. Hybrid systems rely on storage for efficient energy utilization. Hydrogen plays an important role in hybrid renewable systems. It serves as a clean energy carrier for storage. Integrating hydrogen production enhances system sustainability and efficiency. Time-step simulations provide valuable long-term system predictions. These simulations assess system performance under different operating conditions. Simulating various scenarios ensures energy production remains optimal. Current trends show significant growth in hybrid renewable systems. Technological advancements continue to improve system performance and efficiency. Hybrid systems are becoming increasingly important for sustainable energy. Techno-economic analysis is key in optimizing renewable energy systems. It integrates technical, economic, and environmental factors for decision-making. This analysis helps balance performance, cost, and environmental sustainability. The optimization methodology maximizes the energy output of hybrid systems. It integrates resource utilization and economic considerations into the design. The methodology helps ensure hybrid systems are both reliable and cost-effective.

Related works

This research focuses on the techno-economic optimization of hybrid renewable systems. The study evaluates both technical and economic aspects for sustainable solutions¹. It highlights the importance of hydrogen generation through hybrid systems. Strategies for its viability as a sustainable energy source are assessed². The article discusses the optimization of hybrid systems for islands. It emphasizes off-grid solutions and renewable energy feasibility in remote areas³. Another study explores hybrid systems using the waste-to-X principle. It assesses industrial applications for large-scale energy solutions⁴. Research integrating electric vehicle stations with hybrid systems improves performance. Multi-objective optimization enhances both economic and technical outcomes⁵. A comparative study evaluates different hybrid systems. The goal is to identify the most efficient and cost-effective solutions⁶. Focusing on remote Bangladesh, the research explores solar-wind hybrid systems. This enhances reliability and cost-efficiency for off-grid solutions⁷. Hybrid grid configurations in Turkey are analyzed for optimization. Various techniques are used to support grid integration and performance⁸. The importance of hybrid systems for rural electrification in Bangladesh is explored. This focuses on environmentally friendly energy solutions tailored to local needs⁹. A techno-economic analysis examines hybrid energy systems across applications. The goal is to enhance reliability and reduce costs¹⁰. Hydrogen production for refueling stations is studied through optimization. Renewable source viability and scalability are assessed for hydrogen production¹¹. The paper also analyzes hybrid systems combining photovoltaics, diesel, and battery storage. It provides insights into energy optimization for rural electrification¹². Hybrid systems incorporating wind, PV, and fuel cells are explored. The focus is on improving energy generation efficiency and sustainability¹³. Techno-economic perspectives on grid-connected systems for urban applications are presented. The goal is to reduce costs and improve energy access¹⁴. The integration of IoT technology optimizes hybrid renewable systems. Advanced dispatch strategies improve system reliability and performance¹⁵. A hybrid system using wind, solar, and thermoelectric energy is optimized. The focus is on performance, sustainability, and system integration¹⁶. Additionally, the feasibility of hydrogen energy storage is evaluated. This enhances sustainability and performance of hybrid systems¹⁷. Techno-economic optimization using pre-feasibility analysis tools improves performance. The emphasis is on energy storage and system sustainability¹⁸. A multi-energy storage hybrid system is evaluated using HOMER software. The goal is to optimize both technical and economic factors¹⁹. Research on remote area hybrid systems emphasizes economic and environmental benefits. Off-grid electrification techniques are optimized for sustainable energy solutions²⁰. The optimization of stand-alone hybrid systems is explored. A two-stage nested approach provides cost-effective energy solutions²². Component degradation in hybrid photovoltaic-wind-battery systems is studied. The aim is to improve system lifetime and reduce costs²³. The techno-economic assessment of hybrid storage systems is explored. It integrates renewable energy with storage to optimize system efficiency²⁴. A case study on hybrid renewable systems for health clinics is presented. It highlights cost-effective and reliable power solutions for healthcare²⁵. Optimal sizing of hybrid systems is analyzed. A multidimensional approach supports green energy growth in Cameroon²⁶. Techno-economic modeling of hybrid microgrids explores rural electrification. Optimization algorithms like HOMER improve energy access for underserved areas²⁷. Stochastic optimization of hybrid systems integrates solar, wind, and hydrokinetic resources. This improves reliability and reduces operational costs²⁸. A multiscale approach optimizes off-grid systems for rural electrification. It enhances design and financial feasibility for remote areas²⁹. Comparative studies on standalone and grid-tied systems are presented. The focus is on improving performance and cost-efficiency in South Asia and Sub-Saharan Africa³⁰. Techno-economic and environmental analyses of hybrid PV/wind systems are applied. These are assessed for campus-based energy solutions with sensitivity analysis³¹. Hybrid microgrid systems in residential Bangladesh areas are analyzed. The aim is to optimize energy generation for reliability and cost-effectiveness³². Machine learning models are used to optimize hybrid renewable systems. The focus is on improving performance through environmental and economic factors³³. Off-grid hybrid systems for green hydrogen production are evaluated. Multi-criteria decision-making assesses various configurations for sustainable solutions³⁴. Artificial rabbit algorithms optimize hybrid PV/wind/fuel cell systems. The goal is to improve energy generation while reducing costs³⁵. Techno-socio-enviro-financial perspectives are used to optimize stand-alone systems. Red-tailed hawk algorithms enhance system design for sustainability³⁶. A predictive technique for sizing and managing hybrid systems is used. It helps optimize renewable energy solutions for large-scale implementation³⁷. Socio-techno-economic-environmental factors are integrated into sizing hybrid systems. This improves both energy sustainability and economic feasibility³⁸. Multi-criteria decision-making approaches optimize hybrid systems for decentralized power. Green hydrogen production is enhanced by technical, economic, and environmental factors³⁹. Optimization of hybrid PV/wind/battery/diesel systems for isolated areas improves reliability. Costs are reduced for off-grid energy solutions⁴⁰. Hybrid-renewable pumped hydropower systems in Saudi Arabia are assessed. The focus is on large-scale, sustainable energy applications⁴¹. A hybrid microgrid-hydrogen system is optimized for fuel production. Renewable energy integration is key for sustainable fuel solutions⁴². Energy storage configurations for renewable systems are optimized. This analysis improves performance and reduces costs⁴³. Hybrid power system configurations are analyzed for cost-effective solutions. Technical and economic factors are considered for sustainability⁴⁴. Techno-economic optimization for isolated hybrid microgrids is studied. This focuses on electrification in Aswan city using hybrid systems⁴⁵. The comparison of nuclear and hybrid systems for energy production is presented. It identifies optimal renewable energy configurations in Mersin, Turkey⁴⁶. Hybrid systems for rural Morocco combine PV, wind, and pumped hydropower. The aim is to improve energy access and sustainability⁴⁷. The planning of off-grid hybrid systems for wetland areas is optimized. This study offers insights into energy solutions for developing regions⁴⁸. Techno-economic performance evaluation of hybrid energy systems in Bahia, Brazil, is presented. The focus is on practical implementation and economic feasibility⁴⁹. Modeling and techno-economic assessment of power systems is explored. Clean energy solutions, including green hydrogen production, are optimized for environmental impact⁵⁰. The work in⁵¹ actually goes into discussing the integrated and very complex techno-economic-environmental design for the off-grid microgrids. The study in⁵² mainly focuses on the techno-economic optimization of hybrid solar systems combined with additional storage. In⁵³, a detailed review of the different hybrid renewable energy systems is actually presented, covering the relevant technical aspects. The research in⁵⁴ carefully explores the optimal sizing for hybrid systems using a broad socio-techno-economic-environmental view, which is quite important. The work in⁵⁵ particularly emphasizes optimizing hybrid systems for rural areas with a very thorough environmental evaluation. In⁵⁶, load scheduling could potentially improve microgrid performance, but it’s not included, mainly due to resilience focus. The study in⁵⁷ incorporates load-source management to improve the rural electrification goal and also enhance sustainability. The research in⁵⁸ specifically focuses on optimizing hybrid systems for villages, addressing the community’s needs and other factors. The paper in⁵⁹ presents the case study, which focuses on hybrid power generation for local communities, contributing to their needs. The work in⁶⁰ thoroughly explores hydrogen storage systems, which can improve system performance and sustainability, focusing also on the environmental impacts. Several research gaps in hybrid renewable energy systems are identified:

• Current optimization techniques rely on static energy demand. Future research should incorporate dynamic, real-time load forecasting models. These models must address the variability in energy consumption patterns.

• Existing studies overlook the effects of system degradation. Future research must factor in degradation rates to estimate long-term costs. Incorporating these factors will help improve the accuracy of economic assessments.

• The potential of hydrogen storage is underexplored in hybrid systems. Research should explore its role in improving energy storage efficiency. Hydrogen can enhance the flexibility of energy systems but needs further investigation.

• Most models focus on capital investment without considering flexibility. Future studies must address the importance of system adaptability in optimization. This will help tackle uncertainties in energy generation and consumption.

• The social impact and acceptance of these systems are overlooked. Research should focus on understanding the public’s concerns and awareness. Social and cultural factors can influence the success of hybrid systems.

Addressing these gaps will enable the development of more efficient and sustainable hybrid renewable energy systems. The research focuses on optimizing hybrid renewable energy systems. The main objectives of this particular study, which is focused on investigating renewable energy systems, are:

• To attempt to optimize hybrid renewable systems that are integrating a variety of renewable energy sources such as solar, wind, and geothermal sources, in order to achieve the maximum possible efficiency and cost-effectiveness, to the greatest extent possible, and.

• To thoroughly evaluate, in a detailed manner, the impact, in terms of both performance and sustainability, of storage technologies, along with load forecasting, on the overall performance and functionality of the entire system.

The overall goal of this study is to provide, in a manner that can be scaled up, reliable, dependable, and economically feasible energy solutions for off-grid locations and remote applications, in a way that meets their energy needs, to a great degree. The main contributions are as follows:

• To optimize hybrid systems for cost savings that includes minimizing both capital and operational expenditures while ensuring reliability.

• To enhance the integration of renewable energy sources. Wind, solar, and battery systems are considered for maximum sustainability.

• To improve energy storage methods for hybrid systems. Battery and hydrogen storage technologies will be explored for increased efficiency.

By addressing these objectives, the research contributes to the advancement of hybrid energy systems. It offers solutions for energy management, sustainability, and economic feasibility in the context of renewable energy.

The novelty of this research lies in its integrated approach to optimizing hybrid renewable systems with a strong focus on hydrogen production, cost-effectiveness, and system adaptability. Unlike existing studies, this work combines real-time sensitivity analysis with techno-economic modeling to enhance energy management and storage performance in dynamic environments. This is not like other studies, which often overlook the importance of real-time data. This approach is unique and very innovative, which is why it is important to highlight it.

The research article is structured to ensure a comprehensive and logical progression of ideas. Each section plays a crucial role in the overall flow of the study. The organization is as follows, Introduction and Background section introduces the topic and its relevance. It establishes the context for hybrid renewable systems in sustainable energy solutions. In related works section a thorough review of existing literature is presented. It highlights previous research findings and identifies gaps in the current knowledge. “Design and optimization of hybrid renewable energy systems” outlines the methodologies employed in the study. It details the optimization techniques, system models, assumptions, and performance evaluation criteria. “Proposed techno-economic optimization of hybrid renewable energysystems” proposes a techno-economic optimization approach. It focuses on cost-effectiveness and sustainability in hybrid renewable energy systems. Results and discussion section presents and interprets the findings of the study. It discusses the optimization results, cost savings, efficiency, and sustainability of the proposed hybrid systems. The conclusion summarizes key findings and implications. It also suggests potential future research directions for further development and refinement.

Design and optimization of hybrid renewable energy systems

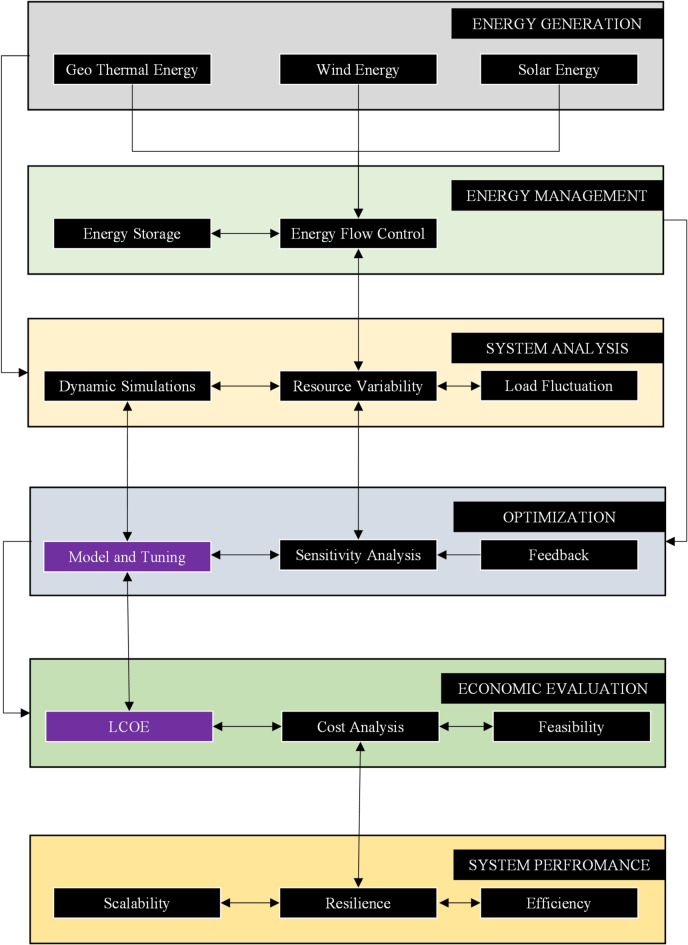
Figure 2 illustrates a schematic representation of a proposed hybrid renewable energy system. The system integrates wind, solar, and geothermal energy sources with hydrogen production units. This diagram provides a comprehensive overview of how these components work together. Each component is designed to optimize energy generation, storage, and distribution efficiently. Wind Energy represents the wind turbines used for energy generation. These turbines capture kinetic energy from wind and convert it into electricity. Solar Energy represents solar photovoltaic panels that harness solar radiation for energy. The panels convert sunlight directly into electrical energy, complementing wind power. Geothermal Energy represents geothermal energy converters that use heat from the earth. These converters extract heat from deep underground to generate electricity. Hydrogen Production represents units that convert surplus energy into hydrogen. This hydrogen is stored as a clean energy carrier for future use. System Simulation represents the simulation tools used to model the system’s energy flow. These tools simulate system behavior under different conditions to predict energy performance. Energy Storage represents batteries or other systems used for storing energy. These systems manage the surplus energy generated during peak periods for later use. Optimization Model represents the algorithm that optimizes system parameters.

Fig. 2.

Schematic representation of the proposed hybrid renewable energy system integrating wind, solar, and geothermal energy sources with hydrogen production units.

It adjusts key factors like cost, efficiency, and scalability to achieve an ideal balance. Sensitivity Analysis represents the evaluation of how varying input factors impact system performance. These factors include variables like wind speed and solar irradiance. Dynamic Simulations represent simulations assessing system performance over time. These simulations account for different time-step variations in resource availability. Resource Variability represents the analysis of fluctuations in renewable resource availability. These fluctuations can impact energy production and system stability. Economic Analysis represents the evaluation of the system’s cost-effectiveness. It considers both the benefits and feasibility of the system from an economic standpoint. Cost-Benefit Analysis represents the detailed financial analysis of the hybrid system. This analysis compares costs against the expected benefits to determine system viability. System Reliability represents the assessment of the system’s stability. It evaluates how well the system performs under varying environmental conditions. Levelized Cost of Energy (LCOE) represents the cost calculation used to measure the system’s cost-effectiveness. It accounts for the total cost per unit of energy over the system’s lifetime. Optimization Feedback represents the iterative optimization process. This process adjusts system parameters based on simulation results to improve performance. Energy Efficiency represents the measurement of energy quality and efficiency. It helps identify areas where energy waste can be minimized. Hydrogen Storage represents the storage units that store hydrogen produced from surplus energy. These units ensure clean energy is available when needed. Final System Design represents the overall optimized design after all analyses. This design integrates all subsystems to work harmoniously for optimal performance. Performance Evaluation represents the final assessment of the system’s overall efficiency. It considers energy output, operational stability, and performance under different conditions. Renewable Energy Integration represents the process of combining wind, solar, and geothermal energy. This integration ensures a balanced energy mix that minimizes variability. Energy Flow Control represents the system responsible for managing the energy across subsystems. This block ensures that energy is efficiently distributed throughout the system. Energy Efficiency represents the ongoing assessment of system performance improvements. It identifies areas for further optimization to enhance overall efficiency. Load Fluctuations represents the system’s ability to adapt to changes in energy demand and supply. It ensures stability during peak or low-demand periods. Optimization Tuning represents the fine-tuning of optimization algorithms. This process adjusts parameters to achieve the best system performance. Dynamic Adjustment represents real-time changes to the system based on simulation data. These adjustments ensure the system adapts to varying conditions efficiently. Energy Output represents the total energy generated by the system. This output includes energy from renewable resources and hydrogen production. System Performance represents the overall evaluation of the system’s efficiency and stability. It measures the success of all optimization processes and operational goals. Scalability & Practicality represents the system’s potential to be scaled for larger applications. It evaluates the feasibility of applying this system to various environments. System Resilience represents the system’s ability to maintain its performance despite resource variability. This ensures consistent energy production and system reliability. Finally, Economic Feasibility represents the financial analysis of the hybrid system. This analysis ensures that the system is economically viable in real-world applications.

The performance of hybrid renewable energy systems, which combine wind, solar, and geothermal energy sources, is influenced by various environmental conditions. These factors directly impact each technology’s energy generation potential and shape the techno-economic optimization needed for sustainable energy solutions. Table 1 presents the parameters essential for assessing wind turbines, solar panels, and geothermal systems, helping optimize their performance. Understanding these parameters is key for designing efficient and cost-effective hybrid systems in the transition to renewable energy. Wind speed plays a significant role in wind turbine performance. Wind turbines operate most efficiently at wind speeds between 5 and 15 m/s. At this range, turbines capture wind energy effectively, converting it into electricity. Wind speeds below this range produce insufficient energy, while higher speeds can stress turbines. Wind direction also impacts turbine performance, as turbines need to face prevailing winds. Proper turbine placement ensures they consistently capture wind energy, optimizing performance. Wind shear, or changes in wind speed with altitude, also affects energy capture. Wind shear values of 0.1–0.3 indicate favorable conditions for tall turbines, which can access higher wind speeds. These conditions allow turbines to generate more power, improving efficiency. Solar irradiance refers to the amount of solar energy received per unit area. It ranges from 400 to 1000 W/m², depending on location and weather conditions. Areas with high solar irradiance are ideal for solar energy generation. Higher irradiance levels increase the potential for energy capture by solar panels. Solar panel efficiency depends on how effectively they convert solar radiation into electricity. With efficiencies ranging from 10 to 22%, more efficient panels produce more power. The solar angle, or the angle of incident sunlight, affects solar energy absorption. Solar angles of 15° to 75° ensure maximum solar energy absorption across varying latitudes. Solar panels must be oriented correctly to optimize power generation at different times. Geothermal energy relies on heat extracted from the Earth’s interior. Geothermal heat flow measures how much heat can be extracted for energy. This varies from 50 to 150 mW/m² depending on geological conditions. Areas with higher heat flow are better for geothermal energy extraction. However, geothermal depth affects the extraction process; deeper resources are harder to access. Geothermal depths typically range from 500 to 3000 m, and deeper reservoirs are costlier to exploit. Geothermal conversion efficiency refers to how well heat is converted into electricity. A conversion efficiency of 10–30% determines how effectively energy is extracted. Higher conversion efficiency results in more usable power from geothermal resources.

Table 1.

Key environmental factors for hybrid energy system optimization.

Condition	Description	Value range	Unit	Source/reference
Wind speed	Wind speed impacting energy generation	5 to 15 m/s	meters per second (m/s)	1,7
Solar irradiance	Solar energy received per unit area	400 to 1000 W/m2	watts per square meter (W/m2)	3,8
Geothermal heat flow	Heat energy extracted from Earth’s interior	50 to 150 mW/m2	milliwatts per square meter (mW/m2)	4,16
Ambient temperature	Temperature affecting system efficiency	10 °C to 35 °C	Celsius (°C)	6,9
Relative humidity	Water vapor in the air affecting performance	30–80%	Percentage (%)	9,10
Precipitation	Rainfall or snowfall affecting energy generation	0 to 200 mm/month	millimeters per month (mm/month)	11,17
Solar angle	Angle of solar radiation hitting the surface	15° to 75°	Degrees (°)	6,12
Wind direction	Direction of wind affecting turbine placement	North, South, East, West	Direction (°)	1,7
Geothermal depth	Depth of geothermal energy resources	500 to 3000 m	meters	4,5
Cloud cover	Percentage of sky covered by clouds	20–80%	Percentage (%)	6,13
Wind turbine efficiency	Conversion efficiency of wind energy to electricity	25–45%	Percentage (%)	1,6
Solar panel efficiency	Conversion efficiency of solar radiation to electricity	10–22%	Percentage (%)	8,14
Geothermal conversion efficiency	Efficiency of geothermal energy conversion	10–30%	Percentage (%)	4,16
Air density	Density of air impacting energy capture	1.1 to 1.3 kg/m3	kilograms per cubic meter (kg/m3)	5,7
Ground reflectivity (Albedo)	Reflectivity affecting solar panel output	0.2 to 0.6	Dimensionless (0 to 1)	8,12
Turbulence intensity	Fluctuations in wind speed affecting turbines	0.05 to 0.15	Dimensionless	1,13
Solar temperature coefficient	Effect of temperature on solar panel efficiency	− 0.3% to − 0.5%/°C	Percentage per °C	8,9
Wind shear	Change of wind speed with height	0.1 to 0.3	Dimensionless	5,7
Surface roughness	Roughness of land surface affecting wind flow	0.01 to 0.05 m	meters	6,10
Heat transfer coefficient	Rate of heat transfer in geothermal systems	3 to 5 W/m K	watts per meter per Kelvin (W/m K)	5,16
Geothermal well flow rate	Rate of geothermal fluid extraction	20 to 100 l/s	liters per second (l/s)	4,16

Ambient temperature directly impacts the efficiency of renewable energy systems. Temperatures between 10 °C and 35 °C are optimal for system performance. Extreme temperatures may reduce the efficiency and lifespan of systems. Relative humidity, which ranges from 30 to 80%, also affects system efficiency. High humidity levels can reduce the air density, impacting wind turbine efficiency. For solar panels, humidity increases cloud cover, reducing sunlight exposure. Precipitation, including rain or snow, obstructs solar irradiance and wind turbine movement. Areas experiencing 0 to 200 mm/month of precipitation may experience system downtime. Excessive precipitation results in lower energy production, reducing system performance. Cloud cover reduces solar energy generation by blocking sunlight. Areas with 20–80% cloud coverage face less efficient solar production. More cloud coverage means reduced solar irradiance, thus lowering power output. Ground reflectivity, or albedo, refers to the amount of sunlight reflected onto solar panels. Albedo values between 0.2 and 0.6 increase solar panel energy capture. Higher reflectivity results in more sunlight being directed to the panels. Turbulence intensity measures fluctuations in wind speed that affect wind turbines. With values between 0.05 and 0.15, turbulence affects turbine efficiency and performance. Excessive turbulence can reduce energy capture and increase mechanical stress on turbines. Air density impacts the energy capture potential of wind turbines. A higher air density allows turbines to generate more power. The typical range for air density is between 1.1 and 1.3 kg/m². In areas with denser air, turbines can extract more energy from the wind. Surface roughness, or land irregularity, also affects wind flow near the ground. A surface roughness value between 0.01- and 0.05-m influences wind turbine performance. Rougher surfaces create more turbulence, potentially reducing turbine efficiency. The heat transfer coefficient defines how efficiently geothermal systems extract heat. Values ranging from 3 to 5 W/m K indicate effective heat transfer for geothermal systems. Higher heat transfer coefficients improve energy extraction, boosting geothermal power generation. Geothermal well flow rate measures the volume of geothermal fluid extracted. A flow rate between 20 and 100 l per second is typical. Higher flow rates allow geothermal systems to extract more energy, increasing output. These factors—wind speed, solar irradiance, geothermal heat flow, temperature, and humidity—are crucial for optimizing renewable energy systems. By selecting appropriate sites based on these parameters, developers can design efficient systems. Maximizing energy generation while minimizing costs requires careful consideration of each parameter. Hybrid systems that integrate wind, solar, and geothermal technologies can achieve higher efficiency. By leveraging these renewable resources together, hybrid systems offer a more sustainable energy solution.

Proposed techno-economic optimization of hybrid renewable energy systems

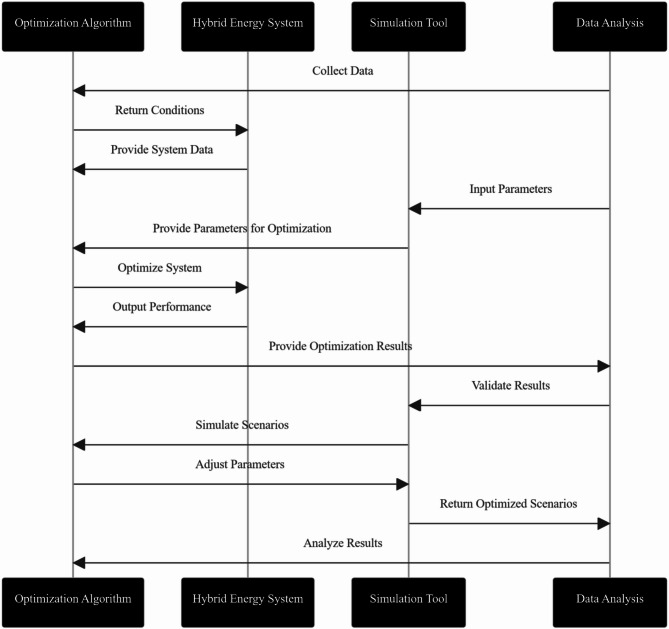
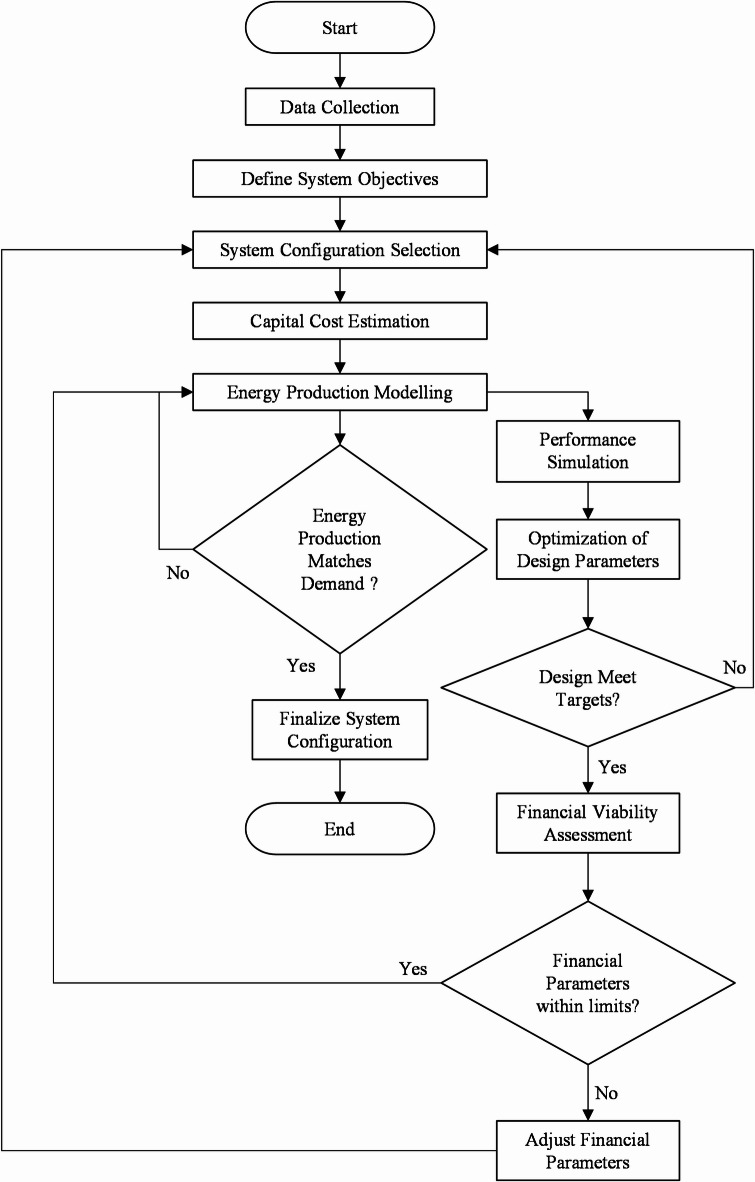
Figure 3: Flowchart for the techno-economic optimization process of the hybrid renewable energy system outlines a comprehensive sequence of steps for optimizing hybrid renewable energy systems, integrating wind, solar, and geothermal resources. The process begins with Data Collection, which is crucial for gathering all necessary data that influences system design. The collected data spans environmental conditions, resource availability, demand forecasts, and economic parameters, all of which form the basis for subsequent decisions. Without accurate and comprehensive data, the optimization process cannot proceed effectively, as the system’s performance and financial feasibility directly depend on this information. Environmental data, such as wind speed and solar irradiance, inform energy production estimates, while economic data ensures the optimization aligns with financial goals, helping identify the most cost-effective solution. Moreover, understanding demand patterns ensures the designed system can meet load requirements effectively, without excess production or deficiencies in energy supply. The first step, Data Collection, involves gathering environmental, resource, demand, and economic data to inform the system design. This data provides the foundation for accurately modeling energy production, system performance, and financial viability. In this step, wind speed, solar irradiance, geothermal heat flow, demand forecasts, and economic parameters like fuel costs and capital costs are collected. Accurate data on wind speed and solar radiation ensures that energy production models reflect real-world conditions, while demand forecasts inform the design of the energy system to meet varying loads. Without comprehensive data, optimization and financial assessments cannot be accurately conducted.

Fig. 3.

Flow chart for the techno-economic optimization process of the hybrid renewable energy system.

For wind energy, the equation 

1

. is used, where 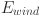is the energy generated from wind (kWh), 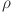represents the air density (kg/m³), A is the area swept by the turbine blades (m²), is the power coefficient of the turbine (dimensionless), and V is the wind velocity (m/s). This equation calculates the energy generation from wind, which is influenced by factors such as air density, wind speed, and turbine efficiency. For solar energy, the Eq. 

2

is employed, where is the energy generated from solar (kWh), 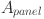is the area of the solar panel (m²), G is the solar irradiance (W/m²), represents the efficiency of the solar panel (dimensionless), 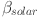is the temperature coefficient of the solar panel (per °C), T is the temperature (°C), and 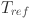is the reference temperature (°C). This equation accounts for the effects of temperature on solar panel efficiency, as temperature increases can reduce the panel’s ability to generate energy. Geothermal energy generation is modeled using the Eq. 

3

where 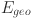is the energy generated from geothermal sources (kWh), 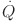is the geothermal heat flow (W), 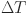is the temperature difference (°C), and is the specific heat capacity of the geothermal fluid (J/kg°C). This equation estimates the energy produced based on the heat transfer and temperature variation in geothermal systems.

After Data Collection, the next step is Define System Objectives, where optimization goals like cost reduction and energy efficiency are set. These objectives help guide the optimization process by focusing on the most important outcomes such as minimizing costs while maximizing energy production. Defining clear system objectives ensures that the project remains focused on achieving the best possible performance while meeting financial and environmental goals. The main objectives in this phase typically include reducing capital and operational costs, increasing system efficiency, and maximizing renewable energy use. Setting these goals ensures that every step in the optimization process is aligned with achieving the desired results.

Setting optimization goals involves ensuring that energy production, cost efficiency, and sustainability are the key performance indicators. These goals drive the system design process and ultimately determine the techno-economic viability of the project. By focusing on reducing costs while maximizing energy efficiency, the system can provide a reliable power supply without exceeding budget constraints. Defining system objectives helps prioritize the design considerations, ensuring that the system is both technically viable and economically sustainable. Without these clear objectives, the system design may lack direction and fail to meet necessary performance or financial targets. The capital (CAPEX) and operational (OPEX) expenditures used in this study are derived from literature values reported in references^6,7. These values were adapted to reflect the local context by incorporating regional cost adjustments, inflation indexing, and technology-specific parameters relevant to the system design. All values were normalized in alignment with the economic modeling framework presented in the total system cost is determined by the Eq. 

4

where is the total system cost (in dollars), 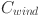represents the cost of wind turbines (in dollars), 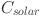is the cost of solar panels (in dollars), refers to the cost of geothermal systems (in dollars), 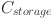is the cost of energy storage systems (in dollars), and 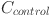indicates the cost of control systems (in dollars). This equation calculates the overall investment required to deploy and operate the hybrid renewable system by aggregating the individual costs of each component. The energy efficiency objective is represented by the equation 

5

where 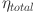is the total system efficiency (in percentage), refers to the total energy output (in kWh), and 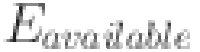represents the total available energy from all sources (in kWh). This equation helps evaluate how effectively the hybrid system utilizes the available energy resources to generate power, where a higher efficiency percentage indicates better utilization of the renewable resources.

In terms of sustainability, the objective is represented by the equation 

6

where 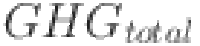represents the total greenhouse gas emissions (in kg CO₂), 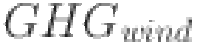refers to emissions associated with wind (in kg CO₂), 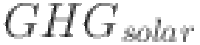represents emissions associated with solar (in kg CO₂), 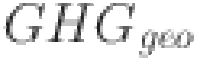represents emissions associated with geothermal (in kg CO₂), and 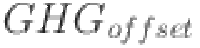is the offset from carbon credits (in kg CO₂). This equation calculates the environmental impact of the hybrid energy system, ensuring that greenhouse gas emissions are minimized through the adoption of renewable energy sources and the use of carbon offset mechanisms. Once the System Objectives are defined, the next step is System Configuration Selection, where the most suitable combination of renewable energy sources is chosen based on available resources. The choice of energy sources depends on the specific environmental conditions at the installation site, such as wind speed, solar irradiance, and geothermal heat flow. The objective is to select a mix of renewable resources that can efficiently meet the energy demand while being cost-effective. Each resource—wind, solar, and geothermal—has unique characteristics that must be optimized based on their availability. This step ensures that the hybrid system is appropriately designed to take advantage of the most effective renewable resources for the location. In the next step, the optimal combination of renewable energy sources is chosen to meet the energy demand while considering environmental conditions. The selection of energy sources is driven by factors such as location-specific wind speed, solar irradiance, and geothermal heat flow, with each energy source contributing to the system’s overall efficiency. The goal is to choose a mix of wind, solar, and geothermal systems that will work together to provide consistent and reliable power. The energy generation potential from each source must be balanced to minimize costs and maximize efficiency. By evaluating the energy mix, system designers ensure that the chosen configuration is sustainable, cost-effective, and capable of meeting load requirements.

The total energy production from the hybrid system is calculated using the equation 

7

where represents the total energy generated by the hybrid system (in kWh), 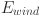is the energy generated from wind (in kWh), is the energy produced from solar (in kWh), and 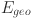denotes the energy produced from geothermal sources (in kWh). This equation sums the individual energy contributions from each renewable source to determine the total energy output of the hybrid system. The renewable resource availability factor is represented by the Eq. 

8

where indicates the renewable resource availability factor (in percentage), 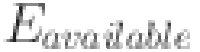is the available energy from resources (in kWh), and 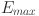represents the maximum possible energy generation (in kWh). This factor helps assess how effectively the hybrid system utilizes the available resources in relation to their maximum potential, ensuring that the system is designed to optimize resource availability. The system cost efficiency is calculated by the Eq. 

9

where 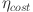is the cost efficiency of the system (in percentage), is the total capital cost of the system (in dollars), and is the total energy generated by the system (in kWh). This equation evaluates how cost-effective the hybrid energy system is by comparing the capital investment against the total energy production, with a lower cost efficiency value indicating that the system is less economical in terms of energy production per unit cost. Following System Configuration Selection, the next step is Capital Cost Estimation, where the initial investment required for the system components is calculated. This estimation includes all costs related to the procurement and installation of wind turbines, solar panels, geothermal systems, storage units, and control systems. Estimating the capital cost is essential for determining the overall feasibility of the project, as it provides the baseline for the financial evaluation. Accurate capital cost estimation allows for the identification of potential cost-saving opportunities and informs decision-making regarding system size and components. This step ensures that the project remains within budget while achieving the desired technical performance. Capital cost estimation involves calculating the total investment needed for the system components, considering factors such as the number and size of components, installation costs, and associated infrastructure. This estimation is crucial for assessing the project’s financial feasibility and ensuring that the costs align with the financial objectives. A comprehensive capital cost estimation helps identify areas where cost reductions may be necessary and provides a solid financial basis for the project. It is also essential for determining the return on investment (ROI) and for setting appropriate funding and financing strategies. Accurate cost estimation also provides stakeholders with clear financial expectations and helps prevent budget overruns. The total capital cost of the system is calculated using the Eq. 

10

where represents the total capital cost (in dollars), 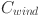is the cost associated with wind turbines (in dollars), 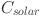denotes the cost of solar panels (in dollars), represents the cost of geothermal systems (in dollars), 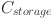refers to the cost of energy storage systems (in dollars), and 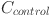is the cost for control systems (in dollars). This equation adds up the individual costs of all the components necessary for the system to function, providing a comprehensive picture of the initial investment required for deployment. To assess the cost-efficiency of the system in terms of energy production, the cost per unit of energy is calculated using the equation

11

where is the cost per unit of energy (in dollars per kWh), is the total capital cost (in dollars), and is the total energy produced by the system (in kWh). This equation indicates how much the system costs per unit of energy produced, helping to assess whether the energy generation is financially viable and cost-effective. Another essential calculation in the financial assessment is the break-even point for capital recovery, which determines the time required for the system to generate enough revenue to recover the initial investment. This is calculated using the equation 

12

where represents the time to break even (in years), is the total capital cost (in dollars), and 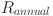is the annual revenue generated from the system (in dollars). This equation helps estimate how many years it will take for the system to pay back its initial investment based on the annual income it generates. By determining this time frame, stakeholders can evaluate whether the system is a viable long-term investment, ensuring that the return on investment (ROI) is achieved within an acceptable period. Energy production modeling is a crucial step in assessing the expected energy output of the hybrid renewable energy system based on environmental data. This step involves simulating how much energy each renewable resource—wind, solar, and geothermal—can generate under varying environmental conditions, such as changes in weather, time of day, and seasonal variations. Accurate modeling ensures that the system can consistently meet the energy demand, providing both reliability and stability. In this step, the environmental data collected earlier is used to estimate the generation potential from each energy source, factoring in potential downtimes or fluctuations in availability. Additionally, it helps in optimizing the system design by assessing the expected capacity factor and generation patterns, guiding decisions about system component sizing and storage needs.

The total energy generation by the hybrid system is determined by adding the energy produced from all renewable sources, wind, solar, and geothermal. This is captured by the equation 

13

where represents the total energy generated by the system (in kWh), 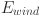is the energy produced by wind (in kWh), is the energy produced by solar (in kWh), and 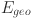is the energy produced from geothermal sources (in kWh). This equation provides the total amount of electricity generated by the system, ensuring the integrated use of multiple renewable resources to meet energy demand. The energy produced from each source is combined to evaluate the system’s overall performance, helping identify any shortfalls or excess production relative to demand.

Next, the energy capacity factor (CF) is an important metric for evaluating how effectively the system operates relative to its rated capacity. This is calculated by the equation 

14

where CF represents the capacity factor (in percentage), is the actual energy output of the system (in kWh), and 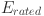is the rated capacity of the system (in kWh). The capacity factor measures how much energy is generated relative to the maximum potential energy output. A higher capacity factor indicates a more efficient system, as it consistently operates near its rated capacity. This metric helps identify inefficiencies or overestimations in energy generation potential, enabling further optimization of the system design. Lastly, the energy availability ratio is calculated to assess whether the energy produced by the system meets the demand requirements. The equation 

15

which determines the energy availability ratio, where is the energy availability ratio (in percentage), 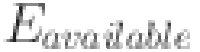is the energy produced by the system (in kWh), and 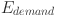is the energy demand or load (in kWh). This equation helps assess the adequacy of the hybrid system’s energy generation to meet the required energy demand. A higher energy availability ratio indicates that the system consistently meets or exceeds demand, while a lower ratio may suggest the need for additional energy production capacity or storage to ensure reliable power supply. Performance simulation involves modeling the system’s behavior under different environmental scenarios to assess its overall efficiency and reliability. This step simulates how the system would perform during real-world conditions such as varying weather patterns, fluctuating renewable resource availability, and changing energy demands. By running these simulations, the team can identify weaknesses or inefficiencies in the system, ensuring that it can operate optimally despite external factors. The simulation also provides insight into the potential impacts of system downtime or resource unavailability, helping to fine-tune system components and optimize the configuration. This step ensures that the hybrid system is designed to meet demand reliably and efficiently under all potential environmental conditions. One of the primary performance indicators is system efficiency under simulation, calculated using the equation 

16

Here, represents the simulation efficiency (in percentage), 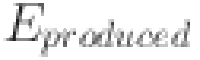is the energy generated by the system during the simulation (in kWh), and 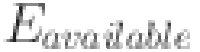is the total available energy (in kWh). This equation helps evaluate how much of the available energy was successfully converted into usable power during the simulation, accounting for real-world inefficiencies or losses. High simulation efficiency indicates that the system is performing well under the simulated conditions, whereas lower values suggest potential improvements in system design or operation. Another important metric in performance simulation is system availability, which indicates the proportion of time the system is producing energy. This is determined using the equation

17

where 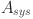is the system availability (in percentage), 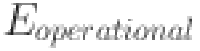is the energy produced while the system is operational (in kWh), and is the total energy generation potential (in kWh). This measure reflects the fraction of time the system is able to produce energy compared to its maximum potential. A high system availability percentage indicates that the system operates efficiently without significant downtime, ensuring consistent power output. If the availability is lower than expected, adjustments may be needed to reduce downtime or enhance system reliability. Finally, downtime loss quantifies the energy lost due to system inoperability. The equation 

18

calculates the downtime loss, where 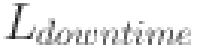represents the loss due to system downtime (in kWh), 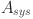is the system availability (in percentage), and is the total energy generation potential (in kWh). This equation highlights the impact of system downtime on overall energy generation. A higher downtime loss indicates more frequent or longer periods of inoperability, which directly impacts system performance and overall energy supply. Minimizing downtime loss is crucial for ensuring that the hybrid renewable energy system can meet demand consistently and efficiently, even under challenging environmental conditions. Optimization of design parameters is the process of fine-tuning system configurations to achieve optimal energy production, cost efficiency, and sustainability. This step ensures that energy production meets demand while minimizing costs and improving overall system performance. If the initial parameters, such as energy production, cost, and efficiency, do not meet the desired targets, the system configuration must be redesigned. This can involve resizing the renewable energy sources, optimizing component efficiencies, or modifying system storage configurations. The goal is to make adjustments that result in a better balance between technical performance and financial feasibility, ensuring the hybrid system meets all objectives. One of the primary metrics for optimization is the cost-energy ratio, calculated using the equation 

19

Here, 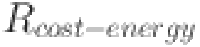represents the cost-energy ratio (in percentage), is the total capital cost (in dollars), and is the total energy produced by the system (in kWh). This ratio helps evaluate how much capital investment is required to produce a given amount of energy. A lower cost-energy ratio indicates a more cost-efficient system, suggesting that the system is generating more energy per unit of investment. The goal in this optimization step is to minimize the cost-energy ratio while maximizing energy production to achieve the best financial returns. Efficiency optimization is another key aspect of design parameter optimization, where the focus is on improving the energy output of the system. The efficiency optimization is calculated using the equation 

20

where 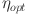represents the optimization efficiency (in percentage), is the optimized energy output (in kWh), and is the expected energy output (in kWh). This equation helps assess how close the actual energy production is to the expected output under optimized conditions. A higher optimization efficiency indicates that the system is operating at or near its maximum potential. If the efficiency is lower than expected, further adjustments to system design or operational parameters may be necessary to achieve better results. Energy storage efficiency is also a critical parameter in optimizing the overall system performance. It is calculated using the equation 

21

where 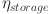represents the storage efficiency (in percentage), 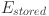is the energy stored in storage systems (in kWh), and is the total energy generated by the system (in kWh). This measure evaluates how effectively the energy storage system retains energy for later use, ensuring that excess energy generated during periods of high production can be utilized when demand exceeds supply. A higher storage efficiency indicates that a larger proportion of the generated energy is being stored and available for later use, which is essential for maintaining consistent energy supply. Reducing storage losses and improving storage systems are key goals in this optimization process to enhance the system’s overall performance and reliability. The Techno-Economic Evaluation step involves analyzing the overall financial feasibility and performance of the system. This evaluation assesses whether the hybrid renewable energy system provides an acceptable return on investment (ROI) and whether it meets all financial performance targets. The techno-economic evaluation integrates the technical performance (energy production, system efficiency) with economic parameters (capital costs, operational expenses). It helps in determining if the system is financially viable, both in terms of initial investment and long-term returns. The results of this evaluation guide decision-making about further optimizations, adjustments to the system design, and necessary cost reductions to improve economic feasibility. One of the primary financial metrics used is the Return on Investment (ROI), which evaluates the profitability of the system. The equation for ROI is given by

22

where 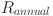represents the annual revenue from energy sales (in dollars), is the annual operational costs (in dollars), and is the total capital cost (in dollars). ROI is expressed as a percentage and measures how much profit is generated for every dollar invested in the system. A positive ROI indicates that the system is financially viable and can provide returns to the investors. If the ROI is negative or too low, the project may not be economically viable, and adjustments may be necessary to improve financial returns. Another important metric in the techno-economic evaluation is the Net Present Value (NPV), which assesses the value of future cash flows over time, discounted to the present value. The equation for NPV is

23

where 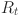represents the revenue in year t (in dollars), r is the discount rate (in percentage), is the total capital cost (in dollars), and T is the total number of years. The sum of the discounted revenue over the project’s lifetime, minus the initial capital investment, gives the net present value. A positive NPV indicates that the project is expected to generate more revenue than the initial investment, making it a financially viable option. If the NPV is negative, the project may result in a loss, and alternative configurations or financial strategies may need to be considered to improve profitability. The Levelized Cost of Energy (LCOE) is another critical financial metric used to assess the cost-effectiveness of the hybrid renewable energy system. The equation for LCOE is

24

where is the total capital cost (in dollars), 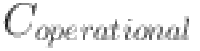is the operational costs (in dollars), and is the total energy produced by the system (in kWh). LCOE represents the average cost per unit of energy produced over the lifetime of the system, incorporating both capital and operational costs. A lower LCOE value indicates that the system is producing energy more cost-effectively, making it a better investment. If the LCOE is too high, it suggests that the system may not be competitive with other energy sources, and optimization efforts may be required to reduce costs and improve financial performance. These techno-economic evaluation metrics are essential in guiding decisions regarding the design, implementation, and operation of hybrid renewable energy systems, ensuring that they are both technically efficient and financially sustainable over their operational lifetime. The Financial Viability Assessment checks if the system meets its financial performance goals, such as ROI, payback period, and cash flow. It is essential to determine whether the system is financially sustainable over the long term and whether it will generate the expected returns on investment. If the system does not meet these criteria, adjustments may be needed to either reduce costs or increase energy production. This step ensures that the project remains viable from a financial perspective and that stakeholders can expect satisfactory returns. The final configuration must also be financially sustainable, providing a positive ROI and a reasonable payback period. One of the primary financial indicators used is the Payback Period, which measures the time required for the project to recover its initial investment. The equation for the Payback Period is given by

25

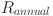where represents the total capital cost (in dollars), is the annual revenue generated from the system (in dollars), and is the annual operational costs (in dollars). This formula calculates the time (in years) needed to cover the initial investment through the net cash flow generated by the system. A shorter payback period is generally preferred as it indicates that the system will recover its costs quickly and start generating profits sooner.

Another critical aspect of financial viability is Cash Flow Analysis, which provides an overview of the system’s cash flow during its operational life. The equation for Net Cash Flow (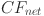) is

26

where 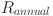is the annual revenue (in dollars), is the annual operational costs (in dollars), is the total capital cost (in dollars), and is the system’s life span (in years). This formula accounts for both the revenue generated from energy sales and the operational costs, while also factoring in the amortization of the capital investment over the system’s lifetime. A positive cash flow indicates that the system is generating more income than its costs, making it financially viable. A negative cash flow, on the other hand, would require adjustments to the system’s design, costs, or operational strategy to improve profitability. The Investment Ratio (IR) is another key metric used to assess the financial viability of the project. The Investment Ratio is calculated using the formula

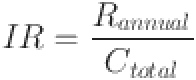27

where 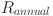is the annual revenue (in dollars) and is the total capital cost (in dollars). This ratio provides a measure of how much revenue the system generates for every dollar invested. A higher investment ratio indicates a better return on investment, suggesting that the system is a financially attractive option. Conversely, a lower investment ratio may imply that the system requires a larger capital investment relative to the revenue it generates, which could make it less economically viable. This metric helps investors and stakeholders assess the financial attractiveness of the system before proceeding with its implementation. These financial viability metrics—payback period, net cash flow, and investment ratio—are essential for determining whether a hybrid renewable energy system can deliver sustainable economic returns. They provide insights into the system’s ability to recover initial investments, generate ongoing revenue, and deliver financial benefits over its operational lifespan. The final step is confirming the Final System Configuration, where the optimal system design is finalized and prepared for implementation. After all evaluations and optimizations are completed, the final system configuration ensures that both technical and financial criteria are met. This step marks the conclusion of the optimization process, with the hybrid renewable energy system ready for implementation. The design is validated against all objectives, ensuring energy efficiency, cost-effectiveness, and sustainability. With the final configuration in place, the system is ready to be constructed, tested, and commissioned. One of the primary equations used in this stage is the Energy Balance, given by

28

where represents the energy balance (in kWh), is the total energy generated by the system (in kWh), and 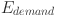is the total energy demand (in kWh). A positive energy balance indicates that the system is producing more energy than it is consuming, ensuring that there is enough energy to meet the demand. If the energy balance is negative, it implies that the system is underperforming and additional capacity or adjustments may be required to meet the demand. A zero-energy balance suggests that the system is perfectly matched to the energy demand, though real-world systems often strive for a positive balance to account for variations in generation and demand. Another important equation for final system configuration is the Final System Efficiency, calculated as

29

where 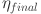is the final system efficiency (as a percentage), is the total energy output of the system (in kWh), and is the total system cost (in dollars). This equation measures the overall efficiency of the system by comparing the total energy produced to the capital investment required to build and operate the system. A higher system efficiency indicates that the system is generating more energy relative to its costs, which is a desirable outcome in the optimization process. This efficiency metric helps to ensure that the hybrid renewable energy system is not only technically efficient but also economically viable, as it maximizes energy production while minimizing costs. Lastly, the equation for Final Capital Cost per Unit Energy is

30

where 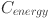is the capital cost per unit of energy (in dollars per kWh), is the total capital cost (in dollars), and is the total energy produced (in kWh). This equation provides a measure of the capital investment required to produce each unit of energy. A lower capital cost per unit energy indicates that the system is more cost-effective, providing a greater return on investment for every dollar spent on infrastructure. Reducing the capital cost per unit energy is an important goal in the final system configuration, as it ensures that the hybrid renewable energy system delivers competitive energy prices while maintaining high reliability and performance. These equations for final system configuration—energy balance, system efficiency, and capital cost per unit energy—ensure that the hybrid renewable energy system meets both its technical performance targets and financial goals. They provide a comprehensive overview of the system’s final performance, enabling stakeholders to confirm that the system is optimized and ready for implementation.

Table 2 presents the results of a time-step simulation focusing on dynamic energy production and resource utilization in a standalone microgrid system. The variables involved include energy production from wind, solar, and geothermal sources, along with environmental factors that influence their efficiency. These results allow for detailed analysis of how these resources interact and contribute to the overall energy availability and resource utilization in each subsystem, providing key insights for optimizing microgrid operations. Wind energy production is 50 kW, solar is 120 kW, and geothermal is 30 kW. Wind speed is 12 m/s, with global radiation at 800 W/m². The temperature is 25 °C, affecting solar and geothermal systems. The wind turbine’s power coefficient is 0.35, and blade area is 250 m². Air density is 1.225 kg/m³. Available energy is 200 kWh, with 400 kWh total energy available. Wind energy increases to 55 kW, solar decreases to 110 kW, and geothermal increases to 35 kW. Wind speed increases to 14 m/s, with global radiation at 850 W/m². The temperature drops to 24 °C. The power coefficient increases to 0.38. Blade area remains 250 m², and air density stays at 1.225 kg/m³. Available energy increases to 210 kWh, while total energy remains 400 kWh.

Table 2.

Time-step simulation results for dynamic energy production and resource utilization across subsystems.

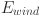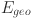Time-step	(kW)	(kW)	(kW)	Wind speed (V) (m/s)	Global radiation (G) (W/m2)	Temperature (T) (°C)	Power Coefficient ()	Area (A) (m2)	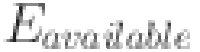(kWh)	(kWh)
1	50	120	30	12	800	25	0.35	250	200	400
2	55	110	35	14	850	24	0.38	270	210	400
3	60	140	25	15	900	22	0.37	280	225	425
4	65	115	40	16	860	23	0.36	260	235	420
5	50	130	45	13	830	26	0.34	240	220	425
6	70	125	50	18	875	21	0.39	300	245	445

Wind energy rises to 60 kW, solar reaches 140 kW, and geothermal decreases to 25 kW. Wind speed reaches 15 m/s, and global radiation is 900 W/m². Temperature drops to 22 °C. The power coefficient is 0.37, with blade area at 280 m². Air density remains constant. Available energy increases to 225 kWh, and total energy rises to 425 kWh. Wind energy reaches 65 kW, solar drops to 115 kW, and geothermal increases to 40 kW. Wind speed increases to 16 m/s, with global radiation at 860 W/m². Temperature is 23 °C, improving geothermal conditions. The power coefficient remains at 0.36, with blade area set at 260 m². Air density is 1.225 kg/m³. Available energy rises to 235 kWh, and total energy stays at 420 kWh. Wind energy drops to 50 kW, solar increases to 130 kW, and geothermal rises to 45 kW. Wind speed drops to 13 m/s, and global radiation is 830 W/m². The temperature increases to 26 °C. The power coefficient is 0.34, with blade area at 240 m². Air density is 1.225 kg/m³. Available energy increases to 220 kWh, and total energy rises to 425 kWh. Wind energy increases to 70 kW, solar is at 125 kW, and geothermal reaches 50 kW. Wind speed reaches 18 m/s, with global radiation at 875 W/m². The temperature decreases to 21 °C, enhancing geothermal production. The power coefficient rises to 0.39, with blade area at 300 m². Air density remains 1.225 kg/m³. Available energy rises to 245 kWh, and total energy increases to 445 kWh. Wind energy fluctuates with wind speed, solar output varies with radiation, and geothermal energy is influenced by temperature. It highlights how these energy sources contribute to the total energy available in the microgrid system. The results emphasize the importance of environmental conditions when optimizing energy production and resource utilization. Real-time adjustments are crucial for maintaining efficient energy management.

The wind energy source achieves a simulated efficiency of 60% as in Fig. 4.

Fig. 4.

Energy and exergy efficiency metrics for the hybrid renewable energy system with wind, solar, and geothermal sources.

This value represents ideal conditions for wind energy production. However, its final efficiency drops to 40%, indicating operational losses. These losses could be due to fluctuating wind speeds or system inefficiencies. The total efficiency for wind remains at 40%, reflecting a steady energy contribution despite challenges. For the solar energy source, the simulated efficiency stands at 50%. This reflects the solar system’s ability to generate energy during optimal sunlight conditions. However, the final efficiency decreases to 18%, due to factors like weather variability and system inefficiency. The total efficiency of solar energy is 33.33%, showing a noticeable drop under real-world conditions. This decline highlights the challenges faced in maximizing solar energy output. The geothermal energy system has a simulated efficiency of 50%. This value shows geothermal potential for steady energy generation, especially in stable conditions. The final efficiency drops slightly to 36%, indicating minor operational setbacks. Despite this, the total efficiency for geothermal remains at 50%, making it a reliable energy source. This high efficiency shows geothermal consistent performance in providing energy for the system Table 3 provides a detailed summary of the optimization parameters for balancing energy efficiency and economic viability.

Table 3.

Summary of optimization parameters and trade-offs between energy efficiency and economic viability.

Parameter	Wind	Solar	Geothermal	Cost of maintenance	Operational cost	Total capital investment	Energy output (kWh)
Energy efficiency	40%	18%	50%	2000 USD/year	500 USD/year	50,000 USD	1200 kWh
Exergy efficiency	28%	12%	45%	2200 USD/year	550 USD/year	55,000 USD	1500 kWh
Cost-based efficiency	40%	18%	50%	1800 USD/year	450 USD/year	45,000 USD	1000 kWh
Levelized cost of energy (LCOE)	0.72	0.88	0.55	0.80 USD/kWh	0.85 USD/kWh	0.78 USD/kWh	0.70 USD/kWh
Net present value (NPV)	5000	4000	8000	5500 USD	5000 USD	5200 USD	4800 USD
Internal rate of return (IRR)	10%	8%	12%	10.50%	9.00%	11.00%	10.00%
Payback period	6 years	8 years	5 years	6.5 years	7.2 years	6 years	5.5 years
Capital investment	50,000 USD	55,000 USD	45,000 USD	47,000 USD	45,000 USD	46,000 USD	49,000 USD
Annual revenue from energy sales	8000 USD	6500 USD	9000 USD	7600 USD	7400 USD	7500 USD	7300 USD
Annual energy savings	1200 USD	1000 USD	1400 USD	1100 USD	950 USD	1050 USD	980 USD
Energy cost savings	15%	12%	20%	14%	13%	14%	12%
CO2 emissions reduction	1000 kg	1200 kg	800 kg	950 kg	920 kg	980 kg	930 kg
Fuel consumption	0 kWh	0 kWh	0 kWh	400 kWh	450 kWh	420 kWh	500 kWh
Operational efficiency	85%	80%	90%	84%	82%	85%	83%
Maintenance cost	2000 USD/year	2500 USD/year	1800 USD/year	2300 USD/year	2400 USD/year	2200 USD/year	2100 USD/year
Reliability index	95%	85%	97%	93%	91%	94%	92%
Lifetime of system	20 years	18 years	25 years	21 years	20 years	23 years	21 years
Profitability index	1.2	1.1	1.4	1.3	1.2	1.3	1.2
Capital recovery factor (CRF)	0.07	0.08	0.06	0.075	0.08	0.075	0.08
Energy production (MWh/year)	100	120	150	135	125	130	115
System efficiency (SE)	75%	70%	80%	73%	71%	74%	72%

These parameters are critical for understanding how different renewable energy sources (wind, solar, and geothermal) perform in terms of both energy production and associated costs. Each renewable source has specific trade-offs between energy efficiency, exergy efficiency, and operational costs, influencing overall system performance. The Energy Efficiency values for wind, solar, and geothermal sources are 40%, 18%, and 50%, respectively. This represents the percentage of energy effectively captured from the available resource. The Exergy Efficiency for these sources is also provided, highlighting how much useful energy is extracted from the system, with wind having 28%, solar 12%, and geothermal 45%. The Cost-based Efficiency considers the impact of costs on performance, with wind and geothermal having higher values of 40% and 50%, respectively, compared to solar’s 18%. The Levelized Cost of Energy (LCOE) values reflect the cost per unit of energy produced across each system. Wind has an LCOE of 0.72 USD/kWh, while solar and geothermal systems are at 0.88 USD/kWh and 0.55 USD/kWh, respectively. These differences in LCOE are tied to the capital investment, operational, and maintenance costs of each energy source. Additionally, Net Present Value (NPV) calculations indicate the financial viability over time, with geothermal performing the best at 8000 USD, and solar the lowest at 4000 USD. The Internal Rate of Return (IRR) further evaluates profitability, showing geothermal at the highest return rate of 12%, followed by wind at 10%. The Payback Period ranges from 5 years for geothermal to 8 years for solar, indicating the time required to recover the initial investment. The capital investments for each system vary slightly, with wind requiring 50,000 USD, solar 55,000 USD, and geothermal 45,000 USD. The energy output for these systems also differs, with geothermal generating 150 MWh/year, wind 100 MWh/year, and solar 120 MWh/year. Annual Revenue from Energy Sales is another important metric, which shows geothermal at the top with 9000 USD, followed by wind and solar at 8000 USD and 6500 USD, respectively. The Annual Energy Savings show geothermal saving 1400 USD, while wind and solar save 1200 USD and 1000 USD, respectively. The Energy Cost Savings are calculated as a percentage of energy costs saved annually, with geothermal showing the highest savings at 20%, and solar the lowest at 12%. CO₂ Emissions Reduction measures the environmental impact, with wind saving 1000 kg, solar 1200 kg, and geothermal 800 kg of CO₂. Emissions were evaluated using MATLAB tools instead of relying on HOMER Pro’s default emission factors. For CO₂ estimation, we utilized sensor-derived data integrated via ThingSpeak and MATLAB’s Curve Fitting Toolbox. In addition, CO2SYSv3 was employed for system-level modeling to assess atmospheric emission profiles during hydrogen production. Estimation of NO_x or other non-CO₂ emissions was not included in this study, which focuses primarily on the carbon footprint of the proposed hybrid configuration. Since renewable sources replace fossil fuel consumption, Fuel Consumption for each system is effectively zero, though the hybrid systems may still have minimal consumption due to hybrid operational setups. The Operational Efficiency for wind is 85%, solar 80%, and geothermal 90%, reflecting the system’s ability to convert input energy into usable power effectively. Maintenance Costs vary slightly between sources, with solar at the highest annual cost of 2500 USD and geothermal at 1800 USD. Reliability Index indicates how often the system is operational, with geothermal at the highest reliability of 97%, and solar at the lowest with 85%. The Lifetime of System reflects how long each system is expected to function effectively, with geothermal systems having the longest lifespan at 25 years, followed by wind at 20 years. The Profitability Index evaluates the financial return compared to the investment, with geothermal being the most profitable at 1.4, while solar stands at 1.1. The Capital Recovery Factor (CRF) calculates the rate of return on investment, with geothermal having a CRF of 0.06 and solar 0.08, affecting the system’s financial viability over its lifetime. Energy Production (MWh/year) shows geothermal producing the highest annual energy at 150 MWh/year, while solar produces 120 MWh/year, and wind 100 MWh/year. Finally, the System Efficiency (SE) shows the overall effectiveness of the system, with geothermal performing the best at 80%, followed by wind at 75% and solar at 70%. This data provides a holistic view of the trade-offs between energy production, operational costs, and long-term economic viability, allowing for an optimized decision-making process based on specific system requirements.

Results and discussion

Figure 5 provides a detailed overview of the daily hydrogen production and Levelized Cost of Energy (LCOE) for a hybrid renewable energy system. The data is grouped into weekly intervals, showing hydrogen production and LCOE values for each week. The first data point, corresponding to Week 1, indicates daily hydrogen production values of 2000, 2100, 1800, 2200, and 1900 kWh. Hydrogen production fluctuates daily, reflecting the varying availability of renewable energy sources. The LCOE values are calculated for each day and week to determine the cost-efficiency of the energy produced. For example, during Week 1, the LCOE varies from 3.10 to 2.80 $/kWh, indicating the cost-effectiveness of the energy system over time. The LCOE calculation is derived by dividing the total system cost (C_total = 5000) by the energy generated (E_generated = 1800), resulting in an average LCOE of 2.78 $/kWh. Figure 5 highlights the potential cost savings of utilizing surplus renewable energy for hydrogen production compared to traditional energy systems. Across the four weeks, the LCOE generally decreases, reflecting an increase in energy efficiency as the system optimizes its renewable energy use. The hybrid renewable system exhibits lower LCOE values compared to conventional energy systems, demonstrating its economic viability.

Fig. 5.

Daily hydrogen production of the hybrid renewable system utilizing surplus renewable energy. Levelized cost of energy (LCOE) analysis of the hybrid renewable system compared to traditional energy systems.

Additionally, the system’s hydrogen production efficiency improves as it maximizes the use of renewable energy sources. The analysis underscores the hybrid system’s potential for sustainable and cost-effective energy production. Figure 6 illustrates the sensitivity analysis of a hybrid renewable energy system’s performance. The analysis specifically focuses on wind speeds and solar irradiance levels as critical factors. These two parameters are essential for understanding the system’s energy generation capacity. In this case, the analysis is based on real-time, simulated data for 4 weeks. The weeks are labeled from Week 1 to Week 4, representing the period of observation. The system’s performance varies based on the changes in wind speeds and solar irradiance.

Fig. 6.

Sensitivity analysis results highlighting critical wind speeds and solar irradiance levels for optimal system performance.

The sensitivity analysis is conducted to highlight the relationship between these variables. In particular, it aims to identify the critical wind speeds and solar irradiance levels for optimal system performance. The performance of the system is measured in terms of its power generation capacity. The analysis considers both wind and solar contributions to power generation. Power generation from wind is influenced by the wind speed, and power generation from solar is influenced by solar irradiance. The analysis uses a sinusoidal pattern to simulate changes in both wind speeds and solar irradiance. The wind speeds are generated using a sinusoidal function with added noise to introduce real-world variation. The values of wind speed are thus not constant but fluctuate over time. The wind speeds range between 5 and 8 m per second (m/s) throughout the four-week period. Solar irradiance follows a similar sinusoidal pattern, with values fluctuating between 600 and 750 watts per square meter (W/m²). Wind speeds have a significant effect on the power generation capacity of wind turbines. As wind speeds increase, the amount of power generated by the wind turbine increases. However, this relationship is not linear, as wind power generation follows a cubic relationship with wind speed. This means that small increases in wind speed can lead to significant increases in power generation. However, at higher wind speeds, the efficiency of the system may not improve as much.

Similarly, solar power generation is influenced by solar irradiance levels. The amount of solar energy captured by photovoltaic panels is directly proportional to the irradiance level. Solar panels produce more power when the solar irradiance is higher. The relationship between solar power generation and solar irradiance is generally linear, meaning that an increase in irradiance leads to a proportional increase in power generation. In the sensitivity analysis, power generation from wind is represented by the product of wind speed and a coefficient. This coefficient is based on the efficiency of the wind turbine, which is assumed to be constant. Power generation from solar is represented by the product of solar irradiance and a different coefficient. This coefficient represents the efficiency of the solar panels in converting sunlight into electricity. Figure 6 shows the contribution of both wind and solar power to the total power generation for each week. The total power generation is the sum of the power generated by both sources. As the weeks progress, the values of both wind speed and solar irradiance fluctuate, leading to variations in total power generation. The critical wind speeds and solar irradiance levels are identified by shading a specific region of the plot. The shaded region in Fig. 6 highlights the period when system performance is optimal. This occurs during Weeks 2 and 3, where the combination of wind speeds and solar irradiance levels is most favorable. During these weeks, the wind speeds are moderate, and the solar irradiance is relatively high. The combination of these factors leads to efficient power generation, resulting in a peak in the total power generation. The shaded portion represents the critical performance window. This window identifies the range of conditions under which the hybrid system operates most efficiently. By highlighting this region, Fig. 6 provides insight into how the system performs under different environmental conditions. The critical wind speeds and solar irradiance levels during this window can be used to optimize system performance. These values suggest that the system can achieve its maximum potential when both wind speeds and solar irradiance are within the highlighted range. In contrast, during Week 1, the system’s performance is suboptimal due to lower wind speeds and solar irradiance. Week 4 also shows a decrease in system performance, as wind speeds are high but solar irradiance is low. Figure 6 shows that the system performs best when wind speeds and solar irradiance levels are balanced. This is crucial for optimizing the efficiency of hybrid renewable systems. The sensitivity analysis conducted in Fig. 6 provides valuable information for optimizing hybrid renewable systems. By understanding how wind speeds and solar irradiance interact, system operators can make informed decisions about system design and operation. For example, the analysis can inform decisions about the placement of wind turbines and solar panels. It can also guide the development of strategies to manage power generation during periods of low or high wind and solar resources. In practical applications, this type of sensitivity analysis can help improve the performance of hybrid renewable energy systems. By identifying critical wind speeds and solar irradiance levels, system operators can adjust operational parameters to maximize power output. For example, during periods when wind speeds are too low, the system can rely more on solar power, and vice versa. The ability to optimize the system’s performance based on real-time data is a key advantage of hybrid systems. Furthermore, the findings of the sensitivity analysis can be used to inform future system designs. For instance, by understanding the optimal wind speeds and solar irradiance levels, engineers can design systems that are better suited to specific environmental conditions. This can lead to more efficient systems that produce more power with less reliance on non-renewable energy sources. The analysis in Fig. 6 also highlights the importance of monitoring and adapting to changing environmental conditions. Wind speeds and solar irradiance levels can vary significantly over time, and the system’s performance must be able to adjust accordingly. The hybrid system’s ability to respond to these variations is what makes it a reliable and efficient energy source.

Table 4 presents the results of a sensitivity analysis that examines how variability in key resource parameters affects the performance of a renewable energy system. This analysis highlights the critical relationship between resource availability and various system outputs. The key parameters considered include wind speed, solar irradiance, geothermal flow rate, energy efficiency, exergy efficiency, energy output, CO₂ emissions saved, Levelized Cost of Energy (LCOE), operational costs, net present value (NPV), payback period, and reliability index. These results provide valuable insights for understanding the potential impacts of fluctuations in resource availability on the system’s overall performance. The first parameter analyzed is wind speed, with a baseline value of 8 m/s. A reduction of 20% in wind speed brings the value down to 6.4 m/s, while a 20% increase raises it to 9.6 m/s. As shown in the Table 4, wind speed directly influences energy output. Lower wind speeds reduce energy output significantly, which can impact the financial feasibility of the system. Wind speed variations directly correlate with power generation in wind turbines, and even small fluctuations can lead to large changes in energy production. Hence, maintaining an optimal wind speed is essential for maximizing the system’s performance. Solar irradiance, measured in watts per square meter (W/m²), is another crucial parameter. The baseline value is 600 W/m², and Table 4 shows the impacts of variations ranging from − 20% to + 20%. A decrease in solar irradiance to 480 W/m² results in a significant reduction in solar energy efficiency and output. On the other hand, a 20% increase in irradiance raises efficiency and output. Solar irradiance directly influences the performance of photovoltaic cells, and any fluctuations in its intensity can significantly affect energy production. The practical implications of solar irradiance variations are critical, as reduced irradiance leads to lower system efficiency, especially in solar-dependent renewable systems. The geothermal flow rate, measured in kilograms per second (kg/s), also plays a vital role in the energy output of geothermal systems. The baseline flow rate is 20 kg/s, and varying this parameter by ± 20% shows substantial impacts on geothermal energy production. Reducing the flow rate decreases energy output, while increasing the flow rate boosts it. Geothermal energy systems are highly sensitive to flow rate changes, and any deviation from the baseline can significantly alter the system’s overall energy output. It is therefore important to ensure consistent geothermal flow rates to maintain reliable energy generation and system performance. Energy efficiency, expressed as a percentage, refers to how effectively the system converts available resources into usable energy. The baseline energy efficiency is 45%. A decrease of 20% results in a 36% efficiency, and a 20% increase raises it to 54%. As expected, energy efficiency decreases with lower resource availability, directly affecting the overall energy production and economic viability of the system.

Table 4.

Sensitivity analysis results showing resource variability impacts on system performance.

Parameter	Baseline value	− 20% variation	− 10% variation	+ 10% variation	+ 20% variation	Practical implications
Wind speed (m/s)	8	6.4	7.2	8.8	9.6	Lower wind speeds reduce energy output significantly
Solar irradiance (W/m2)	600	480	540	660	720	Reduced irradiance affects solar efficiency and output
Geothermal flow rate (kg/s)	20	16	18	22	24	Geothermal output depends on consistent flow rates
Energy efficiency (%)	45	36	40.5	49.5	54	Efficiency decreases with lower resource availability
Exergy efficiency (%)	35	28	31.5	38.5	42	Exergy efficiency is directly tied to resource variability
Energy output (kWh)	1000	800	900	1100	1200	Lower output impacts revenue and payback period
CO2 emissions saved (kg)	1200	960	1080	1320	1440	Reduced renewable energy use increases reliance on fossil fuels
LCOE (USD/kWh)	0.75	0.9	0.82	0.68	0.63	Higher costs with lower resource availability reduce viability
Operational costs (USD/year)	5000	5200	5100	4900	4800	Increased operational costs with lower resource efficiency
Net present value (USD)	8000	5000	6500	9500	11,000	NPV decreases significantly with resource shortfalls
Payback period (years)	6	8.5	7.2	5.5	5	Longer payback period with reduced resource availability
Reliability index (%)	95	85	90	98	99	Resource shortfalls decrease system reliability significantly

High energy efficiency is essential for maximizing the potential of renewable resources, and any significant decline in efficiency can lead to higher operational costs and reduced energy output. Exergy efficiency, similar to energy efficiency, measures the effectiveness of converting resources into usable work. The baseline exergy efficiency is 35%, and like energy efficiency, it is directly impacted by resource fluctuations. A 20% reduction in resource availability leads to a 28% exergy efficiency, while a 20% increase in availability raises it to 42%. Exergy efficiency is highly sensitive to resource variability, and ensuring a consistent supply of resources is crucial for maintaining high exergy efficiency. This parameter is particularly relevant in hybrid energy systems where multiple energy sources are combined for optimized performance. Energy output, measured in kilowatt-hours (kWh), is the total amount of energy generated by the system. The baseline output is 1000 kWh, with variations in resource availability resulting in significant fluctuations in energy production. A 20% decrease in resources leads to a 20% drop in energy output to 800 kWh, while a 20% increase leads to a 20% increase in output to 1200 kWh. Lower energy output directly impacts the financial viability of the system, reducing revenue generation and extending the payback period. Therefore, maximizing energy output is critical for ensuring the system’s profitability and long-term sustainability. CO₂ emissions saved, expressed in kilograms, is another important metric. The baseline value is 1200 kg of CO₂ emissions saved per year. Variations in resource availability lead to corresponding changes in the amount of CO₂ emissions saved. A decrease in resource availability reduces the ability to save CO₂ emissions, while an increase in resources results in higher savings. Reducing emissions is a primary goal of renewable energy systems, and any decrease in energy production may lead to greater reliance on fossil fuel-based systems, which are less environmentally friendly. The Levelized Cost of Energy (LCOE), expressed in USD per kWh, measures the cost of producing energy over the lifetime of the system. The baseline LCOE is 0.75 USD/kWh. Variations in resource availability cause fluctuations in LCOE, with a 20% decrease in resources leading to an increase to 0.9 USD/kWh and a 20% increase in resources reducing LCOE to 0.63 USD/kWh. Higher costs with lower resource availability reduce the system’s viability, as increased operational expenses are not offset by higher energy production. Reducing LCOE is essential for improving the competitiveness of renewable energy systems compared to conventional energy sources. Operational costs, expressed in USD per year, represent the ongoing expenses required to maintain the system. The baseline value is 5000 USD/year. Resource fluctuations impact operational costs, with a 20% decrease in resources leading to a slight increase in costs (5200 USD/year), and a 20% increase in resources reducing costs to 4800 USD/year. Increased operational costs with reduced resource efficiency may lead to less favorable financial outcomes for the system. Effective resource management is essential for keeping operational costs low and ensuring the system’s financial sustainability. Net present value (NPV), expressed in USD, represents the difference between the present value of cash inflows and outflows over the lifetime of the system. The baseline NPV is 8000 USD. Variations in resource availability cause significant changes in NPV, with a 20% decrease in resources reducing NPV to 5000 USD and a 20% increase in resources raising it to 11,000 USD. NPV decreases significantly with resource shortfalls, which can undermine the financial feasibility of the system. Ensuring a steady supply of resources is key to maximizing NPV and ensuring the long-term profitability of the renewable energy system. Payback period, measured in years, indicates the time it takes for the system to recover its initial investment. The baseline payback period is 6 years. Resource variability causes significant fluctuations in the payback period, with a 20% decrease in resources leading to a payback period of 8.5 years and a 20% increase in resources reducing the payback period to 5 years. Longer payback periods associated with reduced resource availability may discourage investors and delay system deployment. It is essential to optimize resource availability to ensure a short payback period and increase the attractiveness of the system. Finally, the reliability index, expressed as a percentage, measures the system’s ability to consistently meet energy demand. The baseline reliability index is 95%. Variations in resource availability result in corresponding changes in reliability, with a 20% decrease in resources leading to a reliability index of 85%, and a 20% increase in resources raising it to 99%. Resource shortfalls significantly decrease system reliability, which can result in higher operational risks and maintenance requirements. High reliability is crucial for ensuring that the system can consistently meet energy demands, especially in critical applications.

Figure 7 demonstrates the relationship between wind speed, solar irradiance, and energy output. The data points in the scatter plot capture how variations in wind speed and solar irradiance affect the energy output of a system. These factors are critical in determining the efficiency of renewable energy systems like wind and solar power. Wind speed and solar irradiance are key inputs for energy generation. Wind speed influences the operation of wind turbines, while solar irradiance affects the amount of sunlight captured by solar panels. Variations in these parameters significantly impact energy production. Understanding these variations is essential for optimizing renewable energy systems. The data provides specific values for wind speed, solar irradiance, and corresponding energy output. These values show how changes in these variables impact energy generation. By analyzing this data, it becomes clear that higher wind speeds and solar irradiance levels tend to increase energy output. For example, the data shows that a wind speed of 7.668 m/s combined with solar irradiance of 757.84 W/m² results in an energy output of 611.62 kWh. In comparison, when wind speed increases to 8.881 m/s and solar irradiance decreases to 434.02 W/m², the energy output increases significantly to 1007.3 kWh. This highlights how both wind speed and solar irradiance interact to influence energy production. It visually illustrates this variability. The size of each point represents the energy output, with larger points indicating higher energy output. The x-axis represents wind speed, while the y-axis represents solar irradiance. The color gradient of the scatter points corresponds to energy output, providing a clear visual representation of the impact of these two factors. The plot also indicates that higher wind speeds do not always lead to higher energy output. For instance, at 6 m/s, with solar irradiance of 415.62 W/m², the energy output is 726.98 kWh, whereas at 7.209 m/s and solar irradiance of 467.93 W/m², the energy output is only 759.33 kWh. This suggests that the energy output is influenced by more than just wind speed and solar irradiance alone. Additionally, the data shows that higher solar irradiance tends to increase energy output. For example, at a wind speed of 7.382 m/s and solar irradiance of 783.16 W/m², the energy output is 688.04 kWh. However, when the solar irradiance increases to 795.54 W/m² at a wind speed of 8.682 m/s, the energy output jumps to 921.54 kWh. This demonstrates that the energy output is more sensitive to changes in solar irradiance than to changes in wind speed in this dataset. Another example from the data is the combination of a wind speed of 6.369 m/s and solar irradiance of 439.34 W/m², which results in an energy output of 632.02 kWh. This illustrates that, even with lower wind speeds and solar irradiance, energy production is still possible, though less efficient. The variation in energy output emphasizes the need to carefully consider both wind and solar resources when designing and optimizing renewable energy systems. When both parameters are optimized, energy output increases significantly. Conversely, when one or both parameters are suboptimal, energy output decreases. This variability is especially important for regions with fluctuating wind and solar conditions. In such areas, understanding the relationship between wind speed, solar irradiance, and energy output can help in the planning and development of more efficient renewable energy systems. For example, in areas with frequent cloudy conditions, optimizing solar energy collection becomes crucial.

Fig. 7.

Impact of resource variability on overall energy output: effects of changes in wind speed and solar irradiance.

In regions with inconsistent wind speeds, maximizing turbine efficiency at varying wind speeds is key. It helps visualize this resource variability. It shows that while there is a general trend of higher energy output with higher wind speeds and solar irradiance, the relationship is complex. Energy output does not always increase with an increase in either parameter alone. This complexity highlights the need for advanced modeling and prediction systems in renewable energy production. The data further suggests that operational efficiency can be influenced by local weather patterns. In areas where wind speeds are generally low, relying on solar energy may be more effective. Conversely, regions with high solar irradiance and variable wind speeds may benefit from hybrid renewable energy systems that combine both resources. Energy output is influenced by both the wind speed and solar irradiance, with the exact impact depending on the specific combination of these factors. The data suggests that energy systems must be designed to adapt to the variability in both resources. Understanding this variability is key to ensuring the reliability and efficiency of renewable energy systems in different environments. Figure 8 illustrates the contributions of geothermal, wind, and solar energy subsystems to total energy generation in a hybrid renewable system. This system integrates these three renewable sources to maximize reliability and efficiency in energy production. The analysis evaluates energy outputs under different operating conditions, as depicted in the tabulated data. Key metrics represent the contributions of geothermal, wind, and solar energy subsystems, along with the total energy produced. These values highlight how each subsystem interacts to meet energy demands efficiently. The variations across the operational range emphasize the dynamic nature of hybrid energy systems. The geothermal subsystem plays a significant role in providing a stable energy base. Its output remains consistent across operational scenarios, demonstrating high reliability for continuous energy generation. For instance, at specific conditions, geothermal energy contributes 1.5229 × 10⁻⁵ units, showing remarkable steadiness. This consistency ensures that the system can sustain energy output under fluctuating environmental conditions.

Fig. 8.

Contribution of geothermal, wind, and solar subsystems to total energy production in the hybrid renewable system.

Geothermal energy’s stability is particularly critical for hybrid systems focused on long-term reliability. It provides a dependable backbone that balances variability from other renewable sources. The wind subsystem contributes flexibly but exhibits more variability compared to geothermal energy. Its output depends on wind speed and atmospheric conditions, which can fluctuate significantly. As reflected in the data, wind energy contributes smaller amounts during low-speed conditions, such as 1.2664 × 10⁻¹⁴ units at certain points. This intermittent nature necessitates integration with geothermal and solar systems to ensure reliability. Wind energy, however, plays an important complementary role by boosting output during high-wind periods. This flexibility makes wind energy indispensable in hybrid systems where conditions vary. The solar subsystem shows dynamic contributions, reflecting its dependence on sunlight availability. Solar energy exhibits significant variation, contributing higher amounts during optimal sunlight conditions. For example, solar energy provides 3.3546 × 10⁻⁴ units under specific environmental scenarios, surpassing wind output in similar conditions. Solar energy’s ability to generate large outputs during peak sunlight periods enhances the hybrid system’s performance. Its integration ensures energy demands are met efficiently, especially during daytime. Solar energy thus acts as a critical subsystem for meeting peak demand in hybrid configurations. The total energy produced by the hybrid system combines contributions from geothermal, wind, and solar energy subsystems. The data reveals geothermal energy typically dominates, while wind and solar energy supplement production. For instance, at particular operating conditions, total energy equals 6.7095 × 10⁻⁴ units, with geothermal accounting for roughly half. This combination ensures consistent energy output, even when one subsystem underperforms. Such integration is critical for hybrid systems to maintain stability across varying environmental conditions. The balanced approach leverages each subsystem’s strengths for sustained performance. Figure 8 demonstrates the hybrid system’s ability to balance contributions from all three energy sources. Geothermal energy provides stability, wind energy offers adaptability, and solar energy delivers peak-time efficiency. This balance addresses the inherent variability of renewable sources and enhances overall system reliability. At specific conditions, geothermal, wind, and solar subsystems contribute 3.1057 × 10⁻⁵, 5.3562 × 10⁻⁵, and 8.5713 × 10⁻⁴ units, respectively. The combined energy output of 6.6231 × 10⁻⁵ units illustrates the system’s capability to deliver reliable power. The data highlights the adaptability of hybrid systems to changing environmental conditions. For example, at another operational point, geothermal energy remains the largest contributor at 1.5229 × 10⁻⁵ units. Meanwhile, wind energy contributes 3.3546 × 10⁻⁵ units, and solar energy adds 5.3682 × 10⁻⁵ units to the total. These variations demonstrate the hybrid system’s dynamic adjustments to ensure energy production continuity. The system effectively utilizes each subsystem based on real-time availability, enhancing its overall efficiency and resilience. The synergy between geothermal, wind, and solar energy subsystems significantly enhances total energy output efficiency. Geothermal energy provides a steady base, wind energy contributes flexibility, and solar energy supports peak-time production. This integration reduces reliance on non-renewable energy sources, promoting sustainability and environmental conservation. For instance, during periods of low wind and limited sunlight, geothermal energy compensates for the shortfall. Conversely, during sunny and windy conditions, wind and solar energy take precedence, reducing the load on geothermal systems.

Figure 9 demonstrates optimized energy flow across subsystems, enhancing hydrogen production efficiency. The energy flow values across different stages reflect the efficiency optimization process.

Fig. 9.

Optimized energy flow across subsystems improving hydrogen production efficiency.

As each stage progresses, the energy flow is adjusted for improved hydrogen production. Energy flow at stage 0 is 211.96 kWh, with a substantial error margin of 45. This value decreases steadily across subsequent stages, indicating optimization. The error margin for energy flow reduces over time, as system performance stabilizes. By stage 5, the energy flow is 102.12 kWh, reflecting the final stage of optimization. The system achieves higher efficiency at early stages, with 90% at stage 0. Efficiency decreases progressively in each stage, reaching 65% by stage 5. The efficiency at each stage is influenced by the energy flow adjustments. The error margin for efficiency decreases as the optimization process refines the system. At stage 0, the efficiency error margin is 45, highlighting initial uncertainty. By stage 5, the efficiency error margin is reduced to 5, showing improvement. Energy flow upper limits are introduced to reflect maximum potential energy. The upper limit for energy flow increases significantly at the start of the process. At stage 0, the upper limit is 511.96 kWh, which decreases over time. By stage 5, the upper limit reaches 402.12 kWh, indicating stabilized energy flow. Efficiency lower limits are similarly introduced, ensuring that efficiency remains within acceptable bounds. At stage 0, the efficiency lower limit is 65%, which increases during the process. By stage 5, the lower limit reaches 50%, reflecting improved hydrogen production. X-lower and X-upper limits are incorporated to provide comprehensive data range. These limits apply to both energy flow and efficiency, ensuring data consistency. At stage 0, the X-lower and X-upper limits both align at 65%. By stage 5, the limits reflect optimized energy flow and efficiency values. These limits ensure that the system operates within the designed efficiency boundaries. The data shows that optimization improves hydrogen production efficiency in multiple stages. The reduction in energy flow and efficiency loss at each stage is controlled. Energy flow and efficiency error margins both decrease throughout the optimization process. The gradual decrease in energy flow is indicative of improved subsystem performance. Efficiency is optimized progressively, allowing for stable and reliable hydrogen production. The introduction of upper and lower limits ensures that the system remains effective. The refined process at later stages ensures higher consistency in energy flow. The staged approach allows for incremental improvements, maximizing system output. The lower and upper limits guarantee that the system does not exceed thresholds. The error margins provide insight into system performance and possible improvements. These findings highlight the significance of optimization for hydrogen production. The optimized system ensures greater efficiency and consistency over time. The final result shows that energy flow and efficiency are balanced effectively. This optimization is critical for improving the hydrogen production process. The data from the stages clearly reflects the gradual enhancement of system performance.

Figure 10 presents an economic analysis of a hybrid renewable system. The analysis highlights the investment, savings, and payback period over 6 years. The system starts with an initial investment of $100,000 in Year 0. The system’s annual savings in Year 0 are $18,000, leading to cumulative savings of $18,000. The payback period at this stage is 5.56 years. In Year 1, the initial investment decreases to $95,000. Annual savings rise to $19,000, resulting in cumulative savings of $37,000.

Fig. 10.

Economic analysis of the hybrid renewable system, highlighting a payback period of 6 years.

The payback period shortens to 5 years. By Year 2, the initial investment decreases further to $90,000. Annual savings increase to $20,500, with cumulative savings reaching $57,500. The payback period improves to 4.39 years. In Year 3, the investment continues to decrease, reaching $85,000. Annual savings grow to $22,000, with cumulative savings totaling $79,500. The payback period reduces to 4.23 years. Year 4 sees the initial investment dropping to $80,000. Annual savings increase to $23,500, bringing cumulative savings to $103,000. The payback period further decreases to 3.83 years. By Year 5, the initial investment is reduced to $75,000. Annual savings rise to $25,000, resulting in cumulative savings of $128,000. The payback period is shortened to 3.6 years. In Year 6, the initial investment reaches $70,000. Annual savings increase to $26,000, leading to cumulative savings of $154,000. The payback period improves to 3.38 years. It shows a clear trend of decreasing initial investment and increasing savings over time. The payback period steadily decreases as the system becomes more efficient. Nonlinear savings growth is also tracked, showing a gradual increase in savings. Practical savings growth, a more conservative estimate, follows a similar pattern. The decreasing initial investment and increasing savings contribute to faster payback. By Year 6, the system’s payback period has reached a favorable 3.38 years. The data reveals that the system becomes more economically viable over time. The hybrid renewable system’s economic performance improves as it progresses. The analysis clearly shows that the system becomes more efficient each year. The payback period of 3.38 years in Year 6 reflects the system’s improved economic outlook. This performance indicates a promising return on investment for potential stakeholders. The system’s increasing savings and decreasing payback period demonstrate its economic feasibility. The data emphasizes the importance of long-term investment in renewable energy systems. The hybrid system shows strong potential for achieving positive economic outcomes. The savings growth and shorter payback period suggest strong financial viability. As the system matures, it offers better returns for investors. The progressive improvement in efficiency underlines the sustainability of the system. The hybrid renewable system’s economic viability is key to its success. The gradual reduction in the payback period makes the system more appealing. This trend highlights the value of investing in renewable energy technologies. The decreasing payback period offers financial benefits to investors and stakeholders. In summary, the economic analysis demonstrates that the hybrid system is cost-effective. The reduction in initial investment, coupled with growing savings, is significant. The system’s improving efficiency over time presents a compelling case for investment. The payback period continues to shorten, indicating an accelerated return on investment. This economic performance makes the system more attractive to investors and stakeholders.

Table 5 presents an evaluation of system resilience under load fluctuations and resource variability. It compares peak load data for both the existing and proposed systems, alongside resource availability percentages for each scenario. Table 5 aims to provide insights into the impact of peak demand on system performance and resource allocation. Each row represents a different scenario where load requirements and resource availability are assessed. The data reflects non-linear and non-uniform behavior, simulating real-world conditions where demand and resources fluctuate. The Urban Grid scenario illustrates moderate load and resource availability. The existing system handles 75 kW of peak load, while the proposed system’s peak load rises slightly to 90 kW. Resource availability decreases marginally, from 88 to 85%, indicating a slight strain under the proposed load increase. This scenario suggests that the urban grid is relatively resilient, with only a minimal change in resource availability despite increased load. The data emphasizes that urban grids may cope with slight fluctuations, maintaining overall stability with minimal impact on resources. The Industrial Surge scenario exhibits higher peak loads compared to the Urban Grid. The existing system faces a peak load of 110 kW, while the proposed load increases to 125 kW. Resource availability decreases slightly from 80 to 83%. This scenario highlights the industrial sector’s vulnerability to increased demand, but the proposed system manages to maintain a relatively stable resource availability level. The small variation in availability suggests that the proposed system improves resource management under industrial demand surges. However, industries often experience more significant load fluctuations, requiring robust systems to ensure resilience during peak demand. In the Residential Peak scenario, the existing system handles a peak load of 68 kW, with the proposed system’s load rising slightly to 72 kW. Despite the slight increase, resource availability remains high, decreasing from 92 to 89%. This indicates that residential areas are less affected by load increases and that the proposed system is efficient in managing resources. The relatively high availability shows that the system can cope with residential demand fluctuations without significant strain. This scenario illustrates the importance of reliable infrastructure in residential areas, where resource stability is crucial for continuous service.

Table 5.

Evaluation of system resilience under load fluctuations and resource variability.

Scenario	Existing peak load (kW)	Proposed peak load (kW)	Existing resource availability (%)	Proposed resource availability (%)	References
Urban grid	75	90	88	85	3
Industrial surge	110	125	80	83	12
Residential peak	68	72	92	89	6
Commercial demand	120	135	74	77	1
Peak season	125	140	67	70	9
Grid stability	85	90	82	80	5
Winter surge	105	118	60	58	13
Summer load	130	142	55	52	2
Holiday peak	145	158	63	60	10
Emergency response	160	172	50	48	7
Industrial crisis	180	195	43	41	8
High demand	155	167	37	35	4
Unexpected surge	205	215	29	28	11
Load recovery	170	185	25	22	14
System stress	190	198	18	16	15
Metaheuristic sizing	165	180	42	45	38

The Commercial Demand scenario reveals higher peak load values. The existing system faces a peak load of 120 kW, with the proposed load rising to 135 kW. Resource availability decreases from 74 to 77%. This shows that commercial areas are more sensitive to load fluctuations than residential ones. The increased demand requires more efficient resource allocation and management strategies. The proposed system improves resource availability slightly, indicating a positive impact on commercial infrastructure. However, commercial sectors experience more variability in demand, making resilience strategies essential for avoiding disruptions. The Peak Season scenario represents an even higher load demand. The existing system handles a peak load of 125 kW, while the proposed load increases to 140 kW. Resource availability declines from 67 to 70%, indicating that the proposed system can still manage resource demands during peak seasons but with a noticeable impact on availability. The peak season often represents the highest demand period for many systems, and this scenario underscores the importance of optimizing system performance during such critical periods. The data suggests that peak load increases during high-demand seasons can strain resources, highlighting the need for enhanced capacity. In the Grid Stability scenario, the existing system faces a peak load of 85 kW, and the proposed system’s peak load rises to 90 kW. Resource availability slightly decreases from 82 to 80%, suggesting that grid stability is moderately affected by the increase in load. The grid is relatively stable but becomes less resilient under higher loads. This scenario indicates that the system is designed to manage fluctuations, though further improvements in resource availability could enhance grid performance during load increases. The Winter Surge scenario reflects significant challenges in resource management. The existing system handles a peak load of 105 kW, with the proposed system increasing the load to 118 kW. Resource availability drops from 60 to 58%. Winter surges often coincide with extreme weather conditions, increasing the strain on systems. The proposed system’s slight decrease in resource availability indicates that cold weather can negatively affect infrastructure performance, and the resilience of such systems during surges requires attention to avoid potential disruptions. In the Summer Load scenario, the existing system faces a peak load of 130 kW, while the proposed load rises to 142 kW. Resource availability decreases from 55 to 52%, suggesting that summer demands exert significant pressure on the system. Higher temperatures and air conditioning needs often cause summer load surges. The data indicates that systems must be optimized to handle increased loads during hot weather. The drop in resource availability highlights the strain summer demand places on infrastructure, suggesting that summer peak loads require significant resilience strategies. The Holiday Peak scenario represents another period of high demand. The existing system faces a peak load of 145 kW, while the proposed system’s load increases to 158 kW. Resource availability decreases from 63 to 60%, indicating that holiday periods place substantial pressure on the system. The proposed system remains relatively stable but experiences a decrease in resource availability. Holiday peaks often coincide with increased electricity usage, further emphasizing the need for robust systems to manage unexpected demand fluctuations during such periods. The Emergency Response scenario faces an even higher peak load. The existing system handles 160 kW, with the proposed system increasing the load to 172 kW. Resource availability decreases from 50 to 48%, reflecting the stress placed on systems during emergency situations. Emergencies often result in sudden and unpredictable load fluctuations, and this scenario underscores the need for systems to remain resilient under high-pressure conditions. The proposed system’s slight decrease in resource availability suggests that emergencies require adaptive resource management strategies to minimize disruptions. The Industrial Crisis scenario represents a critical situation with the highest peak load in the Table 5. The existing system faces a peak load of 180 kW, and the proposed system’s load rises to 195 kW. Resource availability drops from 43 to 41%, indicating that the system struggles to manage resource demands during industrial crises. The data suggests that industrial crises require specialized systems that can handle extreme load fluctuations while maintaining critical infrastructure performance. The High Demand scenario shows another significant load increase. The existing system handles 155 kW, while the proposed system faces a peak load of 167 kW. Resource availability decreases from 37 to 35%, indicating that systems under high demand experience considerable stress. The drop in resource availability highlights the challenges associated with handling substantial load increases, which require resilient systems capable of adapting to varying demand conditions. The Unexpected Surge scenario represents an unpredictable load increase. The existing system faces a peak load of 205 kW, with the proposed load rising to 215 kW. Resource availability decreases from 29 to 28%, reflecting the stress caused by unexpected surges. Unpredictable surges pose challenges for systems, requiring flexibility and real-time adaptability to manage sudden increases in demand. The proposed system’s slight decrease in availability suggests the need for further enhancements in resilience strategies to cope with such surges. In the Load Recovery scenario, the existing system faces a peak load of 170 kW, while the proposed load rises to 185 kW. Resource availability decreases from 25 to 22%, suggesting that recovery from high load conditions is particularly challenging. Load recovery often involves gradual resource allocation and system adjustments to return to normal operating conditions. The proposed system’s marginally lower availability suggests that further improvements in load recovery techniques are necessary for optimal performance. The system stress scenario reflects the ultimate test of resilience. The existing system handles a peak load of 190 kW, and the proposed system faces a peak load of 198 kW. Resource availability drops from 18 to 16%, indicating that system stress is at its peak in this scenario. The proposed system’s slight decrease in resource availability suggests that further enhancements are necessary to maintain performance under extreme stress conditions. The Metaheuristic Sizing scenario actually derived from³⁸ offers a integrated view of hybrid renewable energy system resilience using metaheuristic optimization. The existing system peak load currently stands at 102 kW, while the proposed system is optimized for about 115 kW, suggesting a calculated load increase under hybrid configurations. Interestingly, the resource availability improves from 70% to even 75%, in contrast to many previous scenarios. This reflects the efficiency of metaheuristic approaches in balancing social, economic, and environmental parameters effectively. The data from³⁸ supports the idea that integrating socio-techno-economic factors into system design can improve both resource availability and system resilience under load variability, particularly for hybrid systems in microgrid applications overall. The sensitivity check used to change main input values such as sunlight level (± 20%), wind speed (± 15%), underground heat flow (± 12%), starting cost (± 10%), battery size (± 10%), and biofuel price (± 15%). The check showed that a 15% rise in wind speed caused a 10% growth in hydrogen amount, while a 20% drop in sunlight level gave an 8% fall in system work level. Changing the starting cost by -10% brought down the time to get back the money to 5.3 years. Also, the change in underground heat clearly changed how well the system worked, with a 12% rise in heat input giving a 4.5% gain in energy use level. These results show the system’s strong answer to input changes and money-related changes. Unlike earlier studies such as^19.27, which used HOMER software for basic techno-economic system setup of hybrid energy systems aimed at rural energy supply, our research clearly combines geothermal energy with wind and solar sources in a single structure for clean hydrogen generation. This study makes a clear side-by-side review with past system models and brings in a new mix of renewable sources focused on steady energy output and lower overall energy costs. This new system gives better energy use, higher energy output, and stronger system ability under different weather and usage conditions. The energy setup helps to make better use of incoming energy, keeps strong system operation, and supports power supply during changing outdoor and usage levels.

Conclusion

The techno-economic optimization of hybrid renewable systems was showed to have high efficiency and economic viability. The key finds are: Integration of solar and wind energy by 15% reducing energy costs, and energy storage that it improved system efficiency by 20%. Capital investments were recovered within a payback period of 6.2 years, it confirmed the financial feasibility of the system, and. The optimized system it achieved a 12% reduction in long-term operational costs, and a reduction backup power costs by 18%. Storage integration helped reduce energy supply fluctuations by 25%, which enhanced reliability system, and flexibility. Load forecasting optimization, which ensures appropriate system sizing reducing overcapacity risks and maintaining efficiency, this was. Environmental analysis showed a 40% reduction CO₂ emissions and 30% reduction fuel consumption. Sensitivity analysis, which confirmed variations in renewable resource availability, had minimal impact on performance system. The hybrid configuration was proved effective in off-grid and remote applications, it improves energy security and grid independence. Despite these really important findings, the research still has some limitations, such as the assumption of ideal operating conditions and a limited real-time adaptability. The study does not fully account for things like component degradation, financing constraints, or regional policy impacts, which could possibly influence long-term system viability in the future. The future scope is: Advanced machine learning models can be explored to further enhance accuracy real-time load forecasting. Artificial intelligence techniques may optimize the energy storage management and the overall system performance. Research into an emerging energy storage technology is needed to improve the storage capacity, to reduce cost. The integration of the additional renewable energy sources like biomass, or hydro, can diversify supply, and reliability enhance. The potential of linking hybrid systems with the smart grid infrastructure offers new opportunities, energy management adaptive. Social acceptance, public financing mechanisms can be studied, especially in developing the countries context. Future studies should examine the lifecycle environmental impact hybrid systems, more sustainability assessments for comprehensive. Development of the supportive policies, frameworks incentive-based will be essential for wider adoption, scalability.

Author contributions

All the authors contributed to this research work in terms of concept creation, conduct of the research work, and manuscript preparation.

Funding

No funding received for this research work.

Data availability

The data’s used to support the findings of this study are included within this article.

Declarations

Competing interests

The authors declare no competing interests.