Evaluating the agreement between sensitivity and primary analyses in observational studies using routinely collected healthcare data: a meta-epidemiology study

Abstract

Background

Sensitivity analysis is a crucial approach to assessing the “robustness” of research findings. Previous reviews have revealed significant concerns regarding the misuse and misinterpretation of sensitivity analyses in observational studies using routinely collected healthcare data (RCD). However, little is known regarding how sensitivity analyses are conducted in real-world observational studies, and to what extent their results and interpretations differ from primary analyses.

Methods

We searched PubMed for observational studies assessing drug treatment effects published between January 2018 and December 2020 in core clinical journals defined by the National Library of Medicine. Information on sensitivity analyses was extracted using standardized, pilot-tested collection forms. We characterized the sensitivity analyses conducted and compared the treatment effects estimated by primary and sensitivity analyses. The association between study characteristics and the agreement of primary and sensitivity analysis results were explored using multivariable logistic regression.

Results

Of the 256 included studies, 152 (59.4%) conducted sensitivity analyses, with a median number of three (IQR: two to six), and 131 (51.2%) reported the results clearly. Of these 131 studies, 71 (54.2%) showed significant differences between the primary and sensitivity analyses, with an average difference in effect size of 24% (95% CI 12% to 35%). Across the 71 studies, 145 sensitivity analyses showed inconsistent results with the primary analyses, including 59 using alternative study definitions, 39 using alternative study designs, and 38 using alternative statistical models. Only nine of the 71 studies discussed the potential impact of these inconsistencies. The remaining 62 either suggested no impact or did not note any differences. Conducting three or more sensitivity analyses, not having a large effect size (0.5–2 for ratio measures, ≤ 3 for standardized difference measures), using blank controls, and publishing in a non-Q1 journal were more likely to exhibit inconsistent results.

Conclusions

Over 40% of observational studies using RCD conduct no sensitivity analyses. Among those that did, the results often differed between the sensitivity and primary analyses; however, these differences are rarely taken into account. The practice of conducting sensitivity analyses and addressing inconsistent results between sensitivity and primary analyses is in urgent need of improvement.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12916-025-04199-4.

Background

Observational studies using routinely collected healthcare data (RCD) to investigate drug treatment effects are increasingly being published and used to support regulatory decisions [1–4]. Such studies, however, are prone to variable misclassification, unmeasured confounding, and treatment changes, potentially leading to biased effect estimates [5–8]. Recently, concerns have been growing regarding the validity of study findings when using RCD to explore treatment effects [9–15].

Sensitivity analyses are commonly used to assess the “robustness” of research findings. They have been recommended for studies that assess treatment effects because they can elucidate the extent to which potential unaddressed biases or confounders could affect the results. Sensitivity analyses are a fundamental part of the study protocol for randomized controlled trials (RCTs) supported by specific guidelines and recommendations for planning, implementation, and reporting [16]. They have become equally important for evaluating the validity of the findings of observational studies [17], in which, sensitivity analyses are typically applied to examine three key aspects [17]: alternative study definitions (using alternative coding or algorithms to identify/classify exposure, outcome, or confounders) [18], alternative study design (using alternative data source or changing inclusion period of study population) [19], and alternative analyses (changing the analysis models, modifying the functional form, using alternative methods to handle missing data, or testing model assumptions such as calculating the E-value) [20].

However, in observational studies using RCD, significant knowledge gaps remain regarding how sensitivity analyses are applied. The divergent results resulting from the associations drawn from the sensitivity analyses being inconsistent with those from the primary analysis may threaten the validity of the inferences. Such inconsistencies are not rare in observational studies using RCD. Previous research has shown that 18.2%–45.5% of studies yield differential effect estimates when using alternative definitions or algorithms to identify health status [6]. However, no studies to date have systematically examined the methods and interpretation of sensitivity analysis in observational studies to explore treatment effects. Prior studies have focused on specific issues (e.g., missing data and unmeasured confounding) [21–23], and all have suggested the practice of sensitivity analyses in observational study is inadequate, with underuse or misuse. A review of the reporting and handling of missing data found that only 11% of the included studies conducted sensitivity analyses to assess the impact of missing data [22]. Another review of E-value applications, a method designed to quantify sensitivity to unmeasured confounding, revealed poor reporting (38% of studies only reported point estimates without confidence intervals) and insufficient interpretation (61% failed to explain the E-value with known but unmeasured confounders) [21]. In real-world observational studies using RCD, it remained poorly understood how sensitivity analyses were conducted, how often findings diverge from primary analyses, and to what extent these discrepancies affect interpretation of the findings.

Therefore, we conducted a methodological systematic review to investigate the application of sensitivity analyses in observational studies using RCD. The following research questions were explored: (1) whether and how sensitivity analyses were conducted, (2) the extent to which the results diverge between sensitivity and primary analyses and the factors associated with this divergence, and (3) how the results of the sensitivity analyses are interpreted.

Knowledge of these issues could provide insights into the implementation of sensitivity analyses in observational studies, facilitate improvements in current sensitivity analysis practice, and enhance the transparency and reproducibility of the findings of observational studies.

Materials and methods

This study is part of a major research project investigating observational studies using RCD. Previous studies have examined the reporting and methodological issues in observational studies using RCD [5, 6, 24, 25]. This study aimed to systematically evaluate the application of sensitivity analyses according to the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) 2020 [26].

Eligibility criteria

We included observational studies that used RCD to evaluate the effectiveness or safety of drug treatments. The exclusion criteria were as follows: (1) studies with actively collected data for a pre-specified research purpose, (2) studies with an unspecified type of data, and (3) studies evaluating the treatment effects of complementary or alternative medicines.

Literature search and screening

We used both MeSH terms and free words to conduct a systematic search of PubMed for paper published between January 1, 2018, and December 31, 2020. The search strategy, which was peer-reviewed by specialists, was detailed in a previously published article [24].

Paired methodology-trained investigators independently screened the abstracts and full texts. In cases of disagreement, a third investigator with expertise determined whether the studies met the eligibility criteria.

Data extraction

A general survey had extracted characteristics of the included studies, including sample size, primary outcome, and comparator. Our study further extracted information regarding sensitivity analyses. We recorded whether a sensitivity analysis was performed for each included study. The answer “yes” only applied to studies that explicitly stated that sensitivity analyses were conducted. Other types, such as additional or exploratory analyses, were not considered.

We applied the following approach to select the primary analysis and its corresponding sensitivity analyses for each study. First, we selected the analysis specified as the primary analysis. If not specified, the primary analysis was designated as the first reported multivariable analysis. Next, the analysis of the specified primary outcome (if multiple primary outcomes were reported or no primary outcome was specified, we used the first reported outcome) was selected. We then extracted the first 10 sensitivity analyses explicitly identified by the authors to assess the robustness of the primary analysis results. Analyses were excluded if they were performed to address different target treatment effects, such as changes outcome (e.g., using acute coronary syndrome or all-cause death as the outcome in the primary analysis, but restricting all-cause mortality in sensitivity analyses [27]) or substitution of comparator groups (e.g., changing the reference group of non-β-blockers prescription in the main analysis to calcium-channel blockers in the sensitivity analysis [28]).

We also documented the number and types of sensitivity analyses conducted in each study. To avoid omissions, the sensitivity analyses presented in the Results and Methods sections were considered. Following a guide provided by the Agency for Healthcare Research and Quality (AHRQ), sensitivity analyses were categorized into three main dimensions: alternative study definitions (exposure/control/outcome/confounder), alternative study design (population under study), and alternative modeling (approaches to handling missing data or statistical strategies and models, including the E-value) [17].

We calculated the ratios of effect estimates between the sensitivity and primary analyses to assess the extent of divergence in the results. We extracted effect indicators (i.e., risk ratio, hazard ratio, odds ratio, rate difference, and mean difference), point estimates of treatment effect, and confidence intervals for the primary and first 10 reported sensitivity analyses.

A pre-designed pilot-tested form was used to extract the aforementioned information. Paired investigators conducted independent extractions for each study, and any discrepancies were resolved through discussion or consultation with a third investigator with expertise in methodology.

Statistical analysis

R software version 4.3.2 was used for statistical analysis. The basic characteristics of the studies that conducted sensitivity analyses were depicted. Categorical data were described using frequency and proportion. Continuous data were presented as means and standard deviation if they followed a normal distribution. For non-normally distributed continuous data, the median and interquartile range (IQR) were used. We conducted univariable and multivariable logistic regression analyses to examine the factors associated with performing sensitivity analyses. The examined factors included sample size (> 40,000 vs. ≤ 40,000), primary outcome type (effectiveness vs. safety), comparator type (active vs. blank control), impact factor level of the published journal (Q1 journal vs. other), and whether a protocol was reported (yes vs. no).

For studies with clearly reported sensitivity analyses, we recorded how often the treatment effects estimated in the primary analysis were inconsistent with the interpretation of the sensitivity analysis (treatment effect estimates were significant in primary analysis but not in sensitivity analysis, and vice versa), the estimates were in opposing directions, the confidence interval from primary analyses did not include the effects estimated by sensitivity analyses, and the confidence intervals of the analyses did not overlap. Sensitivity analysis methods that did not provide the same estimates as the primary analysis (e.g., E-value calculations) were not included in the direct comparison of results between sensitivity and primary analyses.

We compared the differences between the primary and sensitivity analyses using the ratios in each study. The point estimate of the ratio was obtained by dividing the point estimate of each sensitivity analysis by that of the primary analysis, provided that the effect indicators of the two analyses were identical. The variance of the ratio was calculated as ${\mathit{var}}_{\mathit{ratio}}=1/4({\mathit{var}}_{\mathit{sen}}+{\mathit{var}}_{\mathit{pri}}+2r\sqrt{{\mathit{var}}_{\mathit{sen}}}\sqrt{{\mathit{var}}_{\mathit{pri}}})$, where the ${\mathit{var}}_{\mathit{sen}}$ and ${\mathit{var}}_{\mathit{pri}}$ denote the variances of the sensitivity and primary analysis estimates, respectively, and $r$ is the correlation coefficient. The sensitivity and primary analyses were from the same studies; therefore, their estimates were not independent. We assumed a moderate correlation (r = 0.5) in the primary ratio calculations. The 95% CI of the ratio was calculated based on the variance and point estimates of the ratio, assuming that it followed a normal distribution [29]. The 95% CI of the ratios not crossing 1 indicated a significant difference in the results. Furthermore, we conducted sensitivity analyses for the ratios to adjust the correlations to 0.8 and 0.2.

We used a random effects model to conduct meta-analyses of these ratios and summarized the extent of disagreement between the sensitivity and primary analyses. To measure the absolute difference between the estimates from the primary and sensitivity analyses, we first standardized the direction of the ratios by inversing those that were less than 1. Given the inherent non-independence of multiple sensitivity analyses within individual studies (for example, different analytical approaches in a study where effect size is large tend to yield robust estimates, leading to the ratios clustering around 1), we conducted a multilevel meta-analysis, decomposing variance into within-study and between-study components [30]. In our primary analysis, we treated each ratio as a level 1 unit and each study as a level 2 unit. A random effects model with inverse-variance weighting was used to pool effect estimates. Interstudy heterogeneity was evaluated using the Cochran Q statistic. We also conducted sensitivity analyses for the meta-analyses by selecting either the ratio from the first sensitivity analysis or the highest ratio within each study. Subsequently, each meta-analysis was stratified according to the type of sensitivity analysis used.

Univariate and multivariate logistic regression analyses were performed to examine the potential association of study characteristics with the consistency between the primary and sensitivity analyses. Specifically, we included the following categorical variables: number of sensitivity analyses (> 3 vs. ≤ 3), sample size (> 40,000 vs. ≤ 40,000) [31, 32], effect size (large effect [i.e., > 2 or < 0.5 for ratio measures; > 3 for standardized difference measures] vs. non-large effect) [33, 34], primary outcome type (effectiveness vs. safety) [35], comparator type (active vs. blank control) [36, 37], whether a protocol was reported (yes vs. no), and impact factor level of the published journal (Q1 journal vs. other). Journal tiers (Q1/non-Q1) were defined using 2020 Journal Citation Reports impact factor percentiles.

Results

A total of 256 studies met our eligibility criteria (Additional file 1: Table S1). A flowchart of the study inclusion process was shown in Additional file 1: Fig. S1. Among these studies, 152 (59.4%) that conducted sensitivity analyses were included. Of these, 138 (90.8%) were published in Q1 journals, and 47 (30.9%) reported a pre-specified protocol. The comparator type was active controls in 69 (45.4%) studies and blank controls in 83 (54.6%). Regarding the primary outcome, 75 (49.3%) of the studies assessed drug effectiveness, whereas 77 (50.7%) assessed safety. Multivariate analyses showed that the studies published in a Q1 journal (adjusted odds ratio [OR] 4.56, 95% CI 2.25–9.22) and with a protocol (adjusted OR 3.20, 95% CI 1.48–6.94) were more likely to perform sensitivity analyses (Table 1).

Table 1.

Study characteristics and their association with conducting sensitivity analyses

Variables	Number of studies (%)			Univariable analysis		Multivariable analysis
	Total (N = 256)	Studies conducted sensitivity analyses (N = 152)	Studies did not conduct sensitivity analyses (N = 104)	OR (95% CI)	P value	Adjusted OR (95% CI)	P value
Sample size
≤ 40,000	156 (60.9)	81 (53.3)	75 (72.1)	1.00 (reference)		1.00 (reference)
> 40,000	100 (39.1)	71 (46.7)	29 (27.9)	2.27 (1.33, 3.87)	0.003	1.50 (0.83, 2.72)	0.180
Type of primary outcome
Safety	113 (44.1)	77 (50.7)	36 (34.6)	1.00 (reference)		1.00 (reference)
Effectiveness	143 (55.9)	75 (49.3)	68 (65.4)	0.52 (0.31, 0.86)	0.012	0.65 (0.37, 1.16)	0.146
Type of comparator
Blank control	146 (57.0)	83 (54.6)	63 (60.6)	1.00 (reference)		1.00 (reference)
Active control	110 (43.0)	69 (45.4)	41 (39.4)	1.28 (0.77, 2.12)	0.344	0.94 (0.53, 1.65)	0.828
Journal impact factor tier
Non-Q1	53 (20.7)	14 (9.2)	39 (37.5)	1.00 (reference)		1.00 (reference)
Q1	203 (79.3)	138 (90.8)	65 (62.5)	5.91 (3.00, 11.65)	< 0.001	4.56 (2.25, 9.22)	< 0.001
Whether there was a protocol
No	199 (77.7)	105 (69.1)	94 (90.4)	1.00 (reference)		1.00 (reference)
Yes	57 (22.3)	47 (30.9)	10 (9.6)	4.21 (2.01, 8.79)	< 0.001	3.20 (1.48, 6.94)	0.003

OR Odds ratio, CI Confidence interval

Table 2 presents the characteristics of sensitivity analysis practices. Of the 152 included studies, the median number of sensitivity analyses was three (IQR, 2–6). Thirty-five (23.0%) studies conducted only one sensitivity analysis, 72 (47.4%) conducted two to five sensitivity analyses, 33 (21.7%) conducted six to ten, and 12 (7.9%) conducted more than ten. In addition, 99 (65.1%) studies applied alternative study definitions (exposure/control 66, 43.4%; primary outcome 49, 32.2%; and covariates 28, 18.4%), 74 (48.7%) adopted alternative study designs with different eligibility criteria for the population, 85 (55.9%) used alternative modeling approaches (statistical strategies/models 74, 48.7%; approach to handling missing data 12, 7.9%; E-value 7, 4.6%), and 24 (15.8%) used sensitivity analyses with multiple alternatives.

Table 2.

Characteristics of studies conducting sensitivity analyses, n (%)

Characteristics	Number of studies (N = 152)
Number of sensitivity analyses (median [IQR])	3 (2.6)
Only one sensitivity analysis	35 (23.0)
2 to 5 sensitivity analyses	72 (47.4)
6 to 10 sensitivity analyses	33 (21.7)
More than 10 sensitivity analyses	12 (7.9)
Type of sensitivity analysis
Alternative study definitions	99 (65.1)
Exposure/control	66 (43.4)
Primary outcome	49 (32.2)
Covariates	28 (18.4)
Exposure/control and primary outcome	1 (0.7)
Alternative study design	74 (48.7)
Population under study	74 (48.7)
Alternative modeling	85 (55.9)
Statistical strategy/model	74 (48.7)
Approach to handling of missing data	12 (7.9)
E-value	7 (4.6)
Multiple alternatives	24 (15.8)
Reporting results of sensitivity analyses
Reporting least one result of sensitivity analyses	131 (86.2)
Reporting no results of sensitivity analyses	21 (13.8)

IQR Interquartile range

Notably, 131 (86.2%) studies reported the results of at least one sensitivity analysis, whereas the remaining 21 (13.8%) failed to report the results of any sensitivity analyses. The following analyses were based on these 131 studies.

Agreement of results from primary and sensitivity analyses

Of the 131 studies, 48 (36.6%) yielded differential interpretations by primary versus at least one sensitivity analyses based on the statistical significance, of which nearly half (23, 47.9%) showed changes in statistical significance with more than one sensitivity analysis (Table 3). Most of these 48 studies (35, 72.9%) reported statistically significant effects in the primary analyses but not in the sensitivity analyses. The estimates were in opposing directions between the primary and sensitivity analyses in 26 (19.8%) studies, and the confidence intervals from the primary and sensitivity analyses did not overlap in 19 (14.5%) studies.

Table 3.

Comparison of results from primary analyses and sensitivity analyses, n (%)

Comparison category	Total (N = 131)	Number of sensitivity analyses consistent with primary analysis
		Only 1	More than 1
Ratios showed significant differencea	71 (54.2)	37 (28.2)	34 (26.0)
Change in statistical significance of effect estimates	48 (36.6)	25 (19.1)	23 (17.6)
Primary analysis had statistical significance but sensitivity analyses did not	35 (26.7)	16 (12.2)	19 (14.5)
Primary analysis had no statistical significance but sensitivity analyses had	13 (9.9)	9 (6.9)	4 (3.0)
The point estimates of sensitivity analyses outside the CI of primary analyses	53 (40.5)	32 (24.4)	21 (16.1)
Opposite direction of effect estimatesb	26 (19.8)	11 (8.4)	15 (11.5)
Non-overlapping CIsc	19 (14.5)	8 (6.1)	11 (8.4)

CI, confidence interval

^a95% CI of the ratio of estimates from sensitivity and primary analyses did not cross 1

^bOpposite direction of effect estimates from sensitivity and primary analyses

^cNon-overlapping CIs of sensitivity and primary analyses

Among the 131 studies, 71 (54.2%) showed significant differences between the primary analyses and at least one sensitivity analysis (i.e., 95% CI of the ratio did not cross 1), with 37 studies showing inconsistencies with one sensitivity analysis, and 34 showing inconsistencies with more than one. Within the 71 studies, 145 (27.3%) sensitivity analyses showed significant differences compared to the primary analyses, with 59 (40.7%) using alternative study definitions (alternative exposure/control 28, 19.3%; alternative primary outcome 23, 15.9%; alternative covariates 4, 2.8%; and alternative exposure/control and primary outcome 4, 2.8%), 39 (26.9%) using alternative study designs, 38 (26.2%) using alternative statistical models (alternative statistical strategy/model 36, 24.8%; alternative approach to handling of missing data 2, 1.4%), and 9 (6.2%) using multidimensional alternatives. The agreement of the results of the different types of sensitivity analyses with the primary analysis is shown in Additional file 1: Fig. S2.

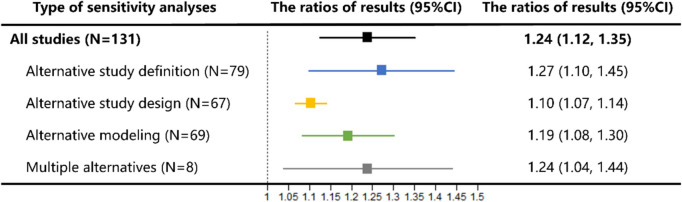
The random effects summary ratios for all studies were 1.24 (95% CI 1.12–1.35), indicating an average difference of 24% in the effect estimates from the primary analyses and sensitivity analyses (Fig. 1). For different types of sensitivity analyses, the largest difference in effects was observed between sensitivity analyses using alternative study definitions and the primary analyses (summary ratio 1.27, 95% CI 1.10 to 1.45). The results of all alternative sensitivity analyses were consistent with those of the primary meta-analyses conducted in this study. When the first reported sensitivity analysis was included, the summary ratio was 1.15. When including the maximum ratio sensitivity analysis with respect to the primary analysis, the summary ratio was 1.29 (Additional file 1: Fig. S3). The summary ratios combined using different correlation coefficients were extraordinarily similar (Additional file 1: Fig. S4). The forest plot of ratios in the primary meta-analysis was presented in Additional file 1: Fig. S5.

Fig. 1.

Meta-analysis of ratios of sensitivity analysis results to primary analyses in studies reporting sensitivity analysis results

Factors influencing consistency between sensitivity and primary analysis results

As shown in Table 4, multivariable analyses showed that studies that conducted more than three sensitivity analyses were more likely to exhibit inconsistencies between sensitivity and primary analysis results compared to studies that conducted no more than three sensitivity analyses (adjusted OR 3.26, 95% CI 1.39–7.62). Studies with a large effect size (adjusted OR 0.23, 95% CI 0.07–0.77), use of active controls (adjusted OR 0.26, 95% CI 0.11–0.61), and published in Q1 journals (adjusted OR 0.13; 95% CI 0.02–0.91) were more likely to show consistent results.

Table 4.

Study characteristics of studies conducted sensitivity analyses and their association with agreement of treatment effects estimated by primary analyses and sensitivity analyses

Variables	Number of studies (%)			Univariable analysis		Multivariable analysis
	Total (N = 131)	Statistically significant ratio (N = 71)	Non-significant ratio (N = 60)	OR (95% CI)	P value	Adjusted OR (95% CI)	P value
Number of sensitivity analyses
≤ 3	67 (51.1)	30 (42.3)	37 (61.7)	1.00 (reference)		1.00 (reference)
> 3	64 (48.9)	41 (57.7)	23 (38.3)	2.20 (1.09, 4.44)	0.028	3.26 (1.39, 7.62)	0.006
Sample size*
≤ 40,000	68 (51.9)	35 (49.3)	33 (55.0)	1.00 (reference)		1.00 (reference)
> 40,000	63 (48.1)	36 (50.7)	27 (45.0)	1.26 (0.63, 2.50)	0.515	1.84 (0.81, 4.18)	0.144
Effect size†
[Ratio (0.5, 2); difference ≤ 3]	111 (84.7)	64 (90.1)	47 (78.3)	1.00 (reference)		1.00 (reference)
[Ratio < 0.5 or > 2; difference > 3]	20 (15.3)	7 (9.9)	13 (21.7)	0.40 (0.15, 1.07)	0.067	0.23 (0.07, 0.77)	0.017
Type of primary outcome
Safety	65 (49.6)	31 (43.7)	34 (56.7)	1.00 (reference)		1.00 (reference)
Effectiveness	66 (50.4)	40 (56.3)	26 (43.3)	1.69 (0.84, 3.38)	0.139	2.25 (0.98, 5.19)	0.056
Type of comparator
Blank control	70 (53.4)	46 (64.8)	24 (40.0)	1.00 (reference)		1.00 (reference)
Active control	61 (46.6)	25 (35.2)	36 (60.0)	0.36 (0.18, 0.74)	0.005	0.26 (0.11, 0.61)	0.002
JCR category quartile of journal
Non-Q1	11 (8.4)	9 (12.7)	2 (3.3)	1.00 (reference)		1.00 (reference)
Q1	120 (91.6)	62 (87.3)	58 (96.7)	0.24 (0.05, 1.15)	0.073	0.13 (0.02, 0.91)	0.039
Whether there is a protocol
No	86 (65.6)	47 (66.2)	39 (65.0)	1.00 (reference)		1.00 (reference)
Yes	45 (34.4)	24 (33.8)	21 (35.0)	0.95 (0.46, 1.95)	0.886	1.28 (0.55, 2.98)	0.572

OR Odds ratio, CI Confidence interval

^*The categories were classified based on the median sample size from the studies included in this analysis, rounded to the nearest practical value

^†The categories were classified based on Grading of Recommendations Assessment, Development and Evaluation (GRADE) guidelines

Interpretation of inconsistent between sensitivity and primary analysis results

Of the 71 studies with statistically significant difference between the sensitivity and primary analysis results, nine (12.6%) indicated potential uncertainty in the primary analysis results, 31 (43.7%) indicated no impact on the robustness of the results, and 31 (43.7%) studies did not discuss the impact of these inconsistencies.

In 48 studies in which inconsistencies in statistical significance were observed between the primary and sensitivity analyses, 17 (35.4%) implied that these inconsistencies did not compromise the robustness of the results, and 23 (47.9%) did not assess the impact. Even in 23 studies with changes in statistical significance between the primary analysis and more than one sensitivity analysis, only 4 (17.4%) discussed the potential uncertainty of the primary results.

Discussion

Summary of findings

Over 40% of the included studies did not conduct sensitivity analyses for potential bias. Compared to studies with sensitivity analyses, these studies demonstrated significantly lower Q1 journal publication rates (adjusted OR 4.56, 95% CI 2.25–9.22) and reduced protocol availability (adjusted OR 3.20, 95% CI 1.48–6.94). These findings collectively suggest improvements in study design and analysis of observational studies using RCD are needed.

In studies that conducted sensitivity analyses, significant differences between the results of sensitivity and primary analyses were often found in observational studies. More than half (71/131, 54.2%) of the studies had at least one sensitivity analysis that was inconsistent with the primary analysis results. And 36.6% of the studies show different interpretations for inconsistencies in the statistical significance of the primary and sensitivity analyses. However, all studies drew conclusions based on the results of the primary analysis, and only nine studies considered that the discrepancies may affect the inference of the treatment effect.

Discrepancies were most pronounced when using alternative study definitions, showing the largest treatment effect deviations. Alternative designs and modeling approaches demonstrated similar inconsistency frequencies.

Multivariable analysis identified four factors associated with increased reporting of inconsistent results: conducting more than three sensitivity analyses, investigating a relatively moderate treatment effect, using blank controls, and publishing in non-Q1 journals.

Comparison with other studies

Observational studies are conducted in a complex environment where causal inferences are particularly vulnerable to multiple sources of bias. Sensitivity analysis is easy to implement and is an important tool for assessing the robustness of these findings. Current methodological research has primarily focused on developing novel sensitivity analysis approaches to address inherent challenges in observational studies such as unmeasured confounding, multiple comparisons, and recurrent events [38–42]. However, no studies have been conducted to investigate the sensitivity analysis practices, nor have guidelines been developed on how to conduct sensitivity analyses in observational studies.

For RCTs, the sensitivity analysis plan should be pre-specified in the protocol, and relevant guidelines for performing sensitivity analyses are available [43–45]. Based on these guidelines, four principles for conducting and evaluating sensitivity analyses in RCTs have been proposed [16]. While the core principles of sensitivity analyses remain broadly applicable, the sources of bias and approaches of sensitivity analyses differ between RCTs and observational studies. RCTs primarily address deviations from randomization, typically comparing intention-to-treat with per-protocol analyses to assess violations of randomization. Observational studies, however, primarily consider the potential unmeasured confounders or unaddressed bias. Accordingly, approaches such as E-value and negative control analyses have been proposed for sensitivity analyses.

Implication of findings

Sensitivity analysis is a very useful and highly recommended approach to uncover the uncertainty caused by hidden biases and to assess the robustness of findings in observational studies [17], but it is underused. Over 40% of the studies did not conduct sensitivity analyses to investigate potential biases. Among those that did, over half demonstrated discrepancies between the primary and sensitivity analysis results. Previous research indicates that only around 10% of observational studies have accessible protocols [5], suggesting that the majority of sensitivity analyses are not pre-planned and may involve post hoc analyses. This survey found that studies published in high-impact journals were more likely to exhibit consistent results. Inconsistency between the primary and sensitivity analyses may be selectively reported and underestimated.

However, with the frequently significant discrepancies, their impact were not adequately considered. For example, most studies tended to report a statistically significant result as the primary analysis, but selected non-statistically significant estimates as sensitivity analyses. It would be unacceptable to drawing conclusions based only on the primary analysis without assessing these differences. Inconsistency between sensitivity and primary analyses suggests that unobserved bias may alter the conclusion drawn from the primary analyses. The investigators should explain the possible source and magnitude of the bias, and the conclusion should be claimed considering the potential impact of this bias.

In addition, there may be a need for more guidance on how to conduct sensitivity analyses in observational studies as both the number and type of sensitivity analyses in empirical studies vary widely. Indeed, the key assumptions or sources of uncertainty in studies may vary from case to case, but basic principles may still be helpful. For example, investigators should at least identify the assumptions or uncertainties arising from the three main dimensions: study definition of key variables, study design and analysis modeling, and then plan sensitivity analyses accordingly.

Last but not least, in an observational study, an active control may be more appropriate than a blank control for assessing treatment effects, as it has been shown to alleviate indication confounding [36].

Incorporating our findings and the principles for RCTs, we proposed four recommendations and corresponding application examples for conducting sensitivity analyses in observational studies (Table 5). Investigators should carefully consider the potential unaddressed biases and test their impact on the effect estimates. Typically, sensitivity analyses could be designed to test three major dimensions of uncertainty sources: study definitions of key variables, study design, and analysis modeling. The investigators should clearly specify the uncertainty being tested. Special consideration should be given to the key sources of bias in observational studies, including unmeasured confounding, misclassification bias, immortal time bias, and time-varying confounding. To address these issues, specific sensitivity analysis methods should be employed—for example, the E-value or negative control analyses to assess unmeasured confounding. In addition, the rationale and implementation of alternative approaches should be explained. The detailed results of the primary and sensitivity analyses, including point estimates and confidence intervals of the primary and sensitivity analyses, should be clearly reported. When assessing the agreement between the results of the primary and sensitivity analyses, not only should the point estimates and the statistical significance of the treatment effect be considered, but the statistical uncertainty should also be compared, for example, by assessing the overlap of the confidence interval. Finally, if the results of the primary and sensitivity analyses are inconsistent, the investigators should highlight the differences and discuss the possible reasons for the divergence: whether some underlying assumptions are violated, and how strong they are. Conclusions should then be drawn the based on this assessment.

Table 5.

Recommendations for conducting sensitivity analyses in observational studies

Recommendation 1: Consider the potential unmeasured confounders or unaddressed bias that may alter the study’s underlying assumptions
Explanation
• In observational studies using RCD, unmeasured confounders or unaddressed bias often threaten the validity of the inferences • Carefully considering the potential unmeasured confounders or unaddressed bias and testing how these violations may change the effect estimates is essential to strengthen the validity of the inferences • Typically, an observational study’s underlying assumptions can be altered along three dimensions: study definition, study design, and analysis modeling
Example
• A real-world cohort study investigated the effect of dipeptidyl peptidase-4 (DPP-4) inhibitors on the incidence of inflammatory bowel disease (IBD) among patients with type 2 diabetes [18]. In this study, the authors conducted sensitivity analyses including the following three dimensions: ✓ Using alternative exposure definition: a stricter exposure definition that DPP-4 inhibitor use was redefined as receipt of at least four prescriptions (patients were considered exposed after first prescription in the primary analysis), and alternative outcome definition, restricting in IBD events to those supported by clinically relevant events (diagnoses of IBD with or without clinically relevant events in database for the primary analysis); ✓ Changing the study design: with alternative eligibility of study population, excluding patients treated with thiazolidinediones at any time before cohort entry (prior use of thiazolidinediones was not considered in the primary analysis); ✓ Using alternative analysis modeling: such as performing a competing risk analysis by death from any cause using the Fine and Gray sub-distribution model (using time-dependent Cox model in the primary analysis). The marginal structural model was used for testing the potential impact of time-varying confounding and the rule-out method was applied to test for unmeasured confounding
Recommendation 2: Carefully select and clearly report the approaches used to conduct sensitivity analyses
Explanation
•Select appropriate approaches to provide quantitative assessments of the robustness of the primary analysis to violations of the assumption of no unmeasured confounders or unaddressed bias; •As observational studies are always subjected to unmeasured confounding, methods such as E-value and negative control are important to apply to assess the impact; • The sources of uncertainty being tested in each sensitivity analysis should be clearly stated; •The basic rationales and implementations of alternative approaches should be provided
Example
• A cohort study by Crellin et al. investigated association between trimethoprim use for urinary tract infection and risk of adverse outcomes in older patients [46]. In the Method section, the uncertainty being tested, methods, and rationales for the sensitivity analyses were provided as follows: “Finally, to ensure that we were comparing similar groups (to reduce confounding by indication), we examined the risks of all three outcomes after propensity score weighting (inverse probability of treatment weighting) of trimethoprim and amoxicillin users (full details in web appendix 1). In inverse probability of treatment weighting, patients are reweighted according to the inverse of their probability of receiving the treatment they actually received.”
Recommendation 3: Clearly report the sensitivity analysis results and compare the differences between primary and sensitivity analyses
Explanation
• Clearly report effect point estimates and confidence intervals for each sensitivity analysis; • Systematically evaluate the consistency between primary and sensitivity analyses by comparing the point estimates, confidence intervals, and statistical significance
Example
• Filion et al. summarized point estimates and confidence intervals of adjusted hazard ratios for the primary and sensitivity analyses in one table [47]. As clearly shown in one column, point estimates and statistical uncertainty were easy to compare; • Shapiro et al. summarized point estimates and confidence intervals of adjusted hazard ratios for the primary and sensitivity analyses in one figure [48]. Presenting a forest plot with the number of point estimates and 95% confidence interval is a good reporting example
Recommendation 4: Highlight the differences and discuss the reason for the divergence when primary and sensitivity analyses yield different inferences
Explanation
• When sensitivity analyses result in changed effect estimates, researchers should highlight the differences and discuss the potential reason for the inconsistency; • The investigators should also reconsider the underlying assumptions, and interpret the findings with caution
Example
• A cohort study by Abrahami et al. investigated the use of incretin-based drugs and risk of cholangiocarcinoma among patients with type 2 diabetes [18]. In the Results section, the authors highlighted the inconsistent results between sensitivity and primary analyses: “The sensitivity analyses led to generally consistent results (supplementary tables 4–13), except for the lagged analyses with hazard ratios ranging from 1.31 to 1.62 for DPP-4 inhibitors and 1.42 to 2.38 for GLP-1 receptor agonists. The stricter exposure definition generated hazard ratios that excluded the null for both DPP-4 inhibitors (1.77, 95% confidence interval 1.01 to 3.11) and GLP-1 receptor agonists (2.46, 1.04 to 5.85).” • Suchard et al. assessed the effectiveness and safety of first-line antihypertensive drug classes [49]. Two different analysis strategies, on-treatment analysis vs. intention-to-treatment analysis, yielded differential results ✓ The following difference was noted: “On-treatment time results in shorter follow-up than intention to treat. As expected, we saw blunted estimates of differential effectiveness and risks between drug class new users under an intention-to-treat design.” ✓ The authors explained the reason for the difference: “On-treatment follow-up also helps to assess differential adherence to initial treatment. Except in the Columbia University Medical Center database, median on-treatment time was modestly shorter (0–38 days) for thiazide or thiazide-like diuretics versus angiotensin-converting enzyme inhibitors new users. Such differences, if meaningful, are also less likely to confound on-treatment estimates where time-at-risk ends with treatment discontinuation. Further, claims databases reported drug fulfilment whereas electronic health records reported prescriptions. Because fulfilment more directly reflects actual drug taking, one might expect differential adherence to generate notable effect estimate differences across data sources; we did not observe such differences in comparing thiazide or thiazide-like diuretics versus angiotensin-converting enzyme inhibitors new users.” ✓ The results were interpreted as follows: “We found, however, that patients initiating treatment with a thiazide or thiazide-like diuretic had a significantly lower risk of seven effectiveness outcomes, including acute myocardial infarction, hospitalisation for heart failure, and stroke, as compared with angiotensin-converting enzyme inhibitors new users, while patients remain on-treatment with their initial drug class choice.”

Strengths and limitations

This is the first study to systematically evaluate the application of sensitivity analyses in observational studies using RCD including the differences between the primary and sensitivity analyses, the potential factors influencing the differences, and the interpretation based on the differences. In addition, the methods used in this survey to identify and screen studies, and to extra and analyze data were rigorous. This survey also included a relatively large number of studies, which can provide comprehensive information on the methodology and reporting characteristics of sensitivity analyses in observational studies.

This study also has several limitations. First, our study was based on reporting. Due to selective reporting and publication, our results may underestimate the proportion and magnitude of inconsistencies between primary analyses and sensitivity analyses. Second, given the inherent correlation between the primary and sensitivity analyses in the same study, a moderate correlation (0.5) was assumed to quantify the difference between the primary and sensitivity analyses, addressing the violation of the independence assumptions for ratio calculations. While sensitivity analyses using alternative analyses with strong correlation (0.8) and weak correlation (0.2) yielded consistent results, indicating that the significant differences between analyses are robust. Third, we only searched for publications between 2018 and 2020. Thus, our findings may not be generalized to other years. However, it is unlikely to incur significant improvement in the practice of sensitivity analysis in observational studies during a relatively short period. To further confirm it, we investigated the practice of sensitivity analyses in a sample of studies published between 2021 and 2024. We searched PubMed for RCD studies published from 2021 to 2024. For each year, we ordered the searched reports in the chronological order of their publication and selected the first 20 reports that met the eligibility criteria (80 articles in total). The results showed that the characteristics of sensitivity analyses and their consistency with the primary analyses did not change significantly to the studies published from 2018 to 2020. There were 51 (63.8%) studies performing sensitivity analyses with 47 reporting the results. Among the 47 studies, the median number of sensitivity analyses was three (IQR 1–6), with 37 (72.5%) using alternative definitions, 25 (49.0%) using alternative designs, and 28 (54.9%) using alternative analysis models (Additional file 1: Table S2). A total of 28 (59.6%) showed significant differences between the primary analyses and at least one sensitivity analysis (i.e., 95% CI of the ratio did not cross 1), with 12 studies showing inconsistencies in more than one sensitivity analysis (Additional file 1: Table S3). We also evaluated the impact of COVID-19 pandemic on sensitivity analysis practices by stratifying studies into pre-2020 and post-2020 publications. The two periods showed comparable patterns in the proportion of studies conducting sensitivity analyses (58.9% [pre-2020] vs. 60.2% [post-2020]); the number of sensitivity analyses performed (median 3 [IQR 1–6] vs. 3 [2–7]); and agreement between the primary and sensitivity analyses (52.4% vs. 57.1% showing significant differences with CIs of ratios not crossing 1).

Fourth, this survey exclusively included observational studies utilizing RCD. While some conclusions may not be generalizable to observational studies employing alternative data sources, the findings overall align with the general characteristics of observational studies.

Conclusions

The number and choice of sensitivity analyses conducted in observational studies showed high heterogeneity. Significant divergences were also found between the results of the sensitivity and primary analyses, with those using alternative study definitions representing the majority. However, the impact of these discrepancies was not comprehensively assessed or addressed, with only a limited number of studies noting the potential bias indicated by the sensitivity analyses. Systematic efforts are urgently needed to improve the performance of sensitivity analyses and interpretation of their findings, especially when they are inconsistent with the primary findings.

Abbreviations

AHRQ

Agency for Healthcare Research and Quality

IQR

Interquartile range

OR

Odds ratio

RCD

Routinely collected healthcare data

RCT

Randomized controlled trials

SD

Standard deviation

Authors’ contributions

JYX and YNW undertook the statistical analysis and drafted the initial manuscript. QH and SYX handled data extraction. SF and XFW structured the article and suggested revisions. WW and XS reviewed the content and results, and suggested revisions. The corresponding author attests that all listed authors meet authorship criteria and that no others meeting the criteria have been omitted. All authors read and approved the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 82225049, 72104155, 72304198) and 1.3.5 project for disciplines of excellence, West China Hospital, Sichuan University (Grant No. ZYGD23004). The funder played no role in the study design; collection, analysis, and interpretation of data; writing of the report; or decision to submit the article for publication.

Data availability

Data is provided within the manuscript or Additional file 1.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.