Spatial frequency and orientation tuning dynamics in area V1

Abstract

Spatial frequency (SF) and orientation tuning are intrinsic properties of neurons in primary visual cortex (area V1). To investigate the neural mechanisms mediating selectivity in the awake animal, we measured the temporal dynamics of SF and orientation tuning. We adapted a high-speed reverse-correlation method previously used to characterize orientation tuning dynamics in anesthetized animals to estimate efficiently the complete spatiotemporal receptive fields in area V1 of behaving macaques. We found that SF and orientation tuning are largely separable over time in single neurons. However, spatiotemporal receptive fields also contain a small nonseparable component that reflects a significant difference in response latency for low and high SF stimuli. The observed relationship between stimulus SF and latency represents a dynamic shift in SF tuning, and suggests that single V1 neurons might receive convergent input from the magno- and parvocellular processing streams. Although previous studies with anesthetized animals suggested that orientation tuning could change dramatically over time, we find no substantial evidence of dynamic changes in orientation tuning.

Spatial frequency (SF) and orientation tuning are two of the most prominent features of neuronal selectivity in primary visual cortex (area V1) (1). The dynamics of SF and orientation tuning and their interactions are of particular interest to neurophysiologists because they can reveal important information about the specific circuits and mechanisms of neuronal selectivity (2). Dynamic tuning properties may also be critical for understanding natural vision, where eye movements can introduce complex temporal stimulus dynamics (3, 4).

We simultaneously measured the temporal dynamics of both SF and orientation tuning in single V1 neurons in the awake primate. Conventional methods for estimating selectivity in V1 use stationary or drifting gratings of constant SF and orientation. Stimuli are presented for relatively long periods (0.3–1 s), and responses are quantified by mean firing rate. Often one stimulus parameter is varied at a time (e.g., orientation tuning is measured at the best SF). Although this approach can yield accurate orientation and SF tuning estimates, it fails to capture both stimulus interactions and temporal response dynamics that can be obscured by nonspecific onset transients. In addition, methods based on static stimuli can be time-consuming. Efficient characterization methods are particularly important when working with behaving animals, where time is almost always at a premium.

One efficient way to characterize tuning that also captures temporal response dynamics is to estimate spatiotemporal receptive fields (STRFs) by using reverse correlation. The STRF describes the probability that a particular spatial stimulus will elicit a spike at a particular latency. In effect, the STRF provides a linear model of a neuron's spatiotemporal filtering characteristics (5, 6).

In the visual system, STRFs are traditionally estimated by stimulating neurons with white noise and reverse correlating recorded spike trains with the stimulus (5, 7, 8). This approach can also be time-consuming, particularly in higher visual areas where white noise often fails to elicit strong responses. Recently, Ringach et al. (2, 9) described an alternative to white noise that significantly reduces the time required to characterize V1 neurons. Their method used high-speed (60 Hz) dynamic sequences of sinusoidal gratings varying randomly in orientation and phase. They obtained spatiotemporal orientation tuning functions by reverse correlating responses with grating orientation.

We extended the method described by Ringach et al. (2, 9) to estimate STRFs in area V1 of awake, behaving macaques. To do this we constructed grating sequences varying in SF as well as orientation and phase. These sequences were divided into short, overlapping segments and each segment was presented during a single fixation trial. STRFs estimated by this method yielded robust estimates of spatial frequency and orientation tuning dynamics after as little as 3–5 min of visual stimulation. STRFs obtained with this method were then used to characterize linear separability and the temporal dynamics of SF and orientation tuning in V1.

Methods

Data were obtained from two awake, behaving adult male monkeys (Macaca mulatta). All procedures conformed to National Institutes of Health guidelines and were approved by either the University of California, Berkeley or Massachusetts Institute of Technology Animal Care and Use Committees. Surgical and recording methods have been described in detail (10, 11).

Recording Techniques.

Single-neuron activity was recorded by using either glass-coated Pt/Ir (1 MΩ) or epoxy-coated tungsten (20 MΩ) electrodes advanced perpendicular to the cortical surface. Single-neuron activity was amplified (×10–1,000), bandpass filtered (0.5–10 kHz), and discriminated with a level detector. Spike times and eye position (1 kHz and 100–500 Hz, respectively) were recorded continuously during each trial. Stimulus generation, behavioral task, and data recording were controlled with either custom software (Indigo²; SGI, Mountain View, CA) or the CORTEX program (Laboratory for Neuropsychology, National Institute of Mental Health; on an IBM-PC).

Stimuli and Behavioral Task.

Stimuli were presented on 20- or 21-inch cathode ray tubes (Sony GDM; 54–83 cm viewing distance; Sony, Tokyo). Single neurons were isolated and classical receptive fields mapped with manually positioned bars and gratings. Manual receptive field estimates were confirmed quantitatively under computer control with either drifting bars or flashed spots (8, 11).

Animals were trained to maintain fixation on a small target (<0.1°) for 5–10 s. Eye movements were monitored with a scleral search coil (12), and trials were aborted if eye movements exceeded a fixed threshold (0.25° or 0.35°). After each complete fixation animals were rewarded either immediately or after saccading to a peripheral, high-contrast target. Liquid rewards were used, and fluid intake was controlled to maintain animal health and consistent motivational state.

Dynamic Grating Stimuli.

Grating sequences (100–300 s at 60 or 72 Hz) were synthesized off line. Each video frame contained a sinusoidal grating masked by a circular aperture; the outer 10% of each grating was blended into a neutral gray background by using a linear ramp. Apertures were chosen to be one to four times the size of each cell's classical receptive field. In most cases responses were obtained by using multiple aperture sizes. Our preliminary analysis revealed no significant effect of stimulus size on orientation or SF selectivity, other than a general improvement in signal-to-noise ratio associated with larger stimuli. For the remainder of this article, we report only responses to the largest stimulus size used with each neuron (most frequently 2× classical receptive field). In 54 of 63 cases 50% Michelson contrast gratings were used and orientation, SF, and phase were drawn with replacement from a continuous uniform distribution (orientation and phase, 0–180°; SF, 0.5–5.0 cycles per degree). In the remaining 9 of 63 cases, gratings were 100% contrast and orientation and SF were selected from a discrete uniform distribution (0–180° in 22.5° steps and 0–5 cycles per degree in 1.0 cycle per degree steps), while spatial phase was held constant. No systematic differences were observed in the data obtained by using these two slightly different procedures.

The 100- to 300-s stimulus sequence was divided into 5- to 10-s segments. On each trial, one segment was chosen at random for presentation. Segments were presented until the entire sequence had been presented one to five times. To minimize the contribution of nonspecific onset transients, segments were selected to overlap by 200 ms, and responses to the first 200 ms of each segment were excluded from analysis. In most cases, we presented only one repetition of the full sequence (about 40 behavioral trials).

Results

We studied 63 well isolated V1 neurons. Receptive fields were parafoveal (3.0 ± 1.5° eccentricity, mean ± SD) with a mean receptive field diameter of 0.7 ± 0.3°.

Spatiotemporal Receptive Fields.

STRFs were estimated by reverse correlation (13). For each neuron, the STRF was estimated by correlating the peristimulus time histogram with the stimulus sequence (stimulus orientation and SF over time). For stimuli drawn from a continuous distribution, the stimulus sequence was discretized before STRF estimation (SF, 10 bins of 0.5–2.5 cycles per degree; orientation, 18 bins of 10°). Peristimulus time histograms were computed at either 1-ms resolution or the video frame rate (14 or 16 ms) depending on the analysis. At each time, t, a counter corresponding to stimulus SF and orientation at time t – Δt was incremented by the peristimulus time histogram value at time t. Each counter was then divided by the frequency of occurrence of the corresponding SF-orientation pair. The complete STRF was estimated by repeating this procedure for a range of Δt values (–100 to + 200 ms in 1-, 14-, or 16-ms steps).

In theory, STRFs can be computed at arbitrary temporal resolution. However, for reasons discussed more fully below, STRFs can be biased by temporal correlations in the stimulus sequence when the stimulus frame rate is lower than the data acquisition rate. We therefore estimated STRFs at two temporal resolutions: 1 kHz (the rate used to acquire spike data) and 60 or 72 Hz (the video frame rate). We found that basic tuning parameters (i.e., preferred SF and orientation) did not differ at the two rates.

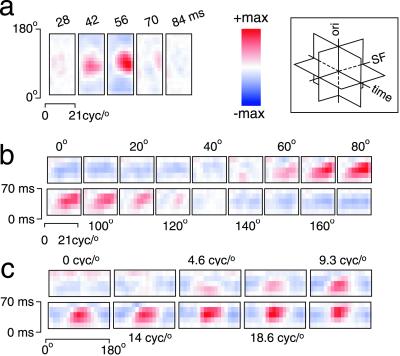
Fig. 1 shows the STRF of a typical V1 neuron. The complete STRF is a three-dimensional matrix (time × SF × orientation). The STRF can be sliced perpendicular to any of the three axes. Fig. 1a shows six consecutive time slices. Each slice represents the probability of particular SF-orientation combinations occurring at the indicated time (Δt) before a spike. The prominent peak at 56 ms indicates that this cell was most likely to spike with a latency of 56 ms after the appearance the optimal SF-orientation pair. Fig. 1b shows the same STRF sliced perpendicular to the orientation axis, highlighting the temporal evolution of SF tuning. Each slice shows SF tuning over time in a single orientation channel. Similarly, Fig. 1c shows the STRF sliced perpendicular to the SF axis, highlighting the temporal evolution of orientation tuning within each SF channel.

Figure 1.

Complete STRF for a typical V1 neuron. STRFs described in this report are three-dimensional matrices with dimensions of time, SF, and orientation, as indicated by the schematic Inset. The complete STRF can be visualized as three sets of slices cut perpendicular to the cardinal axes. (a) Slices perpendicular to the time axis represent joint SF-orientation tuning at different response latencies. The color in each slice indicates the relative probability that each SF-orientation combination will elicit spikes at the indicated latency. (b) Slices perpendicular to the orientation axis represent the temporal evolution of SF tuning within a single orientation channel. (c) Slices perpendicular to the SF axis represent the temporal evolution of orientation tuning within a single SF channel. STRFs are depicted here by using a color map that spans the range ± max (|STRF|). cyc, cycles.

Neurons in our sample with sufficient data for complete STRF estimation (n = 52) typically exhibited single-peaked, narrow-band orientation tuning and bandpass SF tuning. These tuning characteristics are similar to those reported in studies of area V1 using flashed or drifting gratings (14, 15).

Temporal Responses.

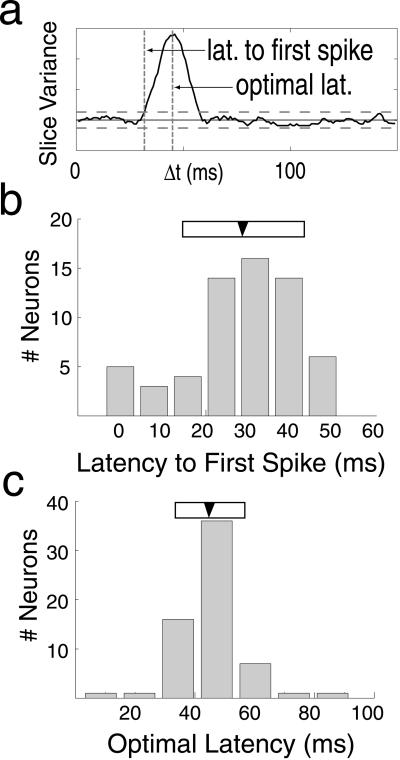
The STRF provides detailed information about the time course of selectivity, including response latency and time-to-peak sensitivity. We developed a simple method to characterize the time course of selectivity independent of tuning (Fig. 2a). Because neurons are causal, stimuli occurring after a spike (Δt < 0) cannot affect firing probability. Consequently, STRF slices at Δt < 0 are nearly flat and have very low variance. As Δt approaches the response latency, neuronal tuning produces peaks and troughs in the STRF, which increases the variance. We defined the latency of the first spike as the time at which the variance first deviates from baseline by more than two standard deviations (baseline mean and SD calculated from Δt < 0; horizontal dashed lines in Fig. 2a). The time when variance is maximal indicates the latency at which the neuron is best tuned and gives the latency of the most probable spike after the appearance of the optimal stimulus. We refer to this as the optimal latency and quantified it as the mean of the best-fit Gaussian of the variance profile.

Figure 2.

Latency measurements from STRFs. The time course of tuning can be visualized by plotting the overall variance of each SF-orientation slice as a function of Δt. (a) Solid line indicates the variance profile for a single V1 neuron. Horizontal solid and dashed lines indicate the mean ± 2SD (computed from Δt < 0; see text for details). (b) Latency to first spike is defined as the first time point when the variance exceeds twice the SD of the noncausal region of the STRF. Very short latencies apparent in the histogram (<20 ms) are caused by noise. Artifactually short estimates of the latency to first spike are caused by spurious peaks in the variance profile that can push the profile over the 2SD threshold. (c) Optimal latency, the latency at which the cell is maximally selective, is given by the peak of the variance curve (see text for details). For both histograms, the filled arrowheads and open horizontal bars indicate the mean ± SD.

Fig. 2 b and c shows the distributions of latency to first spike and optimal latency for our sample. The mean latency to first spike is 28.0 ± 13.4 ms (mean ± SD, n = 62) and the mean optimal latency is 44.8 ± 11.4 ms (n = 63). These values are similar to those reported in studies of area V1 (16). Note that although the latency to first spike is a simple statistic, it is not particularly robust. Consequently, several neurons in the sample have unrealistically short (for V1) latencies to first spike (<20 ms; see Fig. 2b).

Separability of Spatial Frequency and Orientation Tuning.

The relationship between SF and orientation tuning in single neurons can be characterized by their separability. If SF and orientation are separable, then they can be safely measured independently (orientation tuning at best SF and vice versa). In addition, theoretical models of orientation tuning in V1 make specific predictions about SF-orientation separability (17, 18).

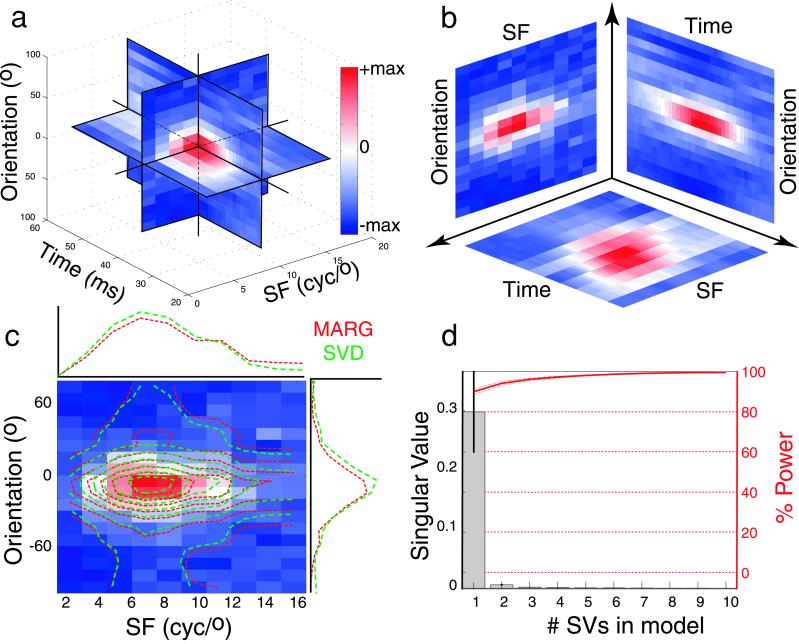
We used two methods to assess SF-orientation separability. First, we determined how well joint SF-orientation tuning could be reconstructed from simple SF and orientation tuning curves. For each cell, we extracted a single SF-orientation slice at the optimal latency (Fig. 3). One-dimensional SF and orientation tuning curves were calculated by summing over the orientation and SF dimensions, respectively (red marginal plots in Fig. 3). The resulting marginal vectors represent SF tuning independent of orientation and vice versa. The two-dimensional matrix product of these vectors represents the separable SF-orientation tuning surface (red contour plot, Fig. 3c).

Figure 3.

Separability of SF, orientation, and time. (a) Complete STRF for a single V1 neuron. (b) Separability is evaluated in orthogonal SF-orientation, SF-time, and orientation-time planes (see text for details). (c) Linearly separable reconstruction of joint SF-orientation tuning for a typical V1 neuron based on simple marginal sums (red lines) and the first singular vector (green lines). The underlying color map shows measured SF-orientation tuning, and the overlying contours indicate the separable predictions. (d) Histogram shows the mean (±SEM) of the first 10 singular values from the SF-orientation SVD analysis for 52 V1 neurons. The red curve represents the mean (±SEM) percent STRF power accounted for by successive inclusion of additional singular vectors (see text for details). This analysis reveals a high degree of SF-orientation separability in V1. cyc, cycles.

Separability was quantified for each cell by computing the squared correlation (r²) between measured and predicted separable SF-orientation tuning. The mean r² was 0.74 ± 0.18 (n = 52), indicating that the separable model accounts for about 74% of the observed joint SF-orientation tuning variance. Thus, SF and orientation tuning are largely, but not completely independent in V1.

We also used singular value decomposition (SVD) to assess SF-orientation separability. For each cell, SVD was used to transform the measured SF-orientation tuning surface at the optimal latency (a two-dimensional matrix) into the form U^TνV, where U and V are the singular vectors and ν is a diagonal matrix of singular values. U and V are sets of orthogonal vectors that, when combined with the singular values in ν, completely reconstruct the original matrix.

For a perfectly separable neuron the complete tuning surface can be represented by the first singular vectors, so only the first diagonal term of ν will be nonzero (19, 20). To quantify separability, we computed the relative magnitude of the first singular value by using the following index: si = λ(1)²/[Σ_iλ(i)²], where λ(i) is the i-th diagonal term of ν; si ranges from near 0 (nonseparable) to 1 (separable; for a similar metric see ref. 20).

Fig. 3c compares the reconstruction of the joint SF-orientation tuning surface based on the marginal product (red lines) to that based on the first singular vectors (green lines) for one neuron. Fig. 3d shows the mean singular values from our sample, and the power explained as additional singular vectors is included in the reconstruction (red curve). It is clear that the contribution of the first singular vector is substantially larger than the remaining ones. The mean si is 0.90 ± 0.09 (n = 53), indicating that for V1 neurons 90% of the power in the linear transfer function at the optimal latency is captured by the separable portion of the STRF (20).

The STRF marginals explicitly represent SF and orientation tuning; the marginal analysis explicitly measures the independence of these dimensions. The r² statistic computed from the matrix product of the marginal vectors reflects the portion of measured response variance accounted for by the separable model. In contrast, each singular vector in the SVD analysis can represent a complex combination of SF and orientation tuning, and si quantifies the power contributed by the first two singular vectors to the cell's transfer function. These statistics are related, but not identical (r² = 0.74 vs. si = 0.90). However, we can make the two analyses more comparable by computing an r² value based on the matrix product of the first singular vectors. For joint SF-orientation tuning, the mean r² value for the singular value reconstruction is 0.78 ± 0.18, very close to that obtained by using the marginal vectors.

Despite these subtle differences, both the marginal matrix product and SVD analyses lead to essentially the same conclusion: SF and orientation tuning are largely, but not completely, independent in macaque area V1 neurons.

Separability of SF Tuning and Time.

We also examined the relationship between preferred SF and latency by calculating SF-time separability, using the marginal reconstruction and SVD methods described above. For each STRF, we analyzed the SF-time slice at best orientation (SF-time planes in Fig. 3 a and b). The mean r² value for the marginal reconstruction was 0.83 ± 0.10 (n = 52), and the mean si obtained by SVD for the same slices was 0.93 ± 0.04 (n = 52). This result indicates that SF and time are also largely independent. However, about 20% of the variance reflects a nonseparable interaction between SF and time. We return to this issue below.

Separability of Orientation Tuning and Time.

Ringach et al. (2) reported dynamic changes in orientation tuning throughout the time course of the response in area V1 in anesthetized primates. We sought to identify similar orientation tuning dynamics by measuring STRF separability in the orientation-time plane. For each neuron we selected the orientation-time slice containing the neuron's best SF and characterized the slice by using marginal reconstruction and SVD (orientation-time planes in Fig. 3 a and b). We found a mean r² for the marginal reconstruction of 0.84 ± 0.12 (n = 52) and a mean si of 0.95 ± 0.03 (n = 52) for the SVD. This indicates that the orientation-time plane, like the SF-orientation and SF-time planes, is also largely separable.

Dynamic Changes in Tuning over Time.

The SF-time and orientation-time separability analyses presented above demonstrate that both SF and orientation tuning are relatively stable over time. However, the separable portion of the STRF does not capture all of the observed response variance; about 20% of the variance remains unaccounted for. In principle, this nonseparable residual could reflect either measurement error (noise) or dynamic changes in tuning over time.

Our ability to detect dynamic shifts in SF and orientation tuning is limited both by the relatively small size of the residuals and by the temporal structure of the dynamic grating stimuli. Although we presented stimuli at 60 Hz or greater, each video frame is still relatively long compared with the temporal envelope of STRFs observed in area V1. Our STRFs are typically less than 30 ms in duration, which means only two time points are available if data are sampled at the frame rate. Two points are insufficient for estimating the significance of dynamic tuning shifts. Ringach et al. (2) addressed this problem by computing STRFs at a higher rate (1 kHz). However, interpreting STRFs computed at 1 kHz is problematic because they are biased by 60-Hz temporal correlations present in the original stimulus sequence. This bias effectively smoothes the tuning data in time. As a result, even extremely small changes in tuning can seem to be statistically significant, and the true significance of changes in SF or orientation tuning cannot easily be assessed. Our preliminary analyses indicated that it is impractical to try to remove this brief (<14 ms) stimulus correlation bias from our data. This left us with few options for detecting dynamic shifts in SF or orientation tuning.

To assess shifts in SF tuning we took advantage of the fact that such shifts might be distributed asymmetrically. Low SFs are preferentially represented by the magnocellular pathway and high SFs by the parvocellular pathway. Because magnocellular neurons have shorter latencies than parvocellular neurons (21, 22), low SF stimuli might evoke responses in V1 with shorter latency than high SF stimuli. This would be reflected in an asymmetric distribution of SF shifts in measured STRFs. In contrast, artifactual shifts caused by temporal correlation bias should be distributed symmetrically.

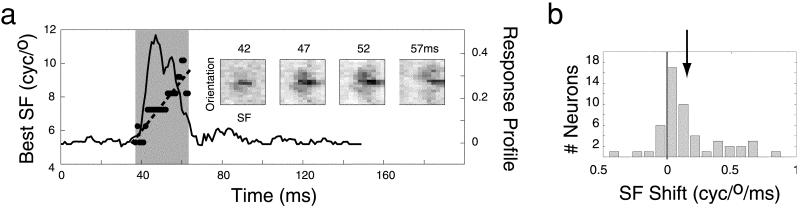
For each neuron, we fit a line to the best SF vs. Δt function (Fig. 4a). The best SF was defined as the SF with the highest probability of eliciting a spike in each SF-orientation slice of the STRF. The distribution of slopes, which give the rate and direction of shifts in preferred SF, is shown in Fig. 4b. In 38 of 52 neurons, responses to low SF stimuli occurred at shorter latencies than responses to high SF stimuli. The mean slope is significantly different from zero (two-tailed t test, P < 0.01) and represents a significant bias in shift direction (nonparametric sign test, P < 0.01). Thus, about three-quarters of the V1 neurons in our sample show a small but significant dynamic shift in preferred SF from lower to higher frequencies.

Figure 4.

Dynamic changes in SF tuning. (a) The solid curve indicates the time course of tuning of a typical V1 neuron (see Fig. 2a), the gray highlighted region shows the time window in which the neuron is responding (2 SD units around the mean of the best-fit Gaussian, as defined in the text). Filled circles represent the SF most likely to elicit a spike (i.e., the best SF) at each time slice (dashed line is the best linear fit). This cell shows an extreme change in SF tuning over time; in less than 25 ms, the best SF shifts by more than an octave from low to high SF. (Inset) Joint SF-orientation tuning at indicated latencies. (b) Distribution of SF shifts for all 52 neurons. Positive slopes indicate short latency responses to low SFs and long latency responses to high SFs (arrow indicates mean shift = +0.15 ± 0.25 cycles/degree per ms; mean ± SD). cyc, cycles.

Unfortunately, orientation is a circular quantity and there is no physiological reason to expect any sort of systematic bias in the distribution of orientation shifts. We therefore used a different method to evaluate orientation shifts. In this case we simply compared measured shifts in best orientation to the orientation-tuning bandwidth (at the optimal latency) of each neuron.

For each neuron in our sample, we estimated peak orientation and orientation bandwidth of each STRF time slice from the mean and SD of the best-fit Gaussian (1 SD is ≈40% of the width at half-maximum). Only 2 of 63 neurons exhibited shifts in peak orientation tuning larger than one SD. In both of these cases, later time slices developed prominent side peaks orthogonal to the preferred orientation, consistent with the earlier report of Ringach et al. (2). However, the frequency with which such shifts were observed is not substantially greater than that expected from chance (2 of 63 represents <5%).

Discussion

The STRF estimation procedure described here efficiently reveals detailed structure of SF tuning, orientation tuning, and temporal responses of V1 neurons in awake behaving macaques. These measurements are all similar to those reported for macaque area V1 (15, 16). In addition, estimated STRFs can be used to assess quantitatively the linear separability of constituent tuning dimensions and to identify interesting temporal response dynamics related to SF or orientation tuning.

Separability of SF and Orientation Tuning.

Some feed-forward models of V1 predict that orientation bandwidth should decrease at higher SFs (17, 18), whereas others predict that orientation and SF tuning should be linearly separable (23). These predictions are clearly in conflict, because changes in orientation-tuning bandwidth with SF are inconsistent with separability. However, this conflict remains unresolved in the experimental literature. Some studies report a lack of separability (24, 25), whereas others support separability (26).

Our results demonstrate that SF and orientation tuning in V1 are largely separable. SF-orientation tuning in our sample is more than 70% linearly separable (marginal analysis), with a mean separability index of 0.90 (SVD analysis). For most cells we could not determine whether the nonseparable SF-orientation residuals were meaningful or were merely caused by measurement noise. However, in 9 of 52 of the neurons in our sample, we observed a slight trend toward decreasing orientation-tuning bandwidth with increasing SF. If true, this effect would be consistent with predictions of feedforward models of orientation tuning in area V1 (17). However, the current data are inconclusive and this issue must be investigated further.

Separability of SF, Orientation, and Time.

If SF and orientation tuning are constant across all STRF time slices then both dimensions should be separable with respect to time. We found that most V1 neurons were largely SF-time and orientation-time separable. However, the STRFs also contained small residual nonseparable components in both the SF-time and orientation-time planes.

Spatial Frequency-Tuning Dynamics.

The nonseparable residual of V1 STRFs showed an interesting dynamic property: preferred SF tended to shift from lower frequencies at short latencies to higher frequencies at longer latencies. Neurons in the magnocellular stream are typically more sensitive to low spatial frequencies and have shorter response latencies than those in the parvocellular stream (21, 22). Consistent with other recent studies (27, 28), this finding suggests that single V1 neurons receive convergent input from the magno- and parvocellular processing streams.

Orientation-Tuning Dynamics.

Ringach et al. (2), with a method similar to that described here, reported that orientation tuning varied dynamically during the first 80 ms after stimulus onset in 56% of V1 neurons in anesthetized primates. Although our method is sensitive enough to reveal similar dynamic changes in SF tuning, we found little evidence of dynamic changes in orientation tuning in our data.

Several possible explanations exist for this discrepancy. First, the orientation shifts reported by Ringach et al. (2) may simply be too small to detect by using our methods. The shifts reported by Ringach and colleagues occurred at relatively long latencies where the absolute probability of response is relatively low. Because our stimulus sequences were typically one-third the length of those used by Ringach and colleagues, and varied in both SF and orientation, the signal-to-noise ratio in our data might be lower. A reduced signal-to-noise ratio could obscure small shifts in orientation tuning.

Second, more recent results from Ringach's laboratory (D. L. Ringach, personal communication) suggest that dynamic orientation tuning shifts may occur substantially less frequently than originally reported (2), perhaps occurring in as few as 5% of all V1 neurons. Our data are consistent with this revised estimate.

Third, our study may have used a different normalization procedure than that used in the earlier experiments of Ringach et al. (2). We normalized STRFs by dividing each bin by the frequency of occurrence for the corresponding SF-orientation pair; because this frequency distribution was flat, it corresponds to a simple scaling operation. Ringach et al. apparently normalized orientation tuning curves at each time slice to have unity area (see ref. 2, legend for figure 2). This normalization procedure may have increased the apparent magnitude and significance of small peaks in the orientation-tuning curves, particularly at long latencies where the overall probability of any stimulus eliciting a spike is relatively low.

Fourth, we have discovered that spatiotemporal correlations present in dynamic grating sequences presented on a video monitor introduce subtle biases that must be considered during data analysis. Specifically, STRFs estimated by simple parametric reverse correlation are contaminated by the temporal autocorrelation of the stimulus sequence (6). For a video signal like the dynamic grating stimuli, the stimulus autocorrelation function is triangular, with a peak at the center of each video frame and a basewidth equal to twice the video refresh period. The effect of this temporal correlation is to smooth the STRF in time. Both signal and noise are smoothed, so noise in the estimated kernels seems to vary smoothly over time. Because the smooth orientation shifts observed both by us and Ringach et al. (2) could be an artifact of the stimulus correlation, we demanded that such shifts be reasonably large before we would accept them as real. Temporal correlations in the stimulus sequence also affect the SF-time data. However, the finding that SF shifts tend to occur in one direction (low to high) is unlikely to be the result of any temporal correlation artifact.

Conclusions.

V1 neurons are largely separable in the SF-orientation, SF-time, and orientation-time planes. However, a small, nonseparable component remains. In the SF-time plane this nonseparable residual reflects a systematic shift in SF tuning; low-frequency stimuli elicit spikes at shorter latencies and high-frequency stimuli at longer latencies. This finding suggests that single V1 neurons receive convergent input from the magno- and parvocellular processing streams. Although the orientation-time plane also has a nonseparable residual, we find significant shifts in orientation selectivity in less than 5% of the cells. The general lack of complex orientation-tuning dynamics in V1 suggests that orientation selectivity emerges from the convergence of afferent inputs with similar temporal response properties.

Abbreviations

STRF

spatiotemporal receptive field

SF

spatial frequency

SVD

singular value decomposition