Global organization of the Wordnet lexicon

Abstract

The lexicon consists of a set of word meanings and their semantic relationships. A systematic representation of the English lexicon based in psycholinguistic considerations has been put together in the database Wordnet in a long-term collaborative effort. We present here a quantitative study of the graph structure of Wordnet to understand the global organization of the lexicon. Semantic links follow power-law, scale-invariant behaviors typical of self-organizing networks. Polysemy (the ambiguity of an individual word) is one of the links in the semantic network, relating the different meanings of a common word. Polysemous links have a profound impact in the organization of the semantic graph, conforming it as a small world network, with clusters of high traffic (hubs) representing abstract concepts such as line, head, or circle. Our results show that: (i) Wordnet has global properties common to many self-organized systems, and (ii) polysemy organizes the semantic graph in a compact and categorical representation, in a way that may explain the ubiquity of polysemy across languages.

A pressing issue in linguistics, philosophy, and brain science is the formal characterization of meaning, i.e., the formalization of our intuition of conceptual content. Language is a privileged window into the mind in its proposed double role of mediator and shaper of concepts (1), and lexical semantics, the mapping between word form and word meanings, is a testing ground for the problem of characterization of meaning within the domain of linguistics. Against the classical empiricist and reductionist interpretations of meaning as the character of the link of individual concepts and the external world, the holistic view proposes that mental concepts arise as an emergent property of their interrelationships rather than as a property of their individual experiential correspondence (2, 3). As an example of how meanings can be related through long chains of semantic relationships, when the words “stripes” and “lion” are presented, one thinks of the word “tiger,” establishing the trajectory lion–feline–tiger–stripes. Dictionaries also make evident the intrinsic holistic nature of languages, as all individual entries must be bootstrapped from other entries in a self-referential fashion. If meaning not only results from a correspondence with external objects, but also depends on the interrelationships with other meanings, an understanding of the lexicon as a collective process implies a characterization of the structure of the graph, i.e., the global organization of the lexicon.

A word form is a label that identifies a meaning. However, meanings are not mapped to word forms in a one-to-one fashion. Two word forms corresponding to the same meaning are said to be synonyms; a word form that corresponds to more than one meaning is said to be polysemous. All known languages are polysemous, but it is not yet clear whether the existence of polysemy is an historical accident, a nuisance that an “ideal” language should avoid, or whether it may be important for generic thought processes (4).

We will investigate the statistics and organization of the following semantic relationships: antonymy, hypernymy (hyponymy), and meronymy (holonomy) (parentheses refer to inverse relationships). Although antonymy is well known and needs no explanation, the other two relationships are less familiar. A hyponym is a meaning that acquires all of the features of its hypernym, which is a more generic concept; for example, tree is hypernym of oak. Dictionaries make implicit use of the hypernym relationship by defining a word as its hypernym (which encompassed all of the basic features) and its specific attributes (5). Meronymy is the relation of being part of; for example, branch is a meronym of tree. Meanings can also be related through common word forms (polysemy); for example, a body of persons officially constituted for the transaction or superintendence of some particular business and a flat slab of wood are two meanings that are related through the word form board. This relationship may seem arbitrary, accidentally linking unrelated meanings. In many cases, however, a chain linking the two different meanings may be established. For instance, the Oxford English Dictionary makes the relationship between the two meanings of the word board explicit: “A table at which a council is held; hence, a meeting of such a council round the table.”

The lexicon then defines a graph, where the points are the different meanings and semantic relationships are the links. The vertices are nouns, adverbs, verbs, or adjectives; in what follows we will present results based on an analysis of the set of nouns. Graph theory provides a number of indicators or measurements that characterize the structure of a graph: the statistical distribution of links, which gives an idea of the homogeneity and scaling properties of the graph, the mean shortest distance between any two points of the graph, which gives an idea of its size or diameter, the clustering index, which provides a measure of the independency of neighboring links, and the traffic, which measures the number of trajectories passing through each vertex, and so identifying the most active hubs. Fig. 1 shows examples of different toy graphs and how the graph theoretic measurements help to identify them.

Figure 1.

Graph measurements. Toy graphs to show how different structures can be identified by using different measurements (clustering, mean length or diameter, and traffic). Both graphs have the same number of nodes and the same distribution of links; each vertex is labeled with a color that indicates the number of links (yellow, 1 link; green ,2 links; blue, 3 links; red, 4 links; and orange, 6 links). Despite having the same statistics, the two graphs are obviously different. Graph A (Upper) gives the impression of being more compact than graph B (Lower). This difference is quantitatively measured by the diameter, i.e., the longest of all of the shortest paths within any pair of vertices in the graph. This path is illustrated with the red dotted line. The two most distant points in graph A are 6 links apart, whereas the two most distant points in graph B are 17 links apart. The characteristic length is the median (not the maximum) of the length of all minimal paths; graph B is the longer one, because of its structure of long branches in which long navigations are required to go from one point to another. A second salient structure of graph B is the pentagon-like structure of nodes linked to each other. This structure is prominent in clustering analysis, i.e., number of connected neighbors as a function of all possible connected neighbors. This pentagon also acts as a center of the graph, i.e., most trajectories connecting two vertices (but not all of them) go through it, and so these particular nodes are highly traversed. Graph A shows that traffic and connectivity are not necessarily related. The red node is not the most connected one; however, it is the one with most traffic (which places it in the center of the graph). The importance of this vertex (central to the structure of the graph) would not have been revealed without traffic analysis. These measures allow the identification of the structure and organization of a graph in cases (as in the lexicon) in which it is not obvious by simple inspection and visualization.

The general properties of the organization of social and biochemical networks and the organization and dynamics of the World Wide Web have been characterized with these graph theoretic measurements, revealing common features of self-organized systems of highly connected elements (6–9). We used similar tools to show several global properties of the set of nouns: (i) all semantic relationships are scale invariant, typical of self-organizing graphs; whereas the semantic network is dominated by the hypernymy tree, which works as the skeleton of the set of nouns, the inclusion of polysemy produces a drastic global reorganization of the graph, namely (ii) it is converted into a small world (8, 10), where all meanings are closer to each other, (iii) simplexes (subgroups of fully connected meanings) become the regions of more traffic, and (iv) distances across the network are not in correspondence with their deepness in the hypernymy tree.

Methods

Grouping all semantic relationships in different classes is ultimately an arbitrary decision, although this grouping was based on a long history of research in psycholinguistics (5). In Wordnet, the relation of meronomy is actually a class of relations including meronomy of component (i.e., branch is component-meronomy of tree), member (tree/forest), and stuff (glass/bottle). Our study did not discriminate between different types of meronomy; another semantic relationship between nouns that we have not explored in this work is the relation of attribute. The minimal distance between vertices was computed adapting a publicly available version of Dijkstra's algorithm (11). For a vertex i, the average minimal length was calculated by averaging the minimal distance from i to all of the other vertices in the graph, 〈d〉_i = (1/66025)∑_{j∈{Meanings}} dist_min(i, j). The characteristic length was computed as the median of the distribution of average minimal lengths across all vertices in the graph. Clustering (C_l) was computed as the ratio of connected neighbors (CN) to the maximal possible number of connected neighbors, given by the formula C_l = 2⋅CN/[N⋅(N + 1)], where N is the number of neighbors. All semantic graphs were obtained from the Wordnet database. Semirandom graphs were generated as controls, by adding random links to the original hypernymy graph. A different number of random links were added to generate graphs of equivalent number of links, to control for the different graphs I–III, I–IV, and I–III–IV. Fig. 3a shows an example of each of these graphs. To calculate the characteristic length and clustering of the semirandom graphs, we generated seven different graphs for each condition and the averages are shown. Standard deviations were not shown because in all cases they were below 1%. The traffic was computed as the limit of the exponentiation of the graph: for an integer N and a graph g, g computes the number of trajectories of length N connecting vertices i and j. For N → ∞, the exponentiation (where λ_i is the ith eigenvalue and u_i its corresponding eigenvector) can be approximated by the largest eigenvalue λ₁ of g (the matrix g is symmetric and positive-definite, hence λ_i ≥ 0∀i, and the first eigenvalue will be set to the largest one) largest eigenvalue is the first one) and its corresponding eigenvector g^N ≈ λ 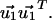Because the composition of a trajectory with a loop gives a trajectory with the same path, but longer N, this limit is guaranteed to converge to the maximum number of paths and therefore 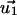measures the limiting behavior of trajectories throughout the graph, i.e., the “traffic” (11). In particular, u represents the number of loops passing through the i-th node, relative to the other nodes.

Figure 3.

Inclusion of polysemy results in a small world organization of the semantic graph. (A) The histogram of average minimal length (see Methods) and the plot of connected neighbors (CN) as a function of neighbors (N) is plotted for different graphs. The maximal number of CN is given by CN_max = [N⋅(N + 1)]/2 and is plotted in the dashed blue line. Points close to this line are highly clustered, whereas the ones close to the horizontal axis are not. Because each graph has different number of links, for each one (except the hypernymy tree) we generated a control graph consisting of hypernymy + random links, to match the number of the original graphs. Data from the original plots are displayed in the two leftmost columns, and data from the semirandom graphs in the two rightmost columns. The length and clustering are shown for the hypernymy tree (first row), hypernymy + meronomy (second row), hypernymy + polysemy (third row), and hypernymy + meronomy + polysemy (fourth row). As can be seen, the addition of polysemy (or word forms) reduces the characteristic length as much as the addition of random links (compare right and left columns), but with a considerable increase of clustering (even for highly connected nodes). In addition, the inclusion of polysemy adds vertices (green dots) of high connectivity and high clustering. Those correspond to clusters of meanings that are connected through a common word. (B) Characteristic length for all possible graphs combining the hypernymy tree and the different semantic relationships (see text). As can be seen in the column corresponding to {I–IV}, the addition of polysemy reduces the characteristic length as much as random relations do. (C) Addition of polysemy on top of hypernymy increases the clustering of the graph. Thus polysemy results in a clustered and compact graph, a small world.

Results

According to the latest version of Wordnet (wordnet1.6), the number of noun meanings is 66,025, although this number is, of course, arbitrary and variable. In this work we will consider four types of relationships: hypernymy (I), antonomy (II), meronomy (III), and polysemy (IV). Antonomy and polysemy relationships are symmetric, whereas hypernymy and meronymy have hyponomy and holonomy as inverses. We will consider the set of hypernyms–holonomys as type I relationships, antonomy as type II relationships, meronomy–holonomy as type III relationships, and polysemy as type IV relationships.

To address scaling in the network of meanings, we computed the distribution of links (first-neighbor connections). Antonomy was excluded, because each meaning has 0 or 1, or rarely 2, antonyms. All relationships showed power-law behaviors reflecting scale invariance in this graph (Fig. 2). The relationship of hypernymy is the one with more links, relating at most 400 meanings. The word-form relationship relates up to 32 meanings through the most polysemous word, head. The statistics of links provides a local measure to characterize a graph, of how uniform it is in the number of neighbors. Crystalline graphs, for example, have a fixed number of links. The power-law distribution of polysemy states that there are very few words that connect a high number of meanings, rendering them as particularly important words. It has been shown that graphs with power-law distribution of links are very sensitive to the removal of these particular nodes (12). Moreover, power-law distributions are a hallmark of self-organizing systems (13), providing support to the idea that the semantic network is dominated by autonomous and self-referential processes, and at the same time reflecting the high quality of Wordnet despite the necessary arbitrariness with which it was built.

Figure 2.

Scale-invariant distribution of all semantic links. The histogram shows the distribution of meanings as a function of number of links for the hypernymy–hyponymy (blue), polysemy (green), and meronymy–holonomy relationships. They all follow a power law (scale invariant) behavior, as seen by the linear dependence in the log–log plot.

The statistics of links, however, does not fully characterize a graph; as seen in the toy model of Fig. 1, two graphs with equal distribution of links may be radically different. We therefore proceeded to calculate more global and characteristic measures of the graph: the characteristic length and the clustering. The characteristic length is the median of the minimal distance between pairs of vertices, and it essentially gives an idea of the diameter of the graph, measuring how far apart from each other two meanings typically are. Clustering is a measure of local structure, as it results from averaging the probability of two meanings being connected to each other given that they are both connected to a third common meaning. It is well known that social networks, for instance, are highly clustered: if A is friend of C, and B is friend of C, then A and B are also likely to be friends. Clusters define islands within the graphs, regions of very high internal connectivity.

We studied the changes in clustering and characteristic length resulting from the inclusion of the different semantic relationships to study their impact on the organization of the graph. We used the hypernymy tree as a base graph, and we generated eight different graphs that result from adding the different semantic relationships to the hypernymy tree (graph {I}). The graph {I,II} has all links of hypernymy and antonymy, the graph {I,IV} hypernymy and word-forms and so on. The graph {I,II,III,IV} contains all of the possible links. All of the graphs have the same number (66,025) of vertices. Overall, as links are being added to a graph of fixed number of vertices, the characteristic length decreases and the clustering increases; however, the particular distribution of links may have very different effects on the length as well as the clustering of the graph (10). To provide a measure of normalization, we generated semirandom graphs by adding random links to the hypernymy graph. For each semantic graph, we generated a corresponding semirandom graph with the same number of links, which works as a control comparing the effect of adding the specified links to just adding random links.

Fig. 3 B and C summarizes the averaged results for the eight graphs, and Fig. 3A provides details for four individual examples: the hypernymy tree alone (first row), the hypernymy and meronomy relationships (second row), the hypernymy and polysemy relationships (third row), and the hypernymy, meronomy, and polysemy relationships (fourth row). The characteristic length of the graph of hypernymy + meronomy links (approximately the maximum of the histogram of characteristic length, first column, second panel) is significantly larger than that of the graph constructed by adding the same number of random relationships to the hypernymy tree (second panel, third column). In comparison, the addition of polysemous relations results in a graph (third column, first panel) of characteristic length comparable to the one that results from adding random relationships to the hypernymy graph (third panel, third column). The fourth panel shows that adding meronomy after the inclusion of polysemy does not result in considerable changes. The impact of adding antonyms to the graph is very low, as can be seen in the averaged results of Fig. 3B. Although this essentially results from the fact that there are very few (1,849) antonym relationships, a small number of links may have a profound impact on the global organization of the graph (10).

Summarizing the exhaustive inspection of the effect of the different relationships revealed that the most important changes in characteristic length result from adding the polysemy relationship (Fig. 3A). In addition, the inclusion of polysemy produces a considerable number of vertices (green dots) with high connectivity and clustering (points close to the blue line, second column third panel). On average, the inclusion of polysemy reduces the characteristic length from 11.9 to 7.4 and increases the clustering from 0.0002 to 0.06. In a way, the inclusion of polysemy creates what is known as a small world (10), a clustered short-range graph.

Given that polysemy has a profound impact on the clustering and characteristic length, we investigated the effect of polysemy in the relationship between mean distance and deepness in the hypernymy tree (minimal distance to the root). In the hypernymy graph, the way to go from one meaning to another is climbing up and down the tree. For example, to go from dog to oak, one would follow the trajectory: dog–canine–carnivore–placental–mammal–chordate–animal–life form–plant–woody plant–vascular plant–tree–oak. As predicted, the mean distance from a node to the rest of the vertices progresses as one goes deeper in the tree. Moreover, the vertices are correlated with a slope of 1, indicating that for every step down in the tree, a vertex is on average one more link apart from the rest of the nodes (Fig. 4, blue). When polysemy is added, this correlation, though still present, becomes very weak (Fig. 4, red).

Figure 4.

Correlation between mean distance and deepness in the hypernymy tree. The figure displays a scatter of average minimal distance versus depth in the hypernymy tree with and without the inclusion of polysemy. In the hypernymy tree (blue), distance scales with E with a tight correlation (r = 0.902). After adding polysemy (red), the correlation is very weak (r = 0.54), showing the hierarchy of hypernymy has low impact in distance between meanings in the full semantic graph.

A complementary measure of global organization in a graph is the traffic through any given vertex, counting the number of trajectories between other vertices passing through it (see Methods and ref. 11). When polysemy is not present, different taxonomic groups are the meanings with more traffic. This result is a consequence of the presence of a large number of related genera: in a tree structure the root is the center of traffic only if the branches are homogeneous; otherwise, highly connected child-vertices take over. The most active vertices in the graph {I–II–III} correspond to meanings with high number of hyponyms (Fig. 5 Middle, blue dots). This is essentially because all of the corresponding hyponyms have to pass through their hypernymy to navigate to the rest of the graph. When polysemy is added the distribution of vertices with high traffic forms clusters (Fig. 5 Top, red dots) corresponding to central abstract meanings such as head (red arrow), line (pink arrow), or point (orange arrow). Interestingly, these three clusters correspond to the groups of meanings of the most polysemous words, respectively, head (P = 30), line (P = 29), and point (P = 24). Moreover, traffic becomes essentially independent of connectivity (Fig. 5 Middle, red dots). In this case, a good local indicator of traffic is the number of connected neighbors as shown in Fig. 5 Bottom. Thus, after the inclusion of polysemy, the heavy clusters (a large group of vertices all connected to each other through a polysemous word) become the center of traffic.

Figure 5.

Polysemy converts meanings related through the most polysemous words in the hubs of the graph. The value of the first eigenvalue (a measure of traffic, see Methods) for the graphs with all relations (red) and without polysemy (blue) as a function of distance (Top), connectivity (Middle), and number of connected neighbors (Bottom). (Top) The word forms produce clusters (marked with the arrows), which correspond to the most polysemous words: head (green arrow), point (pink arrow), and line (orange arrow). (Middle) Traffic is independent of connectivity after the inclusion of polysemy (red dots). In the hypernymy tree, however, the points with most hyponyms, and thus the most connected ones, become hubs. (Bottom) After the inclusion of polysemy, the nodes with more traffic are the ones with most connected neighbors, which form big clusters of fully connected nodes. These two graphs present examples in which the traffic is dominated by the most connected nodes (without polysemy) or to the heavy clusters (with polysemy). The transitions between the graph without and with polysemy is highlighted by arrows in Middle and Bottom marking the highest values for traffic as a function of connectivity and connected neighbors, respectively.

Discussion

Graph Theoretical Analysis.

Our results have been based on three measurements used to characterize the structure of a graph: characteristic length, clustering, and traffic. Although the first two measurements have been widely used to understand the organization of different networks, the latter has been less explored, among other reasons, because traffic and connectivity are often strongly connected. However, in many examples of biological or social networks, the measure of traffic through a vertex (a global measure that establishes how centered it is within the graph) may be more relevant than connectivity. Fig. 1 shows a toy graph in which a node (c) with only four connections is the one with more traffic, given that all trajectories connecting a vertex in two different quadrants of the graph go necessarily through node c. Clearly, the presence of such a central node would not be revealed without a traffic analysis. In our analysis of Wordnet, we have observed a nontrivial relationship between traffic and connectivity after the inclusion of polysemy, which produces the following changes: (i) the characteristic length decreases and (ii) the graph becomes clustered; these two properties define a small-world network. Finally, (iii) the polysemous clusters (which do not include the most connected vertices) become the hubs of the graph.

Beyond the strict analytic content of the present study, we would like to discuss a number of possible implications of our results regarding the neural correlates of concepts.

Implications for polysemy.

The existence of polysemous words has remained a central challenge to artificial language (14). With a one-to-one mapping of meanings to words, decoding meanings from word forms would be, of course, a trivial problem. Why then are all languages polysemous? Our investigation of the impact of different relationships within the lexicon (Wordnet) on its global organization shows that inclusion of polysemy drastically reorganizes the semantic web so as to render it a small-world network, where meanings are typically closer to each other and central concepts (which are the most polysemous, and also the most familiar; ref. 15) become the center of more trajectories, the hubs of the lexicon. This finding formalizes the proposal that polysemy may be crucial for metaphoric thinking, imagery, and generalization (4), and establishes a possible role for polysemy.

Implications for mental navigation.

Different lines of research have provided evidence of mental navigation in the semantic network, implying that our observations of global graph properties might be important for the understanding of the mental representation of meaning (16–20). Word-priming studies have demonstrated that when subjects are asked to judge whether a string of letters is a word, judgments occur more rapidly after a semantically related item than an unrelated item (21). Subliminal presentation of a word can also improve reaction times when a subsequently presented word is semantically related to the first one (22, 23). An ambiguous (polysemous) word primes the different meanings associated with it (24). Finally, classical models of lexical retrieval have shown that the reaction time to a given word is decreased if it has a number of neighbors with similar orthographic or phonological mapping (25, 26). Thus the relation of polysemy may be extended to a word-form neighbor relationship, and consequently two meanings may be related through similar (but not necessarily identical) word forms. This adds yet another dimension to the possible organization of the set of meanings so as to provide it with a more efficient lexical retrieval mechanism. Irrespective of the specifics of the neuronal implementation, we can reason that the small-world property is a desirable one in a navigation network, given that it strikes a balance between the number of active connections and the number of steps required to access any node. Moreover, taking mental navigation for granted, we would also expect that the hubs of network traffic should display distinct and recognizable physiological features, as well as a statistical bias for priming in association and related tasks. Despite the tentative nature of these suggestions, they provide a number of experimentally testable hypotheses to further the understanding of mental navigation processes.