The role of intersection topography in bond selectivity of cis-trans photoisomerization

Abstract

Ab initio methods are used to characterize the ground and first excited state of the chromophore in the rhodopsin family of proteins: retinal protonated Schiff base. Retinal protonated Schiff base has five double bonds capable of undergoing isomerization. Upon absorption of light, the chromophore isomerizes and the character of the photoproducts (e.g., 13-cis and 11-cis) depends on the environment, protein vs. solution. Our ab initio calculations show that, in the absence of any specific interactions with the environment (e.g., discrete ordered charges in a protein), energetic considerations cannot explain the observed bond selectivity. We instead attribute the origin of bond selectivity to the shape (topography) of the potential energy surfaces in the vicinity of points of true degeneracy (conical intersections) between the ground and first excited electronic states. This provides a molecular example where a competition between two distinct but nearly isoenergetic photochemical reaction pathways is resolved by a topographical difference between two conical intersections.

One of the simplest means to convert light into mechanical motion at the atomic scale is cis-trans photoisomerization, and it is widely used in photoactive proteins. Retinal protonated Schiff base (RPSB) is the best known biological chromophore, with five double bonds capable of undergoing photoisomerization. A long-standing question has been the mechanism that selects the isomerizing bond, particularly the role of the protein environment in “steering” reactivity. The availability of the structures of rhodopsin (1) and bacteriorhodopsin (2–5), coupled with characterization of RPSB solution-phase photochemistry (6–11), provides a unique opportunity to identify this mechanism. Conical intersections (CIs), geometries where two electronic states are truly degenerate, providing doorways from excited to ground electronic states, are widely believed to be important in photochemistry (12–14), and their role in photoinduced isomerization has been well documented (14–22). However, their role in bond torsion selectivity has yet to be established. In this paper, we show that the topography, or shape, around CIs determines this selectivity in RPSB. This direct connection between CI topography and photochemical selectivity has significant implications for understanding protein “steering” and the rational design of molecular optoelectronic devices.

Investigations of the photochemistry of RPSB have established that the protein is not an idle spectator; quantum yield, selectivity, and time scales are all significantly different in solution and protein environments. In the protein environment, isomerization occurs exclusively around a single bond, e.g., 11-cis → all-trans in rhodopsin and all-trans → 13-cis in bacteriorhodopsin. In contrast, illumination of the all-trans chromophore in solution results in several photoproducts with 11-cis being the most dominant (6–8). The isomerization quantum yield is greater than 50% in proteins (23), but rarely exceeds 20% in solution (6–10). Finally, the time scale for isomerization in solution has been measured to be 10 ps (9), while it is faster than 2 ps in protein environments (24, 25). Understanding the solution photochemistry is critical because it provides the standard against which one can quantify the steering role of the protein environment. Although steric (26, 27) and electrostatic (28, 29) considerations have been invoked to rationalize the bond selectivity observed in protein environments, they do not explain the solution data for photoisomerization of all-trans RPSB. Entropic considerations associated with the large amplitude motion of isomerization in a confined solution environment would erroneously predict 13-cis to be the favored product. Consideration of ground state stability again erroneously predicts 9-cis and 13-cis to be the dominant products, primarily because of the steric crowding induced by the two methyl groups on the RPSB backbone in the 11-cis conformer. (See the supporting information published on the PNAS web site, www.pnas.org, for calculations of the energies of the different conformers.) Finally, increasing solvent polarity increases the dominance of the 11-cis product in solution, while the charged environment of bR favors the 13-cis conformer. In this work, we show that the intersection topography of the ground and excited state potential energy surfaces, as computed by ab initio quantum chemistry, can explain the observed selectivity in solution photochemistry of all-trans RPSB.

It is now widely recognized that CIs are ubiquitous in the manifold of excited electronic states and that they serve as efficient funnels for nonradiative decay back to the ground state (12–14, 30). These CIs usually form a locus of points or hypersurface; they are not isolated points like local minima or transition states. Nevertheless, the lowest energy point along a CI hypersurface (minimal energy CIs) can serve as the photochemical analog to the transition state that dominates theoretical models of ground state chemical reactions. When several minimal energy CIs leading to different products are present, one may expect the products that arise from the lowest energy intersection to dominate, just as one would expect the reaction path with the lowest barrier to be most important in a ground state chemical reaction with competing reaction paths. Much of the previous work on photochemical mechanisms has concentrated on the energetic location of minimal energy CIs when rationalizing selectivity, in complete analogy to the barrier height for ground state reactions. (Of course there can be exceptions, just as ground state reactions can be nonstatistical.) Although there has been some previous speculation that the topography or shape of the CI might also be an important factor in selecting between alternate photochemical mechanisms (31, 32), no concrete molecular examples have been reported. Here we draw a direct connection between CI topography and selectivity for the most prevalent chromophore in photobiology. The two minimal energy CIs relevant for isomerization around the C₁₃⩵C₁₄ and C₁₁⩵C₁₂ bonds are isoenergetic and both essentially coincide with a twisted local minimum on the excited (S₁) electronic state. However, the local topography of the two CIs is qualitatively different and we attribute the observed bond selectivity to this difference in intersection topography.

The calculations detailed here use accurate ab initio quantum chemistry methods, which are necessary for a suitable description of electronic excited states in molecules. Computational considerations prohibit direct application of these methods to RPSB itself, let alone the chromophore and protein. Hence, the calculations described are done in vacuo by using an RPSB analog slightly shorter than RPSB itself, but containing all the double bonds that can isomerize in RPSB. Sketch 1 shows the RPSB chromophore and the model Schiff base all-trans-3,7-dimethylnona-2,4,6,8-tetraenmethylmminium cation used in our calculations. The model includes 10 conjugated π electrons, the two methyl groups on the RPSB backbone, and an additional methyl group replacing the link to the protein (Lys216 in bR). The β-ionone ring is neglected because it is unlikely to have a significant effect on the electronic structure of the conjugated backbone.

The calculations were carried out with a state-averaged (equally weighting S₀ and S₁) complete active space self-consistent field (CASSCF) electronic wavefunction (33). All 10 π electrons and orbitals are included in the active space and the 6-31G* basis set is used. This SA-2-CASSCF(10, 10) wavefunction includes a large portion of the static correlation energy and provides a satisfactory description of the ground and first excited states. Although it is certainly important to include the dynamic correlation energy, e.g., with multireference perturbation theory or configuration interaction, to accurately predict vertical excitation energies in conjugated molecules like RPSB (34, 35), previous studies of ethylene (21) and RPSB analogs (16) suggest that these dynamic correlation effects are less important to the locations and relative energetics of conical intersections. Hence, we believe that the conclusions in this work would not be greatly affected by an improved treatment of dynamic correlation. For example, in a smaller RPSB analog with three double bonds, the Robb and Olivucci groups found that conical intersections determined at the CASSCF level remain nearly degenerate when perturbation theory corrections are included with CASPT2 (16).

Our calculations, performed with the molpro quantum chemistry program (38), concentrate on the two most important possibilities for photoinduced isomerization: torsion around the C₁₁⩵C₁₂ and C₁₃⩵C₁₄ bonds. We have optimized molecular geometries for local minima on the S₀ and S₁ electronic states and also for minimal energy CIs connecting S₀ and S₁. In addition to these unconstrained optimizations, we have also calculated minimum energy paths for torsion around the C₁₃⩵C₁₄ and C₁₁⩵C₁₂ bonds. The relative energies of the local minima and minimal energy CIs that we have located are depicted in Fig. 1. (For the geometries of the various species, see the supporting information.) The electronic excitation promotes an electron from a (predominantly) π-like bonding orbital to a (predominantly) π*-like antibonding orbital, leading to a reversal of single-double bond character in S₁ if the molecule is constrained to remain planar. Relaxation along this bond alternation coordinate yields a stabilization of ≈9 kcal/mol. The local minima associated with isomerization around C₁₁⩵C₁₂ and C₁₃⩵C₁₄ are essentially isoenergetic, differing by ≈0.5 kcal/mol. The local minima are found in both cases to lie in close geometric and energetic proximity to the corresponding minimal energy CIs. This proximity of local minima and minimal energy CIs has been found in other unsaturated hydrocarbons (20, 21) but is of uncertain generality. Given the relatively long S₁ lifetime in solution for RPSB, this equivalence implies an increased importance for a minimal energy CI compared to other points on the hypersurface of intersection. Following electronic excitation, RPSB is predicted to relax to its new equilibrium position on S₁ predominantly via bond alternation and torsion, in agreement with previous results of Gonzalez-Luque et al. (14). As either of the S₁ local minima corresponding to twisted C₁₁⩵C₁₂ or C₁₃⩵C₁₄ are approached, the molecule may encounter CIs which furnish a gateway back to the ground electronic state.

Figure 1.

Relative energies of various stationary points for the model RPSB analog (see Sketch 1 in the text). Blue and red are used to denote ground and excited state energies, respectively. The ground state equilibrium geometry (which is completely planar) is at the center of the plot and to its left and right are the minima and conical intersections associated with torsion around the C₁₁⩵C₁₂ and C₁₃⩵C₁₄ bonds, as well as the planar relaxed minimum on the first excited state (for clarity this is shown on both sides of the Franck-Condon point). The arrow illustrates the electronic excitation and the three graphical renderings illustrate the structure of the analog at the planar geometries (Center), twisted around C₁₁⩵C₁₂ (Left) and twisted around C₁₃⩵C₁₄ (Right). (See the supporting information for details of bond lengths and angles at the various stationary points.) vmd (37) was used to generate the figures.

The degeneracy of the two intersections and associated local minima implies that in the absence of an intervening barrier, the two isomerization pathways are equally probable and hence so should be the two photoproducts: 11-cis and 13-cis. However, this is not the case in either protein or solution environments. Especially relevant in the present context are the solution results, where a clear preference for the 11-cis photoproduct is observed (6–8). One possible explanation is the existence of barriers (of quite different heights) between the Franck-Condon geometry and the minimal energy CIs. Because the results shown in Fig. 1 do not preclude the existence of such barriers, we have calculated the minimum energy isomerization pathway for the two relevant bonds in an analog where the two backbone methyl groups (on C₁₃ and C₉ in Sketch 1) are replaced by H atoms. As shown in the left panel of Fig. 2, and in agreement with previous theoretical work on a slightly different RPSB analog (14), no significant barrier for isomerization around either of the two torsional coordinates is detected. As shown in Fig. 2b, this conclusion is unchanged if the H atoms are replaced by methyl groups (without reoptimization of the molecular geometry.) One should also expect an entropic barrier in the confined solution environment, but because the volume of isomerization for the all-trans → 11-cis pathway is larger than for the all-trans → 13-cis pathway, such a barrier cannot explain the preference for 11-cis product.

Figure 2.

(a) Minimum energy path on S₁, along the C₁₃⩵C₁₄ (gray lines and circles) and C₁₁⩵C₁₂ (black lines and triangles) torsional coordinates. In these calculations, the two backbone methyl groups of the retinal analog are replaced with H atoms. Energies are measured relative to the energy of the planar minimum on S₀ and in each case (C₁₃⩵C₁₄ and C₁₁⩵C₁₂) we show both the ground and excited state energies. We have also performed the calculations mutating the methyl groups back, but leaving all other geometrical parameters fixed at the optimal values determined with H atoms (b). These latter calculations provide an upper bound to the energies that would be obtained by complete minimization including the two methyl groups for a fixed torsion angle. Both sets of calculations fail to predict any significant barrier along the torsional coordinate. (Table 13 in the supporting information lists the energies plotted here.)

Assuming that there is either no barrier to isomerization or that there is a small barrier of similar magnitude for both isomerization pathways, the results presented so far do not explain the dominance of the 11-cis product in solution RPSB photochemistry. In fact, these results all point to 13-cis as the favored product, in contradiction with experiment. Thus, we have also characterized the topography of the ground and excited state potential energy surfaces (PESs) in the vicinity of the two minimal energy CIs as a function of the two coordinates that are most effective in promoting efficient internal conversion from S₁ to S₀. These two coordinates are given by the difference gradient and nonadiabatic coupling vectors (13), denoted as g⃗ and h⃗, respectively:

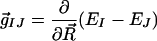1

2

where R⃗ denotes the nuclear coordinates and E_I and ψ_I denote the energy and wavefunction for the Ith electronic state. (The subscripts I and J are given in these equations for generality. Throughout this paper, we drop the subscripts with the understanding that the electronic states involved are S₀ and S₁.) For RPSB, these two coordinates are well described by the relevant C⩵C torsion and bond alternation along the conjugated backbone. (Tables 8–11 in the supporting information contain the Cartesian components of the two vectors at the two geometries.) The resulting two-dimensional PESs are shown in Fig. 3 for both C₁₁⩵C₁₂ and C₁₃⩵C₁₄ minimal energy CIs. The local topographies of the two CIs are quite different; the C₁₁⩵C₁₂ CI (CI_11⩵12) is “peaked” and the C₁₃⩵C₁₄ CI (CI_13⩵14) is “sloped” (31). These two different topographies are expected to result in quite different dynamics (31, 32). On the upper (S₁) PES, the peaked CI is more effective than the sloped CI in directing (i.e., “funneling”) population to the point of intersection. On the lower (S₀) PES, the peaked CI is more effective than the sloped CI in directing population away from the intersection, thereby reducing the probability of S₀ → S₁ “up-funneling” (32, 36). The arrows sketched on the two surfaces demonstrate the expected dynamics for a typical wavepacket approaching the conical intersection from the Franck-Condon region. In the case of a peaked CI, the excited state trajectory is clearly directed toward the intersection, and once it quenches to the ground state, it is directed away from the CI. When the intersection is sloped, however, the quenched wavepacket is not strongly directed away from the intersection. In fact, one easily sees that it may recross back to the excited state. The scenarios predicted for the two different topographies are analogous to recrossing effects that are familiar in the context of transition state theory (TST) for reactions occurring on a single electronic state. If the wavepacket crosses the CI only once, a single photoproduct (11-cis in the case of RPSB) will be formed; the CI is a true configuration of no return. However, if the wavepacket funnels down and up (i.e., crosses from S₁ to S₀ and then back) many times, the distribution of photoproducts will become statistical (i.e., half 13-cis and half back to all-trans)—the same situation which leads to failure of TST. In this analogy, the ground and excited electronic states play the role of products and reactants in TST and we have implicitly assumed that the nuclear motion is diabatic, i.e., electronic state changes occur with high probability when wavepackets approach a CI. Detailed simulation of the quantum mechanical dynamics is needed for a quantitative prediction of the product branching ratios. Nevertheless, a simple estimate based on the above considerations is in qualitative accord with the experimental data—2:1 for 11-cis relative to 13-cis compared to experimental results, which range from 2:1 to 8:1 depending on solvent and excitation wavelength.

Figure 3.

The ground and first excited electronic states, computed with ab initio electronic structure methods, of the RPSB analog as a function of displacement along the two coordinates that are most effective in promoting internal conversion from S₁ to S₀ (g⃗ and h⃗). All other coordinates are fixed at their values at the C₁₁⩵C₁₂ (Left) or C₁₃⩵C₁₄ (Right) conical intersections. The C₁₃⩵C₁₄ conical intersection has a sloped topography while the C₁₁⩵C₁₂ conical intersection is strongly peaked. The three graphical renderings depict the structure of the analog at the planar-relaxed geometry, C₁₁⩵C₁₂ CI, and C₁₃⩵C₁₄ CI (Center, Left, and Right, respectively). The arrows drawn on the computed surfaces provide a qualitative representation of the expected wavepacket dynamics.

Yarkony has recently introduced a quantitative measure of the “peaked” or “sloped” character of an intersection (32). This measure considers only the linear variation of potential energy surfaces around the intersection and is therefore not guaranteed to be informative; as can be seen in Fig. 3, a first-order Taylor series expansion is valid only very close to the intersections for RPSB. Nevertheless, it is instructive to determine whether the topographical difference between CI_11⩵12 and CI_13⩵14 is reflected in this measure. Introducing the “seam coordinate,” s⃗_IJ:

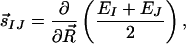3

denoting g and h as the lengths of g⃗ and h⃗, and defining

4

Yarkony defines three dimensionless variables that characterize the intersection through first-order:

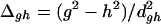5

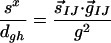6

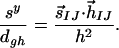7

The asymmetry of the intersection is given by Δ_gh, with Δ_gh = 0 corresponding to a completely symmetric CI where the degeneracy is raised at the same rate for displacements along g⃗ and h⃗. The degree of sloped character for displacements along g⃗ and h⃗ is given by s^x/d_gh and s^y/d_gh, respectively. For a perfectly peaked CI, all three of these parameters vanish. The values we obtain for CI_11⩵12 and CI_13⩵14 are given in Table 1. Neither CI is symmetric, and this measure suggests that CI_13⩵14 is the more symmetric of the two. CI_13⩵14 has more sloped character, as evidenced by the fact that s^x/d_ghfor CI_13⩵14 is the largest of all the listed s^x/d_gh and s^y/d_gh. For the present case, this quantitative measure confirms the assignment of peaked versus sloped CIs, made by appealing to Fig. 3.

Table 1.

Parameters characterizing the first-order topography of the C₁₁⩵C₁₂ and C₁₃⩵C₁₄ CIs

	Δgh	sx/dgh	sy/dgh
C11⩵C12	−0.71	0.0085	0.48
C13⩵C14	0.40	−0.76	0.17

We have investigated the origin of bond selectivity in RPSB using accurate ab initio quantum chemistry methods and a realistic chemical model. Our results suggest that in the absence of any specific interactions with the environment (e.g., discrete ordered charges or H-bonding), bond selectivity originates in the topographies of the S₀ and S₁ PESs around the minimal energy CIs associated with C₁₃⩵C₁₄ and C₁₁⩵C₁₂ torsion. In contrast to energetic considerations that fail to explain bond selectivity, the strikingly different topographies of the two minimal energy CIs are consistent with the observed preference for the 11-cis photoproduct in solution.

Figure.

Sketch 1.

Abbreviations

CI

conical intersection

RPSB

retinal protonated Schiff base

CASSCF

complete active space self-consistent field

PES

potential energy surface