Influence of anthropogenic aerosol on cloud optical depth and albedo shown by satellite measurements and chemical transport modeling

Abstract

The Twomey effect of enhanced cloud droplet concentration, optical depth, and albedo caused by anthropogenic aerosols is thought to contribute substantially to radiative forcing of climate change over the industrial period. However, present model-based estimates of this indirect forcing are highly uncertain. Satellite-based measurements would provide global or near-global coverage of this effect, but previous efforts to identify and quantify enhancement of cloud albedo caused by anthropogenic aerosols in satellite observations have been limited, largely because of strong dependence of albedo on cloud liquid water path (LWP), which is inherently highly variable. Here we examine satellite-derived cloud radiative properties over two 1-week episodes for which a chemical transport and transformation model indicates substantial influx of sulfate aerosol from industrial regions of Europe or North America to remote areas of the North Atlantic. Despite absence of discernible dependence of optical depth or albedo on modeled sulfate loading, examination of the dependence of these quantities on LWP readily permits detection and quantification of increases correlated with sulfate loading, which are otherwise masked by variability of LWP, demonstrating brightening of clouds because of the Twomey effect on a synoptic scale. Median cloud-top spherical albedo was enhanced over these episodes, relative to the unperturbed base case for the same LWP distribution, by 0.02 to 0.15.

Aerosol particles serve as nuclei for formation of cloud droplets in the earth's atmosphere. As enhanced concentrations of aerosol particles from industrial activities lead to increased concentrations of cloud droplets, it was pointed out some time ago by Twomey (1, 2) that such enhanced cloud droplet concentrations would be expected to increase cloud reflectivity for a given cloud liquid water content. This enhancement of cloud albedo would be expected to have resulted in reduction in absorption of solar radiation by the Earth-atmosphere system over the industrial period and a cooling influence on climate. Estimates of the global average magnitude of this effect suggest that it is substantial in the context of climate forcing by increased concentrations of greenhouse gases over the industrial period (3–7). Enhancement of albedo of marine stratus clouds globally by 0.03 would result in a global-mean radiative forcing of −1.8 W m⁻² (3, 4), the negative sign indicating a cooling influence. Such a global mean forcing would more than offset the warming influence caused by increased CO₂ (8). Current estimates of this indirect aerosol forcing are mainly model-based and highly uncertain (5–10). The uncertainty arises from uncertainties in both the global distribution and loading of anthropogenic aerosols and the relation between aerosol loading and cloud microphysics and reflectivity. A recent global modeling study (11) showed high sensitivity of the indirect forcing to the relation assumed between sulfate loading and increased cloud droplet concentration; depending on the relation assumed, the global and annual mean forcing caused by the modeled sulfate distribution ranged from −0.4 to −1.78 W m⁻². Because of such uncertainties in model-based estimates, it is imperative to obtain measurement-based estimates of the aerosol indirect forcing.

As aerosols are short-lived in the troposphere (about 1 week), their distribution is quite inhomogeneous spatially and temporally, indicative of the need for rather detailed global characterization, that is, by satellite. Several studies combining in situ measurements and aircraft and/or satellite remote sensing have demonstrated increases in cloud droplet concentration and albedo because of anthropogenic aerosol on local to regional scales (e.g., refs. 12–18), but such studies are expensive and necessarily limited in scope. Satellite surveys alone might be expected to permit characterizing and quantifying indirect forcing on large scales but have thus far been of limited utility. Large-scale surveys have shown cloud-drop effective radius of warm clouds to be systematically lower (19, 20) and number concentration systematically greater (21) in the anthropogenically influenced Northern Hemisphere than in the relatively unperturbed Southern Hemisphere, consistent with the Twomey mechanism of indirect aerosol forcing. Likewise, fairly strong spatial correlations have been reported of monthly mean aerosol optical depth and number concentration with effective radius (negative correlation) and optical depth (positive correlation) of low clouds, all of which would be consistent with the Twomey effect (22, 23). However, the expected enhancement of cloud albedo caused by the Twomey effect has not been identified in interhemispheric comparisons (20, 24). Likewise, examination for aerosol enhancement of monthly mean cloud albedo as a function of distance off of continents has been negative (25) or shown only marginal indication of enhancement (26); evidence has been presented of enhanced reflectivity of marine stratocumulus clouds locally in the vicinity of copper smelters in Peru under conditions of offshore flow (27).

Recently we demonstrated the ability to use satellite measurements to detect influences of anthropogenic aerosols on cloud properties in a situation where enhanced aerosol loading was indicated by a chemical transport model (28). This approach uses a chemical transport model driven by archived output of a numerical weather prediction model to identify locations and times of higher or lower aerosol loading. This approach also takes advantage of the high dynamic range of aerosol loading that results from synoptic-scale variation in meteorology responsible for transport, conversion, and removal of tropospheric aerosols. Examination of cloud-drop effective radius and number concentration in conjunction with modeled sulfate concentration allowed identification of the influence of sulfate. Here we extend this approach to examine the aerosol influence on cloud optical depth and albedo taking advantage of the ability to simultaneously determine these quantities and cloud liquid water path (LWP) from the satellite data, thereby allowing the strong influence of LWP on cloud albedo to be accounted for.

Approach

The chemical transport and transformation model (29), which represents mixing ratios of sulfur dioxide and sulfate as functions of location, altitude, and time, is driven by the 6-hour forecast data of the European Centre for Medium Range Weather Forecasts (ECMWF, ref. 30). Briefly, the model represents transport of geographically distributed anthropogenic emissions (31) of SO₂ and sulfate and biogenic emissions of dimethyl sulfide (DMS) by the controlling three-dimensional wind fields. DMS is oxidized to SO₂ and methanesulfonic acid (MSA), and SO₂ is oxidized to sulfate by gas- and aqueous-phase reactions; SO₂, MSA, and sulfate are removed from the atmosphere by dry deposition and precipitation. The model, which has horizontal grid spacing of 1.125° and 15 vertical levels with increased resolution near the surface, outputs mixing ratios of SO₂ and sulfate at each grid cell at 6-hour time intervals. The model, which has been extensively evaluated by comparison with in situ measurements (32), provides a fairly accurate, albeit not exact, indicator of the sulfate loading as a function of location and time.

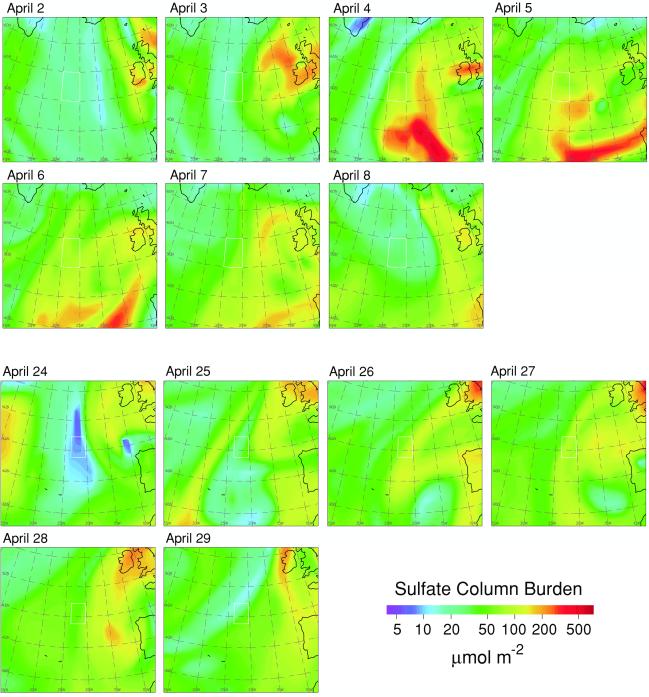
This study focuses on two episodes during April, 1987, during which modeled concentration of sulfate aerosol at locations over the North Atlantic well removed from local sources exhibited substantial increase and subsequent decrease resulting from transport from anthropogenic continental sources. The meteorological conditions giving rise to these episodes are presented and analyzed in ref. 33, which includes animations of the sulfate transport events. Fig. 1 depicts the sulfate column burden (vertical integral of concentration) during these episodes and shows the study areas selected because of the presence throughout the episodes of extensive low-level clouds mostly unobscured by higher level clouds. During the first episode (April 2–8), sulfate from western Europe was transported westward over the North Atlantic under the influence of a persistent intense cut-off low-pressure system. Mean cloud-top temperatures in the 5° × 5° study area (25–30°W, 50–55°N, about 1100 km west of Ireland) ranged from 270 to 262 K, with corresponding cloud-top heights ranging from 1.5 to 2.7 km. The study area is situated toward the edge of the region most strongly influenced by the transported continental sulfate. Modeled sulfate in the study area, which was distributed vertically mainly between the surface and 3 km, reached a maximum on April 5 (Fig. 2a Left). During the second episode (April 24–29), the model indicates advection of air containing high sulfate concentrations from the northeastern United States, in part under the influence of a cut-off low-centered northwest of the Iberian peninsula (33). Cloud microphysical properties were retrieved for a 3.375° × 3.375° study area (20.25–23.625°W; 43.875–47.25°N, about 1100 km WNW of the northwest tip of Spain). Cloud-top temperatures were indicative mainly of liquid-water clouds with average cloud-top heights ranging from 1.3 to 1.9 km. Multiple cloud layers were indicated on April 24 and 29, but cloud properties inferred from satellite measurements show no appreciable differences for the several layers. Modeled sulfate was present mainly between the surface and 4 km; sulfate column burden peaked on April 27 (Fig. 2a Right). Although aerosol from other sources would certainly have been present in both episodes, sulfate from continental sources is expected to have been a major aerosol species at these remote marine locations under these flow conditions.

Figure 1.

Sulfate column burden (vertical integral of concentration) in mid North Atlantic at 1800 Universal Time Coordinated on April 2–8, 1987, and April 24–29, 1987, as evaluated with a chemical transport and transformation model. Note logarithmic scale. Boxes denote areas chosen for analysis of satellite retrievals of cloud properties.

Figure 2.

Time series of sulfate column burden from chemical transport model and pixel-average (1 × 4 km) cloud properties determined from satellite retrievals over mid-North Atlantic, 25–30°W, 50–55°N, April 2–8, 1987 (Left), and 20.25–23.625°W, 43.875–47.25°N, April 24–29, 1987 (Right). (a) Modeled sulfate column burden, obtained by interpolation of model output at 6-h intervals. (b) Effective radius at cloud top, r_e. (c) Optical depth, τ_c. (d) Cloud-top spherical albedo, α_sph. (e) Cloud-top temperature (note inverted scale). (f) LWP. (g) Enhancement of cloud-top spherical albedo relative to that calculated for April 2 (Left) or April 24 (Right) for the same LWP distribution. Bars denote central 80% of the data; ticks denote upper, median, and lower quartiles. Two sets of data are shown for April 8, 27, and 28, for which the study area was within range of the satellite on two successive overpasses. Dates and times are Universal Time Coordinated.

Cloud properties were obtained by using global area coverage data from the Advanced Very High Resolution Radiometer (AVHRR) aboard the NOAA-9 polar orbiting satellite, which overflew the study areas daily at about 2:30 p.m. local time. Details of the retrievals are given in ref. 28. Briefly, pixels (1 × 4 km at nadir) filled by low-level clouds were selected by minimum variance relative to adjacent pixels (34). Cloud microphysical properties were determined by using radiance measurements in the visible (0.58–0.68 μm) and short-wave infrared (3.55–3.93 μm). The two radiance measurements were converted to optical depth τ_c and effective radius near cloud top r_e by a table-lookup procedure based on radiative transfer calculations as a function of solar and viewing geometry (35); visible radiance is sensitive mainly to optical depth, whereas short-wave infrared radiance is sensitive mainly to effective radius. The effective radius, the ratio of the third moment of the cloud droplet size distribution to the second moment, is a measure of the droplet size that contributes most strongly to the radiance (36). Because visible radiance plateaus at high optical depth, the retrieval is insensitive to optical depths greater than 70, and hence values of τ_c ≥ 70 were set to 70; values of τ_c < 3 were excluded to eliminate pixels that could be covered by haze but not clouds. Errors in τ_c and r_e are estimated as less than 15% (35, 37), and retrieved values agree with those obtained by a refined technique typically within 1 optical depth unit and 20%, respectively (38). Values of r_e obtained from AVHRR data by the latter technique agree with in situ measurements typically within 1–2 μm (38).

Cloud LWP was evaluated (19, 23, 39) under the assumption of adiabatic clouds (28) as

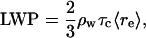1

where ρ_w is the density of water and 〈r_e〉 denotes the cloud-average effective radius taken as 5/6 r_e (16). Cloud-top spherical albedo—the ratio of reflected to incident flux averaged over all angles of incident radiation (40)—was calculated for visible and near-visible radiation (0.25–1.19 μm) according to the asymptotic expression for conservative scattering of Harshvardhan and King (41):

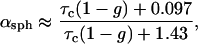2

where the asymmetry parameter g, evaluated according to Slingo (42), ranges from 0.834 for r_e = 6 μm to 0.872 for r_e = 19 μm.

Results and Discussion

The satellite data reveal a systematic trend in effective radius over the course of the two episodes (Fig. 2b). In episode 1, r_e decreases from 15.7 ± 1.6 μm (median and interquartile range) on April 2 to 7.6 ± 1.2 on April 5, and in episode 2 from 16.3 ± 3.7 μm on April 24 to 8.8 ± 1.1 μm on April 26. In each episode, the decrease in r_e is concomitant with the increase in modeled sulfate burden, with subsequent return to higher values as the sulfate decreased toward the end of the episode. In contrast, cloud optical depth (Fig. 2c) and spherical albedo (Fig. 2d) exhibit little evident systematic trend over the episodes that would be consistent with expectation of enhancement associated with greater aerosol loading or decreased effective radius. For example, from April 24 to 26 as r_e decreased from 16.3 ± 3.7 μm to 8.8 ± 1.1 μm α_sph increased, as expected, from 0.65 ± 0.05 to 0.83 ± 0.06. In contrast, despite r_e being considerably greater on April 29 than on April 26 (13.7 ± 2.3 μm vs. 8.8 ± 1.1 μm), α_sph was roughly the same (0.80 ± 0.04 vs. 0.83 ± 0.06). This lack of evident systematic trend in spherical albedo is attributed to variation in LWP within a given day and from day to day, as discussed below.

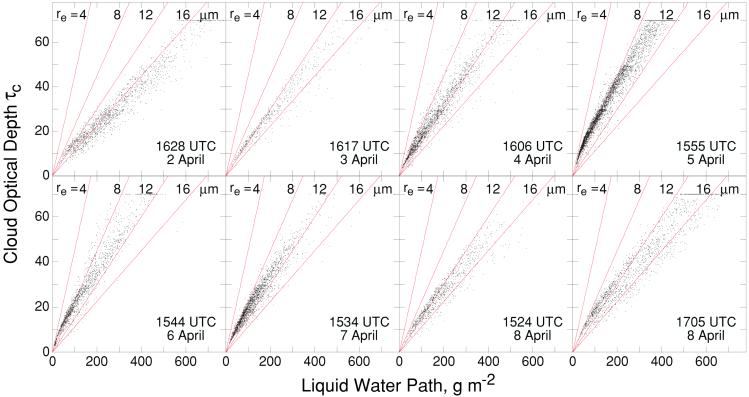
Scatterplots of cloud optical depth against LWP for individual pixels (shown in Fig. 3 for the first episode) show wide variation in both quantities within the study area on any given day. The influence of LWP on cloud optical depth is manifested in the strong dependence of τ_c on LWP observed on any day. For all but one of the 16 scenes examined in the two episodes, the variance in LWP accounted for more than 83% of the variance in τ_c (square of the Pearson product-moment correlation coefficient of a linear fit of τ_c vs. LWP), confirming the supposition that the variation in LWP is responsible in large part for the difficulty in discerning day to-day differences in cloud optical depth and spherical albedo. On each day optical depth data exhibited a roughly linear dependence on LWP, as expected from Eq. 1, but with slope that varied systematically from day to day. Also plotted in Fig. 3 are lines representing the dependence of τ_c on LWP (Eq. 1) for values of cloud-top effective radius r_e of 4, 8, 12, and 16 μm. For each of the several days the cluster of the data points exhibits a near linear dependence consistent with the effective radii indicated in Fig. 2 Left. Comparison of the scatterplots for the several days allows the day to day differences of cloud optical depth to be readily discerned as differences in slopes of the clusters of points, despite the difficulty in discerning differences in optical depth values themselves. The chemical transport model calculations allow these differences to be related to the sulfate loading.

Figure 3.

Pixel-average cloud optical depth τ_c as a function of vertical cloud LWP for eight satellite overpasses over the study area 50–55°N, 25–30°W, for April 2–8, 1987. Data points with τ_c > 70 are plotted at τ_c = 70 because of insensitivity of retrieval method at high optical depth; these points are evident as horizontal clusters at τ_c = 70. Data points with τ_c ≲ 3 have been excluded to eliminate pixels that could be covered by haze but not clouds. Lines denote cloud optical depth for indicated constant values of effective radius near cloud top, r_e.

An influence of anthropogenic aerosol on the slope of a plot of τ_c vs. LWP and the relation of this slope to r_e have been noted in in situ measurements by Boers et al. (15). Likewise Han et al. (19) have presented graphs of satellite-derived monthly and zonal-mean cloud optical thickness vs. LWP in which the data especially for midlatitude continental clouds in the Northern Hemisphere exhibited a steeper slope than those of marine clouds or clouds at other latitudes, consistent with lower effective radius of droplets in these clouds.

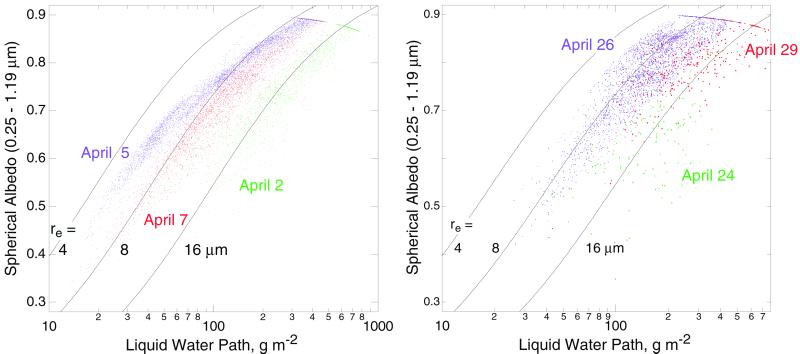
Marked day to day differences are readily apparent also in scatterplots of cloud spherical albedo vs. LWP, examples of which are given in Fig. 4. The clusters of data points for the several days are distinctly segregated, manifesting the different dependencies on the several days. Also shown in the figure are curves representing the dependence of α_sph on LWP for specific values of cloud-top effective radius, r_e = 4, 8, and 16 μm. These curves, which may be directly compared with those given by Twomey (1), explicitly show the increase in modeled spherical albedo with decreasing drop radius for a given LWP. The aerosol influence is similarly manifested in the data by the points at a given LWP exhibiting a higher spherical albedo on days with higher aerosol loading. For example, for the first episode, although the aerosol influence is not evident in comparisons of the aggregate spherical albedo for several days (Fig. 2d Left), at any given LWP α_sph is greater on April 5, at the peak of the sulfate incursion, than on April 7, toward the end of the episode, or on April 2, before the episode. Likewise in the second episode, the aerosol influence is again evident by comparison of spherical albedo at any LWP. Fig. 4 Right shows that the similarity in aggregate spherical albedo on April 26, at the peak of the incursion, and April 29, toward the end of the event is attributable to the increase in LWP on April 29 compensating the effect of the increase in effective radius. In contrast, because of the similarity in LWP on the two days, the increase in spherical albedo from April 24, before the onset of the sulfate incursion, to April 26, at the peak of the event, is evident not just in the scatterplot but also in the aggregate data (Fig. 2d Right).

Figure 4.

Pixel-average cloud spherical albedo as a function of vertical cloud LWP, for three satellite overpasses for the first episode (Left), study area 25–30°W, 50–55°N, and for the second episode (Right), study area 20.25–23.625°W, 43.875–47.25°N, for indicated dates in April, 1987. Clusters of points at albedo ∼0.88 represent points with τ_c > 70 for which spherical albedo was calculated as if τ_c = 70. Curves denote cloud albedo for indicated constant values of effective radius near cloud top, r_e.

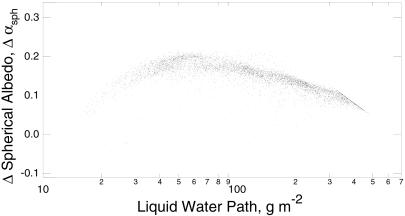
Because cloud LWP is highly variable on account of cloud dynamics and thermodynamics that are independent of aerosol loading, quantification of aerosol influence on cloud albedo would seem to require comparison not of the albedo values themselves but of the enhancement in albedo relative to that expected for the same LWP but with a lower aerosol concentration. Fig. 5 shows the difference in spherical albedo between the high-sulfate low-r_e day at the peak of the sulfate incursion in the first episode (April 5) and the low-sulfate high-r_e day before the incursion (April 2). Specifically, Δα_sph is the difference between α_sph calculated by Eq. 2 from τ_c and r_e obtained from satellite data for April 5, and α_sph calculated for the same LWP by using a linear fit of τ_c to LWP for the April 2 data. This plot thus shows the amount by which α_sph was enhanced over what it would have been with the same LWP but with r_e characteristic of the unperturbed day, consistent with Twomey's (1, 2) mechanism for albedo enhancement by anthropogenic aerosols. Plotting the enhancement against LWP shows maximum enhancement at intermediate values of LWP, for which sensitivity to increased cloud-drop number concentration is the greatest (1, 4). The enhancement in α_sph relative to April 2 evaluated in this way for the entire episode (Fig. 2g) mirrors the excursions in effective radius and sulfate over this period. The magnitude of enhancement in spherical albedo for the second episode is similar.

Figure 5.

Enhancement of pixel-average cloud spherical albedo Δα_sph on April 5, 1987, relative to that on April 2, as a function of LWP, for the study area 25–30°W, 50–55°N. Δα_sph was evaluated for each datum of April 5 as the difference between α_sph obtained by Eq. 2 from τ_c and r_e obtained from satellite data for that date and the value at the same LWP calculated by using a linear fit of τ_c to LWP for the April 2 data. Data points for τ_c > 70 (592 data of a total of 6,443) were calculated for τ_c = 70 and lie along the diagonal line at the upper right of the cluster of points.

This analysis shows substantial enhancement in α_sph correlated with enhanced aerosol loading that is not evident in direct comparisons of the values of α_sph for the several days, because the comparisons are conducted for the same LWP. Whether this comparison is entirely appropriate is an open question (20). It has been suggested (43), with support from in situ studies (e.g., ref. 44), that a decrease in cloud-drop radius caused by enhanced aerosol particle concentration might suppress precipitation and thereby lead to increased liquid water concentration, opposite in direction to the tendency in LWP observed in the first episode (Fig. 2f). Any such increase in LWP would further increase the values of Δα_sph beyond those reported here. As LWP is influenced by a variety of processes including local-scale turbulent fluctuations and synoptic-scale gradients of temperature and humidity, and as LWP greatly influences cloud optical depth and albedo, comparisons of these cloud radiative properties from one situation to another that do not take into account differences in LWP cannot be expected to provide very sensitive measures of aerosol influences. Consequently, it seems imperative that such comparisons take into account the LWP characterizing a given situation.

A potential concern regarding the present analysis is the assumption of conservative scattering by clouds, especially in the presence of potentially absorbing substances in continentally derived air, which affects both inference of r_e and τ_c from satellite radiance measurements and calculation of α_sph from these measurements. Although cloud absorption of visible radiation is generally thought to be small, the validity of this assumption needs further examination.

The magnitude of enhancement of cloud albedo indicated in Figs. 5 and 2g would lead to an indirect aerosol radiative forcing that is quite substantial in the context of radiative forcings over the industrial period; as noted above an average increase of albedo of marine stratus clouds by 0.03 globally would result in a global mean radiative forcing of −1.8 W m⁻² (3, 4). Differences of such magnitude are not readily discernible in direct comparisons of cloud optical depth or spherical albedo (Fig. 2), whereas they are readily ascertained in comparisons that take LWP into account, underscoring the importance of such an approach.

Although a one to one correspondence between modeled sulfate and cloud properties cannot be expected because of model inaccuracy, variation in aerosol properties, the presence of aerosol species other than sulfate, and spatial heterogeneity over the several-hundred kilometer areas chosen for this analysis, the use of the model to distinguish the sulfate loading on the several days permits attribution of the variation in the dependence of optical depth and cloud-top albedo on LWP to the influence of anthropogenic aerosol and thereby provides a demonstration on a synoptic scale of aerosol enhancement of cloud albedo because of the Twomey effect.

Summary

Examination of the dependence of cloud optical depth and spherical albedo on LWP allows the first-order dependencies of these quantities on this macroscopic cloud property to be accounted for and thereby permits the second-order dependencies on cloud microphysical properties to be readily identified, despite the fact that day to day differences in the values of the quantities themselves are not discernible (Fig. 2 c and d). Chemical transport model calculations allow these differences in cloud properties to be related to modeled sulfate loading. The influence of the aerosol is manifested not in the values of optical depth and spherical albedo themselves, but rather in the dependencies of these quantities on LWP (Figs. 3 and 4), or alternatively, in the change in cloud spherical albedo relative to that at the same LWP for a low-aerosol reference case. Mapping out the dependencies of cloud optical depth and spherical albedo on LWP takes explicit advantage of the inherent variation in LWP of low-level marine stratiform clouds on a several-hundred-kilometer scale.

As these cloud microphysical properties can be routinely determined from satellite measurements (19, 21, 38), examination of the dependence of cloud optical depth or spherical albedo on LWP may be expected to be broadly applicable globally as a diagnostic of the Twomey effect of the influence of aerosol loading on cloud albedo. Additionally, this approach leads to a quantitative pixel by pixel estimate of the magnitude of albedo enhancement because of aerosols by comparison to a reference case at the same LWP. This approach may be expected as well to provide the basis for a systematic evaluation of the performance of chemical transport models for aerosols that can then be used with enhanced confidence to represent indirect forcing in climate models.

Abbreviation

LWP

liquid water path