The neural basis of intermittent motor control in humans

Abstract

The basic question of whether the human brain controls continuous movements intermittently is still under debate. Here we show that 6- to 9-Hz pulsatile velocity changes of slow finger movements are directly correlated to oscillatory activity in the motor cortex, which is sustained by cerebellar drive through thalamus and premotor cortex. Our findings suggest that coupling of 6- to 9-Hz oscillatory activity in the cerebello–thalamo–cortical loop represents the neural mechanism for the intermittent control of continuous movements.

We perceive continuous movements as smoothly changing. Yet, movements of finger, arm, and eyes actually exhibit pulsatile velocity changes at a frequency of about 8 Hz (1–3). The changes have been regarded as peripheral manifestation of intermittent output from motor areas in the brain. However, a direct link has not yet been demonstrated and the underlying neural mechanisms remain unknown. Here, we make use of the combined spatiotemporal information available with noninvasive magnetoencephalography (MEG) recordings and a recently developed analysis technique, dynamic imaging of coherent sources (DICS) (4), to demonstrate that slow finger movements are controlled by a cerebello–thalamo–cortical loop, synchronized at about 8 Hz.

Methods

Recordings and Paradigm.

Nine healthy, right-handed subjects (7 male, 2 female, 24–43 years old) participated in this study. Subjects were asked to perform continuous sinusoidal flexion and extension movements in a horizontal plane with their right index finger. The movement range was about 25°. Three conditions were studied, i.e., visual tracking with and without feedback and self-paced movements at the same frequency. In each condition, data were collected during three periods of 2 min. The subjects were allowed to rest for 1 min after each period. The target consisted of a vertical bar projected on a screen that moved sinusoidally left and right at a frequency of 0.5 Hz. Feedback was provided by a second vertical bar. Subjects were instructed to fixate on a stationary dot in the middle of the presentation screen and to perform the movements as smoothly and accurately as possible.

Brain activity was recorded with whole-head MEG (5) at a sampling rate of 1,011 Hz with passband of 0.03–330 Hz. Simultaneously, surface electromyograms (EMG) from the right first dorsal interosseus, flexor digitorum superficialis, and extensor digitorum communis muscles were obtained. In addition, the position of the tip of the right index finger was continuously measured by a three-dimensional ultrasound localization device (Zebris, Isny, Germany; sampling rate, 66 Hz).

Tomographic Coherence Mapping.

DICS (4) was used to determine the spatial distribution of coherent oscillatory activity from the MEG signals recorded at 122 sensors. Coherence quantifies the linear dependency of two signals in the frequency domain and is normalized between 0 and 1. The main features of DICS are explained in this section. Further mathematical details are provided in the Appendix and in ref. 4.

In the first step we performed the transition from time to frequency domain by using the fast Fourier transform (FFT). The FFT was applied to all MEG and EMG signals in 1-s-long data segments (after applying a Hanning window) and the cross-spectral density C was computed between all combinations of MEG and EMG signals. The complex spectrum C was finally averaged across the whole recording period. One element C_i,j of the final cross-spectral matrix consists of the cross spectrum of signals i and j, i.e., signals seen by two different sensors.

In the second step we extracted the mean cross-spectral density of all sensor combinations in a selected frequency band as a complex N × N matrix, where N was the number of signals (MEG and EMG). Computation of cerebro-muscular coherence used the cross spectrum between the EMG signal and all MEG signals, whereas the cerebro–cerebral coherence required the cross spectra of all combinations of MEG signals.

The third step consisted of the application of a spatial filter in the frequency domain (4). This procedure allows the estimation of coherence between two points in the brain (cerebro–cerebral coherence) or between a point in the brain and an external reference signal (here cerebro-muscular coherence). To create tomographic maps, the spatial filter was applied to a large number of voxels covering the entire brain, assigning to each voxel a specific value of coherence to a given reference point or signal. A voxel size of 6 mm was used for our study.

The final analysis of significant group results was performed on the coherence maps in spm99 (Wellcome Department of Cognitive Neurology, Institute of Neurology, London). The coherence maps were spatially normalized to SPM–MNI space by using the corresponding individual T1-weighted magnetic resonance images. The normalized maps were spatially smoothed (15-mm width) and subjected to a one-sample t test. Only areas with P < 0.05 (corrected) were considered.

Synchronization and Directionality Indices.

Time courses of activity were computed from the recorded data for the voxels showing highest coherence (see Appendix). These signals were then band-pass filtered around the peak frequency of movement discontinuities (±2 Hz) and Hilbert-transformed to obtain the instantaneous phases. Two measures were computed from the phases. The first one was the synchronization index ρ (6), which quantifies the degree of coupling of the phases of two signals and ranges from 0 (no coupling) to 1 (strongest coupling). The directionality index (DI; ref. 7) quantifies the direction of coupling between two oscillators with −1 and 1 corresponding to unidirectional coupling (away and toward the reference area, respectively) and 0 corresponding to symmetric bidirectional coupling. The results from the analysis of phase synchronization were used for the quantification of coupling strength and direction because these measures are more sensitive and robust than coherence and phase difference and independent of amplitude dynamics (8).

Results

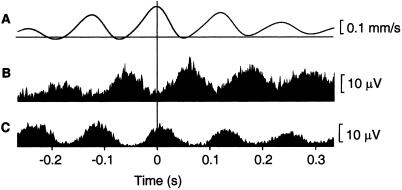
Movement discontinuities were evident in kinematic and EMG signals in all subjects. The EMG power spectra showed peaks at 7.9 ± 1.1 Hz (mean ± SD, range: 6–9 Hz). Fig. 1 illustrates the characteristics of the discontinuities in traces of movement velocity and EMG, averaged time-locked to maxima of the 6- to 9-Hz velocity component. In this subject, peaks in the averaged velocity are separated by about 120 ms corresponding to modulation at 8 Hz (Fig. 1A). The averaged EMG signals reveal a slightly asymmetric alternating agonist-antagonist burst pattern (Fig. 1 B and C). The strongest discontinuities were found during self-paced movements. Because results across conditions did not differ concerning frequency, localization, and direction of cerebro-muscular and cerebro–cerebral coupling, only findings for the self-paced condition are presented here.

Figure 1.

Averages of velocity and EMG signals. Averages of velocity (A), and EMG of first dorsal interosseus (B) and extensor digitorum communis (C) muscle during index finger extension in a typical subject. The trigger points were 300 maxima of the velocity signal, which were found by band-pass filtering the signal at 6–9 Hz and by performing a Hilbert transformation to obtain the instantaneous phase and amplitude. The averaging was done according to the procedure described by Gross et al. (6). The average represents the part of the signal timelocked to discontinuities in the finger velocity.

The 6- to 9-Hz EMG signal from the right extensor digitorum communis muscle was significantly coherent (P < 0.05) (9) to left sensorimotor cortex in all nine subjects (peak frequency 7.0 ± 0.9 Hz) and to right cerebellum in seven subjects (7.3 ± 1.3 Hz). The area with significant coherence in the region around the central sulcus included parts of pre- as well as postcentral cortex. To disentangle possible afferent and efferent components of the coherence map at the interesting frequency of 6–9 Hz, a plane with an extent of 35 mm and a grid size of 5 mm was centered on the point of maximum cortico-muscular coherence. The plane approximated the local brain surface with the edges parallel to the central sulcus. We computed the DI (7) to identify the dominant direction of coupling between EMG activity and the signal of each grid point on the plane.

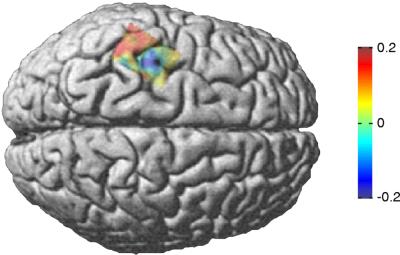
Fig. 2 illustrates the average of spatially normalized individual DI maps, overlaid on a standard brain. The sign of the DI changes across the central sulcus, representing a spatial separation of efferent drive from primary motor cortex (M1) to muscle and afferent input to sensory cortex (S1). The maximum and minimum of the map were used as functional localizations of S1 and M1 for further analysis. The DIs of S1 (0.2) and M1 (−0.16) to EMG were significantly different (P < 0.01, Wilcoxon test; Table 1). The synchronization index ρ was significant for both the M1–EMG coupling (ρ = 0.17, P < 0.05) and S1–EMG coupling (ρ = 0.15, P < 0.05). As for the EMG–cerebellum connection, the mean DI from muscle to cerebellum across subjects was positive indicating a dominant afferent component (Table 1).

Figure 2.

Localization and direction of 6- to 9-Hz sensorimotor-muscle coupling. The DI between muscle and cortical activity was computed on a grid (5-mm resolution) covering the sensorimotor cortex for each individual subject. The individual directionality maps were spatially normalized, averaged over all subjects, and mapped onto a brain normalized with SPM99. Blue and red colors represent predominantly efferent and afferent coupling, respectively.

Table 1.

Summary of cerebro–muscular connectivities

	M1	S1	Cerebellum
DI	−0, 16	0, 2	0, 17
ρ	0, 17	0, 15	0, 2
n	8	9	7

Connectivities from right extensor digitorum communis muscle to contralateral primary motor cortex (M1), primary sensory cortex (S1), and ipsilateral cerebellum are characterized by three numbers: first, the DI; second, the mean synchronization index ρ; and third, the number of subjects n showing the same sign of the DI as the mean (i.e. the dominant direction). Positive DI corresponds to a coupling direction from muscle to brain. 

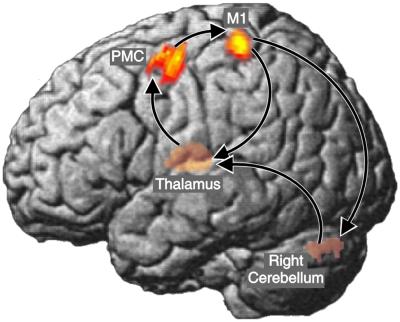
Because the focus of the study was the identification of the cerebral network generating the peripheral discontinuities, we used M1 as the reference region in the analysis of cerebro–cerebral coherence to identify the areas contributing to the generation of 6- to 9-Hz activity at M1. Accordingly, DICS was used to compute a tomographic map of coherence from M1 to all other voxels in the brain. The results of the group analysis in spm99 are summarized in Fig. 3. Left premotor cortex (PMC), left thalamus, and right cerebellum exceeded the significance level of 0.05 (corrected). The group results using SPM were corroborated by the DICS maps in individual subjects. Coherent voxels were consistently located in the M1/S1 and PMC (see Table 2). For the right cerebellum and left thalamus, the spatial variability was larger than in the cerebral cortex. This effect is caused by the increasing uncertainty of localization in deeper brain structures, inherent to the MEG method.

Figure 3.

Map of 6- to 9-Hz cerebral connectivities. The SPM map represents spatial distribution of coherence with the left primary motor cortex as reference region. Only areas with P < 0.05 (corrected, one-sample t test) are shown. Note that left thalamus and right cerebellum are projected to the left surface for easier visualization. The dominant coupling direction (mean DI) is indicated by arrows. Talairach–MNI coordinates are (−35–27 53) for M1, (−40 20 32) for PMC, (−13–25 6) for thalamus, (20 −61–27) for cerebellum.

Table 2.

Summary of cerebral connectivities

From	To
	M1	PMC	Thalamus	Cerebellum
M1	–	0, 29	0, 17	0, 17
PMC	0, 24/6	–	0, 17	0, 16
Thalamus	−0, 32/6	0, 25/6	–	0, 18
Cerebellum	−0, 15/6	0, 10/3	0, 28/7	–

The coupling strength between brain areas is quantified by the mean synchronization index ρ above the diagonal of the table. Fields below the diagonal show the mean DI and the number of subjects with the same sign of the DI as the mean DI (i.e., the dominant direction). 

The time courses of activity in the coherent areas were subjected to a synchronization analysis quantifying the strength and direction of coupling (Table 2). All coherent areas showed significant phase synchronization. The dominant coupling direction led from cerebellum to thalamus, to PMC, to M1, to cerebellum. Cortico–muscular and cerebro–cerebral coupling was evident not only during self-paced movements but—to a lesser extent—also during paced movements with and without visual feedback.

Discussion

The results of the present study show that synchronized 6- to 9-Hz oscillatory activity in the cerebello–thalamo–cortical loop modulates output of the primary motor cortex resulting in pulsatile velocity changes of slow finger movements, which in turn cause oscillatory input to sensory cortex and cerebellum.

Thus, our findings refine and corroborate existing hypotheses of motor control during slow movements in general and the origin and functional significance of 6- to 9-Hz movement discontinuities in particular. Slow movements seem to consist of successive “micromovements,” which are carried out as an agonist burst followed by an antagonist burst. This possibly preprogrammed command pattern is corrected and adjusted by the evaluation of sensory information. Indeed, the afferent signal contains a separate coding of deceleration and acceleration (10), thus allowing for accurate shaping of the discrete pulsatile motor output by adjusting the relative amplitude and timing of both bursts.

Because of its properties, the cerebello–thalamo–cortical system is an appropriate candidate for this task. The cerebellum subserves the optimization and correction of ongoing movements by using sensory information (11, 12), provides accurate timing for movements (13, 14), and influences magnitude and timing of agonist and antagonist muscle activity (15–17). Our results indicate that the cerebellum plays an important role in the generation of 6- to 9-Hz discontinuities. Afferent input, which is reflected in the coupling from muscle to cerebellum, provides the necessary information for the control of ongoing movements. The coupling from M1 to cerebellum likely represents the efference copy, which is needed to predict the consequence of motor output.

A 10-Hz clock involving the cerebellum has been suggested to play a role for motor timing (18). The frequency of the 6- to 9-Hz cerebello–thalamo–cortical synchronization in the present study is strikingly similar. It is therefore tempting to regard the 10-Hz range as a fundamental frequency for the motor system to synchronize oscillatory activity of spatially separate areas, resembling the function of gamma-band synchronization in perceptual binding (19). This hypothesis receives further support from reports of 6- to 9-Hz discontinuities in slow movements of wrist (2) and eyes (3), which thus do not entirely depend on biomechanical properties but seem to reflect a fundamental feature of the motor system. The requirements of limited computational load and the necessity for a stable and robust control loop in the presence of delays in sensory and motor pathways may favor or even demand discrete motor control.

Here, we have shown that the 6- to 9-Hz frequency paces slow finger movements through a cerebello–thalamo–cortical loop. We propose that the 6- to 9-Hz oscillations represent the neural mechanism of intermittent motor control, providing common timing for synergistic muscles, which ensures constant duration of micromovements across muscles.

Abbreviations

MEG

magnetoencephalography

DICS

dynamic imaging of coherent sources

EMG

electromyogram

PMC

premotor cortex

DI

directionality index

Spatial Filter

DICS uses one spatial filter in the frequency domain for the computation of tomographic coherence maps and another spatial filter in the time domain for the computation of time courses of activations of selected areas. The spatial filters represent linear transformations whose characteristics are defined by the transformation matrix A. The transformations used here are solutions of a constrained minimization problem (4) where the output power of the transformed signal is minimized subject to the constraint that the activity at the point of interest is passed with unit gain. The output thus represents the activity of the point of interest irrespective of the activity of other areas (20).

In the frequency domain the transformation for point r at frequency f is.

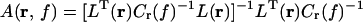1

with C_r(f) = C(f) + α I, where C(f) is the cross spectral density matrix at f, I is the unit matrix, α is the regularization parameter, and superscript T indicates the matrix transpose. The columns of L(r) contain the solution of the forward problem for two orthogonal tangential unit dipoles at r. The forward problem is solved numerically by using a realistic boundary element model.

Coherence between two points r₁ and r₂ is computed as the squared absolute cross spectrum of the activity of both areas c(r₁,r₂,f) divided by the product of their individual power spectra c(r₁,r₁,f) c(r₂,r₂,f). c(r₁,r₂,f) is computed according to

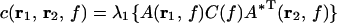2

where λ₁ indicates the largest singular value of the expression in braces and A* represents the complex conjugate of A.

In the time domain transformation the cross-spectral density matrix is replaced by the moment matrix of the data. Matrix A can than be applied to the measured data to get the time series of the activation.