Abstract
Wear is the main failure mode of small modulus gear. Due to the influence of the installation error, tolerance grade and lateral clearance, the wear process has randomness and slow time-varying characteristics, which leads to its reliability changing with time, and the requirements of different precision grades will bring great challenges for design and use. To solve this problem, this paper proposes a dynamic reliability model for small modulus gears based on Wiener process, and predicts the residual life of small modulus gear by analyzing the change rule of reliability. Firstly, the numerical simulation results demonstrate that the wear process of the small modulus gear conforms to the Wiener process with a drift coefficient, and the regression model is used to analyze the wear at each position of the tooth profile. Secondly, by integrating the basic Wiener process model, a dynamic reliability model for gear wear is established using the Fokker–Planck–Kolmogorov (FPK) equation. Thirdly, considering various precision grades, the dynamic reliability of wear under different accuracy requirements is solved, the rule of its reliability is analyzed and the residual life is calculated to optimize the design parameters of the small modulus gear while considering the precision grades. This is beneficial for the design and selection of small modulus gears, thereby improving their reliability and service life.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-025-09419-8.
Keywords: Small modulus gear, Tooth surface wear, Dynamic reliability, Wiener process
Subject terms: Mechanical engineering, Statistics
Introduction
Small modulus gears are widely used in aerospace1–3, medical equipment4 and other fields due to their compact structure and high transmission efficiency. Compared with standard involute gears (modulus greater than 1 mm), higher requirements for the selection of accuracy grades for small modulus are put forward due to their delicate structure. When the design tolerance is unreasonable or the assembly error is large, it may lead to severe wear of the tooth surface, tooth bending, tooth root fracture, etc5,6. Among them, wear is one of the most common failure modes of small modulus gears. To ensure the stable operation of mechanical equipment, it is of great significance to analyze and evaluate the wear of transmission devices. However, the wear process is affected by a large number of random factors, which brings great difficulties to wear modeling and reliability analysis.
Currently, research on wear reliability has been predominantly focused on static reliability, where the reliability of components is assumed to be constant. However, the reliability of components varies over time due to the influence of numerous random factors, such as material properties, initial state and lubrication conditions7,8. Therefore, it is necessary to consider the time-varying characteristics when studying the wear reliability of small modulus gears. Sarper et al.9 analyzed the rule of the reliability of each component in a single-stage cylindrical gear transmission system changing with time. On the basis of nonlinear fatigue damage accumulation theory, Lin et al.10 proposed a prediction model of gear residual strength, and established a dynamic reliability function for gears. The curve of reliability with time was obtained JC method. Considering the time dependence and randomness of the wear process, Liu et al.11 established a dynamic reliability model and a life probability distribution model for rapid prediction of wear, which provided a quantitative idea of wear reliability for engineering applications.
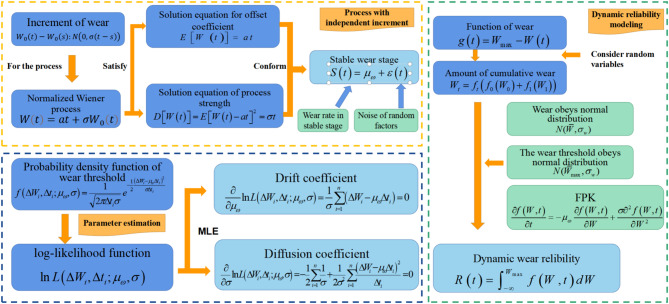
With the development of stochastic process theory, an increasing number of stochastic process modeling methods have been applied to gear wear process description and wear dynamic reliability12,13. Mainstream stochastic process modeling methods for wear degradation include the Wiener process14,15, the Gamma process, etc. The degradation modeling based on the Gamma process is applicable only in cases where the degradation trajectory of the equipment is strictly monotonous. In contrast, the Wiener process is highly effective for addressing nonlinear degradation behaviors, making it more suitable for complex wear processes. Moreover, the parameter estimation of the Wiener process is relatively simple, with good mathematical properties that facilitate the use of methods such as maximum likelihood estimation, making it easier to calculate the system’s remaining useful life and reliability. Additionally, the Wiener process has flexibility and extensibility, allowing for the introduction of random effects or nonlinear extensions to adapt to complex degradation processes. Consequently, the degradation modeling approach based on the Wiener process is more appropriate for such scenarios. And the Wiener process assumes that increments are independent within two non-overlapping time intervals, providing a more accurate description of the mean, variance and auto-correlation function of the wear-related stochastic process16.
There are many research gaps in current reliability modeling techniques. The first is the difficulty of parameter estimation. The Wiener process model relies on two unknown parameters: the drift coefficient and the diffusion coefficient. For small modulus gears, it is challenging to determine these parameters due to environmental noise and measurement errors. The second is the determination of wear thresholds. There is no unified standard for determining wear thresholds. In current gear wear reliability analyses, wear thresholds are primarily determined through empirical methods, which leads to issues with the accuracy of reliability predictions. Moreover, the wear process is affected by random factors such as temperature and lubrication, resulting in non-monotonic degradation trajectories. Based on the above, degradation modeling based on the Wiener process is more suitable for such scenarios, but the application of this method in current research is not yet widespread. Current research mainly focuses on static reliability models, particularly the stress-strength interference model. Although some studies have explored dynamic reliability in terms of strength degradation over time, other key time-varying factors are often overlooked. However, in actual operation, other time-varying factors, including gear wear, play a significant role. Therefore, it is essential to incorporate these additional time-varying factors into the analysis and study dynamic reliability. In view of the above problems, this paper introduces Wiener process analysis on the basis of numerical simulation, and models and analyzes the wear dynamic reliability of small modulus gears according to the requirements of different tolerance grades in the gear design manual.
Some scholars have also conducted extensive research on the innovation of the Wiener process. Wang18 took the gearbox of a high-speed EMU as the research object, and realized the performance degradation modeling and reliability analysis of gearbox based on Wiener process and machine learning method. Long et al.20 structurally integrated the bidirectional GRU model with Wiener process to estimate the remaining service life of bearings from the perspective of information fusion theory. Taking the bearing wear of a helicopter transmission device as an example, Zhao et al.19 applied a wear degradation model of multi-stage Wiener process based on historical degradation data, and verified the applicability of the proposed method. Zhang et al.21 established the relationship between wear volume, degradation characteristic life and drift parameters by combining the two-dimensional Wiener process with the wear model, and verified the efficiency of the proposed method. Shang Wei et al.22 studied the traction components of high-speed trains and used the Wiener process to model the degradation data of locomotive wheel wear, and conducted dynamic reliability analysis. Therefore, on the basis of the numerical simulation of wear, considering the influence of the accuracy level (tolerance level, types of lateral clearance) of small modulus gears, the Wiener process performance degradation modeling method is used to model the random wear process, and the wear reliability and wear life of gears under different accuracy levels are comprehensively evaluated.
The major contributions of our study concentrate on the following aspects: (1) Proposed a Wiener process-based dynamic reliability model for small module gears, offering a probabilistic prediction method for gear wear life and verifying the model’s applicability to describing the wear process of small module gears. (2) Quantified the relationship between tolerance grades and lateral clearance types with the wear life of small module gears, and a gear optimization design scheme that meets dynamic reliability requirements was proposed, providing reference for design and selection. The main contents of this paper are as follows: “Introduction” briefly describes the background and significance of this paper, and expounds the random factors of gear wear and the dynamic reliability technology of wear. “Modeling and analysis of small modulus gear wear considering friction factors” discusses the influence of randomness factors in the meshing process of small module gears, demonstrates that the gear wear process conforms to the Wiener process with drift coefficients, establishes a wear process model for micro planetary reduction devices based on the Wiener process, and proposes a model basis for estimating wear reliability and wear residual life. “Dynamic reliability analysis of small modulus gear wear based on Wiener process” establishes a reliability model of small modulus gear wear based on the FPK formula. The wear dynamic reliability and wear residual life of small modulus gears are analyzed and evaluated, and the better tolerance parameters that satisfy the design life of the equipment are selected. Section 4 summarizes the main work of the thesis. The main process of the full text is shown in Fig. 1.
Fig. 1.
The flow chart of the overall structure.
Modeling and analysis of small modulus gear wear considering friction factors
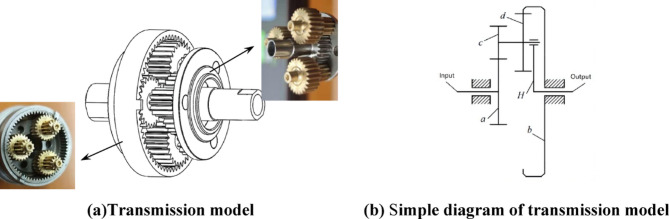
Many random factors such as initial state of the tooth surface, gear material, lubrication condition and friction temperature causes the wear process to exhibit obvious randomness and time-varying characteristics23.Therefore, considering the influence of these random factors, the wear process is considered as a random process for quantitative analysis to more accurately reflect the actual wear situation24–27.The research object of this paper is a small modulus planetary gear transmission device, as shown in Fig. 2. The specific parameters are shown in Table 1.
Fig. 2.
Transmission diagram of the compound planetary gear train.
Table 1.
Basic parameters of the miniature planetary transmission device.
| Basic parameters | Value | Basic parameters | Value |
|---|---|---|---|
| Module m/mm | 0.4 | Tooth width of a-c b/mm | 6.3 |
| Number of teeth za of sun gear a | 29 | Tooth width of d-b b/mm | 4 |
| Number of teeth zc of compound Planetary gear c | 12 | The coefficient of displacement x1 of sun gear a | − 0.6 |
| Number of teeth zd of compound Planetary gear d | 24 | Coefficient of displacement x2 of planetary gear c | 0.5 |
| Number of teeth zb of outer ring gear b | 65 | Coefficient of displacement x3 of planetary gear d | -0.05 |
| Pressure angle α/(°) | 25 | Displacement coefficient x4 of outer ring gear b | 0 |
Wear process analysis and basic wear model
Most of the degradation in engineering practice can be described by stationary stochastic processes28. However, in the actual working process, many factors affecting wear are random throughout the whole wear process, and sometimes this randomness increases or decreases with the passage of time, which constitutes the non-stationarity of the wear process. The Wiener process is a typical non-stationary random process. The application of the Wiener process to gear wear is based on four fundamental assumptions: (1) Independent increment assumption: The wear increments are independent of each other in non-overlapping time intervals. This means that the wear amount in any two non-intersecting time periods are independent random variables. (2) Gaussian increment assumption: The wear increments follow a Gaussian distribution. This implies that the wear amount in any time interval can be considered as a normally distributed random variable29. (3) Stationarity assumption: In the stable wear stage, the statistical characteristics of the wear process, such as the mean and variance, are time-invariant. This means that the wear process maintains a relatively stable state over a long period, with the mean and variance not changing significantly over time. And in the prediction of railway track wear and the service life of rolling bearings, this assumption has been validated in the research30. (4) Linear relationship assumption: The wear amount is approximately linearly related to time. This implies that in the stable wear stage, the wear amount can be expressed as a linear function of time21. Let 
denote a Wiener process, and its mathematical model can be expressed as
 |
1 |
where 
follows a normal distribution with parameters 
, in which the parameter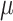 
is the drift coefficient and the parameter 
is the diffusion coefficient.
denotes the standard Brownian motion, that is, 
, then 
has the following basic features:
satisfies the requirement of an independent incremental process, and for any 
, the incremental 
has the same distribution density function.For any
, the increment 
has a Gaussian distribution density function.
 |
2 |
-
3
For the wear process, after entering the stable wear stage, the wear rate is approximately constant, and the wear loss and its fluctuation value within a fixed time interval remain unchanged, which basically conforms to the description of the Wiener process, where the drift coefficient 
can represent the wear rate. In particular, when the Wiener process is used to describe the random wear process, the two key unknown parameters (the drift coefficient 
and the diffusion coefficient 
) can be estimated according to the actual engineering experience or numerical simulation results.
The description of the random wear process needs to meet the following basic assumptions: (1) After a short running-in period, the friction pair enters a stable wear stage; (2) The wear state of the stable wear stage is continuous and uniform. From the above analysis, the average wear rate of the stable wear stage is stable, denoted as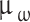 
, and the influence of random factors in the process is denoted as 
, so the stable wear stage can be expressed as
 |
3 |
In the Eq. (3), the deterministic trend process 
is a constant term, which is determined by the working state, material properties and working environment.According to the characteristics of the wear process, process 
is generated by a large number of microscopic factors during wear, which can be defined as a random noise term with a mean value of zero.In the small modulus wear process model, the key is to determine the random noise term.
The cumulative wear of the gear tooth surface at time t is 
. If the wear generated by various random factors during the running-in period is not considered, according to the basic assumption (2), the random process 
is differentiable, and its derivative is still a random process.The expected function relationship between the stochastic process 
and its derivative can be expressed as
 |
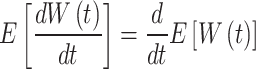4 |
 |
5 |
The above formulas satisfy
 |
6 |
According to Eqs. (5) and (6), combined with the definition and description of the Wiener process, 
is a Wiener process, where the mean value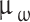 
of the wear rate in the stable wear stage is the drift coefficient of the Wiener process, and 
is the diffusion coefficient in the Wiener process. According to the properties of the above Wiener process, if 
, there are wear increments 
at each time interval that are independent of each other, and these independent increments obey the Gaussian distribution. According to probability theory, the joint distribution of 
is also Gaussian, and the wear process is also Gaussian. The amount of cumulative wear 
at time t can be expressed as
 |
7 |
where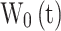 
is the integral of Gaussian white noise 
of the normalized Wiener process, expressed as
 |
8 |
The one-dimensional distribution probability density function of cumulative wear, which is the basic model of the wear process, is represented as
 |
9 |
For increment 
 |
10 |
According to the above analysis, the wear process generally conforms to the Wiener process, so that Wiener process model is used to describe the wear process in the paper. To use the exact Wiener process to describe the process of gear wear, it is necessary to estimate the two parameters of the drift coefficient and the diffusion coefficient.
For worn gears, the amount of wear at the initial time 
is recorded as 
, and the corresponding amount of wear at time 
is recorded as 
, respectively. Note that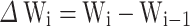 
represents the wear of the gear at time 
. On the basis of the properties of the Wiener process, it can be inferred that
 |
11 |
Then, the likelihood function can be expressed as
 |
12 |
The logarithmic likelihood function can be expressed by taking the logarithm of Eq. (12).
 |
13 |
The derivation of the parameter can be expressed as
 |
14 |
The maximum likelihood estimates of the drift coefficient 
and the diffusion coefficient 
are expressed as
 |
15 |
Stochastic process modeling of small modulus gear wear
To obtain the drift coefficient and diffusion coefficient, this paper combines the numerical simulation results, and the data comes from our contribution to the ABAQUS finite element simulation31.We establish a wear analysis framework based on Archard wear model and Hertz contact theory. Considering the influence of the installation error and position tolerance, starting from the small screw displacement (SDT) and space coordinate transformation theory, the tooth contact analysis (TCA) model of a small modulus gear is established, and the tooth surface wear law of a small modulus gear is obtained by numerical analysis and the finite element analysis method[Appendix C]. The results show that when the installation error is large, the contact trajectory deviates greatly from the standard installation, the contact stress and amount of wear will increase, and the wear life of the standard installation is approximately 2.5 times that of the limit installation position. The wear calculation and analysis process is shown in Fig. 3.
Fig. 3.
Overall framework for wear analysis of small module gears28.
Moreover, the maximum likelihood estimation (MLE) method is used to estimate the two parameters of drift coefficient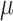 
and diffusion coefficient 
on the basis of the numerical simulation results31. The reason for choosing the Maximum Likelihood Estimation (MLE) method for parameter estimation is that it has a mature calculation method and excellent statistical properties. MLE can well adapt to the assumption that the wear process conforms to a Wiener process, providing accurate parameter estimates. Moreover, by introducing Gaussian white noise terms, MLE can effectively handle the randomness in the wear process, making the model more closely match the actual wear conditions. When estimating the drift coefficient and the process intensity, if the initial values are not chosen appropriately, it can lead to inaccurate estimation results, which in turn affect the subsequent reliability analysis and life prediction. Moreover, MLE is typically based on some strict assumptions. In practical applications, the random noise in the wear process may not fully conform to the assumption of Gaussian white noise, or the wear data may exhibit certain correlations, all of which can impact the results of the MLE. The fitting results of the numerical simulation curve are shown in Appendix A, and the fitting function is a quadratic polynomial and relatively stable, in which the order of magnitude of the quadratic term coefficient reaches 
or even smaller, so the quadratic term can be ignored, and the amount of wear is approximately linearly related to time. Considering the influence of a large number of micro random factors in the running-in stage and stable wear stage, a random noise term with a mean value of zero and a variance of 
, as well as a random noise term with a mean value of zero and a variance of 
are introduced into the numerical simulation results of the two-stage transmission respectively. The parameter estimation values of each position of the gear are shown in Appendix B. Our results demonstrated that when the noise term is introduced, the mean value of the drift coefficient changes little, which indicates that the development trend of wear is not affected by the noise term. The parameter estimation of the diffusion coefficient increases, which indicates that when the randomness is fully considered, the wear process of the gear will change from the original relatively stable process to a relatively non-stationary process.
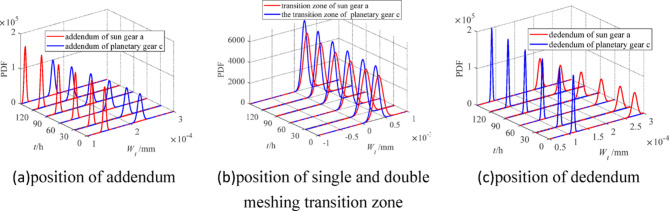
Taking transmission a–c as an example for analysis, according to Eq. (8), the Wiener basic model and incremental change process of each addendum, single and double meshing transition zone and dedendum are obtained without introducing a random noise term, as shown in Fig. 4.
Fig. 4.
Wear of gears in different positions of transmission a-c.
Figure 4a shows that over time, the average increment of the addendum of the sun gear a and the planetary gear c gradually decreases, which is due to the decrease in the time step of the transmission a–c reaching the single wear threshold each time during the numerical simulation. From Fig. 4b, the results confirm that the mean value of the independent increment of the fixed time interval at the transition between the single and double meshing zones of the sun gear a and the planetary gear c remains relatively stable, but the variance of the independent increment of the planetary gear c is smaller than that of the sun gear a. It can be deduced from Eq. (15) that this is because the wear of each time step of the planetary gear c is relatively small, which makes it possible to have relatively large changes, thereby affecting the estimated value of diffusion coefficient 
.From Fig. 4c, the results confirm that the mean and variance of the independent incremental process at the dedendum of each gear are basically consistent with the change trend at the addendum of the tooth, which indicates that the independent incremental process at both the dedendum and the addendum is relatively stable and consistent with the numerical simulation results. In general, the mean and variance of the independent increment in the wear process are very small, which indicates that the wear loss based on the numerical simulation is relatively stable according to the Wiener process principal, and its randomness is not significant, as well as the trend is basically the same as that in Appendix A. The independent increment process at the transition of the single and double meshing zones is more obvious than that at the dedendum and addendum of the tooth, which further explains the approximate linear relationship between Fig.A.1 and Fig.A.2 and the nonlinear relationship of Fig.A.3.
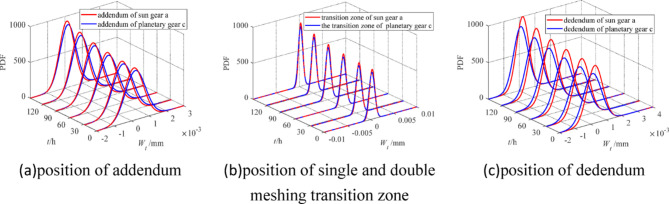
Figure 5 shows the Wiener basic model and incremental change process of each position of the gear when the noise random term is added. Compared with Fig. 4, the mean value of the wear process is not significant, but the randomness of the wear in the independent incremental process is greater, which is consistent with the parameter results of Appendix B.
Fig. 5.
Wear of gears in different positions of transmission a–c after adding noise.
Assuming that the tooth surfaces of the gear are measured, the number of tooth surfaces is denoted as m, and for tooth surface j, the initial wear at time 
is denoted as 
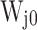. At times 
,the corresponding wear amounts are denoted as 
, respectively.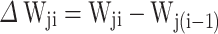
is the amount of wear of the gear at time 
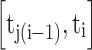, and Eq. (12) can be expressed as
 |
16 |
According to the maximum likelihood estimation method, the drift coefficient 
and diffusion coefficient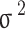 
can be expressed as follows
 |
17 |
Dynamic reliability analysis of small modulus gear wear based on Wiener process
For small module planetary gear transmission devices, it is required to operate smoothly, safely, and reliably during use. Reliability analysis of this type of transmission device can provide reference for design on the one hand, and on the other hand, it can predict the dynamic reliability and remaining life of the device, providing a reference for improvement of the design. The wear reliability analysis process based on Wiener process is shown in Fig. 6.
Fig. 6.
Flow chart of the reliability calculation.
Wear reliability modeling based on wiener process
Wear is a time accumulation process. When modeling the wear reliability, the key is to measure the relationship between the time-varying wear and the maximum allowable wear (wear threshold). When the amount of cumulative wear reaches the wear threshold, it is considered that the parts have wear failure.In engineering practice, the wear threshold 
is generally a random variable, and its distribution law satisfies 
, the mathematical expectation is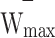 
, and the standard deviation is 
. Assuming that the actual amount of wear also submits to the normal distribution, the probability density function is expressed as
 |
18 |
The wear reliability can be expressed as
 |
19 |
represents the cumulative wear of tooth surface, which is composed of the wear of the running-in period and the wear of the tooth surface in the stable wear stage. Hence, the wear failure probability can be expressed as
 |
20 |
The wear reliability at time t can be expressed as
 |
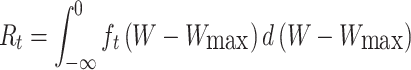21 |
Before the gear reliability modeling, the following assumptions are made: (1) The gear strength decays continuously and steadily with time, and the wear speed is uniform in the stable wear stage; (2) The noise term caused by a large number of microscopic random factors is regarded as Gaussian white noise.
According to Eq. (20), the reliability or failure probability of gears at time t can be determined by the probability density function 
of the wear process, which can be determined by Eq. (22):
 |
22 |
The boundary condition of Eq. (22) is expressed as
 |
23 |
Equation (23) shows that 
is a free boundary condition and 
is a Dirac function.The probability density function 
of the wear process 
can be obtained by the simultaneous Eq. (22) and Eq. (23),which can be expressed as
 |
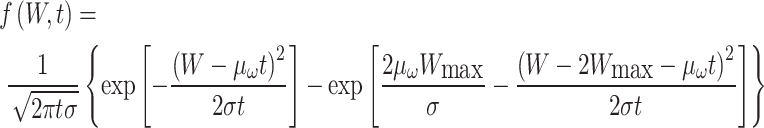24 |
where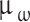 
represents the average wear rate, and 
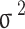represents the diffusion coefficient. Substituting Eq. (24) into Eq. (19), the reliability of gear wear process can be expressed as
 |
25 |
Substituting Eq. (25) into Eq. (20), the failure probability distribution function can be expressed as
 |
26 |
It can also be expressed as
 |
27 |
If 
and 
, then Eq. (27) can be converted into
 |
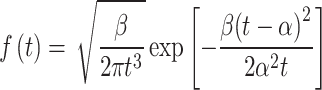28 |
The above derivation reveals that the failure probability density function is an inverse Gaussian distribution. If the wear threshold 
is considered as a constant in the analysis of wear reliability, the distribution is determined only by the drift coefficient 
and diffusion coefficient 
of the Wiener wear process.
Wear reliability analysis of the small modulus gear
When the reliability analysis considering wear degradation is carried out, it is usually considered that the part fails when the degradation reaches the safety threshold for the first time. However, there is no uniform standard for the determination of wear threshold. In the current research, the threshold is determined mainly by empirical method, maximum tooth thickness deviation method and maximum lateral clearance method in the analysis of gear wear reliability. This paper takes transmission a–c as an example for reliability analysis, the simulation parameter settings can refer to Appendix C, and other numerical simulations and finite element comparisons can be found in reference31.
Reliability analysis based on empirical method
Reference31 noted that for standard gears, failure occurs when the wear depth exceeds 5% of the tooth thickness. For small modulus gears, higher wear thresholds are required due to their precise structure.
 |
29 |
The failure probability density function and life reliability distribution of sun gear a and planetary gear c can be obtained from the formula, as shown in Fig. 7.
Fig. 7.
Failure probability density distribution and reliability of transmission a–c.
From Fig. 7, the results confirm that compared with the wear life of the sun gear a, the wear life of the planetary gear c is longer than that of the sun gear a. The reliability and wear life at the dedendum of the addendum of the sun gear a are both smaller than those at the addendum of the tooth, and the reliability and wear life at the transition between the single and double meshing zones are the smallest. According to Section 2, this is because the amount of wear at the transition between the single and double meshing zones is the highest. The reliability and wear life at the tip of the planetary gear c are less than those at the dedendum of the tooth, and the transition between the single and double meshing zones is the smallest. According to the minimum weak link theory32, the sun gear a is used as the reliability and life evaluation standard of the transmission device. When the reliability is 99%, the wear life of the transmission device is approximately 110 h.
Reliability analysis based on the maximum tooth thickness deviation method
Simply using the empirical method for reliability evaluation and analysis can only predict the empirical life of the gear pair. And small modulus gears need to consider their tolerance level design in the design process. The wear threshold can be determined according to the allowable tooth thickness deviation of the gear accuracy level. When the tooth surface wear reaches the maximum tooth thickness deviation, it is considered that the gear has experienced wear failure. Considering the influence of running stability, operating requirements and initial deviation, this paper takes one-third of the maximum tooth thickness deviation as the wear threshold. The upper and lower deviations of the tooth thickness of the small modulus gear can be expressed as
 |
30 |
where 
represents the upper deviation of the average length of the common normal line, 
represents the lower deviation of the average length of the common normal line, and the upper and lower deviations of the average length of the common normal line can be found according to GB/T 2363-1990.Taking the gear with a pitch circle diameter of less than 26 mm, a modulus of less than 0.5 mm, and a lateral clearance type f as an example, the upper and lower deviations of the average length of the common normal of different precision grades and the upper and lower deviations of the tooth thickness are shown in Appendix D. Figure 8 shows the failure probability density distribution of wear and life-reliability curves of the gear at the transition between the single and double meshing zones of the transmission a–c.
Fig. 8.
Failure probability density distribution and reliability of the transition between the single and double meshing ares of transmission a–c.
Similar to the empirical method, Compare Fig. 8a–d, the wear reliability and wear life of planet gear c are greater than that of sun gear a. Considering that when the wear of the gear is high, it may lead to the phenomenon of unstable motion of the gear pair during the meshing process. Therefore, for the transmission device with high stability, the stability and safety of equipment operation should be considered comprehensively when selecting the tolerance grade of group I, so as to avoid vibration and impact between gear pairs caused by excessive tooth thickness deviation. For this type of device, the medium tolerance grade (grade 7, grade 8) can be selected while ensuring the service life. For the high-precision transmission device of the consumption type, the tolerance grade can be more stringently required, and the wear detection and replacement of the gear of the transmission device can be carried out when the estimated service life is reached.
Reliability analysis based on maximum clearance method
The above two evaluation criteria are all constraints on the wear of a single gear of the transmission device. In practice, more attention should be given to the common wear reliability and life of a pair of meshing gear pairs. The maximum lateral clearance method is a requirement for a pair of meshing gear pairs. During the wear development process, the gears that mesh with each other are worn. When the total wear exceeds the allowable value of the maximum lateral clearance, the accuracy of motion transmission and load transmission will be affected, which is considered as wear failure. The minimum lateral clearance 
of the gear pair is specified in GB/T 2363-1990.Table 2 shows the minimum lateral clearance value under the requirements of different lateral clearance types when the center distance is less than 12 mm. However, there is no clear stipulation on the maximum lateral clearance in the national standard. In fact, with the wear of the gear pair, the lateral clearance of the gear pair will continue to increase, which will affect the transmission accuracy, vibration noise and so on. Especially for the gear transmission with precision, high stability and high reliability requirements, it is particularly important to stipulate the maximum lateral clearance. In addition, the lateral clearance of the gear pair is also related to the installation error. When the tight center distance is used for installation, it is difficult for the lubricating oil to enter the surface of mutual meshing, resulting in a large friction and temperature rise. At this time, the minimum lateral clearance needs to be reached; when the loose center distance is installed, vibration impact problems can easily occur.
Table 2.
Value of the minimum lateral clearance 
(GB/T 2363-1990)
| Types of lateral clearance | g | f | e | d |
|---|---|---|---|---|
|
6 | 9 | 15 | 22 |
The maximum lateral clearance requirement can be calculated by the practical formula, which is expressed as
 |
31 |
where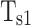 
and 
represent the tooth thickness tolerances of the gear pair respectively, 
represents the center distance tolerance, and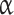 
represents the gear pressure angle. According to GB/T 2363-1990, the center distance tolerance of the gear is subject to tolerance grade I. Table 3 shows that the center distance of the gear pair is less than 12 mm, and the center distance tolerance and the maximum lateral clearance requirements under different tolerance grade I under the precision of the lateral clearance grade f .
Table 3.
Center distance tolerance and maximum clearance requirements under different accuracy levels.
| Tolerance grade I | Center distance tolerance
|
Maximum lateral clearance 
|
|---|---|---|
| 6 |
|
19.85 |
| 7 |
|
25.9247 |
| 8 |
|
29.6021 |
| 9 |
|
36.2667 |
The amounts of wear of sun gear a and planetary gear c at time t are 
and 
, respectively, and the total wear at time t is 
.According to Wiener random process theory, the drift coefficient and diffusion coefficient of different meshing regions are obtained as shown in Table 4.
Table 4.
Parameter Estimation of the total wear of gear pair a–c.
| Gear pair | The position of meshing | Drift coefficient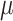 
|
Diffusion coefficient 
|
|---|---|---|---|
| a–c | The addendum of sun gear a and the dedendum of planetary gear c |
|
|
| The transition zone of sun gear a and planetary gear c |
|
|
|
| The dedendum of sun gear a and the addendum of planetary gear c |
|
|
As an example, the probability distribution function and reliability of gear wear failure for lateral clearance type f at the transition meshing region of a single and double meshing zone are shown in Fig. 9.
Fig. 9.
Failure probability density distribution and reliability of the transition zones of sun gear a and planetary gear c (lateral clearance types of f).
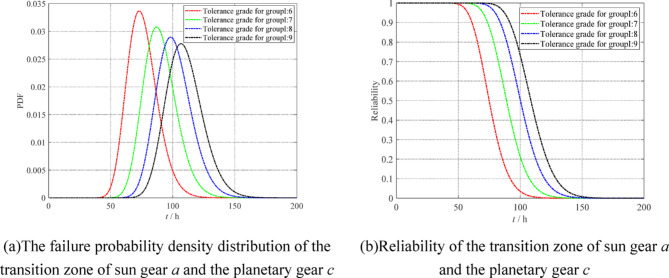
Consistent with the gear analysis process of the lateral clearance types of f, the failure probability distribution function and reliability of gear wear at the transition a–c of single-double meshing zone with lateral clearance types of g, e and d are obtained as shown in Figs. 10, 11 and 12.
Fig. 10.
Failure probability density distribution and reliability of the transition zones of sun gear a and planetary gear c (lateral clearance types of g).
Fig. 11.
Failure probability density distribution and reliability of the transition zones of sun gear a and planetary gear c (lateral clearance types of e).
Fig. 12.
Failure probability density distribution and reliability of the transition zones of sun gear a and planetary gear c (lateral clearance types of d).
With the change of the type of lateral clearance, the minimum lateral clearance of the gear pair gradually increases, which is beneficial for lubrication. However, at this time, on the one hand, the allowable maximum lateral clearance becomes larger, and on the other hand, the allowable wear of the gear pair also increases, which affects the accuracy of motion transmission and the stability of load transmission. Therefore, for transmission devices with high precision requirements and high consumption, the types of lateral clearance g and f can be selected under the premise of ensuring service life.
From Fig. 8, with the change in tolerance grade of group I, the wear life of the gear pair is approximately two times; From Figs. 9, 10, 11 and 12, with the change in the type of lateral clearance, the wear life of the gear pair varies by approximately 1.8 times.
Life evaluation and accuracy grade selection of the small modulus gear
The design requirement of the micro planetary device involved in this paper is to work for 2000 cycles, and the duration of each cycle is 30s, so the total design life is approximately 17 h. In the initial design, the safety factor n (n = 2.5) may be introduced to measure the influence of the installation error on the wear, so the converted design life should be selected as 45 h.According to the maximum clearance method in “Reliability analysis based on maximum clearance method”, the tolerance requirements, wear reliability and corresponding wear service life of the micro planetary gear transmission device can be optimized as shown in Table 5.
Table 5.
Optimal tolerance and wear reliability of the micro planetary device.
| Tolerance grade I | Center distance tolerance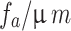
|
Types of lateral clearance | Reliability of wear | Life of wear/h |
|---|---|---|---|---|
| 7 |
|
g / f | 0.9767/0.9981 | 45 |
| 8 |
|
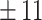
g | 0.9990 | 45 |
According to Table 5, to ensure that the service life of the micro planetary transmission device meets the design requirements, the accuracy grade of the gear can be selected as 7g. At this time, the maximum allowable center distance tolerance of the gear pair is 11 
, the parallelism tolerance in the shaft plane of the gear pair is 9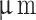 
, and the parallelism tolerance in the vertical plane is 5 
, and the wear reliability is 0.9767.The accuracy grade of the gear can also be selected as 7f, and the tolerance of the gear pair is the same as that of the accuracy level of 7g, and the wear reliability is 0.9981. For the transmission pair with higher reliability requirements, the accuracy grade of the gear can be selected to be 8g.At this time, the maximum allowable center distance tolerance of the gear pair is 11 
, the parallelism tolerance in the shaft plane of the gear pair is 11 
, and the parallelism tolerance in the vertical plane is 6 
,and the wear reliability is 0.9990.
Taking the accuracy grade of 8g as an example, the failure probability of the micro planetary transmission device is 0.001.Considering the functional safety of the transmission device, referring to the relationship between the failure probability and the safety integrity level (SIL)shown in Table 6 of the standard IEC61508, the safety integrity level of the micro planetary transmission device can be obtained as 2, which indicates that the safety of the micro planetary transmission device is higher under this accuracy grade.
Table 6.
Classification of security integrity.
| SIL | 4 | 3 | 2 | 1 |
|---|---|---|---|---|
| Failure probability |
|
|
|
|
Taking the maximum lateral clearance method as the evaluation standard, the wear service life of small module transmission devices under different tolerance grades, different types of clearance and different reliability requirements can be obtained. According to the curve of reliability R in Figs. 9, 10, 11 and 12, the reliability standards are selected as 90%, 95% and 99% respectively, and the service life of the small module transmission device under different tolerance grades and types of lateral clearance is calculated, as shown in Fig. 13. The analysis data are summarized and organized as shown in Table 7.In the process of designing a small modulus transmission device, the accuracy grade of the gear can be selected according to Table 7.
Fig. 13.
Wear service life of small modulus transmission devices with different reliability.
Table 7.
Relationship between the wear service life and tolerance grade.
| Reliability R | Tolerance grade | Center distance tolerance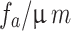 
|
Types of lateral clearance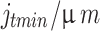 
|
Types of lateral clearance 
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| g | f | e | d | g | f | e | d | |||
| 6 | 9 | 15 | 22 | 6 | 9 | 15 | 22 | |||
Maximum tooth thickness deviation
|
Design and service life of wear/h | |||||||||
| Service life of wear after conversion/h | ||||||||||
| 90% | 6 | 8 | 14 | 17 | 24 | 28 | 39 | 43 | 61 | 76 |
| 15 | 17 | 24 | 30 | |||||||
| 7 | 11 | 21 | 23 | 30 | 33 | 51 | 58 | 74 | 89 | |
| 20 | 23 | 29 | 35 | |||||||
| 8 | 11 | 28 | 29 | 39 | 43 | 61 | 68 | 84 | 97 | |
| 24 | 27 | 33 | 38 | |||||||
| 9 | 18 | 32 | 34 | 46 | 50 | 70 | 85 | 92 | 109 | |
| 28 | 34 | 36 | 43 | |||||||
| 95% | 6 | 8 | 14 | 17 | 24 | 28 | 36 | 40 | 58 | 72 |
| 14 | 16 | 23 | 28 | |||||||
| 7 | 11 | 21 | 23 | 30 | 33 | 48 | 55 | 70 | 85 | |
| 19 | 22 | 28 | 34 | |||||||
| 8 | 11 | 28 | 29 | 39 | 43 | 58 | 64 | 80 | 92 | |
| 23 | 25 | 32 | 36 | |||||||
| 9 | 18 | 32 | 34 | 46 | 50 | 67 | 80 | 87 | 104 | |
| 26 | 32 | 34 | 41 | |||||||
| 99% | 6 | 8 | 14 | 17 | 24 | 28 | 32 | 36 | 52 | 66 |
| 12 | 14 | 20 | 26 | |||||||
| 7 | 11 | 21 | 23 | 30 | 33 | 43 | 49 | 63 | 77 | |
| 17 | 19 | 25 | 30 | |||||||
| 8 | 11 | 28 | 29 | 39 | 43 | 52 | 58 | 73 | 84 | |
| 20 | 23 | 29 | 33 | |||||||
| 9 | 18 | 32 | 34 | 46 | 50 | 60 | 73 | 80 | 96 | |
| 24 | 29 | 32 | 38 | |||||||
Conclusion
In this paper, the wear dynamic reliability analysis and wear life prediction of small modulus gears are carried out on the basis of the Wiener process and determination of three wear threshold methods, which consider the randomness of the wear process .Based on the numerical simulation results of gear wear process, combined with the description and basic model of the Wiener random process, the random reliability model of small modulus gear is established by FPK formula, and the life distribution is given. Combined with the requirements of the gear accuracy grade (tolerance grade, type of lateral clearance), the wear reliability and life of the micro planetary gear transmission device with different accuracy requirements are calculated and evaluated, and the optimal tolerance parameters that meet the design life requirements of the equipment considering the installation error are selected. The main conclusions of this study are as follows :
According to the numerical simulation results, the linear Wiener model is used to analyze the wear rate of small modulus gears. The mean value of the drift coefficient in the Wiener equation represents the wear rate. When the noise term is added, the mean value of the drift coefficient changes little, which indicates that the development trend of wear is not affected by the noise term. The parameter estimation of the diffusion coefficient increases, which indicates that when the randomness is fully considered, the wear process of the gear will change from the original relatively stable process to a relatively non-stationary process. In general, the results of the Wiener process show that the wear rate of each time step is relatively stable, which is consistent with the wear rule of the stable wear stage of the gear.
From the perspective of tolerance, with the change of tolerance level, the wear life of small modulus gear is approximately 2 times different. In order to prevent the phenomenon that excessive tooth thickness deviation and wear from leading to vibration and noise in the device, for a planetary transmission device with high reliability, the medium tolerance grade (grade 7 or grade 8) can be selected while ensuring its service life.
From the perspective of the type of lateral clearance, as the minimum lateral clearance increases, the allowable wear also increases, so that the life of the small modulus gear gradually increases.For the planetary gear transmission device with high reliability and high consumption requirements, tolerance grade of group I of the middle and high grades should be selected, which is beneficial for controlling the minimum lateral clearance of the gear pair, and ensuring the accuracy of motion transmission and the stability of load transmission while ensuring good lubrication.
Considering the tolerance grade and type of lateral clearance of the micro planetary gear transmission device, the optimal precision grade is 7g, 7f or 8g for the micro planetary gear transmission device studied in this paper, which can satisfy the life requirements of the equipment while ensuring high wear reliability.
This research thoroughly examines the impact of randomness in the wear process on the reliability and lifespan of small modulus gears, and investigates the optimization effects of various design parameters (such as tolerance grades and types of lateral clearance) on their wear life. The results indicate that the proper selection of tolerance grades and types of lateral clearance can significantly enhance the service life and reliability of small modulus gears, while ensuring stable operation of the equipment under high precision and high reliability requirements. This research provides a theoretical foundation for the design of micro planetary gear reduction devices and offers new perspectives for the reliability analysis and optimization design of small modulus gear wear in related fields.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
This research was supported by the National Natural Science Foundation of China(grant numbers:52075389),the National Key Research and Development Program of China(grant numbers:2022YFF0607402).
Author contributions
Y.S., Y.L. and C.G. wrote the main manuscript text. Q.Z. and K.C. provided the guidance on software usage. All authors reviewed the manuscript.
Data availability
The data that support the findings of this study are available on request from the corresponding author, upon reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Shuai, M. et al. Research on time-varying meshing stiffness of wind turbine gearbox considering tooth surface wear. Proc. Inst. Mech. Eng.237(7), 1583–1602 (2023).
- 2.Al-Shyyab, K. A non-linear dynamic model for planetary gear sets. Proc. Inst. Mech. Eng. Part k-J. Multi-body Dyn.221(4), 567–576 (2007).
- 3.Experimental investigation of. three-body wear for rubber seals in abrasive slurry environment. Wear. 534, 535205131 (2023).
- 4.Ke, F. J. C. J. et al. A novel vibration-based prognostic scheme for gear health management in surface wear progression of the intelligent manufacturing system. Wear. 522 (2023).
- 5.Zhong, A. et al. A running-in strategy based on an efficient wear simulation model for double circular-arc spiral bevel gears. Proc. Inst. Mech. Eng. Part j-J. Eng. Tribol. (2023).
- 6.Sánchez, M. B., Pleguezuelos, M. & Pedrero, J. I. Influence of profile modification on the transmission error of spur gears under surface wear. Mech. Mach. Theory. 191, 105473 (2024).
- 7.Flodin, A. & Andersson, S. Simulation of mild wear in spur gears. Wear. 207 (1-2), 16–23 (1997). [Google Scholar]
- 8.Wallbridge, N. C. et al. Distribution of wear rate data and a statistical approach to sliding wear theory. Wear. 119 (3), 295–312 (1987). [Google Scholar]
- 9.Sarper, H. Reliability analysis of descent systems of planetary vehicles using bivariate exponential distribution. In Proceedings of the Annual Reliability and Maintainability Symposium, 165–169 (2005).
- 10.Xiaoyan, L. et al. Gear residual strength model and dynamic reliability. J. Harbin Eng. Univ.38 (09), 1476–1483 (2017). [Google Scholar]
- 11.Qin, L., Juan, L. & Yin, L. Modeling and example analysis of wear random process. Acta Armamentarii. 31 (10), 1379–1382 (2010). [Google Scholar]
- 12.Zhu, L. et al. Time-dependent reliability of spur gear system based on gradually wear process. Eksploatacja I Niezawodnosc - Maintenance Reliab.20 (2), 207–218 (2018). [Google Scholar]
- 13.Chen, C. & Wang, H. A novel method for gear gravimetric wear prediction based on improved particle swarm optimization and non-stationary random process probability distribution fitting. Eng. Comput. (2020).
- 14.Zhang, Z. X., Si, X. S., Hu, C. H. & Lei, Y. G. Degradation data analysis and remaining useful life estimation: A review on Wiener-process-based methods. Eur. J. Oper. Res.271 (3), 775–796 (2018). [Google Scholar]
- 15.Ye, Z. S., Wang, Y., ,Tsui, K. L. & Pecht, M. Degradation data analysis using wiener processes with measurement errors. IEEE Trans. Reliab.62 (4), 772–780 (2013). [Google Scholar]
- 16.Songyu, L. & Yabin, S. Research on the wear reliability of the transmission system assembly Ofhelicopter based on wiener process. Helicopter Tech. 2016(03), 6–12.
- 17.Zhou, D., Zhang, X. & Zhang, Y. Dynamic reliability analysis for planetary gear system in Shearer mechanisms. Mech. Mach. Theory, 105244–105259 (2016).
- 18.Tai, W. The Research of EMU Gearbox Reliability Based on Degradation Analysis (Southwest Jiaotong University, 2017).
- 19.Zhao, Z. A., Zhang, Y., Liu, G. J. & Qiu, J. Sample selection of prognostics validation test based on multi-stage wiener process. J. Risk Reliab.233 (4), 605–614 (2019). [Google Scholar]
- 20.Long, W. et al. GRU-AE-wiener: A generative adversarial network assisted hybrid gated recurrent unit with wiener model for bearing remaining useful life Estimation. Mech. Syst. Signal Process. 111663 (2024).
- 21.Zhang, H. et al. Research on two-dimensional Wiener stochastic degradation model based on the wear model. In MATEC Web of Conferences, 169 (2018).
- 22.Wei, S. Reliability and Reliability-based Sensitivity Analysis of Traction Components of High-speed Train (Northeastern University, 2017).
- 23.Bai, Z. F. & Ning, Z. Y. Dynamic responses of the planetary gear mechanism considering dynamic wear effects. Lubricants11 (6), 255 (2023). [Google Scholar]
- 24.Zuo, F. J. et al. Reliability analysis of gear transmission with considering failure correlation. Eksploatacja I Niezawodnosc-Maintenance Reliab.17 (4), 617–623 (2015). [Google Scholar]
- 25.Yuantao, S. et al. Reliability analysis of new RMG lifting driving system based on correlation theory. In International Conference on Advances in Construction Machinery and Vehicle Engineering (2019).
- 26.Wang, X. et al. Remaining useful life prediction based on the wiener process for an aviation axial piston pump. Chin. J. Aeronaut.29 (3), 779–788 (2016). [Google Scholar]
- 27.Xing, J. P. et al. Study on wear dynamic reliability of gear system based on markov diffusive process. J. Tribol. 1–12 (2021).
- 28.Song, J. et al. Study on dynamic reliability of permanent magnet gear transmission system with wear and failure correlation. Eng. Fail. Anal. 131 (2022).
- 29.Wang, Y. et al. Cutting tool wear prediction based on the multi-stage wiener process. Int. J. Adv. Manuf. Technol.129, 5319–5333 (2023). [Google Scholar]
- 30.Guan, Q., Wei, X., Jia, L., He, Y. & Zhang, H. RUL prediction of railway PCCS based on wiener process model with unequal interval wear data. Appl. Sci.10, 1616 (2020). [Google Scholar]
- 31.Yuantao, S. et al. Wear analysis and simulation of small module gear based on Archard model. Eng. Fail. Anal.144 (2023).
- 32.Rajnish, K. et al. Influence of test specimen geometry on probability of failure of composites based on Weibull weakest link theory. Materials. 15 (11), 3911–3911 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author, upon reasonable request.