α-Helical stabilization by side chain shielding of backbone hydrogen bonds

Abstract

We study atomic models of the thermodynamics of the structural transition of peptides that form α-helices. The effect of sequence variation on α-helix formation for alanine-rich peptides, Ac-Ala₂₁- methyl amide (A21) and Ac-A₅ (AAARA)₃A-methyl amide (Fs peptide), is investigated by atomic simulation studies of the thermodynamics of the helix-coil transition in explicit water. The simulations show that the guanidinium group in the Arg side chains in the Fs peptide interacts with the carbonyl group four amino acids upstream in the chain and desolvates backbone hydrogen bonds. This desolvation can be directly correlated with a higher probability of hydrogen bond formation. We find that Fs has higher helical content than A21 at all temperatures. A small modification in the amber force field reproduces the experimental helical content and helix-coil transition temperatures for the Fs peptide.

Detailed all-atom molecular simulation of protein folding has been limited by the inadequacy of sampling and possible inaccuracies of the semiempirical force fields used in classical simulations. The development of techniques for efficient sampling and the refinement of semiempirical force fields are crucial for modeling protein folding, structure prediction, and complex formation. Small peptides have many of the complexities associated with the energy landscape of proteins (1) and are ideal systems to understand the role of competing interactions in determining protein structures. In this work, we study the thermodynamics of the helix-coil transition of short peptides for which ample experimental data exist. We use highly parallel algorithms that enable the efficient sampling of configurational space. We validate our results through comparison with experimental data and test the sensitivity of our results to small changes in the semiempirical force field.

The elucidation of α-helical formation energetics is relevant for understanding protein folding mechanisms. In spite of the large number of experimental studies conducted in peptides, there is still much debate concerning the propensity of Ala residues to stabilize α-helices. Ingwall et al. (2) studied runs of Ala_n, with n = 10–1,000, flanked by Lys runs, and concluded that short (n ∼ 10) sequences of Ala peptides do not form helices in water (2, 3). Similar conclusions were drawn from studies of Ala-rich random sequences. However, short (13–21) Ala-rich peptides containing interior charged amino acid side chains are found to form helices with 70–90% helical content (4–7), and short runs of Ala_n (n = 13) flanked by two ornithine charged amino acid are found to be about 40% helical in water (8, 9). These data have been interpreted in terms of a large intrinsic propensity of Ala residues to form helices in water. Within the Lifson–Roig (10, 11) and Zimm–Bragg (12) models for the helix-coil transition, the intrinsic propensity of an amino acid to form a helix is a measure of the interactions of the amino acid with its own and nearest-neighbor amino acid backbone (11, 13). Theoretical (14) and experimental studies on prenucleated synthetic peptides (15) have suggested that the high helical propensity of Ala-containing peptides is a consequence of the neighboring side chains and is an effect extrinsic to the Ala side chains. Specifically, Vila et al. (14) have argued that the high helical propensity of Ala-rich peptides containing large charged side chains is stabilized by the effect of the side chains in reducing the accessibility of the peptide backbone to water. It has also been argued that backbone desolvation by large side chains is responsible for helix destabilization (16, 17). Theoretical studies suggest that desolvation of the peptide CO and NH groups is energetically unfavorable (18). Atomic simulations of the helix-coil transition of peptides will help elucidate the role of charged side chains in the stabilization of the helical state.

We present all-atom simulations of the thermodynamics of the helix-coil transition with explicit aqueous solvent. Molecular dynamics (MD) simulations have been applied to describe the unfolding of α-helices (19, 20) and helix formation kinetics on short peptides (21–27). Hummer et al. (26, 27) provided a detailed analysis of the helix formation kinetics of pentapeptides of A₅, AAGAA, and G₅, over a broad range of temperatures. The nucleation mechanism was found to be diffusive for helix formation, whereas it showed an Ahrenius behavior for helix breaking. Helix formation (and nucleation) for this pentapeptide showed no temperature dependence, in agreement with the interpretation of nucleation originally described by Zimm and Bragg (12). Recently, Daura et al. (28, 29) published an exhaustive analysis of the helix-coil transition of β peptides by MD simulations. These simulations constitute the most detailed kinetics and stability analysis of the helix-coil transition from MD simulations to date.

We apply the replica exchange MD (REMD) method to the equilibrium folding/unfolding thermodynamics of a 21-aa peptide with a large propensity of forming α-helical structures in water at room temperature. We simulated a 21-residue peptide containing Arg, Ac-A₅ (AAARA)₃A-methyl amide (NMe) (Fs peptide, where Fs stands for folded short), which has been widely described in the experimental literature (30–34). To establish the role of sequence variation in the formation of α-helices, we also simulated a peptide containing only Ala residues, Ac-A₂₁-Nme (A21). The folding of these peptides is completely modeled by the force field, and the results are shown to be independent of initial configurations of the systems. A21 is not easily accessible to experimentation due to its limited solubility. However, sequences containing long runs of Ala flanked by charged amino acids have been widely studied (2, 8, 9).

The explicit treatment of the aqueous solvent with the TIP3P model (35) provides molecular evidence for the stabilization of α-helices by large side chains. Extensive REMD simulations (36, 37) exceeding 1.5 μs of sampling over a broad temperature range (275–550 K) show that peptides containing Arg are significantly more stable than peptides containing only Ala.

The enhanced stability of shielded hydrogen bonds can be explained in terms of the competition for backbone hydrogen bonds between water molecules and backbone donors and acceptors. Thermal fluctuations can cause local opening and closing of backbone CO⋅⋅⋅NH hydrogen bonds. When the local environment is shielded from access to water, the hydrogen bond-breaking event is energetically unfavorable, because the availability of water molecules to participate in favorable H-bonding interactions near unshielded carbonyls can stabilize local opening of the hydrogen bond, as has been observed in crystal structures (38). The destabilization of the water-bridged opened CO⋅⋅⋅NH hydrogen bonds by side chain shielding results in the stabilization of the shielded hydrogen bond conformation, which contributes to the overall stability of helical conformations. The Arg side chain partially shields the carbonyl oxygen of the fourth amino acid upstream from the Arg. The favorable positively charged guanidinium ion interaction with the carbonyl oxygen atom also stabilizes the shielded conformation.

Given the large amount of data on the thermodynamics of the Fs peptide, we validate the adequacy and sensitivity of the force field in describing the helix-coil transition. We find that by applying a small modification of the Cornell et al. (39) force field, we can reasonably reproduce the melting temperature (T) of the Fs peptide. This force field also gives values for the helix propagation and nucleation parameters for Ala measured by Yang et al. (9) but in disagreement with other experimental measurements (2, 3). Our calculations show that the Arg side chain significantly stabilizes the helix state of the Fs peptide, in agreement with Williams et al. (15) and Vila et al. (14). However, we also find that A21 is 34% helical at 275 K, consistent with Spek et al. (8) and in disagreement with an estimate of 1% helical content calculated from the helix nucleation and propagation parameters extracted from measurements by Ingwall et al. and Platzer et al. (2, 3).

Methods

The Ac-A₂₁-Nme peptide is contained in a cubic box containing 2,640 TIP3P water molecules (35). The initial configurations for the replicas are generated by a 1.0-ns simulation of the extended peptide, in vacuo, at 1,000 K. Configurations sampled during the last 0.9 ns are clustered on the basis of their pairwise rms distance (rmsd). We select 32 structures from different clusters. Each of the structures is at least 2.5 Å in rmsd from any structure belonging to other clusters. No biases are imposed regarding secondary structure or energy. The selected configurations are solvated and randomly assigned as initial configurations for the 32 replicas. The dimensions of the solvated system cubic box are each 43.5 Å, which is 1.5 times the linear dimension of the folded α-helix. To test the reliability of the equilibrium sampling, we performed two studies of the A21 peptide, starting from different configurations: random configurations and α-helical configurations.

The Fs peptide [Ac-A₅(AAARA)₃A-Nme] is contained in a cubic box with a side of 43.7 Å containing 2,660 TIP3P water molecules. The Arg residues are modeled in their charged state. The initial configurations are selected from a 1-ns simulation at 700 K of 42 identical solvated systems, starting from an α-helical configuration and random velocities. The helical content of the starting configurations ranges from 15 to 73%. The Fs peptide is simulated in the T range of 275–551 K.

The solvated systems are subjected to 500 steps of steepest-descent energy minimization and a 100-ps MD simulation at constant pressure and temperature, with P = 1 atm (1 atm = 101.3 kPa) and T = 300 K. We use the force field of Cornell et al. (39) and the suite of programs in amber 4.1 (40), modified to include the generalized reaction field treatment of electrostatic interactions (41, 42) (with a cutoff of 8.0 Å) and the REMD algorithm. Nonbonded pair lists were updated every 10 integration steps. The integration step in all simulations is 0.002 ps. The system is coupled to an external heat bath with relaxation time of 0.1 ps (43). All bonds involving hydrogen atoms are constrained by using shake with a tolerance of 0.0005 Å (40). We study the full thermodynamic stability of the Fs and A21 peptides by the REMD algorithm described by Sugita and Okamoto (36, 37). The temperatures of the replicas are chosen to maintain an exchange rate among replicas of 8–20%. Exchanges are attempted every 125 integration steps (0.25 ps).

For A21 with random initial configurations, we simulate 32 replicas with T = 275–456 K, spanning a range of T in which the peptide samples folded and unfolded states. We also simulate 48 replicas with T = 275–501 K for A21 with annealed α-helical configurations. For the Fs peptide, we simulate 42 replicas with T = 275–550 K. We also perform simulations of the A21 (42 replicas with annealed α-helical initial configurations) and Fs peptides (46 replicas with annealed α-helical configurations) by using a modified force field described below. All systems are simulated for 8 ns/replica. The total simulation time for the A21 and Fs peptides is 976 and 704 ns, respectively.

We analyze the configurations generated by the REMD simulations in terms of the backbone (φ, ψ) dihedral angles, helical content, and the coordination number of water molecules to the carbonyl oxygen atoms. Equilibrium quantities, based on ensemble averages at each temperature, are evaluated over the last 4 ns/replica of each simulation. Hydration properties are calculated over the last 1 ns of the trajectories. Block averages over 0.25 ns are performed to estimate errors in the ensemble averages. Unless otherwise specified, we are reporting the results for the 32-replica system for A21 that started from random configurations. We show below that the helical contents as a function of T for both systems are within one standard deviation. Sampled configurations are labeled by a sequence of 21 h or cs, depending on the φ and ψ angles of each amino acid. We labeled (φ, ψ) pairs as hs if the φ = −60 ± 30 and ψ = −47 ± 30 degrees, and as cs, otherwise. Calculations of the helical content follow the Lifson–Roig model, where n (n ≥ 3) consecutive hs make a helical segment of length n − 2. Acetylated and amidated peptides with 21-aa sequence can have a maximum helical length of 19. We expect calculations of the helical content based on local variations in the structure (i.e., from dihedral angles) to be similar to IR and Raman measurements but larger than CD measurements (30).

Results and Discussion

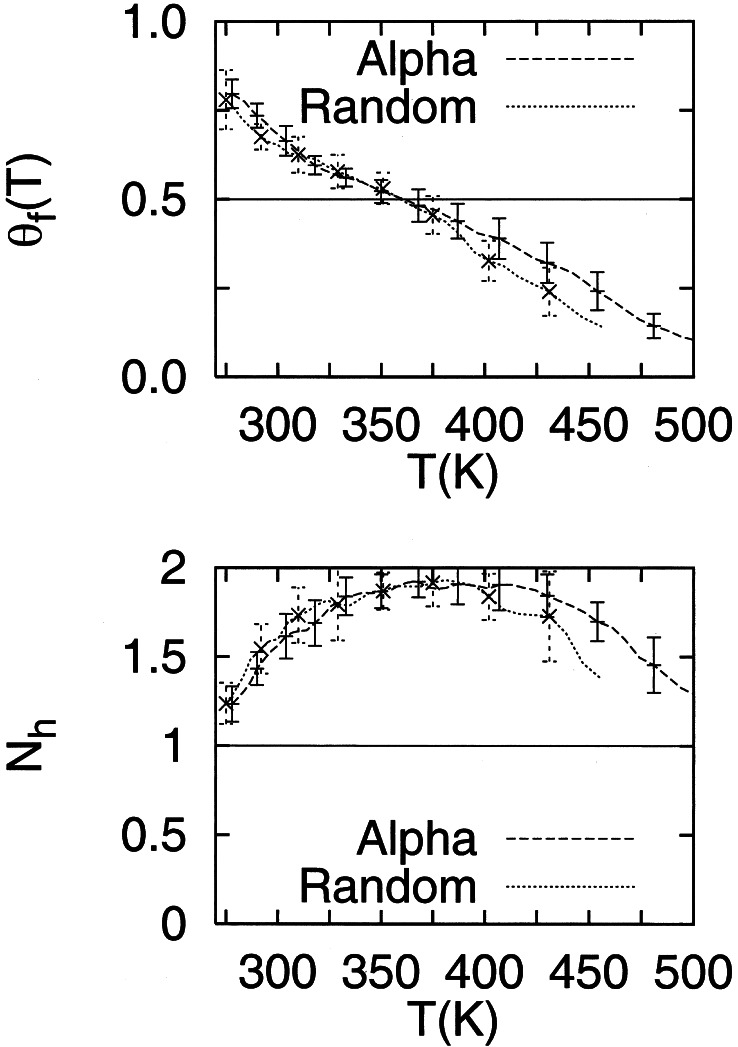
First, we verify that the REMD method gives reliable thermodynamics by showing the independence of the results obtained in different calculations. Fig. 1 shows the average helical content as a function of temperature for A21, for two different simulations, one for the 32-replica system (with random starting configurations) and the other for the 48-replica system (with all α-helical starting configurations). The helical content profile describes a moderately cooperative helix-coil transition, with T_1/2 = 357 K, where T_1/2 is the temperature at which the helical content is 0.5. The helical content at 275 K is 90% and below 10% at 450 K. The two curves are within one standard deviation, with the exception of very high temperatures, where the 32-replica system shows slightly lower helical content, a result of the larger number of replicas and the higher temperature range of the 42-replica system. The T_1/2 for both systems is the same (357 K). The bottom curves in Fig. 1 show the average number of helical segments as a function of temperature. The largest average number of helical segments occurs near T_1/2. The similarity of the two melting curves is an indication that the REMD simulations are equilibrated within the 8.0 ns simulated here.

Figure 1.

Helical content of A21 as a function of T over the whole simulated T range. The two curves show results obtained from two simulations containing different numbers of replicas and initial conditions. The dotted line shows the helical content as a function of T for a system of 32 replicas with random initial configurations. The dashed line shows the helical content as a function of T for a system of 48 replicas with initial α-helical configurations. The bottom plot shows the average number of helical segments as a function of T. The average number of helical segments is largest near T_1/2. Error bars are calculated by block averaging over the last half of the configurations.

The simulations of the helix-coil transition of Fs are similar to those of A21; however, an important distinction is the enhanced thermostability of Fs, T_1/2 ≈ 400 K. The transition T measured by IR spectroscopy is 334 K (30), which is higher than the estimated value by CD (31–33). The helical content at 275 K is 90%. Thompson et al. estimate this value to be 80% for a fluorescent labeled peptide, whereas Agadir predicts 85% for the acetylated peptide (33, 44). The helix-coil transition temperatures (taken as T_1/2) are higher than those experimentally observed for the Fs peptide. The T_1/2 for A21 is not known but is clearly overestimated in our calculations. The Lifson–Roig helix propagation and nucleation parameters for A21 with the Cornell et al. (39) force field are found to be w₀ = 2.58 and v₀ = 0.755 at 273 K, which correspond to s₀ = 1.47 and σ₀ = 0.06 (11). The calculated values for σ are in disagreement with reported values of 0.0008 (2, 3, 13) and 0.004 (9).

We use our equilibrated thermodynamics calculations on the Fs and A21 peptides to test the reliability and sensitivity of the force field. The force fields used in classical modeling are semiempirical in nature and rely on their validation by comparison with experimental data. It has been argued that the Cornell et al. force field (39) overestimates the helical propensities of peptides (45). Kollman et al. have developed the parameter set termed parm96, which consisted only of the modification of the torsion potential for φ and ψ angles (46, 47). Using the parm96 force field, we performed REMD calculations and found that parm96 gives negligible helical content for the Fs peptide and gives large populations of β hairpins (unpublished results). The changes made in parm96 motivated us to modify the Cornell et al. (parm94) force field, by setting the torsion potential for φ and ψ to zero and by using this modified force field as a bare force field that can be further modified by perturbations.

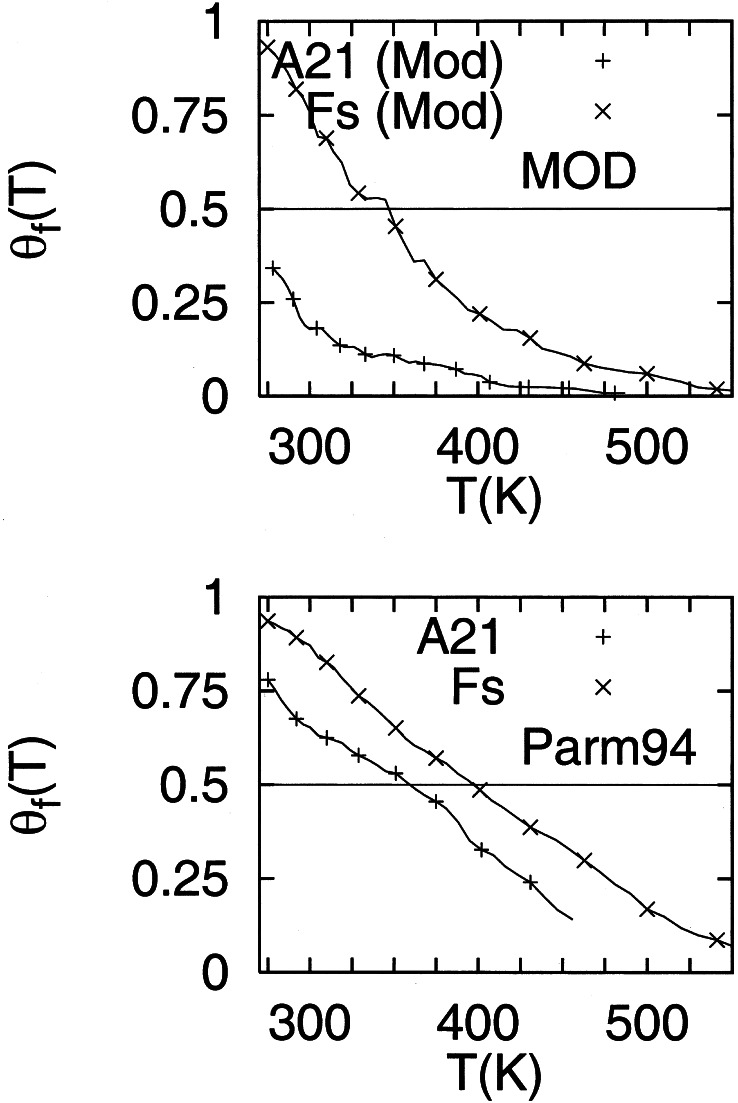
Fig. 2 shows a comparison of the helix content profiles as a function of T for the Fs and A21 peptides with the parm94 and modified force fields. From the helical percentages at various T, we estimate that the force field variation results in 3.7 kJ/mol and 0.8 kJ/mol free energy differences for A21 and Fs, respectively, at 300 K. The difference in free energy between A21 and Fs, with the modified force field, at 350 K, is 5.8 kJ/mol. This difference in stability results from the Arg side chain. The modified force field gives T_1/2 of 345 K and 90% helical content at 275 K for the Fs peptide. The results obtained with the modified force field are in much better agreement with experimental data for Fs (30–33). For A21, we obtained a 34% helical content at 275 K. Spek et al.'s data suggest the helical content of A13 flanked by charged amino acid side chains is near 40% at 273 K in 1 M NaCl solution (8). Ingwall et al.'s (2) measurements would suggest a 1% helical content for A21. The Lifson–Roig helix propagation and nucleation parameters for A21 with the modified force field are found to be w₀ = 1.37 and v₀ = 0.076 at 273 K, which correspond to s₀ = 1.3 and σ₀ = 0.004 (11). Our values for σ are in agreement with Yang et al. (9) (σ₀ = 0.004 ± 0.002 for assumed values of s₀ = 1.4 − 1.7) and in disagreement with those of Scheraga (13) (s₀ = 1.08 and σ₀ = 0.0008, at 273 K). Our calculations are consistent with intrinsic helix formation by Ala.

Figure 2.

Comparison of the helical content of A21 and Fs peptides as a function of temperature obtained with the Cornell et al. force field (39) (labeled Parm94) and with the modified force field described in the text (labeled MOD). The transition temperatures are 400 K for Fs (Parm94), 345 K for Fs (MOD), 357 K for A21 (Parm94), and below 275 K for A21 (MOD).

We fit the Zimm–Bragg helix propagation parameter to a thermodynamic model to extract the enthalpy (ΔH) and entropy (ΔS) changes associated with helix propagation. Assuming a linear T dependence on the specific heat, and taking the unfolded state as reference, we get ΔH(273 K) = −4.6 kJ/mol, ΔS(273 K) = −15 J/K-mol, and ΔC_p(273 K) = −60 J/mol⋅⋅⋅K, and ΔC_p(383 K) = 0. A similar fitting of the nucleation parameter gives ΔH_σ(273) = 8.1 kJ/mol, and ΔS_σ(273) = −15 J/K-mol.

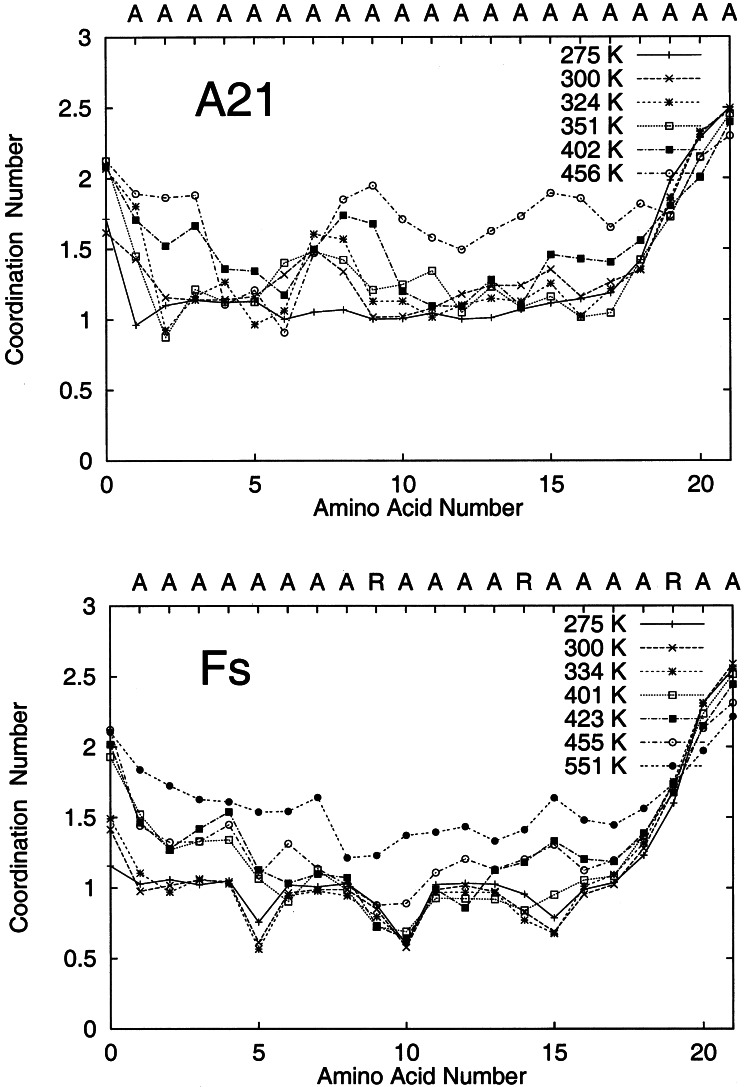
Simulations using the modified and original force fields describe higher stability of the Fs peptide over A21. To test the hypothesis that chain desolvation might be responsible for this stabilization (14) and to provide a molecular description of the shielding, we study the coordination of water to the peptide backbone over the last 2 ns/replica of the simulations. Fig. 3 shows the water coordination number for the peptide backbone carbonyl oxygen. Carbonyl oxygen atoms involved in backbone hydrogen bonding, on average, have one coordinated water molecule. End carbonyl oxygen atoms not participating in hydrogen bonds have two coordinated water molecules. Shielded carbonyl oxygen atoms have zero coordinated water molecules. At low T, the peptide is in the α-helical conformation and has a coordination number of one. At high T, the peptide is in the coil conformation and shows a coordination number between 1.0 and 2.0, which is the case for the Ala21 peptide. The low coordination number of carbonyl oxygens at high T (for example, at position 6 of A21 at 456 K, shown in Fig. 3) is a consequence of multiple intramolecular hydrogen bonds that are not necessarily consistent with an α-helical conformation.

Figure 3.

Water coordination to the backbone carbonyl oxygen atoms along the peptide sequence. The average coordination number for backbone atoms in A21 is 1 when the system forms an α-helix and 2 when the system is a random coil. The coordination number is not uniform along the sequence for the unfolded (high T) averages, because the peptides maintain approximately 15 intramolecular (native and nonnative) hydrogen bonds at high T. For Fs, the coodination number is 1, except when the carbonyl group is four amino acids before an Arg side chain. The Arg side chain shields the carbonyl oxygen atom from exposure to water.

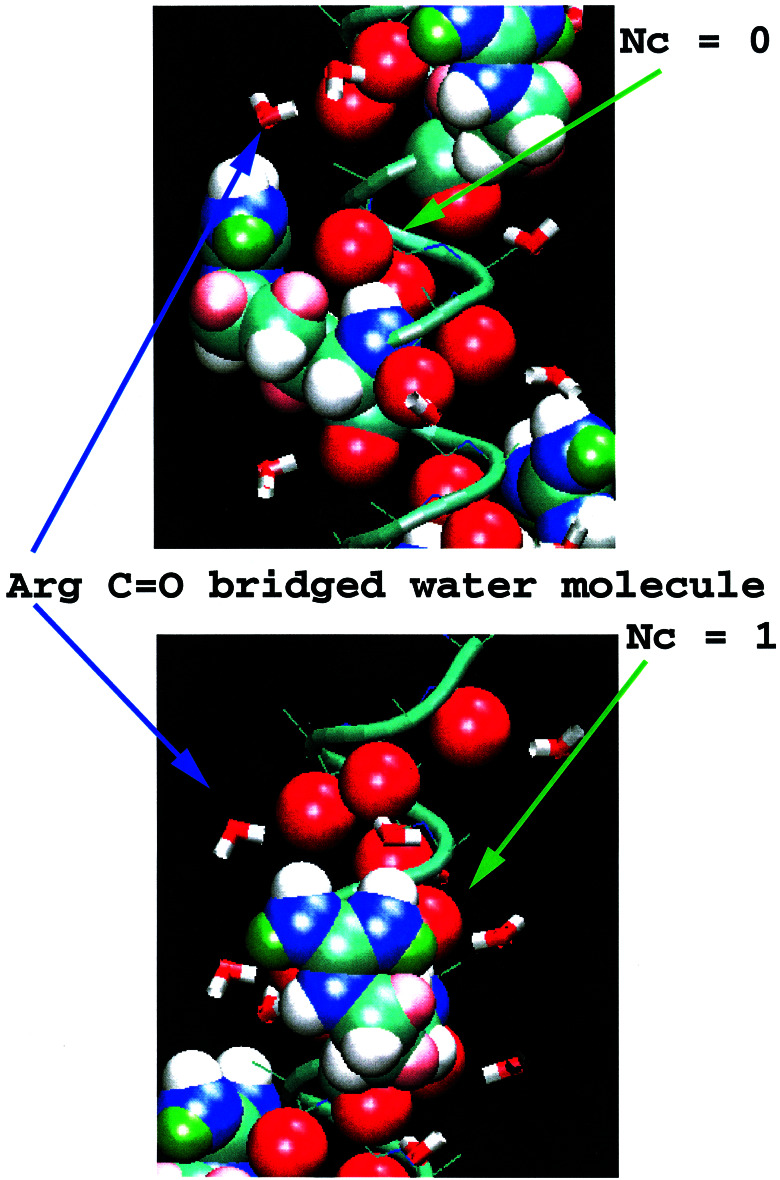
For the Fs peptide, we observe that at low T, the coordination number adopts a number of 0.5 at three positions along the sequence. The atoms with low coordination correspond to carbonyl oxygens four residues before Arg side chains, which are shielded from water by the Arg side chain. There are two configurations, shown in Fig. 4, which yield coordination numbers of 1 and zero. On average, they are equally populated, yielding a coordination number of 0.5. The coordination number patterns did not change with the force field at the lowest temperatures.

Figure 4.

Illustration of the shielding of the backbone carbonyl oxygen atoms by the Arg side chain of Fs. The Arg side chain preferentially adopts configurations where the side chain rests on the helix backbone. The nature of the Arg side chains stabilizes this configuration by a favorable guanidinim group interaction with a carbonyl oxygen four amino acids upstream of the Arg in sequence and by the bridging of water molecules that coordinate to carbonyl oxygens five amino acids upstream of the Arg in sequence. Two equally populated configurations show the carbonyl oxygen to be exposed (N_c = 1) and shielded by the side chain (N_c = 0). The average coordination number for these carbonyl oxygens is ≈ 0.5 for residues 5, 10, and 15.

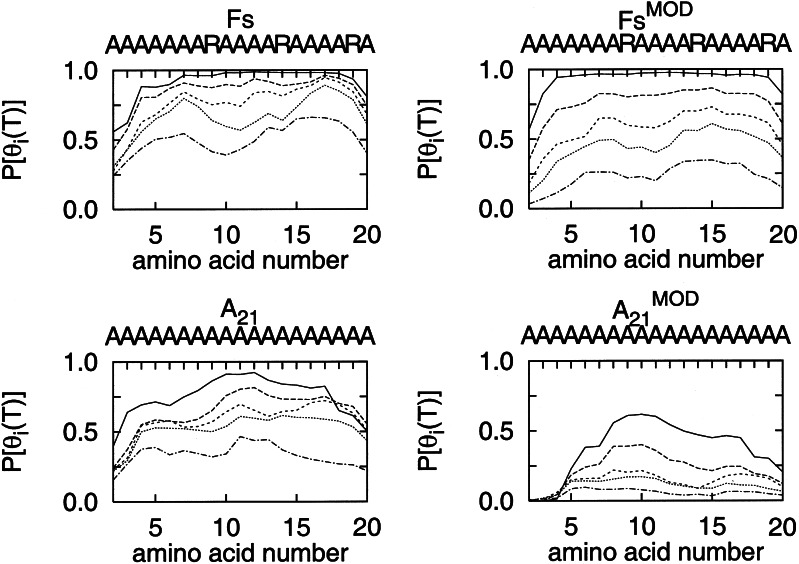
The shielding of the backbone carbonyl atoms by the Arg side chains can be directly correlated to hydrogen bond formation probabilities along the peptide chain. Fig. 5 shows the amino acid probability of participation in an α-helical conformation as a function of temperature, for T = 275, 300, 325, 350, and 400 K. Although the amount of α-helical formation changes with the modification of the force field, the patterns of relative helical content along the sequence, at each T, are similar: the end amino acids have a lower probability of sampling the helical region of the φ–ψ map. The probability increases toward the center of the chain and decreases toward the C terminus. This pattern is maintained at all temperatures, but with a lower overall probability at higher temperatures. For the Fs peptide below 350 K, we observe high helical propensity, relative to neighboring amino acids, for amino acids 7, 12, and 17. The Arg residues are at positions 9, 14, and 19, and the low-coordination number carbonyl oxygens are at positions 5, 10, and 15. The amino acids with larger relative helical propensities correspond to the central amino acid, i, between the shielded carbonyl oxygen, i − 2, and the Arg, i + 2. The shielded hydrogen bond is between the carbonyl oxygen at i − 2 and the amino group at i + 2.

Figure 5.

Probability of participation in an α-helical conformation for each amino acid (amino acids 2–20) in the A21 and Fs peptides, at temperatures near 275, 300, 325, 350, and 400 K. Lower T show larger α-helical formation probabilities. The curves are shown for calculations using the Cornell et al. force field (39) (side plots, Left) and the modified force field described in the text (side plots, Right).

Conclusion

We have used the REMD algorithm to study the effect of sequence variation on α-helix formation for Fs peptide and A21. This is, to our knowledge, the first all-atom calculation of the helix-coil transition thermodynamics of peptides in explicit solvent over a wide temperature range. The helix-coil transitions are moderately cooperative over a broad temperature range, in agreement with experimental data (30–33) and with the Lifson–Roig nearest-neighbor model for short peptides (11).

Analysis of the coordination number of water molecules to the backbone carbonyl oxygens along the sequence and over a broad T range indicates that the additional stabilization observed for the Fs peptide relative to the A21 peptide is produced by the partial shielding of the backbone hydrogen bonds from water. This shielding is provided by the Arg side chains. Vila et al. (14) proposed that α-helical stabilization is induced by bulky side chains (both polar and nonpolar), which sequester water away from backbone atoms. They modeled this effect in Monte Carlo simulations with an implicit treatment of hydration effects. Our simulations verify this and provide a microscopic description of the side chain-shielding effect in terms of the desolvation of the backbone hydrogen bonds using an explicit treatment of the solvent. Details of the shielding not described by Vila et al. (14) are the shielding by Arg at site i of the carbonyl oxygen at i − 4 and the energetically favorable interaction of the charged side chain with the carbonyl oxygen. Simulations of sequences containing Lys and Glu side chains show that the Lys side chain has an interaction with the backbone similar to Arg in the Fs peptide (T. Ghosh, S. Garde, & A.E.G., unpublished results). The stabilizing effect of the charged side chain interaction with the carbonyl oxygen may explain why Ala-to-Leu substitutions destabilize helix formation (17).

We use our equilibrated thermodynamics calculations to validate the force field used and to test the sensitivity of the results to details in the force field. We find that a slight modification of the force field (39) gives a transition temperature for the Fs peptide that is in good agreement with the experimentally determined T. The modified force field estimates the helical content of A21 to be 34% at 275 K, and the T_1/2 is estimated to be near 240–270 K, based on extrapolation of the calculated helical content profile. The helical propagation and nucleation parameters obtained for A21 at 273 K (s₀ = 1.3 and σ₀ = 0.004) are consistent with intrinsic helix formation by Ala. Periodic Ala-to-Arg substitutions, as in Fs, increase the helical propensity. The exhaustive sampling and validation of simulations results with experimental data done in our studies provide a reliable method for further refining semiempirical force fields.

Abbreviations

MD

molecular dynamics

REMD

replica exchange MD

NMe

methyl amide