Network of coupled promoting motions in enzyme catalysis

Abstract

A network of coupled promoting motions in the enzyme dihydrofolate reductase is identified and characterized. The present identification is based on genomic analysis for sequence conservation, kinetic measurements of multiple mutations, and mixed quantum/classical molecular dynamics simulations of hydride transfer. The motions in this network span time scales of femtoseconds to milliseconds and are found on the exterior of the enzyme as well as in the active site. This type of network has broad implications for an expanded role of the protein fold in catalysis as well as ancillaries such as the engineering of altered protein function and the action of drugs distal to the active site.

A relationship between the motion of protein structural elements and activity has been implicated in enzyme catalysis (1–3). Evidence for the existence of promoting vibrations or modes that augment catalytic activity has been sought for a number of enzymes. At the amino acid level, motions of residues both in and distal to the active site have been proposed to participate in catalysis. The identification, characterization, and clarification of the function of such proximal and distal promoting motions present a challenging task. Recently the importance of coupled motions sampled in differing time domains involving distal residues in the enzyme dihydrofolate reductase (DHFR; EC 1.5.1.3) has been suggested by a combination of NMR experiments (microsecond to picosecond) (4), classical molecular dynamics simulations (nanosecond) (5), and kinetic experiments for site-directed mutants (millisecond to second) (6, 7). Here we report the results of genomic analysis, kinetic measurements of multiple mutations, and mixed quantum/classical molecular dynamics simulations (8) of the hydride transfer step in DHFR. Based on the crystal structure framework, these results provide a description of specific residue motions and their linkage to enzyme catalysis.

DHFR is required for normal folate metabolism in prokaryotes and eukaryotes. It catalyzes the reduction of 7,8-dihydrofolate (DHF) to 5,6,7,8-tetrahydrofolate (THF) by using nicotinamide adenine dinucleotide phosphate (NADPH) as a coenzyme. Specifically, the pro-R hydride of NADPH is transferred to the C6 of the pterin with concurrent protonation at the N5 position. This reaction is essential to maintain necessary levels of THF needed to support the biosynthesis of purines, pyrimidines, and amino acids, fostering DHFR as a pharmacological target. As a result of its importance, DHFR has been studied extensively with a wide range of methodologies.

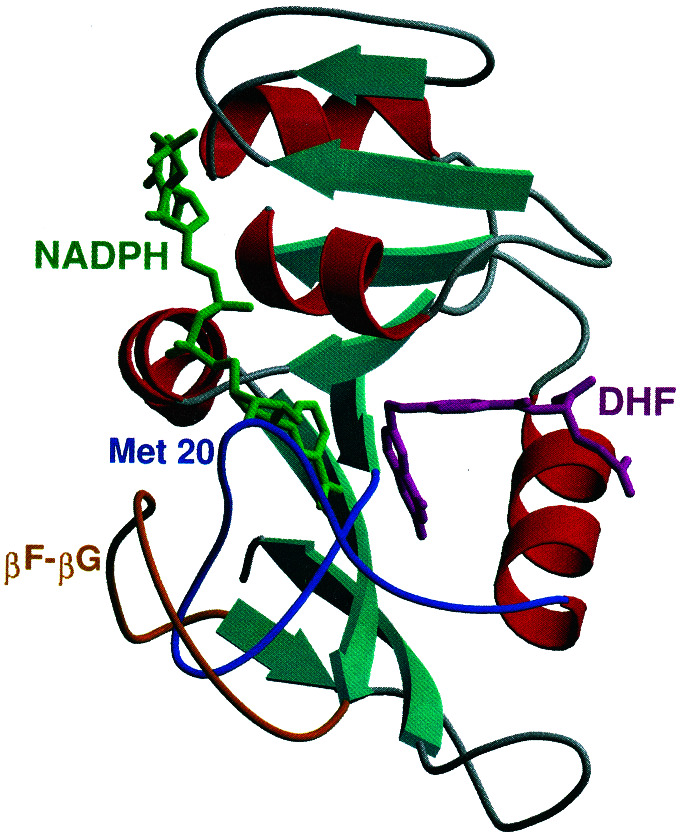
X-ray crystallographic studies indicate that the Escherichia coli DHFR enzyme contains an eight-stranded β-sheet and four α-helices interspersed with flexible loop regions that connect these structural elements (ref. 9; see Fig. 1). Depending on the nature of the bound ligand, three different conformations have been observed for a surface loop formed by residues 9–24 (denoted the Met-20 loop). When the DHF substrate and NADPH coenzyme are bound, the Met-20 loop adopts the closed conformation, in which the Met-20 loop residues interact strongly with NADPH. The closed conformation is stabilized by hydrogen bonding interactions with the βF–βG loop (residues 117–131). Specifically, the amide backbone of both Gly-15 and Glu-17 in the Met-20 loop forms hydrogen bonds with Asp-122 in the βF–βG loop. These hydrogen bonds are not present in the alternative occluded and open conformations of the Met-20 loop. Thus, the closed conformation provides a preorganized structure that juxtaposes the substrate and coenzyme in an orientation conducive to reaction (10). NMR experiments indicate that the Met-20 loop conformational changes regulate ligand binding (11).

Figure 1.

Secondary structure of DHFR. The Met-20 and βF–βG loops, as well as the NADPH coenzyme and DHF substrate, are labeled. All structural figures in this paper were generated by using the programs MOLSCRIPT and RASTER3D.

Previous kinetic studies on site-directed mutants provide evidence that an interaction between the Met-20 and βF–βG loops participates in the hydride transfer step required for catalysis. Replacement of the central portion of the Met-20 loop (residues 16–19) with a single glycine decreased the rate of hydride transfer 400-fold (12). Mutagenesis of Asp-122 to asparagine, serine, or alanine indicated a significant correlation between hydrogen bonding ability and the rate of hydride transfer (13), suggesting that the hydrogen bond between Asp-122 and the Met-20 loop residues plays a role in catalysis. Further indication of the importance of an interaction between the two loops is that mutagenesis of the neighboring residue Gly-121 to alanine, leucine, valine, or proline decreased the rate of hydride transfer by as much as 400-fold (14).

As neither the static x-ray crystal structures nor the inferential kinetic analysis provides direct evidence for molecular motions, NMR and classical molecular dynamics have been used to investigate DHFR dynamics. NMR relaxation experiments revealed that the binding of the substrate and coenzyme alters the motion of the enzyme not only in the active site, but also in regions far from the binding sites (4, 15). Of particular note are changes in the amide backbone observed in the Met-20 loop, as well as the βF–βG loop. Classical molecular dynamics simulations identified strong correlated and anticorrelated side-chain motions involving spatially distinct protein regions for the DHFR⋅NADPH⋅DHF complex but not for the product complexes with THF, implying that these motions might be tied to catalysis (5). Moreover, these correlated and anticorrelated motions involve many of the same regions of the protein implicated by the dynamic NMR measurements, including the Met-20 and βF–βG loops. One interpretation of these data is that such motions constitute a collective reaction coordinate for the ternary enzyme complex.

These data suggest that particular residues found throughout the protein may act as a coupled network to promote catalysis. In this paper we perform a genomic analysis for sequence conservation across 36 diverse species of DHFR from E. coli to human to identify residues that might participate in this coupled network. We also perform kinetic studies of hydride transfer in DHFR for double mutations involving conserved residues that are distal to the active site. In addition, we perform mixed quantum/classical molecular dynamics simulations for the hydride transfer reaction with a recently developed hybrid approach (8). This hybrid approach includes the dynamics of the entire solvated enzyme, as well as nuclear quantum effects such as zero point energy, hydrogen tunneling, and nonadiabatic transitions (16). The power of this hybrid approach is that it provides a wealth of information concerning molecular motions on two disparate time scales (millisecond and femtosecond to picosecond).

Methods

The genomic analysis was performed by aligning the DHFR sequences using the program Clustal-W (17) and then editing and refining by using structural data. The 36 species used are E. coli; Citrobacter freundii; Enterobacter aerogenes; Klebsiella aerogenes; Haemophilus influenzae; Salmonella typhimurium; Bacillus subtilis; Neisseria gonorrhoeae; Staphylococcus haemolyticus; Deinococcus radiodurans; Staphylococcus epidermidis; Staphylococcus aureus; Streptococcus pneumoniae; Haloferax volcanii; Enterococcus faecium; Enterococcus faecalis; Mycobacterium tuberculosis; Mycobacterium avium; Zymomonas mobilis; Aeromonas salmonicida; Lactococcus lactis; Lactobacillus casei; Heliothis virescens; Pneumocystis carinii; Chlamidia pneumoniae; Proteus mirabilis; Homo sapiens; Candida albicans; Herpesvirus saimiri; Aedes albopictus; Drosophila melanogaster; Chlamidia trachomatis; Caenorhabditis elegans; Mus musculus; Shigella sonnei; and Shigella flexneri. Furthermore, these sequence conservation patterns were also noted in a more comprehensive alignment of 121 DHFR sequences that were obtained from SWISS-PROT and TrEMBL database searches. The kinetic studies of multiple mutations involved the construction of mutants and the measurement of rate constants for hydride transfer by stopped-flow techniques at pH 7.0 as described (18).

The mixed quantum/classical molecular dynamics simulations were performed with the hybrid approach described in ref. 8. The specific reaction studied here is hydride transfer from NADPH to protonated DHF to produce NADP⁺ and THF. (Previous calculations imply that the protonation of N5 of DHFR occurs before hydride transfer; ref. 19.) The initial coordinates of the enzyme were obtained from the 1rx2 crystal structure for the E. coli DHFR⋅NADP⁺⋅folate complex, which exhibits the closed conformation of the Met-20 loop (9). The simulation system contains the protein, an NADPH cofactor, a protonated DHF substrate, and 4,122 water molecules in a truncated octahedral periodic box with a distance of 66.61 Å between opposing square faces.

Both electronic and nuclear quantum effects are included in these simulations. The potential energy surface is described with a two-state empirical valence bond potential (20, 21) based on the GROMOS force field (22), including Morse potentials for the donor-hydride and acceptor-hydride bonds. This potential allows chemical bonds to break and form during the hydride transfer reaction. The energy difference and coupling between the two valence bond states were fit to reproduce the free energy of reaction and the free energy of activation calculated from the experimentally determined maximal forward and reverse rates for hydride transfer (18). The transferring hydride nucleus is represented by a three-dimensional vibrational wave function calculated on a cubic grid centered between the donor and acceptor carbon atoms (23). In this manner, nuclear quantum effects such as zero point motion and hydrogen tunneling are incorporated during the generation of the free energy profiles and dynamical trajectories.

In this hybrid approach, the free energy profile is generated as a function of a collective reaction coordinate including motions of the entire solvated enzyme (20). This collective reaction coordinate is defined as the difference between the energies of the product and reactant valence bond states averaged over the ground state hydrogen vibrational wave function. To adequately sample all relevant regions of the reaction coordinate, a series of independent equilibrium simulations with different biasing potentials (i.e., mapping potentials) are performed. The individual pieces of the free energy curve along the collective reaction coordinate are connected by implementation of the thermodynamic integration method. This approach provides a continuous free energy curve along the entire collective reaction coordinate. The transition state theory rate constant is calculated from the free energy barrier. As mentioned above, the empirical valence bond potential was parametrized to reproduce the experimentally determined maximal forward and reverse rates for hydride transfer (18). Moreover, we calculated the deuterium kinetic isotope effect to be 3.4 ± 0.8, in agreement with the experimental value of 3.0 ± 0.4 (18).

In addition to these equilibrium simulations, real-time dynamical trajectories are initiated at the transition state and propagated backward and forward in time. Analysis of an ensemble of these real-time dynamical trajectories allows the calculation of the transmission coefficient (8, 24), which accounts for dynamical barrier recrossings, as well as correlations between specific enzyme motions and the degree of barrier recrossing. The molecular dynamics with quantum transitions method (16) is used to incorporate hydrogen tunneling effects during the generation of these trajectories.

This approach allows the investigation of both thermally averaged enzyme motions that impact the activation free energy and dynamical motions that impact the degree of barrier recrossing (25). Analysis of the series of equilibrium simulations used to generate the free energy profile provides information about changes in thermally averaged geometrical properties along the entire range of the collective reaction coordinate (i.e., as the reaction evolves from reactant to transition state to product). Based on experimental kinetic measurements of hydride transfer in DHFR, the changes in average geometrical properties between the reactant and the transition state were determined to occur on the millisecond time scale. In addition, analysis of the real-time dynamical trajectories initiated at the transition state provides information about motions occurring on the femtosecond to picosecond time scale. Thus, this approach elucidates the millisecond motions directing the system to the transition state, as well as the faster motions occurring in the critical transition state region.

The results illustrating the changes in thermally averaged motions were obtained from a series of individual simulations sampling different regions of the collective reaction coordinate. These individual simulations were smoothly connected with the thermodynamic integration method. Three complete sets of data were obtained from independent fully equilibrated molecular dynamics simulations at 298 K of 140-ps, 160-ps, and 100-ps durations, respectively. Each data set was composed of a series of individual simulations for at least nine different mapping potentials. Note that trapping in metastable minima is problematic in this methodology. To investigate the quality of the sampling, the velocities were randomized according to a Boltzmann distribution every picosecond for the 160-ps simulation. All data presented here are from the initial 140-ps simulation, but the observed trends were reproduced in the other independent data sets. We emphasize that, despite the relatively short duration of the individual simulations, the complete series of simulations provides information on the millisecond time scale because it spans the entire range of the collective reaction coordinate as the reaction progresses from reactant to transition state to product.

Results and Discussion

Fig. 2 summarizes the results of our genomic analysis. The crystal structures of the members of this set show the protein fold to be invariant despite an overall sequence homology of only 30%. As illustrated in Fig. 2, many of the conserved residues are in the active site and hence impact the binding of the substrate and coenzyme. On the other hand, several conserved residues are in distal regions of the enzyme (i.e., residues 41–43, 60–63, and 121–123). Residues 122 and 15, which are hydrogen bonded in the closed conformation of the Met-20 loop, are absolutely conserved. Although some of these distal residues may be conserved for structural purposes, others may be conserved to preserve a network of coupled promoting motions.

Figure 2.

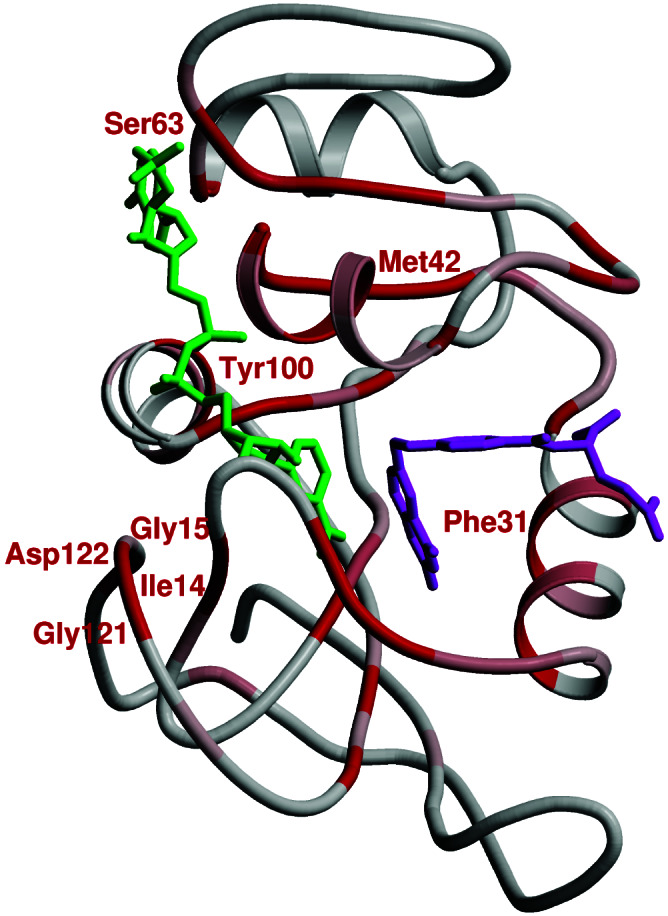
Sequence conservation in DHFR. Regions of conservation are mapped onto the structure of E. coli DHFR by using a gradient color scheme (gray to red, where red is the most conserved). NADPH and DHF are in green and magenta, respectively.

Motivated by this genomic analysis, we performed kinetic studies of hydride transfer in DHFR for double mutations involving conserved residues that are distal to the active site. Table 1 presents results for the double mutation involving Gly-121 and Met-42 (conserved residues distal to the active site and separated by ≈19 Å, as shown in Fig. 2). These double mutations exhibit nonadditivity effects (i.e., the effect of a double mutation is greater than the sum of the effects of the single mutations (26), suggesting a coupling of the βF–βG loop to distant regions of the enzyme. Note that site-specific mutagenesis does not distinguish between nonadditivity effects resulting from changes in conformation and those effects resulting from changes in molecular motions.

Table 1.

Nonadditive mutational effects on forward hydride transfer rates

DHFR	khyd, s−1	khyd ratio, wild type/mutant*	Additivity factor†	Nonadditivity‡
Wild type (ref. 18)	228  ± 8	1.0  ± 0.1
M42F	159  ± 17	1.4  ± 0.2
G121A (ref. 14)	38  ± 3	6.0  ± 0.5
G121S	3.7  ± 0.4	62  ± 7
M42F-G121A	1.3  ± 0.2	175  ± 28	8.4  ± 1.4	21  ± 5
M42F-G121S	0.46  ± 0.08	496  ± 89	87  ± 16	5.7  ± 1.5

^*The factor by which k_hyd is lowered for each mutant enzyme relative to wild-type DHFR. 

^† The factor by which k_hyd for the double mutants would be lowered based on an additive effect of the individual mutations. For example, the k_hyd of M42F-G121A would decrease 1.4 × 6.0 = 8.4-fold. 

^‡ Note that the additive effect of the individual mutations does not match the actual reduction for both double mutants. For M42F-G121A, k_hyd is lowered 175/8.4 = 21-fold more than predicted by a simple additive effect. 

To relate these genomic and kinetic results to molecular motions in DHFR, we performed mixed quantum/classical molecular dynamics simulations for the hydride transfer reaction. Figs. 3 and 4 present the results of our equilibrium simulations, which provide insight into the changes of average geometrical properties required for the millisecond hydride transfer reaction. The geometrical properties within the substrate and coenzyme change dramatically during the reaction. As shown in Fig. 4A, the donor–acceptor distance decreases from 3.4 to 2.7 Å as the reaction evolves from the reactant to the transition state. In addition, Fig. 4B shows that the angle between the acceptor carbon and the methylene amino linkage in DHF increases from 114° to 117° as the reaction evolves from the reactant to the transition state. This movement occurs simultaneously with the puckering of the pterin ring, as illustrated in Fig. 4C, implying an alteration of the electronic structure of the substrate. A localized molecular orbital analysis (27) on representative reactant and transition state structures confirms that the double bond between the acceptor carbon atom and the neighboring nitrogen is significantly weakened at the transition state, thereby promoting hydride transfer to the acceptor carbon.

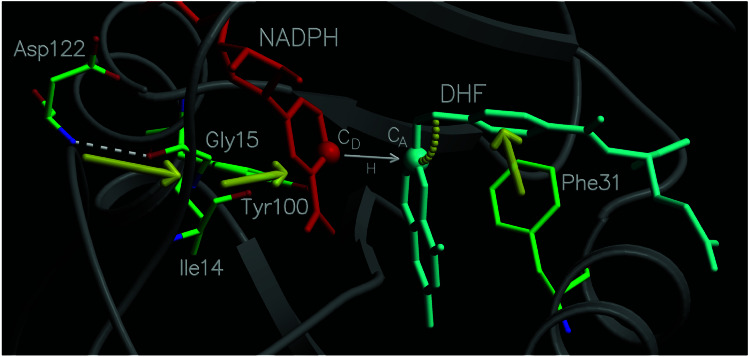
Figure 3.

Diagram of a portion of the network of coupled promoting motions in DHFR. The yellow arrows and arc indicate the coupled promoting motions.

Figure 4.

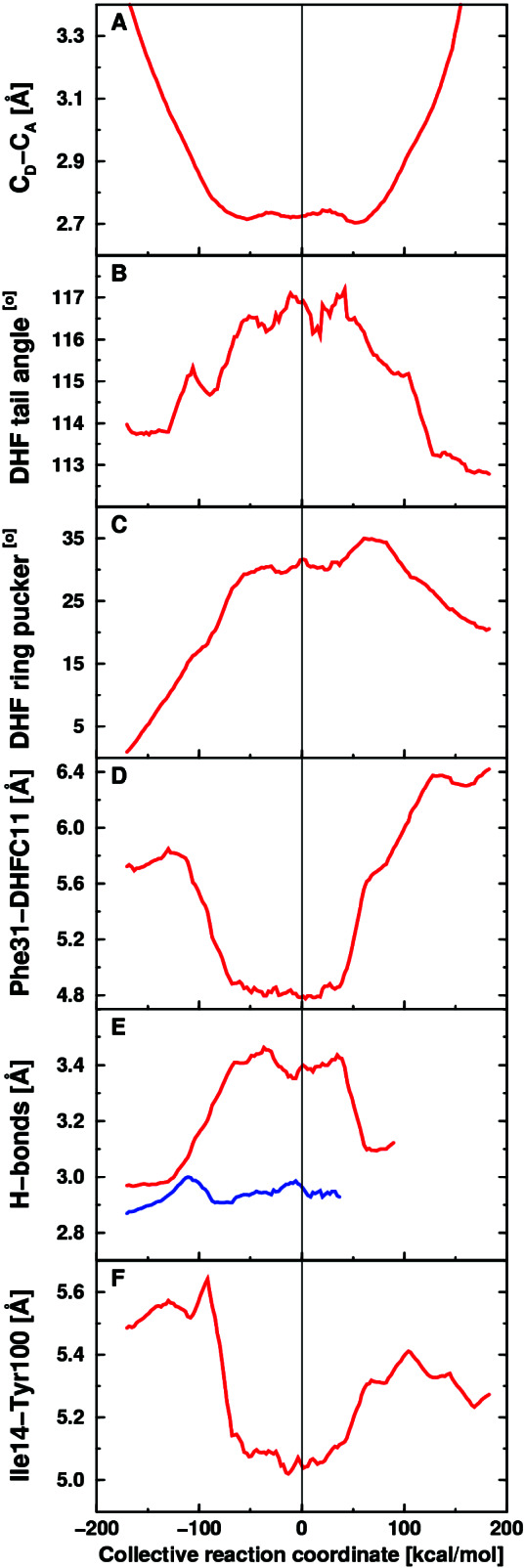
Equilibrium averages of geometrical properties along the collective reaction coordinate. (A) Donor–acceptor distance. (B) Angle between the acceptor and methylene amino linkage in DHF. (C) DHF pterin ring puckering angle. (D) Distance between C_ζ of Phe-31 and C11 of DHF. (E) Hydrogen-bonding distance between N of Asp-122 and O of Gly-15 (red) and between O of Ile-14 and carboxamide N of NADPH (blue). (F) Distance between C_δ of Ile-14 and the side-chain oxygen of Tyr-100.

The motions of amino acid residues in the active site relative to the coenzyme and substrate are also important. For example, as shown in Fig. 4D, the distance between C_ζ of Phe-31 and C11 of DHF decreases by ≈1 Å as the reaction evolves from the reactant to the transition state. As the Phe-31 moves closer to the substrate, the angle between the acceptor carbon and the methylene amino linkage in DHF increases and the donor–acceptor distance decreases, suggesting that the Phe-31 motion directs these changes. These motions are indicated in Fig. 3. Note that Phe-31 is tightly conserved, and mutations of this residue have been found to significantly decrease the rate of hydride transfer (28).

A more unexpected result is that the motion of a residue on the exterior of the enzyme was found to be important for catalysis. Specifically, the motion of Asp-122 relative to Gly-15 was found to contribute to the reaction coordinate. Fig. 4E illustrates that the hydrogen bond between these two residues increases by ≈0.4 Å as the reaction evolves from the reactant to the transition state. In contrast, this figure shows that the hydrogen bond distance between the Ile-14 and the NADPH coenzyme is nearly constant (≈2.95 Å) as the reaction evolves from the reactant to the transition state. (Note that these hydrogen bonding motions are susceptible to difficulties with metastable states.) As Gly-15 moves away from Asp-122, the donor–acceptor distance decreases, suggesting that the neighboring residue Ile-14, which is hydrogen-bonded to the NADPH, directs the donor toward the acceptor. This pathway is illustrated in Fig. 3. Note that Asp-122, Gly-15, and Ile-14 are all absolutely conserved residues, and mutations of Gly-121 and Asp-122 have been found to significantly decrease the rate of hydride transfer (13, 14).

In addition to the role of Ile-14 in terms of backbone hydrogen bonding to NADPH, the motion of the side chain of Ile-14 also contributes to the collective reaction coordinate. Fig. 4F illustrates the motion of C_δ of Ile-14 relative to the side-chain oxygen of Tyr-100, which is in close contact with the nicotinamide ring of NADPH, and is also a tightly conserved residue. The distance between these two atoms decreases by ≈0.6 Å as the reaction evolves from the reactant to the transition state. Tyr-100 remains within contact distance (3.6–3.8 Å) of the donor carbon as the reaction evolves from the reactant through the transition state, suggesting that the motion of the side chain of Ile-14 assists in directing the donor toward the acceptor. This observation provides an explanation for the absolute conservation of Ile-14.

We have also investigated the motion of the other conserved residues. We found that many of these residues maintain strong hydrogen bonds to each other or to NADPH throughout the simulations. For example, Thr-46 and Ser-63 are hydrogen bonded to NADPH, and Met-42 is hydrogen bonded to Ile-60 and Leu-62 throughout the simulations. Similarly, Asp-27, Trp-22, and Thr-113 are involved in a hydrogen bonding network with DHF in the active site. We found that the motion of Gly-96 relative to the donor carbon also contributes to the reaction coordinate, increasing by ≈0.6 Å as the reaction evolves from the reactant to the transition state. Gly-95 and Gly-96 flank the nicotinamide ring of NADPH and are absolutely conserved.

These collective simulation data suggest a network of coupled promoting motions in DHFR. Here promoting motions refer to systematic changes of thermally averaged geometrical properties as the reaction evolves from the reactant to the transition state. We emphasize that the majority of distances monitored did not exhibit systematic changes along the collective reaction coordinate. Moreover, the network shown in Fig. 3 is most likely not complete or unique. In addition, this analysis is unable to differentiate between motions playing an active role in catalysis and motions responding to alterations caused by catalysis.

In addition to these average motions occurring on the millisecond time scale of the hydride transfer reaction, we analyzed real-time dynamical trajectories initiated at the transition state to elucidate motions on the femtosecond to picosecond time scale in the transition state region. Here we focus on the motion of the residues involved in the double mutations with experimentally determined hydride transfer rates presented in Table 1. Fig. 5 depicts the time evolution of the donor–acceptor distance and the distance between C_α of Gly-121 and C_β of Met-42 for a representative real-time vibrationally adiabatic trajectory initiated at the transition state. These data implicate protein vibrations of several different frequencies, ranging from the femtosecond to the picosecond time scale. The transition state is attained when both distances are near a minimum. These qualitative trends were observed for six dynamical trajectories with different transition state configurations. Note that these individual real-time trajectories reflect the conformations implicated in single-molecule experiments (29). These data imply that the motions of the well-separated residues Gly-121 and Met-42 are coupled to each other and participate in the overall network of coupled motions. This coupling is consistent with the nonadditivity of the double mutations involving Gly-121 and Met-42.

Figure 5.

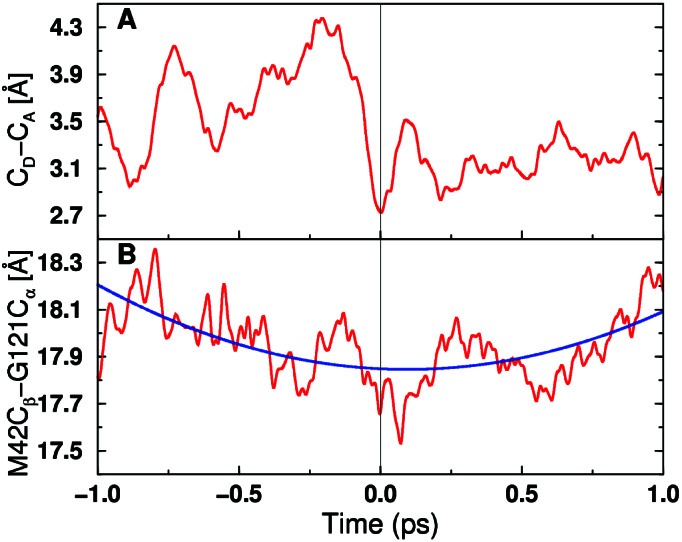
Time evolution of two select distances for a representative real-time vibrationally adiabatic trajectory. (A) Donor-acceptor distance. (B) Distance between C_α of Gly-121 and C_β of Met-42. Time t = 0 corresponds to the transition state, and the reaction evolves toward the reactant/product as the time becomes negative/positive. For B, the blue curve indicates a fit to a frequency on the picosecond time scale.

The results presented here identify a network of coupled promoting motions in the enzyme DHFR. This type of network has broad implications for protein engineering because of the consequences arising from the interruption of coupled motions. The inadvertent uncoupling of such networks by protein engineering protocols adds further complexity to a rationale based primarily on structural changes. On the other hand, the presence of coupled networks offers an alternative perspective for understanding allostericity (30) and the effects of pharmacaphores distal to the active site.

Abbreviations

DHFR

dihydrofolate reductase

DHF

7,8-dihydrofolate

THF

5,6,7,8-tetrahydrofolate