Abstract
Following a pretest, 11 participants who were naive with regard to various algebraic and trigonometric transformations received an introductory lecture regarding the fundamentals of the rectangular coordinate system. Following the lecture, they took part in a computer-interactive matching-to-sample procedure in which they received training on particular formula-to-formula and formula-to-graph relations as these formulas pertain to reflections and vertical and horizontal shifts. In training A-B, standard formulas served as samples and factored formulas served as comparisons. In training B-C, factored formulas served as samples and graphs served as comparisons. Subsequently, the program assessed for mutually entailed B-A and C-B relations as well as combinatorially entailed C-A and A-C relations. After all participants demonstrated mutual entailment and combinatorial entailment, we employed a test of novel relations to assess 40 different and complex variations of the original training formulas and their respective graphs. Six of 10 participants who completed training demonstrated perfect or near-perfect performance in identifying novel formula-to-graph relations. Three of the 4 participants who made more than three incorrect responses during the assessment of novel relations showed some commonality among their error patterns. Derived transfer of stimulus control using mathematical relations is discussed.
Keywords: mutual entailment, combinatorial entailment, mathematical relations, stimulus equivalence, novel relations, matching to sample, relational frame theory
Mathematicians have often assumed that their students can, or should, be able to relate various formulas to their graphical representations rather spontaneously. For example, one commonly used precalculus textbook advises the reader that particular types of formulas are critical to the understanding of all mathematical relations and states, “Whenever you encounter one of them, you should see a mental picture of its graph” (Sullivan & Sullivan, 1996, p. 114).
Nevertheless, a wide range of mathematical concepts remains elusive for large segments of our population, and a lack of mathematical preparation handicaps students who attempt postsecondary education and cannot compete in traditional math courses. Seventy-five percent of community college students and 50% of university freshmen lack the requisite skills to succeed in traditional college-level math courses (Burley, 1997; Center for Science, Mathematics, and Engineering Education, 1996; “CUNY Trustees,” 1999; “Educational Catch-Up,” 1998; Ravitch, 1997). In addition, 50% of all college students fail developmental course offerings (EnabLearning, 2002). In Texas, 70% of community and technical college students fail the statewide assessment exam and need developmental courses (Texas Higher Education Coordinating Board, 1999).
Until recently, the analysis of problem solving and similar cognitive phenomena has been almost exclusively the domain of cognitive psychology (cf. Reese, 1992). Particularly, as these issues pertain to the exploration and understanding of mathematical concepts (e.g., Anderson, Corbett, Koedinger, & Pelletier, 1995) or related problem-solving and analogical concepts, cognitive psychology (e.g., Vosniadou & Ortony, 1989) has sustained a long and vigorous applied research agenda (e.g., Vygotsky, 1978). The study of equivalence relations (e.g., Lane, Clow, Innis, & Critchfield, 1998) and relational frame theory (RFT; Hayes, Barnes-Holmes, & Roche, 2001) offer functional analytic alternatives to cognitive theorizing in the form of derived relational responding.
Using matching-to-sample (MTS) procedures, researchers train participants to select a particular stimulus, B, from an array of comparisons in the presence of A. Similarly, C is trained as the correct selection in the presence of B. Following such an experimental history, participants are likely to select A from an array of alternatives when B is displayed (symmetry), B from an array when C is displayed (symmetry), A when C is displayed (transitivity), and C when A is displayed (equivalence). This series of derived performances confirms that participants are able to relate the training stimuli as equivalent forms of the same objects or events.
Stimulus equivalence strategies have provided a functional system for generating a wide range of complex behaviors in low-functioning humans (e.g., Sidman, 1977; Sidman & Cresson, 1973; Trace, Cuvo, & Criswell, 1977). In one early illustration, Mackey and Sidman (1984) taught students with mental retardation to identify colors verbally and to assemble the names of colors with alphabetic characters. Then, students matched these printed words to colors and the colors to their respective printed words. This MTS procedure allowed students to verbally identify the names of the printed words.
Interestingly, there have been very few applied studies on stimulus relations that address the learning of mathematical operations. One exception is Lynch and Cuvo (1995), who developed a protocol wherein low-performing fifth- and sixth-grade students were trained to match fraction ratios (A) to their graph or pictorial representation (B). Then, participants were trained to match the graphs or pictures (B) to their matching decimal values (C). Upon emergence of equivalence, participants' generalization to other, untrained fraction-to-decimal relations was assessed. Although generalization was demonstrated for several students, this study limited its scope to fractions and their decimal equivalents; application to more advanced mathematical concepts has not been explored. One item of note is that Lynch and Cuvo's study employed a computer voice synthesizer to provide a pretraining procedure that instructed participants regarding response contingencies; however, the participants never received information on rules regarding the trained mathematical relations, either from the voice synthesizer or the experimenter. Participants' correct MTS responses resulted in a computer-generated affirmation of accuracy in the form of “yes.” However, Lynch and Cuvo reported that generalization might have been enhanced by “teaching students to develop general rules during training and posttest trials” (p. 125).
In a somewhat similar procedure, Leader and Barnes-Holmes (2001) trained fraction–decimal relations to 24 5-year-old preschool children using fractions, decimals, and partially shaded pictures. Prior to MTS, this study employed a two-part training system. During demonstration trials, participants were told and shown how to point to correct comparison stimuli (e.g., circles divided into shaded quadrants) when samples were presented in the form of fractions. During subsequent no-help trials, the experimenter presented samples and the participants independently pointed to comparison stimuli. Reinforcement was provided, contingent on correct identification of comparison stimuli, and inaccurate responses resulted in immediate verbal corrections. MTS test trials were conducted in the same format as no-help trials; however, no systematic consequences were provided. Following tests for equivalence, follow-up experiments confirmed that these preschool children were better able to generalize their performances to more complex pictorial representations of fractions (in the form of a square composed of 16 shaded or nonshaded segments) when generalization tests were administered according to a progression of increasingly novel comparisons. Here, as in the Lynch and Cuvo (1995) study, the relations among stimuli were expressed using the equivalence paradigm, and although instructions detailed how participants should point to particular objects under various conditions, verbal rules were not employed to train specific stimulus relations.
The potential for humans to demonstrate other types of stimulus relations has been explored (Steele & Hayes, 1991), and several types of relational responses are described by RFT (see Hayes et al., 2001, for a discussion). From an RFT perspective, responding in accordance with stimulus relations includes the properties of mutual entailment, combinatorial entailment, and the transformation of function. With respect to the property of mutual entailment, if a given stimulus is related to another, such that Stimulus A is the same as Stimulus B, then the derived relation B same as A is mutually entailed. This property operates in a manner consistent with symmetry (Sidman, 1986). However, if A is greater than B, then the relation B less than A is mutually entailed. In another form of relations, if A is the opposite of B, then B opposite of A is mutually entailed. At the same time, if B is the opposite of C, then C opposite of B is mutually entailed. Given all of the above, the relation C same as A and A same as C is derived and described by RFT as combinatorial entailment (O'Hora, Roche, Barnes-Holmes, & Smeets, 2002).
Behavioral researchers are now exploring innovative methodologies to investigate stimulus relations pertaining to sameness, opposite, more than, and less than (e.g., Dymond & Barnes, 1995); opposite and same (e.g., Dymond & Barnes, 1996); temporal, spatial, and deictic (e.g., Barnes & Roche, 1997); and opposition, distinction, analogical, and metaphorical (e.g., Stewart, Barnes-Holmes, Hayes, & Lipkens, 2001; Stewart, Barnes-Holmes, & Roche, in press; Stewart, Barnes-Holmes, Roche, & Smeets, 2001). Even before most of these controversial studies addressed the potential value of new approaches to multiple stimulus relations (see Galizio, 2003, for a discussion), Hayes and Barnes (1997) argued for the development of more basic and applied research to explore verbal learning and problem-solving applications (see Barnes-Holmes & Hayes, 2003, for a response to Galizio). In our view, these studies do not contradict stimulus equivalence. However, RFT tries to identify additional variables that may interact with the emergence of new types of derived stimulus relations.
In this vein, we were interested in determining if RFT preparations might have practical problem-solving applications for instruction of particular types of mathematical relations. For example, several fundamental formulas (e.g., linear, square root functions, logarithmic, exponential, sine, tangent, etc.) have graphical functions, such that each type of formula operates on the coordinate axis in a way that is analogous to other types of mathematical functions. Very much like the arbitrary stimuli used in computer-interactive MTS procedures, for individuals with limited mathematical histories, formulas and their graphical representations may seem completely ambiguous and arbitrary. However, an individual who has learned the relations between particular types of formulas and the graphs of these functions may be well positioned to identify new relations insofar as different types of formulas generate graphs (as well as other types of formulas) that are analogous.
Most RFT, as well as stimulus equivalence, researchers have refrained from appealing to rule governance to explain the formation of stimulus relations or even to develop training procedures that employ complex instructions (see Hayes, Barnes-Holmes, & Roche, 2003, for a discussion). In computerized procedures (e.g., Stewart, Barnes-Holmes, Roche, & Smeets, 2002), the sample stimuli often appear in one sector of the screen while comparison stimuli are contrasted in separate partitions of the display. Participants click on what they believe to be the correct comparison stimulus and receive accuracy feedback from the computer. Although this is an elegant system for studying arbitrary stimulus relations (cf. Horne & Lowe, 1996), it is not, nor was it intended to be, particularly efficient in teaching complex verbal relations in an academic setting. And, practically speaking, mathematics instructors (or designers of computer-assisted mathematics software) would find it untenable to ask their students or software users to become skilled at complex mathematical operations without introducing them to precise rules for solving the problems in question (Ninness, McCuller, & Ozenne, 2000). Nevertheless, we believe that computer-interactive MTS platforms with instructional applications might incorporate functional analytic strategies based on stimulus equivalence and RFT protocols.
In a recent study by Ninness et al. (in press), participants demonstrated mutual entailment on formula-to-graph and graph-to-formula relations and were assessed for 36 novel variations of the original training formulas and their graphical representations. Many of the participants demonstrated perfect or near-perfect performance on all novel relations. Nevertheless, other participants made several errors during the first assessment of novel formula-to-graph relations. Error patterns were classified with the help of a self-organizing map (Kohonen, 2001), and a new training protocol was developed to remediate the dominant error patterns exhibited during the first experiment. Following training on the revised protocols, all participants demonstrated a substantial reduction in errors relative to their earlier performance.
The present investigation continues to focus on the transformation-of-function graphs (not transformation of stimulus functions, as discussed in RFT); however, we have attempted to expand our training protocols. In reviewing strategies for training formula-to-graph relations, it became apparent that most textbooks and software systems do not incorporate explanations in conjunction with direct practice in addressing formula-to-graph relations (cf. Zaskis, Liljedahl, & Gadowsky, 2003). This seems to be particularly true when the standard forms of formulas contain −1 coefficients in the leading x variable [e.g., y = log(−x − 4)]. The present study extends our previous research in this area by employing a brief lecture followed by a computer-interactive program to train the relations between standard formulas to more easily understood factored formulas and factored formulas to their graphical representations. The lecture was followed by computer-interactive training and MTS procedures that assessed mutual entailment and combinatorial entailment. Subsequently, participants were probed over an array of novel and complex formula-to-graph relations.
It is worth noting that the formulas employed as sample or comparison elements were not unique, and any number of rearranged formulas might have generated the same graphs. Participants were not trained to relate a specific formula and graph as unitary stimuli; rather, they were trained to identify relations contained within the samples and comparisons. That is, we attempted to train participants to identify the relations contained within the formulas to the relations contained within other formulas and graph analogues. RFT, with its emphasis on conceptual and empirical analyses of identifying relations, seemed most appropriate for this type of experimental preparation. In training A-B, standard formulas (highest power variables first and constants last) served as samples and factored formulas served as comparisons. In training B-C, factored formulas served as samples and graphs served as comparisons. Combinatorial entailment testing assessed participants' understanding of the relations between the graphical versions of the formulas (C) and the original standard formulas (A) as well as C-A relations. Following demonstration of combinatorial entailment, participants responded to 40 novel standard and factored formulas relative to their respective graphed functions.
Method
Participants and Setting
Eleven participants, ranging in age from 15 to 37 years, were recruited among university students and employees from a local hospital rehabilitation facility and their family members. Following informed consent and a pretest to determine level of familiarity with various mathematical functions, individuals who demonstrated any familiarity with algebraic or trigonometric transformation of functions were excluded from the experiment. Specifically, any potential participant who answered more than 2 of 15 pretest items correctly was eliminated from the participant pool.
One participant required a specialized training format. Participant 6 was a 15-year-old boy who had previously been diagnosed as dyslexic. During training, he was unable to read most of the directions on the computer screen for the formula-to-graph modules, so the experimenter read the directions on the screen for the A-B and B-C modules to him. However, no other form of assistance was provided during any part of the training session, and the participant performed all items on the assessment of novel relations independently.
Undergraduate and graduate student participants earned 3 extra points toward their final class examination grade. Hospital employees and their family members were recruited through personal contacts and received financial reimbursement ($10) for their participation. In addition, all participants were paid 10 cents for every correct response during the assessment-of-novel-relations phase of the study (maximum of $4). After completion of the experiment, all participants were debriefed and compensated. The experimental sessions were carried out in empty classrooms of the university campus or offices of the hospital rehabilitation facility. These settings were arranged to preclude distractions or interruptions, and they remained free of noise throughout the study.
Apparatus and software
All software for this study was developed on a Dell Dimension® 4400 computer (Pentium 4 1.8-GHz processor with 768 MB RAM). The mathematical instructional and MTS modules were written in Microsoft® Visual Basic 6 for IBM PC-compatible machines by the first author. The software provided math instructional tutorials and displayed graphs, and it assessed and recorded the speed and accuracy of user performance during all phases of the study. In addition, the first author modified the self-organizing map algorithm in C++ to categorize error patterns based on Kohonen's logic for these algorithms (see Kohonen, 2001, for a discussion). The experimental procedures were conducted on a Hewlett-Packard Pavilion® ze5170 (Pentium 4 2-GHz processor with 512 MB RAM) with an attached infrared mouse. A microphone sat adjacent to the computer, and it was conspicuously attached to the side port of the computer.
Design and Procedure
Following informed consent, participants who demonstrated no familiarity with algebraic and trigonometric functions relative to vertical and horizontal shifts were asked to continue with the experiment. Following a brief pretraining presentation, participants were escorted to their respective computers in isolated rooms and computer-interactive training was initiated. Procedures included training and testing of A-B and B-C relations and the assessment of mutually entailed (B-A and C-B) and combinatorially entailed (A-C and C-A) relations. The program then assessed participants on 40 novel relations between formulas and the graphs of these functions (see Table 1).
Table 1. Sequence of Training and Assessment Conditions.
| Stage 1. Pretraining presentation on basic relations | |||
| Provide A-B rules | Provide A-B exemplar with formulas | ||
| Provide B-C rules | Provide B-C exemplar with formula and graph | ||
| Stage 2. Computer-interactive training and testing of complex relations | |||
| Trained relations | Mutual entailment | Combinatorial entailment | Novel relations |
| A1-B1 | B1-A1 | A1-C1 | [e.g., y = −sin(x) + 6] |
| B1-C1 | C1-B1 | C1-A1 | |
| A2-B2 | B2-A2 | A2-C2 | |
| B2-C2 | C2-B2 | C2-A2 | |
| A3-B3 | B3-A3 | A3-C3 | |
| B3-C3 | C3-B3 | C3-A3 | |
| A4-B4 | B4-A4 | A4-C4 | |
| B4-C4 | C4-B4 | C4-A4 | |
Stage 1: Pretraining presentation of basic mathematical relations
The presenter conducted pretraining lectures in small groups (2 or 3 participants at a time) and included projections of formulas and graphs on an overhead screen above the lectern. The presenter read rules regarding basic mathematical operations directly from the overhead transparency and responded to questions from participants only insofar as they were directed at sample-to-comparison items (A-B or B-C). At no time were the relations of B-A, C-B, A-C, and C-A displayed or discussed.
Step 1: Provide A-B rules. In pretraining A-B rules, it was explained that a negative coefficient of x inside the standard form of a formula often complicated the graphing of a function. It was further explained that the standard form of the square root formula could be factored to remove any negative signs that precede the x variable.
In describing this and all A-B relations, standard formulas (highest power variables first and constants last) served as illustrations of samples, and factored formulas served as comparisons. The participants were shown a basic square root function in its standard form and how it can be expressed when a −1 coefficient is factored out of the argument. In the pretraining and computer training, we used the words negative sign rather than −1 coefficient and conducive rather than factored because most of our participants had no familiarity with, or misleading interpretations of, the latter terms.
Step 2: Provide B-C rules. Because many of our participants were unacquainted with the rectangular coordinate system, the presenter explained that the horizontal number line is called the x axis and that the vertical number line is referred to as the y axis. Further, it was explained that various types of formulas were called functions and could be used to generate graphs on the coordinate axes. In describing functions for B-C relations, factored formulas served as samples and graphs served as comparisons. Using an overhead transparency, the presenter read rules explaining that a negative sign inside the radical reflects the graph over in (about) the y axis and that a negative sign outside the radical or the parentheses reflects the graph down in (about) the x axis. Similarly, the presenter explained that a constant value added or subtracted outside the radical or the parentheses moves the graph up or down the y axis in the same direction indicated by the sign. The overhead transparency was identical to a screen later used by the computer-interactive program that followed this lecture.
Step 3: Provide A-B exemplar. In this step, participants were shown an example of an A-B test screen, where A was represented as a standard square root formula and B as one of six factored square root formulas or comparisons. The presenter explained that a very similar type of selection format would be employed in the forthcoming computer-interactive training session and used a pencil to tap the letter of the correct comparison item displayed on the overhead.
Step 4: Provide B-C exemplar. The participants were shown an example of a B-C test screen, where B was the factored formula and C was one of six possible graphical representations of that function. Again, the presenter used a pencil to tap the letter of the correct comparison item displayed on the overhead. (These A-B and B-C examples were not arranged in the same positions as those employed during the actual computer-interactive training used in Stage 2.)
All participants were exposed to the same pretraining presentation regarding the fundamentals of the rectangular coordinate system and the relation between the square root formula and its graphical representation. The entire presentation required approximately 15 min. Following the small-group presentations, participants were escorted to their respective computers, each of which was located in a separate room. Before allowing the participants to initiate the computer-interactive training and assessment program, the presenter demonstrated a point-and-click response on a sample screen and verified that the participants could perform the same response independently.
Stage 2: Computer-interactive training and testing of mathematical relations
During computer-interactive training in Stage 2, our program emphasized giving participants visual displays and audio output in the form of mathematical rules and having participants repeat these rules immediately by reading them into a microphone. In conjunction with the rule rehearsal, participants engaged in repeated practice of the behaviors specified by the rules. After training and assessing formula-to-formula (A-B) relations and formula-to-graph (B-C) relations, participants were assessed for mutually entailed formula-to-formula (B-A) relations and graph-to-formula (C-B) relations. Subsequently, the combinatorially entailed relations between the graphical versions of the formulas and the original standard formulas (C-A), and the standard form of the formulas and their respective graphical representations (A-C), were assessed.
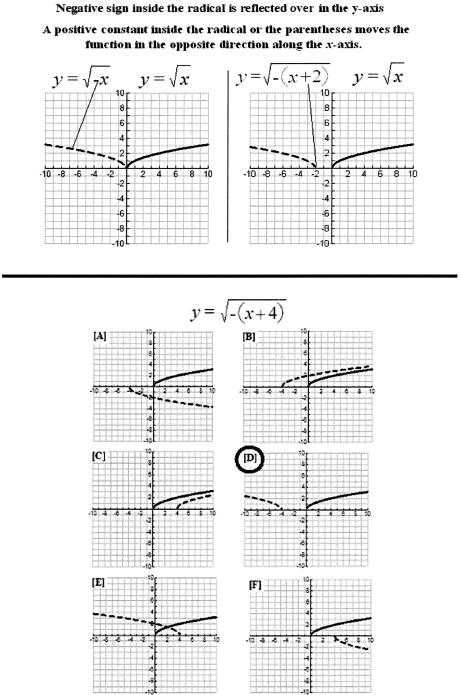
Step 1: Train A-B relations, test A-B. Computer-interactive training of A-B relations included several of the details described to the participants during the pretraining presentation. The computer provided prerecorded audio output and displayed mathematical rules on each screen. Following the audio expression of the rule, the participants read the same computer-posted rules into the microphone. For example, participants heard and recited rules indicating that the standard form of the square root formula could be factored to remove any negative signs that precede the x variable (see Figure 1, top). After participants heard and recited these rules twice, clicking “next” moved to them to a screen that assessed A-B performance (as shown in Figure 1, bottom).
Figure 1. Two training screens are displayed. The top screen shows standard and factored (conducive) forms of the square root formula when a negative coefficient precedes the x variable and a subtraction operation (−2) is provided inside the argument.
Below, an A-B test shows the correct response to the trained relations circled.
Step 2: Train B-C relations, test B-C. The same type of audio output, display, and rule-recitation format was employed to train B-C, test B-C performance. Training B-C relations included having the participants hear and recite rules regarding reflections and vertical and horizontal shifts associated with various functions on the coordinate system. The screen displayed solid blue lines to represent the basic square root function and dashed red lines to show various transformations of the square root functions. As illustrated in Figure 2 (top), these rules indicated such mathematical relations as, “Negative sign inside the radical is reflected over in the y axis. A positive constant inside the radical or the parentheses moves the function in the opposite direction along the x axis.” (We used the words over in rather than the traditional about in response to pilot testing that suggested this phrasing seemed to be easier for many participants to follow.) After participants heard and recited these rules twice, clicking “next” moved them to a screen that assessed B-C performance, as illustrated on the lower half of Figure 2. Note that although the assessment screens varied the specific values of the constants within the formulas, the correct answers were always obtainable by behaving in accordance with the rules displayed on the previous screens.
Figure 2. On top, a formula-to-graph illustration and mathematical rules pertaining to square root function transformations are displayed.
All mathematical rules, formulas, and graphical representations for horizontal and vertical shifts as well as those describing reflections in the x axis and y axis were presented in a similar format. A line drawn from the formula to the graph indicates the reason for the transformed function. At the bottom of the figure, a B-C test screen shows the correct response to the trained relation. The solid lines indicate the graph of a basic square root function (y=\sqrt x). The dashed lines indicate the possible transformation of the graph according to the sample formula. In each case, the correct response has been circled.
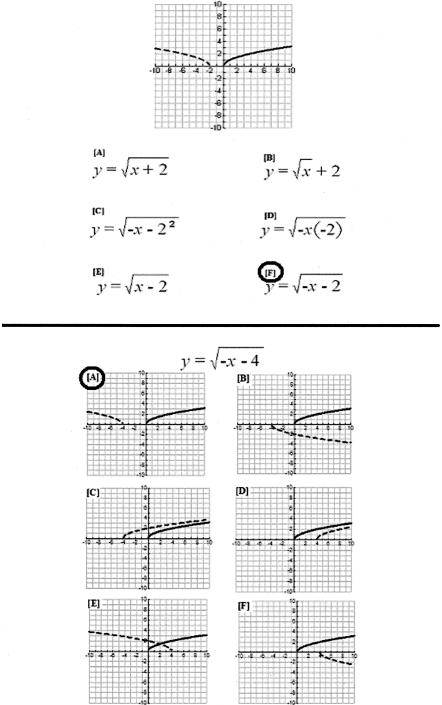
Step 3: Test B-A, test C-B, test A-C, and test C-A. This step examined the mutually entailed B-A and C-B relations as well as the combinatorially entailed relations between the graphical versions of the formulas and the original standard formulas (C-A) (Figure 3, top). Likewise, the combinatorial relations between the standard forms of the formulas and their respective graphical representations (A-C) were assessed (Figure 3, bottom).
Figure 3. On top, a test for the combinatorial relation between the graphical version of a formula and the standard formula (C-A) is displayed.
Beneath, the combinatorial relation between the standard forms of the formula and its graphical representation (A-C) is assessed. Solid lines indicate the basic square root function (y=\sqrt x), and the dashed line indicates the possible transformation of the graphs according to the sample formula. In each case, the correct response has been circled.
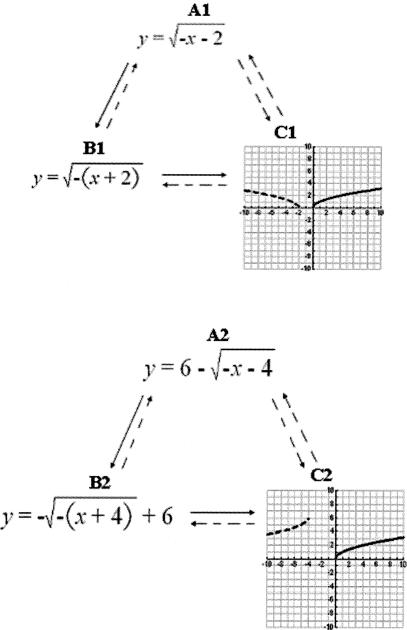
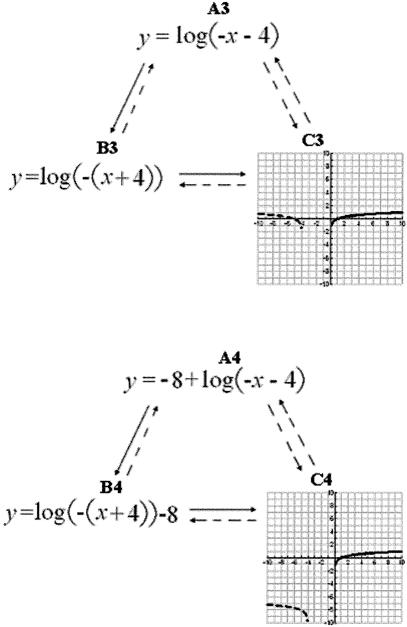
In total, the program aimed to develop four three-member classes of relations made up of formula-to-formula and formula-to-graph relations. All mathematical rules, formulas, and graphical representations for horizontal and vertical shifts as well as for reflections in the x axis and y axis were presented according to this format. Specifically, the program provided training and testing on two versions of the square root function and two versions of the common logarithmic function. Figures 4 and 5 illustrate the trained, mutually entailed, and combinatorially entailed relations. Figure 4 specifies the elements of basic square root function as A1, B1, and C1 and a more complex square root function as A2, B2, and C2. Figure 5 shows the training and testing form for the log functions A3, B3, and C3 followed by a more complex log function of A4, B4, and C4. After each trained (A-B and B-C) relation, the program assessed for mutually entailed (B-A and C-B) relations as well as combinatorially entailed (C-A and A-C) relations. If a participant failed to produce a correct response during any MTS tests, they were reexposed to the entire relational training and testing cycle, beginning with the first (A1-B1) training screen.
Figure 4. The top section shows the trained and tested elements of basic square root function A1, B1, and C1.
Below, a more complex square root function A2, B2, and C2 is displayed.
Figure 5. The top screen shows training and testing of the log functions A3, B3, and C3, followed a more complex log function of A4, B4, and C4 at the bottom.
Note that in the graphical representation of our logarithmic functions, we do not show f(x) continuing − ∞.
Correction procedures and mastery criteria
Our mastery criterion required participants to complete one errorless sequence of all four classes of relations, each consisting of six MTS problems (A-B, B-C, B-A, C-B, A-C, and C-A). Mastery was comprised of 24 consecutive correct MTS responses. A participant who made an error during the assessment of trained, mutually entailed, or combinatorially entailed relations was cycled back to the beginning of the program and was reexposed to the entire training and testing sequence. Here, the program randomized all comparison elements before initiating the new training cycle. In the event that a participant required more than five training cycles, the program terminated, and the participant was paid, debriefed, and excused from the experiment.
Assessment of novel relations
Following demonstrations of mutual entailment and combinatorial entailment on both versions of the square root functions and both versions of the common logarithmic functions, the program assessed participants on novel relations between formulas and their graphically represented functions. Novel algebraic and trigonometric functions were composed of 40 complex variations of the originally trained mathematical relations. Each test item required participants to match a new formula with a graph from an array of six that had not been employed during any of the training and assessment screens. (The comparison graphs were all of the same type of mathematical function; e.g., a logarithmic formula was compared only against variations of logarithmic graphs.) No form of accuracy feedback or recycled training was provided during any of the tests for novel relations. This task entailed identifying graphs that represented formulas with new combinations of positive and negative constants preceding and following various square root and logarithmic functions. Moreover, testing novel relations included multiple combinations of reflections and vertical and horizontal shifts for complex exponential, square, cubic, tangent, and sine functions.
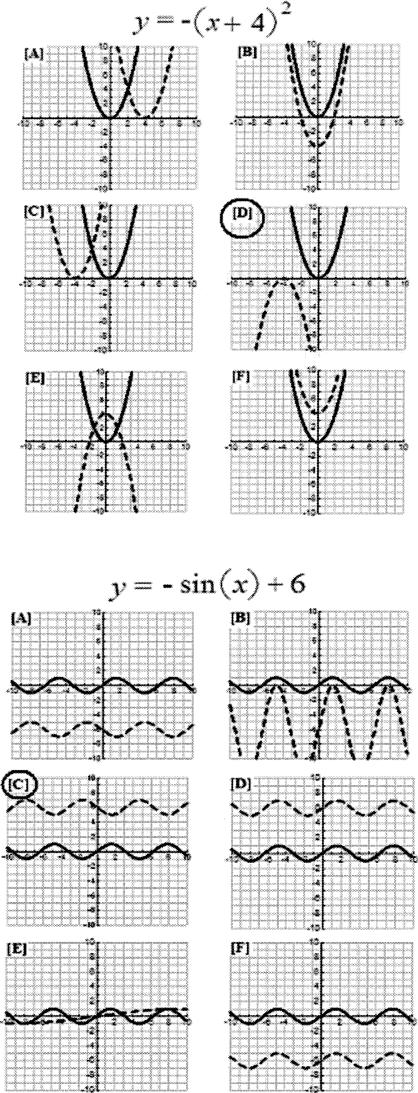
Figure 6 shows two of the 40 tests for novel relations. When presented with a formula for a squaring function that included a leading negative one coefficient preceding the argument and positive constants within the argument, a participant who answered correctly would select D as the graphed reflection and accompanying shift along the x axis. If shown a formula of a sine function in which a −1 coefficient preceded the argument and a positive constant was placed after the argument, a participant who identified the transformation of function correctly would select C.
Figure 6. Two of the 40 tests of novel formula-to-graph relations are shown.
The solid lines represent the basic squaring function (y = x2), and the dashed lines indicate the possible transformation when the formula becomes more complex. On top, a participant who identified a novel variation of formulas that include a negative one coefficient in front of the argument and a positive constant within the argument would select D. Beneath, the solid lines represent the basic sine function [y = sin(x)], and the dashed lines indicate the possible transformation when the formula becomes more complex. A participant who identified the transformation that occurs with a negative one coefficient in front of the argument and a positive constant is placed after of the argument selected C as the correct response.
As additional probes of novel relations, three of the novel formulas contained correct but somewhat misleading constant values as prefix and postfix operations (−1 with +1 and −4 with +4); specifically, participants were shown the following: y = −1 + log (−x − 4) + 1 and y=-4+\sqrt{-(x+4)}+4. The third formula also contained redundant negative coefficients in the prefix: y = −(x + 4)2. Again, all three probes were algebraically correct and consistent with an assessment of novel mathematical relations, but they were unlikely to be encountered as actual formulas within most texts or software systems. All of the other sample formulas in the assessment of novel relations were presented in their usual standard or factored forms.
Results
Ten participants completed all training modules within twenty or fewer training screens. Voice recordings of these participants' recitations of rules were audible and complete. Table 2 shows the number of exposures needed for the 10 participants to complete the trained A-B and B-C relations. Most participants mastered the computer-interactive training sequence in a relatively small number of exposures.
Table 2. Number of Training Exposures Required to Attain Mastery.
| Participant | A1-B1 | B1-C1 | A2-B2 | B2-C2 | A3-B3 | B3-C3 | A4-B4 | B4-C4 | Total |
| 1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 10 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 14 |
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 20 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 8 |
| 5 | 3 | 3 | 3 | 3 | 2 | 2 | 1 | 1 | 18 |
| 6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 8 |
| 7 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 20 |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 8 |
| 9 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 12 |
| 10 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 18 |
Errors for each participant are displayed in Figure 7. The number of MTS errors on each tested relation is represented with shaded digits 1 or 2, corresponding to the number of errors made. Open blocks of zeros represent the absence of an error during the assessment of a given relation. Figure 7 shows that 7 of the 10 participants made one or more errors in deriving A-C or C-A combinatorial relations. Participants 1 and 10 made errors in identifying C1-A1 when the comparison formula included a leading negative coefficient of x in the argument in the standard form of the square root function (Figure 4). Participants 5, 7, and 9 failed to derive the combinatorial relation C2-A2. This square root formula involved a constant (6) and a negative coefficient in front of the argument. It also included a negative coefficient of x and a negative constant inside of the argument. Participant 7 made this same error in the form of A2-C2 when he attempted to identify the graph that matched this formula. Accordingly, he was cycled back to the beginning of the program on two separate occasions and received three training exposures (Table 2). Participants 2 and 3 made errors in deriving C3-A3 combinatorial relations when the logarithmic formula contained a negative x followed by a negative constant inside the argument (refer to Figure 5). Participant 3 made the same incorrect response on two consecutive occasions and was recycled through the program accordingly. Participants 4, 6, and 8 made no errors during the assessment of trained or derived relations.
Figure 7. Errors for each participant are displayed.
The number of MTS errors on each tested relation is represented with shaded digits 1 or 2. A 0 represents the absence of an error on a given test.
Only 2 participants made errors with regard to the property of mutual entailment. During her second cycle through training and testing, Participant 5 failed to derive C3-B3 when the sample graph reflected about the y axis and shifted in the negative direction along the x axis. The correct comparison formula was a negative logarithmic function in its factored form (refer to Figure 5). Participant 10 made a similar error during her second cycle in deriving C4-B4 when the sample graph reflected about the y axis, shifted in the negative direction along the x axis, and shifted in the negative direction along the y axis. The correct comparison formula was in its factored form of the logarithmic formula. As shown in Table 2, both participants were cycled back to the beginning of training when these errors occurred.
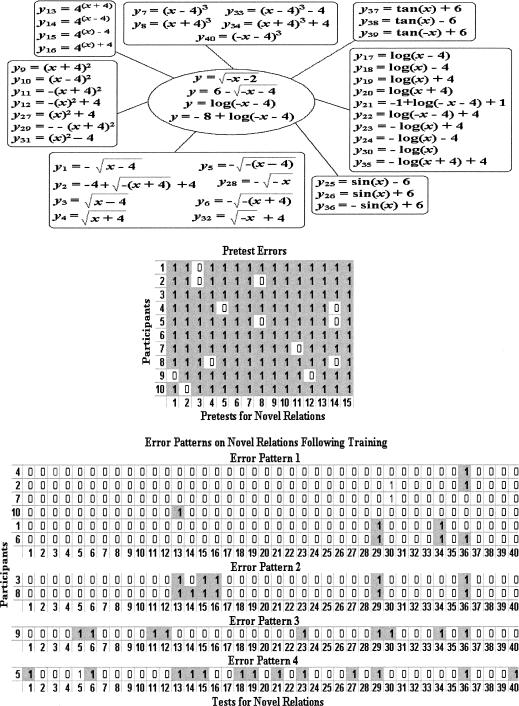
The top of Figure 8 shows the standard forms of the original four formulas (A1, A2, A3, and A4) in their standard forms employed during training. These four formulas (in the center of the illustration) served as the foundation for developing the trained and derived relations. The periphery shows the 40 formulas that were employed in probing novel formula-to-graph relations. The y subscripts identify the order in which these formulas appeared in the assessment sequence (e.g., y14 = 4(x−4) was the 14th item on the test of novel relations).
Figure 8. The top shows the four standard functions (four formulas within the center oval) employed during training and assessment of stimulus relations.
Formulas on the periphery were used as sample stimuli in testing novel formula-to-graph relations. The middle block shows the correct and incorrect responses on the pretest. Problem numbers are listed along the x axis for each of the 10 participants. Accurate responses contain the digit 0; errors are shaded blocks that contain 1.
The center of Figure 8 shows the pretest errors on 15 formula-to-graph test items. The density of pretest errors in this middle block confirms that our participants were unfamiliar with the formula-to-graph relations prior to training.
The four bottom blocks show the same participants' errors following MTS training, as classified and grouped by the self-organizing map. The first 15 items were the same as those used in the pretest but were novel in terms of the participants' MTS training experience. The remaining 25 items (16 through 40) consisted of an additional 25 novel stimuli that were not used during any part of training or pretraining.
Error Pattern 1 contains data for the 6 participants who completed training with perfect or near-perfect performance, obtaining at or above 92.5% accuracy in identifying novel algebraic and trigonometric formula-to-graph relations. With only a few exceptions, the small number of errors was associated with not recognizing graphical representations when the formula contained redundant negative signs preceding the argument (y29 in Figure 8) or when a negative one coefficient preceded a sine function (y36 in Figure 8). Participant 6 demonstrated the largest number of errors in this group. These included items that addressed a double negative coefficient, an exponential function that included a constant following the argument, and a negative sine function. Participants 7 and 10 misidentified only one of the novel formula-to-graph relations.
Error Pattern 2 shows 2 participants who commonly misidentified formula-to-graph relations of exponential and negative sine functions as well as errors associated with formulas containing double negative signs preceding the argument. Error Pattern 3 includes 1 participant who made a series of incorrect responses that have much in common with those in Error Pattern 2. Errors for this participant were associated with several different types of formulas that contained negative or double negative signs preceding their arguments. This participant also misidentified a cubic function and a negative sine function. Error Pattern 4 shows outcomes for the only participant who demonstrated a somewhat more diversified and scattered series of errors across a wider range of novel formula-to-graph relations. Participants averaged 38 min (range, 26 min to 57 min) to complete training, MTS testing, and probing of novel mathematical relations.
There appears to be little correspondence between the total number of training cycles to reach mastery and the number of errors obtained during the assessment of novel relations that followed. For example, Participant 5 was exposed to a total of 18 training screens and made the largest number of errors during the assessment of novel relations. Participant 10 was exposed to a total of 18 training screens and made only two errors in the assessment of novel relations.
Discussion
These results are consistent with our previous study (Ninness et al., in press), in which participants demonstrated mutual entailment on formula-to-graph functions and subsequently identified relations between new formulas and their respective graphically displayed representations. The present results advance the previous work by employing MTS strategies that assess mutual entailment and combinatorial entailment and propagate a more extensive repertoire of formula-to-graph relations. Novel formula-to-graph relations included identifying graphical functions when formulas involved combinations of constants in new positions inside and outside function arguments, combinations of positive and negative signs in the prefix and postfix operations, and several new and more detailed algebraic and trigonometric functions (sine, exponential, cubic, and tangent functions) that included new combinations of variables and constants inside and outside the arguments of these novel formulas. We are not suggesting that, following this brief training and MTS exercise, participants understood all of the mathematical dynamics of these functions; however, having learned to factor particular types of formulas and to identify particular graphical functions with a limited array of exemplars, participants demonstrated a generalized ability to derive a wider range of more complex formula-to-graph relations.
Although several participants had taken intermediate algebra, none of them had any familiarity with the procedures provided during training. Preexperimental inquiry and pretesting revealed that they had no understanding of mathematical functions addressing vertical and horizontal shifts or reflections. Moreover, they were unable to factor standard versions of formulas correctly. In fact, any potential participant who answered more than 2 of 15 pretest items correctly was eliminated from the participant pool. As noted above, Participant 6 was a 15-year-old boy who had previously been diagnosed as dyslexic. During training, he was unable to read most of the directions in the formula-to-graph modules, so the experimenter read the directions for the A-B and B-C modules to him. However, no other form of assistance was provided during any part of the session. This participant proceeded to get every B-A, C-B, A-C, and C-A comparison correct on the first trial throughout all test screens. The assessment of novel relations that followed did not require any reading of directions, and he performed this phase of the study independently. He missed only three of the 40 complex variations of the original formula-to-graph relations.
Caveats
Our interactive training software is not sufficiently developed for general dissemination. Nevertheless, the general approach described in this study might well be adapted to traditional modalities of instruction. Indeed, Lynch and Cuvo (1995) and Leader and Barnes-Holmes (2001) conducted a series of instructional procedures that employed many of the steps described herein. In addition, we are developing a Web-based version of this project on our Web site at www.lcsdg.com/psychStats. Upon completion, it will be freely available to interested users.
This study did not attempt to differentiate the influence of the pretraining lecture from the effects of computer-interactive MTS training procedures that followed. Because most of our participants were unfamiliar with the x, y coordinate system, some minimal level of preparation was required for them to interact effectively with the computerized training program. Nonetheless, future research should attempt to isolate the entry level of skills critical to initiating training on such platforms.
Four participants displayed five or more errors during tests of novel relations. The dominant error pattern among these participants was failure to recognize the graphs associated with exponential functions. This may not have been due to the inherent complexity of the function per se as much as the particular elements within these functions. That is, the four sample formulas that we employed in our assessment of novel exponential functions all included a base of 4 in conjunction with various forms of exponents of 4 (e.g., y = 4(x+4)). The simultaneous use of 4 in the base and exponent within these novel formulas may have compounded the ambiguity of the expressions. The error patterns of 2 other participants showed most of the above errors plus several diversified and idiosyncratic errors. Future research should attempt to identify variables that interact with such error patterns.
Tests for Novel Relations in Applied Settings
Manipulating symbols to identify new relations among variables is a ubiquitous characteristic of human behavior. Most conspicuously, problem solving in science and technology requires the abstraction and reorganization of complex stimuli into new relations among objects and events. Tests for novel relations allow participants to identify different and more complex sequences of stimulus relations not included in the training protocol.
The mathematical relations reported by participants in the current study (formula to graph) are not specifically symmetrical. Showing participants novel formulas allowed them to identify a vast network of relations extending from the exemplars provided during training. It might be argued that if our participants were learning to form four three-member classes made up of formulas and graphs in the same way as they would in using completely arbitrary shapes or nonsense syllables, then we might expect less adequate performance in tests involving novel stimuli. However, one interpretation is that they were not relating formulas and graphs as unitary stimuli but were identifying the relations contained within the samples and comparisons. This view is consistent with findings from previous basic research investigating relational frames pertaining to same as, more than, and less than (e.g., Dymond & Barnes, 1995) as well as temporal, spatial, and deictic relations (e.g., Barnes & Roche, 1997). One advantage to this perspective is that it may lend itself to the development of better MTS training platforms and allow students to learn composite relations among more complex operations.
As in Ninness et al. (in press), our outcomes suggest that error patterns displayed by participants are not necessarily due to negligence, nor are they necessarily the result of insufficient practice. Debriefing revealed that many participants made incorrect inferences regarding problem-solving strategies. In some of our pilot and earlier research in related areas (e.g., Ninness & Ninness, 1998, 1999), we found that several incorrect problem-solving strategies produced correct answers intermittently and thus perpetuated intermittent errors as well as occasional accurate responses throughout the experimental sessions. Given these fairly common circumstances in working with many types of math problems (Ashlock, 2002), it is hardly surprising that some students become confused and exasperated while trying to learn mathematical relations. Our present adaptation of the self-organizing map operates somewhat like a descriptive analysis insofar as it classifies error patterns across various types of problems within the study. These error patterns may be useful in refining the next generation of computer-interactive training platforms. Although it is true that a rigorous visual inspection of errors would eventually produce a similar pattern of correct and incorrect responses within and between participants, the self-organizing map performs this operation almost instantly while allowing the user to calibrate the software at specific levels of precision.
In a previous study (Ninness et al., in press), 10 of 15 participants required supplemental training to derive nearly all relations successfully. Having access to a pattern of errors allowed us to intervene more efficiently with a second level of MTS procedures. Error patterns classified by the self-organizing map allowed us to provide specific remediations regarding formula-to-graph relations that participants found particularly challenging. However, in the current version of our experimental architecture, based on previously identified error patterns, we provided a more intensive training platform than existed in any of our previous attempts. In this study, MTS procedures repeatedly assessed participants for mutual entailment and combinatorial entailment on two versions of a square root function and two versions of a log function before allowing them to be assessed on novel relations. Following training, 8 of 10 participants in this study obtained at or above 85% accuracy on tests of novel relations, and 6 of these 10 obtained 92.5% or better. Following training, participants were no more likely to make errors associated with novel variations of A-C [e.g., y = (−x − 4)3] than they were to make errors that were novel variations of B-C [e.g., y = (x − 4)3]. This result suggests that linear training procedures that incorporate tests for mutual entailment may be fairly efficient in terms of generating expanded mathematical repertoires.
Future MTS procedures might focus on mutually entailed and combinatorially entailed mathematical relations that emerge from more robust and sophisticated computer-interactive MTS platforms. Such investigations might survey the combination of MTS preparations in conjunction with feedback from the self-organizing map to identify error patterns within and between participants. At the same time, training that focuses on the combinatorially entailed properties of more complex trigonometric and calculus functions and their graphical representations might prove beneficial for applied and basic research purposes.
Similarly, procedures that further explore the rudiments of relational skills in algebra still are needed. For example, a quadratic function expressed as y = x2 − 6x entails factoring (completing the square) to obtain y = (x − 3)2 − 9. This factored version of the formula may allow a student who has learned to identify formula-to-graph relations by way of the above experimental exercises to identify y = (x − 3)2 − 9 as a graph that shifts horizontally by three units (to the right) and vertically nine units. Pilot research in our laboratory suggests that several individuals who had difficulty identifying graphs of quadratic functions were able to learn these relations more efficiently following the type of MTS training used in this study. Moreover, learning to identify these relations appears to be generative, which may be useful in training higher levels of mathematical operations. In calculus, for example, it may be beneficial to consider an intricate function as the sum, difference, product, or quotient of a less complex network.
Research that moves beyond the present study to more sophisticated architectures and more extensive MTS procedures might provide a much wider range of combinatorially entailed formula-to-graph and graph-to-formula relations. Of course, as in the teaching of phonics via direct-instruction procedures, there are exceptions to the rules of nonarbitrarily derived mathematical relations. For example, there are numerous odd functions in which negative coefficients positioned outside or inside the argument generate identical graphs. As one illustration, the function y = −sin(x) is graphically indistinguishable from y = sin(−x). Nevertheless, odd (and even) trigonometric functions are explicitly governed by shifts and reflections that are variations of the basic strategies employed in this experiment. From our perspective, most basic and advanced formula-to-graph relations are well coordinated within a hierarchical network of relational frames that could be addressed within a more comprehensive computer-interactive tutorial that emphasizes MTS training. One functional alternative to waiting for students to construct improved schemas of mathematical understanding might include the development of improved MTS protocols.
Acknowledgments
We gratefully acknowledge the contributions, continual encouragements, and technical insights provided by our recently departed friend and colleague, Morris Lang, in the development of this project. His memory serves as an inspiration and guiding light for our current research.
Study Questions
Given Stimuli A, B, and C, of which A-B and B-C are directly trained in matching relations, what stimulus relations emerge according to (a) a stimulus equivalence account and (b) a relational frame theory account, and what are these relations called?
What were the three mathematical forms (A, B, C) that were of interest in the current study?
Briefly describe the training and testing of mathematical relations (Stage 2).
What was the mastery criterion, and what consequence was arranged for incorrect responding?
Briefly describe the assessment of novel mathematical relations.
Describe the data depicted in Figure 7. What do these results show with respect to effects of training?
The authors stated that participants were unfamiliar with novel formula-to-graph relations prior to training. What data support this statement?
How might the data on the bottom panel of Figure 8 be used in a prescriptive manner?
Questions prepared by Pamela Neidert and Erin Camp, University of Florida
References
- Anderson J.R, Corbett A.T, Koedinger K, Pelletier R. Cognitive tutors: Lessons learned. Journal of Learning Sciences. 1995;4:167–207. [Google Scholar]
- Ashlock R.B. Error patterns in computation: Using error patterns to improve instruction. Upper Saddle River, NJ: Prentice Hall; 2002. [Google Scholar]
- Barnes D, Roche B. A behavior-analytic approach to behavioral reflexivity. The Psychological Record. 1997;47:543–572. [Google Scholar]
- Barnes-Holmes D, Hayes S.C. A reply to Galizio's “The Abstracted Operant: A Review of Relational Frame Theory: A Post-Skinnerian Account of Human Language and Cognition.”. The Behavior Analyst. 2003;26:305–310. doi: 10.1007/BF03392084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burley H. From policy to learning: The effectiveness of developmental education at Texas community colleges. [Retrieved April 22, 2003];1997 from http://www.thecb.state.tx.us/CTC/perfdata/deved/BurleysReport.doc.
- Center for Science, Mathematics, and Engineering Education. From analysis to action: Undergraduate education in science, mathematics, engineering, and technology. Washington, DC: National Academy Press; 1996. [Google Scholar]
- CUNY trustees reaffirm commitment to remediation cutbacks. Black Issues in Higher Education. 1999. [Retrieved April 21, 2003]. p. 10. from Academic Search Premier database.
- Dymond S, Barnes D. A transformation of self-discrimination response functions in accordance with the arbitrarily applicable relations of sameness, more than, and less than. Journal of the Experimental Analysis of Behavior. 1995;64:163–184. doi: 10.1901/jeab.1995.64-163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dymond S, Barnes D. A transformation of self-discrimination response functions in accordance with the arbitrarily applicable relations of sameness and opposition. The Psychological Record. 1996;46:271–300. doi: 10.1901/jeab.1995.64-163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Educational catch-up. Christian Science Monitor. 1998. [Retrieved April 21, 2003]. p. 8. from Academic Search Premier database.
- EnabLearning. EnabLearning, Inc. partners with Mass community colleges in ground-breaking math initiative. 2002. Oct 29, [Retrieved April 17, 2003]. from http://www.enablearning.com/AboutUs/FISPE.html.
- Galizio M. Hayes S.C, Barnes-Holmes D, Roche B, editors. The abstracted operant: A review of Relational Frame Theory: A Post-Skinnerian Account of Human Language and Cognition. The Behavior Analyst. 2003;26:159–169. doi: 10.1007/BF03392084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes S.C, Barnes D. Analyzing derived stimulus relations requires more than the concept of stimulus class. Journal of the Experimental Analysis of Behavior. 1997;68:235–270. doi: 10.1901/jeab.1997.68-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes S.C, Barnes-Holmes D, Roche B, editors. Relational frame theory: A post-Skinnerian account of human language and cognition. New York: Kluwer Academic/Plenum; 2001. [DOI] [PubMed] [Google Scholar]
- Hayes S.C, Barnes-Holmes D, Roche B. Behavior analysis, relational frame theory, and the challenge of human language and cognition: A reply to the commentaries on Relational Frame Theory: A Post-Skinnerian Account of Human Language and Cognition. The Analysis of Verbal Behavior. 2003;19:39–54. doi: 10.1007/BF03392981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horne P.J, Lowe C.F. On the origins of naming and other symbolic behavior. Journal of the Experimental Analysis of Behavior. 1996;65:185–241. doi: 10.1901/jeab.1996.65-185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohonen T. Self-organizing maps. 3rd ed. Berlin: Springer-Verlag; 2001. [Google Scholar]
- Lane S.D, Clow J.K, Innis A, Critchfield T.S. Generalization of cross-modal stimulus equivalence classes: Operant processes as components in human category formation. Journal of the Experimental Analysis of Behavior. 1998;70:267–279. doi: 10.1901/jeab.1998.70-267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leader G, Barnes-Holmes D. Establishing fractional-decimal equivalence using a respondent-type training procedure. The Psychological Record. 2001;51:151–165. [Google Scholar]
- Lynch D.C, Cuvo A.J. Stimulus equivalence instruction of fraction-decimal relations. Journal of Applied Behavior Analysis. 1995;28:115–126. doi: 10.1901/jaba.1995.28-115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackey H.A, Sidman M. Teaching new behaviors via equivalence relations. In: Brooks P.H, Sperber R, MacCauley C, editors. Learning and cognition in the mentally retarded. Hillsdale, NJ: Erlbaum; 1984. pp. 493–513. [Google Scholar]
- Ninness H.A.C, McCuller G, Ozenne L. School and behavioral psychology: Research in human-computer interactions, functional assessment and treatment. Norwell, MA: Kluwer Academic; 2000. [Google Scholar]
- Ninness H.A.C, Ninness S.K. Superstitious math performance: Interactions between rule-governed and scheduled contingencies. The Psychological Record. 1998;48:45–62. [Google Scholar]
- Ninness H.A.C, Ninness S.K. Contingencies of superstition: Fallacious rules and irrelevant responding during second-order schedules of reinforcement. The Psychological Record. 1999;49:221–243. [Google Scholar]
- Ninness C, Rumph R, McCuller G, Vasquez E, Harrison C, Ford A.M, et al. A relational frame and artificial neural network approach to computer-interactive mathematics. The Psychological Record. in press. [Google Scholar]
- O'Hora D, Roche B, Barnes-Holmes D, Smeets P.M. Response latencies to multiple derived stimulus relations: Testing two predictions of relational frame theory. The Psychological Record. 2002;52:51–75. [Google Scholar]
- Ravitch D. Do it right the first time. [Retrieved April 21, 2003];Forbes. 1997 159:80. from Academic Search Premier database. [Google Scholar]
- Reese H.W. Rules as nonverbal entities. In: Hayes S.C, Hayes L.J, editors. Understanding verbal relations. Reno, NV: Context Press; 1992. pp. 121–134. [Google Scholar]
- Sidman M. Reading and auditory-visual equivalences. Journal of Speech and Hearing Research. 1977;14:5–13. doi: 10.1044/jshr.1401.05. [DOI] [PubMed] [Google Scholar]
- Sidman M. Functional analysis of emergent and verbal classes. In: Thompson T, Zeiler M.A, editors. Analysis of interaction of behavioral units. Hillsdale, NJ: Erlbaum; 1986. pp. 213–235. [Google Scholar]
- Sidman M, Cresson O. Reading and crossmodal transfer of stimulus equivalence in severe retardation. American Journal of Mental Deficiency. 1973;77:513–523. [PubMed] [Google Scholar]
- Steele D.L, Hayes S.C. Stimulus equivalence and arbitrarily applicable relational responding. Journal of the Experimental Analysis of Behavior. 1991;56:519–555. doi: 10.1901/jeab.1991.56-519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart I, Barnes-Holmes D, Hayes S.C, Lipkens R. Relations among relations: Analogies, metaphors, and stories. In: Hayes S.C, Barnes-Holmes D, Roche B, editors. Relational frame theory: A post-Skinnerian account of human language and cognition. New York: Kluwer Academic/Plenum; 2001. pp. 73–86. [Google Scholar]
- Stewart I, Barnes-Holmes D, Roche B. A functional-analytic model of analogy using the relational evaluation procedure. The Psychological Record. in press. [Google Scholar]
- Stewart I, Barnes-Holmes D, Roche B, Smeets P.M. Generating derived relational networks via the abstraction of common physical properties: A possible model of analogical reasoning. The Psychological Record. 2001;51:381–408. [Google Scholar]
- Stewart I, Barnes-Holmes D, Roche B, Smeets P.M. A functional-analytic model of analogy: A relational frame analysis. Journal of the Experimental Analysis of Behavior. 2002;78:375–396. doi: 10.1901/jeab.2002.78-375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan M, Sullivan M., III . Precalculus: Enhanced with graphing utilities. Upper Saddle River, NJ: Prentice Hall; 1996. [Google Scholar]
- Texas Higher Education Coordinating Board. The effectiveness of developmental education at Texas public institutions of higher education. 1999. Retrieved from http://www.thecb.state.tx.us/reports/PDF/0177.pdf.
- Trace M.W, Cuvo A.J, Criswell J.L. Teaching coin equivalence to the mentally retarded. Journal of Applied Behavior Analysis. 1977;10:85–92. doi: 10.1901/jaba.1977.10-85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vosniadou S, Ortony O. Similarity and analogical reasoning. New York: Cambridge University Press; 1989. [Google Scholar]
- Vygotsky L.S. Mind and society. Cambridge, MA: Harvard University Press; 1978. [Google Scholar]
- Zaskis R, Liljedahl P, Gadowsky K. Conceptions of function translation: Obstacles, intuitions, and rerouting. Journal of Mathematical Behavior. 2003;22:435–448. [Google Scholar]