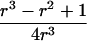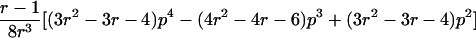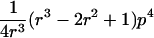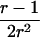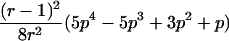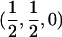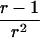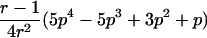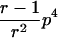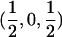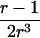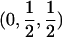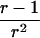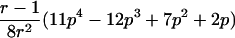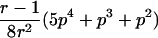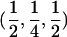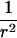Abstract
For the analysis of affected sib pairs (ASPs), a variety of test statistics is applied in genomewide scans with microsatellite markers. Even in multipoint analyses, these statistics might not fully exploit the power of a given sample, because they do not account for incomplete informativity of an ASP. For meta-analyses of linkage and association studies, it has been shown recently that weighting by informativity increases statistical power. With this idea in mind, the first aim of this article was to introduce a new class of tests for ASPs that are based on the mean test. To take into account how much informativity an ASP contributes, we weighted families inversely proportional to their marker informativity. The weighting scheme is obtained by use of the de Finetti representation of the distribution of identity-by-descent values. We derive the limiting distribution of the weighted mean test and demonstrate the validity of the proposed test. We show that it can be much more powerful than the classical mean test in the case of low marker informativity. In the second part of the article, we propose a Monte Carlo simulation approach for evaluating significance among ASPs. We demonstrate the validity of the simulation approach for both the classical and the weighted mean test. Finally, we illustrate the use of the weighted mean test by reanalyzing two published data sets. In both applications, the maximum LOD score of the weighted mean test is 0.6 higher than that of the classical mean test.
Introduction
A standard approach to mapping complex genetic diseases is the ascertainment of several affected sib pairs (ASPs). A variety of test statistics has been proposed for this study design, and most of the test are based on the identity-by-descent (IBD) value of an ASP. For some genetic markers, the IBD value can be determined uniquely for a given family. However, other markers may not be completely informative, so that the IBD distribution is ambiguous and has to be estimated from the observed marker data. Still, the ASP statistics can be applied by use of this estimated IBD distribution. One example of this application is the mean test statistic, which is often employed because of its elegance, simplicity, and optimality (Knapp et al. 1994; Whittemore and Tu 1998). The question of whether incomplete marker informativity affects the power of the utilized statistic remains.
The following example illustrates that incomplete informativity may lead to a decrease in the LOD score. Consider a small sample of 20 ASPs, all with an IBD value of 2. The mean test statistic gives a LOD score of 8.69. However, if the total sample comprises an additional 20 noninformative ASPs, the mean test LOD score drops to 4.34. Thus, the 20 noninformative ASPs do not increase the available information but, instead, lead to an extreme power loss. In most software packages, those completely noninformative ASPs would have been omitted from the analysis. If they are only slightly informative, sib pairs remain in the statistical calculation, although this does not alter the substantial LOD score drop.
The reason for this rather obscure observation is simple: all sib pairs receive the same weight in the linkage analysis, although their information content varies substantially. This defies basic statistical ideas summarized under the term “Horvitz-Thompson estimation” (Horvitz and Thompson 1952). On the basis of those ideas, observations should be weighted according to their informativity: the greater the degree of informativity, the greater the weight of an observation.
Weighting by informativity has already been proposed in the context of linkage studies for quantitative traits. For example, Amos et al. (1989) extended the classic Haseman-Elston method (Haseman and Elston 1972) by introducing a generalized least-squares approach in which the squared phenotypic difference of a sib pair is weighted proportional to its Fisher information. Sham and Purcell (2001) also weighted sib pairs by phenotypes. They linearly combined squared differences and squared sums, and the weights were determined by the overall trait correlation between the sibs in a population. Both statistics may lead to a substantial gain in power.
Unlike in studies that use quantitative phenotypes, in ASP studies, sib pairs cannot be weighted according to their phenotypic informativity, because both sibs are affected. An alternative method might be to increase power by weighting families according to marker informativity, which has already been proposed for quantitative traits. The recent regression method introduced by Sham et al. (2002) takes into account ambiguous IBD sharing by an appropriate specification of the variance-covariance matrix of IBD sharing between pairs of relatives. Sham et al. (2002) have derived the limiting distribution of the proposed test statistic and have validated their results by Monte Carlo simulations. Jacobs et al. (2003) weighted individual sib pair families for Haseman-Elston linkage analyses according to marker informativity, as measured by the difference between the allele sharing at the marker and the allele sharing at a noninformative marker. We have recently demonstrated, however, that this results in increased type I error fractions (Franke et al., in press). This led us to the conclusion that Haseman-Elston analysis with marker informativity weights should be used only in conjunction with empirical P values until the valid limiting distribution has been derived.
Weighting by informativity has been proven to be successful in the context of meta-analyses in which studies, not individual families, have been weighted (Loesgen et al. 2001; Dempfle and Loesgen 2004). The effect estimates from the single studies in the meta-analytic approach approximately follow a normal distribution by the central limit theorem, so the limiting distribution of the combined estimator can be derived easily.
In this contribution, we introduce a novel weighted mean test statistic that weights individual sib pairs according to marker informativity. Weights are based on the Euclidian distance between the IBD distribution of the marker under study and the IBD distribution of a noninformative marker. We derive the limiting distribution of the novel test statistic. We discuss the applicability of existing Monte Carlo permutation or simulation approaches, argue that previously published methods cannot be applied to the weighted test statistic, and introduce a novel method for simulating P values in ASP studies. We validate our new test statistic and the proposed simulation method in a Monte Carlo simulation study. Finally, we illustrate the application of the novel weighted mean test by reanalyzing two published data sets.
The Classical Mean Test
For the classical mean test, consider a sample of n independent ASPs, and let 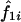 and
and 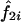 denote the estimated probability that sib pair i shares 1 or 2 alleles IBD, respectively. Further, let
denote the estimated probability that sib pair i shares 1 or 2 alleles IBD, respectively. Further, let 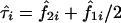 be the observed proportion of alleles shared IBD for sib pair i. Under the null hypothesis of no linkage between the marker and trait loci, the expected mean proportion of alleles shared IBD by an ASP is 1/2. In other words, if we let
be the observed proportion of alleles shared IBD for sib pair i. Under the null hypothesis of no linkage between the marker and trait loci, the expected mean proportion of alleles shared IBD by an ASP is 1/2. In other words, if we let
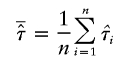 |
be the observed mean proportion of alleles shared IBD, then 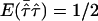 under the null hypothesis. The mean test statistic is given by
under the null hypothesis. The mean test statistic is given by
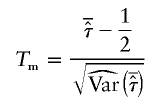 |
(see, e.g., Olson 2002), where the denominator may be replaced by 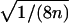 under the null hypothesis of no linkage. In this case, Tm asymptotically follows a standard normal distribution, and its mean is >0 for ASPs under linkage.
under the null hypothesis of no linkage. In this case, Tm asymptotically follows a standard normal distribution, and its mean is >0 for ASPs under linkage.
Greater power of the mean test statistic and a better approximation to the normal distribution can be achieved by replacing the denominator with an empirical variance estimate. For example, in the software package S.A.G.E. (2004, p. 221, eq. [10.1]), 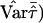 is replaced by
is replaced by 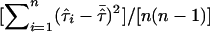 , and we denote the resulting test statistic by Tmev.
, and we denote the resulting test statistic by Tmev.
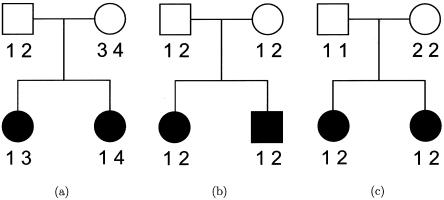
Figure 1 illustrates the fundamental shortcoming that underlies the standard mean test for ASPs. It displays marker data of a notional locus for three nuclear ASP families. The IBD value of ASP (a) can be uniquely determined, whereas uncertainty remains for the other two pedigrees, (b) and (c). Although these families have markedly different degrees of informativity for linkage analysis, they share the same proportion of alleles IBD—namely, 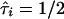 . They thus contribute equally to Tm, since
. They thus contribute equally to Tm, since 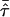 is an unweighted mean. Our alternative suggestion is to take marker informativity of a sib pair into account, and a measure for marker informativity is delineated in the next section.
is an unweighted mean. Our alternative suggestion is to take marker informativity of a sib pair into account, and a measure for marker informativity is delineated in the next section.
Figure 1.
Three ASP families with varying degrees of informativity. Sib pair (a) shares 1 allele IBD; sib pair (b) shares either 0 or 2 alleles IBD, with equal probabilities; and sib pair (c) is completely uninformative for linkage. For all three sib pairs, the proportion of alleles shared IBD is 0.5.
Simplex Weighting Scheme
Let us begin by considering the space of IBD distributions that can be represented by an equilateral triangle of height 1, termed the “de Finetti triangle” (Franke et al., in press). If an ASP is completely noninformative at a genetic marker, its IBD distribution is (1/4,1/2,1/4). A natural approach to measure distance is Euclidian distance, and we (Franke et al., in press) have shown that the Euclidian distance between an uninformative marker and the actual IBD distribution f=(f0,f1,f2) is given by
 |
Therefore, d=0 for a sib pair that is completely noninformative at a marker locus. In contrast, d equals 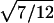 for sib pairs sharing 2 or 0 alleles IBD and equals 1/2 for sib pairs sharing 1 allele IBD. These different distances for sib pairs sharing 2 or 0 alleles versus 1 allele IBD naturally reflect the variability in informativity of sib pairs sharing 1 allele IBD, depending on the underlying genetic model. Thus, one expects a sharing of 2 alleles IBD under a recessive model of inheritance, whereas 1 or 2 alleles shared IBD are reasonably expected for a simple dominant genetic model.
for sib pairs sharing 2 or 0 alleles IBD and equals 1/2 for sib pairs sharing 1 allele IBD. These different distances for sib pairs sharing 2 or 0 alleles versus 1 allele IBD naturally reflect the variability in informativity of sib pairs sharing 1 allele IBD, depending on the underlying genetic model. Thus, one expects a sharing of 2 alleles IBD under a recessive model of inheritance, whereas 1 or 2 alleles shared IBD are reasonably expected for a simple dominant genetic model.
By use of equation (1), Euclidian distance weights wi are defined as the normalized Euclidian distance between the noninformative marker situation and the estimated IBD sharing information for ASP i, with 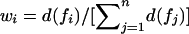 such that
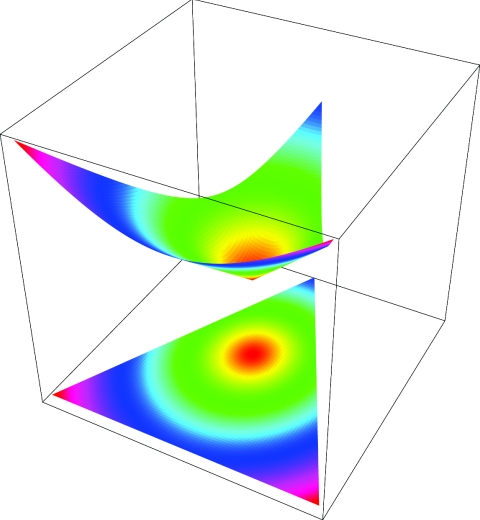
such that 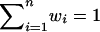 . Figure 2 illustrates the Euclidian distances in both a three-dimensional representation of di, plotted over the triangular space of IBD distributions, and a two-dimensional representation. Points with identical colors have identical weights.
. Figure 2 illustrates the Euclidian distances in both a three-dimensional representation of di, plotted over the triangular space of IBD distributions, and a two-dimensional representation. Points with identical colors have identical weights.
Figure 2.
Euclidian distances in the space of IBD distributions. The curved plane shows the relation between the informativity of a specific IBD distribution and the weight assigned to this distribution. Weights increase with increasing distance from (1/4,1/2,1/4), which is the center of the displayed circles. The triangle below the plane is an orthogonal projection of the contours of the plane above.
The Weighted Mean Test
As a test for linkage, we propose to replace the original unweighted mean from the classical mean test with the weighted mean
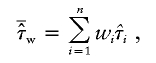 |
where wi are the Euclidian distance weights. 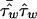 has variance
has variance 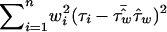 , so that a weighted mean test statistic is given by
, so that a weighted mean test statistic is given by
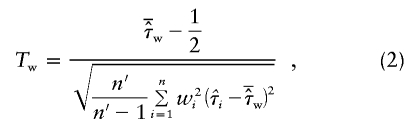 |
since its mean is 1/2 under the null hypothesis of no linkage for both ASPs. Here, n′ denotes the number of ASPs that are not completely uninformative—that is, for which wi>0. The weighted mean test statistic reduces to the classical mean test with the empirical variance estimate if wi=1/n for all i and n′=n.
In equation (2), we treat the weights as fixed, although they are estimated from the present sample. Therefore, the asymptotic properties are not obvious at first glance. However, Tw can also be derived from a generalized estimating equations (GEE) model with independence working covariance matrix (Ziegler et al. 1998). For this purpose, we assume that we can additively decompose τi into τ+ɛi for all n independent sib pairs. Furthermore, E(τi)=τ, and Var(τi)=wi. If a generalized least squares estimator is used with weight matrix diag(wi) for estimating τ, then the Wald statistic of equation (2) is obtained if the robust estimator of variance (Ziegler et al. 1998) is employed for this model. Therefore, Tw asymptotically follows a standard normal distribution under the null hypothesis of no linkage. To avoid slightly increased type I error, especially for small sample sizes, we recommend the use of the central t distribution, with n-1 df, in applications.
Monte Carlo Simulation of P Values
At the beginning of this project, it was not certain whether we would discover the limiting distribution of our novel weighted mean test statistic, because weights are estimated from the current sample, thus introducing an extra random element. We therefore investigated the applicability of existing Monte Carlo permutation or simulation approaches, which can be grouped into three basic procedures, as follows.
-
1.
For linkage analysis of quantitative traits in sib pairs and for case-control association studies, one may permute phenotypes or genotypes to disperse the dependency of genotypes and phenotypes (Wan et al. 1997; Zhao et al. 2000). In ASP studies, however, all sib pairs have identical phenotypic values, and this approach is not applicable.
-
2.
One may generate new marker genotypes under the null hypothesis of no linkage with a prespecified heterozygosity (see, e.g., Zinn-Justin et al. 2001). This, in turn, alters the weights, and thus the degree of informativity is not adequately reflected.
-
3.
Zhao et al. (1999) proposed a randomization procedure for the inheritance vectors obtained from the Lander-Green algorithm (Idury and Elston 1997; Kruglyak and Lander 1998). Again, this approach does not hold the weights wi constant and therefore does not adequately reflect the informativity of the individual sib pairs.
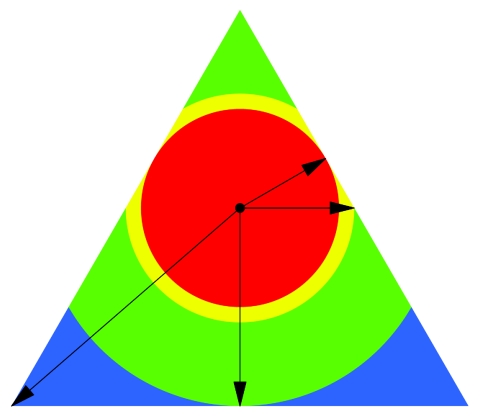
To conclude, all existing approaches do not keep the weight constant for an individual sib pair. They are therefore not suitable for the proposed weighted mean test, and we suggest instead the use of the following approach. If we consider lines tracking the circles around the IBD distribution of an uninformative marker, we see that these represent ASPs with identical informativity and, thus, equal weights. Although the weights are constant, their specific IBD distribution may vary, as shown by a specific position on the circle. For a given weight wi, we therefore simulate new ASPs on the line describing the circle belonging to weight wi, as shown in figure 3.
Figure 3.
Space of IBD distributions and resampling restrictions. The figure visualizes the regions defined in table 1. The red area is obtained by a circular expansion from the point of noninformativity—that is, (1/4,1/2,1/4). The intersection of the circle with the side of the triangle is obtained by an orthogonal projection along the side of the triangle. The yellow circle segments are bounded by the triangle parallel to the X-axis. The green area is obtained by an expansion of the circle segments to the bottom line of the triangle. The blue area represents the remaining part of the triangle and is limited by the corners of the triangle.
With increasing weights, circles around (1/4, 1/2, 1/4) do not completely fit into the triangle of IBD distributions in figure 3. In this situation, one could first simulate a point on the corresponding circle, as before, and, second, check whether the point corresponds to a valid IBD distribution by lying within the triangle. This may, however, be quite inefficient. For example, in the most extreme case (i.e., a sib pair with either 2 or 0 alleles shared IBD), the circle intersects the triangle at only those two points. Consequently, the probability that a point on the circle exactly corresponds to one of the two possible IBD distributions is 0. For this reason, we mathematically derived the circles and circle segments, given a specific weight. Four areas have to be distinguished, as shown in figure 3. The first area is the red circle, which is obtained by moving from (1/4, 1/2, 1/4) in all directions toward the sides of the triangle. The first intersection is obtained orthogonal to f0 and f2. The second area, marked in yellow, is bounded by the intersection orthogonal to the Y-axis. The third area, displayed in green, is limited by the intersection orthogonal to the X-axis. The remaining area is shown in blue.
Areas according to Euclidian distances and corresponding valid IBD distributions are calculated using polar coordinates (d,t). These specify the valid angles t (in radians) for any distance d (table 1). With the angles t, given the distance d, the following simulation algorithm for ASPs may be employed.
-
1.
Compute the weighted mean test statistic Tw, using the original n sib pairs. Keep the Euclidian distances di and weights wi.
-
2. For sib pairs i, from 1 to n,
-
a. Draw ti from a continuous uniform distribution in accordance with table 1.
-
b. Calculate the simulated IBD sharing values
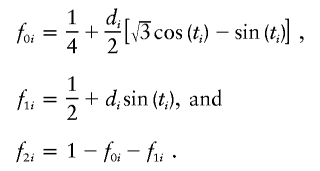
-
a.
-
3.
Compute the simulated test statistic, Tsim, of the resampled pairs, using weights wi.
-
4.
Repeat steps 2 and 3, say, M times.
-
5.
Compute the empirical P value, Pemp, by #{Tsim⩾Tw}/M. Here, # denotes the number operator.
To explain step 2a of the algorithm in greater detail, we consider the following example. If the estimated IBD distribution is f=(1/2,1/4,1/4), then one obtains 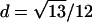 , corresponding to case 4 in table 1. This distance d falls within the interval
, corresponding to case 4 in table 1. This distance d falls within the interval 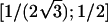 . With
. With 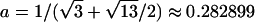 ,
, 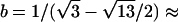 −14.1393,
−14.1393, 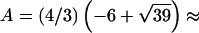 0.326664, and
0.326664, and 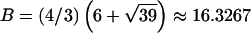 , t is drawn from a continuous uniform distribution, with values that fall within the interval
, t is drawn from a continuous uniform distribution, with values that fall within the interval
 |
Table 1.
Mapping Rules[Note]
| Case | Distance d | Range of t |
| 1 | 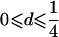 |
0⩽t<2π |
| 2 | 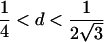 |
0<t⩽2arctan(3-1/2-a-A)2arctan(3-1/2-a+A)⩽t⩽2arctan(-3-1/2+b-B)-2arctan(3-1/2-b-B)⩽t<ππ⩽t⩽2π |
| 3 | 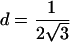 |
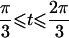 π⩽t⩽2π π⩽t⩽2π
|
| 4 | 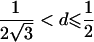 |
2arctan(3-1/2-a+A)⩽t⩽2arctan(-3-1/2+b+B)2π-2arctan(3-1/2-b+B)⩽t⩽2π-2arctan(-3-1/2+a+A) |
| 5 | 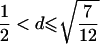 |
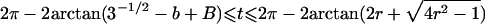 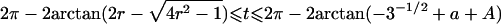
|
Note.— Valid IBD distributions are calculated in terms of polar coordinates (d,t) with origin in (f0,f1,f2)=(1/4,1/2,1/4). These rules specify, for any d, the valid angles t (in radians), so that the pair (d,t) maps back to a valid IBD sharing value. Except for the first area, which describes a whole circle, distances d correspond to the union of different circle segments. In addition, 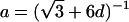 ,
, 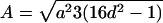 ,
, 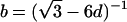 , and
, and 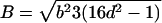 .
.
Simulation Studies
In this section, we demonstrate the validity of the proposed weighted mean test and the Monte Carlo simulation approach. Furthermore, we show the gain in power that can be achieved by the weighted mean test, in comparison with the classical mean test.
In the simulation study, we wanted to avoid computer time–consuming simulation of parental alleles, segregation of alleles to offspring, disease assignment, and subsequent calculation of IBD values in a two-point setting. We therefore derived the probabilities for the seven possible IBD distributions for ASPs at an unlinked marker locus with r equifrequent alleles (table 2). A similar distribution has been presented by Risch (1990) for identity-by-state values. We also deduced the probabilities of the seven possible IBD distributions for ASPs, assuming an autosomal dominant and recessive disease with complete penetrance, no phenocopies, a diallelic trait locus with minor-allele frequency p, θ=0, and a marker locus with r equifrequent alleles. Both loci are assumed to be in Hardy-Weinberg equilibrium, and there is no linkage disequilibrium between the loci.
Table 2.
Possible IBD Distributions (f0,f1,f2) and Their Probabilities at a Marker Locus with r Equifrequent Alleles
Displays the probability of an ASP for a specific IBD distribution at an unlinked autosomal genetic marker—that is, θ=0.5.
The probability of an ASP for a specific IBD distribution at a linked genetic marker with θ=0 for an autosomal dominant disease (dominant model) or a recessive disease (recessive model) with complete penetrance and a diallelic trait locus with minor-allele frequency p. Both loci are in Hardy-Weinberg equilibrium, and there is no linkage disequilibrium between the loci.
Parameters subject to variation were the probability of the disease allele (p=1/100,000), the number of families (n=50 and n=200), and the number of equally frequent alleles at the marker locus (r). The scenario r=2 corresponds to a heterozygosity of 0.5, which is comparable to the usual two-point situation. The scenario r=4 (i.e., heterozygosity of 0.75) is similar to the informativity in a microsatellite genome scan, and r=100 corresponds to an almost completely informative chromosomal position, which can be achieved in genomewide scans with SNP chips.
The number of replications was set to 100,000 under the null hypothesis, H0, for the unlinked marker and to 1,000 for a completely linked marker locus. Asymptotic P values were obtained from the t distribution, with n-1 df, for the standard mean tests and the weighted mean test. The number of simulations was set to M=10,000 for the computation of empirical P values for both Tmev and Tw. For the empirical determination of P values, data were simulated on circles or circle segments. Distances, however, were ignored in the computation of Tmev by setting weights to 1/n. Power at type I error level α was determined by using the upper α fractile from both the asymptotic and the empirical distribution of P values simulated under the null hypothesis of no linkage. All Monte Carlo simulations were performed by a fast and flexible simulation utility in C++, which is available upon request.
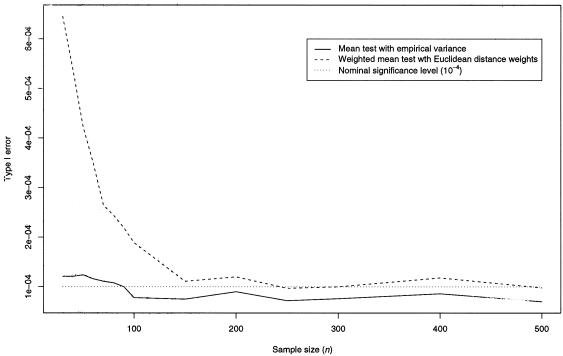
Simulation results for type I error fractions and power for the dominant genetic model are summarized in tables 3 and 4, respectively. As displayed in figure 4, asymptotic type I error levels based on the t distribution agree well with the nominal levels, if the sample size is at least n=100, and the approximation improves with sample size, regardless of the underlying marker informativity. Asymptotic normality begins to take effect later for the novel weighted mean test (dashed line in fig. 4) than for the classical mean test with empirically estimated variance (solid line in fig. 4) because of the extra random element introduced by the weight wi. However, differences are negligible when the sample size exceeds 150 (fig. 4). No such pattern can be observed for empirically determined type I errors. Here, the nominal level coincides well with the simulated level for both mean tests, regardless of the sample size and marker informativity (table 3), except for n=50 and r=2, for which the weighted mean test appeared to be slightly conservative.
Table 3.
Asymptotic and Empirical Type I Error Fractions for the Classical Mean Test with Empirical Variance (Classic) and the Weighted Mean Test with Euclidian Distance Weights (Euclid)[Note]
|
Type I Error |
||||||||||||
|
n = 50; r = 2 |
n = 50; r = 4 |
n = 50; r = 100 |
n = 200; r = 2 |
n = 200; r = 4 |
n = 200; r = 100 |
|||||||
| Nominal α | Classic | Euclid | Classic | Euclid | Classic | Euclid | Classic | Euclid | Classic | Euclid | Classic | Euclid |
| Asymptotic: | ||||||||||||
| .001 | .00113 | .00146 | .00098 | .00195 | .00098 | .00183 | .00091 | .00132 | .00077 | .00089 | .00097 | .00104 |
| .01 | .00986 | .01377 | .01025 | .01357 | .00965 | .01195 | .00952 | .01024 | .00960 | .01011 | .01010 | .01023 |
| .02 | .02049 | .02598 | .01972 | .02398 | .02115 | .02197 | .01973 | .02049 | .01940 | .01952 | .02040 | .02026 |
| .03 | .03058 | .03764 | .02999 | .03406 | .03127 | .03204 | .02967 | .03062 | .02918 | .02977 | .03092 | .03024 |
| .04 | .04085 | .04869 | .04033 | .04426 | .04013 | .04251 | .03991 | .04117 | .03908 | .03974 | .04084 | .04008 |
| .05 | .05034 | .05989 | .04907 | .05462 | .04979 | .05315 | .05019 | .05141 | .04908 | .05002 | .05109 | .05062 |
| Empirical: | ||||||||||||
| .001 | .00117 | .00051 | .00083 | .00078 | .00099 | .00130 | .00121 | .00096 | .00100 | .00072 | .00092 | .00097 |
| .01 | .01071 | .00819 | .01026 | .01000 | .00957 | .01042 | .01060 | .00892 | .01009 | .00955 | .01032 | .01011 |
| .02 | .02025 | .01756 | .01982 | .01991 | .01995 | .02044 | .02119 | .01853 | .02033 | .01891 | .02061 | .02027 |
| .03 | .03037 | .02808 | .02953 | .02978 | .02971 | .03033 | .03133 | .02845 | .03021 | .02880 | .03094 | .02999 |
| .04 | .04040 | .03812 | .03992 | .03970 | .04007 | .04029 | .04149 | .03879 | .04006 | .03910 | .04128 | .03956 |
| .05 | .05029 | .04855 | .04918 | .05000 | .05002 | .05075 | .05167 | .04929 | .05058 | .04907 | .05153 | .05010 |
Note.— Error values were calculated for n ASPs and r equifrequent alleles. Asymptotic type I errors are obtained from the t distribution with n-1 df. Empirical type I error fractions are estimated from the novel Monte Carlo simulation approach.
Table 4.
Asymptotic and Empirical Power of the Classical Mean Test with Empirical Variance (Classic) and the Weighted Mean Test with Euclidian Distance Weights (Euclid)[Note]
|
Power |
||||||||||||
|
n=50;r=2 |
n=50;r=4 |
n=50;r=100 |
n=200;r=2 |
n=200;r=4 |
n=200;r=100 |
|||||||
| Nominal α | Classic | Euclid | Classic | Euclid | Classic | Euclid | Classic | Euclid | Classic | Euclid | Classic | Euclid |
| Asymptotic: | ||||||||||||
| .001 | .01734 | … | .78372 | … | 1.00000 | … | .27522 | .69777 | .99991 | 1.00000 | 1.00000 | 1.00000 |
| .01 | .06973 | … | .86694 | … | 1.00000 | … | .39528 | .88785 | .99999 | 1.00000 | 1.00000 | 1.00000 |
| .02 | .13617 | … | .91924 | … | 1.00000 | … | .53396 | .93070 | .99999 | 1.00000 | 1.00000 | 1.00000 |
| .03 | .17692 | … | .93668 | … | 1.00000 | … | .59950 | .94601 | .99999 | 1.00000 | 1.00000 | 1.00000 |
| .04 | .20631 | … | .95779 | … | 1.00000 | … | .62774 | .95875 | .99999 | 1.00000 | 1.00000 | 1.00000 |
| .05 | .24086 | … | .96311 | … | 1.00000 | … | .65765 | .96887 | .99999 | 1.00000 | 1.00000 | 1.00000 |
| Empirical: | ||||||||||||
| .001 | .02291 | .05394 | .78853 | .90693 | .99901 | .99870 | .28467 | .69713 | .99900 | 1.00000 | 1.00000 | 1.00000 |
| .01 | .07334 | .23344 | .86252 | .98124 | 1.00000 | 1.00000 | .39984 | .88308 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| .02 | .14210 | .34297 | .91689 | .98798 | 1.00000 | 1.00000 | .54142 | .92321 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| .03 | .18063 | .41545 | .93584 | .99095 | 1.00000 | 1.00000 | .60576 | .94377 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| .04 | .21263 | .49261 | .95330 | .99401 | 1.00000 | 1.00000 | .63758 | .95470 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| .05 | .24729 | .56199 | .96008 | .99606 | 1.00000 | 1.00000 | .65720 | .96530 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
Note.— Power was calculated for n ASPs under an autosomal dominant genetic model with complete penetrance, no phenocopies, and θ=0 in a two-locus setting. The linked marker was assumed to have r=2, r=4, and r=100 equally frequent alleles. Empirical P values are based on 100,000 simulations. The asymptotic weighted mean is liberal for a sample size of n=50; therefore, we present asymptotic power of the weighted mean test only for n=200.
Figure 4.
Asymptotic type I error of the classical mean test with empirical variance and of the weighted mean test with an increasing number of sib pairs (n). Under H0, 1,000,000 samples of size n were simulated. P values were obtained by use of Student's t distribution, with n-1 df and at a nominal significance level of α=10-4.
Because the weighted mean test with the use of the asymptotic distribution is liberal for n=50, power for this test is presented only for a sample size of n=200 (table 4). As expected, power increases with the number of ASPs and the number of alleles at the linked marker locus. Power varies only slightly between asymptotically and empirically determined type I error levels. There is, however, a remarkable gain in power between the classical mean test with empirically estimated variances and the weighted mean test, for many configurations. For instance, for a significance level of 0.001, with n=200 ASPs and a low heterozygosity of 50%, corresponding to r=2, the power increases from 28% to 70%. Furthermore, there is no configuration in our simulations for which the classical mean test has greater power than the weighted mean test.
Application to Sample Data
As a first example, we reanalyzed the ASP sample data given by Risch (1990, table 1), which are displayed in table 5. Only 32 of the 74 ASPs have definite information about IBD. The mean test statistic Tm, with variance fixed to 1/(8n), gives a LOD score of 1.95 (table 6) when Tm statistics are converted to LOD scores via T2m/(2ln10). As expected, the mean test statistic with empirical variance Tmev has a higher LOD score of 2.63. The weighted mean test statistic outperforms both mean test statistics Tm and Tmev, with a LOD of 3.09, because the ASPs with IBD values equal to 2 receive greater weight than the ASPs with IBD values equal to 1.
Table 5.
Sample Data for Comparison of Test Statistics in Table 6
| No. ofSib Pairs | f2 | f1 | f0 |
| 14 | 1 | 0 | 0 |
| 16 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 |
| 22 | 2/3 | 1/3 | 0 |
| 13 | 0 | 1/3 | 2/3 |
| 7 | 1/2 | 0 | 1/2 |
Table 6.
Comparison of MLS, Holman’s TTS, and the Mean Test Statistics for the Sample Data in Table 5
|
LOD Score for |
||
| Test Statistica | Informative Families | All Families |
| MLS and TTS | 2.20 | 2.79 |
| Tm | 1.95 | 1.90 |
| Tmev | 2.63 | 2.55 |
| Tw | 3.09 | 3.20 |
Tm is the classical mean test statistic with variance evaluated under the null hypothesis, H0. Tmev is the classical mean test statistic with empirical variance. Tw is the weighted mean test statistic.
The IBD distribution estimated from the completely informative ASP sample is 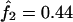 ,
, 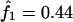 , and
, and 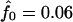 , and it therefore lies in the possible triangle (Holmans 1993). Subsequently, the maximum LOD score (MLS) and the triangle test statistic (TTS) have identical LOD scores of 2.20. Nevertheless, the asymptotic distributions of these test statistics are different (for details, see Holmans 1993).
, and it therefore lies in the possible triangle (Holmans 1993). Subsequently, the maximum LOD score (MLS) and the triangle test statistic (TTS) have identical LOD scores of 2.20. Nevertheless, the asymptotic distributions of these test statistics are different (for details, see Holmans 1993).
When the incompletely informative families are added to the sample, the LOD scores of both classical mean tests decrease. In contrast, the weighted mean test shows an increase in the LOD score to 3.20. A higher LOD score of 2.79 can also be observed for the MLS and TTS. The IBD distribution estimated for the complete sample is an inner point of the possible triangle, so that the LOD scores are identical. Nonetheless, the LOD score of the weighted mean test statistic Tw is higher than the LOD score of the MLS and TTS.
As a second example, we consider the data of Mein et al. (1998). On the basis of a genomewide scan that included a total of 356 ASP families collected in the United Kingdom, they reported a susceptibility locus on chromosome 16q22-q24 (D16S515–D16S520) for type 1 diabetes (see fig. 1b in Mein et al. 1998). Seventeen of the ASPs were drawn from families with three affected offspring, from which a single ASP was selected that comprised the proband and the next diagnosed individual; thus, a sample of independent ASPs was assembled. Details on subjects, genotyping, and map construction can be found in the work of Mein et al. (1998). The information content varied between 65% and 90% for chromosome 16 (for details, see fig. 1a in Mein et al. 1998), and it was ∼80% at the peak position.
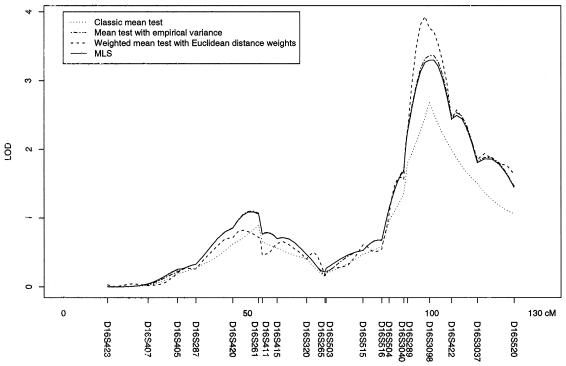
Mein et al. (1998) used the TTS under the assumption of dominance variance, as implemented in Genehunter (Kruglyak and Lander 1998) for multipoint linkage analysis. We reanalyzed the published data with use of the TTS, the classical mean test with variance evaluated under H0, the mean test with empirical variance, and the weighted mean test (fig. 5). While the maximum LOD for Tm is 2.8, both Tmev and TTS have maximum LOD scores of ∼3.4. They are outperformed by the Tw, which shows a LOD of 3.9 at D16S3098. It is important to note that the general shapes of the LOD score curves look similar for all displayed test statistics.
Figure 5.
Multipoint linkage analysis of chromosome 16 with use of the data from Mein et al. (1998). Multipoint TTS statistic was calculated under the assumption of dominance variance. The classical mean test with variance was evaluated under H0, and the weighted mean test with Euclidian distance weights was computed from the same individual ASP IBD estimates.
Discussion
Informativity of families for linkage analysis is an important issue in human genetics, and, consequently, it has been studied by several investigators using different concepts. Teng and Siegmund (1998), for example, analytically compared differences between two-point and multipoint analyses. They showed that multipoint analyses exploit available information better than two-point analyses. However, even in multipoint situations, the IBD value cannot be determined unambiguously for every chromosomal position, since markers are not placed at any genomic location and the number of distinct alleles at each marker locus is restricted. Therefore, weighting by marker informativity, as proposed here, can still increase power to detect linkage.
Another focus in the consideration of informativity is the family size, since families of different sizes also have different degrees of informativity. This has been studied by Hodge (1984) for linkage analysis with ASPs. Hodge examined the Shannon information contained in sibships of size s and showed that a complete sibship contains (2s-3+0.5s-1)/1.5 pair-equivalents of information. Thus, a sibship of size 4 has the informativity of ∼3.4 independent ASPs, although 6 different pairs can be constructed. Hodge therefore proposed to downweight multiple sibships accordingly. For the more general case of affected relative pairs, weighting on the basis of pedigree structure has also been discussed in the context of the nonparametric linkage (NPL) statistic (see, e.g., Whittemore 1996; Kong and Cox 1997; Teng and Siegmund 1997).
A third interpretation for informativity has been employed successfully in meta-analyses in which studies have been weighted according to their information content (Loesgen et al. 2001; Dempfle and Loesgen 2004). Weighting families by marker informativity has already been incorporated in the analysis by Sham et al. (2002), who specified and estimated the covariance matrix of IBD sharing between relative pairs in the framework of a new regression-based method for linkage analysis of quantitative traits.
If marker informativeness is neglected in the analyses, a severe loss of power can occur, as recently discussed (Abecasis et al. 2004; Cordell 2004; Mukhopadhyay et al. 2004; Schork and Greenwood 2004a, 2004b; Sieberts et al. 2004; Visscher and Wray 2004). A simple solution to the problem is to remove uninformative relative pairs from the analysis. This corresponds to a discrete weighting scheme with all-or-nothing weights, which is already implemented in some software packages. However, Schork and Greenwood (2004b) also pointed out that, in practice, it will be difficult to decide which pairs should be discarded from the analyses. They have, therefore, also proposed to consider the use of more complicated test statistics that downweight partially informative relative pairs in some way.
In this article, we have taken up this idea and have weighted ASP families by marker informativity: the greater the degree of informativity of an ASP, the greater its weight in linkage analysis. We thus extended the classical mean test, proposed a weighted mean test, and derived its limiting distribution. Because weights are estimated from current data, asymptotic normality begins to take effect later for the novel weighted mean test than for the classical mean test. Although significance levels of 10-4, which correspond to a LOD score of 3, can be maintained for ∼50 ASPs with the classical mean test, between 100 and 150 ASPs are required for the weighted mean test. However, for most applications, this should not be a relevant restriction. In cases in which the number of ASPs is low, our new method for simulation of P values may be employed instead. This keeps Euclidian distance weights fixed, and new ASPs are generated using a continuous uniform distribution on the corresponding circle or circle segment. Our simulation method clearly shows that the weighted mean test is, in principle, able to detect any deviation from the null hypothesis. This is in contrast to the TTS, for which IBD estimates for the whole sample are restricted to the so-called possible triangle.
Weighting as discussed here may be employed in some other tests as well. Whittemore and Tu (1998), for example, derived a set of constraints for the IBD probabilities of affected sib triples and used common features of the shapes of the two constraint sets to introduce the minmax tests. For other test statistics, weighting by marker informativity seems to be impossible. For instance, in likelihood-ratio statistics like the MLS, the weights cancel out in both the numerator and the denominator. Here, an all-or-none weighting scheme seems to be the only possibility to exclude partially informative families from the analysis. Uninformative families are already discarded. For a sample consisting of ASPs only, the standard NPL statistic is equivalent to the classical mean test with theoretical variance (see, e.g., Cordell 2004). Though weighting is meaningful for the standard NPL statistic, different degrees of marker informativity are adequately considered in the further development by Kong and Cox (1997).
For validation of results, it may be worthwhile to investigate the effect of additionally recruited discordant sib pairs (DSPs), in which one offspring is affected and the other is unaffected (Guo and Elston 2000; Elston et al. 2005). Because the classical mean test has been used for the analysis of DSPs (Risch and Zhang 1996; Guo and Elston 2000), the weighted mean test is adopted easily for this situation—instead of a higher sharing under linkage, it should be <1/2 for DSPs. The weighted mean test for ASPs and DSPs will soon be available in the software package S.A.G.E., which can be obtained for free by nonprofit organizations.
In two applications, we have illustrated the use of the weighted mean test in two-point and multipoint analyses. However, our new approach is currently restricted to independent ASPs. Two approaches to overcome this restriction are possible. First, large sibships can be treated as independent ASPs, as shown by Blackwelder and Elston (1985). This result is based on asymptotic arguments with identical weights; thus, P values are possibly too liberal in small samples. In addition, the generalization of the argument used by Blackwelder and Elston (1985) for the classical mean test to the weighted mean test needs to be demonstrated in a Monte Carlo simulation study. Second, the same GEE technique that has been used for deriving the asymptotic normality of the proposed weighted mean test may be employed here, with a correction for large sibships. Similarly, our approach for simulation of P values requires extension to large sibships.
Another area of possible improvement is our use of Euclidian distance weights for the novel weighted mean test. We validated the asymptotic distribution of the proposed test statistic with Euclidian distance weights in a Monte Carlo simulation study and demonstrated that the power of the weighted mean test can be substantially higher than the power of the classical mean test. However, our simulations were based on simple Mendelian traits—that is, fully penetrant without phenocopies. Furthermore, we did not study the effect of missing parental genotypes and of misspecified allele frequencies. Use of the diabetes data in our example yielded results consistent with findings from our simple simulation studies. However, we recognize that diabetes is a more complex genetic disease, and we therefore presume that our weighted mean test is also powerful in more complex models.
Since we did not show the optimality of the proposed weights, other weighting schemes based on different distance or informativity measures, such as Shannon’s entropy or the Fisher information, may be even more powerful. We cannot exclude the notion that the classical mean test with empirical variance might be more powerful in some configurations. Although the numerical derivation of optimal weights is possible in principle, a theoretical result most likely cannot be derived, since weights appear in both the numerator and the denominator of the weighted mean test statistic. Further research is required to extend the weighted mean test to large sibships, or even to affected relative pairs.
Acknowledgments
We are grateful to Inke R. König for helpful discussions on a previous version of the manuscript. We gratefully acknowledge the Juvenile Diabetes Research Foundation/Wellcome Trust Diabetes and Inflammation Laboratory for providing genotype data (from Mein et al. [1998], data version 1.0) for independent analysis by our group. This work was supported by Deutsche Forschungsgemeinschaft grant ZI 591/12-1.
Web Resources
The URL for data presented herein is as follows:
- S.A.G.E. software, http://darwin.cwru.edu/ (Note: the weighted mean test will be available soon from S.A.G.E. Nonprofit organizations can obtain S.A.G.E. for free.)
References
- Abecasis G, Cox N, Daly MJ, Kruglyak L, Laird N, Markianos K, Patterson N (2004) No bias in linkage analysis. Am J Hum Genet 75:722–723 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amos CI, Elston RC, Wilson AF, Bailey-Wilson JE (1989) A more powerful robust sib-pair test of linkage for quantitative traits. Genet Epidemiol 6:435–449 10.1002/gepi.1370060306 [DOI] [PubMed] [Google Scholar]
- Blackwelder WC, Elston RC (1985) A comparison of sib-pair linkage tests for disease susceptibility loci. Genet Epidemiol 2:85–97 10.1002/gepi.1370020109 [DOI] [PubMed] [Google Scholar]
- Cordell HJ (2004) Bias toward the null hypothesis in model-free linkage analysis is highly dependent on the test statistic used. Am J Hum Genet 74:1294–1302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempfle A, Loesgen S (2004) Meta-analysis of linkage studies for complex diseases: an overview of methods and a simulation study. Ann Hum Genet 68:69–83 10.1046/j.1529-8817.2003.00061.x [DOI] [PubMed] [Google Scholar]
- Elston RC, Song D, Iyengar SK (2005) Mathematical assumptions versus biological reality: myths in affected sib pair linkage analysis. Am J Hum Genet 76:152–156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke D, Kleensang A, Elston RC, Ziegler A. Haseman-Elston weighted by marker informativity. BMC Genet (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo X, Elston RC (2000) Two-stage global search designs for linkage analysis. II. Including discordant relative pairs in the study. Genet Epidemiol 18:111–127 [DOI] [PubMed] [Google Scholar]
- Haseman JK, Elston RC (1972) The investigation of linkage between a quantitative trait and a marker locus. Behav Genet 2:3–19 10.1007/BF01066731 [DOI] [PubMed] [Google Scholar]
- Hodge SE (1984) The information contained in multiple sibling pairs. Genet Epidemiol 1:109–122 10.1002/gepi.1370010203 [DOI] [PubMed] [Google Scholar]
- Holmans P (1993) Asymptotic properties of affected–sib-pair linkage analysis. Am J Hum Genet 52:362–374 [PMC free article] [PubMed] [Google Scholar]
- Horvitz DG, Thompson DJ (1952) A generalization of sampling without replacement from a finite universe. J Am Stat Assoc 47:663–685 [Google Scholar]
- Idury RM, Elston RC (1997) A faster and more general hidden Markov model algorithm for multipoint likelihood calculations. Hum Hered 47:197–202 [DOI] [PubMed] [Google Scholar]
- Jacobs KB, Gray-McGuire C, Cartier KC, Elston RC (2003) Genome-wide linkage scan for genes affecting longitudinal trends in systolic blood pressure. BMC Genet Suppl 4:82 10.1186/1471-2156-4-S1-S82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapp M, Seuchter SA, Baur MP (1994) Linkage analysis in nuclear families. I. Optimality criteria for affected sib-pair tests. Hum Hered 44:37–43 [DOI] [PubMed] [Google Scholar]
- Kong A, Cox NJ (1997) Allele-sharing models: LOD scores and accurate linkage tests. Am J Hum Genet 61:1179–1188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Lander ES (1998) Faster multipoint linkage analysis using Fourier transforms. J Comput Biol 5:1–7 [DOI] [PubMed] [Google Scholar]
- Loesgen S, Dempfle A, Golla A, Bickeböller H (2001) Weighting schemes in pooled linkage analysis. Genet Epidemiol Suppl 21:142–147 [DOI] [PubMed] [Google Scholar]
- Mein CA, Esposito L, Dunn MG, Johnson GC, Timms AE, Goy JV, Smith AN, et al (1998) A search for type 1 diabetes susceptibility genes in families from the United Kingdom. Nat Genet 19:297–300 10.1038/991 [DOI] [PubMed] [Google Scholar]
- Mukhopadhyay I, Feingold E, Weeks DE (2004) No “bias” toward the null hypothesis in most conventional multipoint nonparametric linkage analyses. Am J Hum Genet 75:716–718 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson JM (2002) Linkage analysis, model free. In Elston RC, Olson JM, Palmer L (eds) Biostatistical genetics and genetic epidemiology. John Wiley & Sons, New York, pp 460–472 [Google Scholar]
- Risch N (1990) Linkage strategies for genetically complex traits. III. The effect of marker polymorphism on analysis of affected relative pairs. Am J Hum Genet 46:242–253 (erratum 51:673–675) [PMC free article] [PubMed] [Google Scholar]
- Risch NJ, Zhang H (1996) Mapping quantitative trait loci with extreme discordant sib pairs: sampling considerations. Am J Hum Genet 58:836–843 [PMC free article] [PubMed] [Google Scholar]
- S.A.G.E. (2004) Statistical analysis for genetic epidemiology. Statistical Solutions, Cork, Ireland [Google Scholar]
- Schork NJ, Greenwood TA (2004a) Got bias? The authors reply. Am J Hum Genet 75:723–727 [Google Scholar]
- ——— (2004b) Inherent bias toward the null hypothesis in conventional multipoint nonparametric linkage analysis. Am J Hum Genet 74:306–316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sham PC, Purcell S (2001) Equivalence between Haseman-Elston and variance-components linkage analyses for sib pairs. Am J Hum Genet 68:1527–1532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sham PC, Purcell S, Cherny SS, Abecasis GR (2002) Powerful regression-based quantitative-trait linkage analysis of general pedigrees. Am J Hum Genet 71:238–253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sieberts SK, Broman KW, Gudbjartsson DF (2004) Conventional multipoint nonparametric linkage analysis is not necessarily inherently biased. Am J Hum Genet 75:720–722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teng J, Siegmund D (1997) Combining information within and between pedigrees for mapping complex traits. Am J Hum Genet 60:979–992 [PMC free article] [PubMed] [Google Scholar]
- ——— (1998) Multipoint linkage analysis using affected relative pairs and partially informative markers. Biometrics 54:1247–1265 [PubMed] [Google Scholar]
- Visscher PM, Wray NR (2004) Conventional multipoint nonparametric linkage analysis is not necessarily inherently biased. Am J Hum Genet 75:718–720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan Y, Cohen J, Guerra R (1997) A permutation test for the robust sib-pair linkage method. Ann Hum Genet 61:79–87 [DOI] [PubMed] [Google Scholar]
- Whittemore AS (1996) Genome scanning for linkage: an overview. Am J Hum Genet 59:704–716 [PMC free article] [PubMed] [Google Scholar]
- Whittemore AS, Tu IP (1998) Simple, robust linkage tests for affected sibs. Am J Hum Genet 62:1228–1242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao H, Merikangas KR, Kidd KK (1999) On a randomization procedure in linkage analysis. Am J Hum Genet 65:1449–1456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao JH, Curtis D, Sham PC (2000) Model-free analysis and permutation tests for allelic associations. Hum Hered 50:133–139 10.1159/000022901 [DOI] [PubMed] [Google Scholar]
- Ziegler A, Kastner C, Blettner M (1998) The generalised estimating equations: an annotated bibliography. Biom J 40:115–139 [DOI] [Google Scholar]
- Zinn-Justin A, Ziegler A, Abel L (2001) Multipoint development of the weighted pairwise correlation (WPC) linkage method for pedigrees of arbitrary size and application to the analysis of breast cancer and alcoholism familial data. Genet Epidemiol 21:40–52 10.1002/gepi.1017 [DOI] [PubMed] [Google Scholar]