Eukaryotic cells are dynamically ordered or critical but not chaotic

Abstract

Two important theoretical approaches have been developed to generically characterize the relationship between the structure and function of large genetic networks: The continuous approach, based on reaction-kinetics differential equations, and the Boolean approach, based on difference equations and discrete logical rules. These two approaches do not always coincide in their predictions for the same system. Nonetheless, both of them predict that the highly nonlinear dynamics exhibited by genetic regulatory systems can be characterized into two broad regimes, to wit, an ordered regime where the system is robust against perturbations, and a chaotic regime where the system is extremely sensitive to perturbations. It has been a plausible and long-standing hypothesis that genomic regulatory networks of real cells operate in the ordered regime or at the border between order and chaos. This hypothesis is indirectly supported by the robustness and stability observed in the phenotypic traits of living organisms under genetic perturbations. However, there has been no systematic study to determine whether the gene-expression patterns of real cells are compatible with the dynamically ordered regimes predicted by theoretical models. Using the Boolean approach, here we show what we believe to be the first direct evidence that the underlying genetic network of HeLa cells appears to operate either in the ordered regime or at the border between order and chaos but does not appear to be chaotic.

It is an essential property of living organisms to be robust against perturbations. As noted by de Visser et al. (1), “robustness is the invariance of phenotypes in the face of perturbation.” This robustness is observed at various levels of biological organization, ranging from gene-expression and cell-cycle regulation to the adaptation of the whole organism to new environments. Two important questions arise in the study of robustness: What are the mechanisms that produce robust behavior? How can robustness be detected and measured? The answer to these questions will depend on the level of organization under consideration. At the genetic level, several mechanisms yielding robust behavior have been proposed. In most of them, such as gene redundancy and buffering epistasis, genetic robustness is associated with a small set of genes responsible for the expression of a specific phenotypic trait (1, 2). However, there is evidence suggesting that genetic robustness might also be associated with the structural and dynamical properties of the entire genetic network and not only with a particular set of genes (3-5). In this kind of “distributed robustness,” one would have to know all of the regulatory interactions among all of the genes to actually determine the dynamical properties of the whole network. Despite significant recent progress, a complete description of a genetic regulatory network, even for well characterized organisms, remains elusive.

A different strategy to determine and characterize the genetic robustness in living organisms is to compare the general dynamical properties of model genetic regulatory networks with those present in real systems. Over the last 35 years a great variety of model genetic networks have been developed, ranging from continuous models based on differential equations for the temporal evolution of gene product concentrations, to Boolean models where genes can be in only two states of activity (“on” or “off”) and the dynamics evolve in discrete time steps. Continuous models have been considered as more realistic and complete for the description of intracellular processes than Boolean models. However, although the Boolean approach might seem to be an oversimplification of intracellular processes, recent work has shown that this approach actually captures the essential aspects of the gene-regulation dynamics, accurately reproducing the experimental gene-expression profiles of some real organisms (3, 4, 6-9). In this work, we will adopt the Boolean approach for the modeling of genetic networks.

In this context, the genetic network of an organism is represented by a set of N Boolean variables (genes), σ₁, σ₂,..., σ_N, each acquiring the values 1 or 0 corresponding to the two possible states of gene activity (either the gene is expressed or it is not). To each gene σ_n we assign a set of k_n randomly chosen genes, σ_n1, σ_n2,..., σ_nkn, which will control the value of σ_n through the equation σ_n(t + 1) = f_n(σ_n1(t),..., σ_nkn(t)). In this equation, the Boolean function f_n of k_n arguments is randomly chosen from the ensemble of all possible Boolean functions such that, for each configuration of its k_n arguments, f_n = 1 with probability p. [For a detailed description of this model, usually known as a random Boolean network (RBN), see refs. 10-12.] One of the main characteristics of RBNs is the occurrence of dynamical attractors. Starting out from a given initial configuration, after a transient time each particular realization of a RBN will fall into a pattern of cyclic activity called, as noted, an attractor. A network can have many attractors, but at least one must exist. It has been hypothesized that the dynamical attractors in a Boolean network correspond to the different cell types or cell fates in an organism (11). In other words, the phenotypic traits of the organism are encoded in the dynamical attractors of its underlying genetic regulatory network. This hypothesis has partially been corroborated in recent works (3, 4, 6-9, 13).

Another important aspect of RBNs is the existence of two dynamical regimes, ordered and chaotic, and a phase transition between the two (12, 14). Networks operating in the ordered regime are intrinsically robust. This robustness is reflected in the dynamical stability of the attractors both under structural perturbations (mutations to the wiring or function rules) and transient perturbations (changes to the activity or state of a gene). Contrary to this, in the chaotic regime the dynamical attractors are extremely sensitive to such small perturbations. The phase transition between the ordered and chaotic regimes is governed by the value of the so-called expected network sensitivity, defined as S = 2Kp(1 - p), where K is the average network connectivity and p is the probability of gene expression (15). For S < 1 the network is in the ordered regime, whereas the chaotic regime is attained for S > 1. The phase transition occurs at S = 1. It is important to mention that the existence of the ordered and chaotic regimes mentioned above is not particularly associated with the Boolean approach but rather with the highly nonlinear behavior exhibited by genetic regulatory systems. Ordered and chaotic dynamics are also known to occur in continuous and hybrid models of genetic regulatory systems (16).

The robustness and stability observed in living organisms at the genetic level seem to point to the possibility that their underlying genetic networks operate in the ordered regime. For instance, cellular states are very robust to a large variety of perturbations, and evidence of the existence of robust attractors representing cell types and cell functions has been reported (3, 4). Moreover, cellular oscillations, such as the cell division cycle or the respiratory cycle (17, 18), have periods astonishingly small compared with the number of genes in the genome, which is a typical characteristic of networks in the ordered regime. All of these observables can be interpreted as indirect evidence favoring the idea that gene-regulation networks operate in the ordered regime. Nevertheless, such qualitative indirect evidence is not enough to assert whether the underlying machinery of intracellular processes is robust in part because it operates in the ordered phase of some appropriate dynamical space. For example, numerical simulations show that even RBNs in the chaotic regime can have relatively short-period attractors (and vice versa). For such networks, one has to probe the entire configuration space to detect chaotic behavior. Therefore, to determine whether the dynamics of the genetic networks of real organisms are ordered or chaotic, or even more, if order and chaos have any meaningful manifestation in such systems, we need a quantitative measure of robustness that does not depend on particular attractor structures (such as the attractor length). This requirement leads us to the second important question about robustness, namely, how to measure it, especially in the absence of knowledge about the specific network structure.

Methods and Results

The gene-expression patterns of real cells can be generated by using high-throughput transcriptional profiling technologies such as cDNA microarrays. From such data we would like to determine whether the underlying genetic network is ordered, critical, or chaotic. One possible approach is to first infer the underlying architecture and logical rules of the genetic network from the time-course gene-expression data and then analyze or simulate this network to determine the regime in which it operates. Such an approach, however, can be highly problematic, in part because it requires one to solve a much more difficult problem to answer a relatively simpler question. Indeed, using today's technology, genetic network inference is highly challenging and involves issues such as small-sample error estimation, variable selection, and, in the context of our central question, a thorough understanding of the way in which the inherent network estimation uncertainty affects our estimate of the degree of “chaoticity.” It would thus be more prudent to attempt to answer our question directly by using the observed dynamical network behavior without having to first infer the network structure.

To this end, we compare the complexity of time series microarray data of real cells with that of mock data generated by RBNs operating in the ordered, critical, and chaotic regimes. There are different ways to measure the “complexity” of a time sequence, most of them aiming to measure the amount of information stored in the sequence. Here, we use the Lempel-Ziv (LZ) measure of complexity (19, 20), which applies to a sequence over a finite alphabet and counts the number of substrings (words) as the sequence evolves from left to right. Although there are numerous variants of this approach, the algorithm essentially parses the sequence into shortest words that have not occurred previously and the complexity is defined as the number of such unique words, with the possible exception of the last word, which may not be unique. Because it is known that the LZ complexity of a random binary sequence is asymptotically Gaussian with a defined mean and standard deviation being a function of the sequence length, it can also be used for statistical tests of randomness (21).

Rather than give the mathematical formulation of the LZ complexity, which can be found in ref. 19, let us illustrate it by means of an example. Consider the sequence 01100101101100100110. The first digit, 0, is a new word because we have not seen it before. So is the second digit, 1. However, the third digit, also a 1, is one that we have seen before, so we increase the length of the word by one, resulting in the new word 10. Next, starting with the fifth digit, we see that the smallest new word is 010. If we repeat this process, the sequence gets parsed as follows: 0·1·10·010·1101·100100·110, where the dots delimit the new words. Thus, the LZ complexity of this word is 7. Note that all words, with the exception of the last one, are unique and that in this definition of LZ complexity, our search for previous occurrences of a word can span across previously seen word boundaries. Repetition results in lower LZ complexity. For example, the complexity of the sequence 01010101010101010101 is 3. In general, time series with repetitive or simple patterns have a low LZ complexity, whereas series with a rich pattern structure exhibit high LZ complexities. Our simulations show that RBNs operating in the ordered or critical regimes exhibit lower LZ complexities of the sequences generated by each gene due to their pattern-like behavior over time, as compared with networks in the chaotic regime, which give rise to more random gene behavior with high LZ complexities.

We measured the LZ complexities of the time series obtained from the gene-expression patterns in eukaryotic cells. In particular, the cell data we used are in the public domain (22) and are derived from synchronized (in early S phase by double thymidine block) HeLa cells, on which cDNA microarray analyses were performed for 48 time points, representing two to three synchronous cell cycles. A total of 43,198 probes were used in these experiments representing an estimated 29,621 distinct genes. After filtering out genes that were flagged as unreliable by the experimenter, the data consist of a time series of length 48, at 1-h intervals except for the first two intervals, which were 30 min, for each of 42,159 gene probes. We used no additional data filters. To analyze these data, we used the absolute intensities from synchronized HeLa cells, normalizing each array by its median expression level across all genes.

Because the mock data generated by the RBNs are binary, the HeLa gene-expression data had to be binarized. We used the well known k-means algorithm (23) with two groups (or clusters), corresponding to the two binary values.∥ Briefly, the general method consists of clustering n data points x₁, x₂,..., x_n into k disjoint clusters U₁, U₂,..., U_k. In our case, the number of clusters is k = 2. The clustering is carried out in such a way as to minimize the sum

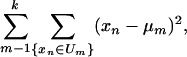where μ_m is the centroid of the cluster U_m. We iterate the following two steps: (i) Assign each data point to the cluster that has the closest centroid (e.g., mean). (ii) Recalculate the positions of the centroids. The algorithm minimizes the sum of point-to-centroid distances for all clusters. The method is guaranteed to converge to a local optimum.

There are many sources of variation and noise in microarray data (25, 26). In the binary domain, the compound effect of noise amounts to a certain percentage of values in the time series data being flipped from zero to one or vice versa. There is another, related issue: Many genes are expressed at levels that are below those corresponding to pure noise. That is, spots that are empty (i.e., have no probe) nonetheless produce some measurable signal, which corresponds to noise due to autofluorescence or other factors. Thus, only those genes that are legitimately expressed above this “noise floor” should be considered for further analysis. Fortunately, by using the HeLa data, it is possible to estimate both the binary noise probability and the global noise floor level as follows.

There are 963 empty spots on the HeLa microarrays. As a conservative estimate, for each of the 48 microarrays, we used the 95th percentile of the values of the empty spots as the noise floor level for that array. Accordingly, only those genes whose values exceed this global threshold at all time points are included for further analysis. Hence, our criteria are very stringent. To estimate the noise probability, we made use of the replicated probes available on the arrays. We sorted the data based on clone ID, and if two consecutive clone IDs were identical, signifying the same probe printed in different spots, we considered that pair to be a replicate pair.** This resulted in 2,001 duplicate gene profiles of 48 time points. Keeping only those that exceeded the global threshold, we binarized each of the duplicate profiles with the k-means algorithm and computed the normalized Hamming distance, which is the fraction of values binarized differently in the duplicate profiles, for each such pair. The estimated normalized Hamming distance, and, hence, the probability of noise, was approximately equal to q̂ = 0.35 with a 95% confidence interval of ≈[0.32,0.38], computed by using the bootstrap method (27). It is worth emphasizing that one of the advantages of working with binary data is that the compound effect of all sources of noise, whether it comes from irregularities in the intracellular processes or just from error measurements, is reflected in the binarized data in the fact that some spots are flipped to 1 when they must have actually been 0, and vice versa.

To determine whether the HeLa cells operate in the ordered, critical, or chaotic regimes, we compared the LZ complexity of the binarized microarray data with the LZ complexity of the time series obtained from random Boolean networks operating in those three regimes. Thus, we constructed RBNs with 29,621 model on/off genes tuned to the chaotic, critical, or ordered regimes. Specifically, we used three methods to do this. First, we constructed standard RBNs with a fixed gene-expression probability p = 1/2 and where each gene has exactly K randomly chosen inputs. By varying K, we can make the system transition from one regime to another: K = 1 networks are in the ordered regime (sensitivity S = 1/2), K = 2 networks are critical (S = 1), K = 3 networks are slightly chaotic (S = 3/2), and K = 4 networks are more chaotic (S = 2). Our second method consisted in constructing Boolean networks where each gene has K = 4 randomly chosen inputs but varying now the probability of gene expression p to match the same sensitivities as before. The values we used were p = 0.93301 (ordered, S = 1/2), p = 0.85355 (critical, S = 1), p = 0.75 (slightly chaotic, S = 3/2), and p = 0.5 (more chaotic, S = 2).

Our third method consisted in constructing RBNs with more realistic topologies. Real genetic networks do not have a fixed number of inputs, K, per gene. Some evidence supports a scale-free output distribution in Escherichia coli and an exponential or scale-free input distribution in yeast (28-31). Scale-free RBNs also show ordered and chaotic regimes with a phase transition between them (32, 33). The phase transition is governed by the same parameter S previously defined, with the difference that now the average network connectivity K = K(γ) depends on the value of the scale-free exponent γ. We used values of p and γ such that the expected average sensitivities S in this case matched those of standard RBN with K = 1, 2, 3, 4, and 5.

There is another technical point worth mentioning. Our random Boolean networks are synchronous. A state of the network is the current value, 1 or 0, of each of the 29,621 genes. If started at an initial state, at a clocked moment, each gene evaluates the activities of its inputs, consults its Boolean function, and assumes the proper next value, 1 or 0. Hence, at each clocked moment the network passes from one state to another. To obtain mock time series 48 entries long from our model genetic networks, we started each network in a random initial state, ran the network forward in time for 200 time steps, then took the next 48 entries as the time series for each of the 29,621 model binary genes. The networks in the ordered or critical regimes we used had reached their attractors after 200 time steps. Because the attractor length of networks in the chaotic regime can be much larger than 48 time steps, for such networks it does not matter whether they have reached their attractors after 200 time steps.

As mentioned before, to properly compare the complexities of the time series from HeLa cells with those obtained from the RBN, we have to take into account the noise q observed in the microarray data. To parameterize and model this noise, each binary value in our mock time series data was flipped with probability q ranging from 0 to 0.5 in increments of 0.05. We generated 75 RBNs in each ensemble and for each value q of the noise.

Because the LZ complexities of the mock data change from one network realization to another, we do not expect the LZ complexities from any particular RBN realization to perfectly match the LZ complexities from the experimental data. Therefore, it is a better procedure to compare the probability distributions of LZ complexities rather than the LZ complexities themselves. Because there is a finite number of possible LZ complexities for a 48-element binary sequence, the resulting LZ distributions are discrete, meaning that they are essentially normalized histograms (see Fig. 1 for an example). If we represent as P = [p₁,..., p_m] and Q = [q₁,..., q_m] the LZ distributions corresponding to the HeLa data and mock data, respectively, it is clear that the actual form of the Q distribution will change according to whether the Boolean network is operating in the ordered, critical, or chaotic regime. (The distribution P corresponding to experimental data is given and cannot be changed.) There are different ways to compute the “distance” between two probability distributions. Here, we use the Euclidean distance, defined as 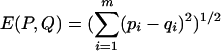, and the Kullback-Leibler (KL) distance, also called the relative entropy, defined as 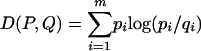. Note that if the distributions P and Q are identical, then E(P, Q) = D(P, Q) = 0. The more different the distributions P and Q, the larger the values of the Euclidean and KL distances. The purpose of using two different distances is to show that the results do not depend on the particular measure used.

Fig. 1.

LZ distributions generated from random binary vectors, and k-means binarized gene-expression data from HeLa cells.

Fig. 2 shows the results of comparing the experimental distribution Q with the distributions P corresponding to RBNs operating in different regimes. In each plot, either the Euclidean distance (Fig. 2 a and c) or the KL distance (Fig. 2 b and d) is plotted against the noise probability q. The four plots in each figure correspond either to the cases K = 1, 2, 3, and 4 with p = 0.5 (Fig. 2 a and b) or to the cases p = 0.93301, 0.85355, 0.75, and 0.5 with K = 4 (Fig. 2 c and d), and each is an average taken over the 75 RBNs in each ensemble and for each value of q. In each figure, the estimated noise probability and its confidence interval are indicated by vertical lines.

Fig. 2.

Euclidean (a and c) and KL (b and d) distances between the LZ complexity distributions corresponding to the HeLa data and Boolean networks operating in different regimes, plotted against the noise probability, q. The four plots in each panel correspond either to the cases K = 1, 2, 3, and 4 with P = 0.5 (a and b) or to the cases P = 0.93301, 0.85355, 0.75, and 0.5 with K = 4 (c and d). The estimated noise probability q̂ = 0.35, along with its confidence interval, are indicated by vertical lines.

It is evident from Fig. 2 a-d that in all cases, within the 95% confidence interval around the estimated noise level, the lowest Euclidean or KL distance, hence highest similarity between model and HeLa LZ distributions, corresponds to the ordered regime characterized by a sensitivity S = 1/2 (K = 1 with p = 0.5 or p = 0.93301 with K = 4), although these distances are extremely close to the ones corresponding to the critical phase S = 1 (K = 2 with p = 0.5 or p = 0.85355 with K = 4, respectively). Additionally, we reran all network simulations with the estimated probability of noise q̂ = 0.35096 and compared the distances (e.g., K = 1 vs. K = 2) using a t test and the Mann-Whitney test on samples generated from 75 random networks. In all cases but one, the distance corresponding to the ordered regime was smaller (with a P value ≪ 0.001) than the distance corresponding to the critical regime, although their distributions exhibited considerable overlap: The difference in their means constituted ≈1% of the distances corresponding to either of the chaotic regimes. For the case of the KL distance, there was no statistically significant difference between p = 0.93301 and p = 0.85355.

The general behavior of the distances relative to the noise levels observed in Fig. 2 is consistent with intuition. Recall that the LZ complexity is a measure of how much information can be stored in a sequence (how many different words). A random sequence can store, in principle, much more information than a fully ordered repetitive sequence. Networks in the chaotic regime produce random-like sequences with relatively high LZ complexities. Therefore, at low levels of noise (q), the LZ complexities of the real (noisy) data are more similar to those of chaotic networks, because the latter generate time series that appear more random than do ordered networks. As q is increased, the distance to the chaotic networks increases somewhat but not significantly so (especially the most chaotic networks, such as K = 4, p = 1/2), presumably because they are already “noisy,” ultimately saturating at a value of ≈0.35 for maximum noise (q = 1/2). On the other hand, ordered and critical networks generate more or less ordered sequences with extremely low values of LZ complexities. Hence, these sequences are considerably more distant from the real noisy data at very low noise levels. But as q is increased, they rapidly fall below those of chaotic networks and, in particular, within the range of noise estimated from the data. At very high levels of noise, the difference between ordered, critical, and chaotic networks disappears, as expected.

Finally, Fig. 3 a and b shows the Euclidean and KL distances computed for the scale-free networks whose expected average sensitivities match those of standard Boolean networks with K = 1, 2, 3, 4, and 5. The results are entirely consistent with the other two methods described above: The smallest distances at the estimated probability of noise are achieved by the ordered or critical regimes.

Fig. 3.

Euclidean (a) and KL (b) distances between the LZ complexity distributions corresponding to the HeLa data and scale-free Boolean networks operating in different regimes, plotted against the noise probability, q. The five plots in each panel correspond to scale-free networks whose sensitivities correspond to the cases K = 1, 2, 3, 4, and 5 in standard Boolean networks. The estimated noise probability of q̂ = 0.35, along with its confidence interval, are indicated by vertical lines. (Insets) Blowup around the estimated noise probability.

We conclude from this analysis that, given the estimated levels of noise in the binarized data, the HeLa time series data correspond, vis-à-vis the LZ complexity, to a time series characteristic of a model genetic network that is operating in the ordered regime but close to the phase-transition boundary. This conclusion is reached on the basis of three different means to cross the order-chaos threshold, implying that HeLa binarized time series data are consistent with HeLa cells lying in the ordered or critical regimes.

Discussion

To draw an inference from Boolean networks about cells requires taking a step from a mathematical model to a real genetic system. However, such a step appears to be always necessary. For suppose that we did not have a model mathematical system and tried to define order and chaos in terms of some property, such as sizes of avalanches in response to perturbations. Our criterion would then merely be heuristic and unjustified by simply looking at cells, and it would only be able to be made precise by reference to a model class. Here, we have used the first and simplest model class, Boolean networks, for which the notions of order and chaos are well defined, to draw the inference that eukaryotic cells, namely HeLa cells, are ordered or critical. Future work can examine alternative model classes for which the ordered or chaotic regime and a phase transition between them can be well defined and for which a reasonable measure of complexity can be established.

The global dynamical behavior of the genetic regulatory system in cells is itself a legitimate biological observable. We do not yet know the structure, logic, and dynamics of cell regulatory networks. We make use of the LZ measure of time series complexity for gaining insight into the dynamical behavior of the underlying genetic regulatory network latently generating the observed time-series gene-expression data. We used the Euclidean and KL distances to compare the similarities of two LZ distributions computed from HeLa time-series data binarized with k-means and mock data generated with random Boolean networks in the ordered, critical, and chaotic regimes. All simulations were run (and distances computed) with different values of the noise probability, q, which was also estimated, along with confidence bounds, from the HeLa data itself by using the available replicated probes. Additionally, genes below the “noise floor” levels, computed from the available empty spots, were discarded.

We used three techniques to cross the order-chaos phase transition: varying the number of inputs per model gene, K, from 1 to 4; fixing K at 4 and varying the bias, p, between 0.93301 and 0.5; and finally, varying the scale-free exponent parameterizing the distribution of inputs in a network with scale-free topology. The results strongly suggest that the underlying genetic network of HeLa cells operates in the ordered regime or is critical. To the best of our knowledge, this is the first attempt to analyze the global dynamics of genetic regulatory systems in eukaryotic cells. HeLa is a cancer cell line. Similar analyses need to be carried out for normal as well as more malignant cell lines. Perhaps cancer cells, as they progress, become more chaotic, or more ordered, in their dynamical behavior.

The hypothesis that cells are in the ordered regime is open to a variety of different tests, which should be carried out to further characterize the global dynamics of cells. Experimentally, if cells are in the ordered regime, then nearby states of the network should lie on dynamical trajectories that approach one another over time—a hallmark of homeostasis. This can, in principle, be tested by transiently perturbing a small fraction of gene activities and comparing test and control cell populations by gene arrays to see whether the distance between their gene activity patterns decreases with time. A number of other tests are possible, such as predicting the distribution of genes whose activities are altered by deletion or transient perturbation of single genes, and measuring the “Derrida” curve for cells (14). Critical K = 2 networks appear to predict the distribution of genes whose activities are altered in several hundred knockout mutants of yeast (34). It is not yet known whether critical networks in general predict this knockout distribution.

Furthermore, the proportion of Boolean functions belonging to certain classes of functions is known to influence the degree of order of the network (35, 36). It will be of interest to compare the time series of such ensembles of Boolean networks across the phase transition with binarized HeLa data. In addition, piece-wise linear network models show the same phase transition from order to chaos as do classical random Boolean nets (37). It will also be of interest to compare the binarized behavior of such model networks in the ordered, critical, and chaotic regimes with HeLa and other cell data.

Finally, we note a difficulty. Adjacent time moments in a synchronous random Boolean network, or scale-free network, are well defined discrete time moments in the dynamics of the Boolean network. Real cells have no central clock, have genes whose natural dynamics may show a range of time scales, and may be intrinsically noisy. It will be important to use more realistic ensembles of model genetic networks embodying these features to test whether our conclusions hold. In any case, we would not expect any model of genetic network, whether continuous, discrete, or hybrid, to predict that cells operate in the chaotic phase of the dynamical space, for this would not be consistent with the robust behavior exhibited by living organisms at all levels of organization.