Abstract
Although randomized controlled trials (RCTs) are a cornerstone of comparative effectiveness, they typically have much smaller sample size than observational studies due to financial and ethical considerations. Therefore there is interest in using plentiful historical data (either observational data or prior trials) to reduce trial sizes. Previous estimators developed for this purpose rely on unrealistic assumptions, without which the added data can bias the treatment effect estimate. Recent work proposed an alternative method (prognostic covariate adjustment) that imposes no additional assumptions and increases efficiency in trial analyses. The idea is to use historical data to learn a prognostic model: a regression of the outcome onto the covariates. The predictions from this model, generated from the RCT subjects’ baseline variables, are then used as a covariate in a linear regression analysis of the trial data. In this work, we extend prognostic adjustment to trial analyses with nonparametric efficient estimators, which are more powerful than linear regression. We provide theory that explains why prognostic adjustment improves small-sample point estimation and inference without any possibility of bias. Simulations corroborate the theory: efficient estimators using prognostic adjustment compared to without provides greater power (i.e., smaller standard errors) when the trial is small. Population shifts between historical and trial data attenuate benefits but do not introduce bias. We showcase our estimator using clinical trial data provided by Novo Nordisk A/S that evaluates insulin therapy for individuals with type 2 diabetes.
Keywords: causal inference, diabetes, historical data, prognostic score, randomized trials
1. Introduction
Practical, financial, and ethical concerns often preclude large randomized trials, which limits their power [1], [2], [3]. On the other hand, historical (often observational) data are often plentiful, and there are many existing methods for including historical data in trial analyses in order to boost power [4]. “Data fusion” methods simply pool trials with historical data [5], [6], [7]. Bayesian methods, which naturally rely on assumptions in the form of specified priors from historical data, are also popular in the literature [8], 9]. Similar problems have also been addressed in the generalizability and transportability research [6], 10], 11]. Recent studies proposed machine learning methods to integrate prior observational studies into trial analyses [12], 13]. Although pooled-estimators are an active research field – integrating historical with trial data, (for example, Dang et al. [14]) we focus on improving trial analysis alone.
Unfortunately, the aforementioned approaches that rely on validity of historical data are all sensitive to unobservable selection biases and must therefore be used with extreme care. The fundamental problem is that the historical population may differ systematically from the trial population in ways that impact both treatment assignment and outcome. For example, if the historical population did not have access to a modern standard-of-care, adding historical controls would artificially make any new drug seem more effective than it really is. Observable differences in populations can potentially be corrected under reasonable assumptions, but shifts in unobserved variables are impossible to detect or correct.
We take the approach of covariate adjustment to increase efficiency. In recognition of using covariates to reduce estimation uncertainty, the U.S. Food and Drug Adminstration recently released guidance on adjusting for covariates in randomized clinical trials [15]. See Van et al. [16] for summarized methods using covariate adjustment [16]. Our research builds on Schuler et al. [17], who suggest using the historical data to train a prognostic model that predicts the outcome from baseline covariates [17]. They then adjust for the model’s predictions on the trial data in the trial analysis using linear regression, namely the “prognostic adjustment”. A similar research proposed by Holzhauer and Adewuyi [18] recommends using a “super-covariate,” combining multiple prognostic models into a single covariate for adjustment [18]. However, both these methods are limited to trial analyses using linear regression models.
Our task in this paper is to extend the prognostic adjustment approach beyond linear regression, specifically, to “semiparametrically efficient” estimators. Semiparametrically efficient estimators are those that attain the semiparametric efficient variance bound, which is the smallest asymptotic variance that any estimator can attain. The use of efficient estimators thus tends to reduce the uncertainty of the treatment effect estimate. These estimators leverage machine learning internally to estimate the treatment or the outcome model, or both; for example, the augmented inverse probability weighting estimator (AIPW) and the targeted maximum likelihood estimator (TMLE) are commonly used to evaluate the average treatment effect [19], [20], [21], [22], [23]. These estimators have been shown to improve the power of trials over unadjusted or linearly adjusted estimates [24].
In this study, we aim to improve power even further by incorporating historical data via prognostic adjustment. Our approach guarantees asymptotic efficiency of the trial treatment effect and more importantly, promises benefits in small-sample efficiency and robust inference.
2. Framework and notation
We follow the causal inference framework and roadmap from Petersen and van der Laan [25]. First, we define each observational unit i ∈ {1, …, n}, as an independent, identically distributed random variable, O i with true distribution P. In our setting, each random variable O = (W, A, Y, D) contains associated p baseline covariates , a binary treatment indicator A, denoting whether a unit is in the control group (A = 0), or in the treatment group (A = 1), an outcome Y, and an indicator D denoting whether a unit is in either the trial (D = 1) or historical (D = 0) data sample.
We will assume that the trial data is generated under the setting of an RCT, such that P (A = a|W, D = 1) = π a , with some positive constant π a denoting the treatment probability for a ∈ {0, 1}. Define μ a (W) = E P [Y|A = a, W, D = 1] as the conditional outcome means per treatment arm in the trial. Let ρ d (W) = E [Y|W, D = d] denote the prognostic score for a dataset d [26]. When referenced without subscript (ρ) we are referring to the prognostic score in the historical data D = 0.
The fundamental problem of causal inference comes from not being able to observe the outcome under both treatment types. We assume that for each individual, Y = Y(A), i.e., we observe the potential outcome corresponding to the observed treatment. To calculate the causal parameter of interest, we define the (unobservable) causal data to be (Y 1, Y 0, A, W, D), generated from a causal data generating distribution P*. In this study, we are interested in the causal average treatment effect (ATE) in the trial population:
which due to randomization in the trial is equal to the observable quantity:
where μ a (W) = E P [Y|A = a, W, D = 1] is the conditional mean outcome in treatment arm a ∈ {0, 1} from the observable data distribution.
Let (W, Y) denote a dataset with observed outcome Y = [Y 1, …, Y n ] and the observed covariates W = [W 1, …, W n ], where . Furthermore, let denote a machine learning algorithm that maps (W, Y) to a learned function f that estimates the conditional mean E [Y|W]. The algorithm may include detailed internal model selection and parameter tuning, and the algorithm works with predictors and data of any dimension (i.e., m, n are arbitrary). Let represent the historical dataset of size , which is a draw from . We use (or just ) to refer to an estimate of prognostic score learned from the historical data. Let (Y, A, W) represent the trial data set of size n, which is a draw from P n (Y, A, W|D = 1). In a slight abuse of notation, let denote the mapping between trial data and our estimate using an efficient estimator. For example, could denote the cross-fit AIPW estimator described in Schuler [27].
3. Proposed method
3.1. Efficient estimators with prognostic score adjustment
Our proposed method for incorporating historical data with efficient estimators is simple: we first obtain a prognostic model by performing an outcome prediction to fit the historical data (D = 0) using a machine learning algorithm . We then calculate the value of the prognostic score in the trial by feeding in all units’ baseline covariates: . This prognostic score can be interpreted as a “pre-learned” dimension reduction for the trial covariates. Lastly, we estimate the ATE from the trial data, augmented with the prognostic score as an additional covariate, using an efficient estimator: .
In practice, we suggest using a cross-validated ensemble algorithm (also called “super-learner”) for [28]. The super learner is known to perform as well as the best machine learning algorithm included in the library [28], 29]. The library in the super learner should include a variety of nonparametric and parametric learners, such as gradient boosting, random forest, elastic net, and linear models [28], 29].
For an efficient estimator, adding a fixed function of the covariates as an additional covariate will not change the asymptotic behavior [30], 31]. Thus our approach will never be worse than ignoring the historical data (as it might be if we pooled the data to learn the outcome regression). However, it also means that our approach cannot reduce asymptotic variance (indeed it is impossible to do so without making assumptions).
Nonetheless, we find that the finite-sample variance of efficient estimators is far enough from the efficiency bound that using the prognostic score as a covariate generally decreases the variance (without introducing bias) and improves estimation of the standard error. Mechanistically, this happens because the prognostic score “jump-starts” the learning curve of the outcome regression models such that more accurate predictions can be made with fewer trial data. This is especially true when the outcome-covariate relationship is complex and difficult to learn from a small trial. It is well-known that the performance of efficient estimators in RCTs is dependant on the predictive power of the outcome regression. Therefore improving this regression (by leveraging historical data) can reduce variance.
We expect finite-sample benefits as long the trial and historical populations and treatments are similar enough. But even if they are not identical, the prognostic score is still likely to contain very useful information about the conditional outcome mean.
In the following Subsections 3.2 to 3.5, we theoretically show how adjusting for a prognostic score with an efficient estimator can improve estimation in a randomized trial. In an asymptotic analysis where the historical data grows much faster than the trial data, we show that using the prognostic score speeds the decay of the empirical process term in the stochastic decomposition of our estimator. The implications are that small-sample point estimation and inference should be improved even though efficiency gains will diminish asymptotically. The material assumes expertise with semiparametric efficiency theory and targeted/double machine learning. We present our results at a high level and do not present enough background details for readers not specialized in semiparametric inference. Two good starting points for this material are Schuler and van der Laan and Kennedy [32], 33]. The casual reader may skip this section and if they are comfortable with the above heuristic explanation of why prognostic adjustment may improve performance.
3.2. No asymptotic efficiency gain
Before showing how adjusting for a prognostic score for an efficient estimator can benefit estimation, we show that adding any prognostic score to an efficient estimator cannot improve asymptotic efficiency. To see this, we will start by considering the counterfactual means ψ a = E [E [Y|A = a, W]] = E [μ a (W)] for any choice of a ∈ {0, 1}. We will return to the ATE shortly, but for now, it will make our argument clearer to only consider counterfactual means. Consider any efficient estimator for ψ a in a semiparametric model (known treatment mechanism) over the trial data (Y, A, W). The influence function of an estimator completely determines its asymptotic behavior. By definition, any efficient estimator of E [μ a (W)] must have an influence function equal to the canonical gradient, which is referred to as the efficient influence function:
where I is the indicator function and π a = P (A = a) is the fixed, known propensity score.
The efficient influence function in an RCT (where the propensity score is known) is the same as for an observational study (where the propensity score is unknown) as shown by Hahn [34]. Consider now a distribution over (Y, A [W, R]), where R = g(W) for any fixed function g playing the role of a prognostic model. The efficient influence function in this setting is the same as the above. To see this formally one must observe that the tangent space of the factor P (R|Y, A, W) is {0} and does not contribute to the projection of the influence function of e.g. the difference-in-means estimator. Intuitively this is because observing R = g(W) does not add any additional information that can be exploited since it is a fixed, known transformation of the observed covariates.
The fundamental issue is that the asymptotic efficiency bound cannot be improved without considering a different statistical model, e.g. distributions over (Y, A, W, D). The problem is that in considering a different model we must also introduce additional assumptions to maintain identifiability of our trial-population causal parameter. For example, Li et al. [13] consider precisely this setup and rely on an assumption of “conditional mean equivalence” E [Y|A, W, D = 1] = E [Y|A, W, D = 0] to maintain identification while improving efficiency [13]. Similarly, an analysis following Chakrabortty et al. [35] shows that efficiency gains are also possible if we assume the covariate distributions are the same when conditioning on D [35]. In this paper, we take the covariate adjustment approach, incorporating the external data without these explicit assumptions and therefore we have to look for benefits in finite sample improvements.
3.3. Improving point estimation
To understand the benefits of prognostic adjustment we must consider the non-asymptotic behavior of our estimator. As above we will consider estimation of the treatment-specific mean ψ a , but from now on we will omit the a subscripts to reduce visual clutter.
Consider the following decomposition:
This sort of decomposition is common in the analysis of efficient estimators [32], 33]. As above, ϕ here denotes the efficient influence function of ψ. We use the empirical process notation to denote a sample mean, to denote a population mean (not averaging over randomness in ), and a plug-in estimate of ϕ with μ estimated by regression. We will analyze each term and see what difference adjusting for the prognostic score makes in this general decomposition. Note that for an efficient estimator, the last term by construction. Eliminating this “plug-in bias” term is the purpose of bias correcting schemes such as TMLE or efficient estimating equations [32], 33].
Of the remaining terms, the first is the efficient influence function term, P n ϕ. We have already shown that an efficient estimator leveraging the prognostic score has the same influence function as one without. It is also known that the remainder term can be bounded in absolute value by the product of estimation errors in the outcome and propensity regressions [32], 33]. This is exactly zero in a randomized trial since the propensity score is known. Therefore both of these terms are unaffected by prognostic adjustment.
That leaves us with only the “empirical process” term . With cross-fitting this term can be shown to be [32], 33]. In our setting, the estimated influence function depends only on the estimated outcome regression and we thus have . This is o P (n −1/2) in all cases where the regression is L 2 consistent, but the actual rate can be faster depending on how quickly converges. We’ll use t n to denote this rate, i.e., . This is the mechanism by which prognostic adjustment improves efficient estimators. When the prognostic score is used to estimate , the norm is generally smaller than it otherwise would be.
We can formalize this asymptotically. Recall that n denotes the trial sample size and denotes the historical sample size. Consider a historical sample much larger than the trial in the limit: . For example, presume in which case r n = 1/n. Presume that the historical distribution of covariates and outcome is the same as that in the trial control arm, or simply that ρ(w) = μ 0(w) (this is a best-case scenario). Presume we have a learning algorithm that in some large nonparametric function class can learn functions in an L 2 sense at rate t n . Let be the prognostic score learned from the historical samples using this learner.
Instead of fitting our trial outcome regression with the prognostic score as a covariate, presume that we directly take . In other words, we use our prognostic model as the control outcome regression in the trial, ignoring the trial data. That’s sensible in this hypothetical setting because 1) the prognostic model will indeed converge to the true outcome function and 2) the amount of omitted trial data is vanishingly small relative to the historical data. We can also interpret this as an estimator of in the trial data (i.e., our prognostically adjusted outcome regression): we should expect that when the prognostic model is good, our learner will simply return the prognostic score untouched to model the control counterfactual outcome. Or, more formally, if a parametric learner is used on top of the prognostic score (e.g. a working model ) then the total error will be composed of a root-n term from learning the parameters and a higher order empirical process term. If we used our learner to fit the outcome regression from trial data alone, our rate on the L 2 norm of the outcome regression would be t n , e.g. n −1/10 for example. However, if we use the prognostic score the rate is ( instead of n), e.g. . But recalling (r n = 1/n, for example), we can express as (t n r n )/n. Essentially we can plug in into to see . This can dramatically increase the speed at which in terms of n and consequently affect the rate of convergence of the empirical process term, making it decay faster than it would without the prognostic adjustment.
The result of making the empirical process term higher order is to reduce finite-sample variance of our point estimate. With cross-fitting the empirical process term is exactly mean-zero [32], 33], so finite-sample bias is unaffected.
3.4. Improving standard error estimation
We can apply similar arguments to show that the performance of the plug-in estimate of asymptotic variance (based on our estimated influence function ) is also improved by prognostic adjustment. The difference between the estimate and the true asymptotic variance Pϕ 2 can be decomposed as
The first term here is a nice empirical mean which by the central limit goes to zero at a root-n rate and is unaffected by prognostic adjustment. The second term is similar to the empirical process term discussed above in the context of point estimation and by identical arguments this term decays faster when prognostic adjustment is used (note L 2 convergence of implies the same for under regularity conditions that are satisfied in our setting because π is a known constant bounded away from 0). This term is always higher-order than n −1/2 and thus asymptotically negligible, but possibly impactful in small samples. It is also mean-zero. Together, this means that its improved rate with prognostic adjustment translates to less finite-sample variability in our estimate of the standard error.
The last term is bounded by , so this term also decays faster with prognostic adjustment. This term contributes to both bias and variance of the standard error estimate. Unlike the equivalent norm that appears in the bound for the empirical process term, the norm here is not divided by and so this term may be of leading order (slowest decaying) in the overall stochastic decomposition, thus asymptotically relevant. Since prognostic adjustment increases the rate, the term may go from leading order to higher-order. Therefore prognostic adjustment may, in some cases, make the plug-in standard error an asymptotically linear estimator (i.e. standard error of the standard error should decrease at a n −1/2 rate).
3.5. Caveats
Although we do not need additional assumptions for identifiability and thus retain unbiased estimation in all cases, all of the possible benefits described above do rely on the assumption that the historical and trial data-generating processes share a control-specific conditional mean. If this is not the case, then the amount by which the prognostic score speeds convergence of the control outcome regression will be attenuated, but not necessarily eliminated. For example, if the true outcome regression is the same as the prognostic score up to some parametric transformation that is learnable at a fast rate by a learner in our library , then we should still expect benefits.
Until now we have also focused on the control counterfactual mean. The influence function for the ATE is the difference of those for the two counterfactual means and consequently we can decompose the empirical process term into two terms which are and where μ a = E [Y|A = a, W] denote the counterfactual mean functions. Therefore, the overall order of the empirical process term is dominated by whichever of these terms is lower-order. For the treatment regression to leverage the historical data, we need to assume some prognostic information can be transferred from the control to the treatment arm. For example, we might expect satisfactory information transfer from the historical data to the trial treatment arm when there is a constant treatment effect c (i.e. μ 1(w) = μ 0(w) + c) or there is some other parametric, easily-learnable relationship between the two conditional means. Otherwise, the slower convergence rate for μ 1 dominates and we obtain less benefit from prognostic adjustment. A worst-case scenario would be when the two conditional means depend on mutually exclusive sets of covariates: if this is the case, no transfer should be possible and benefits should be limited or absent.
Our analysis shows that use of the historical sample via prognostic score adjustment produces less-variable point estimates in small samples as well as more stable and accurate estimates of standard error. Unfortunately, asymptotic gains in efficiency are not possible without further assumptions.
However, these benefits are contingent on the extent to which the covariate-outcome relationships in both treatment arms of the trial are similar to the equivalent relationship in the historical data. In particular, differences between historical and trial populations and high heterogeneity of effect may both attenuate benefits. Nonetheless, these problems can never induce bias. Therefore, relative to alternatives, prognostic adjustment of efficient estimators provides strict guarantees for type I error, but at the cost of limiting the possible benefits of using historical data.
4. Simulation study
4.1. Setup
This simulation study aims to demonstrate the utility of an efficient estimator with the addition of a prognostic score. We examine how our method performs in different data generating scenarios (e.g., heterogeneous vs. constant effect), across different data set sizes, and when there are distributional shifts from the historical to the trial population. The simulation study is based on the structural causal model in DGP [1], [2], [3], [4], [5], [6], [7], [8], [9], [10]. In total there are 20 observed covariates of various types and a single unobserved covariate.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
Notice that m a (W, U) is the mean of the counterfactual conditioned on both the observed and unobserved covariates. Our observable conditional means are thus μ a (W) = E [m a (W, U)|W]. We examine two different scenarios for the conditional outcome mean m a . In our “heterogeneous effect” simulation:
| (11) |
| (12) |
where the I represents the indicator function and propensity score π is written without the subscript a since the treatment probability is the same. To illustrate our results with another specification, we also include a second “heterogeneous effect” simulation to illustrate our results.
| (13) |
| (14) |
Our “constant effect” simulation is computed as:
| (15) |
| (16) |
To begin, we use the same data generating process (DGP) for the historical and trial populations except the fact that A = 0 deterministically in the historical DGP. But in what follows, we loosen this assumption by changing the historical data generating distribution with varying degrees of observed and unobserved covariate shifts.
We examine several scenarios: first, we analyze the trial (n = 250) under the heterogeneous and constant treatment effect DGPs, where the historical sample ( = 1,000) is from the same DGP [1], [2], [3], [4], [5], [6], [7], [8], [9], [10] as the trial sample. Second, we vary the historical and trial sample sizes for the heterogeneous treatment effect simulation. To vary the historical sample sizes, we first fix the trial sample size (n = 250) and vary the historical sample size (with = 100, 250, 500, 750, and 1,000). To vary the trial sample sizes, we first fix the historical sample size ( = 1,000) and vary the trial sample size (with n = 100, 250, 500, 750, and 1,000). We also vary n and together to demonstrate asymptotic benefits in the estimation of the standard error (as discussed in Section 3).
Third, we examine the effect of distributional shifts between the historical and trial populations. In these cases, we draw trial data from the DGP [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], but draw our historical data from modified versions. To simulate a “small” observable population shift we let W 1|D = 0 ∼Unif (−5, − 2) and to simulate a “large” observable population shift we let W 1|D = 0 ∼Unif (−7, − 4). To simulate a “small” unobservable population shift we let U|D = 0 ∼Unif (0.5, 1.5) and to simulate a “large” unobservable population shift we let U|D = 0 ∼Unif [1], 2]. The shifts in the unobserved covariate induce shifts in the conditional mean relationship between the observed covariates and the outcome (see Supplemental Appendix A for an explicit explanation).
We consider three estimators for the trial: unadjusted (difference-in-group-means), main terms only linear regression (with Huber-White (robust) standard errors estimator HC3 [36], [37], [38], and targeted maximum likelihood estimation (TMLE; an efficient estimator [19]). All estimators return an effect estimate and an estimated standard error, which we use to construct Wald 95 % confidence intervals and corresponding p-values. The naive unadjusted estimator cannot leverage any covariates, but both linear and TMLE estimators can. We compare and contrast results from linear and TMLE estimators both with and without the fitted prognostic score as an adjustment covariate (“fitted”) to compare against Schuler et al. [17]. We also consider the oracle version of the prognostic score (“oracle”) for a benchmark comparison; the oracle prognostic score perfectly models the expected control outcome in the trial E [Y|W, A = 0, D = 0]. Unlike the fit prognostic score, the oracle version is not affected by random noise in the historical data and it is not sensitive to shifts between historical and trial populations (indeed it is not affected by the historical data at all). The oracle prognostic score only serves as a best-case comparison and is infeasible to calculate in practice.
For simplification, we include the same specifications of the discrete super learner (cross-validated ensemble algorithm) for both the prognostic model and all regressions required by our efficient estimators. Specifically, we use the discrete super learner – choosing one machine learning algorithm from a set of algorithms for each cross-fit fold via the lowest cross-validated mean squared error. The set of algorithms include linear regression with main terms only, gradient boosting with varying tree tuning specifications (xgboost) [39], and Multivariate Adaptive Regression Splines [40]. Specifications for tuning parameters are in Supplemental Appendix B.
4.2. Results
Our results for the primary heterogeneous effect scenario are summarized in Table 1 and 2. Results for other DGPs are qualitatively similar so these are reported in Supplemental Appendix C along with additional performance metrics.
Table 1:
Empirical bias and variance for the point estimate of the trial ATE in the heterogeneous effect simulation scenario. Results in the table are formatted as “empirical bias (empirical variance)”.
| Prognostic score | TMLE | Linear | Unadjusted |
|---|---|---|---|
| Oracle | −0.066 (4.827) | −0.083 (10.485) | – |
| Fit | −0.081 (4.843) | −0.096 (10.438) | – |
| None | −0.031 (5.918) | −0.005 (11.113) | −0.015 (10.373) |
Table 2:
Empirical bias and variance for the estimated standard error of the trial ATE estimate. Results in the table are formatted as “empirical bias (empirical variance)”.
| Prognostic score | TMLE | Linear | Unadjusted |
|---|---|---|---|
| Oracle | 0.036 (0.004) | 0.037 (0.029) | – |
| Fit | 0.064 (0.005) | 0.037 (0.030) | – |
| None | 0.048 (0.041) | 0.026 (0.026) | 0.009 (0.011) |
Table 1 illustrates the mean of the empirical bias and empirical variance of the ATE point estimate across the 1,000 simulations. The results demonstrate that prognostic adjustment decreases variance relative to vanilla TMLE in the realistic heterogeneous treatment effect scenario (results are similar in other scenarios). The reduction in variance results in an increase in an 10 % increase in power in this case. In terms of variance reduction, fitting the prognostic score is almost as good as having the oracle in this scenario.
Prognostic adjustment also improves the variance of the linear estimator (corroborating Schuler et al. [17]). But overall TMLE convincingly beats the main terms only linear estimator, with or without prognostic adjustment, except for in the constant effect scenario where the two are roughly equivalent with prognostic adjustment. The matching or slightly superior performance of prognostically adjusted linear regression in the constant effect DGP is consistent with the optimality property previously discussed in Schuler et al. [17].
Importantly, the variance is not underestimated in any of our simulations meaning that the coverage was nominal (95 %) for all estimators (and thus strict type I error control was attained; Supplemental Appendix C). Including the prognostic score did not affect coverage in any case, even when the trial and historical populations were different.
Table 2 illustrates the mean of the empirical bias and empirical variance of the estimated standard error of the ATE estimate. The table corroborates the theoretical findings from Section 3, namely that the variance of the estimated variance for an efficient estimator (TMLE) is decreased by prognostic adjustment.
Using larger historical data sets increases the benefits of prognostic adjustment with efficient estimators. Figure 1.A shows a detailed view of this phenomenon in terms of decrease in the average estimated standard error as the historical data set grows in size. In effect, the larger the historical data, the smaller the resulting confidence intervals tend to be in the trial (while still preserving coverage, see Supplemental Appendix C), for the estimators leveraging an estimated prognostic score. Figure 1.B shows the change in estimated standard error as the trial size varies. This illustrates that the relative benefit of prognostic adjustment is larger in smaller trials. Here we see an 10.6 % increase in power comparing the TMLE with versus without fitted prognostic score when n = 250, but an 80 % increase when n = 100. From Figure 1 we again see that the TMLE with the fitted prognostic score performs almost as well as the TMLE with the oracle prognostic score when the historical sample size is increased to around 1,000. The asymptotic standard error bound calculated from the influence function is also shown in Figure 1 for reference (the empirical standard error with 95 % confidence interval is included in Supplemental Appendix D).
Figure 1:
Mean estimated standard errors across estimators when historical and trial sample sizes are varied using the heterogeneous DGP. When the historical sample size is varied (Figure 1.A), the trial is fixed at n = 250. When the trial size is varied (Figure 1.B), the historical sample is fixed at .
When trial sample size n and historical sample size increase together, our theory predicts that the plug-in standard error may become asymptotically linear with prognostic adjustment. This is confirmed by simulation (with 1,000 Monte Carlo simulations): as we increase n with prognostic adjustment, the empirical variance of the estimated standard error times n is closer to a flat line which indicates a near- rate of decay (Figure 2). The same is not true without prognostic adjustment: the variance of the plug-in standard error from TMLE is greater and falls more slowly.
Figure 2:
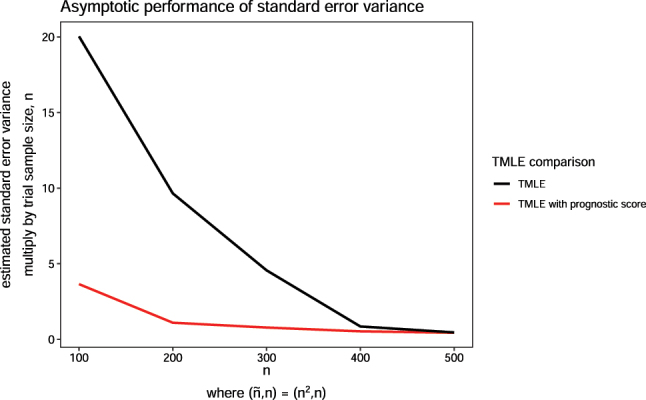
Variance of estimated standard error across estimators when historical and trial sample sizes are varied using the constant effect DGP. The historical sample size, is proportional to trial size n, where .
We also observe that our method is relatively robust to both observed and unobserved distributional shifts between historical and trial populations (Figure 3). When the shifts are large, the prognostic score may be uninformative (most evident in Figure 3.B), but including it may still improve efficiency (as seen in Figure 3.A). We also see that a good prognostic score (no shift in distribution) substantially reduces the variability of the estimated standard error. Variability increases with the magnitude of the covariate shift but still does not exceed that of TMLE without prognostic adjustment.
Figure 3:
Estimated standard errors across estimators when observed (Figure 3.A) and unobserved shifts (Figure 3.B) are present in the historical sample relative to the trial sample.
5. Case study
In this section, we examine the use of TMLE with prognostic covariate adjustment in RCTs involving people diagnosed with type 2 diabetes (T2D). T2D is a chronic disease with a progressive deterioration of glucose control. Glucose control is normally evaluated by long-term blood glucose level, measured by hemoglobin A1C (HbA1C). The analyses are carried out using data provided by Novo Nordisk A/S originating from 14 previously conducted RCTs within the field of diabetes, see Supplemental Appendix E for a full overview of the trials.
We reanalyze the phase IIIb clinical trial called NN9068-4229, where the trial population consisted of insulin naive people with T2D [41]. The participants of this trial were inadequately controlled on treatment with SGLT2i, a type of oral anti-diabetic treatment (OAD). Inadequately controlled was defined as having a HbA1C of 7.0–11.0 % (both inclusive). The aim of the trial was to compare glycemic control of insulin IDegLira versus insulin IGlar as add-on therapy to SGLT2i in people with T2D. The trial was a 26-week, 1:1 randomized, active-controlled, open label, treat-to-target trial with 420 enrolled participants. One participant was excluded due to non-exposure to trial product, yielding n = 419. The efficacy of IDegLira was measured by the difference in change from baseline HbA1C to landmark visit week 26. Our corresponding historical sample came from previously conducted RCTs with a study population also consisting of insulin naive people with T2D, who were inadequately controlled on their current OADs. A total of participants all receiving insulin IGlar, were enrolled in the historical sample.
For the trial reanalysis in our study, we included patient measures of their demographic background, laboratory measures, concomitant medication, and vital signs. The treatment indicator where only used in the NN9068-4229 trial. For details on the specific measurements, covariate distributions, and imputation of missing covariates see Supplemental Appendix F, G, and H. For the continuous covariates we see that the mean and standard deviation are not particularly different between the historical and new trial sample, meaning that both resemble a T2D population with uncontrolled glycemic control. Furthermore we see that the range of continuous covariates for the new trial sample are contained in the range of the historical sample. This indicates that the trial population is largely similar to the historical population, at least in terms of observable covariates. For the categorical covariates the distributions vary between the historical and new trial sample. However, all the categories in the new trial sample are present in the historical sample.
A linear estimator with baseline HbA1C, region and pre-trial OADs as adjustment covariates was used in the original analysis of the primary endpoint in the NN9068-4,229 trial. In this analysis, an average treatment effect estimate of −0.340 (95 % confidence interval [−0.480; −0.200]). In this reanalysis, we report the result of five estimators: unadjusted, linear regression (adjusting for all available covariates), linear regression with a prognostic score, TMLE, and TMLE with a prognostic score. The prognostic score is explicitly defined in Supplemental Appendix I. For this application, we expanded the library of the super learner for a more comprehensive set of machine learning models than the simulation, including random forest [42], k-nearest neighbor, and a more comprehensive set of tuning parameters for the xgboost model in addition to the previously specified library, see Supplemental Appendix B. Separately, we obtained the correlation of the fitted prognostic score against the trial outcome. The prognostic score’s correlation with the outcome is 0.752 with control subjects and 0.622 with treated subjects, indicating that adjustment for the score should result in an improvement over unadjusted estimation [17].
This is a reanalyses of the NN9068-4229 trial using five different estimators where 1:1 randomization was performed. The total sample size is n = 419.
From Table 3, we see that the smallest confidence interval is obtained using TMLE with prognostic score. All methods obtain similar point estimates except from the unadjusted estimator. Notice that the linear estimator with or without a prognostic score yields the same results, since the prognostic model is a linear model in this case (chosen as the model that yielded lowest MSE from 20-fold cross-validation within the discrete super learner).
Table 3:
Estimates for average treatment effect (ATE) and with 95 % confidence levels of change in hemoglobin A1C (HbA1C) from baseline to week 26 for insulin IDegLira versus insulin IGlar as add-on therapy to SGLT2i in people with type 2 diabetes.
| Prognostic score | TMLE | Linear | Unadjusted |
|---|---|---|---|
| With | −0.351 (s.e. 0.145) | −0.355 (s.e. 0.157) | – |
| Without | −0.369 (s.e. 0.150) | −0.355 (s.e. 0.157) | −0.248 (0.192) |
This is a reanalyses of the NN9068-4229 trial using five different estimators where 50 participants from the control and treatment group, respectively, were chosen at random yielding a total sample size of n = 100. The random selection is done 10 times and the reported numbers are the average of the point estimates and standard error.
As illustrated by the simulation study and the asymptotic analysis in Sections 3.3 and 3.4, the relative benefit of prognostic adjustment is larger in smaller trials. To examine this result, we sub-sampled from the NN9068-4229 trial but reanalyzed with selecting 50 participants randomly from each group, resulting in n = 100. This random selection of 50 participants from each group is repeated 10 times and averaged to compute the point estimate and standard error. The average correlation of the prognostic score with the outcome was 0.790 with control subjects and 0.656 with treated subjects. We see an relatively larger reduction in the standard error estimate using TMLE with prognostic covariate adjustment compared to TMLE without in the reanalysis (Table 4).
Table 4:
Estimates for average treatment effect and with 95 % confidence levels of change in hemoglobin A1C from baseline to week 26 for insulin IDegLira versus insulin IGlar as add-on therapy to SGLT2i in people with type 2 diabetes.
| Prognostic score | TMLE | Linear | Unadjusted |
|---|---|---|---|
| With | −0.519 (s.e. 0.307) | −0.544 (s.e. 0.438) | – |
| Without | −0.582 (s.e. 0.349) | −0.544 (s.e. 0.438) | −0.344 (0.399) |
6. Discussion
In this study we demonstrate the utility of incorporating historical data via a prognostic score in an efficient estimator while maintaining strict type I error control. Using the prognostic score via covariate adjustment overall improves the performance of the efficient estimator by decreasing the standard error and improving its estimation. This method is most useful in randomized trials with small sample sizes. Our proposed method is shown to be robust against bias even when the historical sample is drawn from a different population.
Prognostic adjustment requires no assumptions to continue to guarantee unbiased causal effect estimates. However, this comes with a trade-off: without introducing the risk of bias, there is a limit on how much power can be gained and in what scenarios. For example, the method of Li et al. [13] (which imposes an additional assumption) can asymptotically benefit from the addition of historical data, whereas our method can only provide gains in small samples [13]. However, these gains are most important precisely in small samples because estimated effects are likely to be of borderline significance, whereas effects are more likely to be clear in very large samples regardless of the estimator used.
Besides being assumption-free, our method has other practical advantages relative to data fusion approaches. For one, we do not require a single, well-defined treatment in the historical data. Moreover, we do not require an exact overlap of the covariates measured in the historical and trial data sets. This means trial data can have more measured covariates compared to the historical data, but the prognostic score could only be derived from the overlapping measured covariate set. For multiple historical data sets, there is no need to manually select one over another. It is easy to utilize the data sets: if they are believed to be drawn from substantially different populations, separate prognostic scores can be built from each of them and included as covariates in the trial analysis. Additional variable selection procedure (screening) can be performed within the Super Learner specification. As long as one of these scores is a good approximation of the outcome-covariate relationship in one or more arms of the trial, there will be added benefits to power.
Prognostic adjustment with efficient estimators can also be used with pre-built or public prognostic models: the analyst does not need direct access to the historical data if they can query a model for predictions. This is helpful in cases where data is “federated” and cannot move (e.g. when privacy must be protected or data has commercial value).
Our approach is closely related to the transfer learning literature in machine learning. In transfer learning, the goal is to use a (large) “source” dataset to improve prediction for a “target” population for which we have only minimal training data [43], [44], [45]. In this work we use a particular method of “transfer” (adjusting for the source/historical model prediction) to improve the target (trial) predictions, which drives variance reduction. It should also be possible to leverage other more direct forms of model transfer for the outcome regression, such as pre-training a deep learning model on the historical data and then fine-tuning using the trial data.
The theory we developed to explain the benefits of prognostic adjustment in the context of efficient estimation for trials is easily generalizable to estimation of any kind of pathwise differentiable parameter augmented with transfer learning from an auxiliary dataset. The specific breakdown of different terms may differ but the overall intuition should be the same: transfer learning may accelerate the disappearance of higher-order terms that depend on the error rates of regression estimates.
Lastly, since we use efficient estimators, we can leverage the results of Schuler [27] to prospectively calculate power with prognostic adjustment [27]. In fact, we suspect the methods of power calculation described in that work would improve in accuracy with prognostic adjustment since the outcome regressions are “jump-started” with the prognostic score. Verification of this fact and empirical demonstration will be left to future work.
Supplementary Material
Supplementary Material Details
Acknowledgments
The authors would like to thank study participants and staff for their contributions. This research was conducted on the Savio computational cluster resource provided by the Berkeley Research Computing program at the University of California, Berkeley. This computing resource was supported by the UC Berkeley Chancellor, Vice Chancellor for Research, and Chief Information Officer. The authors thank Christopher Paciorek for answering Savio related inquiries. This research was also conducted on Kaiser Permanente advance computing infrastructure platform. The authors thank Woodward B Galbraith and Tejomay Gadgil for their technical support on shortening the simulation computation time.
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/ijb-2024-0018).
Footnotes
Research ethics: Not applicable.
Informed consent:Not applicable.
Author contributions: LDL and AS conceptualized the methodology of this research. LDL wrote the original draft and conducted the investigation, formal analysis, and visualizations. LDL worked closely together with AEH and AS on the research framework and discussion. EH-F collaborated with LDL on the application of the research and ran case study analysis. EH-F wrote the original draft of the updated case study analysis section and result section. EH-F also was involved in simulation discussion with LL and AS. All authors contributed significantly to the review and editing of the paper. The authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Use of Large Language Models, AI and Machine Learning Tools: None declared.
Conflict of interest: Alan E. Hubbard is a co-editors-in-chief of IJB. None of the authors, including Alan E. Hubbard, had a role in the peer review or handling of this manuscript. All other authors state no conflict of interest.
Research funding: This research was made possible by funding from the National Science Foundation (DGE 2146752) to LDL and global development grant (OPP1165144) from the Bill & Melinda Gates Foundation for AEH to the University of California, Berkeley, CA, USA. This research also received funding from Innovation Fund Denmark (Grant number 2052-00044B) for EFD to Novo Nordisk A/S. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Data availability: Not applicable.
Contributor Information
Lauren D. Liao, Email: Liaoldliao@berkeley.edu.
Alejandro Schuler, Email: alejandro.schuler@berkeley.edu.
Supporting information
The following supporting information is available as part of the online article:
Appendix A. Expectation calculation when incorporating unobserved covariate.
Appendix B. Discrete super learner specifications for simulation and case study.
Appendix C. Simulation results for different data generation processes.
Appendix D. Empirical standard error estimates.
Appendix E. Case study data summary.
Appendix F. Summary of continuous measurements of the baseline.
Appendix G. Summary of categorical measurements of the baseline.
Appendix H. Missing pattern of the case study.
Appendix I. Case study prognostic score.
References
- 1.Bentley C, Cressman S, van der Hoek K, Arts K, Dancey J, Peacock S. Conducting clinical trials – costs, impacts, and the value of clinical trials networks: a scoping review. Clin Trials. 2019;16:183–93. doi: 10.1177/1740774518820060. [DOI] [PubMed] [Google Scholar]
- 2.Glennerster R. Chapter 5 – the practicalities of running randomized evaluations: partnerships, measurement, ethics, and transparency. In: Banerjee AV, Duflo E, editors. Handbook of economic field experiments. Vol. 1. Oxford: Elsevier; 2017. pp. 175–243. [Google Scholar]
- 3.Temple R, Ellenberg SS. Placebo-controlled trials and active-control trials in the evaluation of new treatments. Part 1: ethical and scientific issues. Ann Intern Med. 2000;133:455–63. doi: 10.7326/0003-4819-133-6-200009190-00014. [DOI] [PubMed] [Google Scholar]
- 4.Wu P, Luo S, Geng Z. On the comparative analysis of average treatment effects estimation via data combination. J Am Stat Assoc. 2025:1–12. doi: 10.1080/01621459.2024.2435656. [DOI] [Google Scholar]
- 5.Bareinboim E, Pearl J. Causal inference and the data-fusion problem. Proc Natl Acad Sci USA. 2016;113:7345–52. doi: 10.1073/pnas.1510507113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shi X, Pan Z, Miao W. Data integration in causal inference. Wiley Interdiscip Rev Comput Stat. 2023;15 doi: 10.1002/wics.1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Colnet B, Mayer I, Chen G, Dieng A, Li R, Varoquaux G, et al. Causal inference methods for combining randomized trials and observational studies: a review. Stat Sci. 2024;39:165–91. doi: 10.1214/23-STS889. [DOI] [Google Scholar]
- 8.Hill JL. Bayesian nonparametric modeling for causal inference. J Comput Graph Stat. 2011;20:217–40. doi: 10.1198/jcgs.2010.08162. [DOI] [Google Scholar]
- 9.Li F, Ding P, Mealli F. Bayesian causal inference: a critical review. Philos Trans A Math Phys Eng Sci. 2023;381:20220153. doi: 10.1098/rsta.2022.0153. [DOI] [PubMed] [Google Scholar]
- 10.Huang M, Egami N, Hartman E, Miratrix L. Leveraging population outcomes to improve the generalization of experimental results: application to the JTPA study. Ann Appl Stat. 2023;17:2139–64. doi: 10.1214/22-AOAS1712. [DOI] [Google Scholar]
- 11.Degtiar I, Rose S. A review of generalizability and transportability. Annu Rev Stat Appl. 2023;10:501–24. doi: 10.1146/annurev-statistics-042522-103837. [DOI] [Google Scholar]
- 12.Lee D, Yang S, Dong L, Wang X, Zeng D, Cai J. Improving trial generalizability using observational studies. Biometrics. 2021:1213–25. doi: 10.1111/biom.13609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li X, Miao W, Lu F, Zhou XH. Improving efficiency of inference in clinical trials with external control data. Biometrics. 2023;79:394–403. doi: 10.1111/biom.13583. [DOI] [PubMed] [Google Scholar]
- 14.Dang LE, Tarp JM, Abrahamsen TJ, Kvist K, Buse JB, Petersen M, et al. A cross-validated targeted maximum likelihood estimator for data-adaptive experiment selection applied to the augmentation of RCT control arms with external data. arXiv preprint. 2022 doi: 10.48550/arXiv.2210.05802. [DOI] [Google Scholar]
- 15.FDA . Adjusting for covariates in randomized clinical trials for drugs and biological products. Internet: Center for Drug Evaluation and Research, Center for Biologics Evaluation and Research; 2023. [Google Scholar]
- 16.Van Lancker K, Bretz F, Dukes O. The use of covariate adjustment in randomized controlled trials: an overview. arXiv preprint. 2023 doi: 10.48550/arXiv.2306.05823. [DOI] [PubMed] [Google Scholar]
- 17.Schuler A, Walsh D, Hall D, Walsh J, Fisher C, for the Critical Path for Alzheimer’s Disease ; the Alzheimer’s Disease Neuroimaging Initiative ; the Alzheimer’s Disease Cooperative Study Increasing the efficiency of randomized trial estimates via linear adjustment for a prognostic score. Int J Biostat. 2022;18:329–56. doi: 10.1515/ijb-2021-0072. [DOI] [PubMed] [Google Scholar]
- 18.Holzhauer B, Adewuyi ET. “Super-covariates”: using predicted control group outcome as a covariate in randomized clinical trials. Pharm Stat. 2023;22:1062–75. doi: 10.1002/pst.2329. [DOI] [PubMed] [Google Scholar]
- 19.Van Der Laan MJ, Rubin D. Targeted maximum likelihood learning. Int J Biostat. 2006 doi: 10.2202/1557-4679.1043. [DOI] [Google Scholar]
- 20.Van der Laan MJ, Rose S. Targeted learning: causal inference for observational and experimental data. Vol. 4 New York: Springer; 2011. [Google Scholar]
- 21.Diaz I. Machine learning in the estimation of causal effects: targeted minimum loss-based estimation and double/debiased machine learning. Biostatistics. 2020;21:353–8. doi: 10.1093/biostatistics/kxz042. [DOI] [PubMed] [Google Scholar]
- 22.Glynn AN, Quinn KM. An introduction to the augmented inverse propensity weighted estimator. Polit Anal. 2010;18:36–56. doi: 10.1093/pan/mpp036. [DOI] [Google Scholar]
- 23.Chernozhukov V, Chetverikov D, Demirer M, Duflo E, Hansen C, Newey W, et al. Double/debiased machine learning for treatment and structural parameters. Econom J. 2018;21:C1–68. doi: 10.1111/ectj.12097. [DOI] [Google Scholar]
- 24.Rosenblum M, van der Laan MJ. Simple, efficient estimators of treatment effects in randomized trials using generalized linear models to leverage baseline variables. Int J Biostat. 2010;6:13. doi: 10.2202/1557-4679.1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Petersen ML, van der Laan MJ. Causal models and learning from data: integrating causal modeling and statistical estimation. Epidemiology. 2014;25:418–26. doi: 10.1097/ede.0000000000000078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hansen BB. The prognostic analogue of the propensity score. Biometrika. 2008;95:481–8. doi: 10.1093/biomet/asn004. [DOI] [Google Scholar]
- 27.Schuler A. Designing efficient randomized trials: power and sample size calculation when using semiparametric efficient estimators. Int J Biostat. 2021;18:151–71. doi: 10.1515/ijb-2021-0039. [DOI] [PubMed] [Google Scholar]
- 28.van der Laan MJ, Polley EC, Hubbard AE. Super learner. Stat Appl Genet Mol Biol. 2007;6:25. doi: 10.2202/1544-6115.1309. [DOI] [PubMed] [Google Scholar]
- 29.Polley EC, van der Laan MJ. Super learner in prediction. U.C. Berkeley Division of Biostatistics Working Paper Series. 2010;Working Paper 266 https://biostats.bepress.com/ucbbiostat/paper266 [Google Scholar]
- 30. Rothe C. Flexible covariate adjustments in randomized experiments; 2018. . https://madoc.bib.uni-mannheim.de/52249/ [Google Scholar]
- 31.Moore KL, van der Laan MJ. Covariate adjustment in randomized trials with binary outcomes: targeted maximum likelihood estimation. Stat Med. 2009;28:39–64. doi: 10.1002/sim.3445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schuler A, van der Laan M. Introduction to modern causal inference. . 2022. [9 12 2023]. https://alejandroschuler.github.io/mci Accessed.
- 33.Kennedy EH. Semiparametric doubly robust targeted double machine learning: a review. . 2024:207–36. doi: 10.48550/arXiv.2203.06469. Handbook of statistical methods for precision medicine. Boca Raton, FL: Chapman & Hall. [DOI] [Google Scholar]
- 34.Hahn J. On the role of the propensity score in efficient semiparametric estimation of average treatment effects. Econometrica. 1998:315–31. doi: 10.2307/2998560. [DOI] [Google Scholar]
- 35.Chakrabortty A, Dai G, Tchetgen ET. A general framework for treatment effect estimation in semi-supervised and high dimensional settings. arXiv preprint. 2022 doi: 10.48550/arXiv.2201.00468. [DOI] [Google Scholar]
- 36.White H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica. 1980;48:817–38. doi: 10.2307/1912934. [DOI] [Google Scholar]
- 37.MacKinnon JG, White H. Some heteroskedasticity-consistent covariance matrix estimators with improved finite sample properties. J Econom. 1985;29:305–25. doi: 10.1016/0304-4076(85)90158-7. [DOI] [Google Scholar]
- 38.Long JS, Ervin LH. Using heteroscedasticity consistent standard errors in the linear regression model. Am Statistician. 2000;54:217–24. doi: 10.1080/00031305.2000.10474549. [DOI] [Google Scholar]
- 39.Chen T, Guestrin C. Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. KDD ’16. New York, NY, USA: Association for Computing Machinery; 2016. XGBoost: a scalable tree boosting system; pp. 785–94. [Google Scholar]
- 40.Friedman JH. Multivariate adaptive regression Splines. aos. 1991;19:1–67. doi: 10.1214/aos/1176347963. [DOI] [PubMed] [Google Scholar]
- 41.gov C. A clinical trial comparing glycaemic control and safety of insulin degludec/liraglutide (IDegLira) versus insulin glargine (IGlar) as add-on therapy to SGLT2i in subjects with type 2 diabetes mellitus (DUAL TM IX) . 2020. https://clinicaltrials.gov/study/NCT02773368?cond=DUALTMAccessed:2023-9-25 Available from.
- 42.Breiman L. Random forests. Mach Learn. 2001;45:5–32. [Google Scholar]
- 43.Torrey L, Shavlik J. Handbook of research on machine learning applications and trends: algorithms, methods, and techniques. Hershey, PA: IGI Global; 2010. Transfer learning; pp. 242–64. [Google Scholar]
- 44.Zhuang F, Qi Z, Duan K, Xi D, Zhu Y, Zhu H, et al. A comprehensive survey on transfer learning. Proc IEEE. 2021;109:43–76. doi: 10.1109/jproc.2020.3004555. [DOI] [Google Scholar]
- 45.Weiss K, Khoshgoftaar TM, Wang D. A survey of transfer learning. J Big Data. 2016;3:1–40. doi: 10.1186/s40537-016-0043-6. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material Details




