Dynamics of bacterial phenotype selection in a colonized host

Abstract

The population dynamics of Helicobacter pylori during colonization in an infected animal host provide a quantifiable experimental model of in vivo microbial phenotype evolution. Phenotype variability in H. pylori populations can be typed as polymorphic expression of Lewis antigens on their cell surfaces. The high mutational frequency of H. pylori for Lewis expression provides substrate for differential selection by the host. Experimental challenge and successful colonization of mice and gerbils allows tracking of H. pylori phenotype variability from the initial inoculation to the ultimate establishment of a quasispecies. Colonization data provide a quantitative experimental model of phenotype evolution in a relatively large population (>10⁴ individuals) over a relatively long evolutionary time scale (>10³ generations). A mathematical model is developed to interpret the data in terms of the dynamic processes occuring during colonization. The mathematical model distinguishes the roles of selection and mutation; quantifies the effects of initial phenotype diversity, mutational frequency, and selective advantage; and applies generally to phenotype evolution in biological populations.

Microbial populations in infected or colonized hosts are subject to selective forces and thus are dynamic (1). Inquiry into this area largely has aimed at characterizing the genetics, biochemistry, and physiology of the interactions between microbe and host (2). However, only relatively recently have quantitative analyses been done, most successfully with viral infections (3–5). The within-host population dynamics of infections or colonizations are not simply described, because many of the important interactions cannot be measured directly (6). Therefore, the development of mathematical models that can overcome such barriers is critical for understanding forces that determine the abundance, diversity, and distribution of microbial populations.

Microbes, with their large population size and short generation times, also are ideal for exploring evolutionary issues (2). In populations of sufficient size, mutations occur at frequencies that are measurable within reasonable time frames. For microbes that are obligate parasites, the necessity of transfer from host to host creates bottlenecks that magnify the importance of selective forces (7). The ability of the microbial population to generate mutations, and thus diversity, provides substrate for differential selection by the host. Reduction of these phenomena to mathematical relationships that can represent and predict the changes in the system improves our understanding of the biological processes involved. However, such studies require systems in which typing characters are informative and in which change can be quantitated. Analyses of this type have worked well for HIV and hepatitis B and C infections (4–6, 8–10), and we now describe a parallel system for a bacterial infection.

Helicobacter pylori are Gram-negative bacteria that colonize the human stomach (11). Once acquired, the organisms generally persist in their hosts for decades or for life, and their presence is associated with increased risk for the development of peptic ulcer disease and noncardia gastric adenocarcinoma (12). Over the long course of natural colonization, variation in both genotype and phenotype is observed, consistent with the H. pylori population in any host existing as a quasispecies (13); multiple mutational “hot spots” facilitate the generation of genetic diversity (14) in the colonizing H. pylori population. Experimental infection models have been established in a number of animals, including mice (15) and gerbils (16).

The H. pylori lipopolysaccharide may contain the Lewis (Le) histo-blood group antigen oligosaccharides (17). H. pylori cells may express Le^x, Le^y, or both on their surface, and these levels can be quantified (18, 19). In a given host, individual H. pylori colonies may vary greatly in their Le antigen expression (20). Because humans themselves are polymorphic for expression of Le antigens (21), and Le expression in gastric tissue both varies and reflects this polymorphism, one hypothesis is that the host is continuously selecting for H. pylori cells that express particular Le antigens (20, 22). Several of the genes that are required for Le^x and Le^y expression in H. pylori cells now have been characterized, and each contain loci that are highly mutable, involving several different molecular mechanisms (14, 23–25). Thus, the H. pyloriLe phenotype, which varies, is controlled by mutation, can be quantitated, and seems to be under selective pressure (22, 26, ¶), represents a trait that can be used to assess the scale and tempo of in-host evolution.

In this article, we aim to develop a deterministic mathematical model of H. pylori Le-antigen variation in vivo and then test the model with data from experimental animal challenges. We explore the tension between mutation and selection, which we define as a function of the fitness differentials of varying types of Le expression. Such studies are relevant to understanding H. pylori acquisition of antibiotic resistance, ontogeny of the host immune response, and development of vaccination strategies, as well as providing a general model of host selection for microbial phenotype.

Methods

Animals.

Adult female C3H/HeJ mice and outbred Mongolian gerbils were used in these studies as described (27, ‖). After challenge with H. pylori, groups of animals were serially killed, and gastric tissues were obtained for culture. All procedures were approved by the Animal Use Committee at Vanderbilt University.

Bacterial Strain.

H. pylori strain B128, a recent cagA+ isolate from a patient with a duodenal ulcer, which was known to colonize rodents well, was used in these studies, as described (27). Animals were given an inoculum of approximately 10⁸ colony forming units (cfu) 3 times over 3 days. At the time of death, gastric tissues were cultured on selective media, and H. pylori colonies were enumerated as described (16). From each animal, up to 10 individual colonies were picked and saved.

Le Expression.

For each bacterial colony, the expression of Le^x and Le^y was determined by ELISA as described (20). The mean ± SD Le expression for 10 B128 colonies that were in the initial inoculum introduced into gerbils was Le^x = 32 ± 39 OD units (ODU) and Le^y = 851 ± 293 ODU. For the mouse inoculum, Le^x = 20 ± 21 ODU and Le^y = 1210 ± 396 ODU.

Results

Mathematical Model.

We construct a mathematical model to describe the dynamic processes in the evolution of phenotype variation in H. pylori experimental colonization of mice and gerbils. Phenotypes are distinguished by Le antigen (Le^x and Le^y) expression, which vary continuously within the host population (20, ¶). The model is designed to be consistent with the following features of the evolutionary process: (i) phenotype expression varies in a continuum from 0 to a maximum value; (ii) the phenotype distribution evolves gradually in overlapping generations, beginning from an initial phenotype distribution at 1 or 2 weeks after challenge; (iii) the changing distribution of phenotypes is because of the result of mutation and selection forces; and (iv) the total population of all phenotypes is constrained by the carrying capacity of the host environment.

The evolving distribution of phenotypes is quantified mathematically by density functions that depend continuously on the Le antigen variable and continuously on time. We denote these densities by u(x, t) and u(y, t) [with units (ODU)⁻¹], where x represents Le^x antigen expression in ODU, y represents Le^y antigen expression in ODU, and t represents time in weeks. Integration of the density yields the total number of bacteria in a given ODU range at a given time. For example, ∫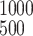 u(x, t)dx is the number of bacteria with Le^x measured between 500 and 1,000 ODU at time t weeks after challenge. The densities thus provide quantitative descriptions of changing Le phenotypes during the colonization and satisfy equations that constitute a deterministic mathematical model for the evolving populations. The equations incorporate mathematical realizations of the mutation and selection processes during colonization. The density u(x, t) of Le^x antigen expression in phenotypes satisfies the partial differential equation

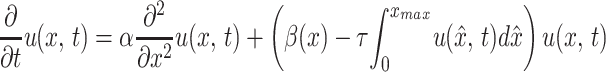1

for 0 ≤ x ≤ x_max and t ≥ t₀. Eq. 1 balances rate of change in time with rate of change in Le^x phenotype distribution.

In Eq. 1 the mutation process is represented by the diffusion term α(∂²/∂x²)u(x, t). The form of this term indicates that mutations occur randomly in all phenotypes, and a mutation event results in a ± incremental change in the phenotype expression of the next generation of offspring. The effect of mutation events on the evolution of the phenotype distribution depends on the number of mutations per generation, the number of generations per unit time, and the average incremental change per mutation event, as controlled by the diffusion parameter α. The assumption that mutation corresponds to a diffusion process means that there is a gradual dispersion away from Le^x concentrations at a rate controlled by the diffusion parameter α.

In Eq. 1 the selection process is represented by the term β(x)u(x, t), which corresponds to change in Le^x expression per unit time because of phenotype fitness of individuals in the host. The distributed parameter β(x) [in units (week)⁻¹] corresponds to differential fitness for Le^x phenotypes and is highest where Le^x phenotypes have a selective advantage. In Eq. 1 the constraint of total population growth within the host is represented by the term − τ∫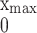u(x̂, t)dx̂ u(x, t), which corresponds to mortality independent of Le^x, but which depends on the total bacterial population. Thus, the model assumes that there is a finite carrying capacity of the host for the bacterial population, as was shown (28, 29). The parameter τ controls the rate at which the carrying capacity is approached as colonization is established. The form of this term is nonlinear and reflects competition among all phenotypes (26, ¶).

The density also satisfies the boundary conditions

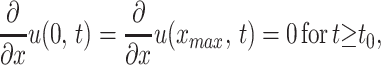2

which means that mutation is neutral with respect to phenotype selection. In the absence of differential selection [i.e., β(x) = a constant], the distribution of phenotypes would evolve to an equal presence of phenotypes throughout the range [0, x_max]. Mutation thus provides the substrate of phenotype variability on which selection acts. Either boundary, x = 0 or x = x_max, may or not be hospitable for phenotypes, with the distinction imposed by the fitness function β(x) at x = 0 or x = x_max.

Lastly, the density satisfies the initial condition

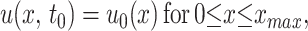3

where the initial distribution u₀(x) of phenotypes is obtained from the data at time t₀ weeks. The initial time t₀ is chosen as 1 or 2 weeks after challenge, at which time the founding population is successfully established from the inoculum. Similar equations hold for u(y, t).

The model 1–3 of phenotype evolution is similar to the continuum of alleles model of Kimura (30, 31) and to Fleming–Viot processes (32, 33). In continuum of alleles models, the type density satisfies a nonlinear integro-partial differential equation balancing mutation and selection, which act independently through overlapping generations. General theoretical results for continuum of alleles models are proved in refs. 34–40. Fleming–Viot processes describe population type frequencies by using measure-valued Markov processes, and use probabilistic methods to model the evolution of types subject to mutation, selection, and random genetic drift (32, 33, 41–43). The model 1–3 is similar to these, but is distinct in additionally incorporating a demographic carrying capacity, thus becoming applicable to the data of Le antigen phenotypes of H. pylori in colonized hosts and in parallel systems of microbial phenotype evolution.

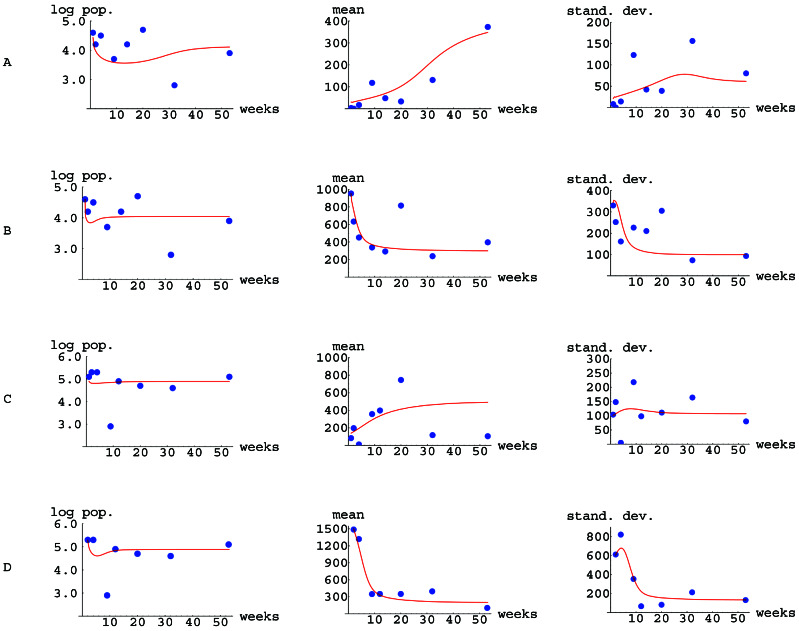
The model 1–3 is deterministic in the sense that once the initial value is prescribed, the solution exists uniquely, and thus predicts the phenotype evolution for all time. In this study, we assign initial and parameters values in 1–3 and then compare model predictions to experimental data. The Le^x and Le^y antigen expression of the H. pylori cells isolated from the experimentally infected mice and gerbils is shown in Tables 1 and 2, respectively. In the two independent experiments (27), over the course of 53 weeks, the mean Le^y expression progressively fell, whereas the H. pylori Le^x expression tended to rise. The experimental data provided an ideal opportunity to analyze the power of the model.

Table 1.

Le^x and Le^y antigen expression in H. pylori cells isolated from experimentally challenged C3H/HeJ mice

Week	Population*	Lex (Mean ± SD)	Ley (Mean ± SD)
0	NA†	20  ±  21	1,210  ± 396
1	104.6	3  ±   8	953  ± 330
2	104.2	0  ±   0	633  ± 252
4	104.5	17  ±  14	451  ± 161
9	103.7	118  ± 123	338  ± 226
14	104.2	48  ±  42	292  ± 210
20	104.7	33  ±  39	815  ± 305
32	102.8	131  ± 156	238  ±  73
53	103.9	373  ±  80	396  ±  93

^*H. pylori population size, in cfu. 

^† NA, not applicable (since original inoculum). 

Table 2.

Le^x and Le^y antigen expression in H. pylori cells isolated from experimentally challenged Mongolian gerbils

Week	Population*	Lex (Mean ± SD)	Ley (Mean ± SD)
0	NA†	32  ±  39	851  ± 293
1	105.1	83  ± 104	322  ± 101
2	105.3	197  ± 148	1,488  ± 612
4	105.3	11  ±   5	1,320  ± 822
9	102.9	357  ± 218	347  ± 354
12	104.9	398  ±  98	350  ±  66
20	104.7	746  ± 111	350  ±  82
32	104.6	117  ± 164	396  ± 213
53	105.1	105  ±  80	103  ± 131

^*H. pylori population size, in cfu. 

^† NA, not applicable (since original inoculum). 

Eqs. 1–3 were solved numerically (programs written in MATHEMATICA are available on request at http://www.math.vanderbilt.edu/faculty/Webb) and the total populations, means, and SDs of the densities were computed for t ≥ t₀. The initial values u₀ [in units (ODU)⁻¹] were assumed to have scaled truncated gaussian form

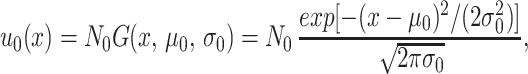with scaling factor N₀, mean μ₀, and SD σ₀ determined from the total population, mean, and SD, respectively, of the data at t₀ weeks. The fitness functions β also were assumed to have scaled truncated gaussian form

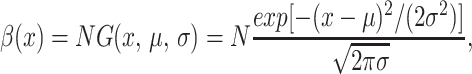with scaling factor N, mean μ, and SD σ determined from the total population, mean, and SD, respectively, from the data at 53 weeks. The parameters N, μ, σ for the fitness function β(x), the diffusion coefficient α, and the carrying capacity τ were not estimated by an optimization process but were chosen instead to provide agreement with the experimental data. The nature of the data is such that the modeling process is intended to develop qualitative understanding of the roles of mutation and selection in the phenotype evolution, as characterized by the five parameters above.

The experimental data from Tables 1 and 2 are compared with simulations of model 1–3 with the initial and parameter values (Table 3) used for each of the four cases (Fig. 1). For the simulations, the initial times were taken as t₀ = 1 week after challenge for Le^x in mice, Le^y in mice, and Le^x in gerbils, and t₀ = 2 weeks after challenge for Le^y in gerbils.

Table 3.

Initial and parameter values

Le	Host	u0	α	β	τ
Lex	mouse	104.6N(x,15,30)	100	350N(x, 400, 200)	0.00005
Ley	mouse	104.6N(y,950,350)	400	1000N(y, 300, 350)	0.0001
Lex	gerbil	105.1N(x,50,150)	400	2000N(x, 500, 500)	0.00002
Ley	gerbil	105.3N(y,1500,650)	900	1000N(y, 200, 500)	0.00001

The initial values u₀ in 3 and the parameter values α, β, and τ in 1 for Le antigen phenotype expression (Le) in the four cases Le^x in mice, Le^y in mice, Le^x in gerbils, and Le^y in gerbils. 

Figure 1.

Comparison of the experimental data from Tables 1 and 2 (dots) and simulations (curves) of the mathematical model 1–3 for the evolution of Lewis antigen phenotype in H. pylori. (A) Le^x in mice. (B) Le^y in mice. (C) Le^x in gerbils. (D) Le^y in gerbils. The total population of H. pylori cells is expressed as log₁₀. The mean and SD of the distribution of Le expression are expressed in ODU.

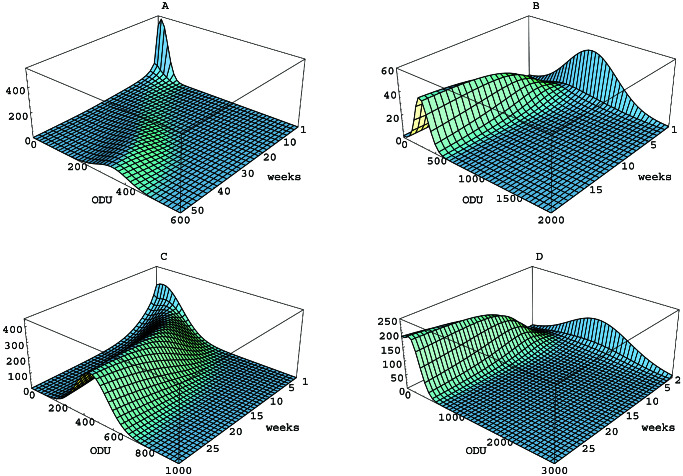
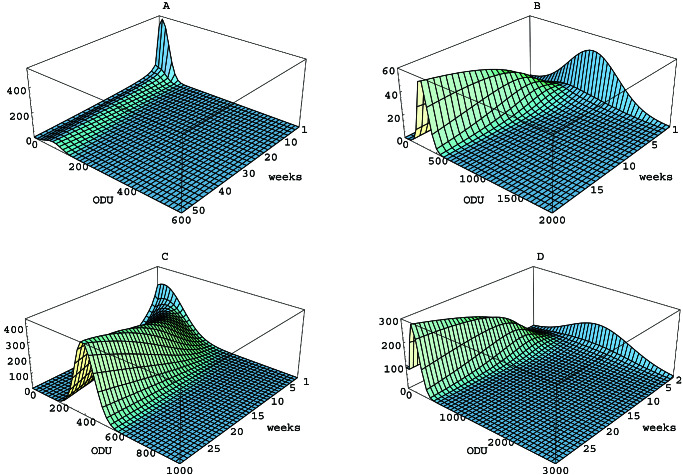
The numerical solutions of 1–3 for the initial and parameter values for each of the four cases in Table 3 are represented as surfaces (Fig. 2). The initial phenotype distributions u₀ are seen in the back face at time t = t₀, and the Le phenotype densities u(x, t) and u(y, t) unfold forward in time as the colonizations evolve.

Figure 2.

Simulations of the mathematical model for Le antigen phenotype evolution in H. pylori. (A) Le^x in mice. (B) Le^y in mice. (C) Le^x in gerbils. (D) Le^y in gerbils. The vertical axis corresponds to u(x, t) in A and C, and u(y, t) in B and D. The colonization stabilized at approximately 50 weeks in A, 20 weeks in B, and 30 weeks in C and D; each simulation is shown to the time of stabilization.

Analysis of the Mathematical Model.

Analysis of the above model (44) has proven that the solutions exist uniquely for given initial values and converge to equilibrium as time advances. Specifically, the solutions of 1–3 exhibit the following asymptotic behavior in time: lim_t→∞u(x, t) = λ₁u₁(x)/τ, where λ₁ > 0 is the principal eigenvalue of the linear problem 1–3 (when τ = 0) and u₁ is its normalized eigenfunction. This asymptotic limit as time approaches infinity is independent of the initial value u₀ in 3, which means that any initial phenotype distribution will migrate over time to the same limiting phenotype distribution. Different initial populations thus approach the same ultimate destination, although the shape and size of the initial population influence the path traveled and the length of time required. The independence of the ultimate and initial phenotype distributions in this model is consistent with the new host playing the principal role in determining phenotype evolution. Other models (44) could exhibit limiting behavior that depends on the initial value, which would indicate the importance of the prior host.

The Role of Mutation in H. pylori Phenotype Evolution.

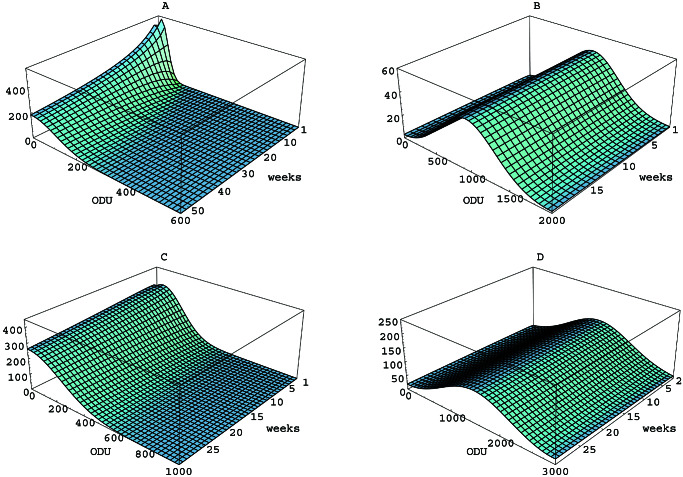
The processes of mutation and selection can be separated in our model of phenotype evolution, thus allowing independent interpretations of their roles. In the model, mutation is viewed as a diffusion process acting on the phenotype variable at a rate determined by the parameter α. If selection is removed from model 1–3 by setting β ≡ 0 and τ = 0, then the phenotype evolution is subject only to the mutation process (Fig. 3).

Figure 3.

Simulations of the model in the absence of selection. (A) Le^x in mice. (B) Le^y in mice. (C) Le^x in gerbils. (D) Le^y in gerbils. The α values used are shown in Table 3. In each case, β ≡ 0 and τ = 0.

The change in the SD σ_t over time in the absence of selection is an indicator of the effect of mutation on the phenotype distribution. In the absence of selection (β ≡ 0 and τ = 0), the SD of the solution u(x, t) is related to the diffusion parameter α by the formula (45) σ_t ≈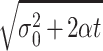. For the values of α for the four cases (Table 3), this formula reveals that in the absence of selection, the change in the SD, and thus the effect of mutation, is a relatively slow dispersion of the initial phenotype concentration (Fig. 3).

The diffusion term α(∂²/∂x²)u(x, t) in 1 incorporates information about the frequency of mutation f per generation, the number of generations g per unit time, and the average incremental ± change d in ODU per mutation event. The quantities f, g, and d are related to the diffusion parameter α by the formula α ≈ (fgd²/2). A value of f ≈ 10⁻³ is consistent with variable Le expression in H. pylori, in which regulation at the level of replication slippage, transcription, and translation (23) of the fucosyl transferase genes permits high frequency phenotypic variation (19, 23, 25). If the in vivo division cycle length of H. pylori is estimated at 1 h (g ≈ 10²), then the formula α ≈ (fgd²/2) allows determination of the value of the average incremental change d in ODU per mutation event for the four cases of our study. For Le^x antigen expression in mice (α = 100), d ≈ 50 or ≈ 8% of the ODU range [0, 600]. For Le^y antigen expression in mice (α = 400), d ≈ 100 or ≈ 5% of the ODU range [0, 2000]. For Le^x antigen expression in gerbils (α = 400), d ≈ 100 or ≈ 10% of the ODU range [0, 1000]. For Le^y antigen expression in gerbils (α = 900), d ≈ 150 or ≈ 5% of the ODU range [0, 3000]. In each of the four cases, daughters of cells that undergo mutation inherit Lewis antigen expression differing from their mother cells by an average of 5–10% of the ODU range of all phenotypes.

The Role of Selection in H. pylori Phenotype Evolution.

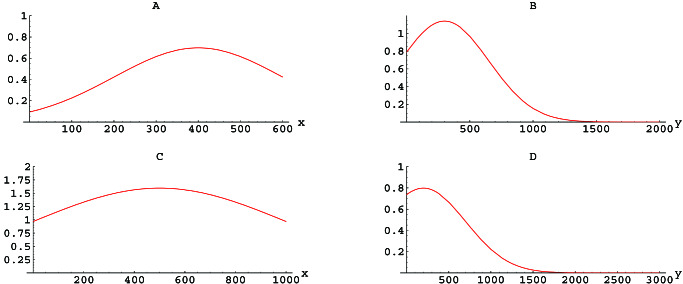
The role of selection in Le antigen phenotype evolution also can be interpreted independently in model 1–3. In 1 the rate of change in u(x, t), which depends on Le^x, is given by the fitness function β(x). The maximum variation in β is ≈ 1/week in each of the four cases (Fig. 4). An estimate of the generation time of H. pylori as approximately 1–2 h ≈ 10⁻²/week, implies that the per capita rate of increase of cells expressing x ODU is approximately (10² + β(x)/week) in the absence of mortality. The relative selective advantage of the most fit quasispecies is thus approximately [(10² + 1) − 10²/10²] ∼ 1% in all four cases.

Figure 4.

The fitness functions β. In A, β(x) (the vertical axis) corresponds to the rate of increase that depends on Le^x per week per cell expressing × ODU (the horizontal axis) of Le^x antigen expression in mice. Similar definitions hold for B (Le^y in mice), C (Le^x in gerbils), and D (Le^y in gerbils). The parameters for calculating β are provided in Table 3.

Although the relative selective phenotype advantage is small in the model simulations, it is sufficient to drive the migration of phenotype distribution to stabilization in each of the four cases. However, the role of mutation would be essential if cells in the initial population with phenotypes that are within the range of the optimally fit phenotypes are extremely uncommon; e.g., if the initial distribution u₀ has little or no population with x or y values where β is highest. When mutation is removed from the model 1–3, by setting α = 0 without changing β or τ (Fig. 5), the phenotype evolution is significantly altered only for the case of Le^x antigen expression in mice, in which the initial population is extremely small in the region of maximal fitness (Fig. 5A). Thus, in most cases, selection is the driving force for the ultimate evolution of phenotypic expression.

Figure 5.

Simulations of the model in the absence of mutation. (A) Le^x in mice (maximal fitness at 400 ODU). (B) Le^y in mice (maximal fitness at 400 ODU). (C) Le^x in gerbils (maximal fitness at 500 ODU). (D) Le^y in gerbils (maximal fitness at 200 ODU). In all four cases, α = 0, and β and τ are as in Table 3.

Discussion

Both mutation and selection play essential but independent roles in this model of phenotype evolution. Mutation is necessary to create the phenotype diversity on which selection acts. This diversity may be produced by mutation in the previous host, and thus be present in the initial population, or may be generated by mutation in the new host after inoculation. In either case, the early population is subject to selective pressure and ultimately stabilizes to a new population of cells, even when their selected phenotypes possess a relatively small fitness advantage in the new host. The mathematical model reveals that the unfolding of phenotype evolution precedes somewhat differently in each of the four cases of our experimental data. For Le^y phenotype evolution in mice (Fig. 1B), there is considerable initial population in the range of the most fit phenotypes, and the population reaches its stable phenotype distribution in approximately 20 weeks. For Le^x and Le^y phenotype evolution in gerbils (Fig. 1 C and D), there is less, but still considerable, initial population in the range of the most-fit phenotypes, and the populations reach their stable phenotype distributions in approximately 30 weeks. For Le^x phenotype evolution in mice (Fig. 1A), the initial population in the range of the most-fit phenotypes is very small, and the colonization requires approximately 50 weeks to stabilize. The relatively slow stabilization in all four cases, requiring hundreds or thousands of generations, results from the gradual dispersion of the initial phenotypes because of mutation, and the relatively small differential in fitness among phenotypes. This view, of coexisting populations of cells varying in Le phenotypes, is consistent with the substantial variation of Le expression usually observed among single H. pylori colonies isolated from single biopsies in the same host (20). The findings in rodents, and our ability to develop appropriate models of phenotype evolution, also are consistent with the hypothesis that the colonizing H. pylori population in humans represents a quasispecies (13), subject to continuous selection based on phenotype expression.

The identification and the interpretation of the parameters in the mathematical model provide quantitative information about the roles of mutation and selection in the evolving populations. The quantification of mutation in the evolution can be inferred from the diffusion parameter α. Because α is related to the frequency of mutation f, the generation time g, and the average incremental change d in Le phenotype expression per mutation event by the formula α ≈ (fgd²/2), these parameters can be related quantitatively. The values f ≈ 10⁻³, g ≈ 10²/week, and d ≈ 5–10% of the range of Le antigen expression in ODU are consistent with the model simulations of the data. The magnitude of selection in the evolving populations can be inferred from the selection function β, which corresponds to the rate of increase of phenotypes that depend on Le^x or Le^y expression. In all four cases, the values of β range from approximately 0/week to 1/week. The rate of increase of phenotypes independent of Le^x or Le^y expression can be assumed as 1/g ≈ 10²/week. The relative selective advantage of favored phenotypes is thus ≈ 1%. Because H. pylori colonization of humans persists for decades, with large populations (46), and seems subject to specific constraints in different microniches (13, 20), small differences in selective advantage would ultimately have profound affects on the composition of the colonizing population (26, ¶).

With these data, we demonstrate an experimental model of phenotype evolution in a natural setting for a large population (10⁴–10⁵ individuals) over a long evolutionary time scale (10³–10⁴ generations). With this mathematical model, we demonstrate that smaller mutation effect, smaller initial population of the most-fit phenotypes, and smaller selective advantage of the most-fit phenotypes all imply relatively slower stabilization. One advantage of this model is that it provides a framework to examine the relative importance of these independent factors in determining the pathway toward stabilization. Similarly, because bacterial evolution does not rely solely on endogenous mutation, but also on recombination, this model provides the first step toward more complex analyses that incorporate such phenomena. The experimental and mathematical models together provide quantitative description and qualitative understanding of the evolutionary processes involved, independent of specific molecular mechanisms (23–25) and thus are generally applicable. Finally, our increasing understanding of H. pylori mutations and the pathways involved in Le expression variation (13, 14, 23–25) will ultimately permit a detailed analysis of the interplay between selective pressure and phenotype variation at a molecular level.

Abbreviations

Le

Lewis

cfu

colony-forming unit

ODU

OD unit