Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1996 Jan;70(1):358–369. doi: 10.1016/S0006-3495(96)79577-2

Deformation and flow of membrane into tethers extracted from neuronal growth cones.

F M Hochmuth 1, J Y Shao 1, J Dai 1, M P Sheetz 1
PMCID: PMC1224934  PMID: 8770212

Abstract

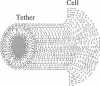
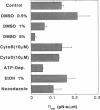
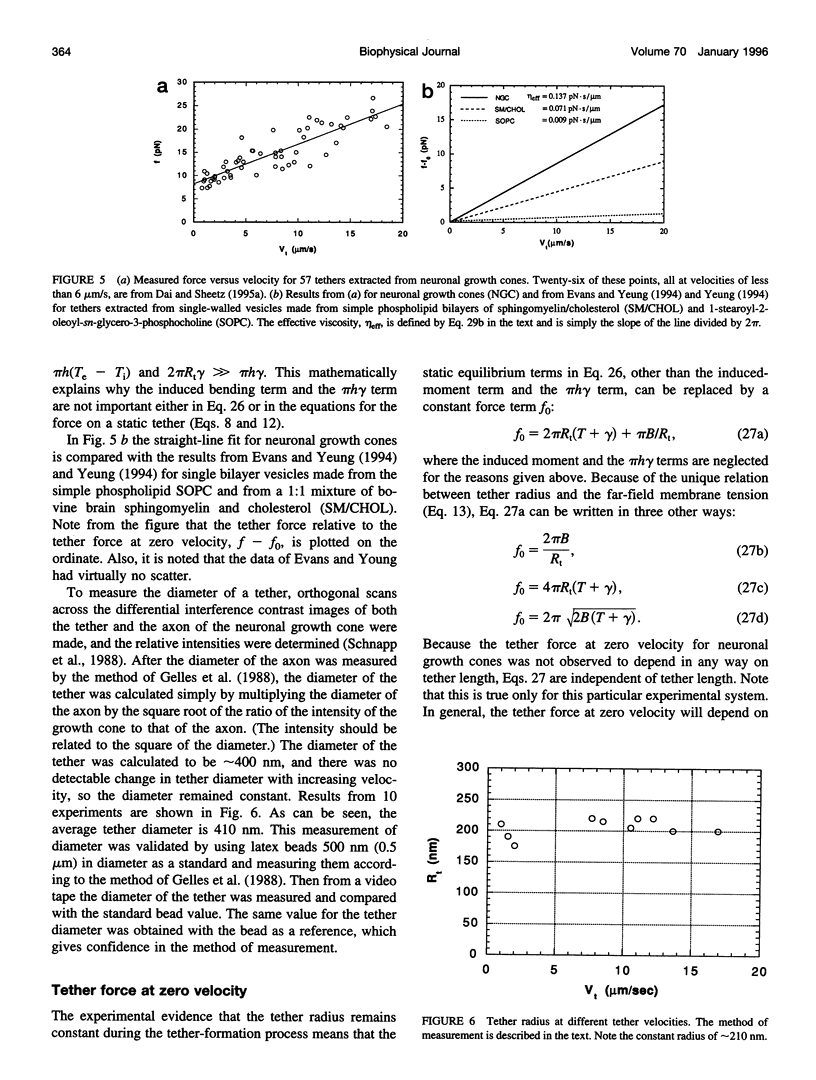
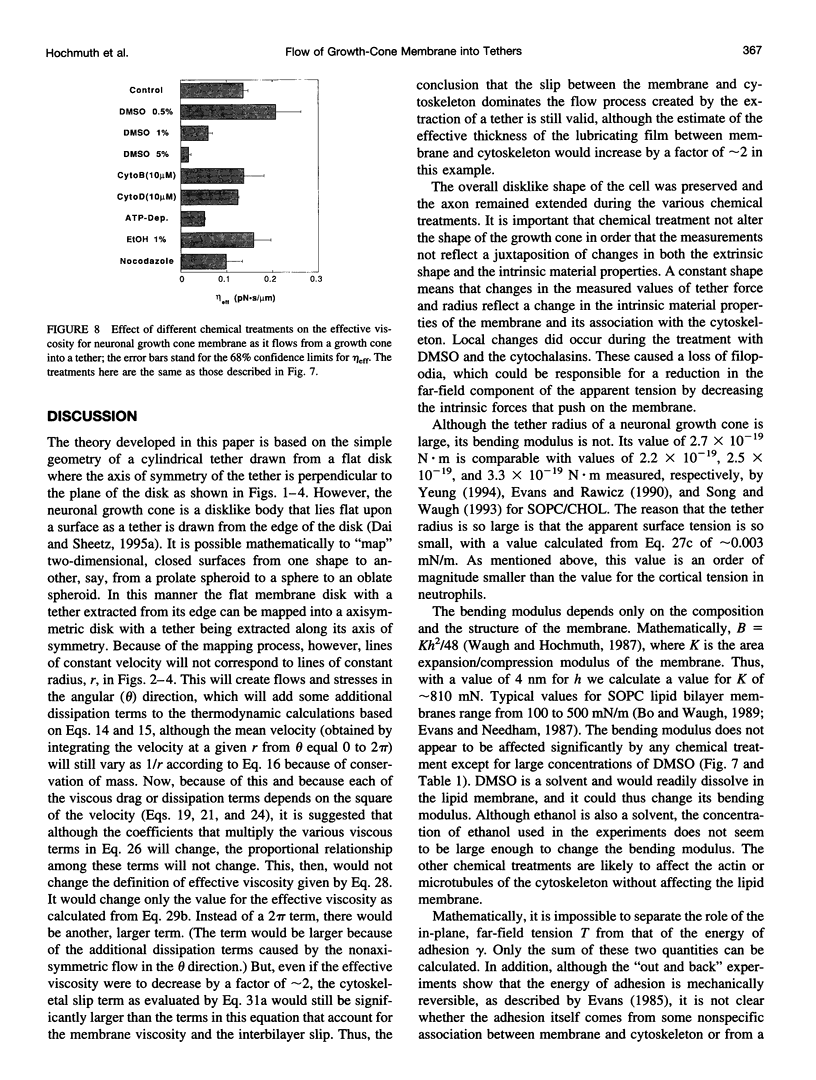
Membrane tethers are extracted at constant velocity from neuronal growth cones using a force generated by a laser tweezers trap. A thermodynamic analysis shows that as the tether is extended, energy is stored in the tether as bending and adhesion energies and in the cell body as "nonlocal" bending. It is postulated that energy is dissipated by three viscous mechanisms including membrane flow, slip between the two monolayers that form the bilayer, and slip between membrane and cytoskeleton. The analysis predicts and the experiments show a linear relation between tether force and tether velocity. Calculations based on the analytical results and the experimental measurements of a tether radius of approximately 0.2 micron and a tether force at zero velocity of approximately 8 pN give a bending modulus for the tether of 2.7 x 10(-19) N.m and an extraordinarily small "apparent surface tension" in the growth cone of 0.003 mN/m, where the apparent surface tension is the sum of the far-field, in-plane tension and the energy of adhesion. Treatments with cytochalasin B and D, ethanol, and nocodazole affect the apparent surface tension but not bending. ATP depletion affects neither, whereas large concentrations of DMSO affect both. Under conditions of flow, data are presented to show that the dominant viscous mechanism comes from the slip that occurs when the membrane flows over the cytoskeleton. ATP depletion and the treatment with DMSO cause a dramatic drop in the effective viscosity. If it is postulated that the slip between membrane and cytoskeleton occurs in a film of water, then this water film has a mean thickness of only approximately 10 A.

Full text

PDF
358

Images in this article

359FIGURE 1
on p.359
362FIGURE 4
on p.362
365FIGURE 7
on p.365
367FIGURE 8
on p.367

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Bo L., Waugh R. E. Determination of bilayer membrane bending stiffness by tether formation from giant, thin-walled vesicles. Biophys J. 1989 Mar;55(3):509–517. doi: 10.1016/S0006-3495(89)82844-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Dai J., Sheetz M. P. Mechanical properties of neuronal growth cone membranes studied by tether formation with laser optical tweezers. Biophys J. 1995 Mar;68(3):988–996. doi: 10.1016/S0006-3495(95)80274-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Evans E. A. Detailed mechanics of membrane-membrane adhesion and separation. I. Continuum of molecular cross-bridges. Biophys J. 1985 Jul;48(1):175–183. doi: 10.1016/S0006-3495(85)83770-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Evans E. A. Minimum energy analysis of membrane deformation applied to pipet aspiration and surface adhesion of red blood cells. Biophys J. 1980 May;30(2):265–284. doi: 10.1016/S0006-3495(80)85093-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Evans E., Kukan B. Passive material behavior of granulocytes based on large deformation and recovery after deformation tests. Blood. 1984 Nov;64(5):1028–1035. [PubMed] [Google Scholar]
  6. Evans E, Rawicz W. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys Rev Lett. 1990 Apr 23;64(17):2094–2097. doi: 10.1103/PhysRevLett.64.2094. [DOI] [PubMed] [Google Scholar]
  7. Gelles J., Schnapp B. J., Sheetz M. P. Tracking kinesin-driven movements with nanometre-scale precision. Nature. 1988 Feb 4;331(6155):450–453. doi: 10.1038/331450a0. [DOI] [PubMed] [Google Scholar]
  8. Hochmuth R. M., Evans C. A., Wiles H. C., McCown J. T. Mechanical measurement of red cell membrane thickness. Science. 1983 Apr 1;220(4592):101–102. doi: 10.1126/science.6828875. [DOI] [PubMed] [Google Scholar]
  9. Hochmuth R. M., Evans E. A. Extensional flow of erythrocyte membrane from cell body to elastic tether. I. Analysis. Biophys J. 1982 Jul;39(1):71–81. doi: 10.1016/S0006-3495(82)84492-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hochmuth R. M., Mohandas N., Blackshear P. L., Jr Measurement of the elastic modulus for red cell membrane using a fluid mechanical technique. Biophys J. 1973 Aug;13(8):747–762. doi: 10.1016/S0006-3495(73)86021-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hochmuth R. M., Wiles H. C., Evans E. A., McCown J. T. Extensional flow of erythrocyte membrane from cell body to elastic tether. II. Experiment. Biophys J. 1982 Jul;39(1):83–89. doi: 10.1016/S0006-3495(82)84493-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kuo S. C., Sheetz M. P. Force of single kinesin molecules measured with optical tweezers. Science. 1993 Apr 9;260(5105):232–234. doi: 10.1126/science.8469975. [DOI] [PubMed] [Google Scholar]
  13. Needham D., Hochmuth R. M. A sensitive measure of surface stress in the resting neutrophil. Biophys J. 1992 Jun;61(6):1664–1670. doi: 10.1016/S0006-3495(92)81970-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Schmidt C. E., Dai J., Lauffenburger D. A., Sheetz M. P., Horwitz A. F. Integrin-cytoskeletal interactions in neuronal growth cones. J Neurosci. 1995 May;15(5 Pt 1):3400–3407. doi: 10.1523/JNEUROSCI.15-05-03400.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Schnapp B. J., Gelles J., Sheetz M. P. Nanometer-scale measurements using video light microscopy. Cell Motil Cytoskeleton. 1988;10(1-2):47–53. doi: 10.1002/cm.970100109. [DOI] [PubMed] [Google Scholar]
  16. Song J., Waugh R. E. Bending rigidity of SOPC membranes containing cholesterol. Biophys J. 1993 Jun;64(6):1967–1970. doi: 10.1016/S0006-3495(93)81566-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Wang N., Butler J. P., Ingber D. E. Mechanotransduction across the cell surface and through the cytoskeleton. Science. 1993 May 21;260(5111):1124–1127. doi: 10.1126/science.7684161. [DOI] [PubMed] [Google Scholar]
  18. Waugh R. E., Bauserman R. G. Physical measurements of bilayer-skeletal separation forces. Ann Biomed Eng. 1995 May-Jun;23(3):308–321. doi: 10.1007/BF02584431. [DOI] [PubMed] [Google Scholar]
  19. Waugh R. E., Hochmuth R. M. Mechanical equilibrium of thick, hollow, liquid membrane cylinders. Biophys J. 1987 Sep;52(3):391–400. doi: 10.1016/S0006-3495(87)83227-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Waugh R. E., Song J., Svetina S., Zeks B. Local and nonlocal curvature elasticity in bilayer membranes by tether formation from lecithin vesicles. Biophys J. 1992 Apr;61(4):974–982. doi: 10.1016/S0006-3495(92)81904-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Waugh R. E. Surface viscosity measurements from large bilayer vesicle tether formation. II. Experiments. Biophys J. 1982 Apr;38(1):29–37. doi: 10.1016/S0006-3495(82)84527-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Weiss L., Asch B. B., Elkin G. Effects of cytoskeletal perturbation on the sensitivity of Ehrlich ascites tumor cell surface membranes to mechanical trauma. Invasion Metastasis. 1991;11(2):93–101. [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES