Abstract
Animals are predominantly risk prone toward reward delays and risk averse toward reward amounts. Humans in turn tend to be risk-seeking for losses and risk averse for gains. To explain the human results, Prospect Theory postulates a convex utility for losses and concave utility for gains. In contrast, Scalar Utility Theory (SUT) explains the animal data by postulating that the cognitive representation of outcomes follows Weber's Law, namely that the spread of the distribution of expected outcomes is proportional to its mean. SUT also would explain human results if utility (even if it is linear on expected outcome) followed Weber's Law. We present an experiment that simulates losses and gains in a bird, the European Starling, to test the implication of SUT that risk proneness/aversion should extend to any aversive/desirable dimension other than time and amount of reward. Losses and gains were simulated by offering choices of fixed vs. variable outcomes with lower or higher outcomes than what the birds expected. The subjects were significantly more risk prone for losses than for gains but, against expectations, they were not significantly risk averse toward gains. The results are thus, in part, consistent with Prospect Theory and SUT and show that risk attitude in humans and birds may obey a common fundamental principle.
Behavioral studies of risk sensitivity (preference for variance) in humans and animals show two main context effects. Humans tend to be risk averse for gains and risk prone for losses (for overviews, see refs. 1 and 2); nonhumans of various species, on the other hand, show weak risk aversion for food amounts and strong risk proneness for delays to food (reviewed in ref. 3). Here, we discuss existing theoretical accounts with the aim of unifying accounts of risk sensitivity and present an experimental study that aims at emulating the gains-vs.-losses human paradigm in a bird species, the European Starling (Sturnus vulgaris). Our favored hypothesis is that human and nonhuman results obey a common perceptual and choice mechanism that causes risk aversion when the subject strives for as large an outcome as possible and causes risk proneness when the subject strives for as small an outcome as possible (4, 5). In this view, the joint explanation of existing results is that humans attempt to maximize gains and nonhumans attempt to maximize amounts of reward, whereas they aim at minimizing losses and delays to reward, respectively. If this hypothesis is correct, the same two effects (risk aversion and risk proneness) are expected for other types of hedonically positive or negative manipulations and, specifically, in animals both risk aversion and risk proneness should obtain in both amounts and delays if the choices are framed with maximizing or minimizing goals. We return later to the rationale underlying this hypothesis, but before that we describe some typical experimental examples and existing accounts.
In a paradigmatic experiment with humans (6), subjects were divided into two groups and were asked to imagine that they were in one of two states differing in initial endowment ($2,000 or $4,000). Then, they were asked to choose between a sure and a probabilistic alternative, the former with final state of $3,000 and the latter leading to final states of either $2,000 or $4,000, with equal probability. Thus, the final states were the same for both groups, but, because of the initial endowment difference, for one group the choice was between a sure and a probabilistic gain, whereas for the other, it was between a sure and a probabilistic loss. Even though the choice was between the same final states for both groups, a group effect occurred. Most subjects in the “gains” group tended to prefer the sure option, whereas those in the “losses” group showed a bias toward the variable, or “risky” option. These results together with various replicates have led to developments such as Prospect Theory (6, 7) and security-potential/aspiration theory (8), in which choice is accounted for by incorporating psychological mechanisms and not just normative criteria.
In the field of animal behavior, “attitudes” towards risky choice have been studied in the context of variance in the amount of food or in the delay to food in a range of foraging tasks (see refs. 3 and 9), and in terms of how payoffs are subjectively evaluated (e.g., refs. 10–13). The experiment reported by Reboreda and Kacelnik (4) is typical. In a within-subject design, they offered European Starlings a choice between fixed and variable food amounts in one treatment and fixed vs. variable delays to food in another. The amounts and delays were programmed so that reinforcement rates of both fixed and variable options were equal between the treatments. The birds preferred the fixed to the variable amount of food (i.e., were risk averse for amounts) but then preferred the variable over the fixed delay to food (i.e., were risk prone for delays). Notice that, as in the human example, the starlings were choosing among equated levels of variance in reward rate and hence in final states.
Biologists are interested in this form of context effect mainly because the effect is hard to accommodate within the standard normative theoretical framework based on fitness maximization. Normative models in biology, as in economics, deal with differences in final, rather than initial states (i.e., what should drive choice is the state consequent to each possible action). In both the human and the starling examples, the final states and the level of uncertainty were equalized as much as possible between groups, and yet, the subjects had definite and diverging preferences. This point can be seen by reference to the dominant approach to risk sensitivity in biological research, Risk Sensitivity Theory (14–16). Risk Sensitivity Theory predicts a switch between risk aversion and risk proneness depending on whether the subject is on a positive or a negative energy (for animals) or earnings (humans) budget (3, 16–18). This prediction depends entirely on the final state.
Prospect Theory, security-potential/aspiration theory, and Scalar Utility Theory (SUT) are examples of approaches with an emphasis on mechanism, and hence they can all deal with path-dependent results. We shall place special focus on SUT for several reasons. First, SUT originates on animal research and hence is closer to our own background and less widely known. Second, we believe that its account is more economical than the alternatives, in that its premises derive from independent psychophysical research built over more than a century outside the realm of risk-related behavior, and that it predicts the required trends without specific assumptions about unobservable differences in utility functions. (We assume utility to be proportional to expected outcome). Reboreda and Kacelnik (4) proposed SUT as an explanation for the starlings' result based on a mechanism of choice that had been applied to time intervals (19). Mathematical details of the theory as applied to animal research with amounts and delays are available elsewhere (3–5). Here, we present a conceptual outline sufficient for the purposes of this study and for the extension to human results we propose.
Scalar Utility Theory
SUT is composed of two hypotheses, one about cognitive representation of the alternatives and the other about the mechanism of choice. The cognitive representation hypothesis postulates that Weber's Law applies to the internal representation of perceived or expected outcomes of choices, which implies that percepts (by “percept” we mean any piece of information acquired by the subject that impinges on choices) are cognitively represented by Gaussian probability density functions that preserve the coefficient of variation (SD/mean) across magnitudes. In the examples discussed above, the relevant percepts are the utilities associated with expected monetary gains or losses, and the hedonic value of expected food amounts or lengths of delay to food. If a behavioral alternative has a fixed outcome, its internal representation takes the form of a normal distribution, whereas if it has a set of different outcomes with associated probabilities, then its representation is the sum of separate Gaussian functions for each possible outcome, weighted by subjective probabilities for humans and relative frequencies in the past history of the subject for nonhumans. The crucial point is that, because the SD of these distributions is proportional to their mean, the internal representation is formed by the sum of narrower distributions for the smaller outcomes and flatter distributions for larger outcomes, leading to an overall representation that is more positively skewed than the veridical distribution of outcomes.
The next element of the SUT is the process of choice. Here SUT emphasizes that the subject does not have access to forthcoming outcomes but only to the cognitive representation of past outcomes or their imagined utilities. To make a choice between two alternatives, the subject draws a pair of samples, one from each of their internal representations and picks the alternative that yielded the most favorable sample. For hedonically positive outcomes, such as monetary gains or amounts of food, the most favorable alternative is the one that yields the larger sample, whereas for hedonically negative kinds of outcome such as monetary losses or delays to food, the preferred alternative is the one that yields a smaller sample. Because of the induced skew in the internal representation, if two options have equal expectation but different variance, the more variable option will yield a smaller sample in more than half of the choices, and hence will be chosen less often if the subject prefers larger outcomes and more often if it prefers smaller outcomes. This can account in a very economical fashion for the results for gains and losses in humans and for amounts and delays for nonhumans.
A weakness of SUT is the hypothetical process of choice. Although for our study animal (the Starling) strong supportive evidence exists in favor of a Weberian internal representation of both delays (20) and amounts (21), the suggested sampling mechanism is speculative and must remain as a working hypothesis. However, the pairwise mechanism of memory sampling for each choice described above is not essential; SUT predicts the same qualitative trends for many mechanisms of choice provided the choice is sensitive to the skew of the internal representation of the alternatives. Kacelnik and Brito e Abreu (5) offer several alternative mechanisms, including rules such as one in which the proportion of choices matches the relative value of the medians of internal representations. For the present purposes, it is not necessary to specify the precise process of choice, only its skew sensitivity.
One way to test the generality of SUT is to apply similar experimental designs to humans and nonhumans, which is difficult because it is not possible to instruct nonhumans about the nature of the choice without using a repetitive training task, whereas for human subjects it is customary to present the alternatives with written or verbal instructions. Further, outcomes in experiments with human subjects are positive or negative changes in the same dimension (often money), but animal data are across food (or water) and time, hence it is not clear that the analogy made above between the two literatures is justified; animal results may be specific to time and food amounts and not to the negative or positive hedonic significance of the outcomes. Here we attempt to test the principle of the theory in an animal simulation of the human paradigm of gains and losses, using the fact that animals (including humans) can be conditioned to expect certain outcomes (e.g., refs. 22 and 23), and furthermore, that information-processing systems make use of relative relationships in assessment (e.g., the perceived magnitude of an outcome depends on its reference class; see ref. 24). Thus, our attempt is driven by the hope that the perceived goodness of a food reward may depend on the size of the food reward with which it is being compared, and in our experiment we try to manipulate this standard. We train the animals to form an expectation for reward size and then offer a choice with expected outcome either higher (“gains”) or lower (“losses”) than the expectation.
Methods
Subjects were 16 wild-caught adult European Starlings (8 males and 8 females), housed in individual flight cages measuring 158 × 56 × 53 cm. Experimental cages were stacked in groups of three in climate controlled rooms maintained at 18°C (±3°C). Automatic timers maintained laboratory lighting on a 14 h light/10 h dark cycle with gradual transition periods at 07:00 h and 21:00 h, respectively. Each cage had two perches, one at each far side of the cage, and an operant panel. The panel had a centrally mounted food hopper (4 × 3.5 cm) that was illuminated whenever food was delivered. The operant panel also had three circular response keys 3 cm in diameter, one in the center of the panel and one on either side. The center key could be illuminated in green, and the keys on either side with black and white projected symbols. Experimental trials were governed by an Acorn A5000 microcomputer running ARACHNID experimental control language (Paul Fray, Cambridge, U.K.). The program controlled and recorded stimuli, rates of work, and pecking key choices. Food rewards were delivered in pellet form (45-mg pellets, manufactured by P.J. Noyes, Lancaster, NH) at a rate of 1 unit/sec from automatic pellet dispensers situated above the cages. At the end of each day, all birds were permitted to feed ad libitum on turkey starter crumbs, Orlux Pellets, and live mealworms from gravity-feeding dispensers clipped to the side of each cage. Cages were cleaned each morning before experimental trials began. Drinking water was available at all times. All birds were weighed periodically to check their body masses.
Pretraining.
Birds were trained by autoshaping. The schedule went through a series of progressively more complex steps until birds would make 10 pecks to a center key to switch on the symbol keys on either side. A single peck to an illuminated side key released the food reward (see details below). After the pretraining process was complete (≈6 weeks), symbols used in training were replaced with new (unfamiliar) symbols.
Experimental Protocol.
Experimental trials consisted of two stages. The first stage was a “work” period, in which subjects had to make 10 pecks to the center green key. This stage was designed to simulate foraging time and effort, to build expectancy and as an attention control that standardized the animal's state at the onset of the second stage. The 10th peck started the second stage. In this stage, the side keys were illuminated with symbols. In “standard” trials, identical symbols (SE; the suffix stands for “expectation”) were projected on both sides. In “choice” trials, two different symbols (SF and SV for “fixed” and “variable”, respectively) were presented randomly with respect to side. SF always gave a fixed payoff of four food pellets, and SV gave a variable payoff of either two or six food pellets with equal probability (thus, the mean outcome of SF and SV was the same, although they differed in variance).
Treatment.
Experimental treatment consisted of manipulating the reward size in standard trial types. In different treatments, the reward delivered by pecking at SE was either one pellet (“gains treatment”) or seven pellets (“losses treatment”). Treatments of each type were presented for 10–14 consecutive days, depending on how fast birds adjusted to pecking keys and payoffs. Standard and choice trials were given in a random sequence, with 90% (pretraining) and 75% (testing) of trials being of the standard type. Because the mean payoff of a choice trial was always four pellets of food, the hypothesis of this experiment is that choice trials should be “framed” as either a gain or loss, depending on whether the subject was used to receiving one pellet or seven pellets, respectively.
Rewards were followed by a fixed intertrial interval of 45 sec (gains treatment) or 320 sec (losses treatment). The different intertrial intervals served to standardize the overall reward rate and thus reduce differences in the subjects' energetic state caused by the difference of standard payoffs in the two treatments. This control was required to avoid confounding with the predictions of risk sensitivity theory, which predicts risk aversion in positive energy budgets and risk proneness in negative energy budgets. Without the intertrial interval manipulation, subjects receiving seven pellets in standard trials would have had higher energy reserves than those receiving one pellet. Notice that, however, the effect of the size of the standard is the opposite for Risk Sensitivity Theory and SUT. The latter predicts risk proneness when expected rewards are high, that is, when the birds receive more pellets in standard trials and hence are more likely to be in a higher energy state.
Experimental trials were presented in four 2-h blocks throughout the day, beginning 2 h after the lights were turned on. Each trial period was separated by 1 h of rest, during which all keys were extinguished and no food was available. Treatments were presented in a balanced reverse A-B-A design. Birds were assigned to one of two groups; the first group had treatments in the order gains-losses-gains, whereas the second had treatments in the order losses-gains-losses. Each group was composed of four males and four females. When treatments were reversed, new symbol keys were used to prevent prior symbol conditioning from contaminating choices. Early in the experiment two of the subjects experienced repeated equipment malfunctions and had to be withdrawn.
Results
Response data were grouped by treatment, summed, and converted into proportions (rounded to the nearest second decimal place) for each bird. For statistical analysis the proportions were normalized by using the arcsine transformation and analyzed by using a general linear model. No effect of sex (F1,11 = 0.12, P = 0.73) was demonstrated, but an effect of treatment order on strength of preference (F1,11 = 5.46, P = 0.04) was demonstrated with birds having treatments in the order loss-gain-loss being more risk-seeking in the gains domain than birds having treatments in the order gain-loss-gain.
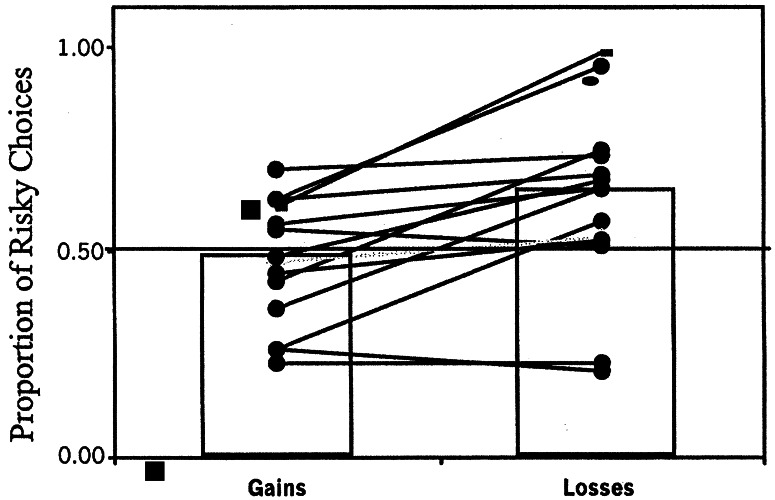
Of the 14 birds, 8 were risk averse in the gains treatment (binomial test, NS), whereas 12 of 14 were risk prone in the losses treatment (binomial test, P = 0.02), so that the prediction of risk proneness for losses is fulfilled but that of risk aversion for gains is not. The individual trends show that most subjects (five of seven birds in the first group and six of seven in the second) were more risk-seeking in the losses treatment than in the gains treatment. Overall, because 11 of 14 subjects were more risk-seeking in the losses domain than in the gains domain, the trend is significant (binomial test, P = 0.02). Fig. 1 shows the individual and mean results.
Figure 1.
Risk preference in relation to treatment. Bars show group means and individual results by symbols joined by lines.
Discussion
We used a within-subjects design, with the behavior of interest being a choice between pecking at a symbol that resulted in a fixed reward of four food pellets and pecking at another that yielded a probabilistic reward of two or six pellets with equal chance. The difference between our two treatments was the context surrounding the choice: in one treatment (gains) the birds were accustomed to receiving one pellet in the majority of trials, and thus all choices were between alternatives that offered a gain with respect to their expectation. The size of these gains were of either three pellets for sure or a gamble of one or five pellets, with equal chance. In the other treatment (losses), they were used to a standard payoff of seven pellets, so that the choice was between a sure shortfall (with respect to expectation) of three pellets and a probabilistic shortfall of one or five pellets, with equal chance. The goal of this manipulation was to create an animal approximation to the human tests for risk attitude in the contexts of gains and losses to test the predictions of SUT. SUT predicts that subjects will be risk averse for outcomes that they wish to be large and risk prone for outcomes they prefer to be small, not because of an intrinsic preference for a level of variance but as a by-product of the way they represent the magnitude of the outcomes and their hedonic value. Our protocol did not ensure that outcomes would be perceived as differences relative to expectation because in absolute terms they were in fact gains in both cases, but this would cause a conservative bias: the lower the effect of the manipulation, the lower should be the difference between groups.
The data yielded partial support for SUT. A significant majority of subjects were more risk prone in the losses than in the gains treatment, but whereas in the losses treatment, significant risk proneness occurred, in the gains treatment, the mean preference was close to neutrality. The fact that the data do not show significant risk aversion for gains is unfortunate for SUT but is informative and not surprising in relation to previous empirical evidence. In animal experiments, risk proneness toward delays is stronger and more pervasive than risk aversion for amounts (see ref. 3).
We surmise that amounts and delays in animal experiments are best understood as special cases of outcomes that are preferred to be large and small, respectively. SUT does not, in its present state, account for the difference in response magnitude to variance in positive and negative dimensions. However, despite these shortcomings, SUT remains successful in unifying empirical results across the human and animal behavior literatures on risk attitude. Other theories could be suitably modified to do the same, hence the task ahead is to propose these theoretical extensions and design experiments that allow a comparison or fusion between surviving theories.
Acknowledgments
This research was funded by a Junior Research Fellowship (New College, Oxford; to B.M.) and Biotechnology and Biological Sciences Research Council Research Grant 43/S13483 (to A.K.).
Abbreviation
- SUT
Scalar Utility Theory
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Kuhberger A. Org Behav Hum Decis Proc. 1998;75:23–55. doi: 10.1006/obhd.1998.2781. [DOI] [PubMed] [Google Scholar]
- 2.Kahneman D, Tversky A, editors. Choices, Values, and Frames. Cambridge, U.K.: Cambridge Univ. Press; 2000. [Google Scholar]
- 3.Kacelnik A, Bateson M. Am Zool. 1996;36:402–434. [Google Scholar]
- 4.Reboreda J C, Kacelnik A. Behav Ecol. 1991;2:301–308. [Google Scholar]
- 5.Kacelnik A, Brito e Abreu F. J Theor Biol. 1998;194:289–298. doi: 10.1006/jtbi.1998.0763. [DOI] [PubMed] [Google Scholar]
- 6.Kahneman D, Tversky A. Econometrica. 1979;47:263–291. [Google Scholar]
- 7.Tversky A, Kahneman D. J Risk Uncert. 1992;5:297–323. [Google Scholar]
- 8.Lopes L. Psychol Learn Motiv. 1995;32:177–220. [Google Scholar]
- 9.Shafir S. Oikos. 2000;88:663–669. [Google Scholar]
- 10.Waddington K D, Gottlieb N. J Insect Behav. 1990;3:429–441. [Google Scholar]
- 11.Richter M R, Waddington K D. Anim Behav. 1993;46:123–128. [Google Scholar]
- 12.Waite T A. Behav Ecol Sociobiol. 2001a;50:116–121. [Google Scholar]
- 13.Waite T A. Behav Ecol. 2001b;12:318–324. [Google Scholar]
- 14.Caraco T, Martindale S, Whittam T S. Anim Behav. 1980;28:820–830. [Google Scholar]
- 15.Stephens D W, Krebs J R. Foraging Theory. Princeton: Princeton Univ. Press; 1986. [Google Scholar]
- 16.McNamara J M, Houston A I. Bull Math Biol. 1992;54:355–378. [Google Scholar]
- 17.Pietras C J, Hackenberg T D. J Exp Anal Behav. 2001;76:1–19. doi: 10.1901/jeab.2001.76-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Houston A I, McNamara J M. Models of Adaptive Behaviour: An Approach Based on State. Cambridge, U.K.: Cambridge Univ. Press; 1999. [Google Scholar]
- 19.Gibbon J, Fairhurst S, Church R M, Kacelnik A. Psychol Rev. 1988;95:102–114. doi: 10.1037/0033-295x.95.1.102. [DOI] [PubMed] [Google Scholar]
- 20.Brunner D, Kacelnik A, Gibbon J. Anim Behav. 1992;44:597–613. [Google Scholar]
- 21.Bateson M, Kacelnik A. Anim Behav. 1995;50:431–443. [Google Scholar]
- 22.Amsel A. Psychol Bull. 1958;55:102–119. doi: 10.1037/h0043125. [DOI] [PubMed] [Google Scholar]
- 23.Festinger L. A Theory of Cognitive Dissonance. Evanston, IL: Row Peterson; 1957. [Google Scholar]
- 24.Hsee C K. In: Choices, Values, and Frames. Kahneman D, Tversky A, editors. Cambridge, U.K.: Cambridge Univ. Press; 2000. pp. 543–563. [Google Scholar]