Rivers dam waves of rabies

Established and emerging infectious diseases of humans and animals are an ever-increasing threat. A key question in disease dynamics is how infection moves in space and time. The most dramatic manifestations of disease spread are waves of infection, often moving across great distances. These waves arise particularly during invasions of pathogens into susceptible territory (1). However, the intrinsically nonlinear “natural enemy” dynamics of infectious diseases can generate waves even when infections are more established (2–4).

Infection waves have spawned a sophisticated theoretical literature, which lays bare the key dynamical issues underlying epidemic waves and their control (1, 2, 5). However, as observed by Smith et al. (6) in this issue of PNAS, a hybrid of dynamic modeling and statistical analysis is required to understand how infection moves across a real, heterogeneous landscape of patchy host populations and natural barriers to their movement. A few human and livestock diseases provide the necessary combination of host and parasite data to analyze the effect of these heterogeneities on disease waves directly (3, 4, 7). However—and particularly for wildlife infections—this approach is frequently inhibited by a lack of information at the right spatial grain.

Smith et al. (6) analyze the spread of rabies through Connecticut during the early 1990s. Rabies is the paradigm for studies of wildlife disease waves (much of this work has focused on the dynamics of rabies in European fox populations and of raccoon rabies in the U.S.; refs. 1, 2, and 5). Smith et al. tackle a basic question in the dynamics of rabies waves: What determines the irregularity of the rabies wave front? Previous theoretical studies of fox rabies have demonstrated the potential of stochastic “sparks” of infection to generate irregular waves (5) and the potential impact of variations in susceptibility ahead of the front (2). However, quantifying the effect of transmission heterogeneities in a particular situation is very difficult, because of a lack of information on host ecology and disease incidence at crucial spatial scales. Smith et al. (6) elegantly address this problem by effectively embedding a simple transmission model within their statistical analysis of the rabies wave. They begin by defining a network model, capturing the adjacency of Connecticut's 169 townships. This formulation allows for potential transmission heterogeneities in host population size (crudely captured by human population density) and barrier effect from rivers between townships. A family of models capturing the impact of these heterogeneities is then fitted to the observed distribution of waiting times to first appearance of rabies in each township. This exercise demonstrates a striking effect of river barriers—rivers reduce local transmission by seven-fold [although rivers can have more complex effects on transmission in some situations (6)]. Smith et al. use a neat trick to illustrate the overall barrier effect: “removing” rivers from the landscape speeds the simulated spread of rabies across Connecticut by around a year. The overall strategy parallels the study of disease diffusion in spatial geography (3), where barriers to stochastic diffusion have been explored by simulation (8). The synthesis of models and data of Smith et al. also allows them to quantify the impact of barriers on an observed epidemic wave. As they discuss, one applied issue here is the analogy between natural barriers and the effects of vaccination (2). Another component of the fitted models of Smith et al.—significant long sparks of rabies beyond the main wavefront—offers a significant challenge to vaccination campaigns. This problem echoes preliminary conclusions from the 2001 Foot and Mouth Disease (FMD) epidemic in the U.K. (7).

What determines the irregularity of the rabies wave front?

The Smith et al. (6) model indicates only a minor influence of human population size, suggesting that it provides a weak measure of raccoon density at the spatial scales considered. As the authors say, detecting further significant sources of transmission heterogeneity is a key area for refinement, which will require host and disease data at a finer spatial scale. One direction that suggests itself here is testing their method against artificial data generated by more mechanistic individual-based transmission models. This exercise might best be done initially for fox rabies, where recent models (5) indicate that the often considerable seasonal dispersal of animals may be important for generating spatiotemporal waves. If the same applies to raccoon rabies, we might therefore expect to see a key role in the spatiotemporal dynamics of the epidemic of natural movements and translocations at a wide range of spatial scales. Comparative studies of fox and raccoon rabies dynamics are potentially very interesting, but also beset with complex and often unquantified differences in host ecology. The Smith et al. approach, perhaps coupled with detailed models, offers a way forward here, particularly because a key aspect of disease dynamics in foxes—the almost complete absence of surviving immune hosts—also seems to be reflected in the temporal dynamics of raccoon rabies (9).

The Smith et al. (6) article also illustrates a number of important general epidemiological issues. First, it highlights the importance of both local contagious disease spread and longer-range sparks of infection. The balance between these forces is much studied in human diseases, where we often see a strongly hierarchical component to long-range spread. The hierarchy is best understood for measles, where infection moves from large “core” centers (where the infection persists) to smaller “satellite” populations (3). Such “sparking” of infection to restart epidemics in small centers has strong analogies to forest fire dynamics (10) and can cause infection waves even when the disease is endemic in the population as a whole (3, 4). For disease invasions into new territory, a significant number of long translocations of infection tend to obscure the wavefront (6). The time scale of this process, and the subsequent spatiotemporal dynamics of infection, also depends on the transmission rate and other aspects of the natural history of the disease (1, 3). Rabies waves move relatively slowly in comparison to some other acute infections. Human influenza A is probably the paradigm here, with rapid seasonal transhemispheric movement of new antigenic variants (3). Diseases of birds (11) and mobile mammals can also spread infection very rapidly; for example, an epidemic of Phocine Distemper virus (a relative of measles) moved many hundred kilometers between North Sea harbor seal colonies in remarkably few months during 1988 (12).

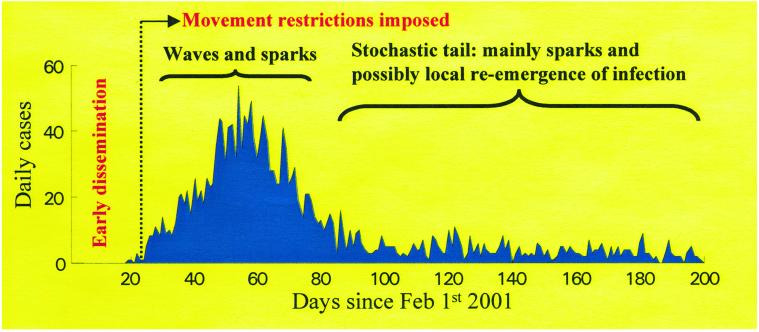
A more complex picture can emerge when disease dispersal varies during an epidemic. The effect is dramatically illustrated by the 2001 FMD epidemic in the U.K. (7, 13), where the relative importance of wave-like local spread and longer range sparks varied over the course of the epidemic (Fig. 1). Before initial detection, the infection was disseminated widely, mainly by means of animal markets. Animal movement restrictions were introduced on February 23rd, shrinking the movement kernel of the infection to intense local spread (which necessitated culling in the neighborhood of infected farms), with rarer long jumps (7). During the main part of the epidemic, infection moved in a complex pattern in “core” areas of high cattle and sheep density. This movement was partly wave-like (7) but modified by patterns of at-risk farms and other variables (13). Topographical barriers and the effects of the road network have not been examined; however, there is considerable scope for analyses in the spirit of Smith et al. (6) to explore these heterogeneities, in the extremely detailed spatial data available for the FMD epidemic. Away from the core areas, the early epidemic took the form of sparks and ensuing small stochastic epidemics. In the long tail of the epidemic (Fig. 1), wave-like spread gave way to this stochastic epidemic behavior.

Figure 1.

Daily reported cases of FMDs during the 2001 U.K. epidemic. The annotation describes the qualitative patterns of epidemic dynamics during different parts of the outbreak. See ref. 7 for more details of the spatiotemporal progression of the infection. Source of data: defra.gov.uk.

The early spread of FMD brings us to a second general epidemiological question raised by Smith et al. (6): How do we predict the course of infectious disease emergence? They identify three components to this question:

• Where will the disease emerge?

• Where and how will it spread?

• Will there be recurrent epidemics and of what nature?

These are key issues and, as the authors say, the first is the most imponderable and least amenable to analysis by models. The lesson of FMD is that the extent of initial dissemination of infection before detection is crucial to subsequent control efforts—after seeing an initial outbreak, how many more foci of infection can we expect? To address this, and the second and third questions for a novel infection, we also require basic epidemiological information. The length of the latent period, before disease appears, influences our ability to detect infection foci. Understanding initial local and longer range spread of infection depends on identifying infection routes and susceptible species, as well as key transmission parameters: the basic reproduction number of infection and infectious periods (14). Subsequent epidemic behavior, notably the tendency for recurrent epidemics, is strongly influenced by what happens after infection—prolonged immunity (or mortality) after infection promotes recurrent epidemic cycles (14), which can be strengthened by seasonal or stochastic fluctuations (4, 15). Ideally, all these parameters are required to chart fully the behavior of a novel infection. However, there are often crucial gaps in our knowledge of even very familiar diseases. For instance, the landscape-scale transmission rate of FMD could be estimated only from the early epidemic pattern itself (7). Pathogen variations caused by strain structure are also a potential complication in this epidemiological detective work.

Finally, the clarification of rabies spread by Smith et al. is only possible because of the availability of detailed spatiotemporal epidemiological surveillance data (16). This is a truth not universally enough acknowledged; understanding the dynamics and control of rabies, FMD, influenza, or any other novel or established infection requires rapid assessment, both of infection in space and time and (ideally) the underlying demographic network of the host population. In my view, glasnost is also extremely important here: a powerful and cost-effective contribution to epidemic planning is to make such data freely available to the epidemiological and population dynamic community. Apart from these applied benefits, the wonderful disease notification data often collected for parasite and host populations (7) allow us to test basic ideas in spatiotemporal population dynamics (17). The next few years should be particularly exciting, given the potential to collect routine data synthesizing, in exquisite spatiotemporal detail, the epidemiology, and molecular ecology of infectious diseases (18). Such an exercise requires staying power, but could be one of the most important outcomes of the genomic revolution for pure and applied population biology.