The gas phase reaction of singlet dioxygen with water: A water-catalyzed mechanism

Abstract

Stimulated by the recent surprising results from Wentworth et al. [Wentworth, A. D., Jones, L. H., Wentworth, P., Janda, K. D. & Lerner, R. A. (2000) Proc. Natl. Acad. Sci. USA 97, 10930–10935] that Abs efficiently catalyze the conversion of molecular singlet oxygen (¹O₂) plus water to hydrogen peroxide (HOOH), we used quantum chemical methods (B3LYP density functional theory) to delineate the most plausible mechanisms for the observed efficient conversion of water to HOOH. We find two reasonable pathways. In Pathway I, (i) H₂O catalyzes the reaction of ¹O₂ with a second water to form HOOOH; (ii) two HOOOH form a dimer, which rearranges to form the HOO-HOOO + H₂O complex; (iii) HOO-HOOO rearranges to HOOH-OOO, which subsequently reacts with H₂O to form H₂O₄ + HOOH; and (iv) H₂O₄ rearranges to the cyclic dimer (HO₂)₂, which in turn forms HOOH plus ¹O₂ or ³O₂. Pathway II differs in that step ii is replaced with the reaction between HOOOH and ¹O₂, leading to the formation of HOO-HOOO. This then proceeds to similar products. For a system with ¹⁸O H₂O, Pathway I leads to a 2.2:1 ratio of ¹⁶O:¹⁸O in the product HOOH, whereas Pathway II leads to 3:1. These ratios are in good agreement with the 2.2:1 ratio observed in isotope experiments by Wentworth et al. These mechanisms lead to two HOOH per initial ¹O₂ or one, depending on whether the product of step iv is ¹O₂ or ³O₂, in good agreement with the experimental result of 2.0. In addition to the Ab-induced reactions, the hydrogen polyoxides (H₂O₃ and H₂O₄) formed in these mechanisms and their decomposition product polyoxide radicals (HO₂, HO₃) may play a role in combustion, explosions, atmospheric chemistry, and the radiation chemistry in aqueous systems.

Recently, Wentworth et al. (1, 2) from the Scripps Research Institute reported the surprising result that Abs, regardless of source or antigenic specificity, have an ability to catalyze the generation of H₂O₂ in a highly efficient manner and by a mechanism that involves the oxidation of H₂O by singlet oxygen molecules, O₂ (¹Δ_g). This potentially aligns recognition and killing within the same Ab molecule. To understand how Abs can carry out this remarkable and unexpected chemistry, we need to understand how ¹O₂ can interact with H₂O to produce H₂O₂. Preliminary mechanistic investigation (2)§ suggested that ¹O₂ might be able to convert H₂O to H₂O₂ via the formation of hydrogen polyoxides, H₂O₃ and H₂O₄.

In this article, we use the quantum chemical (QC) methods described in Computational Details to consider the most likely chemical reaction mechanisms for the oxidation of water by singlet molecular oxygen to generate hydrogen peroxide. Quantum Mechanical (QM) Calculations and Plausible Mechanisms reports investigations of the formation mechanisms for hydrogen polyoxides, H₂O₃ and H₂O₄, and the related polyoxide radicals, HO₂ and HO₃. The results lead to plausible mechanisms in good agreement with the Scripps isotope experiments. The Discussion talks about these results, suggesting that these mechanisms account for the Scripps Ab results and they may also be significant for understanding related processes in biochemistry, combustion, explosions, atmospheric chemistry, and radiation chemistry of aqueous systems.

Computational Details

All QM calculations use the Becke three-parameter hybrid functional with Lee–Yang–Parr correlation functional (B3LYP) flavor of density functional theory (3–7), which includes a generalized gradient approximation and some exact exchange. The 6-31G** basis set (8, 9) was used on all atoms for a full geometry optimization. Vibrational frequencies (from the analytic Hessian) were calculated to ensure that each minimum is a true local minimum (containing only positive frequencies) and that each transition state has only a single imaginary frequency (negative eigenvalue of the Hessian). All QM calculations were carried out with jaguar (10–12). Some of these energetics were included in ref. 2.

To obtain more accurate energetics, we carried out calculations with the cc-pVTZ basis set (13) by using the optimized geometries from the 6-31G** basis. Such QM calculations lead to an accuracy of around 3 kcal/mol for simple organic molecules (14).

For molecules such as ¹O₂ and O₃, which have significant open shell character, standard density functional theory methods often lead to much larger errors. Thus, with B3LYP, the singlet and triplet gap for O₂ is ΔE (¹Δ_g − ³Σ) = 10.4 kcal/mol, in poor agreement with the experimental value of 22.5 kcal/mol (15). Consequently, we used spin projection techniques (16) to ensure a proper description of the complexes involving ¹O₂. This leads to ΔE (¹Δ_g − ³Σ) = 20.5 kcal/mol, in good agreement with experiment.

The calculated vibrational frequencies (with no empirical scaling) were used to calculate the zero point energy and temperature corrections so that all energetics are reported for ΔH (298K), in kcal/mol.

QM Calculations and Plausible Mechanisms

Formation of H₂O₂ from the Reaction Between Two H₂O₃.

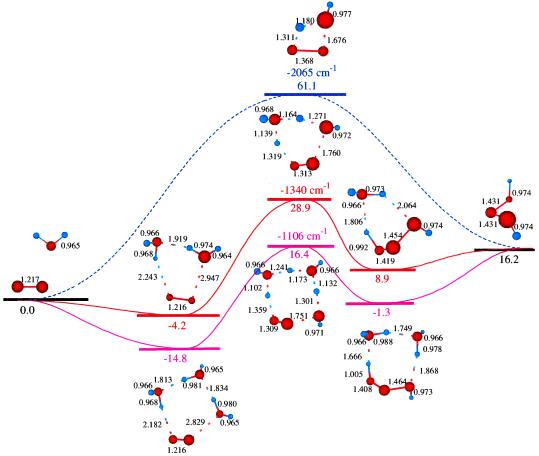
First, we examined the direct reaction of ¹O₂ with H₂O leading to Eq. 0 (See Fig. 1):

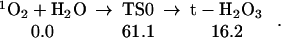0

This barrier of 61 kcal/mol is too high for this reaction to play an important role in the observed processes. Indeed, this barrier is above the reaction heat of ΔH_r = 46.0 kcal/mol for hydrogen abstraction to form of HO and HO₂, which should also have a barrier of ∼46 kcal/mol.

Figure 1.

The reaction of ¹O₂ with H₂O to form H₂O₃. The top pathway (TS0 at 61.1) is uncatalyzed. The middle pathway is H₂O-catalyzed (TS1 at 28.9), whereas the lowest pathway (TS2 at 16.4) is (H₂O)₂-catalyzed. Either reaction (1) or (2) can be part of Pathways I and II.

Thus, we considered the possible role of a second H₂O, as in Eq. 1:

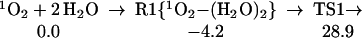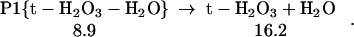1

The structures for the reactant cluster (R1), transition state (TS1), and product cluster (P1) are shown in Fig. 1. TS1 shows that the H₂O on the left plays the role of a catalyst with one H (pointing down) moving onto the left end of the ¹O₂ simultaneous with extracting an H from the right H₂O, leaving an OH that simultaneously attaches to the other end of the ¹O₂. This TS1 is 28.9 kcal/mol above the limits of the free reactants and 33.1 kcal/mol above the energy of the ¹O₂ plus H₂O dimer complex (R1). Although high, this activation barrier is small compared to the first HO bond energy of H₂O (119 kcal/mol), and the bond energy in ¹O₂ (96 kcal/mol). Thus, this is a concerted reaction. The second water acts as a catalyst to dramatically reduce the reaction barrier.

We also find that water dimer can serve as a catalyst (See Fig. 1), with a transition state energy only 16.4 kcal/mol above the energy of the separated reactants (31.2 kcal/mol above the stable complex):

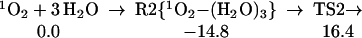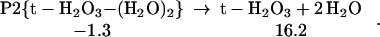2

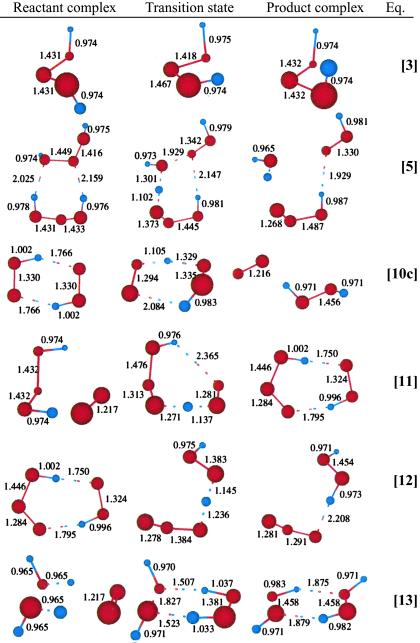
The ground state configuration of the HOOOH product in these reactions is trans (t-H₂O₃ shown in Table 1), but cis (c-H₂O₃ shown in Table 1) is only 2.4 kcal/mol higher in energy (17–21, ¶), see Eq. 3.

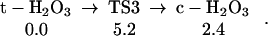3

Considering the reverse reactions, Eq. 0 indicates that the unimolecular decomposition of t-H₂O₃ has a barrier of 44.9 kcal/mol, whereas Eq. 1 indicates that H₂O can catalyze decomposition of t-H₂O₃ with a barrier of 20.0 kcal/mol (from the complex) (22, 23, ‖, ‡‡).

Table 1.

Geometries for some important reaction complexes.

Reaction of HOOOH with HOOOH (Pathway I).

Direct conversion to HOOH.

Starting with two t-H₂O₃, we find (Eq. 4) that the transition state to form directly two HOOH is 57.8 kcal/mol (TS4 is chair-like), a value we consider too high for this to play a plausible role in the observed chemistry.

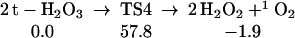4

Conversion of the HOOOH dimer to form the HOO-HOOO intermediate plus H₂O.

Starting with the dimer of c-H₂O₃, we find the low barrier process (16.9 kcal/mol from the complex) to form linear HOO-HOOO, as in Eq. 5.

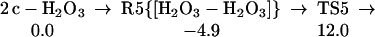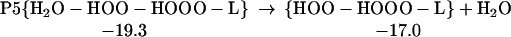5

The structures for R5, TS5, and P5 are shown in Table 1. As indicated in Eq. 6, HOO-HOOO-L can rearrange to form the more active complex, HOOH-OOO.

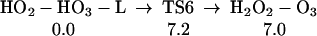6

Next we will follow the subsequent reactions involving H₂O₂-O₃.

Formation of H₂O₄.

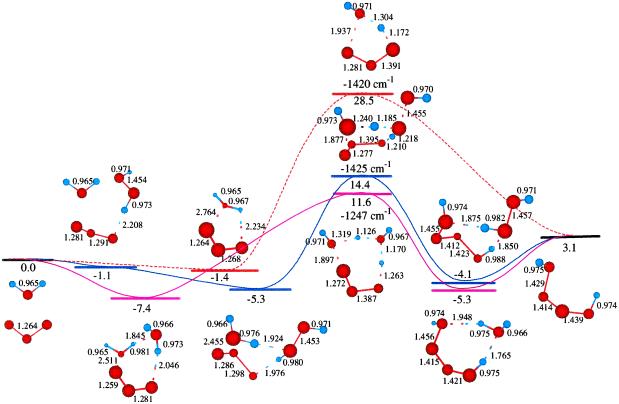
Starting with the product of Eq. 5, and allowing the rearrangement in Eq. 6, leads to the complex R7 (Eq. 7), with two hydrogen bonds: one hydrogen of water points to an OH in H₂O₂, whereas this same OH hydrogen bonds with O₃. Fig. 2 shows the reaction profile for Eq. 7. In TS7 H₂O₂ acts both as a hydrogen donor and a hydrogen acceptor. As the H bonded to the left O of H₂O₂ is transferred to the right O of O₃, to start forming HO₃, the right hydrogen of H₂O is transferred to the left O of H₂O₂ to reproduce H₂O₂. Simultaneously, the remaining HO part of the H₂O combines with the newly forming HO₃, to form H₂O₄. Thus, the H₂O₂ in Eq. 7 catalyzes the formation of H₂O₄ with a barrier of only 20.1 kcal/mol from the complex (14.4 kcal/mol from the separated reactants). This can be compared with the barrier of 28.5 kcal/mol for O₃ to react directly with H₂O to form H₂O₄ (Eq. 8). Eq. 9 shows that a second water reduces the barrier to 11.6 kcal/mol (from separated reactants). This catalytic role of the second water in Eq. 9 is very similar to that in Eq. 1.

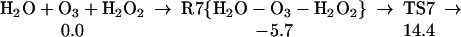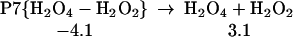7

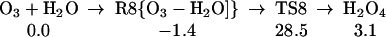8

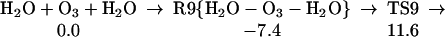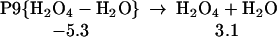9

Figure 2.

The reaction of O₃ and H₂O to form HOOOOH. The top pathway (TS8 at 28.5) is uncatalyzed. The lowest pathway is H₂O catalyzed (TS9 at 11.6), whereas the middle pathway (TS7 at 14.4) is H₂O₂ catalyzed. This latter reaction (7) is part of Pathways I and II.

Conversion of H₂O₄ to H₂O₂ and ¹O₂ or ³O₂.

The strength of the central OO bond of the H₂O₄ produced in Eq. 7 is only 10.2 kcal/mol (Eq. 10a), producing two HO₂ radicals. These can in turn associate to form the cyclic dimer, c-[HO₂]₂, either as a spin singlet or triplet (Eqs. 10b or 10c). In addition there can be interconversion of these spin singlet and triplet as in Eq. 10d. Then, hydrogen transfer from one HO₂ to the other in c-[HO₂]₂ leads to a second H₂O₂ plus ¹O₂ or ³O₂ (Eqs. 10b or 10c). The optimized structures for 10c are shown in Table 1.

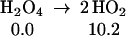10a

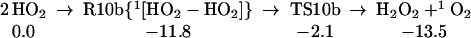10b

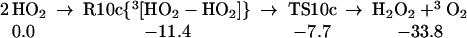10c

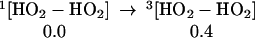10d

Summary of the HOOOH Dimer Mechanism (Pathway I).

The above reactions lead to two simple reaction mechanisms.

Pathway IA.

[Eq. (1 or 2) + (3)] twice, followed by (5) + (6) + (7) + (10ab) (with the ¹O₂ product).

Pathway IB.

[Eq. (1 or 2) + (3)] twice, followed by (5) + (6) + (7) + (10adc) (with the ³O₂ product). Pathway IA leads to a net reaction of

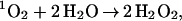A

whereas Pathway IB leads to a net reaction of

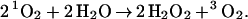B

Both Pathways IA and IB provide plausible mechanisms by which ¹O₂ can react with H₂O to generate H₂O₂. Eqs. A and B indicate that this mechanism can lead to two H₂O₂ per initial ¹O₂ or one, depending on whether step 10b or 10c is used (leading to ¹O₂ or ³O₂, respectively). This is in good agreement with the experimental result (1, 2) of 2.0.

Wentworth et al. (2) carried out studies by using H₂O with ¹⁸O but ¹O₂ with ¹⁶O (and also the reverse case). These are difficult experiments requiring removal of all traces of ¹⁶O H₂O. They found ratios of ¹⁶O:¹⁸O in the product HOOH ranging from 2.0 to 3.8, with the best experiments leading to ∼2.2:1.

In our reaction mechanism, (denoting ¹⁸O as O*):

• Eq. 1 leads to HO*OOH and HOOO*H (equal probability).

• Eq. 5 starts with four cases of the form (HO*OOH)₂.

• The product of Eq. 5 after transferring the H as in Eq. 6 leads to four cases, where: HO*H, O*OO-HOOH HO*H, OOO*-HOOH HOH, O*OO-HOO*H HOH, O*OO-HOO*H

• Eq. 7 (assuming that the reactant H₂O here is the same as the product H₂O in Eq. 5) then leads to: HO*O*OOH + HOOH HO*OOO*H + HOOH HOO*OOH + HOO*H HOO*OOH + HOO*H, leading to a ¹⁶O:¹⁸O ratio of 5:3 in HOOOOH and a ¹⁶O:¹⁸O ratio of 6:2 in HOOH.

• The cyclic (HOO)₂ dimer formed in Eq. 10 has the same ¹⁶O:¹⁸O ratio as in H₂O₄, leading to the product distribution HO*O*-HOO + HOOH → 0.5 (HO*O*H) + 1.5 HOOH HO*O-HO*O + HOOH → 1.0 (HO*OH) + 1.0 HOOH HOO*-HOO + HOO*H → 1.5 (HOO*H) + 0.5 HOOH HOO*-HOO + HOO*H → 1.5 (HOO*H) + 0.5 HOOH.

The net result is 3.5 HOOH + 4.0 HOO*H + 0.5 (HO*O*H), leading to an overall ¹⁶O:¹⁸O ratio of 11:5 = 2.2:1 in the two HOOH products. This is in excellent agreement with the experimental value of 2.2:1, giving strong support to this mechanism. Of course, we have neglected isotope-dependence of the rate constants.

Alternatively, assuming that the H₂O produced in Eq. 5 is lost and replaced with ¹⁸O H₂O in Eq. 7, would lead to

• HO*O*OOH + HOOH → HO*O*-HOO + HOOH → 0.5 (HO*O*H) + 1.5 HOOH

• HO*OOO*H + HOOH → HO*O-HO*O + HOOH → 1.0 (HO*OH) + 1.0 HOOH

• HO*O*OOH + HOO*H → HO*O*-HOO + HOO*H → 1.0 (HOO*H) + 0.5 HOOH + 0.5 (HO*O*H)

• HO*O*OOH + HOO*H → HO*O*-HOO + HOO*H → 1.0 (HOO*H) + 0.5 HOOH + 0.5 (HO*O*H).

The net result is 3.5 HOOH + 3.0 HOO*H + 1.5 (HO*O*H), giving rise to a ¹⁶O:¹⁸O ratio of 10:6 or 1.67:1 in the final product of HOOH. This seems outside the range of the experiments. This suggests that the environment in the Ab responsible for this chemistry is isolated such that the product H₂O remains in this complex.

Pathway II: Formation of H₂O₃ Monomer from ¹O₂.

We also considered an alternative to Pathway I in which the H₂O₃ molecule reacts with ¹O₂ to form a sequence of reaction intermediates leading to H₂O₂.

Reaction of H₂O₃ with ¹O₂.

We find (Eq. 11) that ¹O₂ can react with H₂O₃, extracting one hydrogen to form HOO-HOOO-7r, a cyclic hydrogen-bonded ring with seven atoms. The linear HOO-HOOO formed here can transfer an H to form HOOH-OOO (similar to Eq. 6, but the barrier is larger because HOO-HOOO-7r is 4.8 kcal/mol more stable than HOO-HOOO-L. The structures for HO₂-HO₃-7r, TS12, and H₂O₂-O₃ are shown in Table 1.

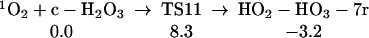11

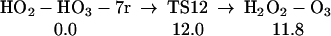12

Adding H₂O to the HOOH-OOO in Eq. 12 leads to in steps (7) + (10) to form HOOH products just as in Pathway I.

Summary of the H₂O₃ Plus ¹O₂ Mechanism (Pathway II).

Pathway IIA.

[Eq. (1 or 2) + (3)] once, followed by (11) + (12) + (7) + (10ab) (with the ¹O₂ product).

Pathway IIB.

[Eq. (1 or 2) + (3)] once, followed by (11) + (12) + (7) + (10adc) (with the ³O₂ product).

These pathways lead to the net reactions in A and B.

Because Eq. 1 leads to one ¹⁸O among the outer two O of H₂O₃, then Eqs. 11 and 12 lead to a product H₂O₂-O₃ in which both O of the H₂O₂ are ¹⁶O, whereas one of the outer two O of the OOO is ¹⁸O. Then, Eq. 7 leads to HOOH with only ¹⁶O, whereas the HOOOOH has one ¹⁸O among the central pair of O and one in the outer pair. The cyclic (HOO)₂ dimer formed in Eq. 10 has one ¹⁸O next to an H and one away from it so that the product HOOH has one ¹⁸O. Thus, the net result is that the two HOOH products have a total of three ¹⁶O and one ¹⁸O, leading to a 3:1 ratio. This is in the range of the experiments, but probably on the high side. Some decrease from 3:1 might result from the ¹O₂ reaction product in Eq. 10b (which involves one ¹⁸O), reacting subsequently with H₂O to form HOOH. It could also result from isotope-dependent rate constants.

Pathway III: Direct Conversion of Singlet Dioxygen to Hydrogen Peroxide.

We also considered the direct conversion of singlet dioxygen to hydrogen peroxide, without formation of the various intermediates:

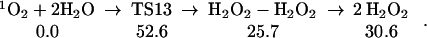13

The structures are shown in Table 1. One hydrogen from each H₂O moves toward the ¹O₂ to form one HOOH while the remaining two HO come towards each other to form the other HOOH. The negative charges on O of these two HO repel each other, leading to a high barrier. Spin recoupling (the necessity to flip the lone pairs and radical orbitals on the two hydroxyls simultaneously to make the O–O bond of the departing peroxide) will further increase this barrier. This pathway is unlikely. The isotope ratio would be ¹⁶O:¹⁸O = 1:1, which is well outside the experimental range.

Discussion

In summary, we find two reasonable pathways by which ¹O₂ plus water can produce HOOH, providing strong support for the experimental observations by Wentworth et al. (1, 2) that Abs and T cell receptors can catalyst the conversion of ¹O₂ plus water to HOOH. In Pathway I, (i) H₂O catalyzes the reaction of ¹O₂ with a second water to form HOOOH; (ii) HOOOH forms dimer, which rearranges to form HOO-HOOO + H₂O; (iii) HOO-HOOO rearranges to HOOH-OOO that subsequently reacts with H₂O to form H₂O₄; and (iv) H₂O₄ rearranges to (HO₂)₂ to form HOOH plus ¹O₂ or ³O₂. Pathway II differs in that step ii is replaced with the reaction between HOOOH and ¹O₂, leading to the formation of HOO-HOOO. This then proceeds to similar products.

For a system with ¹⁸O H₂O, these mechanisms lead to a 2.2:1 ratio of ¹⁶O:¹⁸O in the product HOOH for Pathway I and 3:1 for Pathway II. This is in good agreement with the ratio 2.2:1 observed in isotope experiments by Wentworth et al. These mechanisms lead to two HOOH per initial ¹O₂ or one, depending on whether the product of step iii is ¹O₂ or ³O₂. This is in good agreement with the experimental result of 2.0.

Relevance for Experiments on Abs.

Datta et al. (24) find that the QM structures reported here for the relevant complexes and transition states involved in forming H₂O₃ and H₂O₂ are stabilized at sites unique to Abs and T-cell receptors (TCRs) but not in other structures such as β2-microglobulin. This finding is consistent with the observations from Wentworth et al. (1, 2) that all Abs and TCRs catalyze the oxidation of water, but that other systems, including β2-microglobulin, do not. The predicted sites (24) are at the barrel-like interface of two Greek key domains formed by the light and heavy chains of the Ab (and of the TCR). This structure, referred to as the inter-Greek key domain interface (IGKD) is unique to these systems (24). At these IGKD sites there are several well-ordered crystallographic water molecules spaced just as in water dimers or trimers, providing an environment appropriate for reactions such as Eqs. 1 and 2. In addition, this IGKD region is sufficiently hydrophobic to stabilize both H₂O₃ and ¹O₂ (24). These IGKD sites also stabilize HOOOH and its dimer, providing an environment for the balance of Pathways I and II. Indeed, although these IGKD sites have water dimers and trimers, the lack of exposure to bulk water at these sites may be essential to the chemistry. In particular, this environment is consistent with the product H₂O in Eq. 5 remaining to be the same as the reactant H₂O in Eq. 7, which in turn led to the 2.2:1 isotope ratio, which agrees with experiment (for Pathway I).

Although the only intermediate detected experimentally is HOOH, our mechanism suggests the production of other reactive intermediates (H₂O₃, HO₂-HO₃, HOOH-O₃, O₃, c-(HOO)₂, and H₂O₄), any of which could be responsible for subsequent chemical processes. All these intermediates are expected to form at IGKD sites near the V_H-V_L region that binds the antigen. In this protected region, these active intermediates might live long enough to travel to the antigen-binding site (indeed, some might be detected by the peroxidase assay used to detect the H₂O₂). These intermediates might react with antigen and do other chemistry in addition to the formation of H₂O₂. The function of this chemistry might be to form reactive intermediates next to the antigen that would react with it to nick the protein recognized by the Ab, making it more susceptible to attack by other enzymes in the macrophage. Alternatively, the function of the Ab might be as a ¹O₂ scavenger, converting ¹O₂ to H₂O₂ or other reactive intermediates (like H₂O₃, O₃, or H₂O₄) that are less damaging or eliminated by other enzymes.

Role of H₂O₃ in Other Chemistries.

Reaction of ¹O₂ with H₂O.

There are two distinct pathways for the reaction of ¹O₂ and H₂O.

• Hydrogen abstraction: leading to the formation of HO and HO₂. We calculate that the reaction heat for this process is ΔH_r = 46.0 kcal/mol, which should also be the barrier.

• O₂ addition (Eq. 0): giving rise to H₂O₃. We calculate that this leads to ΔH_r = 16.2 kcal/mol. Thus, losing the π bond in ¹O₂ is nearly compensated by the formation of σ bond in H₂O₃. However, the barrier for this reaction is 61.1 kcal/mol, making less favorable than hydrogen abstraction, despite the high endothermicity. On the other hand, including a second H₂O catalyzes the O₂ addition reaction, reducing the activation barrier from 61.1 to 28.9 kcal/mol (Eq. 1), while a water dimer lowers the effective reaction barrier further to 16.4 kcal/mol (Eq. 2).

If the reaction of ¹O₂ is so favorable, one might wonder why there have been so few observations of this chemistry. Most significant is that although the barrier for unimolecular decomposition of gas phase H₂O₃ is 44.9 kcal/mol (the reverse of Eq. 0), water catalyzes the decomposition reducing the barrier to 12.7 kcal/mol (the reverse of Eq. 1). [First pointed out by Plesnicar and Koller (22).]

Production of H₂O₃.

The existence of higher oxides of hydrogen, such as H₂O₃ and H₂O₄, has been postulated repeatedly since the original suggestion of Berthelot in 1880 (25–34). In electrically dissociated water vapor, H₂O₃ and H₂O₄ have been postulated on the basis of such experimental observations as oxygen evolution on warming, thermal analysis, or phase changes (25, 26). Infrared absorption of the products from electrically dissociated H₂O vapor trapped at liquid nitrogen temperature (26) or photolyzed samples of H₂CO in Ar and glyoxal in Ar (28) also provided spectroscopic support for the existence of H₂O₄. Hydrogen trioxide, H₂O₃, was proposed as a transient intermediate in the oxygenation of alkanes with ozone in superacid media (32) and in the pulse radiolysis of air-saturated perchloric acid solution (25). UV irradiation of H₂O₂ in methyl acetate produced an oxygen-rich intermediate, characterized by ¹H NMR absorption at about δ14.5 ± 1.0 ppm, downfield from Me₄Si. This polyoxide was assigned to H₂O₃ (30–33). More recently, by means of ¹⁷O NMR spectroscopy, Plesnicar et al. (34) concluded that the low-temperature ozonation of isopropyl alcohol and isopropyl methyl ether yields, in addition to the hydrotrioxides of these compounds, hydrogen trioxide H₂O₃.

Production of H₂O₂.

The production of H₂O₂ from H₂O₃ has been postulated (25–27), but no detailed studies have previously been reported. We find three plausible mechanisms.

• H₂O₃ decomposes to form ¹O₂ (catalyzed by the presence of H₂O as discussed above).

• H₂O₃ reacts with ¹O₂ in a hydrophobic region to form HOOH and other intermdidats as in Pathway II, where the activation barrier for ¹O₂ to subtract an H from H₂O₃ is only 8.3 kcal/mol (Eq. 11). The resultant cyclic hydrogen-bonded complex, HO₂-HO₃-7r (BE = 8.1 kcal/mol), retards the decomposition of HO₃.

• H₂O₃ reacts with another H₂O₃ in a hydrophobic region to form HOOH and other intermdidats as in Pathway I. This involves the formation of {H₂O + HO₂-HO₃-L} (Eq. 5, ΔHr = −17.0 kcal/mol and ΔE_a = 12.0 kcal/mol).

Production of H₂O₄.

The existence of H₂O₄ was confirmed spectroscopically by Giguere and Herman (26) and Diem et al. (28). The first theoretical studies of H₂O₄ were reported by Plesnicar et al. (35), but the most accurate and detailed theoretical studies were performed by Schaefer's group (36, ††). Our calculations show that formation of H₂O₄ from H₂O + O₃ is uphill by 3.1 kcal/mol with an effective barrier of 28.5 kcal/mol (Eq. 7). However, H₂O or H₂O₂ can catalyze this reaction, reducing the effective barrier to 11.6 or 14.4 kcal/mol (Eqs. 9 and 7).

Detailed kinetic studies have been reported for the disproportionation of HO₂ to H₂O₂ + O₂ (37–42). This reaction possesses a negative activation barrier (40–42), but no molecular level mechenistic study has been reported. Our results show that two HO₂ form a planar cyclic hydrogen complex with BE = 11.8 kcal/mol for singlet (HO₂)₂ and 11.4 kcal/mol for triplet (HO₂)₂. As one hydrogen in an HOO bends out of the plane, the other hydrogen in the other HOO is pulled over to form HOOH.

The energy surface of singlet (HO₂)₂ coincides almost exactly with that of the triplet (HO)₂, enhancing the rate for singlet to triplet interconversion (Eqs. 10bcd). Because of formation of the cyclic hydrogen-bonded (HO₂)₂, the entire energy surface is below the potential energy surface of 2 HO₂, leading to a negative activation barrier.

Summary

The mechanisms studied here involve the formation of hydrogen polyoxides (H₂O₃ and H₂O₄) and the related polyoxide radicals (HO₂ and HO₃). These mechanisms may be of significance to the understanding of related oxidations in biochemistry, combustion, and explosion chemistry, atmospheric chemistry, and radiation chemistry of aqueous systems. Many of the proposed intermediates and mechanisms might be studied by using spectroscopic and isotope methods.

Abbreviations

QM

quantum mechanical

IGKD

inter-Greek key domain interface

TS

transition state

R

reactant cluster

P

product cluster