Abstract
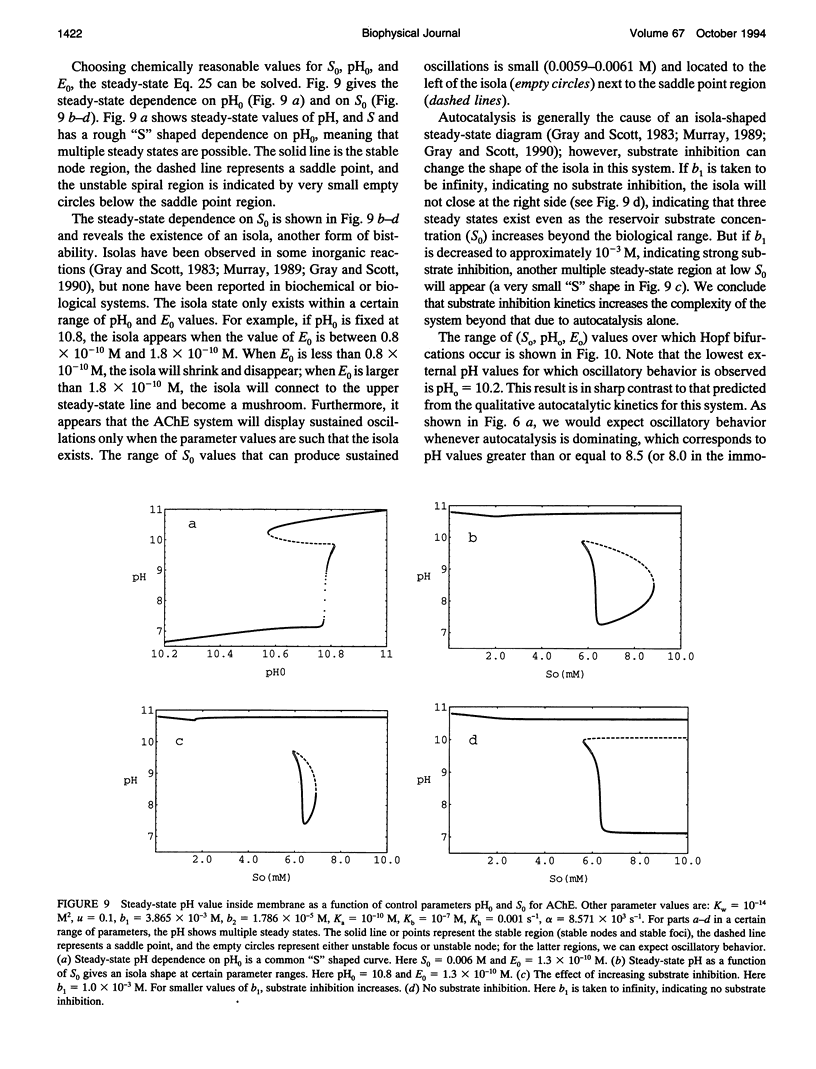
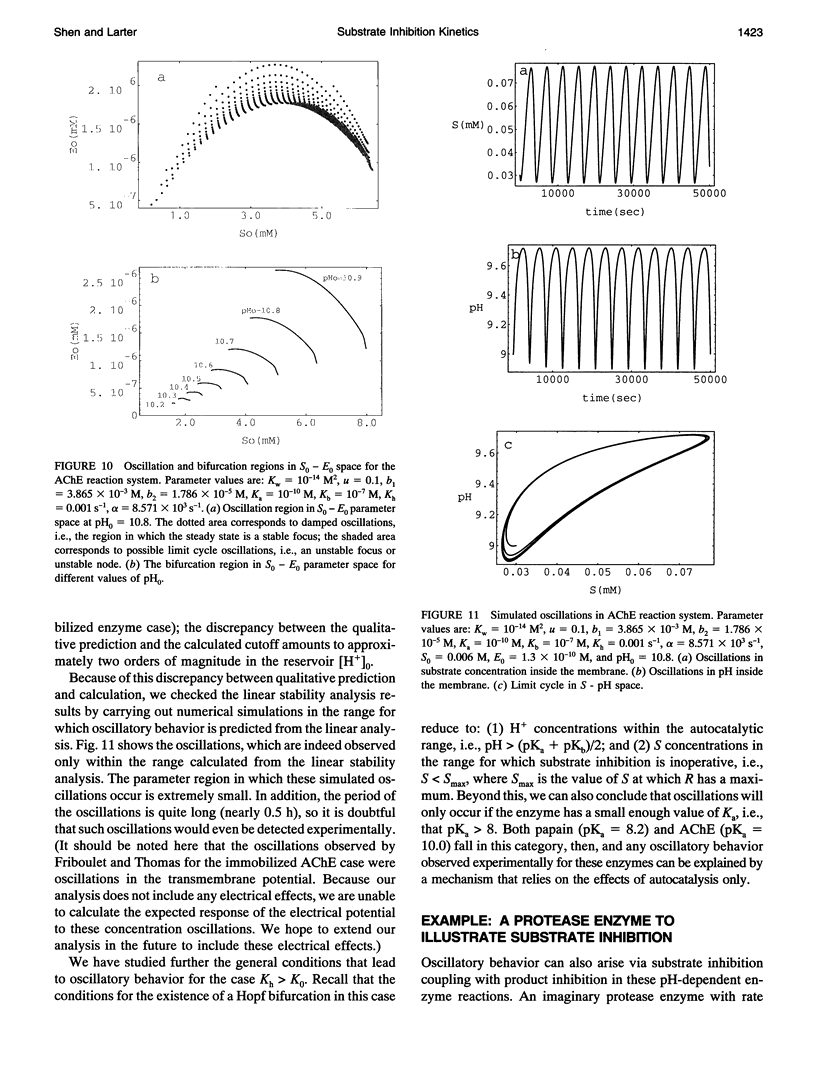
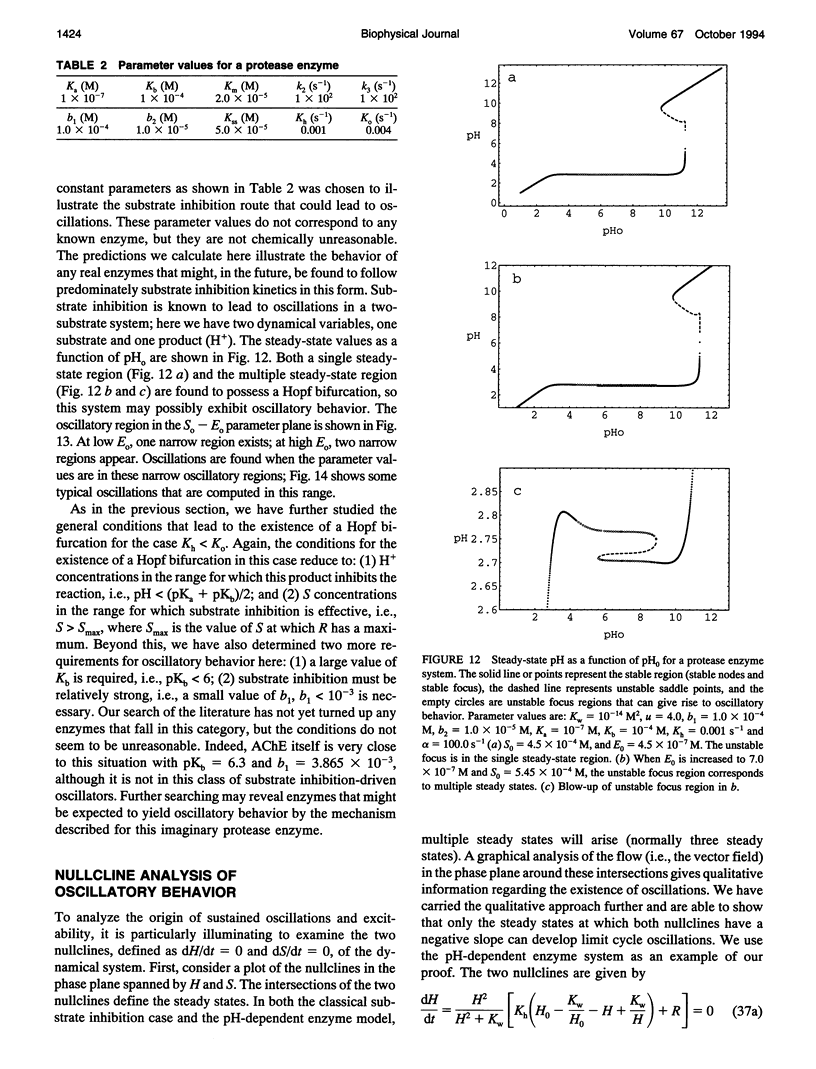
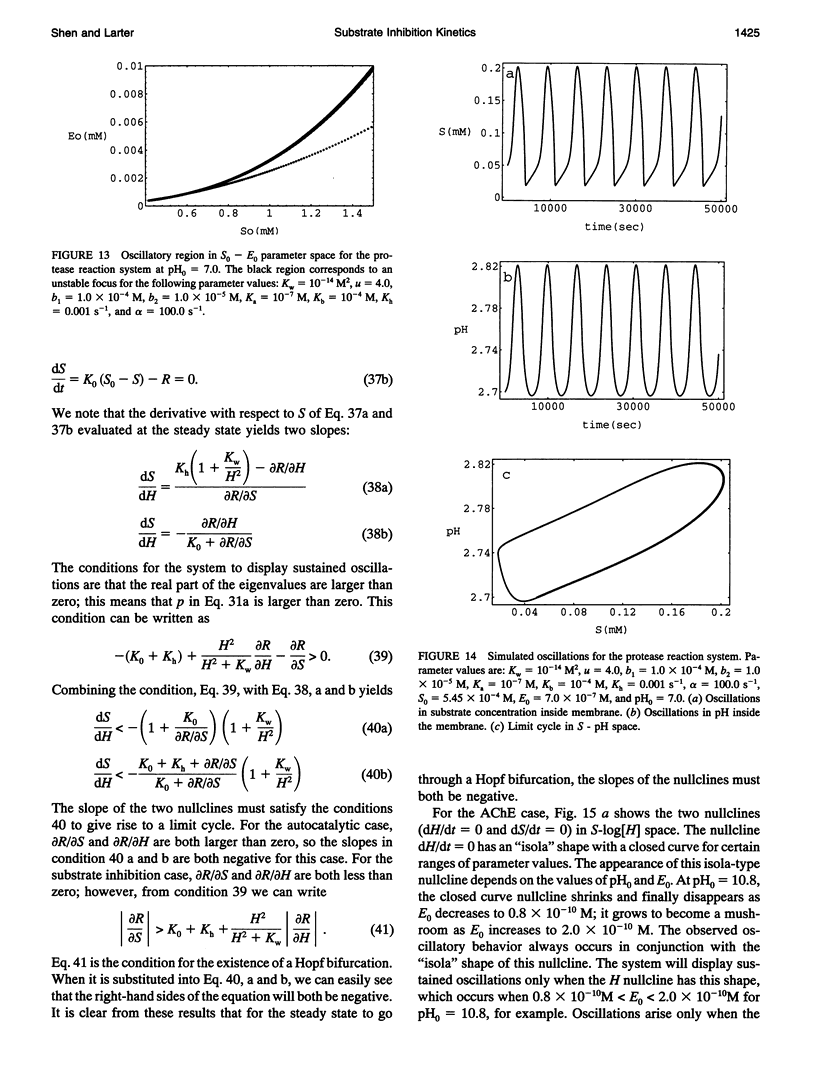
Two chemical kinetic models are investigated using standard nonlinear dynamics techniques to determine the conditions under which substrate inhibition kinetics can lead to oscillations. The first model is a classical substrate inhibition scheme based on Michaelis-Menten kinetics and involves a single substrate. Only when this reaction takes place in a flow reactor (i.e., both substrate and product are taken to follow reversible flow terms) are oscillations observed; however, the range of parameter values over which such oscillations occur is so narrow it is experimentally unobservable. A second model based on a general mechanism applied to the kinetics of many pH-dependent enzymes is also studied. This second model includes both substrate inhibition kinetics as well as autocatalysis through the activation of the enzyme by hydrogen ion. We find that it is the autocatalysis that is always responsible for oscillatory behavior in this scheme. The substrate inhibition terms affect the steady-state behavior but do not lead to oscillations unless product inhibition or multiple substrates are present; this is a general conclusion we can draw from our studies of both the classical substrate inhibition scheme and the pH-dependent enzyme mechanism. Finally, an analysis of the nullclines for these two models allows us to prove that the nullcline slopes must have a negative value for oscillatory behavior to exist; this proof can explain our results. From our analysis, we conclude with a brief discussion of other enzymes that might be expected to produce oscillatory behavior based on a pH-dependent substrate inhibition mechanism.
Full text
PDF




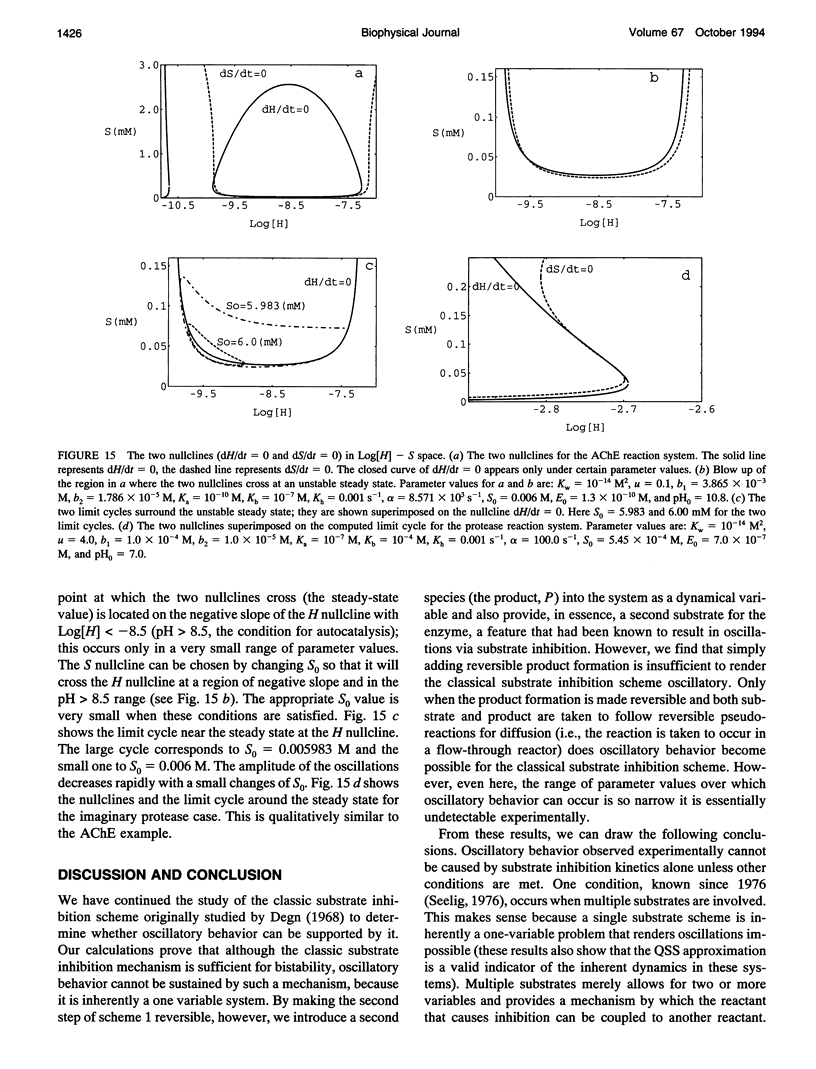


Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Caplan S. R., Naparstek A., Zabusky N. J. Chemical oscillations in membrane. Nature. 1973 Oct 19;245(5425):364–366. doi: 10.1038/245364a0. [DOI] [PubMed] [Google Scholar]
- Chay T. R. A model for biological oscillations. Proc Natl Acad Sci U S A. 1981 Apr;78(4):2204–2207. doi: 10.1073/pnas.78.4.2204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chay T. R. Proton transport across charged membrane and pH oscillations. Biophys J. 1980 Apr;30(1):99–118. doi: 10.1016/S0006-3495(80)85079-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degn H. Bistability caused by substrate inhibition of peroxidase in an open reaction system. Nature. 1968 Mar 16;217(5133):1047–1050. doi: 10.1038/2171047b0. [DOI] [PubMed] [Google Scholar]
- Degn H., Harrison D. E. Theory of oscillations of respiration rate in continuous culture of Klebsiella aerogenes. J Theor Biol. 1969 Feb;22(2):238–248. doi: 10.1016/0022-5193(69)90003-4. [DOI] [PubMed] [Google Scholar]
- Friboulet A., Thomas D. Electrical excitability of artificial enzyme membranes. III. Hysteresis and oscillations observed with immobilized acetylcholinesterase membranes. Biophys Chem. 1982 Oct;16(2):153–157. doi: 10.1016/0301-4622(82)85017-5. [DOI] [PubMed] [Google Scholar]
- Goldstein L. Kinetic behavior of immobilized enzyme systems. Methods Enzymol. 1976;44:397–443. doi: 10.1016/s0076-6879(76)44031-4. [DOI] [PubMed] [Google Scholar]
- Hahn H. S., Nitzan A., Ortoleva P., Ross J. Threshold excitations, relaxation oscillations, and effect of noise in an enzyme reaction. Proc Natl Acad Sci U S A. 1974 Oct;71(10):4067–4071. doi: 10.1073/pnas.71.10.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sel'kov E. E. Self-oscillations in glycolysis. 1. A simple kinetic model. Eur J Biochem. 1968 Mar;4(1):79–86. doi: 10.1111/j.1432-1033.1968.tb00175.x. [DOI] [PubMed] [Google Scholar]
- Spangler R. A., Snell F. M. Transfer function analysis of an oscillatory model chemical system. J Theor Biol. 1967 Sep;16(3):381–405. doi: 10.1016/0022-5193(67)90063-x. [DOI] [PubMed] [Google Scholar]