Ion channel gating: A first-passage time analysis of the Kramers type

Abstract

The opening rate of voltage-gated potassium ion channels exhibits a characteristic knee-like turnover where the common exponential voltage dependence changes suddenly into a linear one. An explanation of this puzzling crossover is put forward in terms of a stochastic first passage time analysis. The theory predicts that the exponential voltage dependence correlates with the exponential distribution of closed residence times. This feature occurs at large negative voltages when the channel is predominantly closed. In contrast, the linear part of voltage dependence emerges together with a nonexponential distribution of closed dwelling times with increasing voltage, yielding a large opening rate. Depending on the parameter set, the closed-time distribution displays a power law behavior that extends over several decades.

Voltage-dependent ion channels of biological membranes are formed by porelike single proteins that poke through the cell membrane. They provide the conducting pathways for the ions of specific sorts (1, 2). Such potassium (K⁺) and sodium (Na⁺) channels participate in many important processes occurring in living cells. For example, these are crucial for the phenomenon of neural excitability (3).

Two features are important for the biological function of these naturally occurring nanotubes. First, they either are dwelling in open conformations, allowing for the ion flow to pass through, or are resting in closed nonconducting conformations. Between these two conformation types the ion channel undergoes spontaneous temperature-driven transitions—the so-called gating dynamics—which can be characterized by the residence time distributions of open, f_o(t), and closed, f_c(t), states, respectively. The mean open and closed residence times, 〈T_o(c)〉 := ∫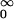 tf_o(c)(t)dt are prominent quantifiers of the gating dynamics. In particular, they determine the mean opening (closing) rates k_o(c) := 〈T_c(o)〉⁻¹. The second important feature refers to the fact that the gating dynamics is voltage dependent. This voltage dependence provides a mechanism for a mutual coupling among otherwise independent ion channels, being realized through the common membrane potential. Both ingredients are central for the seminal model of neuronal activity put forward by Hodgkin and Huxley in 1952 (3).

The dichotomous character of gating transitions yields a bistable dynamics of the Kramers type (4). Therefore, a priori one expects that both the opening and the closing gating rates will expose an exponential Arrhenius-like dependence on voltage and temperature. Indeed, the closing rate of many K⁺ channels follows such a pattern; in clear contrast, however, the opening rate usually does not. To explain the experimental voltage dependence of the activation time constant of the potassium current for a squid giant axon, Hodgkin and Huxley (3) postulated that the gating behavior of a potassium channel is determined by four independent voltage-sensitive gates, each of which undergoes a two-state Markov dynamics with a form (3, 5)

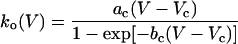1

for the opening rate, which is commonly used in neurophysiology. In Eq. 1, a_c, b_c, V_c are some experimental parameters. Notwithstanding that in their work (3) this kind of dependence has been used for a single gate, the opening rate of the whole K⁺ channel can also be fitted by Eq. 1 (see, e.g., in ref. 6). The same modeling for a whole channel is used also for dendritic K⁺ channels in neocortical pyramidal neurons (5).

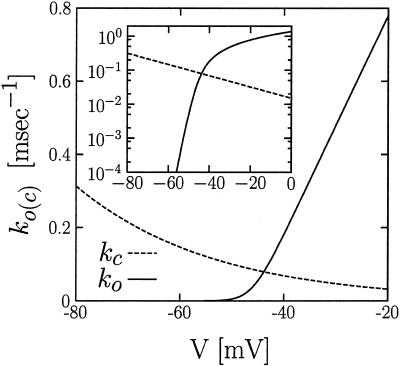
Note that in Eq. 1 the voltage dependence of the opening rate changes in a knee-like manner from an exponential behavior into a linear one (cf. Fig. 1). This typical experimentally observed behavior of delayed rectifier K⁺ channels presently lacks an explanation in physical terms. A qualitative explanation of this gating dynamics has briefly been mentioned in recent work (8). However, a definite analysis leading to the functional form in Eq. 1 is not available. A first main objective of the present work is to fill this gap, and, moreover, to provide additional insight into the voltage behavior of Eq. 1 within an exactly solvable stochastic Fokker–Planck–Kramers model.

Figure 1.

Dependence of opening (k_o) and closing (k_c) rates on voltage for a Shaker IR K⁺ channel from ref. 6 at T = 18°C. The opening rate is described by Eq. 1 with the following parameters (6): a_c = 0.03 msec/mV, b_c = 0.8 mV⁻¹, and V_c = −46 mV. The closing rate is given by k_c = 0.015 exp(−0.038V) msec⁻¹ (V in mV) (6, 7). Inset shows the same dependencies on a semilogarithmic scale.

The ion current recordings made on the level of single ion channels (2) reveal yet another unresolved, interesting, aspect of the gating dynamics. Namely, the distribution of closed residence times of many channels is not exponential. In particular, it has been shown by Liebovitch et al. (9) that the closed residence time distribution f_c(t) in a rabbit corneal endothelium channel can be reasonably fitted by a stretched exponential with only two parameters. This result initiated the construction of the so-called fractal model of ion channel gating (9, 10). Other channels—e.g., K⁺ channels in neuroblastoma × glioma (NG 108-15) cells—exhibit a power-law scaling behavior as well—i.e., f_c(t) ∝ t^−α with α = 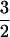(11). To explain this type of fractal-like behavior Millhauser et al. (12) proposed a one-dimensional diffusion model. Similar power laws with α ≠ 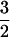have also been reported (13–15), and several variations of diffusion theory have been introduced to explain the gating behavior of different channels (16–19).

The observed nonexponential behavior can be fitted by a finite sum of exponentials; consequently, it can alternatively be explained with a corresponding discrete Markovian scheme (11). These discrete Markovian models have proven their usefulness in many cases (20). Nevertheless, such an approach presents a fitting procedure; as such it is intimately connected with the danger of a proliferation of parameters. In particular, kinetic schemes containing as many as 14 structurally unidentified closed substates have been proposed (21).

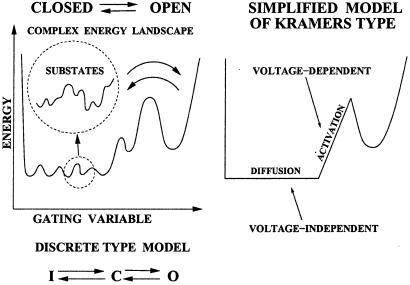
An important lesson to be learned from the detailed studies of a simple protein—myoglobin—by Frauenfelder et al. (22) is that proteins exist in a huge number of quasidegenerate microscopic substates, corresponding to a single macroscopic conformation (cf. Fig. 2). It is thus conceivable that at room temperatures the ion channel dwells in a huge number of almost degenerate (within k_BT) conformational substates. Both the fractal and diffusion models of the ion channel gating have been inspired by this crucial property of proteins. We conjecture that the ultimate theory of the ion channel gating must take this property into account. This program requires a compromise between Markovian discrete state models and a continuous diffusion model. This can be achieved by a Kramers type theory (4, 8). The discrete Markov models can then be considered as a limiting case of more general Kramers type approach (4).

Figure 2.

Gating dynamics as an activated diffusion on a complex free energy landscape. Two global minima correspond to open and closed macroconformations. One assumes a large number of quasidegenerate (within k_BT) and voltage-independent closed substates separated from the open conformation by a voltage-dependent potential barrier. This idea is sketched by a simplified model of the Fokker–Planck–Kramers type, and by a discrete model with open (O), closed (C), and inactivated (I) states.

Theoretical Modeling

The complex structure of the multidimensional conformational space of proteins implies an intricate kinetics despite an apparently simple bistability that is observed (22). Two popular theoretical approaches have been developed to cope with this complexity. A first one uses a simple bistable dynamics as a basis. To model the complexity of the observed kinetics this dynamics is amended by using an additional stochastic time dependence of the energy profile, or kinetic constants. Such an approach is nowadays commonly known under the label of “fluctuating barriers” (23–27). Alternatively, one can attempt to model the complexity of the energy profile itself in the simplest possible way. Our strategy is to find such a minimal model of the second kind that does allow for a rigorous analysis and does reproduce some nontrivial features of the gating dynamics.

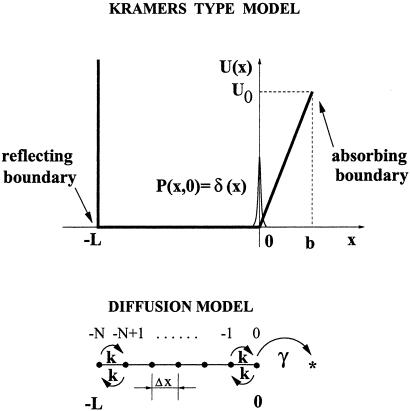
Let us assume that the conformational stochastic dynamics between the open and closed states can be described in terms of a one-dimensional reaction coordinate dynamics x(t) in a conformational potential U(x) (Figs. 2 and 3). Because the distribution of open residence time intervals assumes typically a single exponential (1), in the following we rather shall focus on the behavior of the closed residence time intervals. To evaluate the distribution of closed residence time intervals it suffices to restrict our analysis to the subspace of closed states by putting an absorbing boundary at the interface, x = b, between the closed and open conformations (see Fig. 3). We next assume that the gating dynamics is governed by two gates: an inactivation gate and an activation gate. The inactivation gate corresponds to the manifold of voltage-independent closed substates. It is associated with the flat part, −L < x < 0, of the potential U(x) in Fig. 3. In this respect, our modeling resembles that in ref. 28. The mechanism of inactivation in potassium channels is quite sophisticated and presently not totally established (1). It is well known that inactivation can occur on quite different time scales (1). The role of a fast inactivation gate in Shaker K⁺ channels is taken over by the channel's extended N terminus, which is capable of plugging the channel's pore from the cytosol part while diffusing towards the pore center (29). The slow inactivation apparently is due to a conformational narrowing of the channel pore in the region of selectivity filter (1). In both cases, no net gating charge translocation occurs and the inactivation process does not depend on voltage. When the inactivating plug is outside of the pore, or the selectivity filter is open (x > 0 in Fig. 3) the channel can open only if the activation barrier is overcome.

Figure 3.

Studied model and its diffusion counterpart.

The dynamics of the activation gate occurs on the linear part of the ramp of the potential U(x)—i.e., on 0 < x < b in Fig. 3, as in refs. 18 and 19. Note that for 0 < x < b, the inactivating plug diffuses outside of the channel's pore and the selectivity filter is open. During the activation step a gating charge q moves across the membrane; this feature renders the overall gating dynamics voltage dependent. The channel opens when the reaction coordinate reaches the location x = b in Fig. 3. This fact is accounted for by putting an absorbing boundary condition at x = b. Moreover, the channel closes immediately when the inactivation gate closes (x ≤ 0), or when the activation gate closes. To account for this behavior in extracting the closed residence time distribution we assume that the channel is reset into the state x = 0 after each closure (see below).

The diffusional motion of the inactivated gate is restricted in conformational space. We characterize this fact by the introduction of a conformational diffusion length L (Fig. 3) and the diffusion constant D ∼ k_BT that are combined into a single parameter—the conformational diffusion time

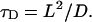2

This quantity constitutes an essential parameter for the theory. We assume that the activation barrier height U₀ is linearly proportional to the voltage bias V (18, 19)—i.e., in terms of the gating charge q we have

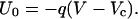3

Moreover, U₀ is positive for negative voltages—i.e., for V < V_c—vanishes at V = V_c, and becomes negative for V > V_c. Thus, for V > V_c the channel “slips” in its open state, rather than overcomes a barrier. In addition, the fraction ξ of the voltage-dependent substates in the whole manifold of the closed states should be very small, implying that

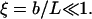4

Analytical Solution.

The corresponding Fokker–Planck equation for the probability density of closed states P(x, t) reads

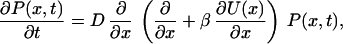5

where β = 1/(k_BT). To find the distribution of closed residence times f_c(t), we solve Eq. 5 with the initial condition P(x,0) = δ(x), in combination with a reflecting boundary condition dP(x, t)/dx |_x=−L = 0, and an absorbing boundary condition, P(x, t)|_x=b = 0 (4). The closed residence time distribution then follows as

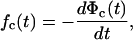6

where Φ_c(t) = ∫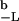 P(x,t)dx is the survival probability of the closed state.

By use of the standard Laplace transform method we arrive at the following exact solution:

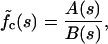7

where

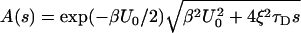8

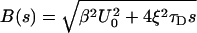9

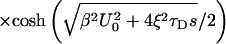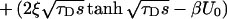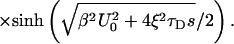The explicit result in 7–9 allows one to find all moments of the closed residence time distribution. In particular, the mean closed residence time 〈T_c〉 = lim_s→0[1 − f̃_c(s)]/s reads

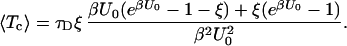10

This very same result 10 can be obtained alternatively if we invoke the well-known relation for the mean first-passage time 〈T_c〉 = 1/D ∫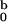 dxe^βU(x) ∫ 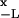dye^−βU(y) (4). This alternative scheme provides a successful validity check for our analytical solution in 7–9.

Elucidation of the Voltage Dependence in Eq. 1.

Upon observing the condition 4, Eq. 10 by use of 3 reads in leading order of ξ

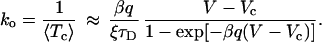11

With the parameter identifications

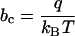12

and

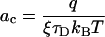13

the result in 11 precisely coincides with Eq. 1. The fact that our approach yields the puzzling voltage dependence in Eq. 1 constitutes a first important result of this work.

Let us next estimate the model parameters for a Shaker IR K⁺ channel from ref. 6. In ref. 6, the voltage dependence of k_o(V) at T = 18°C has been parameterized by Eq. 1 with the parameters given in the caption of Fig. 1. Then, from Eq. 12 the gating charge can be estimated as q ≈ 20e (e is the positive-valued elementary charge). As to the diffusion time τ_D, we speculate that it corresponds to the time scale of inactivation; the latter is in the range of seconds and larger (6). Therefore, we use τ_D = 1 sec as a lower bound for our estimate. The fraction of voltage-dependent states ξ is then extracted from Eq. 13 to yield, ξ ≈ 0.0267. This value, indeed, is rather small and thus proves our finding in Eq. 11 to be consistent.

Analysis for the Closed Residence Time Distribution.

The exact results in Eqs. 7–9 appear rather entangled. To extract the behavior in real time one needs to invert the Laplace transform numerically. With ξ ≪ 1, however, Eqs. 7–9 are formally reduced to

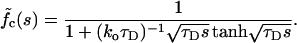14

This prominent leading order result can be inverted analytically in terms of an infinite sum of exponentials, yielding:

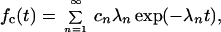15

where the rate constants 0 < λ₁ < λ₂ < … are solutions of the transcendental equation

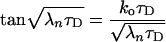16

and the expansion coefficients c_n, respectively, are given by

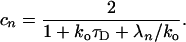17

Note from Eq. 6 that the set c_n is normalized to unity, i.e. Σ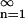 c_n = 1.

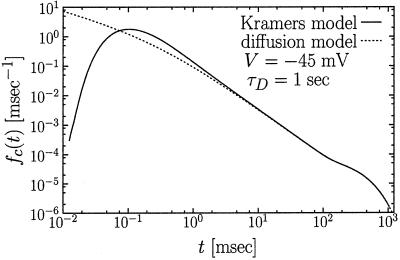
The analytical approximation, Eqs. 15–17, is compared in Fig. 4 with the precise numerical inversion of the exact Laplace transform in Eqs. 7–9. The numerical inversion has been performed with the Stehfest algorithm (30). As can be deduced from Fig. 4, for t > 10 msec the agreement is very good indeed. A serious discrepancy occurs only in the range 0.01 msec < t < 0.1 msec, which lies outside the range of the patch clamp experiments (t ≳ 0.1 msec). Moreover, the agreement improves with increasing τ_D (not shown).

Figure 4.

Closed residence time distribution for a diffusion-limited case. The numerical precise result (solid line) is compared with the analytical approximation in Eqs. 15–17 (broken line). The latter one coincides with the exact solution of the diffusion model by Millhauser et al. (12) in the scaling limit.

Origin of the Power Law Distribution.

The features displayed by the closed residence time distribution f_c(t) depend sensitively on the applied voltage V. When V > V_c—e.g., V = −45 mV, as in Fig. 4—the activation barrier towards the channel opening disappears and the opening dynamics becomes diffusion limited. In this case, the diffusion time τ_D = 1 sec largely exceeds the mean closed residence time 〈T_c〉 ≈ 18.4 msec. Put differently, τ_D ≫ 〈T_c〉 and the closed residence time distribution exhibits an intricate behavior with three distinct regions (see Fig. 4). Most importantly, for the intermediate time scale

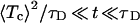18

we find from Eq. 14 (by considering the limit τ_D → ∞) that the closed residence time distribution obeys a power law, reading

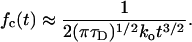19

This type of behavior is clearly detectable in Fig. 4, where it covers about two decades of time. As follows from Eq. 18, an increase of τ_D by one order of magnitude (while keeping 〈T_c〉 fixed) extends the power law region by two orders of magnitude. This conclusion is fully confirmed by our numerics (not shown). This power law dependence, which extends over four orders of magnitude, has been seen experimentally for a K⁺ channel in NG 108-15 cells (11). On the contrary, for channels, where τ_D is smaller, the power law region 18 shrinks and eventually disappears, whereas the mean opening rate defined by Eq. 10 still exhibits a steep dependence on the voltage. Thus, our model is capable of describing for different channels both the emergence of the power law and its absence.

On the time scale t ≥ τ_D the discussed power law distribution crosses over into the exponential tail; the latter is fully described by the smallest exponent λ₁ in Eq. 15, i.e., by

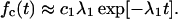20

This feature is clearly manifest in Fig. 4. The transition towards the exponential tail in the closed residence time-interval distribution can be used to estimate the diffusion time τ_D on pure experimental grounds!

Finally, let us consider the opposite limit, τ_D ≪ 〈T_c〉, for V ≪ V_c. For the considered set of parameters this occurs—e.g., for V = −55 mV—when the channel is predominantly closed. Then, the diffusion step in the opening becomes negligible and in the experimentally relevant range of closed residence times, defined by 〈T_c〉, the corresponding distribution can be approximated by a single exponential, 20. A perturbation theory in Eq. 16 yields λ₁ ≈ k_o (1 − (k_oτ_D)/3). For the parameters used we have λ₁ ≈ 0.96k_o and, from Eq. 17, c₁ ≈ 0.95. This is in a perfect agreement with the precise numerical results obtained from Eqs. 7–9. Thus, the distribution of closed residence times is single exponential to a very good degree. Consequently, one and the same channel can exhibit both an exponential and a power-law distribution of closed residence times, as a function of the applied transmembrane voltage. With an increase of τ_D the voltage range of the exponential behavior shifts towards more negative voltages, V < V_c, and vice versa.

Reduction to a Diffusion Model.

Let us relate our model to that introduced previously by Millhauser et al. (12). The latter one is depicted with the lower part in Fig. 3. It assumes a discrete number N of closed substates with the same energy. The gating particle jumps with the equal forward and backward rates k between the adjacent states, which are occupied with probabilities p_n(t). At the right edge of the chain of closed states the ion channel undergoes transition into the open state with the voltage-dependent rate constant γ. To calculate the closed residence time distribution f_c(t) one assumes p₀(0) = 1, p_n≠0(0) = 0, and dΦ_c(t)/dt = −γp₀(t), where Φ_c(t) = Σ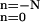 p_n(t) is the survival probability (12, 17).

We consider the continuous diffusion variant of this model (31) in a scaling limit: we put Δx → 0, k → ∞, γ → ∞, N → ∞, keeping the diffusion length L = N Δx, the diffusion constant D = k(Δx)², and the constant k_o = γ/N all finite. The latter one has the meaning of mean opening rate (see below). Note that in clear contrast with our approach, the rate parameter k_o in the diffusion model is of pure phenomenological origin. The problem of finding the closed residence time distribution is reduced to solving the diffusion equation

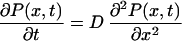21

with the initial condition P(x,0) = δ(x − 0₋), the reflecting boundary condition ∂P(x, t)/∂x |_x=−L = 0 and the radiation boundary condition (32).

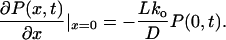22

We emphasize that the radiation boundary condition 22 is not postulated, but is rather derived from the original discrete model in the considered scaling limit. Using the Laplace transform method, we solved this problem exactly and obtained the result in Eq. 14. In conclusion, our approximate result in Eqs. 14–17 provides the exact solution of the diffusion model (12, 17) in the scaling limit! Note, however, that this diffusion model so obtained is not able to resolve the puzzling voltage dependence in Eq. 1.

Synopsis and Conclusions

With this work we put forward a unifying generalization of the diffusion theory of ion channel gating by Millhauser et al. (12, 17). Our theory reproduces the functional form of the puzzling voltage dependence in Eq. 1. The latter had been postulated almost 50 years ago in the pioneering paper by Hodgkin and Huxley (3) and is commonly used in neurophysiology up to now. The proposed model of the Fokker–Planck–Kramers type explains the origin of steep voltage dependence in Eq. 1 within a clear physical picture that seemingly is consistent with both our current understanding of the physics of proteins and basic experimental facts. Our study furthermore reveals the connection between the voltage dependence of the opening rate and the intricate behavior for the closed residence time distribution in corresponding voltage regimes. A particularly appealing feature of our approach is that our model contains only four voltage-independent physical parameters: the diffusion time τ_D, the fraction of voltage-dependent substates ξ, the gating charge q, and the threshold voltage V_c. Several experimental findings could be described consistently while others call for an experimental validation.

In particular, (i) when the activation barrier is very high, i.e., V ≪ V_c, the activation step determines completely the opening rate: the distribution of closed residence times is nearly exponential, as well as the voltage dependence of the opening rate. The channel is then predominantly closed. We remark that the opening rate should exhibit an exponential dependence on temperature as well. This conclusion follows from Eqs. 11 and 12 and the fact that in accord with our model the parameter a_c in Eq. 1 is temperature independent. Indeed, with the diffusion time τ_D being inversely proportional to the temperature—i.e., with τ_D ∼ 1/D ∼ 1/(k_BT)—one obtains a_c ∼ 1/(τ_Dk_BT); i.e., the coefficient a_c is temperature independent (cf. Eq. 13). In contrast, (ii) when the activation barrier vanishes—i.e., the voltage shifts towards the positive direction—the closed residence time distribution becomes nonexponential. On the intermediate time scale given in Eq. 18, this distribution exhibits a power law behavior, f_c(t) ∝ t^−3/2, which crosses over into an exponential one at t > τ_D. The emergence of the exponential tail can be used to determine the conformational diffusion time τ_D experimentally. (iii) When the activation barrier assumes negative values at voltages V > V_c, our result for the opening rate exhibits a linear dependence on voltage and, consequently (see Eq. 11), it no longer depends on temperature. The weak temperature dependence will emerge, however, when we renormalize the diffusion coefficient D due to the roughness of random energy landscape (cf. Fig. 2). Assuming uncorrelated Gaussian disorder, one gets D ∼ k_BT exp(−〈δU²〉/(k_BT)²) (4, 33, 34), where 〈δU²〉 is the mean-squared height of the barrier between substates. Then, k_o ∼ exp(−〈δU²〉/(k_BT)²), and because 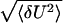∼ k_BT this non-Arrhenius dependence is weak at room temperatures. This result has a clear thermodynamic interpretation: when the activation barrier vanishes the closed-to-open transition is entropy dominated and thus the opening rate will only weakly depend on temperature. In accord with our model, this type of behavior correlates with a nonexponential kinetics.

The temperature behavior of the opening rate (or, equivalently, the mean closed time) presents a true benchmark result of our theory. We are looking forward to seeing this feature being tested experimentally.