A Survey of Affected-Sibship Statistics for Nonparametric Linkage Analysis

Abstract

We have compared the power of a large number of allele-sharing statistics for “nonparametric” linkage analysis with affected sibships. Our rationale was that there is an extensive literature comparing statistics for sibling pairs but that there has not been much guidance on how to choose statistics for studies that include sibships of various sizes. We concentrated on statistics that can be described as assigning scores to each identity-by-descent–sharing configuration that a pedigree might take on (Whittemore and Halpern 1994). We considered sibships of sizes two through five, 27 different genetic models, and varying recombination fractions between the marker and the trait locus. We tried to identify statistics whose power was robust over a wide variety of models. We found that the statistic that is probably used most often in such studies—S_all—performs quite well, although it is not necessarily the best. We also found several other statistics (such as the R criterion, S_robdom, and the Sobel-and-Lange statistic C) that perform well in most situations, a few (such as S_-#geno and the Feingold-and-Siegmund version of S_pairs) that have high power only in very special situations, and a few (such as S_-#geno, the N criterion, and the Sobel-and-Lange statistic B) that seem to have low power for the majority of the trait models. For the most part, the same statistics performed well for all sibship sizes. We also used our results to give some suggestions regarding how to weight sibships of different sizes, in forming an overall statistic.

Introduction

During the past decade there has been a dramatic increase in the number of studies searching for genes influencing susceptibility to complex diseases. Such studies have involved many different laboratory technologies, study designs, and statistical tools. One of the most important statistical tools has been “nonparametric” linkage analysis methods, which base statistical inference on allele-sharing statistics for affected pedigree members. A particularly important class of allele-sharing statistics is that outlined by Whittemore and Halpern (1994). This very general class includes any statistic based on a scoring function, S, that assigns a score to each possible identity by descent (IBD)–sharing configuration, φ, that a pedigree can take on. For a single pedigree, the allele-sharing statistic is written as Σ_φP(φ|markerdata)S(φ). This raw statistic for each pedigree is normalized by subtracting the null-hypothesis (no linkage) mean of each statistic and dividing by the null-hypothesis SD. The normalized statistics are summed over pedigrees, and the sum is asymptotically normally distributed under the null hypothesis of no linkage under reasonable regularity conditions. Statistics of this form have been particularly important in nonparametric linkage analysis, for a number of reasons. On the theoretical side, they are attractive because they are very flexible and because they correctly treat the whole pedigree (rather than a relative pair) as the sampling unit. On the practical side, these statistics are appealing because they separate the calculation of the IBD sharing from the calculation of the statistic. This allows one to estimate the IBD sharing by computationally quite-intensive methods (e.g., see Kruglyak et al. 1996; Sobel and Lange 1996) and then to trivially take those IBD-sharing estimates and score them in various ways, to compute different sharing statistics.

Whittemore and Halpern (1994) discussed two scoring functions, S_pairs and S_all (for descriptions, see table 1), both of which can be applied to any type of pedigree. However, a large proportion (arguably most) of the allele-sharing statistics from the literature, both preceding 1994 and since then, can also be written in the form described above. There are statistics that apply only to sibling pairs, statistics that can be applied to sibships of arbitrary size, and statistics that can be applied to general pedigrees. For example, the most commonly used statistic for sibling pairs, the mean sharing statistic, is of this form. The score for a sibling pair is the sum of the probability that the pair shares two alleles IBD plus half of the probability that the pair shares one allele IBD. Scoring functions that apply to sibships of arbitrary size have been discussed by, for example, Green and Woodrow (1977) and Abel et al. (1998). The literature also now contains a number of general-pedigree scoring functions beyond S_pairs and S_all. These were reviewed recently by McPeek (1999). It should also be noted that any sib-pair scoring function can be extended to larger sibships or even to general pedigrees, by adding it over all affected relative pairs in the pedigree. Such an “all pairs” statistic is still of the Whittemore-and-Halpern form if it is normalized on a pedigree-wise basis rather than on a pairwise basis. Indeed, S_pairs is constructed in this way from the mean sharing statistic.

Table 1.

Statistics of Interest

Statistic	Definition	Reference
R criterion	Sum of no. of repeats of each parental allele among affected siblings; equivalent to Sobel and Lange's (1996) statistic A and recessive LOD-score statistics with q=.1 and q=.01, computed with penetrance vector (.00, .00, .50) at θ=0	Green and Woodrow (1977)
N criterion	Maximum no. of alleles, among affected siblings, from father, + maximum from mother; equivalent to the parental allele–difference method (Abel et al. 1998)	Green and Woodrow (1977)
Spairs	Sum of pairwise IBD sharing, over all affected pairs in pedigree, measured as the no. of pairs sharing two IBD +  1/2the no. of pairs sharing one IBD; equivalent to Sobel and Lange's (1996) statistic D	Whittemore and Halpern (1994)
Sobel and Lange's statistic C (S+L C)	Entropy of alleles among affecteds	Sobel and Lange (1996)
Robust dominant statistic (Srobdom)	Sum, over founder alleles, of 7cl(i)-1, where cl(i) is the no. of affected siblings in the family who have at least one copy of allele i	McPeek (1999)
Sall	Sum of the nos. of nontrivial permutations of all possible sets consisting of one allele from each affected individual	Whittemore and Halpern (1994)
Sobel and Lange's statistic B (S+L B)	Maximum no. of alleles, among affecteds, that are attributable to any one descent tree	Sobel and Lange (1996)
No. of distinct genotypes (S-#geno)	Counts −1 for each distinct genotype among affected siblings	McPeek (1999)
Feingold and Siegmund's version of Spairs (F+S)	Sum of pairwise IBD sharing, over all affected pairs in pedigree, measured as the no. of pairs sharing two IBD +  1/4times the no. of pairs sharing one IBD	Feingold and Siegmund (1997)
Dominant LOD score with q=.1 [ldom(.1)] and q=.01 [ldom(.01)]	LOD score computed with penetrance vector (.00, .50, .50) at θ=0	Ott (1999)

Quite a bit of literature has compared the power of various scoring functions for sib pairs (e.g., see Blackwelder and Elston 1985; Knapp et al. 1994; Davis and Weeks 1997; Feingold and Siegmund 1997; Whittemore and Tu 1998). A few papers have covered the other end of the spectrum, comparing general pedigree scoring functions (e.g., see Krugylak et al. 1996; McPeek 1999; Feingold et al. 2000). In this article, we address the intermediate question of which scoring functions are the best for affected sibships of various sizes. Some previous studies (e.g., see Davis and Weeks 1997; Abel et al. 1998; Abreu et al. 1999) have investigated statistics for sibships, although for somewhat different types of statistics than those which we consider. In addition, most of these previous power analyses calculated power for mixtures of sibships of different sizes. This is a very useful approach, but it is also important to look at sibships of different sizes separately, to find out which scoring functions are the best for each sibship size. In theory, a linkage study need not use the same scoring function for each sibship size; doing so is a matter of convenience (no software package that we are aware of currently allows the user to specify different scoring functions for different types of pedigrees), but there is no statistical reason why it must be done that way.

We have done a literature survey and have extracted most of the statistics of the Whittemore-and-Halpern type that can be applied to sibships, including general-pedigree scoring functions, sibship scoring functions, and sib-pair scoring functions (used over all pairs). We studied the power of these statistics for sibships of sizes two through five. We judged affected sibships of sizes greater than five to be relatively unimportant for complex-trait mapping. Our goal was to find scoring functions whose power is robust over a wide variety of trait models, since, in a typical complex trait–mapping situation, there is not much knowledge of the trait model. We considered 27 models, including dominant, additive, and recessive models, with full and incomplete penetrance and with varying phenocopy rates. All of our models are single-gene models, although we considered fairly high phenocopy rates, which can be thought of as including heterogeneity effects and which also approximate certain interaction models that produce small marginal effects. We computed power for a test of a single marker, with varying recombination fractions between the marker and the trait locus. All of our computations assumed perfect IBD information at the marker. The effect of this assumption is addressed in the Methods and Discussion sections.

Of course, given good statistics for each sibship size, one still needs to know how to weight sibships of different sizes to combine them. The search for good weights is conceptually very similar to the search for good statistics for a given sibship size. For any trait model, one can derive the optimal statistic for each sibship size and the optimal weights for combining sibships of different sizes. Since we do not expect to know the trait model, we want to find statistics and weights whose power is robust over a variety of models. The issue of weights for pedigrees of different sizes has been addressed, for pairwise statistics, by an enormous number of authors (e.g., Suarez and Hodge 1979; Sham et al. 1997; Abel et al. 1998; Greenwood and Bull 1999; Holmans 2001), and, for pedigree-wise statistics, by a few (e.g., Krugylak et al. 1996; Teng and Siegmund 1997; Abel et al. 1998; McPeek 1999). We comment on the weighting issue in the Discussion section, but it is not the main focus of this article.

Methods

Table 1 lists the statistics that we considered in this study. Groups of statistics that are analytically equivalent up to linear transformations are condensed into single listings. In table 1, all references to matching or counting of alleles or genotypes refer to IBD, not to identity by state. We enumerated the IBD-sharing configurations in each sibship, as shown in table 2, labeling the genotypes of the mother and father as “12” and “34,” respectively. This is the same notation used by Whittemore and Halpern (1994). The IBD-sharing configurations are listed from highest-order IBD sharing to lowest-order IBD sharing; by the terms “higher-order” and “lower-order” sharing we mean to indicate generally greater and lesser sharing, although this ordering is not precise, since there are different ways to quantify IBD sharing.

Table 2.

IBD-Sharing Configurations

Label	Configuration
Two siblings:
1	(13 13)
2	(13 14)
3	(13 24)
Three siblings:
1	(13 13 13)
2	(13 13 14)
3a	(13 13 24)
3b	(13 14 23)
Four siblings:
1	(13 13 13 13)
2	(13 13 13 14)
3	(13 13 14 14)
4a	(13 13 13 24)
4b	(13 13 14 23)
5	(13 13 14 24)
6a	(13 13 24 24)
6b	(13 14 23 24)
Five siblings:
1	(13 13 13 13 13)
2	(13 13 13 13 14)
3	(13 13 13 14 14)
4a	(13 13 13 13 24)
4b	(13 13 13 14 23)
5a	(13 13 13 14 24)
5b	(13 13 14 14 23)
6a	(13 13 13 24 24)
6b	(13 13 14 24 24)
6c	(13 13 14 23 24)

To understand both the similarities and the differences among the statistics, we considered how each statistic scores each possible IBD-sharing configuration. Since additive and multiplicative constants are irrelevant to the definitions of the statistics, we can scale the scores for each statistic, to make comparisons among them easier. Tables 3–6 show the scaled scores for all the statistics of interest. They were scaled for each sibship size by subtracting the null hypothesis (i.e., no linkage) mean of each statistic and dividing by the null hypothesis SD. This normalization allows us to directly compare how the different statistics score each IBD-sharing configuration—and thus allows us to make inferences about their power in different situations. A negative value assigned to any configuration means evidence against linkage.

Table 3.

Normalized Sibship Statistics, for Two Affected Siblings

	Normalized Coefficientfor Configuration
Statistic	1 (2 IBD)	2 (1 IBD)	3 (0 IBD)
R criteriona	1.41	.00	−1.41
S+L B	.58	.58	−1.73
S-#geno	1.73	−.58	−.58
F+S	1.67	−.33	−1.00
ldom(.1)	1.14	.23	−1.61
ldom(.01)	.86	.42	−1.70

^aFor two siblings, the R criterion, the N criterion, S_pairs, S+L C, S_robdom, and S_all are all equivalent.

Table 4.

Normalized Sibship Statistics, for Three Affected Siblings

	Normalized Coefficientfor Configuration
Statistic	1	2	3a	3b
R criteriona	2.45	.82	−.82	−.82
S+L B	1.13	1.13	−.88	−.88
S-#geno	2.25	.54	.54	−1.18
F+S	2.89	.58	−.19	−.96
ldom(.1)	1.79	.99	−.62	−.98
ldom(.01)	1.46	1.07	−.77	−.93

^aFor three siblings, the R criterion, the N criterion, S_pairs, S+L C, S_robdom, and S_all are all equivalent.

Table 5.

Normalized Sibship Statistics, for Four Affected Siblings

	Normalized Coefficient for Configuration
Statistic	1	2	3	4a	4b	5	6a	6b
R criterion	3.74	1.60	1.60	−.53	−.53	−.53	−.53	−.53
N criterion	2.67	1.60	.53	.53	.53	−.53	−1.60	−1.60
Spairs	3.46	1.73	1.15	.00	.00	−.58	−1.15	−1.15
S+L C	3.60	1.72	1.30	−.16	−.16	−.57	−.99	−.99
Srobdom	3.70	1.68	1.45	−.30	−.30	−.57	−.80	−.80
Sall	3.68	1.71	1.29	−.25	−.11	−.58	−.91	−1.00
S+L B	1.50	1.50	1.50	−.15	−.15	−.15	−1.81	−1.81
S-#geno	2.67	1.15	1.15	1.15	−.42	−.42	1.15	1.15
F+S	4.08	1.63	.82	.82	−.27	−.54	−.27	−1.36
ldom(.1)	2.57	1.69	1.69	−.09	−.53	−.53	−.09	−1.08
ldom(.01)	2.22	1.76	1.76	−.36	−.54	−.54	−.36	−.82

Table 6.

Normalized Sibship Statistics, for Five Affected Siblings

	Normalized Coefficient for Configuration
Statistic	1	2	3	4a	4b	5a	5b	6a	6b	6c
R criterion	5.47	2.56	2.56	−.37	−.37	−.37	−.37	−.37	−.37	−.37
N criterion	3.63	2.47	1.31	1.31	1.31	.15	.15	−1.02	−1.02	−1.02
Spairs	4.46	2.69	1.78	.87	.87	.01	.01	−.90	−.90	−.90
S+L C	4.83	2.74	2.01	.66	.66	−.08	−.08	−.81	−.81	−.81
Srobdom	5.33	2.72	2.37	.12	.12	−.24	−.24	−.59	−.59	−.59
Sall	5.27	2.80	2.07	.32	.56	−.17	−.10	−.70	−.70	−.77
S+L B	1.92	1.92	1.92	.41	.41	.41	.41	−1.10	−1.10	−1.10
S-#geno	3.15	1.63	1.63	1.63	.07	.07	.07	1.63	.07	−1.45
F+S	5.26	2.74	1.47	1.92	.65	.21	−.23	.21	−.61	−1.05
ldom(.1)	3.58	2.51	2.51	.33	−.21	−.21	−.21	.33	−.21	−.88
ldom(.01)	3.17	2.64	2.64	−.06	−.29	−.29	−.29	−.06	−.29	−.63

To find the power of each statistic under various genetic models, we first calculated the probability of each IBD-sharing configuration, k, under the alternative hypothesis, conditional on having n affected siblings, as

where j and k are any IBD-sharing configuration in sibships of a given size (see table 2). The probabilities P(k) are just the null-hypothesis probabilities. The conditional probability P(n affected siblings|IBD configuration k) can be written as

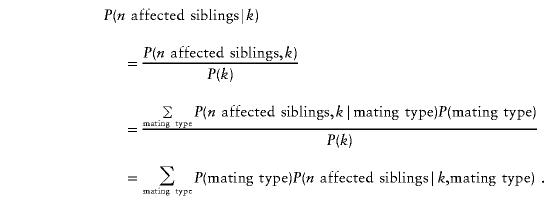For the case of no recombination (θ=0) between the marker and the trait locus, we computed these probabilities analytically and then checked our equations by using MENDEL (Lange et al. 1988) to compute the conditional probabilities P (n affected siblings|IBD configuration k). For the values θ=.05, .10, and .20, we also computed these conditional probabilities by using MENDEL. Including θ values that are >0 is important because, in a real study, it is unlikely that the gene would be in complete linkage with a marker. Furthermore, in a real study, one would not have perfect IBD information, and the effect of reduced IBD information is very similar to the effect of increased distance between the gene and the marker. In the Discussion section, we comment on this issue further.

These probabilities in equation (1) above depend on the genetic model as defined by the allele frequency q and the penetrances f₁, f₂, and f₃. We considered 27 models, which are listed in table 7. In table 7, K is the population prevalence of the disease, and λ_o is the risk ratio to offspring, defined as the recurrence risk divided by the population prevalence (Risch 1990). Models 1–9 all give a disease prevalence of 10%. They include three dominant, three additive, and three recessive models. Each group of three models consists of a full-penetrance–no-phenocopies model, a model with phenocopies, and a model with reduced penetrance. Models 10–18 repeat the same pattern for a disease prevalence of 1%, and models 19–27 do the same for a disease prevalence of 0.1%. We consider models 1–9 to be the most relevant to complex-trait mapping, and we present results primarily for those models. The other models were investigated in order to get a more complete understanding of the effects that allele frequency has on our results.

Table 7.

Genetic Models

Model	q	f1	f2	f3	λo	Description
K=.1:
1	.0513	.0000	1.0000	1.0	5.4	Dominant, no phenocopies, full penetrance
2	.0267	.0500	1.0000	1.0	3.2	Dominant, half of cases are phenocopies
3	.1056	.0000	.5000	.5	2.9	Dominant, reduced penetrance
4	.1000	.0000	.5000	1.0	3.2	Additive, no phenocopies, full penetrance
5	.1000	.0500	.5000	1.0	2.9	Additive, half of cases are phenocopies
6	.2000	.0000	.2500	.5	2.0	Additive, reduced penetrance
7	.3162	.0000	.0000	1.0	3.2	Recessive, no phenocopies, full penetrance
8	.2294	.0500	.0500	1.0	1.8	Recessive, half of cases are phenocopies
9	.4472	.0000	.0000	.5	2.2	Recessive, reduced penetrance
K=.01:
10	.0050	.0000	1.0000	1.0	50.4	Dominant, no phenocopies, full penetrance
11	.0025	.0050	1.0000	1.0	25.7	Dominant, half of cases are phenocopies
12	.0101	.0000	.5000	.5	25.4	Dominant, reduced penetrance
13	.0100	.0000	.5000	1.0	25.8	Additive, no phenocopies, full penetrance
14	.0100	.0050	.5000	1.0	25.3	Additive, half of cases are phenocopies
15	.0200	.0000	.2500	.5	13.3	Additive, reduced penetrance
16	.1000	.0000	.0000	1.0	10.0	Recessive, no phenocopies, full penetrance
17	.0709	.0050	.0050	1.0	4.3	Recessive, half of cases are phenocopies
18	.1414	.0000	.0000	.5	7.1	Recessive, reduced penetrance
K=.001:
19	.0005	.0000	1.0000	1.0	500.4	Dominant, no phenocopies, full penetrance
20	.0003	.0005	1.0000	1.0	250.7	Dominant, half of cases are phenocopies
21	.0010	.0000	.5000	.5	250.4	Dominant, reduced penetrance
22	.0010	.0000	.5000	1.0	250.7	Additive, no phenocopies, full penetrance
23	.0010	.0005	.5000	1.0	250.3	Additive, half of cases are phenocopies
24	.0020	.0000	.2500	.5	125.8	Additive, reduced penetrance
25	.0316	.0000	.0000	1.0	31.6	Recessive, no phenocopies, full penetrance
26	.0224	.0005	.0005	1.0	11.9	Recessive, half of cases are phenocopies
27	.0447	.0000	.0000	.5	22.4	Recessive, reduced penetrance

For each statistic and each model, we used the conditional IBD probabilities described above to compute the sample size (number of sibships of a given size) needed to obtain 80% power with a significance level of .001, using the Z-test. The formula that we used is

where σ₀ and σ₁ are the SDs of the statistic under the null and alternative hypotheses, respectively, and where μ₀ and μ₁ are the corresponding means. We used z_α=3.09 and z_β=0.84. We note that this assumes normality of the statistics but does take account of the fact that they might have different variances under the null and alternative hypotheses. By computing power analytically under the assumption of normality, we fail to account for the fact that some statistics will have skewed distributions for modest sample sizes and thus will have higher power. However, since that higher power is accompanied by higher false-positive rates, we feel that the analytical calculation provides a more appropriate comparison. In a sense, the “fairest” power comparison would be a simulation study using empirical significance cutoffs, but, since empirical cutoffs are seldom used in real studies, it is not clear that such an approach has much more relevance than the much-simpler normality-based comparisons. This issue has also been discussed theoretically by McPeek (1999), and the results of Davis and Weeks (1997) give some indications of how large the effect of the skewness is on the false-positive rates and on the power of some of the statistics.

Results

As indicated in table 1, several groups of statistics are analytically equivalent over all sibship sizes (including sizes larger than five). The R criterion (Green and Woodrow 1977), Sobel and Lange's (1996) statistic A, and recessive LOD scores with penetrance vector (.00, .00, .50) form one such group and are referred to by the label “the R criterion” for the remainder of this paper. The N criterion (Green and Woodrow 1977) and the parental-allele–difference statistic (Abel et al. 1998) form a second group, and we refer to them by the label “the N criterion.” S_pairs (Whittemore and Halpern 1994) and Sobel and Lange's (1996) statistic D form a third group, referred to as “S_pairs.” Furthermore, there are additional equivalencies within the smaller sibship sizes. These can be seen clearly in tables 3–6. For example, table 3 shows that the R criterion, N criterion, S_pairs, S+L C, S_robdom, and S_all statistics are all equivalent for a sibship of size two.

Tables 3–6 also show some basic differences among the statistics. For two siblings, the R criterion, which is the usual mean sharing statistic, considers IBD sharing of one allele to be neutral and derives its linkage information from the relative frequencies of pairs sharing zero and two alleles IBD. This characterization of the mean sharing statistic is fairly well known, but table 3 also allows us to see how the other statistics compare to that. For example, S_-#geno and F+S, statistics that were developed with recessive models in mind, both give negative scores to IBD sharing of one, and we can see that S_-#geno scores it more negatively than does F+S, suggesting that it is a more “recessive” statistic. We can also see surprisingly large differences in the normalized coefficients for the two dominant LOD scores, suggesting that there might be nontrivial power differences between them. For three siblings (table 4), similar patterns are discernible; note that only one statistic, S_-#geno, considers configuration 3a (13 13 24) as providing evidence in favor of linkage. For sibships of sizes four and five (tables 5 and 6), we can see that there is quite a broad range of statistics. One important way to characterize this range is in terms of how high a score each statistic gives to the lower-order–IBD-sharing configurations. For example, considering table 5, we see that the R criterion is the most extreme in this sense, giving positive scores only to the top three sharing configurations and quite negative scores to all the other configurations. It is followed, roughly in this order, by S_robdom, S_all, S+L C, and S_pairs, each of which gives progressively higher scores to configurations 4a and 4b (table 5). The dominant LOD scores are somewhat similar to the R criterion, except that they, unlike the statistics just listed (except S_all), distinguish between configurations 4a and 4b and between configurations 6a and 6b. Similar patterns are seen in table 6. We might expect that statistics, such as the R criterion, that give high scores only to very-high–IBD-sharing configurations will be most powerful for simple genetic models and small values of q. When phenocopy rates are high and/or the marker is farther from the trait locus, we expect that the average IBD sharing will be less, and thus we might get more power from statistics that give somewhat stronger scores to lower-order–IBD-sharing configurations.

Tables 8–11 show our detailed sample sizes for models 1–9 (the models with population trait frequency [K] of 10%) for a recombination fraction (θ) of 0. The sample sizes underlined in these tables are the minima for each model specified.

Table 8.

Approximate Sample Sizes, for Two Affected Siblings

	No. of Familiesa
Model	R criterionb	S+L B	S-#geno	F+S	ldom(.1)	ldom(.01)
Dominant:
1	42	55	70	51	41	45
2	60	82	100	73	61	67
3	64	91	101	75	65	73
Additive:
4	61	81	103	74	61	67
5	112	155	182	133	114	127
6	120	167	195	142	122	137
Recessive:
7	27	64	29	26	32	42
8	39	110	37	34	49	68
9	51	105	60	51	59	74

^aSample sizes that are underlined are the minima for the model.

^bFor two siblings, the R criterion, the N criterion, S_pairs, S+L C, S_robdom, and S_all are all equivalent.

Table 9.

Approximate Sample Sizes, for Three Affected Siblings

	No. of Familiesa
Model	R criterionb	S+L B	S-#geno	F+S	ldom(.1)	ldom(.01)
Dominant:
1	19	20	28	22	18	19
2	21	22	32	25	20	21
3	35	38	50	39	35	36
Additive:
4	35	37	54	41	35	36
5	41	45	65	48	41	42
6	78	87	124	91	80	83
Recessive:
7	22	34	31	23	26	29
8	20	32	25	19	23	27
9	49	68	71	51	56	60

^aSample sizes that are underlined are the minima for the model.

^bFor three siblings, the R criterion, the N criterion, S_pairs, S+L C, S_robdom, and S_all are all equivalent.

Table 10.

Approximate Sample Sizes, for Four Affected Siblings

	No. of Familiesa
Model	R criterion	N criterion	Spairs	S+L C	Srobdom	Sall	S+L B	S-#geno	F+S	ldom(.1)	ldom(.01)
Dominant:
1	14	24	15	14	14	14	18	21	17	13	13
2	13	19	13	13	12	13	16	20	15	12	12
3	31	52	34	32	31	32	41	44	36	30	30
Additive:
4	31	43	32	31	31	31	39	49	37	32	32
5	29	37	28	28	28	28	34	44	32	29	29
6	78	97	75	74	74	73	93	118	85	78	79
Recessive:
7	29	51	33	31	29	31	49	50	34	33	33
8	20	29	21	20	19	20	32	30	21	22	23
9	70	128	80	74	71	74	114	126	86	78	78

^aSample sizes that are underlined are the minima for the model.

Table 11.

Approximate Sample Sizes, for Five Affected Siblings

	No. of Familiesa
Model	R criterion	N criterion	Spairs	S+L C	Srobdom	Sall	S+L B	S-#geno	F+S	ldom(.1)	ldom(.01)
Dominant:
1	13	24	17	15	13	15	21	22	19	13	13
2	10	15	12	11	10	10	14	16	13	10	10
3	35	61	45	40	36	38	54	53	46	34	34
Additive:
4	36	40	34	33	33	32	42	53	39	35	35
5	28	29	25	24	25	24	30	40	29	27	27
6	94	90	79	78	81	77	98	127	90	88	90
Recessive:
7	46	92	64	56	48	53	91	101	69	52	50
8	26	41	31	29	26	28	45	49	33	29	29
9	117	245	168	146	123	137	233	269	183	134	127

^aSample sizes that are underlined are the minima for the model.

Table 8 shows that, for the families with two siblings, the R criterion and ldom(.1) are more powerful than the remaining statistics, under dominant and additive models. Under recessive models, F+S and the R criterion are the most powerful statistics. Overall, the R criterion seems to be the most robust statistic, approximately equaling the power of the best statistic(s) for each trait model. The S+L B and S_-#geno statistics are fairly suboptimal over almost all models. These results also hold true for the rarer-trait models, which we have not shown in detail, except that, for very-rare recessive traits, S_-#geno and F+S are the best statistics.

Table 9 shows that, for the families of three siblings, all the statistics except S_-#geno and F+S perform almost the same under dominant and additive models. For dominant and additive models with reduced penetrance (i.e., models 3 and 6), the S+L B statistic does not perform as well as those best statistics. For the recessive models, F+S and the R criterion are better than the other statistics. Overall, as in the case of families with two siblings, the R criterion appears to be the most robust statistic, having close to the best power for each model. These results also hold true for the rare-trait models that we have not shown in detail, except that F+S is the most powerful statistic for rare-recessive-trait models. For three siblings, S_-#geno is not as good as most other statistics, for rare recessive traits.

Table 10 shows that, for all dominant and additive models, all the statistics except the N criterion, S+L B, S_-#geno, and F+S perform almost the same for the families with four siblings. Under the recessive models, the N criterion, S+L B, and S_-#geno do not perform as well as the other statistics. S_robdom also performs well under the recessive models. As K decreases, under many dominant, additive, and recessive models, the R criterion, S+L C, S_robdom, S_all, and both ldom statistics perform almost the same. Again, the R criterion appears to have the most robust power overall. Results for rarer-trait models are similar, except that, for rare-recessive-trait models, F+S is no longer any better than the R criterion.

Table 11 shows that, under dominant models, the R criterion, S_robdom, and both ldom statistics perform better than the other statistics, for the families with five siblings. Under additive models, S+L C, S_robdom, and S_all are better than the other statistics. For the recessive models, the R criterion and S_robdom statistics do perform better than the other statistics. In general, the R criterion, S_robdom, and both ldom statistics perform well for dominant and additive models. Overall, results for families with five siblings are very similar to those for families with four siblings.

Tables 12–15 show selected sample sizes for the cases in which θ>0, as well as for the cases in which θ=0. The sample sizes underlined in these tables are also the minima for each model specified. For clarity, we show results only for a few representative models and for the better-performing statistics. Not surprisingly, the sample sizes necessary in the case of θ>0 increase substantially over those necessary in the case of θ=0. There are also some important differences in which of the statistics have highest power. As predicted, there is a shift, in power, from the R criterion to some of the statistics—such as S+L C, S_all, and S_robdom—that give higher scores to lower-order–IBD-sharing configurations. This effect is minor for θ=.05 but is quite substantial for θ=.20. The dominant LOD scores also lose power, relative to the other scoring functions, when θ>0. The statistics that perform uniformly poorly when θ=0 continue to do so when θ>0.

Table 12.

Approximate Sample Sizes, for Two Affected Siblings, for θ⩾0

	No. of Familiesa
θ	R criterionb	ldom(.1)	ldom(.01)
Model 3:
.00	64	65	73
.05	99	102	116
.10	160	166	189
.20	514	537	614
Model 6:
.00	120	122	137
.05	185	190	214
.10	298	308	349
.20	950	992	1,131
Model 9:
.00	51	59	74
.05	79	89	111
.10	128	142	173
.20	407	442	525

^aSample sizes that are underlined are the minima for the model.

^bFor two siblings, the R criterion, the N criterion, S_pairs, S+L C, S_robdom, and S_all are all equivalent.

Table 13.

Approximate Sample Sizes, for Three Affected Siblings, for θ⩾0

	No. of Familiesa
θ	R criterionb	ldom(.1)	ldom(.01)
Model 3:
.00	35	35	36
.05	54	54	56
.10	87	88	91
.20	272	281	291
Model 6:
.00	78	80	83
.05	120	123	127
.10	191	198	204
.20	598	626	646
Model 9:
.00	49	56	60
.05	74	83	90
.10	118	131	140
.20	368	399	420

^aSample sizes that are underlined are the minima for the model.

^bFor three siblings, the R criterion, the N criterion, S_pairs, S+L C, S_robdom, and S_all are all equivalent.

Table 14.

Approximate Sample Sizes, for Four Affected Siblings, for θ⩾0

	No. of Familiesa
θ	R criterion	Spairs	S+L C	Srobdom	Sall	ldom(.1)	ldom(.01)
Model 3:
.00	31	34	32	31	32	30	30
.05	49	51	49	48	49	48	48
.10	81	81	79	78	79	80	81
.20	267	250	247	251	248	265	268
Model 6:
.00	78	75	74	74	73	78	79
.05	120	113	112	113	111	121	122
.10	194	179	178	181	178	195	197
.20	620	554	555	571	555	621	630
Model 9:
.00	70	80	74	71	74	78	78
.05	110	119	113	110	113	120	121
.10	182	188	181	178	181	195	197
.20	605	577	568	573	568	631	638

^aSample sizes that are underlined are the minima for the model.

Table 15.

Approximate Sample Sizes, for Five Affected Siblings, for θ⩾0

	No. of Familiesa
θ	R criterion	Spairs	S+L C	Srobdom	Sall	ldom(.1)	ldom(.01)
Model 3:
.00	35	45	40	36	38	34	34
.05	59	66	61	57	60	57	57
.10	102	104	98	95	96	97	98
.20	370	317	308	320	309	344	351
Model 6:
.00	94	79	78	81	77	88	90
.05	147	119	117	125	117	137	141
.10	241	188	186	201	187	223	230
.20	791	577	578	641	585	724	748
Model 9:
.00	117	168	146	123	137	134	127
.05	198	250	224	198	213	218	209
.10	349	392	361	335	349	371	361
.20	1,319	1,201	1,153	1,167	1,142	1,315	1,310

^aSample sizes that are underlined are the minima for the model.

Discussion

We have compared the power of a large number of scoring functions for construction of allele-sharing statistics for affected sibships. Perhaps the most important result is that the scoring function that is most often used for such studies, S_all, performs very well; for almost all of the situations that we examined, it has power at or near the maximum. We found the R criterion to be somewhat better when θ=0, but, for slightly larger values of θ, S_all, S_robdom, and S+L C all did as well as the R criterion. For very large values of θ , these other statistics did better than the R criterion, and S_pairs also did well. The difference in our results as θ varies suggests that one might actually want to choose one’s statistic on the basis of study design and marker informativeness. We considered a fully informative marker, but, if the marker is not fully informative, the result is very similar to that of increasing θ—that is, a degradation of the IBD information and an increase in the frequency of sibships with lower-order–IBD-sharing configurations. In a typical situation, say a genome scan with 10-cM spacing and moderately informative markers, it might be reasonable to take our results for θ=.05 as most realistic. In that case, our results suggest that any of the statistics R criterion, S+L C, S_all, and S_robdom would perform close to equivalently. The R criterion might have a slight edge, but the others are more readily available in software. However, if one were using very uninformative markers or, more likely, using siblings without parental genotypes, the quality of the IBD information might be substantially degraded. In that case, our results for larger values of θ would be more relevant. Our results show that S+L C is generally the best scoring function when θ=.20 but that S_all and S_pairs perform only slightly worse. It seems likely that, if the marker spacing and/or quality of the IBD information were even worse than that in any of our scenarios, S_pairs would be a good choice, since it scores the lesser IBD-sharing configurations slightly higher than does S+L C.

The recessive LOD-score statistics, being equivalent to the R criterion, did surprisingly well over all models. This is consistent with the results reported by Davis and Weeks (1997), who observed that the SIBPAIR program of J. Terwilliger (Satsangi et al. 1996), which computes a LOD score under a recessive model, was quite powerful for sibships of mixed size, over a range of multilocus genetic models. The dominant LOD-score statistics that we examined were reasonably powerful for dominant and additive models, predictably doing best in the cases in which the trait model was close to the model under which the LOD score was calculated. However, even for the dominant and additive models, the dominant LOD-score statistics did not have power higher than that of some of the other statistics (e.g., the R criterion) that also performed well for recessive models. Thus we do not endorse the dominant LOD scores as among the most robust choices. We should note that we do not consider these results to be a full comparison of “parametric” and “nonparametric” approaches, since we considered only the LOD scores at θ=0 and since we did not consider unaffected individuals in any of the pedigrees studied. Our intent was primarily to evaluate the LOD scores as scoring functions within the context of a nonparametric analysis. Both Abreu et al. (1999) and Sham et al. (2000) recently looked at parametric and nonparametric approaches for complex traits on small pedigrees. It is difficult, however, to compare our results to theirs (or theirs to each other), because of major differences in the types of parametric analyses used.

A few of the scoring functions that we evaluated cannot be recommended for any situation. S_-#geno, the N criterion, and S+L B had consistently poor performance over all models, with the single exception that S_-#geno was powerful for rare recessive traits in sib pairs.

We have described most of our results in terms of which statistics had robust power over many models. We should reiterate that the exception to the robustness was always the rare-recessive-trait models (models 25–27). This issue was discussed in greater depth (with a focus on sib pairs) by Blackwelder and Elston (1985) and Feingold and Siegmund (1997). For rare-recessive-trait models, most of the commonly used statistics do not have good power, and special recessively oriented statistics do much better. “Rare recessive” in this case means any trait caused by recessive action of a rare allele. The disease itself need not be rare—for example, in the case of heterogeneity or phenocopies. This special property of rare recessive loci holds only when the allele acts close to purely recessively, and it does not usually hold when there is any amount of heterozygote disadvantage. Thus we feel that using a statistic that is known to work well for all but the rare-recessive-trait case is a good general strategy for complex-trait mapping. However, investigators should be aware that, if they are actually looking at something that is likely to be due to a rare recessive allele, they should not be using these general-purpose statistics. The F+S statistic that we have evaluated here is an “all pairs” version of a statistic proposed by Feingold and Siegmund (1997) for sibling pairs. The sibling-pair statistic was designed to have robust power for both rare-recessive-trait and other models. Our results here show that it does indeed perform quite well for sibling pairs and trios, having, for rare-recessive-trait models, the best power of all the statistics and, for other models, power only slightly lower than that of the best statistics (especially when θ>0). However, this performance did not hold up for sibships of sizes four and five. This is probably due to the limitations of the “all pairs” form, which tends to give high scores to lower-order–IBD-sharing configurations. It is possible that a different adaptation of the statistic proposed by Feingold and Siegmund (1997) could do better—for example, by using the scores that our F+S statistic gives to the higher-order–IBD-sharing configurations but arbitrarily lowering the scores for the lower-order–IBD-sharing configurations to something like what S_all uses.

We do not feel the need to recommend a strategy of using different statistics for different sibship sizes, because we did not find large differences with respect to which statistics are best for different sibship sizes. For sibships of sizes two and three, most of the statistics that performed best are equivalent, and the results for sibships of sizes four and five were similar to each other. However, our results are restricted to sibships. It is not necessarily true that the statistics that are best for sibships would be best for extended pedigrees. The literature comparing general-pedigree statistics (e.g., see Kruglyak et al. 1996; Davis and Weeks 1997; McPeek 1999; Feingold et al. 2000) has, in general, found S_all to be very good for most models, but this result does depend on the type of pedigree. Davis et al. (1997) found that, in situations in which the disease allele is likely to have entered the pedigree more than once (e.g., a recessive disease with a fairly common allele), S_pairs does much better than S_all. Additionally, McPeek (1999) found S_robdom to be very powerful for a pedigree consisting of a sib pair with an affected parent.

Finally, although we have dealt primarily with the issue of which statistic(s) is best for each sibship size, our results also shed some light on the relative value of sibships of different sizes. We found, similarly to previous studies (e.g., Sham et al. 1997; McPeek 1999; Holmans 2001), that larger affected sibships are not necessarily as powerful as one might expect. For the rare-allele models that we examined (i.e., models 19–24), sibships of sizes three, four, and five were roughly equal to 3, 5, and 10–15 sibling pairs, respectively; but, for the more common-allele additive and dominant models (i.e., models 1–6), the sibships of sizes three, four, and five were all worth approximately two sibling pairs. For the common recessive models (i.e., models 7–9), which have the highest allele frequencies, sibships of sizes four and five were worth considerably less than a sibling pair. On the surface, this observation seems to conflict with the common wisdom that larger pedigrees are much more powerful than small ones, but the explanation is that, under many models, a large number of affecteds in a sibship indicates multiple copies of the disease allele, which decreases power. Thus a large extended pedigree should, in fact, have higher power than does a small pedigree, although a pedigree with an unusually large percentage of affecteds might suffer from the same power loss that we see for large affected sibships. All of these results assume that there is no information or selection based on parental phenotypes. If one were, for example, to eliminate pedigrees with two affected parents, then the relative value of large sibships would increase.

The relative values of the sibships of different sizes translate directly into recommended weights for combining them in an overall statistic. Since the optimal weights depend on the trait model, we again favor an approach of trying to find weights that seem robust over a variety of models. Clearly, however, this is a difficult task, since we see such a broad range of relative values for the different-sized sibships. McPeek (1999) noted this problem as well. The literature on pairwise statistics has a long history of examining the weighting question, and a number of authors (e.g., Abel et al. 1998; Holmans 2001) have found high power, for a variety of models, for the so-called 2/N weighting scheme originally proposed by Suarez and Hodge (1979). This scheme equates a sibship of size N with N-1 sibling pairs, which is certainly within the range of what our results suggest. If it is assumed that a typical nuclear-family study will consist of a large number of affected sib pairs, a somewhat smaller number of trios, and relatively few larger sibships, then it is really the weight given to sib trios that is most important. Essentially all of the studies described above, including our own, put that weight in a range of 2–3; this suggests that a good robust statistic could be formed by weighting a sib trio as 2.5 sib pairs and assigning larger sibships almost any reasonable weight.

Finally, we remind the reader that the results presented here are analytical and are based on normality assumptions (which are satisfied if the number of families is large enough). The analytical approach also implicitly assumes that P values for the statistics are computed accurately. In real use, statistics with skewed distributions will have higher false-positive rates and higher apparent power. In addition, accurate P-value computation can be computationally intensive, and so, in their P-value computations, some software packages take shortcuts that may result in conservative P values; use of conservative P values may result in power lower than that which we have presented here. Thus, when one actually applies these statistics to real data, one must be cautious about the potential limitations of the software implementations. For example, GENEHUNTER (Kruglyak et al. 1996) uses a perfect-data approximation to compute P values that can be quite conservative (as clearly described by those authors). Similarly, SimWalk2 (Sobel and Lange 1996) currently uses simulation on underlying inheritance vectors to generate P values that may be conservative, depending on the level of marker informativity. Caveat emptor.