The Ising Model in Physics and Statistical Genetics

Abstract

Interdisciplinary communication is becoming a crucial component of the present scientific environment. Theoretical models developed in diverse disciplines often may be successfully employed in solving seemingly unrelated problems that can be reduced to similar mathematical formulation. The Ising model has been proposed in statistical physics as a simplified model for analysis of magnetic interactions and structures of ferromagnetic substances. Here, we present an application of the one-dimensional, linear Ising model to affected-sib-pair (ASP) analysis in genetics. By analyzing simulated genetics data, we show that the simplified Ising model with only nearest-neighbor interactions between genetic markers has statistical properties comparable to much more complex algorithms from genetics analysis, such as those implemented in the Allegro and Mapmaker-Sibs programs. We also adapt the model to include epistatic interactions and to demonstrate its usefulness in detecting modifier loci with weak individual genetic contributions. A reanalysis of data on type 1 diabetes detects several susceptibility loci not previously found by other methods of analysis.

Introduction

The Ising model (Ising 1925) was originally proposed to explain the structure and properties of ferromagnetic substances. Since the model allows for simplification of complex interactions, it has since been successfully employed in several areas of science: elasticity theory of DNA (Ahsan et al. 1998), hydrophobicity of protein chains (Irback et al. 1996), cooperativity between ion channels (Liu and Dilger 1993), the thermodynamic theory of codon bias in genes (Rowe and Trainor 1983), and several others.

The Ising model may be used to analyze genetic data from affected sib pair (ASP) studies. The data structures of the two systems are identical. Each data point may be represented by a +1 or −1 corresponding to up and down spin states of a magnetic dipole or to an allele being shared and not shared by a sib pair, respectively. The physical interactions between adjacent dipoles are analogous to linkage between adjacent genetic markers on a chromosome. The effect of an applied external magnetic field, acting to align magnetic particles in the direction of the field, is analogous to the effect of a disease gene, causing increased allele sharing at nearby loci.

Analyzing genetic data using the Ising model allows simultaneous consideration of all markers on a chromosome and has the potential to be an effective multipoint ASP analysis method. Multipoint analyses have the advantage of extracting maximum identity-by-descent (IBD)–sharing information from a system where not all markers are fully informative. By considering adjacent markers jointly, multipoint methods also have a lower overall genomewide type I–error rate, because they eliminate spurious peaks due to random variation in individual markers. Below, we demonstrate that the performance of the Ising model is equivalent to that of Allegro (Gudbjartsson et al. 2000), a leading genetics-analysis program, and, in the example considered here, surpasses that of Mapmaker-Sibs (Kruglyak and Lander 1995), another popular analysis package.

Moreover, the Ising model is easily adapted to the analysis of complex genetic models with several genetic effects and with interaction, or epistasis, between the genes. The debate over the use of multilocus search strategies versus the conventional single-locus searches is an ongoing one (see, e.g., Risch 1990; Schork et al. 1993; Cordell et al. 2000). Some complex genetic disorders will either not benefit from multilocus strategies, or the power for their detection may decrease, relative to the power of single-locus methods. However, it is becoming increasingly clear that at least some underlying disease genes will be much easier to detect by joint consideration of the effects of all interacting loci. Several researchers have focused on the development of simultaneous multilocus methods (see Cordell et al. 2000 for a summary). Although many of the current methods are effective in certain situations, they often suffer from computational or mathematical limitations, particularly when more than two genes are considered jointly. The development of a flexible multilocus, nonparametric linkage analysis method is far from complete. Here, we demonstrate the usefulness of the Ising model as both an effective method in conventional nonparametric linkage analysis and a flexible tool for analysis of complex genetic interactions.

Methods

The Ising Model in Physics

In its most general form, the Ising model applies to an ensemble of magnetic particles interacting with each other in the presence of an applied external magnetic field. Here, we use the one-dimensional model, in which the particles are arranged in a chain and are limited to directly interacting only with their nearest neighbors. The external field is a “point” field acting on a given particle. At a particular position (t) along the chain, each particle has a spin value of +1 or −1 (representing parallel or antiparallel alignment with the field). We denote this spin value as x(t). The configuration of the entire chain {x(t)} is determined by specifying x(t) at all positions t. The energy of the configuration of m particles can then be expressed as

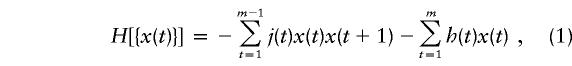where j(t) is the coupling strength between spins x(t) and x(t+1) and h(t) is the local magnetic field at position t. According to statistical mechanics, the probability of observing a specific configuration is given by

where k is the Boltzmann constant, T is the temperature of the chain, and Z is the partition function equal to the sum of energies of all possible configurations:

An applied external magnetic field will cause ferromagnetic particles to align in the direction of the field, with neighboring particles aligning in the same direction. The effect of temperature is to introduce additional randomness into the system. The degree of magnetization of the chain is determined by the strength of the field and coupling energy, relative to the thermal energy.

Adaptation to Genetic Data

For pairs of affected siblings, the main statistic of interest is the number of alleles shared IBD. For a given marker locus, each parent of an ASP either does (x=1) or does not (x=-1) pass the same allele to the two offspring. Thus, the data may be represented in the form of a simple n⋅m matrix with rows corresponding to n parents and columns corresponding to m marker loci. For a given parent i, the status of IBD sharing for each typed marker on a chromosome corresponds to the ith row, and is analogous to a configuration of m particles in the Ising model. It is assumed that the data for each parent represent an independent draw from an underlying probability distribution.

We model the distribution of {x(t)} by P[{x(t)}] given in equations (1) and (2). The first term in equation (1), j(t), represents the fact that if a marker is shared IBD the neighboring markers have an increased chance to be also shared because of genetic linkage. The second term, h(t), is the actual parameter of interest to genetic studies, since a local magnetic field at position t is analogous to a genetic effect causing an increase in IBD sharing at the t locus. In affected siblings, increased IBD sharing is a result of proximity of a causative disease gene. For a simple Mendelian disease, there will be an apparent strong “field” close to the disease gene. For a complex disease, there may be multiple genes that influence the disease with variable strengths. Thus, the model may contain as many as m+m-1=2m-1 parameters, where m is the number of markers. If epistatic interactions between genes are to be considered, the model will consist of additional interaction terms.

There is no direct analogy relating the temperature (T) and the Boltzmann constant (k) in thermodynamics to genetic parameters. The model parameters j/kT and h/kT, which in physical systems correspond to the strength of magnetic coupling and the strength of the applied field relative to the thermal noise of the system, may be respectively viewed as the extent of genetic linkage between markers and the effect of the disease locus in distorting allele sharing, relative to random genetic and environmental effects.

Parameter Estimation and Significance Testing

For a given parent i, the probability of observing a particular IBD sharing configuration, {x_i(t)}, is given by P[{x_i(t)}]. Since the observations for each parent are independent, the probability of observing the entire parent ⋅ IBD-sharing matrix, is the product:

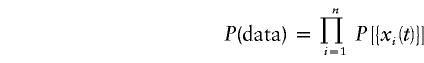This is equivalent to the likelihood, L[{j(t)},{h(t)}]. The parameters of the model, j(t) and h(t) are estimated by use of maximum likelihood—that is, maximizing the probability of observing a particular data set. We implemented the Powell method (Press et al. 1990) to maximize the multivariate likelihood function.

The likelihood function is dependent on Z (eq. [3]), the partition function of the Ising model. The partition function is the sum of the Boltzman weights of all possible configurations of the data set. Since the number of configurations is equal to 2^nm, the running time of the maximization procedure should increase exponentially with the size of the data set. Fortunately, the partition function for the Ising model with only nearest-neighbor interactions can be calculated recursively in linear time (Reichl 1980). The algorithm is outlined in Appendix A.

After maximization of all relevant parameters, the significance of a hypothesis is tested by the likelihood ratio (LR) test. Under the simplest hypothesis of one disease locus at position t₁, only one effect parameter, h(t₁), is maximized in the numerator, whereas all the other effects are kept equal to zero. This gives an LR test with 1 df:

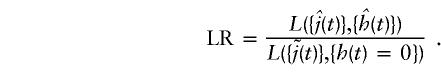Since the genetic effect can only take on positive values, under the null hypothesis of no linkage and no interaction, 2ln(LR) is asymptotically distributed as a 50% mixture of a point mass at zero and a χ² distribution with 1 df. Because we are not interested in the coupling parameters, {j(t)}, we treat them as nuisance parameters, maximizing {j(t)} separately in both the numerator and denominator. This strategy is equivalent to simultaneous estimation of disease-locus position and recombination rates from the data.

In the epistatic model (see the Data and Simulation section), two genetic-effect loci and their interaction are considered jointly. Equation (1) must be modified by an additional interaction term, j(int)·x(t₁)·x(t₂), where t₁ and t₂ are the positions of the two interacting genes, and j(int) is the interaction parameter. In the LR test, two effect parameters, h(t₁) and h(t₂), and the interaction parameter j(int) are estimated by maximum likelihood in the numerator. The locus t₁ is the main effect locus, which is easily identified. Since its position is already known, we treat its effect h(t₁) as a nuisance parameter (i.e., we maximize its value separately in both the numerator and the denominator). This results in an LR test with 2 df:

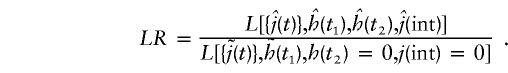Since the genetic effect can only take on positive values, but the interaction term can be either positive or negative, under the null hypothesis of no linkage and no interaction, 2ln(LR) is asymptotically distributed as a 50% mixture of χ² with 1 df and χ² with 2 df. Note that this is the simplest possible example of two-locus epistasis. When additional interaction coefficients and effect loci are added, the model can easily be extended to more-complex genetic systems.

Missing Data and Undetermined IBD-Sharing States

When one or both of the parents are not genotyped, or the markers are not fully informative, the IBD sharing state may be impossible to determine with certainty. In cases with unknown IBD sharing, we calculate the likelihood under the assumption of the unknown state being either +1 or −1. That is, the probability of observing the data is given as the sum of the probabilities for the two possible cases, weighted by any additional information about the IBD sharing (e.g., the knowledge of population allele frequencies or typed unaffected sibs):

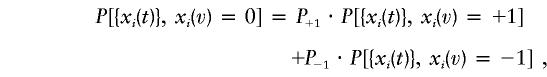where x_i(v)=0 indicates unknown IBD sharing at position v, and P₊₁ and P₋₁ are the probabilities that the undetermined state has a value of +1 or −1, respectively. In this article, all data consists of fully typed parents and sibs, where no additional information can improve the knowledge of IBD sharing, and the two weights (P₊₁ and P₋₁) are set equal.

When multiple unknown IBD states are present within the data set, the running time of the likelihood calculation should increase exponentially with the amount of missing data. However, it is possible to calculate the likelihood in linear time with respect to the total number of marker loci, by use of an algorithm similar to the one used for calculating the partition function (Appendix A).

Data and Simulation

To model an individual genetic effect, we used the program SIMNUCLEAR to simulate a disease trait and genotypes for 100 sib pairs. The data were simulated under the assumption of no dominance variance, heritability, h²=0.06, shared environment variance of 0.40, and the “affected” phenotype cutoff defined as the most extreme 0.01 of the quantitative phenotype. Genotypic data was simulated for parents and children. All marker loci were assumed to have six alleles with equal frequencies. The resulting unambiguous IBD determination rate was ∼75%. IBD sharing status was determined using the sib_ibd module of the ASPEX package, and the single-point IBD-sharing states were then processed using the Ising model to produce a multipoint statistic. For type I–error analysis, null data were simulated as above but without any genetic effect on the quantitative phenotype. This data set was designed to test the effectiveness of the Ising model as a multipoint allele-sharing statistic, as well as the model's ability to extract information from data where IBD sharing cannot always be uniquely determined.

The second data set, used for detection of a weak locus with epistatic interactions, is described in detail by Lucek et al. (1998). Briefly, the genetic model consists of a main-effect locus and a modifier locus (table 1). The main-effect gene is responsible for a majority of the observed disease phenotype. It is easily detectable. The modifier locus, however, has very low expected excess IBD sharing (0.52, vs. the 0.5 expected by chance) and is very hard to detect by ordinary methods. Data for two chromosomes, each consisting of 10 equally spaced (10 cM) markers, were simulated for 2,000 sib pairs. The main effect locus was tightly linked to marker 5 on chromosome 1, whereas the modifier locus was linked to marker 5 on chromosome 2. All parents were heterozygous for distinct marker alleles, and, hence, IBD sharing was always uniquely determined. The data set was used to produce bootstrap replicates of 250 sib pairs each. Then 2,000 bootstrap replicates were used to assess the power to detect linkage at the weak modifier locus. Type I error was estimated using the genetic data described above for chromosome 1, but data for chromosome 2 were generated randomly, without linkage to a disease locus.

Table 1.

Inheritance Model for an Epistatic Two-Locus Trait^[Note]

	Locus 2
Locus 1	BB	Bb	bb
AA	0	0	0
Aa	0	0	1
aa	1	1	1

Note.— Locus 1 is recessive, given genotypes BB and Bb at locus 2, and is dominant, given genotype bb. Disease-allele frequencies are set at p(a)=.01 and p(b)=.02.

The third and final data set comprises real data from the insulin-dependent diabetes mellitus (IDDM) genome screen (Mein et al. 1998): 356 genotyped sib pairs and parents, with an average intermarker distance of about 10 cM. We use these data to demonstrate the usefulness of the Ising model both as a single-locus and as a two-locus (by conditioning on the strong effect of the HLA locus) analysis method.

Results

Multipoint Allele Sharing

We declared linkage to the disease locus if a LOD score exceeded a predetermined cutoff level at any point within a 20-cM interval centered at the locus. This criterion is representative of a study aiming to confirm a previously suggested linkage result. We compared the performance of the Ising model and two leading nonparametric genetic analysis programs: Allegro (Gudbjartsson et al. 2000) and Mapmaker-Sibs (Kruglyak and Lander 1995). We also calculated a single point χ² statistic for the number of shared and nonshared alleles at each marker location. Typical results are shown in figure 1. The power analysis, based on 20,000 replicates of simulated data and various significance cutoffs, corresponding to suggestive, significant, and highly significant linkage (Lander and Kruglyak 1995), is summarized in table 1. Note that the maximum-likelihood statistic (MLS) score in Mapmaker-Sibs is not equivalent to the 1-df likelihood-ratio test score. A correction to the significance cutoff was applied according to Nyholt (2000). For the χ² statistic, the corresponding LOD is calculated using 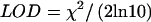. The results in table 2 are for a 2-cM–density marker map.

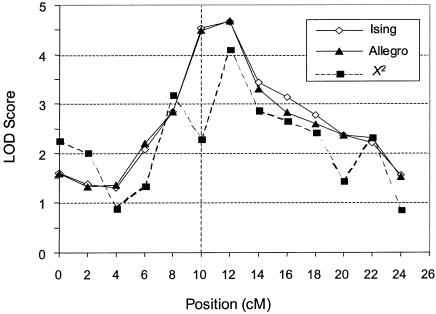
Figure 1.

Example of a typical LOD-score curve comparing the performance of the Ising model, Allegro, and the single point χ² statistic. The disease locus is situated at position 10 cM. The behavior of the Ising model and that of the Allegro exponential pairs statistic are virtually identical. The single-point allele-sharing method has considerably lower power and is subject to greater local fluctuations.

Table 2.

Comparison of IBD Allele-Sharing Statistics^[Note]

	Power at LOD Score Cutoff				Intervalwise Type I Error at Cutoff
Model	2.19 (2.45)	3.00 (3.28)	3.63 (3.93)	5.30 (5.76)	.59 (0.74)	1.18 (1.38)	1.44 (1.66)	2.19 (2.45)
Ising	.834	.654	.497	.178	.151	.041	.023	.005
Allegro (ZLR)	.836	.652	.505	.176	.151	.041	.023	.005
Mapmaker-Sibs (MLSpt)	.818	.646	.495	.168	.165	.045	.026	.005
χ2	.811	.618	.438	.121	.221	.062	.037	.007

Note.— The cut-off levels in parentheses refer to the equivalent MLS_PT score in Mapmaker-Sibs.

Power analysis (table 2) and examination of individual LOD score plots (see fig. 1) shows that the Ising statistic and the Z_LR exponential pairs (Allegro) statistic are practically equivalent. The performance of the Mapmaker-Sibs MLS_pt (the full possible triangle, without the “no dominance” restriction) statistic was inferior to the Z_LR and Ising statistics. The power of the MLS_pt was significantly lower (but note that the difference is small) than that of the Ising statistic (P<.05) at all levels except for the LOD = 3.63 cutoff. As expected, all multipoint methods are superior to the single-point χ² statistic.

In type I–error analysis, a false-positive result was declared when a LOD score exceeded a predetermined cutoff level within a simulated interval of 20 cM, unlinked to the disease locus. This “intervalwise” false-positive rate corresponds to a study aiming to confirm linkage described above and is a useful measure of error for comparison of different multipoint methods. Lower significance cutoff levels were used for type I–error analysis than for power analysis, because the false-positive rates are low and a much larger number of replicates would be necessary to determine error rates at higher levels. The reported levels correspond to single-point P values of .05, .01, .005 and 7.4⋅10⁻⁴ (suggestive linkage). Results for a 2-cM marker map are summarized in table 1.

Once again, the Ising and Z_LR statistics have essentially identical type I–error rates. The MLS_pt has a significantly higher intervalwise false-positive rate (P<.05) than Ising at the first three cutoff levels (i.e., LODs of 0.59, 1.18, and 1.44). A similar result has previously been observed by Shugart and Goldgar (1997). The number of replicates is too low to assess the significance of the differences in type I–error rate at the highest significance level (LOD 2.19). All multipoint statistics have significantly lower type I–error rates than does the single-point χ² statistic.

Epistatic Interaction

In this analysis, we concentrate on the effectiveness of the Ising model to detect weak-effect loci with epistatic interactions. The main-effect locus is easily detectable. We tested the detection of the weak locus, using the Ising model with two effect loci and an interaction, under the assumption that the main locus has already been detected (see the Methods section). In this example, since the markers were fully informative, linkage was declared if the test statistic exceeded a predetermined cutoff at the simulated disease locus. The results are shown in table 3. Although the power to detect the weak locus is low, the Ising model visibly outperforms the single-locus search method—the χ² or the Z_LR exponential-pairs statistic, which are equivalent for independent sib pairs where all markers are fully informative (Sengul et al. 2000). We have also tested another popular strategy based on exclusion of sib pairs sharing two alleles at a “strong” locus (e.g., Mein et al. 1998). Such a strategy removes much of the effect of the major locus, and a single-locus search may then be carried out on the remaining data (i.e., sib pairs sharing 0 and 1 alleles at the major locus 1). Table 3 shows that the Ising model outperforms such a search at all significance levels.

Table 3.

Detection of a Weak Locus with an Epistatic Interaction^[Note]

	Power at Lod Score Cut-Off				Pointwise Type I Error at Cut-Off
Model	.59 (1.13)	.92 (1.50)	1.18 (1.80)	1.44 (2.09)	.59 (1.13)	.92 (1.50)	1.18 (1.80)	1.44 (2.09)
Ising	.377	.263	.190	.138	.030	.013	.008	.006
χ2 (0 and 1 sharers at locus 1)	.326	.189	.113	.064	.044	.018	.008	.004
χ2/Allegro (single-locus)	.286	.176	.119	.088	.049	.020	.009	.005

Note.— The cut-off levels in parenthesis refer to the 2-df LR test in the Ising model with epistatic interaction. The P values corresponding to the LODs shown are .05, .02, .01, and .005, respectively.

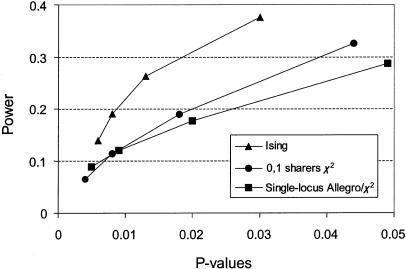
The pointwise significance of all three methods may be determined from the asymptotic behavior of the respective statistics. However, in order to verify the correctness of P values with respect to the particular data set used here, we carried out type I–error analysis by simulating data with a main-effect locus but without the weak locus, as described in the sib-pair data and simulation section. The pointwise type I–error rate is within the theoretically predicted range for the conditional epistatic search (Ising model), splitting by allele sharing at locus 1, and the simple single-locus search. Note that, although pointwise values are presented here, in the case of a genome scan, the conditional epistatic search suffers from exactly the same multiple testing problems as the single-locus search. After correcting for the difference in number of degrees of freedom, same significance criteria should be used for both methods. The power versus type I–error rate curves are shown in figure 2, illustrating the superior performance of the two-locus epistatic model.

Figure 2.

Power versus type I–error rates for analysis of the two-locus genetic model. The conditional epistatic two-locus Ising model is compared with a single-locus analysis, illustrated either by the Allegro exponential pairs statistic or by a χ² statistic (for fully informative markers, the two single-locus methods are equivalent), and with an analysis based on splitting the sample according to the IBD-sharing state at locus 1, followed by a single-locus analysis of only those sib pairs sharing 0 or 1 alleles IBD.

Analysis of IDDM Data

The diabetes data set has been extensively analyzed using various approaches, including single-locus methods, splitting the data by IBD sharing at the HLA locus (Mein et al. 1998), and conditional multilocus methods (Cordell et al. 1995, 2000). We first analyzed the data using the single-locus approach (i.e., considering only one effect locus at a time) followed by a two-locus conditional approach, conditioning on the strong HLA locus and considering a model with an additional effect locus and an epistatic interaction between HLA and the second locus (as in the analysis of simulated data with epistasis above). The analysis presented here is meant predominantly as a confirmation of the performance of the Ising model on real data, rather than a search for novel IDDM loci. However, several interesting results can be observed.

The single-locus results are similar to those already reported in previous analyses. The Ising model detects the HLA locus (IDDM1 ) with a maximum single-locus LOD score of 33.5. The other notable single-locus hits are: IDDM10 (LOD 4.21), D16S908 (LOD 3.19), IDDM2 (LOD 2.72), and D19S226 (LOD 2.06). As expected, the significance levels for the above scores are comparable to those already reported by Mein et al. (1998).

The two-locus conditional analysis is considerably more interesting. The most noteworthy results are shown in table 4. The table contains loci with evidence for a significant genetic effect (P<.05) and a significant epistatic interaction with HLA (P<.05). Several of the detected loci coincide with those reported in the multilocus conditional search by Cordell et al. (2000): D3S1576, D8S88, D16S3098, and D21S120. However, the Ising model suggests several additional epistatic loci. D1S229 has previously been shown to be linked with IDDM by an independent study (Concannon et al. 1998) with a LOD score of 3.31. This locus has not been identified by Cordell et al. (2000). Similarly, D2S301 corresponds to IDDM13. This locus does not exhibit any appreciable excess allele-sharing in a single-locus search but is detected by the epistatic search using the Ising model. Other loci detected uniquely by the Ising model (D7S519 and D13S153) have not been noted in any previous studies and may constitute new candidate IDDM loci.

Table 4.

Two-Locus Conditional Analysis of IDDM Data Using the Ising Model

			LOD Score (P)
Chromosome	Markera	Location(cM)	Single Locusb	Two Locus	Interaction
1	D1S229	238	.003 (NS)	1.43 (.02)	Negative
2	D2S301	215	.0004 (NS)	1.30 (.03)	Positive
2	D2S119	65	.03 (NS)	1.69 (.01)	Negative
3	D3S1560	19	.09 (NS)	1.50 (.02)	Negative
3	D3S1576	152	1.09 (.01)	1.70 (.01)	Positive
4	D4S431 (D4S412)	12 (5)	.90 (.02)	1.57 (.02)	Negative
6	D6S294	79	…	2.26 (.0006)c	…
7	D7S519	69	.09 (NS)	1.17 (.03)	Negative
8	D8S281 (D8S257)	125 (111)	.71 (.04)	1.71 (.01)	Positive
13	D13S153	46	.005 (NS)	1.72 (.009)	Negative
14	D14S276 (D14S75)	56	.93 (.02)	1.65 (.01)	Positive
16	D16S3098	108	3.16 (.00006)	4.32 (.00002)	Positive
21	D21S219	34	0 (NS)	1.22 (.03)	Negative

^aThe results shown are for selected loci where the two-locus conditional model is significant at the P<.05 level and where there is evidence (P<.05) for an interaction between the test locus and the conditional locus (HLA). In cases where the locations of the single-locus and two-locus maximum LOD scores are different, the location for the two-locus peak is indicated in parentheses.

^bNS = not significant.

^cThis is a two-locus conditional LOD score with no additional interaction term. No interaction is necessary, since any genetic interaction between candidate genes is absorbed by the interaction terms due to linkage between markers. The resulting test is a one-sided LR test with 1 df.

An interesting case is illustrated by IDDM15 on chromosome 6. This putative locus is very close to IDDM1, and its considerably smaller contribution is hidden under the high IBD-sharing proportion in the vicinity of the stronger locus. The Ising model can be particularly efficient in detecting such loci. If the presence of two underlying disease genes within a linked chromosomal region is suspected, it is sufficient to use a model with a main locus and a conditional locus, but no interaction term. Any epistatic interaction between the two genes is absorbed in the coupling parameters of the Ising model, already representing genetic linkage due to colocalization. The resulting test has 1 df and should be maximally sensitive for detection of such cases. In fact, the Ising model gives a LOD score of 2.26 at IDDM15, corresponding to P<.0006.

Several putative interactions detected by Cordell et al. (2000) are not picked up by the Ising model. These include TH/INS (IDDM2), FGF3 (IDDM4), and D18S487, further demonstrating that both similarities and differences exist between the two approaches. More studies of different types of genetic interactions will be necessary to determine the conditions under which models such as that of Cordell et al. (2000) or the Ising model described here will be more a powerful approach.

Discussion

The Ising model is a simplified representation of interactions within a complex system. In ASP analysis, the IBD sharing matrix can be analyzed in the context of a signal due to a disease locus and the genetic linkage of each marker locus to its nearest neighbor. By jointly considering all markers on a chromosome and accounting for linkage between them, the Ising model allows the calculation of a multipoint allele-sharing statistic.

The multipoint analysis presented here shows that the Ising statistic is essentially equivalent to the exponential-pairs Z_LR statistic computed by the Allegro program. Figure 1 shows a graphic example of the near-equivalence of the two statistics. The power and type I–error rates estimated from 20,000 simulated data sets are practically identical (table 2). The correspondence of LOD score curves is even more striking for a more dense genome scan but decreases for a less dense map (data not shown). The performance of the MLS_pt, was inferior to the Z_LR and Ising statistics. Both the power and the false-positive rates of the MLS_pt were slightly, but significantly, poorer than the corresponding power and false-positive rates of the Ising statistic.

The above results may be better understood in terms of the genetic models that implicitly underlie most nonparametric statistics. The most general model is represented by the MLS_pt statistic, which independently considers the proportions of sib pairs sharing 0, 1, and 2 alleles (designated by z₀, z₁, and z₂) at a given locus and measures their deviations from the proportions expected under the null hypothesis of no linkage—that is, z₀=0.25, z₁=0.5, and z₂=0.25. By contrast, many popular nonparametric tests compare a weighted sum of z₁+wz₂ with its null expectation. Such 1-df tests implicitly correspond to a particular genetic model. For example, the popular means test considers the sum z₁+2z₂ (i.e., w=2, which is equivalent to measuring the total proportion of alleles shared IBD) and corresponds to an additive genetic model (Whittemore and Tu 1998). The Z_lr (pairs) statistic in Allegro can also be shown to correspond to the additive model (Kong and Cox 1997). The Ising-model statistic depends only on the total number of alleles shared IBD at a given locus (note that IBD states for each parent are considered independent and may be permuted freely without altering the result), and, hence, it too corresponds to an additive genetic model. It is thus not surprising that the Ising and Z_lr statistics are nearly equivalent in the above analysis. It should be noted that the 1-df models are still valid when the true genetic model is not additive, but there should be some loss of power as compared to the most general model (e.g., the MLS_pt statistic). Conversely, Ising and Z_lr statistics are expected to outperform the MLS_pt statistic when the true generating model is closest to additive, as is the case with the simulated data considered here.

As expected, all multipoint methods outperformed the single-point χ² statistic. Combining incomplete information from neighboring markers results in a more precise determination of the IBD-sharing status, while IBD sharing at each single marker may not always be unambiguously determined. The corresponding decrease in type I–error results from sharing of information between neighboring markers to eliminate spurious peaks.

The analysis of a two-locus system with epistasis shows that the Ising model is easily adapted to represent complex genetic systems. The use of a conditional search with epistatic interaction results in a significant increase in power to detect the weak modifier locus in the two-locus genetic model, as compared to a conventional one-locus search. Although the power is low at all significance levels, for levels of P<.02, the power of the conditional search is nearly twice that of the one-locus search. This particular example demonstrates that, for certain complex genetic models, the disadvantage of introducing an extra degree of freedom into the system is more than compensated for by a more accurate representation of the genetic model.

It should be noted, that the Ising model with epistatic interactions remains a model-free method in the genetic sense; no inheritance model is assumed for the trait. When conditioning on the existence of a known locus, the search for epistatic loci depends on specification of at least one other locus and a possible interaction between the two (or more) genes. Any correlation between IBD-sharing states at distinct loci constitutes an epistatic interaction. Furthermore, the model may be used not only for detection of epistatic loci but also to test for the presence of interactions. The appropriate LR test for the latter compares the model with the interaction to the model with the interaction set to zero, providing a simple test for the presence or absence of epistasis. Some information regarding the nature of the interaction may be obtained from the sign of the interaction term. A positive interaction implies positive correlation between IBD-sharing states at different loci, suggesting an additive or a threshold model. An example of negative interaction or negative correlation between IBD-sharing states is presented in the above example of a weak modifier locus.

Analysis of the IDDM data shows that the Ising model performs well in real situations. Single-locus results are comparable to those obtained in previous analyses (e.g., Mein et al. 1998). The conditional, two-locus, epistatic analysis replicates some of the results of Cordell et al. (2000) but also suggests other epistatic loci, some of which correspond to loci detected using independent data (D1S229 and IDDM13) and some of which may represent new IDDM loci (D7S519 and D13S153). However, the Ising model fails to detect some of the epistatic interactions observed by Cordell et al. (2000), demonstrating that the two approaches to analyzing epistatic systems are not equivalent.

As mentioned above, the Ising model is based on detection of deviation of the “mean” overall IBD sharing from the expected proportion, whereas models based on the MLS consider deviations from normal in the proportions of individuals sharing 0, 1, and 2 alleles. Hence, the two-locus Ising model with epistatis requires only one additional parameter to measure the correlation between IBD sharing at two loci, whereas an analogous MLS-based model requires nine additional parameters in order to estimate interactions between 0-, 1-, and 2-allele sharers. Although more comparative analysis with simulated data will be necessary to determine under what conditions the two approaches will differ, it may be expected that the Ising model, because of its underlying additive genetic model, may perform particularly well in detecting additive interactions, whereas the MLS-based approach may be more suitable for detecting general interactions. Also, as illustrated by the example of IDDM1 and IDDM15, because the Ising model includes coupling parameters representing interactions between linked loci, the model may be particularly well suited for detection of epistatic loci within a linked chromosomal region.

The Ising model is also attractive from the perspective of significance testing. The introduction of additional parameters in epistatic models results simply in increasing the number of degrees freedom in the LR test, the asymptotic significance of which can be assessed using a χ² distribution. Unlike the MLS-based approach, simulations are not necessary to calculate P values.

Although the examples considered here are two-locus systems, the Ising model can be extended to systems with a higher number of loci and higher number of interactions. It can be used either as a conditional or a nested method for location of subsequent disease genes or for simultaneous detection of multiple loci (although an appropriate multiple-testing correction would have to be applied in consideration of pairs of loci in a genome scan). The current implementation of the Ising model applies only to sib pairs, but future developments should include extension to other affected relative pairs.

The costs and benefits of multilocus search schemes remain debatable. Clearly, in certain cases, there will be no gain in power—and a likely loss—when complex genetic models are considered (Li and Reich 2000). However, in many cases, virtually the only way to detect loci with weak genetic effects is to view their contribution in the context of the entire genetic pathway (or in as much of the pathway as is known to us). As major disease genes are being discovered and our knowledge of their function increases, multilocus methods should become effective tools for detecting minor genes and their interactions with the known loci. Here, we have adapted a statistical tool developed for the physical sciences to the analysis of genetic data and present it as an efficient method for multipoint, multilocus linkage analysis. The model is easily adapted to the representation of complex genetic systems and allows for testing of diverse hypotheses required for detection of weak loci and interactions in complex disorders.

Appendix A

For a system of m markers, the probability of observing a particular configuration is given by

where H{x(t)_m} is the energy of the configuration:

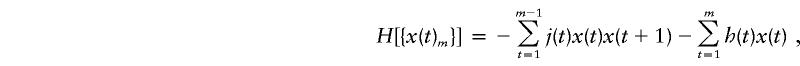and Z_m is the partition function, defined as the sum of energies over all the possible states of the system:

Since, at every position, the system has two possible states, the overall number of states is equal to 2^m. Hence, the number of terms in the above summation increases exponentially with the number of markers, and the calculation may become very time intensive. Fortunately, since the model involves only nearest neighbor interactions, the calculation can be simplified to run linearly in m. First, write Z_m=Z_m++Z_m-, where Z_m+ is the value of the partition function for m dipoles, given that the last (mth) position has a positive spin, and Z_m− is the value of the partition function, given that the last position has a negative spin. We can then write

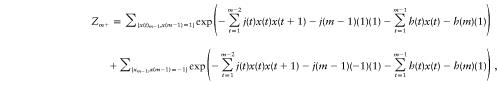where the two summation terms are over all possible configurations {x_m-1} of a system with (m-1) markers, given that the (m-1)th position has the value +1 or −1, respectively.

A similar expression may be written for Z_m-. This simplifies to

and, hence,

and

The partition function Z_m can then be calculated recursively from the above two expressions. The algorithm used in the program calculates Z_m in linear time in m. The above method for calculating the partition function is easily adapted for efficient calculation of the energy of each individual state of the system with missing data, as well as epistatic models involving additional interactions between genetic-effect loci.