Skip to main content
NCBI home page
American Journal of Human Genetics logoLink to American Journal of Human Genetics
. 2001 Apr 13;68(5):1197–1206. doi: 10.1086/320103

Model-Free Linkage Analysis with Covariates Confirms Linkage of Prostate Cancer to Chromosomes 1 and 4

Katrina A B Goddard 1, John S Witte 1, Brian K Suarez 2, William J Catalona 3, Jane M Olson 1
PMCID: PMC1226100  PMID: 11309685

Abstract

As with many complex genetic diseases, genome scans for prostate cancer have given conflicting results, often failing to provide replication of previous findings. One factor contributing to the lack of consistency across studies is locus heterogeneity, which can weaken or even eliminate evidence for linkage that is present only in a subset of families. Currently, most analyses either fail to account for locus heterogeneity or attempt to account for it only by partitioning data sets into smaller and smaller portions. In the present study, we model locus heterogeneity among affected sib pairs with prostate cancer by including covariates in the linkage analysis that serve as surrogate measures of between-family linkage differences. The model is a modification of the Olson conditional logistic model for affected relative pairs. By including Gleason score, age at onset, male-to-male transmission, and/or number of affected first-degree family members as covariates, we detected linkage near three locations that were previously identified by linkage (1q24-25 [HPC1; LOD score 3.25, P=.00012], 1q42.2-43 [PCAP; LOD score 2.84, P=.0030], and 4q [LOD score 2.80, P=.00038]), near the androgen-receptor locus on Xq12-13 (AR; LOD score 3.06, P=.00053), and at five new locations (LOD score > 2.5). Without covariates, only a few weak-to-moderate linkage signals were found, none of which replicate findings of previous genome scans. We conclude that covariate-based linkage analysis greatly improves the likelihood that linked regions will be found by incorporation of information about heterogeneity within the sample.

Introduction

Prostate cancer (CaP [MIM 176807]) is one of the most common causes of cancer mortality among men in the United States and accounts for ∼31,900 deaths annually (Greenlee et al. 2000). Substantial differences in the prevalence of CaP are observed among populations, with African Americans having the highest prevalence of the disease and with Asian populations having the lowest prevalence (Parkin et al. 1993; Whittemore 1994). Individuals either with several affected first-degree relatives or with an affected brother who had an early age at onset have a higher risk of development of CaP (Keetch et al. 1995), suggesting that genetic factors play a role in the development and progression of CaP. Studies of the familial clustering of CaP also indicate a heritable component of the disease, although there have been conflicting reports about the mode of inheritance. Some studies suggest an autosomal dominant mode of inheritance for early-onset disease (Carter et al. 1992; Grönberg et al. 1997), whereas others suggest a recessive or X-linked mode of inheritance (Monroe et al. 1995).

Numerous studies have indicated evidence for linkage to regions that may contain a disease-susceptibility locus for CaP. The first region, reported by Smith et al. (1996), was on chromosome 1q24-25 (HPC1 [MIM 601518]). Subsequent reports presented conflicting results in this region. Some studies showed little or no support for a locus in this region (McIndoe et al. 1997; Berthon et al. 1998; Eeles et al. 1998; Berry et al. 2000a; Goode et al. 2000), whereas others showed moderate support, usually in subsets of the data restricted to families with early age at onset (Hsieh et al. 1997; Grönberg et al. 1999), families meeting the criteria for hereditary CaP (Cooney et al. 1997), or families with male-to-male disease transmission, early age at onset, and a large number of affected individuals (Xu and International Consortium for Prostate Cancer Genetics 2000). A second locus on chromosome 1, located at 1q42.2-43 (PCAP [MIM 602759]), was reported by Berthon et al. (1998). However, additional studies have failed to support the evidence for linkage in this region (Gibbs et al. 1999a; Whittemore et al. 1999; Berry et al. 2000a), although the genome scan by Smith et al. (1996) had earlier reported a small-to-moderate signal in this region. A third locus on chromosome 1, located at 1p36 (CAPB [MIM 603688]), was implicated in families that also have a history of brain cancer (Gibbs et al. 1999b); however, one other study showed negative LOD scores in this region in 13 families with prostate and brain cancer (Berry et al. 2000a).

Additional loci, on chromosomes other than chromosome 1, also have been implicated in CaP and recently were reviewed by Ostrander and Stanford (2000). In brief, Xu et al. (1998) reported a locus, on the X chromosome (HPCX [MIM 300147]), that had supportive evidence of linkage in another study (Lange et al. 1999). Berry et al. (2000b) identified evidence for linkage to a locus on chromosome 20, among pedigrees with no male-to-male transmission, a high average age at diagnosis (⩾66 years), and a relatively small number of affected individuals (fewer than five affected). These families are the least likely to have linkage to the regions that were identified previously. More recently, the HPC2/ELAC2 gene on chromosome 17p was found to be associated with an increased risk of CaP (Rebbeck et al. 2000; Tavtigian et al. 2000). Finally, two recent genome scans have identified suggestive evidence for linkage on chromosomes 2, 12, 15, and 16 (Suarez et al. 2000) and on chromosomes 1, 8, 10, 12, 14, and 16 (Gibbs et al. 2000). The strongest evidence for linkage was found on chromosome 16, in the affected-sib-pair (ASP) study by Suarez et al. (2000), and on chromosomes 8 and 10, under a recessive model, in the Gibbs et al. (2000) study.

The mixed results observed both within and between studies is an indication of the complex nature of CaP. CaP is likely to be a genetically heterogeneous disorder, with several genetic and environmental factors contributing to the development of disease. Two additional factors are likely to contribute to the lack of consistency across studies. First, there may be population differences both within and between studies; for example, in the original report for HPC1, two African American pedigrees contributed substantially to the total LOD score suggesting linkage in the region, whereas many subsequent studies included a large proportion of white families. Second, differences in the ascertainment criteria used to identify pedigrees can lead to different genes segregating in the study population (McCarthy et al. 1998; Goddard 1999). Many of the studies listed above selected large pedigrees with a large number of affected individuals, whereas others included only nuclear families with at least two affected individuals.

Previous analyses have used several methods to deal with heterogeneity, including alternative models in parametric linkage analysis; model-free methods, such as the nonparametric linkage (NPL) score; and stratification of the sample on one or more covariates. An alternative method that may provide additional power to detect linkage is the model-free conditional logistic model for affected-relative-pair (ARP) linkage analysis (Olson 1999), an extension and reparameterization, in terms of log risk ratio, of the Greenwood and Bull (1999) multinomial covariate model for ASPs. Greenwood and Bull established, using simulations, that inclusion of family-specific covariates increases the power to detect linkage, provided that the covariate reflects underlying locus heterogeneity. They also found that inclusion of covariates does not substantially impact the accuracy of asymptotic approximations to the distribution of the appropriate likelihood-ratio statistic, regardless of whether constraints on the mode of inheritance are applied that reduce the number of parameters in the model.

These methods are model free in the sense that model parameters at the trait locus do not need to be specified. Discrete or quantitative covariates included in the model increase power to detect linkage when the covariate measures differences, between families, that are important to locus heterogeneity. The method incorporates locus heterogeneity due to the covariate, by allowing the genetic relative risk to depend on the covariate, so that, in effect, the allele sharing at the marker locus differs for different values of the covariate. The original model proposed by Olson (1999) requires two additional parameters for each covariate and therefore may not provide optimal power. In the present study, we instead use a modification that requires only one additional parameter per covariate.

We apply this modification of the Olson (1999) conditional logistic model to a genome scan of sibships with CaP. We test four covariates: Gleason score, age at onset, male-to-male transmission, and number of first-degree relatives with CaP. In contrast to the original analysis of these data by Suarez et al. (2000), we find strong confirmatory evidence of linkage in four genomic locations, as well as substantial evidence for linkage in several new locations.

Subjects and Methods

Subjects

The recruitment of study subjects has been described elsewhere (Suarez et al. 2000; Witte et al. 2000). For this analysis, a total of 564 men from 254 families with both CaP and measured Gleason scores were available. This sample included 189 families with two affected brothers, 41 families with three affected brothers, 2 families with four affected brothers, and 1 family with two pairs of affected brothers who were cousins (for a total of 326 ASPs). We considered four covariates: (1) the sum of the sib-pair Gleason scores, (2) age at onset (measured as family mean age at diagnosis), (3) an indicator for male-to-male transmission in the nuclear family, and (4) the number of affected first-degree relatives in the nuclear family. Gleason score is a measure of tumor aggressiveness and has been analyzed previously, as an outcome variable, by use of these data (Witte et al. 2000). Family mean age at diagnosis was used in place of the sum of the sib-pair age at onset, because of the large number of missing values for the latter. Overall, 4% of the ASPs had missing values for male-to-male transmission, and 11% of ASPs had missing values for the family mean age at diagnosis. Missing values for covariates other than Gleason score were given the mean value for that covariate.

Genotyping

Genotyping was performed at the Center for Medical Genetics, Marshfield Medical Research Foundation, with DNA from each subject’s peripheral blood, extracted by standard methods. The samples were typed through use of Marshfield Screening Set 9 (Yuan et al. 1997), which includes 364 autosomal simple-tandem-repeat polymorphisms, with ∼9-cM spacing between markers across the genome and an average heterozygosity of 77% (Broman et al. 1998). We confirmed the sib-pair relationship in all sibships, through use of all markers in the screening set, with the program RELTEST from the Statistical Analysis for Genetic Epidemiology (S.A.G.E.) software package, release 4.0 beta. Pairs that were not full siblings or that were MZ twins were excluded from the analysis, as in previous analyses of these data (Suarez et al. 2000; Witte et al. 2000).

Statistical Analysis

To detect linkage in our ASPs, we performed a model-free likelihood analysis that allowed incorporation of covariates. Olson (1999) showed that the original Risch (1990) ASP LOD score can be reparameterized in terms of the natural logarithms of relationship relative risks, by putting λ1=exp(β1) and λ2=exp(β2), where λ1 (λ2) is the relative risk for a pair of relatives that shares exactly 1 (2) alleles identical by descent (IBD) and where β1 (β2) is the natural logarithm of λ1 (λ2). In this analysis, multipoint IBD-sharing estimates for autosomal loci were obtained with the GENIBD program from the S.A.G.E. package, release 4.0 beta, and those for the X chromosome were obtained with MAPMAKER/SIBS (Kruglyak and Lander 1995). Addition of covariates to this model requires two additional parameters for each covariate. Instead, we constrained the relative risks so that λ2=3.634λ1-2.634, reducing, from two to one, both the number of parameters in the basic model and the number of additional parameters needed for each added covariate. This particular constraint was chosen on the basis of work by Whittemore and Tu (1998), who showed that a minmax one-parameter ASP LOD score preserved type I error but had more power for most genetic models than did the usual two-parameter LOD score. Our constraint is simply a reparameterization of the Whittemore-Tu minmax constraint and assumes a genetic model approximately halfway between a recessive and a dominant mode of inheritance. We then incorporated covariates into our analysis by putting 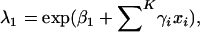Inline graphic where xi, i=1,…,K, are the covariates included in the model and where γi are the corresponding parameters. The same model may be used on X-linked markers after the correct prior and conditional allele-sharing probabilities for X-linked loci and brother-brother pairs are obtained, where the interpretation of λ1 is specific to that pair type.

In this analysis, inclusion of a covariate allows for linkage heterogeneity due to the covariate; for example, a binary covariate indicating population membership allows for population heterogeneity in linkage to a particular location, and including such a covariate is equivalent to analyzing each subpopulation separately and summing the LOD scores. Continuous covariates have a similar interpretation in that they allow for linkage heterogeneity due to the covariate. Using the parameter estimates, one can then calculate sibling relative risks at particular values of the covariate: λs(x)= 1/4+ 1/2λ1(x)+ 1/4λ2(x), subject to the minmax constraint described above.

In our analyses, we assumed that genetic constraints (Holmans 1993) hold at the sample mean covariate value, but not necessarily at other covariate values (see Greenwood and Bull 1999); each covariate was standardized to have mean 0 and variance 1. By centering the covariate around 0, we avoid the need to further constrain γ to be consistent with a genetic model at the mean covariate value (Olson 1999). In addition, the sign of γ indicates the direction of covariate effect on linkage evidence; for example, if linkage is present in families with early age at onset but absent in families with late age at onset, inclusion of x (as mean age at onset [centered]) as a covariate will substantially increase the LOD score, and the estimate of γ will be negative, generating the highest values of λs(x) for the lowest values of x. In addition to centering each covariate, we also standardized by dividing by the estimated SD. The sole purpose was to reduce the number of possible computational problems encountered by the maximization algorithm MAXFUN from the S.A.G.E. package, release 2.2; >15,000 separate maximizations were performed in this analysis.

Critical values for the corresponding likelihood-ratio statistics (LRS; i.e., 4.605×LODscore) can be obtained easily, by use of the methods of Self and Liang (1987). The distribution of the LRS for the basic one-parameter model is a 50:50 mixture of a point mass at 0 and a χ2 distribution with 1 df. Addition of K covariates gives an LRS with a distribution that is a 50:50 mixture of a χ2 with K df and a χ2 with K+1 df. The difference in LRS between nested models that differ by J covariates has a χ2 distribution with J df. One can therefore test both the significance of the contribution of a covariate and the overall evidence for linkage.

Clearly, addition of covariates increases the LOD cutpoint needed in order to allow us to declare that there is significant linkage. As a result, we encourage both a priori selection of candidate covariates to be included in routine linkage analysis and careful differentiation between planned and exploratory analyses. We chose covariates that we believed had a high probability of measuring some aspect of locus heterogeneity and analyzed each covariate individually. In regions where more than one covariate contributed significantly to linkage evidence (P<.05), we obtained parsimonious final models, using multiple-regression methods.

Results

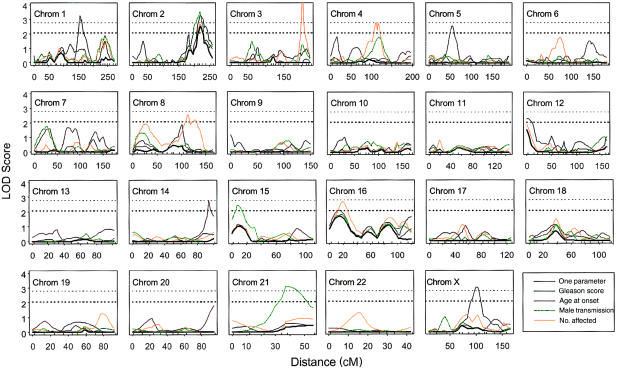
Plots of LOD score versus map distance (in cM) are shown in figure 1, for five models: the one-parameter model, without covariates, and four models, each with one covariate (Gleason score, mean age at onset, male-to-male transmission indicator, or number of affected relatives). The one-parameter model, represented by the black line, is always the smallest of the five LOD scores and can be viewed as a “baseline” in the context of the analysis of covariate effects on linkage. Five regions have baseline LOD scores >1; these regions are summarized in table 1, along with the corresponding two-parameter LOD score and the NPL score reported, by Suarez et al. (2000), for the same data set. The largest one-parameter LOD score is on chromosome 2q (LOD score 2.48). We detected the same regions reported by Suarez et al. (2000), with some differences in relative magnitude of the signal, which, presumably, reflect differences in method power and the fact that Suarez et al. included more markers in these regions and used a larger sample size by including ASPs with no reported Gleason score. Comparison of the one- and two-parameter LOD scores shows the dependence of the results on the constraints that were chosen for the one-parameter model. These results indicate that, at the cost of an additional parameter, the two-parameter model adds little additional evidence for linkage, a finding that is consistent with the results of Whittemore and Tu (1998) that also suggest that the one-parameter model is usually more powerful. Similar increases in the LOD score were found by maximizing over the mode-of-inheritance parameter (two-parameter model) for models that included the covariates (data not shown).

Figure 1.

Figure 1

Open in a new tab

LOD scores for a genome scan of sibships with CaP. Marker locations are indicated by tick marks above the lower axis. Five models are included: the baseline one-parameter model (black) and four models with one covariate each, including Gleason score (blue), age at onset (red), male-to-male transmission (green), and number of affected relatives (yellow). Horizontal lines correspond to LOD score cutpoints at α = .001 for baseline LOD score (cutpoint 2.07) and models including a single covariate (cutpoint 2.78).

Table 1.

Baseline Linkage Results

LOD Score (P Value)
Chromosome Flanking Marker(s) Peak Locationa(cM) One-Parameter Two-Parameter Peak Locationby NPLa(cM) NPL Scoreb(P Value)
2q D2S434, D2S1363 220 2.48 (.0004) 2.79 (.0003) 224 2.78 (.0027)
12p D12S372 0 1.55 (.0038) 1.64 (.0050) 8 2.00 (.0228)
15p D15S165, ACTC 10 1.02 (.0151) 1.10 (.0190) 24 2.77 (.0028)
16p D16S748, D16S764 16 1.70 (.0026) 1.74 (.0039) 32 2.81 (.0025)
16q D16S2624, D16S516 88 1.07 (.0132) 1.13 (.0176) 99 3.15 (.0008)
Open in a new tab
a

Distance is measured from the first marker on the chromosome.

b

From Suarez et al. (2000). N=320 ASPs.

Covariate effects significant at the .01 level are detailed in table 2, as are regions for which the total LOD score (including the covariate) is >2.0. We included considerable detail in this table so that various features of the new models can be observed more easily. Because all covariates were standardized prior to inclusion, covariate-parameter estimates (γ) are interpreted as unit changes in loge offspring relative risk λ1 of the standardized covariate. The means and SDs of the original covariates are given in footnote “b” of table 2.

Table 2.

Significant Covariates

Chromosome and Flanking Marker(s)(Position [in cM]) Z1a β Covariateb Z2c β γ Z2-Z1 P
1:
 D1S534, D1S1653 (156) .03 .019 Gleason 3.25 .110 .311 3.22 .0001
 D1S549, D1S3462 (240) .32 .065 Male 1.90 .106 .236 1.58 .0070
2:
 D2S1360 (35) .00 .000 Gleason 1.52 .000 .115 1.52 .0082
 D2S1384, D2S1649 (204) 1.06 .126 Male 2.79 .171 .266 1.73 .0048
 D2S434, D2S1363 (220) 2.48 .205 Gleason 3.29 .216 −.140 .81 .053
 D2S434, D2S1363 (218) 2.48 .205 Male 3.40 .244 .216 .92 .040
3:
 D3S1768 (61) .00 .000 Male 1.51 .000 .162 1.51 .0084
 D3S1262, D3S2398 (202) .00 .000 No. affected 4.66 .000 −.236 4.66 <.0001
4:
 D4S403, D4S2639 (16) .00 .000 Age at onset 1.80 .012 .168 1.80 .0040
 D4S2623, D4S2394 (110) .06 .030 No. affected 2.80 .096 −.237 2.74 .0038
 D4S2394, D4S1644 (120) .00 .003 Male 1.76 .019 −.116 1.76 .0044
5:
 D5S1457, D5S2500 (56) .00 .000 Gleason 2.57 .023 −.207 2.57 .0006
6:
 GATA184A08, D6S2436 (140) .00 .000 Age at onset 1.53 .033 −.175 1.53 .0079
7:
 D7S1802, D7S1808 (32) .00 .000 Age at onset 1.55 .013 .081 1.55 .0075
 D7S1802, D7S1808 (26) .00 .000 Male 1.75 .012 −.112 1.75 .0045
 D7S3046, D7S2204 (74) .00 .000 Age at onset 1.68 .000 −.139 1.68 .0054
8:
 D8S1106, D8S1145 (28) .04 .016 No. affected 1.92 .022 .139 1.88 .0033
 D8S1119 (101) .39 .066 Gleason 1.88 .096 .123 1.49 .0029
 GAAT1A4, D8S1132 (114) .00 .000 No. affected 2.56 .058 .253 2.56 .0006
12:
 D12S372 (0) 1.55 .200 Gleason 2.32 .179 −.129 .77 .0600
14:
 D14S1434, D14S1426 (94) .03 .051 Age at onset 2.75 .114 .310 2.72 .0040
15:
 D15S165, ACTC (8) 1.02 .114 Male 2.42 .043 .124 1.40 .0110
16:
 D16S764 (19) 1.59 .152 No. affected 2.68 .162 −.096 1.09 .0250
 D16S2621 (120) .13 .040 Gleason 1.65 .064 .137 1.52 .0082
20:
 D20S171 (94) .00 .000 Age at onset 1.81 .000 .127 1.81 .0039
21:
 D21S2055 (37) .32 .060 Male 3.12 .083 −.141 2.80 .0003
X:
 DXS6789, DXS6797 (101) .26 .153 Gleason 3.06 .171 .533 2.80 .0003
Open in a new tab
a

LOD score for one-parameter model.

b

Mean (SD) of covariates—total Gleason score, 11.30 (2.13); age at onset, 63.1 (8.30); Male-to-male transmission, 0.166 (.36); Number of affected relatives, 2.74 (.83).

c

LOD score for model including covariate.

Some of the most interesting results were on chromosome 1. In the region that purports to contain HPC1, a large peak (LOD score 3.25) was found only when Gleason score was included as a covariate. The highest point of our peak was located ∼30 cM centromeric to the most significant marker described by Smith et al. (1996). The LOD score without covariates is only 0.03, and the effect of Gleason score on linkage at this location is highly significant (P=.00012). This signal is the largest Gleason-score effect in our genome scan. The sign of the covariate parameter is positive, indicating that ASPs with high Gleason scores show the strongest evidence for linkage. Sibling relative risks for various Gleason scores are given in table 3, to illustrate the dependence of relative risk on Gleason score; ASPs with total Gleason scores in the upper 2.5% of the sample distribution have sibling relative risks >2.52.

Table 3.

Relative-Risk Estimates, at Chromosome 1q24-25

Relative Risk
Gleason Scorea (x) Offspring [λ1(x)] Sibling [λs(x)]
−2.0 .60 .44
−1.0 .82 .74
0 1.12 1.16
1.0 1.52 1.74
2.0 2.08 2.52
Open in a new tab
a

Sib-pair summed Gleason-score value, in SD.

A second peak on chromosome 1 is in the region of the PCAP signal reported by Berthon et al. (1998). Again, the model without covariates shows little evidence for linkage (LOD score 0.32), whereas the model that includes male-to-male transmission gives a LOD score of 1.90 (P=.007 for the covariate effect). Families that have male-to-male transmission show the most evidence in favor of linkage. In addition, Gleason score and number of affected relatives both are significant at the .05 level. As a result, we fit multiple conditional logistic-regression models (table 4). The best-fitting, most-parsimonious model includes both Gleason score and male-to-male transmission (total LOD score 2.84, P=.003). The interaction term has a negligible effect, indicating an excellent fit to a model in which these covariates affect offspring relative risk λ1 multiplicatively. The signs of the covariate parameters in the final model indicate that ASPs with male-to-male transmission and low Gleason scores contain the most evidence for linkage to the PCAP region on chromosome 1. The number of affected relatives does not add linkage information once Gleason score and male-to-male transmission are taken into account.

Table 4.

Multiple-Regression Analysis of Chromosome 1q42.2-43

Model LOD Score OverallP value LOD-ScoreDifferencea P value
One-parameter .32 .1124 … …
 +Gleason (G) 1.53 .0187 1.21 .0182
 +Age at onset .33 .3427 .01 .930
 +Male-to-male transmission (M) 1.90 .0078 1.58 .007
 +No. affected (N) 1.42 .0243 1.10 .0244
 +G+M 2.84 .00296 .94 .0376
 +G+M+N 2.87 .00723 .03 .710
 +G+M+G*M 2.86 .00738 .02 .762
Open in a new tab
a

To nearest model with one less parameter.

A second large signal due primarily to Gleason score was found on chromosome X (P=.0003 for covariate effect), ∼10 cM telomeric from the androgen-receptor locus (AR [MIM 313700]), an important candidate locus for CaP. CAG- and GGN-repeat polymorphisms in the AR locus have been related to CaP in association studies (e.g., see Giovannucci et al. 1997; Ingles et al. 1997; Stanford et al. 1997; Hsing et al. 2000) but not in linkage studies (Lange et al. 2000). For this signal, the LOD score without the covariate was only 0.26, compared with the LOD score including the covariate, which was 3.06, a strongly significant value (P=.00058). In contrast to what has been observed in the HPCX region (Xu et al. 1998; Lange et al. 1999), we did not observe an increase in the evidence for linkage among families with transmission that was consistent with an X-linked mode of inheritance (i.e., families that did not have male-to-male transmission). We could not examine the chromosome X region previously reported by Xu et al. (1998) because we did not have markers in this region near Xqter.

A third large signal, due entirely to Gleason score, was found on chromosome 5 (P=.00058 for covariate effect), in a location different from the location identified by Witte et al. (2000) when they used Gleason score as a dependent variable in a Haseman-Elston regression. Gleason score also increases the signal on chromosomes 2 (two regions), 8, and 16. The largest effect of age at onset was on chromosome 14, where the linkage signal increased from 0.18 to 2.74. Chromosomes 4, 6, 7, and 20 showed smaller age-at-onset effects, which were significant at the .01 level. The largest effect of male-to-male transmission was found on chromosome 21, where the LOD score increased from 0.32 to 3.12. Chromosomes 1–5 also showed effects from this covariate, which were significant at the .01 level.

The largest effects of the number of affected relatives were on chromosomes 3 (increase in LOD score from 0.00 to 4.66), 4 (from .03 to 2.76), and 8 (from 0.00 to 2.56), with another smaller but significant effect on chromosome 8. The signal on chromosome 4 is in the region of the second-largest signal reported by Smith et al. (1996). In this region, male-to-male transmission also shows an individual effect, which is significant at the .05 level, but it does not add linkage evidence to the model that includes the number of affected relatives. None of the other large covariate effects corresponds to a region for which previous strong linkage evidence has been reported.

The signal on chromosome 3 appears unusually narrow and may be overestimated or improperly maximized. However, we were unable to discover any difficulties with the maximization procedures at this location. An additional indication of possible overestimation is revealed by the fact that the linkage-parameter estimate (β) is 0 but the covariate-parameter estimate (γ) is large in absolute value; in other words, the offspring relative risk for much of the covariate distribution is considerably less than 1. In our analyses, we constrained only the mean covariate value to be consistent with genetic-triangle constraints, because it remains unclear what, if any, genetic constraints should be imposed when a covariate cannot be considered to differentiate subpopulations in which the genetic constraints should separately conform (e.g., different mating populations).

Nonetheless, one generally expects true relative risk values to be ⩾1; on the other hand, if linked and unlinked subsets are indeed present, estimated relative risks in the unlinked subset will be <1, with probability 1/2, by chance alone; in fact, we believe that chance evidence against linkage in unlinked (and unidentified) subsets is one of the primary reasons that linkage is often not detected in the first place. Therefore, we hesitate to discount signals that yield some implausible relative-risk values, while recognizing that, in some regions, the size of the detected covariate effect may be distorted and that the LOD score may be inflated.

Discussion

A reanalysis of the genome-scan data first reported by Suarez et al. (2000) provides confirmatory evidence of linkage in two regions, first reported by Smith et al. (1996), on chromosome 1 (i.e., HPC1) and on chromosome 4, and in one region, highlighted by Berthon et al. (1998), on chromosome 1 (i.e., PCAP), which also had a moderate-sized signal reported by Smith et al. (1996). Our peaks on chromosome 4 and 1q42.2-43 appear to be within 10–20 cM of their previously reported locations. We estimate that our HPC1 peak may be 30 cM centromeric to its previously reported location. In addition, we observed a strong new signal, on chromosome Xq12-13, that appears to be within 10–15 cM of the AR locus, a major candidate locus for CaP. We were able to detect these signals by including in the linkage analysis those covariates that account for some of the genetic heterogeneity presumed to exist in this complex disease. Linkage analysis without covariates failed to detect the signals in these regions. We believe that analyses that include additional phenotypic information will greatly improve the ability of genome scans to detect genetic loci for complex diseases.

Other covariate-based linkage methods have been proposed in addition to those of Olson (1999) and Greenwood and Bull (1999). Schaid et al. (2001 [in this issue]), in the context of model-based linkage analysis, specify the heterogeneity parameter as a function of covariates and apply the method to CaP. Gauderman and Siegmund (2000) have proposed a method in which gene-by-environment interaction is included in ASP linkage analysis. Although linkage analysis with covariates is not yet commonplace, it is similar in spirit to the common practice of subgroup analysis, in that subgroup analysis also aims to account for locus heterogeneity. One advantage of the conditional logistic model is that it provides a more general way in which covariate information can be easily included in the linkage analysis. The form of the model allows for multiple covariates—including quadratic terms and interactions—to be modeled, without the need to subdivide a sample into smaller and smaller portions. For continuous covariates, it is not necessary to choose a cutpoint on the basis of which the data are to be subgrouped. One possible disadvantage is that the model assumes multiplicativity in offspring relative risk; however, this restriction can be partly overcome, if necessary, to provide a better fit, by the inclusion of higher-order terms or by the transformation of covariates.

Addition of covariates increases the LOD-score cutpoint needed in order to allow us to declare significant linkage. In addition, indiscriminate use of covariate analyses can result in greatly increased experiment-wise type I error, because of multiple testing. As a result, we encourage both a priori selection of candidate covariates to be included in routine linkage analysis and careful distinction between prespecified and exploratory analyses. More-rigorous rules for multiple testing await further research.

The influence of missing data on the results of an analysis is always a concern. Here, missing data for covariates were replaced with the mean covariate value. The age-at-onset covariate had the largest proportion of missing data, with 11% of the ASPs having missing values. Removing from the analysis the ASPs having missing values for this covariate slightly reduced the LOD score; however, it is unclear whether this is an indication of a biased result due to use of the mean covariate value or of additional information that is gained by inclusion of the ASPs having missing values.

Witte et al. (2000) analyzed these data by using Gleason score as a dependent variable in a (new) Haseman-Elston regression (Elston et al 2000); there was little, if any, overlap between the signals reported in the present article and the signals reported by Witte et al. We believe that the two analyses detect different types of information relevant to linkage. Using Gleason score as a dependent variable in a sample of ASPs is likely to provide the most power to detect genes that modify tumor aggressiveness in patients with CaP but that do not confer susceptibility to CaP itself—that is, genes that contribute to within-family variability in Gleason score; on the other hand, inclusion of Gleason score as a covariate in an ASP linkage analysis is likely to have the most power to detect genes that confer susceptibility solely to subtypes of CaP that are characterized by aggressive tumors—that is, genes that contribute to between-family variability in Gleason score.

However, we note that, for individual-specific covariates, covariate information relevant to locus heterogeneity may be present in the sib-pair covariate sum, the sib-pair covariate difference, or both. One can include the sib-pair difference as an additional covariate if one believes that between-family differences in within-family variability contribute to locus heterogeneity. For the five largest Gleason-score signals, we added the sib-pair difference to the model but found no significant increase in LOD score. We are currently using simulations to explore these and other models of covariate action, and we plan to report the findings in a future publication. The one-parameter conditional logistic model for ARPs is expected to be available in the next release of S.A.G.E.; a beta version of the program is currently available from the Human Genetic Analysis Resource Web site.

Acknowledgments

This work was supported, in part, by U.S. Public Health Service grants HG01577 from the National Center for Human Genome Research, RR03655 from the National Center for Research Resources, CA88164 from the National Cancer Institute, and MH14677; by U.S. Army Medical Research and Material Command grants DAMD17-00-10108 and DAMD17-98-1-8589; and by grants from the Urologic Research Foundation. Some of the results in this article were obtained by S.A.G.E. software, which is supported by National Center for Research Resources grant RR03655.

Electronic-Database Information

Accession numbers and URLs for data in this article are as follows:

  1. Human Genetic Analysis Resource, http://darwin.cwru.edu/ (for S.A.G.E. software)
  2. Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/ (for CaP [MIM 176807], AR [MIM 313700], HPC1 [MIM601518], PCAP [MIM 602759], HPCX [MIM 300147], and CAPB [MIM 603688])

References

  1. Berry R, Schaid DJ, Smith JR, French AJ, Schroeder JJ, McDonnell SK, Peterson BJ, Wang Z-Y, Carpten JD, Roberts SG, Tester DJ, Blute ML, Trent JM, Thibodeau SN (2000a) Linkage analyses at the chromosome 1 loci 1q24-25 (HPC1), 1q42.2-43 (PCAP), and 1p36 (CAPB) in families with hereditary prostate cancer. Am J Hum Genet 66:539–546 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Berry R, Schroeder JJ, French AJ, McDonnell SK, Peterson BJ, Cunningham JM, Thibodeau SN, Schaid DJ (2000b) Evidence for a prostate cancer–susceptibility locus on chromosome 20. Am J Hum Genet 67:82–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Berthon P, Valeri A, Cohen-Akenine A, Drelon E, Paiss T, Wöhr G, Latil A, et al (1998) Predisposing gene for early-onset prostate cancer, localized on chromosome 1q42.2-43. Am J Hum Genet 62:1416–1424 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Broman KW, Murray JC, Sheffield VC, White RL, Weber JL (1998) Comprehensive human genetic maps: individual and sex-specific variation in recombination. Am J Hum Genet 63:861–869 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Carter BS, Beaty TH, Steinberg GD, Childs B, Walsh PC (1992) Mendelian inheritance of familial prostate cancer. Proc Natl Acad Sci USA 89:3367–3371 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cooney KA, McCarthy JD, Lange E, Huang L, Miesfeldt S, Montie JE, Oesterling JE, Sandler HM, Lange K (1997) Prostate cancer susceptibility locus on chromosome 1q: a confirmatory study. J Natl Cancer Inst 89:955–959 [DOI] [PubMed] [Google Scholar]
  7. Eeles RA, Durocher F, Edwards S, Teare D, Badzioch M, Hamoudi R, Gill S, Biggs P, Dearnaley D, Andern-Jones A, Dowe A, Shearer R, McLennan DL, Norman RL, Ghadirian P, Aprikian A, Ford D, Amos C, King TM, The Cancer Research Campaign/British Prostate Group UK Familial Prostate Cancer Study Collaborators, Labrie F, Simard J, Narod SA, Easton D, Foulkes WD (1998) Linkage analysis of chromosome 1q markers in 136 prostate cancer families. Am J Hum Genet 62:653–658 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Elston RC, Buxbaum S, Jacobs KB, Olson JM (2000) Haseman and Elston revisited. Genet Epidemiol 19:1–17 [DOI] [PubMed] [Google Scholar]
  9. Gauderman WJ, Siegmund KD (2000) Gene-environment interaction and affected-sib-pair linkage. Genet Epidemiol 19:248 [DOI] [PubMed] [Google Scholar]
  10. Gibbs M, Chakrabarti L, Stanford JL, Goode EL, Kolb S, Schuster EF, Buckley VA, Shook M, Hood L, Jarvik GP, Ostrander EA (1999a) Analysis of chromosome 1q42.2-43 in 152 families with high risk of prostate cancer. Am J Hum Genet 64:1087–1095 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gibbs M, Stanford JL, Jarvik GP, Janer M, Badzioch M, Peters MA, Goode EL, Kolb S, Chakrabarti L, Shook M, Basom R, Ostrander EA, and Hood L (2000) A genomic scan of families with prostate cancer identifies multiple regions of interest. Am J Hum Genet 67:100–109 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gibbs M, Stanford JL, McIndoe RA, Jarvik GP, Kolb S, Goode EL, Chakrabarti L, Schuster EF, Buckley VA, Miller EL, Brandzel S, Li S, Hood L, Ostrander EA (1999b) Evidence for a rare prostate cancer–susceptibility locus at chromosome 1p36. Am J Hum Genet 64:776–787 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Giovannucci E, Stampfer MJ, Krithivas K, Brown M, Brufsky A, Talcott J, Hennekens CH, Kantoff PW (1997) The CAG repeat within the androgen receptor gene and its relationship to prostate cancer. Proc Natl Acad Sci USA 94:3320–3323 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Goddard KAB (1999) Study design issues in the analysis of complex genetic traits. PhD thesis, University of Washington, Seattle [Google Scholar]
  15. Goode EL, Stanford JL, Chakrabarti L, Gibbs M, Kolb S, McIndoe RA, Buckley VA, Schuster EF, Neal CL, Miller EL, Brandzel S, Hood L, Ostrander EA, Jarvik GP (2000) Linkage analysis of 150 high-risk prostate cancer families at 1q24-25. Genet Epidemiol 18:251–275 [DOI] [PubMed] [Google Scholar]
  16. Greenlee RT, Murray T, Bolden S, Wingo PA (2000) Cancer statistics, 2000. CA Cancer J Clin 50:7–33 [DOI] [PubMed] [Google Scholar]
  17. Greenwood CMT, Bull SB (1999) Analysis of affected sib pairs, with covariates—with and without constraints. Am J Hum Genet 64:871–885 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Grönberg H, Smith J, Emanuelsson M, Jonsson B-A, Bergh A, Carpten J, Isaacs W, Xu J, Meyers D, Trent J, Damber J-E (1999) In Swedish families with hereditary prostate cancer, linkage to the HPC1 locus on chromosome 1q24-25 is restricted to families with early-onset prostate cancer. Am J Hum Genet 65:134–140 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Grönberg H, Xu J, Smith JR, Carpten JD, Isaacs SD, Freije D, Bova GS, Danber J-E, Bergh A, Walsh PC, Collins FS, Trent JM, Meyers DA, Isaacs WB (1997) Early age at diagnosis in families providing evidence of linkage to the hereditary prostate cancer locus (HPC1) on chromosome 1. Cancer Res 57:4707–4709 [PubMed] [Google Scholar]
  20. Holmans P (1993) Asymptotic properties of affected-sib-pair linkage analysis. Am J Hum Genet 52:362–374 [PMC free article] [PubMed] [Google Scholar]
  21. Hsieh CL, Oakley-Girvan I, Gallagher RP, Wu AH, Kolonel LN, Teh CZ, Halpern J, West DW, Paffenbarger RS, Jr, Whittemore AS (1997) Re: prostate cancer susceptibility locus on chromosome 1q: a confirmatory study. J Natl Cancer Inst 89:1893–1894 [DOI] [PubMed] [Google Scholar]
  22. Hsing AW, Gao Y, Wu G, Wang X, Deng J, Chen Y, Sesterhenn IA, Mostofi FK, Benichou J, Chang C (2000) Polymorphic CAG and GGN repeat lengths in the androgen receptor gene and prostate cancer risk: a population-based case-control study in china. Cancer Res 60:5111–5116 [PubMed] [Google Scholar]
  23. Ingles SA, Ross RK, Yu MC, Irvine RA, La Pera G, Haile RW, Coetzee GA (1997) Association of prostate cancer risk with genetic polymorphisms in vitamin d receptor and androgen receptor. J Natl Cancer Inst 89:166–170 [DOI] [PubMed] [Google Scholar]
  24. Keetch DW, Rice JP, Suarez BK, Catalona WJ (1995) Familial aspects of prostate cancer: a case control study. J Urol 154:2100–2102 [PubMed] [Google Scholar]
  25. Kruglyak L, Lander ES (1995) Complete multipoint sib-pair analysis of qualitative and quantitative trait data. Am J Hum Genet 57:439–454 [PMC free article] [PubMed] [Google Scholar]
  26. Lange EM, Chen H, Brierley K, Livermore H, Wojno KJ, Langefeld CD, Lange K, Cooney KA (2000) The polymorphic exon 1 androgen receptor CAG repeat in men with a potential inherited predisposition to prostate cancer. Cancer Epidemiol Biomarkers Prev 9:439–442 [PubMed] [Google Scholar]
  27. Lange EM, Chen H, Brierley K, Perrone EE, Bock CH, Gillanders E, Ray ME, Cooney KA (1999) Linkage analysis of 153 prostate cancer families over a 30-cM region containing the putative susceptibility locus HPCX. Clin Cancer Res 5:4013–4020 [PubMed] [Google Scholar]
  28. McCarthy MI, Kruglyak L, Lander ES (1998) Sib-pair collection strategies for complex diseases. Genet Epidemiol 15:317–340 [DOI] [PubMed] [Google Scholar]
  29. McIndoe RA, Stanford JL, Gibbs M, Jarvik GP, Brandzel S, Neal CL, Li S, Gammack JT, Gay AA, Goode EL, Hood L, Ostrander EA (1997) Linkage analysis of 49 high-risk families does not support a common familial prostate cancer-susceptibility gene at 1q24-25. Am J Hum Genet 61:347–353 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Monroe KR, Yu MC, Kolonel LN, Coetzee GA, Wilkens LR, Ross RK, Henderson BE (1995) Evidence of an X-linked or recessive genetic component to prostate cancer risk. Nat Med 1:827–829 [DOI] [PubMed] [Google Scholar]
  31. Olson JM (1999) A general conditional-logistic model for affected-relative-pair linkage studies. Am J Hum Genet 65:1760–1769 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ostrander EA, Stanford JL (2000) Genetics of prostate cancer: too many loci, too few genes. Am J Hum Genet 67:1367–1375 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Parkin DM, Pisani P, Ferlay J (1993) Estimates of the worldwide incidence of eighteen major cancers in 1985. Int J Cancer 54:594–606 [DOI] [PubMed] [Google Scholar]
  34. Rebbeck TR, Walker AH, Zeigler-Johnson C, Weisburg S, Martin AM, Nathanson KL, Wein AJ, and Malkowicz SB (2000) Association of HPC2/ELAC2 genotypes and prostate cancer. Am J Hum Genet 67:1014–1019 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Risch N (1990) Linkage strategies for genetically complex traits. II. The power of affected relative pairs. Am J Hum Genet 46:229–241 [PMC free article] [PubMed] [Google Scholar]
  36. Schaid DJ, McDonnell SK, Thibodeau SN (2001) Regression models for linkage heterogeneity applied to prostate cancer. Am J Hum Genet 68:1189–1196 (in this issue) [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Self SG, Liang K-Y (1987) Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under non-standard conditions. J Am Stat Assoc 82:605–610 [Google Scholar]
  38. Smith JR, Freije D, Carpten JD, Gronberg H, Xu J, Isaacs SD, Brownstein MJ, Bova GS, Guo H, Bujnovszky P, Nusskern DR, Damber JE, Bergh A, Emanuelsson M, Kallioniemi OP, Walker-Daniels J, Bailey-Wilson JE, Beaty TH, Meyers DA, Walsh PC, Collins FS, Trent JM, Isaacs WB (1996) Major susceptibility locus for prostate cancer on chromosome 1 suggested by a genome-wide search. Science 274:1371–1374 [DOI] [PubMed] [Google Scholar]
  39. Stanford JL, Just JJ, Gibbs M, Wicklund KG, Neal CL, Blumenstein BA, Ostrander EA (1997) Polymorphic repeats in the androgen receptor gene: molecular markers of prostate cancer risk. Cancer Res 57:1194–1198 [PubMed] [Google Scholar]
  40. Suarez BK, Lin J, Burmester JK, Broman KW, Weber JL, Banerjee TK, Goddard KA, Witte JS, Elston RC, Catalona WJ (2000) A genome screen of multiplex sibships with prostate cancer. Am J Hum Genet 66:933–944 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Tavtigian SV, Simard J, Labrie F, Skolnick MH, Neuhausen SL, Rommens J, Cannon-Albright LA (2000) A strong candidate prostate cancer predisposition gene at chromosome 17p. Am J Hum Genet Suppl 67:7 [Google Scholar]
  42. Whittemore AS (1994) Prostate cancer. Cancer Surv 19–20:309–322 [PubMed] [Google Scholar]
  43. Whittemore AS, Lin IG, Oakley-Girvan I, Gallagher RP, Halpern J, Kolonel LN, Wu AH, Hsieh C-L (1999) No evidence of linkage for chromosome 1q42.2-43 in prostate cancer. Am J Hum Genet 65:254–256 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Whittemore AS, Tu I-P (1998) Simple, robust linkage tests for affected sibs. Am J Hum Genet 62:1228–1242 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Witte JS, Goddard KAB, Conti DV, Elston RC, Lin J, Suarez BK, Broman KW, Burmester JK, Weber JL, Catalona WJ (2000) Genomewide scan for prostate cancer-aggressiveness loci. Am J Hum Genet 67:92–99 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Xu J, International Consortium for Prostate Cancer Genetics (2000) Combined analysis of hereditary prostate cancer linkage to 1q24-25: results from 772 hereditary prostate cancer families from the International Consortium for Prostate Cancer Genetics. Am J Hum Genet 66:945–957 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Xu J, Meyers D, Freije D, Isaacs S, Wiley K, Nusskern D, Ewing C, Wilkens E, Bujnovszky P, Bova GS, Walsh P, Isaacs W, Schleutker J, Matikainen M, Tammela T, Visakorpi T, Kallioniemi OP, Berry R, Schaid D, French A, McDonnell S, Schroeder J, Blute M, Thibodeau S, Trent J (1998) Evidence for a prostate cancer susceptibility locus on the X chromosome. Nat Genet 20:175–179 [DOI] [PubMed] [Google Scholar]
  48. Yuan B, Vaske D, Weber JL, Beck J, Sheffield VC (1997) Improved set of short-tandem-repeat polymorphisms for screening the human genome. Am J Hum Genet 60:459–460 [PMC free article] [PubMed] [Google Scholar]

Articles from American Journal of Human Genetics are provided here courtesy of American Society of Human Genetics

RESOURCES