Segregation Analyses of 1,476 Population-Based Australian Families Affected by Prostate Cancer

Abstract

Segregation analyses aim to detect genetic factors that have a major effect on an individual’s risk of disease and to describe them in terms of mode of inheritance, age-specific cumulative risk (penetrance), and allele frequency. We conducted single- and two-locus segregation analyses of data from 1,476 men with prostate cancer diagnosed at age <70 years and ascertained through population registries in Melbourne, Sydney, and Perth, Australia, and from their brothers, fathers, and both maternal and paternal lineal uncles. Estimation and model selection were based on asymptotic likelihood theory and were performed through use of the software MENDEL. All two-locus models gave better fits than did single-locus models, even if lineal uncles were excluded or if we censored data (age and disease status) for relatives at 1992, when prostate-specific–antigen testing started to have a major impact on the incidence of prostate cancer in Australia. Among the genetic models that we considered, the best-fitting ones included a dominantly inherited increased risk that was greater, in multiplicative terms, at younger ages, as well as a recessively inherited or X-linked increased risk that was greater, in multiplicative terms, at older ages. The recessive and X-linked effects were strongly confounded, and it was not possible to fit them together. Penetrance to age 80 years was ∼70% (95% confidence interval [CI] 57%–85%) for the dominant effect and virtually 100% for the recessive and X-linked effects. Approximately 1/30 (95% CI 1/80–1/12) men would carry the dominant risk, and 1/140 (95% CI 1/220–1/90) would carry the recessive risk or 1/200 (95% CI 1/380–1/100) would carry the X-linked risk. Within discussed limitations, these analyses confirm the genetic heterogeneity, of prostate cancer susceptibility, that is becoming evident from linkage analyses, and they may aid future efforts in gene discovery.

Introduction

Having a family history of prostate cancer (CaP [MIM 176807]) is one of the few well-established risk factors for the disease. The increased risk associated with having at least one affected first-degree relative is approximately twofold (Steinberg et al. 1990; Carter et al. 1992; Hayes et al. 1995; Bratt et al. 1997, 1999; Easton et al. 1997; Ghadirian et al. 1997). In multiplicative terms, this increased risk is greater (a) the younger the age at diagnosis in the affected relative and (b) the younger the age of the person at risk (Gronberg et al. 1996, 1997; Bishop and Kiemeney 1997). A similar pattern is apparent in other cancers; for example, the existence of genes associated with a dominantly inherited high breast-cancer risk that is greater (in multiplicative terms) at younger ages has been predicted by segregation analyses. These predictions have since been confirmed by molecular studies of the susceptibility loci BRCA1 (MIM 113705) and BRCA2 (MIM 600185) (Ford et al. 1998).

For CaP, the increased familial risk also appears to be greater if the affected relative is a brother rather than a father or son (Woolf 1960; Steinberg et al. 1990; Goldgar et al. 1994; Hayes et al. 1995; Monroe et al. 1995; Whittemore et al. 1995; Lesko et al. 1996; Schaid et al. 1998; Cerhan et al. 1999; Schuurman et al. 1999). A greater risk due to an affected sibling than due to an affected parent has been interpreted as evidence of X-linked or recessive inheritance of CaP risk (Monroe et al. 1995; Narod et al. 1995).

Moreover, recently published data suggest that an affected twin brother is associated with an even greater risk: 3-fold if in a DZ pair and up to 10-fold if in an MZ pair (Gronberg et al. 1994; Page et al. 1997; Lichtenstein et al. 2000). There are several plausible reasons why concordances are higher in twins than those in nontwins, and higher still in MZ pairs. First, there may be environmental or lifestyle factors that have an impact on the risk and/or age at diagnosis of disease and that are shared to a greater extent by twins than by nontwins. In particular, diagnosis of CaP in a brother could spur a man to seek screening by the prostate-specific–antigen (PSA) test. The effect that diagnosis in a sibling has on screening behavior could be stronger if the brother is a twin rather than a nontwin and could be stronger within MZ pairs than within DZ pairs. There could also be genetic factors, which would explain at least part, but not necessarily all, of the excess concordance in MZ pairs compared with DZ pairs.

Single-locus segregation analyses aim to identify the mode of inheritance and other characteristics of the most plausible genetic factor(s) that may have a major effect on an individual’s risk of disease. For CaP these analyses have typically supported the role of a rare (allele frequency ∼.005) dominantly inherited set of genetic risk factors that confer a high lifetime risk, of up to 90% by age 85 years (Carter et al. 1992; Schaid et al. 1998), although there is also a report of a more common genetic risk (allele frequency .017), with a lower cumulative probability (63% to age 85 years) (Gronberg et al. 1997). These segregation analyses, however, have analyzed data only from first-degree relatives of affected probands, and, hence, their ability to differentiate between different modes of inheritance has been limited. A recent segregation analysis suggested that a dominant model alone cannot adequately explain family data when probands were diagnosed at age >70 years (Schaid et al. 1998). To the best of our knowledge, segregation analyses considering more than one mode of inheritance do not appear to have been published previously. Much can be learned from segregation analyses that accommodate multiple sources of familial aggregation simultaneously and that use data from more than just nuclear families, as we have demonstrated recently for breast cancer (Cui et al. 2001).

During the past few years, at least six regions of the genome have been identified that may contain loci associated with a high risk of CaP. Based on results of previous single-locus segregation analyses, classic linkage studies of the autosomal chromosomes have presumed dominant inheritance and have used the estimates of both age-specific risk in carriers and allele frequency quoted above. Candidate regions include the following: 1q24-25 (the putative CaP-susceptibility locus HPC1 [MIM 601518]) (Smith et al. 1996; Cooney et al. 1997; Hsieh et al. 1997; Xu et al. 2000), 1q42.2-43 (PCaP [MIM 602759]) (Berthon et al. 1998), 1p36 (CAPB [MIM 603688]) (Gibbs et al. 1999), 16q23.2 (CTRB1 [MIM 118890]) (Paris et al. 2000), and, more recently, 17p (HPC2/ELAC2 [MIM 605367]) (Rebbeck et al. 2000; Tavtigian et al. 2000). For all of these putative autosomal loci, there also exist reports that have failed to find evidence of linkage. There has also been a report of a possible locus on the X chromosome, at the region Xq27-28 (HPCX [MIM 300147]) (Xu et al. 1998). Whereas evidence for linkage to putative loci with a presumed dominant inheritance of risk has almost all come from a small subset of families with CaP that have multiple affected members, usually with early-onset disease, recent evidence for X linkage has come from families with fewer cases and with a later-onset disease (Schleutker et al. 1999).

We have conducted single-locus and two-locus segregation analyses of a large series of families, unselected for family history, based on men with clinically significant CaP diagnosed at age <70 years. The families consist of the proband and his father, brothers, and lineal uncles on both sides of the family. The study was performed during a period when CaP screening by the PSA test was gaining popularity in Australia. Consequently, we have adjusted baseline risks and have conducted analyses in which information on relatives has been censored back to a time prior to the impact of PSA testing, to assess the sensitivity of our model fits.

Subjects and Methods

Subjects

Data on family cancer history were collected by face-to-face interview of participants in a population-based case-control study of risk factors for CaP, conducted in Melbourne, Sydney, and Perth (G. G. Giles, G. Severi, M. R. E. McCredie, D. R. English, M. P. Staples, J. L. Hopper, W. Johnson, P. Boyle, unpublished data). Patients were considered eligible if they were men (1) with a first primary invasive adenocarcinoma of the prostate, with Gleason score >4; (2) diagnosed between April 1, 1994 and December 31, 1997; (3) age at diagnosis <70 years; and (4) resident in the metropolitan areas of these state capital cities. Patients were identified from the state cancer registries of Victoria, New South Wales, and Western Australia and were approached with the permission of their treating urologist. In this analysis, only data from patients (hereafter referred to as the “probands”) and their relatives were used.

Information about date of birth, vital status, and history of cancer in all first-degree relatives and in both maternal and paternal lineal uncles was sought from probands by means of a self-completed questionnaire. Date at diagnosis (and, therefore, age at diagnosis) was recorded for the proband and for all affected relatives. Age at last interview—and age at death, if the individual no longer was alive—were recorded for all unaffected relatives. Information about grandfathers was not collected, because it was found that few probands had reliable information about CaP in grandfathers. To date, we have been able to confirm 45% (165/363) of all reports of CaP in relatives, 56% (62/111) for brothers, 44% (71/163) for fathers, and 36% (32/89) for uncles. No false positives have been detected. The analyses below are based on the proband’s report of family history.

Statistical Analysis

The cumulative probability of CaP in a defined cohort of relatives of the probands—F(t)=1-S(t), where S(t) is the survivor function—was estimated by the Kaplan-Meier product-limit method (Kaplan and Meier 1958), based on the disease status and censored age and calculated by the statistical software STATA, release 6 (Stata Corporation). The variance of the product-limit estimator was estimated by Greenwood’s (1926) formula and was used to calculate confidence intervals. This was performed separately for probands and their brothers, fathers, and lineal uncles on both maternal and paternal sides of each family.

Complex segregation analyses were performed under maximum-likelihood theory, by the software MENDEL (Lange et al. 1988). We fitted what have traditionally been called single-locus and two-locus models of “major gene” effects with different modes of inheritance (autosomal dominant, recessive, codominant, and X linked). To adjust for ascertainment, the likelihood for each pedigree was conditioned on the proband being affected at his age at diagnosis of CaP.

For a single-locus model, let a represent a disease allele and assume a Mendelian mode of transmission. Let p=1-q be the population frequency of all disease alleles at this locus and assume random mating and Hardy-Weinberg equilibrium at this locus (Elandt-Johnson 1971). Note that, despite its historic name, a single-locus model may represent effects with the same mode of inheritance at multiple loci, provided that, at each of these loci, the at-risk genotype (e.g., Aa or aa for dominant inheritance or aa for recessive inheritance) is so rare that it is highly unlikely that more than one locus contributes to this type of genetic risk in any one family.

In accordance with the studies by Ford et al. (1998) and Cui and Hopper (2000), a proportional-hazards model was assumed, in which the hazard function of development of CaP at age t, in calendar year group k (k=1,2,⋅⋅⋅,K), for a male with i disease alleles (i=0,1,2), is given by λ_i(t,k)=HR_i(t)λ₀(t,k), where we set HR₀(t)=1, so that HR_i(t) is the genetic hazard ratio at age t (Benichou 1997) for males with i alleles, compared with that for noncarriers. Here the hazard ratio HR_i(t) depends only on age t, not on calendar-year group k—whereas the absolute hazard, λ_i(t, k), is assumed to be dependent on both age t and calendar-year group k, to reflect the change in CaP incidences since the early 1990s, after the introduction of PSA testing.

We chose the number of calendar-year groups to be K=2, with λ(t, 1) representing the age-specific incidence before 1992 and λ(t, 2) the incidence after 1992. This is because the incidence rate was relatively stable before 1992 and then increased by nearly twofold from 1992 to 1996 (Giles et al. 1992, 1998; McCredie et al. 1996). Incidence rates were calculated using a population-weighted average of age-specific rates from each of the three states. First-, second-, third-, and fourth-order polynomial functions were used to model the log hazard ratio ln[HR_i(t)]. For females, we assumed that λ_i(t,k)=0 for all i.

We modeled ln[HR_i(t)] as a Jth-order polynomial function of age t, given by

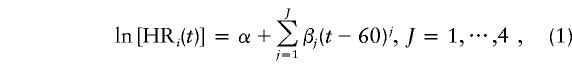where exp(α) is the hazard ratio at age 60 years.

Let λ(t, k) be the population incidence of CaP at age t, in calendar-year group k. If, for simplicity, it is assumed that there is no mortality difference, by genotype, across the age ranges considered (although this could have been implemented; e.g., see Bishop et al. [1988]), then, for an autosomal locus, the hazard function for noncarriers is given by

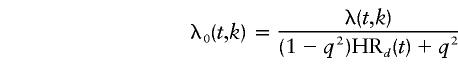under dominant inheritance, where HR₁(t)=HR₂(t)=HR_d(t); by

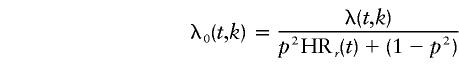under recessive inheritance, where HR₁(t)=1 and HR₂(t)=HR_r(t); and by

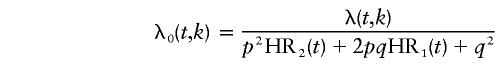under the codominant model, where HR₁(t) and HR₂(t) are not necessarily equal to HR₀(t) or to each other.

For a locus on the X chromosome, the hazard function for noncarriers is given by

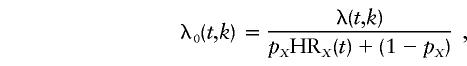where HR₁(t)=HR_X(t), HR₂(t)=0, and p_X is the frequency of all disease alleles at that locus.

We estimated all parameters on the log scale—that is, as ln(p), ln[HR₁(t)], and ln[HR₂(t)]—because on that scale their log-likelihood profiles were close to a quadratic curve. Maximum-likelihood theory, therefore, suggests that their distributions are close to normal and thus valid variance estimates are obtainable from the asymptotic covariance matrix.

The probability that a male with i disease alleles develops CaP at age t, in calendar-year group k (so as to allow for an effect of PSA testing on incidence rate), is given by

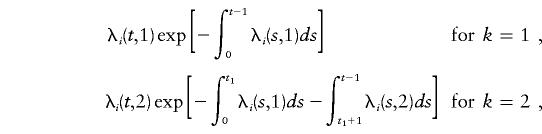where t₁ is the male’s age in 1992. The probability that a male does not develop the disease before age t, in calendar-year group k=2, is given by

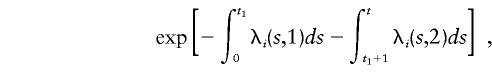where i=0,1,2 indicates the number of disease alleles.

For a two-locus model, without loss of generality, we assume dominant inheritance for the first locus and X-linked inheritance for the second. The interaction between the effects of these two loci was allowed to be multiplicative or additive. Under a multiplicative model, the hazard ratio for carriers of both a dominant and X-linked risk is given by HR_d×HR^′_X, where HR_d is the hazard ratio for carriers of the dominant risk and HR^′_X the hazard ratio for carriers of the X-linked risk; under an additive model, the hazard ratio is HR_d+HR^′_X. The correlations between the estimates of pairs of model parameters (e.g., the dominant and X-linked allele frequencies and the dominant and X-linked hazard ratios) were estimated from the asymptotic correlation matrix given by MENDEL (Lange et al. 1988).

Nested models were compared using the likelihood-ratio test; otherwise, we used Akaike’s (1974) information criterion (AIC), defined as AIC = 2(−maximum log-likelihood + no. of parameters estimated). The AIC serves as a measure for assessing the relative fits of unnested models by adding a penalty to each log-likelihood to reflect the number of parameters estimated under a particular model. The parsimonious model was taken to be that with the minimum AIC.

To examine the possible effects of the introduction of PSA testing, we conducted sensitivity analyses. The age and disease status of all relatives were assumed to be the age and disease status present at the beginning of 1992. To identify the families that were most likely to be contributing to a particular major-gene effect (dominant, recessive, codominant, or X linked), we calculated, for each family, the change that occurred in log-likelihood when that effect was included in a single-locus model, compared with a null model, in which the effect was not included.

Results

Descriptive Statistics and Analysis of Cohorts of Relatives

A total of 1,476 families (based on 437 probands living in Sydney, 786 in Melbourne, and 253 in Perth) contained 8,836 male relatives, of whom 363 (4%) had been diagnosed with CaP. Approximately 80% of the probands (1,192/1,476) did not have a father with CaP or any brothers or uncles with CaP; two probands had three affected brothers; five probands had three affected lineal uncles; and four probands had four affected relatives.

Table 1 shows that 11% (163/1,476) of fathers, 6% (111/1,890) of brothers, and 3.5% (89/2,552) of lineal uncles had been diagnosed with CaP. The median age at diagnosis of CaP was 61 years (mean 61 years, SD 6 years) for the probands, 62 years (mean 63 years, SD 6 years) for the affected brothers, 75 years (mean 74 years, SD 8 years) for the affected fathers, and 75 years (mean 75 years, SD 8 years) for the affected lineal uncles.

Table 1.

Number of Men with CaP, by Age at Diagnosis, for Different Categories of Family Members

	No. (%) of Affected Men
Age atDiagnosis(years)	Proband (n=1,476)	Father (n=1,476)	Brother (n=1,890)	Uncle (n=2,552)
<50	56 (3.8)	1 (.6)	2 (1.8)	0
50–54	183 (12.4)	3 (1.8)	11 (9.9)	1 (1.1)
55–59	412 (27.9)	6 (3.7)	18 (16.2)	2 (2.3)
60–64	366 (24.8)	8 (4.9)	36 (32.4)	7 (7.9)
65–69	459 (31.1)	25 (15.3)	33 (29.7)	11 (12.4)
70–74	0	35 (21.5)	8 (7.2)	22 (24.7)
75–79	0	34 (20.9)	1 (0.9)	20 (22.5)
80–85	0	34 (20.9)	2 (1.8)	17 (19.1)
⩾85	0	17 (10.4)	0	9 (10.1)
Total	1,476	163	111	89

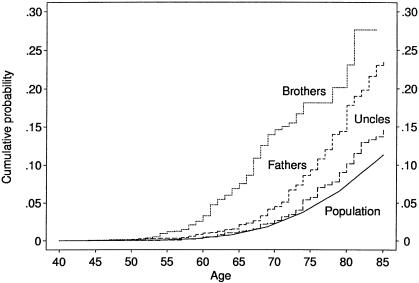
Figure 1 shows the cumulative probability of CaP for the Australian population and for cohorts defined by the brothers, fathers, and lineal uncles of the proband. By the mid-1990s, ∼1% of Australian men were diagnosed with CaP at age <65 years, 5% at age <75 years, and 12% at age <85 years (Giles et al. 1998). For the brothers, ∼8% (95% confidence interval [CI] 6%–10%) were affected by age 65 years and 18% (95% CI 14% - 22%) were affected by age 75 years. When we used data (age and disease status) collected from brothers prior to 1992, 5% were affected by age 70 years, but this estimate was based on just 20 cases, and there was little information on brothers beyond that age. For fathers, ∼9% (95% CI 7%–11%) were affected by age 75 years. There also appeared to be a small excess risk in lineal uncles, at least by age 75 years when ∼6% (95% CI 4%–8%) were affected. There was no discernible difference between paternal and maternal uncles (χ²₍₁₎=3.1, P=.08).

Figure 1.

Age-specific cumulative probability of CaP for the population and for brothers, fathers, and lineal uncles of the probands who had CaP at age <70 years.

Segregation Analyses—Single-Locus Models

Table 2 (top half) shows the best-fitting single-locus models for different modes of inheritance. Under dominant inheritance alone, the log hazard ratio was best described by a quadratic function of age (i.e., β₃=0 in eq. [1]). The cumulative probability of CaP in carriers of at least one copy of the disease allele was estimated to be 7%, 36%, and 79% to ages 60, 70, and 80 years, respectively. These cumulative probability estimates were not changed greatly when different polynomial models for ln[HR_i(t)] were fitted. Under the assumption of constant hazard ratio (results not shown), the estimated allele frequency was .011 (95% CI .006–.021), and the hazard ratio was 36 (95% CI 27–47).

Table 2.

Best-Fitting Segregation Analyses of Single-Locus and Two-Locus Models

	Estimate (95% CI)
		Hazard-Ratio Parametera
Model and Mode of Inheritance	Allele Frequency	exp(α)	β1	β2	β3	Log-Likelihood	AIC
Single-locus models:
Null	0	1	0	0	0	−2,305.23	4,610.46
Dominant	.009 (.006 to .015)	47.9 (31.1 to 73.8)	−.2283 (−.3431 to −.1134)	.0114 (.0047 to .0181)	0	−2,136.79	4,281.58
Recessive	.187 (.160 to .220)	32.2 (24.9 to 44.2)	−.1174 (−.1512 to −.0836)	−.0010 (−.0038 to .0018)	.0005 (.0003 to .0007)	−2,120.60	4,249.20
X linked	.014 (.008 to .026)	48.0 (32.5 to 71.0)	−.1063 (−.1628 to −.0498)	.0015 (−.0031 to .0061)	.0009 (.0004 to .0014)	−2,154.83	4,319.66
Two-locus multiplicative models:
Dominant + rcessive						−2,097.84	4,211.68
Dominant	.017 (.006 to .044)	7.7 (2.2 to 26.6)	−.2555 (−.4187 to −.0923)	.0231 (.0066 to .0396)
Recessive	.084 (.067 to .105)	93.5 (59.6 to 146.5)	.0779 (.0149 to .1409)	−.0010 (−.0090 to .0069)
Dominant + X linked						−2,101.21	4,218.42
Dominant	.012 (.006 to .026)	14.3 (7.3 to 28.2)	−.2272 (−.3525 to −.1019)	.0174 (.0089 to .0258)
X linked	.005 (.003 to .009)	82.4 (49.0 to 138.6)	.0764 (.0121 to .1408)	−.0045 (−.0128 to .0038)

^aThe natural logarithm of the hazard ratio is parameterized as a polynomial in age, according to equation (1).

Under recessive inheritance alone, the best-fitting model of the log hazard ratio was a cubic function of age. The cumulative probability of CaP in homozygote carriers was 14%, 62%, and 96% to ages 60, 70, and 80 years, respectively. Again, the estimated penetrances did not change greatly for different polynomial models. Under the assumption of constant hazard ratio (results not shown), the estimated allele frequency was .15 (95% CI .11–.20), and the hazard ratio was 43 (95% CI 27–70). The estimates under codominant inheritance were similar to those under recessive inheritance.

Under X-linked inheritance alone, the best-fitting model of log hazard ratio was a cubic function of age. The cumulative probability of CaP in carriers of the X-linked risk was 20%, 75%, and 99% to ages 60, 70, and 80 years, respectively. Under the assumption of constant hazard ratio, the estimated allele frequency was .01 (95% CI .004–.022), and the hazard ratio was 62 (95% CI 36–108). On the basis of AIC, the recessive model was the most parsimonious single mode-of-inheritance model.

Segregation Analyses—Two-Locus Models

Table 2 (bottom half) shows the best-fitting two-locus models under the multiplicative assumption; we found that the fits were better if it was assumed that the interaction effects were multiplicative rather than additive (results not shown). The two-locus recessive + X-linked model is not shown because it was not possible to derive estimates, owing to the lack of convergence of the maximization algorithm, presumably reflecting the collinearity of parameters describing these two modes of inheritance when this family design was used. In all two-locus models, the best-fitting description of the log hazard ratio was a quadratic function of age. The two-locus models gave a better fit than did the single-locus models. As judged on the basis of AIC and the likelihood-ratio tests, the dominant + recessive multiplicative model gave a better fit than did the dominant + X-linked model. The strength of dominant effect, in terms of the allele frequency and hazard ratio, was reduced by incorporation of a recessive or X-linked effect. Under the multiplicative assumption, the cumulative probability of CaP to age 80 years in carriers of the dominant risk decreased from 75% to either 69%, when a recessive risk was added, or to 72%, when an X-linked risk was added; on the other hand, the cumulative probability of CaP for carriers of the recessive risk was increased by incorporation of a dominant effect, increasing from 91% to 100% by age 80 years. The corresponding probability for carriers of the X-linked risk also was increased, from 69% to 100% by age 80 years, after incorporation of a dominant effect.

The correlation coefficients between the estimates of the allele frequencies for the two modes of inheritance were small and not significant, being .09 and .07 under multiplicative dominant + X-linked and dominant + recessive models, respectively. Similarly, the correlation coefficients between the estimates of hazard ratios of the two modes of inheritance were all <.20 and not statistically significant.

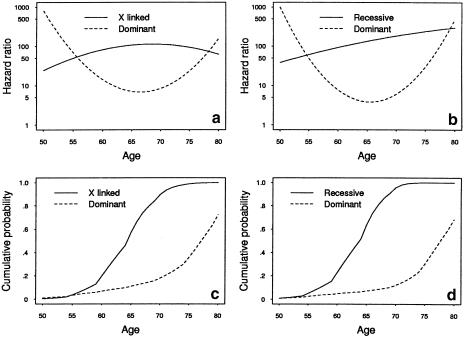
Figure 2a and b shows the estimated best-fitting quadratic hazard ratios under the two-locus models, plotted on a log scale. Similar graphs were evident from fits that allowed for the hazard ratios to be a cubic function of age. The hazard ratio for the dominantly inherited risk decreased rapidly, from ∼800 at age 50 years to 10 at age 70 years. The hazard ratio for the X-linked risk increased from 25 at age 50 years to 110 at age 70 years and then stabilized at that level. The hazard ratio for the recessively inherited risk increased from 40 at age 50 years to ∼180 at age 70 years; that is, the dominant risk was more evident at earlier ages, whereas the X-linked and recessive risks were more evident at later ages.

Figure 2.

Estimated hazard ratios and cumulative probabilities under two-locus multiplicative models

Figure 2c and d shows the estimated cumulative probability of CaP for carriers of the dominantly inherited, X-linked, and recessively inherited risks, based on the estimates given in the bottom half of table 2. The penetrance for carriers of the X-linked risk increased rapidly, from 19% to 89% and 100% at ages 60, 70, and 80 years, respectively, similar to the penetrance for carriers of the recessive risk, which increased from 23% to 94% and 100% at the same ages; irrespective of the mode of inheritance at the other locus, the penetrance for carriers of the dominant risk increased from 7% to 18% and 72%, at the same ages.

Table 3 shows the 10 families for which the change in log-likelihood was greatest as a result of addition of an X-linked single-locus effect to a null model. These families have either multiple brothers affected or lineal maternal uncles affected, if not both. Nine probands were diagnosed at age ⩽60 years, and 80% (14/18) of the affected brothers were diagnosed at age <65 years. The three affected maternal uncles, however, were diagnosed at age >70 years.

Table 3.

Age at Diagnosis of All Affected Members of 10 Families for Which the Change in Log-Likelihood was Greatest When an X-Linked, Recessive, and Dominant Effect Was Added to the Null Model

	Age(s) at Diagnosis(years)
Inheritance andFamily ID	Proband	Father	Brother(s)	Uncle(s)	ΔLLa
X linked:
VIC1216	51	…	61, 68	74b (Maternal)	7.15
VIC50	60	…	59, 66, 67	…	6.77
VIC895	54	…	52, 58	…	6.61
VIC1335	58	72b	57, 60	…	5.85
VIC1805	49	64b	…	74b (Maternal); 54b, 70b (Paternal)	5.10
WA2300	59	…	59,63		5.09
VIC1290	52	…	61	74b (Maternal)	4.90
NSW621	57	…	64b, 64b	…	4.88
NSW831	53	…	63, 65	…	4.81
NSW54	61	…	62, 66	…	4.54
Recessive:
VIC1335	58	72b	57, 60	…	6.69
VIC895	54	…	52, 58	…	6.09
VIC1805	49	64b	…	74b (Maternal); 54b, 70b (Paternal)	5.83
VIC1216	51	…	61, 68	74b (Maternal)	5.39
NSW770	55	78b	54	…	5.33
VIC1132	55	80b	52b	…	5.11
VIC479	55	54b	66b	…	5.08
VIC50	60	…	59, 66, 67	…	5.04
NSW780	55	80b	53	…	4.96
WA1605	60	71b	60	77 (Paternal)	4.89
Dominant:
VIC1335	58	72b	57, 60	…	5.98
VIC1805	49	64b	…	74b (Maternal); 54b, 70b (Paternal)	5.41
VIC895	54	…	52,58	…	5.15
NSW817	55	72	…	76, 82, 82 (Paternal)	5.09
VIC1216	51	…	61, 68	74b (Maternal)	4.91
VIC479	55	54b	66b	…	4.66
NSW770	55	78b	54b	…	4.50
VIC1637	55	70b	54b	…	4.42
VIC1132	55	80b	52b	…	4.39
WA1605	60	71b	60	77 (Paternal)	4.38

^aChange in log-likelihood, compared with the null model.

^bDiagnosed before 1992.

Table 3 also shows the 10 families that provided the most evidence for a recessively inherited risk. These families also have either multiple affected brothers or an affected father or uncles. More than 60% (9/14) of affected brothers were diagnosed at age <60 years. Seven families had an affected father, compared with only two families in the X-linked situation. Five families contributed both to the 10 families most influential for the X-linked mode of inheritance and to the 10 families most influential for the recessive mode of inheritance. Finally, table 3 shows the 10 families that provided the most evidence for a dominantly inherited risk, 8 of which also contributed to those for the recessive model and 4 of which contributed to those for the X-linked model.

We performed two sets of sensitivity analyses, using the age and disease status of relatives prior to 1992 and only first-degree relatives of the probands. Both of the two-locus models still gave a better fit than did the single-locus model, irrespective of how we restricted the data from relatives. Estimates of the allele frequency were smaller when data on relatives were censored. For example, under the constant–hazard-ratio assumption and the multiplicative two-locus model, the allele frequency for the dominant risk was ∼.01, irrespective of whether the other locus was recessive or X-linked, compared with .03 when data for all relatives were used, and the estimated constant hazard ratio was stable, at ∼15. The estimated allele frequency for the X-linked risk was .0001, compared with .005 when data for all relatives were used. Also, the estimated allele frequency of the recessive risk became .05, compared with .08. The estimated constant hazard ratio did not change much for the dominant risk; however, it became ∼60 and ∼160 for the recessive and X-linked risks, respectively.

For the recessive effect, the allele frequency decreased from .08 to .05 when the relatives were censored, and the constant hazard ratio decreased from 110 to 60, with the cumulative probability to age 70 years decreasing from 91% to 75%. For the X-linked effect, the allele frequency decreased from .005 to .001, although the constant hazard ratio increased from 90 to 160, and the cumulative probability to age 70 years increased from 86% to 97%.

When we used only first-degree relatives of the probands, the estimated allele frequency was slightly higher, with a wider 95% CI, than when we used all relatives. The estimated allele frequency of the dominant risk became .04, whereas the estimated allele frequency for recessive and X-linked risks became .09 and .007, respectively. The estimated constant hazard ratio for the dominant risk became ∼20, whereas for recessive and X-linked risk it became ∼100 and ∼80, respectively.

Discussion

Our two-locus segregation analysis, of families with CaP that included uncles of probands, has confirmed the likely genetic heterogeneity of CaP. Segregation analyses aim to detect genetic factors that have a major effect on an individual’s risk of disease; hence, the term “major gene effects” is often used. For CaP we have found that such effects could include two or more of the following: (1) dominantly inherited risks contributing especially to early-onset disease, (2) X-linked risks, and (3) recessively inherited risks, the latter two appearing to contribute more to later-onset disease. Recent linkage and other molecular studies have identified several autosomal regions, as well as one region on the X chromosome, that may contain genes contributing a (dominantly) inherited risk (Ostrander and Stanford 2000).

Most of the previous segregation studies have been single-locus and restricted to nuclear families. They have tended to favor a dominantly inherited risk for CaP (Steinberg et al. 1990; Gronberg et al. 1994; 1996; Hayes et al. 1995; Page et al. 1997). However, some studies have claimed evidence of an X-linked or recessively inherited risk, on the basis of the observation that relative risk due to the presence of an affected brother is greater than that due to the presence of an affected father or son (Monroe et al. 1995; Narod et al. 1995). To the best of our knowledge, ours is the first segregation analysis of CaP that has fitted two-locus models and that has used more than just nuclear families. We found stronger evidence for the co-occurrence of both the dominant and the nondominant modes of inheritance than for the occurrence of either mode alone. The penetrance associated with the nondominant effects appears to be considerably higher than that for the dominant effects, even after the data on relatives are censored so as not to include cases identified by the recent epidemic of PSA-detected CaP in Australia (see below). It was not possible, however, with the family structure of our design, to discriminate between recessive and X-linked effects.

The introduction of PSA testing during the early 1990s in Australia has led to a dramatic increase in the incidence of CaP in the subsequent years. Recent statistical modeling (Etzioni et al. 1998) has suggested that ∼50% of new cases in the United States would have been unlikely to have come to clinical diagnosis in the absence of PSA testing. There is also evidence that men with CaP diagnosed by PSA testing are ∼3–5.5 years younger than those with CaP diagnosed by either digital rectal examination or physical symptoms (Gann et al. 1995; Pearson et al. 1996). In the present study, 82% (91/111) of brothers, compared with 20% (32/163) of fathers and 33% (29/89) of uncles, were diagnosed during or after 1992. To adjust for the changing incidence of CaP over time, we used calendar-time–specific baseline incidences—namely, a lower incidence before 1992 and a higher incidence after 1992—based on Australian cancer-registry data.

We only fitted models for genetic factors that had a strong influence on individual risk. It is possible that familial aggregation could also be due to nongenetic factors shared by relatives. Some segregation analyses claim to fit, if not exclude, so-called “environmental models,” through a convenient but limited parameterization of the transmission probabilities. In reality, the family environment could act in many and much more sophisticated ways. Family and twin analyses of continuous traits have demonstrated that evidence for effects of family environment can be inferred from modeling of the familial trait correlations, through use of both genetic relationship and cohabitation status, provided that the design is such that genetic and nongenetic effects are not highly confounded (as is usually the case with nuclear-family–alone designs); for example, see the report by Harrap et al. (2000). Therefore, interpretation of our model fits must take into account that at least a component of familial aggregation could be due to nongenetic familial factors. In the present study, our aim has not been to tease apart the unmeasured effects of genes and environment, which would be better done by specialized designs such as those involving twin or adoptee families; instead, our aim has been to try to make inferences about the types and characteristics of major-gene effects, primarily to assist efforts aimed at gene discovery.

Environmental or lifestyle factors associated with a substantial risk of disease have yet to be identified. However, given that there is a high prevalence of latent CaP in older men, familial aggregation could, in part, be due to diagnostic zeal. This has become of particular importance in recent years, with the advent of PSA testing. Screening behavior is likely to be correlated within families, particularly between brothers: an unaffected man whose brother has been recently diagnosed with CaP could be prompted to have a PSA test himself, leading to a diagnosis of CaP at an age much earlier than when it otherwise would have occurred (if ever).

To assess the impact of PSA testing on our model fits, we conducted sensitivity analyses, by ignoring information on relatives collected since the beginning of 1992. We found that the estimates of allele frequency and penetrance for the dominantly inherited risk were robust to this censoring. For the recessive effect, both the allele frequency and cumulative probability decreased slightly. For the X-linked effect, however, there was a substantial decrease in the estimate of the allele frequency, as well as an increase in the estimate of the cumulative probability. The instability of estimates for the nondominant effects may be due to the reduction in the number of incident cases among relatives, especially among brothers. Nevertheless, despite ignoring all cases in relatives since 1992, we still found evidence of nondominant genetic effects in addition to dominantly inherited ones. The most realistic model probably lies somewhere between that fitted with all data of relatives and that with the censoring of data at the beginning of 1992.

We modeled the increased risk in carriers by multiplying the age-specific population incidence by a factor (the hazard ratio) and fitted polynomial functions for the log hazard ratio. We used the flexibility of this set of functions to examine nonconstant or nonlinear trends of multiplicative genetic risks in carriers. Implementation of this strategy led to detection of both a decreasing trend with age, for the dominant hazard ratio, and an increasing trend with age, for the X-linked and recessive hazard ratio, at early ages. Both of these trends tended to dissipate at later ages (fig. 2); that is, in multiplicative terms there were quantitatively different patterns for the dominantly inherited increased risk, which was greater at earlier ages, compared with the nondominant risks, which were greater at later ages. This is of interest, given that the linkage study of Schleutker et al. (1999) found evidence for X linkage in families with later mean ages at onset and with relatively few cases, in contrast with the studies finding evidence for dominantly inherited risk at the putative HPC1 region, confined mostly to families with multiple cases of early mean age at diagnosis (Smith et al. 1996; Cooney et al. 1997; Hsieh et al. 1997; Xu et al. 2000).

Nevertheless, our family data still combine both CaP diagnosed prior to PSA testing (in the majority of affected fathers and uncles) and CaP diagnosed during the PSA-testing era (in all probands and in the great majority of brothers); that is, the phenotype does not necessarily have the same definition within a family. (This phenomenon is probably having a major impact on CaP linkage studies, by inducing phenocopies.) In addition to the sensitivity analyses, we have attempted to obtain some uniformity of phenotype definition within and between families, by excluding from recruitment as probands those newly diagnosed cases who had a Gleason score <5; that is, we have focused on clinically significant CaP. Nevertheless, we are still likely to have included a proportion of probands who would not have been diagnosed if not for PSA testing. CaP is a biologically heterogeneous disease. One way to increase disease specificity is to retrieve archival tissue and to perform immunohistochemical studies in order to define homogenous subgroups for future reanalysis. We are pursuing this approach.

The question remains as to the identity of the population about which we are making inferences. We have sampled families through probands with clinically significant CaP diagnosed at age <70 years. Therefore, the genes that are apparently segregating in these families are those which are most likely to cause such early-onset disease. We have, in effect, estimated the penetrance of these genes through use of the disease history of the relatives of the probands, as has been done for mutations in BRCA1 and BRCA2 through use of the families of known mutation carriers (Hopper et al. 1999). In doing so, we have estimated the penetrance function to ages beyond the latest age at diagnosis of the probands.

In summary, our analyses need to be interpreted within the usual caveats that apply to segregation analyses; in particular, that they are trying to determine the best-fitting genetic models, not to differentiate between genetic effects and a broad range of plausible environmental effects. Furthermore, PSA testing has created problems in terms of disease definition and may be contributing to the high incidence rate that has been seen in brothers since 1992—and, thereby, artifactually may be giving more credence to models that include nondominant modes of inheritance. Nevertheless, our analyses suggest that there may be multiple sources of genetic risks for CaP, involving autosomal genes associated with dominantly and recessively inherited risks, as well as one or more genes on the X chromosome. Therefore, in addition to further exploration of dominant inheritance of CaP, future linkage studies might benefit from consideration of recessive effects of high penetrance and should continue to examine the X chromosome, for the presence of cancer-susceptibility genes. The findings in the present study may have implications for future efforts in gene discovery.