Complexity and Power in Case-Control Association Studies

Abstract

A general method is described for estimation of the power and sample size of studies relating a dichotomous phenotype to multiple interacting loci and environmental covariates. Either a simple case-control design or more complex stratified sampling may be used. The method can be used to design individual studies, to evaluate the power of alternative test statistics for complex traits, and to examine general questions of study design through explicit scenarios. The method is used here to study how the power of association tests is affected by problems of allelic heterogeneity and to investigate the potential role for collective testing of sets of related candidate genes in the presence of locus heterogeneity. The results indicate that allele-discovery efforts are crucial and that omnibus tests or collective testing of alleles can be substantially more powerful than separate testing of individual allelic variants. Joint testing of multiple candidate loci can also dramatically improve power, despite model misspecification and inclusion of irrelevant loci, but requires an a priori hypothesis defining the set of loci to investigate.

Introduction

In complex diseases, the genetic component of risk may be spread across several loci, requiring either sufficient statistical power to detect the modest contribution of individual genes or some means of evaluating loci collectively. Risch and Merikangas (1996) considered the former strategy in the context of a single-locus two-allele system and concluded that association tests are powerful enough to detect the modest effects of individual loci in complex disorders. Slager et al. (2000) found that allelic heterogeneity greatly reduced power for tests of individual alleles. A general method of power analysis for complex traits is described here and is used to investigate the power of a broader class of tests in the face of allelic heterogeneity and misclassification, as well as the alternative strategy of collective testing of multiple loci.

The designs considered here involve unrelated controls, as opposed to the parental controls of the transmission/disequilibrium test (TDT) considered in the references above. This is motivated by the continuing practical importance of the case-control design, as well as by recent methodological work permitting recognition and adjustment for potentially confounding population structure (Devlin and Roeder 1999; Pritchard and Rosenberg 1999; Bacanu et al. 2000; Schork et al. 2001). The flexibility of the unrelated control approach, which includes case-case designs and studies of therapeutic efficacy, calls for a flexible power method.

The approach to power analysis is based on the use of exemplary data to calculate noncentrality parameters for the asymptotic χ² distribution of likelihood-ratio statistics. This approach has been described in varying degrees of generality in the statistical literature: in the context of clinical studies by Greenland (1985), in the context of log-linear models by O’Brien (1986), and in the context of generalized linear models by Self et al. (1992), who also consider the matched case-control design. Brown et al. (1999) comment that these methods are not as widespread as their generality would seem to warrant, due to “insufficient appreciation of the straightforward nature of the calculations and the difficulty of formulating reasonable specific alternative hypotheses.” In the present paper, the method is extended to encompass general retrospective sampling, implemented as a set of functions in the S language (Chambers 1998), illustrated on a design problem in genetic epidemiology and further used to address general questions in the design of association studies in the face of complex genetic etiology. Because explicit alternative models are used, the method can accommodate very general models involving incomplete penetrance, phenocopies, allelic and locus heterogeneity, and interactions among genes and between genes and covariables. The emphasis here is on the general method and its application to allelic and genetic heterogeneity. Other types of genetic complexity generate questions about the selection of cases for allele discovery and association testing that are best addressed separately.

The Method

The exemplary data method provides a general way of estimating the power of likelihood-ratio tests in complex models. The general strategy consists of three steps. First, we hypothesize a model, here called “the scenario,” under which we wish to calculate power. This consists of an assumed joint distribution of genetic and nongenetic risk factors and the conditional penetrance, given each configuration of risk factors. We then generate an exemplary data set that represents the expected data under the sampling design. Finally, we analyze the exemplary data set exactly as we would analyze the actual data, calculating any likelihood-ratio test of interest. The resulting likelihood ratio can then be used, as described below, to calculate the power of the same test when applied to observations generated under the scenario. Straightforward extensions permit calculation of sample sizes or detectable effect sizes.

The Likelihood-Ratio Test

In a simple case-control study, n₁ cases and n₂ controls are sampled and compared with regard to the frequency of genotypes. An alternative approach to analysis, particularly useful in more complex settings, is to fit a logistic regression model as if the data had been collected prospectively, taking advantage of the well-known fact that all but the intercept term in a logistic regression model can be consistently estimated from retrospective data (Breslow and Day 1984; Agresti 1990).

Define Y=1 for a case and Y=0 for a control and let p=P(Y=1|X=x) be the penetrance as a function of x, a vector encoding genotype and covariable information (capitals are used here to denote random variables). In the general logistic formulation, we model penetrance, p, by relating the logit of p to a linear model,

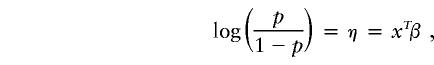where β is a vector of unknown coefficients to be estimated.

In the simplest case, x=(x₁,x₂) where x₁=1 for all individuals, and x₂ takes the value 1 or 0 to denote the presence or absence, respectively, of a putative high-risk genotype. Then η=β₁+x₂β₂, where β₂ is the logarithm of the odds ratio and β₁ is a constant that fits the model to the numbers of case and control subjects sampled. We would then test the hypothesis that β₂=0. The likelihood-ratio test can be computed by fitting both the full model and a second, reduced model, in which β₂ is constrained to equal zero. The goodness of fit of each model can be measured by the deviance (see, e.g., Agresti 1990, p. 83), which is commonly reported by logistic regression software. The difference in deviance between the two fitted models is the likelihood-ratio statistic, which can be referred to a central χ² distribution—in this case, with a single df, because of the elimination of one parameter.

For slightly more generality, consider a single locus with two alleles, denoted “a₁” and “a₂.” Let x₂ be the number of copies of a₂ (allele dose), and let x₃=1 if the individual is heterozygous, and zero otherwise. The likelihood-ratio test statistic, comparing the three-parameter model with the single-parameter null-effect model, would then have 2 df. Use of an alternative parameterization—for instance, x₂ being a binary indicator for the a₁/a₂ genotype and x₃ being the indicator of the a₂/a₂ genotype—would not change the likelihood-ratio test, because either parameterization permits the full model to exactly fit the observed penetrance for each genotype.

With k alleles, there are d=k(k+1)/2 possible distinct genotypes, although rare combinations might be missing from the data. Models with and without d-1 indicator variables can be compared, to yield a likelihood-ratio test with d-1 df. This will be referred to as the omnibus test, because it is not focused on any one set of putative high-risk genotypes. Risch and Merikangas (1996) describe separate testing of each allele in their proposed program of genomewide association testing, and Slager et al. (2000) considered the effect of allelic heterogeneity on similar tests of single alleles. The omnibus test provides a test for the entire locus that neither focuses on a single allele nor ignores the distinctions between other alleles. The 1-df and 2-df tests of a single allele and the multiple-df omnibus test are all tests of the same null hypothesis, but the omnibus test compares the null model to a general alternative hypothesis that admits allelic heterogeneity.

By using additional x variables, the general logistic regression model can accommodate multiple alleles per locus, multiple loci, nongenetic covariables, and interactions among any or all variables. Multiple likelihood-ratio statistics can be defined to test hypotheses about the individual and joint effects of genes, and their interactions with each other and with environmental factors.

The approach to testing can be summarized as follows: we fit a logistic model for penetrance, log(p/1-p)=x^Tβ, partition the parameter as β=(λ,ψ), and use the likelihood ratio to test hypotheses of the form λ=λ₀, provided the intercept is included among the nuisance parameters, ψ.

The Scenario

A scenario can be described by specification of the joint distribution of risk factors, X, and the conditional penetrance, P(Y=1|X=x), for each x—that is, for each configuration of risk factors. Consider an example that arose in the course of determination of the feasibility of detecting genes that may modify the risk of lung cancer caused by tobacco smoke. The CYP2E1 gene of the cytochrome P450 family 2 locus was considered a candidate for a detoxification effect (Matthias et al. 1998). The frequency of the potentially protective c2 allele was expected to be ∼20% in the sampled population. That population was also to be classified with regard to smoking status, as follows: those subjects who had never smoked (34%), those who formerly smoked (44%), and those who currently smoke (22%). Table 1 describes this example by listing all combinations of genetic (CYP2E1) and environmental (smoking) risk factors, along with the relative frequency for each combination in the sampled population, under the assumptions of Hardy-Weinberg genotype proportions and independence of genotype and smoking status.

Table 1.

Scenario: Joint Risk-Factor Distribution and Penetrance

CYP2E1 andSmoking Statusa	P(x)b	P(y=1|x)c
c1/c1:
Never	.2176	.0001
Former	.2816	.0005
Current	.1408	.0010
c1/c2:
Never	.1088	.0001
Former	.1408	.0004
Current	.0704	.0008
c2/c2:
Never	.0136	.0001
Former	.0176	.0002
Current	.0088	.0004

^aCYP2E1 and smoking status are encoded in the vector x (values not shown).

^bP(x) is the relative frequency of each combination of risk factors.

^cP(y=1|x) is the penetrance, given the risk factors.

The last column gives the penetrance for each combination of risk factors. One can either specify each value directly or specify parameters in a penetrance model. The latter is convenient if one is considering many risk factors with few interactions, so that only main effects need to be specified. In the scenario given in table 1, there are two interacting factors, and it is, perhaps, easiest to specify the penetrance values directly. It is assumed that the CYP2E1 genotype is irrelevant to nonsmokers, for whom the penetrance is assumed to be .0001. For the c1/c1 genotype, the penetrance is assumed to be fivefold larger for former smokers and tenfold larger for current smokers. The c2 allele is assumed to have no effect in nonsmokers, but, in former or current smokers, we assume that a single copy protects one in five individuals and that homozygosity for c2 protects three in five individuals.

Because all models to be considered will include an intercept, the baseline penetrance has very little effect on power if the other penetrance values are specified relative to baseline. In consideration of multiple scenarios, it makes a difference whether effects are specified in absolute or relative terms, and the exemplary data method provides a tool for detailed study of the impact of phenocopy and locus heterogeneity—for example, on the marginal effect of a locus and on power.

The key effect sizes in the example are the hypothesized protective effects of the genotypes containing c2 alleles, which were stated in relative terms (one in five protected and three in five protected). It is possible to fix the ratio of the genotype effects, creating a family of models parameterized by a single number that can be optimized to obtain the desired power. If one chooses to solve for such an effect-size parameter or even to report it as a summary, the scenario table provides an explication of the meaning of the effect-size parameter, in addition to organizing the calculations. Subsequent sections, however, make no use of detectable effect calculations.

Expected Data Configurations

To obtain all the possible data configurations, the nine distinct risk-factor combinations are each combined with the two possible disease-status values, as shown in table 2. The column labeled p(y|x) is either the conditional penetrance or its complement, depending on whether y=0 or y=1.

Table 2.

Exemplary Data with Weights^[Note]

y, CYP2E1,andSmokingStatus	P(x)	P(y|x)	P(x,y|s)	Stratum	w
0:
c1/c1:
Never	.2176	.9999	.2177	1	.1088
Former	.2816	.9995	.2816	1	.1408
Current	.1408	.9990	.1407	1	.0704
c1/c2:
Never	.1088	.9999	.1088	1	.0544
Former	.1408	.9996	.1408	1	.0704
Current	.0704	.9992	.0704	1	.0352
c2/c2:
Never	.0136	.9999	.0136	1	.0068
Former	.0176	.9998	.0176	1	.0088
Current	.0088	.9996	.0088	1	.0044
1:
c1/c1:
Never	.2176	.0001	.6400	2	.0960
Former	.2816	.0005	.3509	3	.1228
Current	.1408	.0010	.3509	3	.1228
c1/c2:
Never	.1088	.0001	.3200	2	.0480
Former	.1408	.0004	.1404	3	.0491
Current	.0704	.0008	.1404	3	.0491
c2/c2:
Never	.0136	.0001	.0400	2	.0060
Former	.0176	.0002	.0088	3	.0031
Current	.0088	.0004	.0088	3	.0031

Note.— y=1 for cases, 0 for controls. All combinations of case status and risk factors are listed. P(x) is as in table 1. P(y|x) is the penetrance or its complement. P(x,y|s) is found from Bayes’ rule, renormalizing within strata. The strata are sampled in proportions fixed by design (see text). w is the weight (i.e., the probability for each data configuration in the sample).

If prospective sampling were feasible, with genotypes and covariables fixed by design, the penetrance model alone would determine the power. In fact, most descriptions of the exemplary data method in the statistical literature focus on such prospective designs. In a prospective study, the expected relative frequency of each data configuration is

where π(x) is the relative frequency of configuration x in the design and P(y|x) is the penetrance model. In a retrospective study, we sample cases (y=1) and controls (y=0) separately, so

where π(y) denotes the sampling proportion allocated to cases or controls. We can calculate the conditional probabilities of genotypes (and covariables), via Bayes’ rule, as

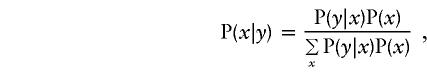where P(x) is the relevant population genotype frequency or, more generally, the joint frequency of genotype and covariates. So, if we consider a specific penetrance model, P(y|x), population genotype frequencies, P(x), and sampling proportions, π(y), the weights, w, provide the expected fraction of the sample with each data configuration.

The example is slightly more complex than a case-control study, in that three strata are defined, to permit oversampling of subjects who had never smoked, who were of interest for a separate objective involving passive exposure to tobacco smoke. Let s be one set in a partition of the full set of (x,y) pairs. Then, for each s and each (x,y) in s, we define w=P(x,y|s)π(s), where π(s) is the fraction of the total sample devoted to stratum s. We can obtain P(x,y|s) by computing P(y|x)P(x) for each configuration, as above, and simply renormalizing separately within strata. Note that the column labeled P(x,y|s) sums to 1 within each stratum. The weights, labeled w, are obtained by multiplying P(x,y|s) by the planned stratum proportions, which are 50% controls, 15% nonsmoking cases, and 35% smoking or formerly smoking cases.

Tests and Sample Size

Once a scenario and retrospective sampling proportions have been specified and the expected data configuration has been arrived at, it remains to specify a likelihood-ratio test and use the exemplary data to calculate its power. Let 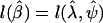be the log likelihood, evaluated at the maximum-likelihood estimates. The hypothesis that λ=λ₀ can be tested by fitting a second model under the constraint (the fitted parameter being denoted “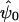”) and calculating the likelihood ratio test statistic

Usually λ₀=0. Operationally, we fit models with and without the components of x corresponding to λ and calculate the difference in deviance.

The test statistic, G², can be referred to its asymptotic χ² distribution, calling G² significant at level α if G²>q, where q=χ²(r,1-α), the (1-α)-quantile of the central χ² distribution with r df, r being the number of parameters fixed by the hypothesis. When the null hypothesis does not hold, the distribution of G² can be approximated by a noncentral χ² distribution; hence, the power can be estimated by a noncentral χ² probability function, F_χ², evaluated at the critical value q, df r, and noncentrality ν—that is,

The key feature that simplifies the power calculations is that the noncentrality parameter, ν, can be estimated simply as the planned test statistic, G², calculated from the exemplary data.

A second simplifying feature is that the noncentrality scales with sample size. If we want to consider doubling both the number of cases and the number of controls, we can simply double the noncentrality parameter, without further model fitting. Symbolically, we have ν(n)=nν(1) in an obvious notation. Many software packages permit easy calculation of the likelihood-ratio statistic using fractional counts. This feature permits finding the sample size necessary for specified power by a simple root-finding algorithm, without the need to recalculate the noncentrality. There are other approaches to power calculations, but this approach has the advantage of generalizing easily to more-complex situations while maintaining good accuracy (O’Brien 1986; Self et al. 1992).

Table 3 shows the analysis-of-deviance table that results from fitting four models to the weighted exemplary data of table 2. Each line represents a model involving the effects listed on that line, as well as all effects listed above, beginning with the “NULL” model which consists of an intercept only. This table permits forming several likelihood-ratio tests. If we compare the model with CYP2E1 main effect (line 3) to the model with smoking, but no genetic effects (line 2), the test statistic is G²=0.003, with 2 df, and the noncentrality is 0.003n. Numerically solving for a .01 level of significance and 80% power, we find that 4,672 subjects would be needed. If we sum the CYP2E1 main effect and the interaction, to obtain a 6-df test statistic comparing the largest model to the smoking model, then the noncentrality is 0.005n and 3,952 subjects are required for the same level and power. With simple case-control sampling (which involves recomputing the exemplary data), the required sample sizes are 3,039 and 3,448, respectively, illustrating both loss of power caused by the oversampling of nonsmoking cases and the fact that the optimal test statistic depends on the design.

Table 3.

Analysis of Deviance for Exemplary Data^[Note]

Effects	df	Deviance	Residualdf	ResidualDeviance
NULL			17	1.386
Smoking	2	.021	15	1.365
cyp2	2	.003	13	1.362
Smoking:cyp2	4	.002	9	1.360

Note.— Each line summarizes a model with the named effect, and all effects on lines above. “df” and “Deviance” are differences in residual df and residual deviance. Deviance values are likelihood-ratio (χ) statistics comparing the models on adjacent lines.

The large sample-size requirement, despite a substantial hypothesized effect and a relaxed level of stringency, suggested that this particular sampling design should be abandoned. It is included here because it exercises the major features of the method.

Computer software for the exemplary data method was written in the form of a set of functions, in the R dialect (Ihaka and Gentleman 1996) of the S language (Chambers 1998), that are available from the author and at his Web site. These do not constitute a stand-alone program, but rather the additional components needed within this particular computing environment. A central component is a function for converting a scenario specification, like table 1, into a weighted exemplary data set, like that in table 2. Native functions are used to create an analysis-of-deviance table, like table 3, and the noncentrality (deviance) and df are passed to sample-size or power functions. Together with some functions to permit simplified specification of a scenario using Hardy-Weinberg allele frequencies and standard notation for specification of a penetrance model, these provide flexible tools for estimation of sample size in complex settings.

Allelic Heterogeneity

The calculation of sample sizes for specific scenarios can be used to address broad questions of study design, as well as plans for specific studies. The effect of allelic heterogeneity on the power of omnibus test statistics is considered here, along with the impact of efforts to detect and classify allelic variation. The power of joint tests of several possibly interacting candidate loci is addressed in the section Genetic Heterogeneity and Multilocus Testing, below.

Although these sample sizes are calculated for explicit penetrance probabilities, rather than from formulae based on relative risk, the noncentrality and sample size are quite insensitive to the overall penetrance for constant relative risk. Unless otherwise stated, all sample sizes are presented for test size α=0.0001, and 80% power. As a rough approximation, halving or doubling the sample sizes yields the numbers required for α=0.01 or α=10^-8. The main conclusions, however, depend on ratios of sample sizes, which are insensitive to test size.

Table 4 illustrates the effect of allelic heterogeneity on sample size, using as an example a single-locus trait, when all the alleles are known and none are rare. Scenarios with both dominant and recessive modes of inheritance are considered, but this is assumed to be unknown to investigators; hence, a 2-df test is used in the diallelic case. In the second and third lines, the high-risk allele is essentially subdivided into four or eight equally frequent alleles. These subdivisions leave the noncentrality unchanged, so the increase in sample size is entirely due to the increasing df. If it could be reasonably hypothesized that the uncommon alleles are all putatively high-risk alleles, perhaps on the basis of a predicted loss of function, they could be pooled for analysis, recovering the power of the 2-df test.

Table 4.

Total Sample Size, n, for A Single Low-Risk Allele and 1, 4, or 8 High-Risk Alleles, in Either Dominant and Recessive Scenarios^[Note]

Allele Frequencies			n
LowRisk	HighRisk	df	DominantScenario	RecessiveScenario
.60	.40	2	749	964
.60	.1×4	14	1,197	1,541
.60	.05×8	44	1,751	2,253

Note.— The df for omnibus tests are shown in the column labeled df. All high-risk genotypes have a relative risk of 2 (penetrance = 0.1 or 0.2). The significance level is α=0.0001 and power is 80%. It is assumed that all alleles are known.

The strategy of separately testing each allele would not work well in this setting. In the dominant scenario of line 2, for example, if one of the four high-risk alleles were singled out for comparison to all other alleles, the single-df test of the dominant effect of that one allele would require 5,891 subjects instead of the 1,197 for the omnibus test. Despite the necessary increase in df, the omnibus test is more powerful because the tests of individual alleles may miss the greater part of the risk attributable to the locus.

Table 5 illustrates a situation with symmetric high-risk and low-risk allele frequencies and a codominant allele-dose mode of inheritance. Sample sizes are given for 1-df (allele-dose) and 2-df tests of a single high-risk allele, in addition to the omnibus test. The slight advantage of the optimal single-df test in the simplest scenario is quickly obliterated by increasing allelic heterogeneity.

Table 5.

Comparison of Multiple-df and Single-df Tests^[Note]

	Omnibus Test		n for Single-Allele Tests
AlleleFrequencies	df	n	1-df Test	2-df Test
2×.5	2	744	684	744
4×.25	9	1,048	2,288	2,561
8×.125	35	1,603	5,493	6,177

Note.— Sample sizes, n, are shown for scenarios with two, four, or eight alleles, half of which are high-risk alleles. An additive mode of inheritance is assumed, with penetrance for 0, 1, or 2 high-risk alleles being, respectively, .001, .002, or .003.

The problem with tests that compare one allele to all others is that, in the presence of allelic heterogeneity, several high-risk alleles are effectively misclassified by the contrast. The power of the omnibus test is robust to allelic heterogeneity, but all of the allelic variants need to be detected if the power is to be fully realized. An example of the effect of undetected alleles is shown in table 6. In each scenario, the combined frequency of high-risk alleles is 5%. The first line gives the sample size in the absence of allelic heterogeneity or if all high-risk alleles are regarded as equivalent. A 72% increase in the sample size is needed to accommodate the df of the underlying allelic heterogeneity in an omnibus test (line 3), but failure to detect the three least common alleles requires an increase of >275% in the required sample size (line 2), despite fewer df. Even with a modest number of alleles, there is a large advantage to detecting the relevant allelic variation.

Table 6.

Sample Sizes, n, for Detected and Undetected Allelic Heterogeneity^[Note]

Allele Frequencies
LowRisk	High RiskDetected	High RiskUndetected	df	n
.95	.05	…	2	624
.95	.02	.01×3	2	1,720
.95	.02, .01×3	…	14	998

Note.— Each of the high-risk alleles is dominant, increasing the risk by a factor of 3 relative to the common allele. The first line is for a scenario with only two alleles, or, equivalently, for an optimal 2-df contrast. Lines 2 and 3 consider 5 alleles, but for line 2, only the most common of the four high-risk alleles is detected, with the other high-risk alleles misclassified as low-risk. “df” denotes degrees of freedom.

In contrast to the problem of failing to detect high-risk alleles, we can consider the effect of detecting and including both low-risk and high-risk alleles among the variants tested. Of course, an omnibus test with multiple df does not require the alleles to be classified into low- and high-risk categories, but, if such a classification is plausible, it could be used to improve power by limiting df. Table 7 describes a scenario with a common low-risk allele and eight uncommon alleles, only four of which elevate the risk (as a dominant effect). The omnibus test (44 df) requires 2.6 times the sample size of the optimal (high vs. low risk) contrast. Both of these assume that all of the allelic variants are detected, but the latter makes use of prior knowledge as to which are high-risk alleles, as well as the dominant mode of inheritance. If all uncommon alleles are lumped together as putative dominant alleles, an intermediate sample size is required. A substantially higher sample size is necessary if only one of the high risk alleles is detected. With two high-risk alleles detected, the sample size is comparable to that of the omnibus test of all alleles.

Table 7.

Sample Size, n, with Undetected High-Risk Mutations and Detection of Irrelevant Mutations^[Note]

Test	df	n
Comparison of nine alleles	44	455
High risk vs. low risk	1	173
One high risk vs. others	1	888
Two high risk vs. others	1	411
Rare vs. common	1	290

Note.— The scenario represents a dominant model, with one common allele of frequency 84%, eight uncommon alleles at 2% each, four of which (high risk) elevate risk from .01 to .05, the other four having no impact on risk.

When the rare-versus-common and the two-high-risk tests—both, to some degree, misspecified—are compared, it is evident that there is a benefit to discovering all of the relevant allelic variation, even if that effort also includes some alleles that do not confer risk. However, the further improvement with correct classification as to high-risk or low-risk status illustrates the value of distinguishing the most important mutations. At one level, we can attempt to distinguish what Sobell et al. (1992) call VAPSEs (variations affecting protein sequence or expression) from silent allelic variation. At another level, single-locus substitutions at evolutionarily conserved sites might be separated from those at nonconserved sites. The advantage of the rare-versus-common contrast over the omnibus test in table 7 suggests that the advantages of such a distinction may be robust to a moderate amount of misclassification.

Genetic Heterogeneity and Multilocus Testing

Table 8 gives the sample size for tests of individual loci and for the joint effect of multiple loci. The four columns of sample sizes correspond to four distinct scenarios involving dominant or recessive effects, either multiplicative (log-additive) or interacting. The first three rows give the sample sizes for tests of single-locus main effects, ignoring the other loci. Rows 4, 5, and 6 give sample sizes for three different tests of the joint effects of the three loci. All three tests involve main effects but differ with regard to the inclusion of interactions in the hypothesis. Regardless of the use of interactions, all three joint-effects tests require smaller samples than do any of the single-locus tests. The last three rows show the effects of including additional candidate genes that are not associated with disease. Each such neutral locus adds 2 df to the test statistic, without changing the noncentrality. In all four scenarios, the overall test of main effects is more powerful than the tests of any single locus, even when half of the loci tested are unrelated to disease.

Table 8.

Sample Size, n, for Single-Locus and Joint-Effects Tests of Three Disease-Related Loci and Three Neutral Loci (D, E, and F)^[Note]

		n for Example
Test	df	1	2	3	4
A locus	2	1,039	459	717	354
B locus	2	901	716	1,138	572
C locus	2	904	1,456	2,169	1,082
A+B+C+AB+AC+BC+ABC	26	612	457	562	327
A+B+C+AB+AC+BC	18	543	405	499	290
A+B+C	6	399	298	464	231
A+B+C+(D)	8	481	359	559	278
A+B+C+(D)+(E)	10	543	405	632	314
A+B+C+(D)+(E)+(F)	12	596	445	693	345

Note.— Example 1: multiplicative loci with dominant alleles; RR = 2. Example 2: multiplicative loci with recessive alleles; RR = 3. Example 3: interacting loci; RR = 2 for each pair of loci with high-risk alleles. Example 4: interacting loci; RR = 2 for each individual high-risk homozygous locus, with an additional multiplicative RR = 3 for each pair of homozygous loci. High-risk allele frequencies at loci A, B, and C are 40%, 30%, and 20%, respectively. A+B denotes additive main effects in a logistic model. A+B+AB denotes inclusion of an interaction term. All sample sizes are for tests comparing the specified model to the null (intercept only) model.

Table 8 serves to illustrate the perhaps obvious fact that, if multiple loci contribute incrementally to penetrance, their collective action will provide a stronger signal than will their individual effects. What is, perhaps, less obvious is that the test of joint main effects can be quite powerful, even if the loci interact strongly, and that the advantages of collecting loci can persist even when half of those loci have no effect on disease.

One difficulty with testing the joint effect of several loci is that rejection of the null hypothesis that none of the loci is associated with disease does not tell us which loci are associated with disease. However, such a finding provides protection of the overall false-positive rate, removing much of the onus of multiple comparisons, and thus indirectly improving the power for detecting individual loci. Allison and Schork (1997) proposed a reformulation of the multiple-comparison problem, which they described as “moving the goal posts” in a useful way. Their proposal concerned the level of significance regarded as compelling in tests of individual loci. The testing of joint effects is different in at least two regards. It can be substantially more powerful than single-locus tests, as is illustrated in table 8, and it does not involve shifting objectives. It is simply a direct test of the global null hypothesis about a specific collection of loci, and it provides a direct and powerful means of protecting the overall false-positive rate when a collection of loci are tested.

Such a test is analogous the Fisher’s use of an omnibus F-test to protect the false-positive rate when multiple treatments are compared in a one-way analysis of variance. If there is a genuine scientific hypothesis that a particular pathway is involved in the genetic etiology of a disease, then the genes involved in that pathway collectively form an a priori hypothesis, and a test of their joint effect is an appropriate level of aggregation for protection of multiple comparisons. So, even though the direct implications of joint-effects tests are less specific that those of single-locus tests, by protecting the overall false-positive rate for a collection of loci, they permit the testing of individual loci to proceed at unadjusted levels of significance, provided, of course, that the collection of loci represent a well-motivated a priori hypothesis.

Discussion

The exemplary-data method provides a way of estimating power for a very large class of likelihood-ratio tests in a variety of both prospective and retrospective study designs. The method relies on asymptotic distributions, but the large sample sizes of case-control studies make this a reasonable area for the exemplary-data approach. Self et al. (1992) consider the accuracy of the method. Brown et al. (1999) suggest that, in critical applications, the method should be augmented by simulation studies. The availability of the exemplary-data table makes Monte Carlo sampling particularly simple. One only needs to generate a vector of counts, or indices, with probabilities given by the weights.

As an illustration, 500 samples were generated to simulate the last line of table 7. Each sample had 145 cases and 145 controls. The nominal P values were calculated for 500 likelihood-ratio tests, of which 347 were <.0001. Another 85 were between .0001 and .001; 47 were between .001 and .01, 16 were between .01 and .05, and 5 were >.05. The simulated power was ∼70%, rather than the targeted 80%, although 80% of simulated samples had P⩽.0004. The method thus seems a reasonable approximation, in light of the uncertainties surrounding the specification of realistic scenarios. The conclusions of the previous sections are based on relative, rather than absolute, sample sizes.

Risch and Merikangas (1996) cast the problem of detecting disease-related genes as a question of obtaining sufficient power to detect the modest contributions of individual loci in a simple two-allele system. Although allelic heterogeneity does not cause serious problems for linkage-based gene mapping (Lander and Schork 1994) it can have a profound impact on the power of association tests (Slager et al. 2000). The large loss of power for single-allele tests can be ameliorated by allele discovery, the use of omnibus tests, and a priori classification of alleles. For testing the effects of the modest number of common alleles expected per locus, the use of one omnibus test per locus, combined with the recent estimate of <40,000 human genes (Venter et al. 2001), requires an individual test size of 1.25×10^-6 to maintain a genomewide false-positive rate of .05 via Bonferroni adjustment, which is somewhat less onerous than the 5×10^-8 considered by Risch and Merikangas (1996).

For loci with numerous uncommon alleles, the detection and classification of mutants is important for implication of the locus in disease etiology. Of course, one would like to know the risk associated with individual genotypes, but a purely empirical estimate may be impossible for rare alleles. The implication of the locus as a whole would seem to offer an important protection against false positives in multiple comparisons, as well as a firmer foundation for interpretations based on the nature of the variants.

Plausible contrasts or groupings of alleles can be defined from consideration of functional implications of mutations and, for some genes, by evolutionary conservation. Such contrasts do not need to be perfect, and moderate misclassification can be tolerated. The greater misclassification problem occurs when a substantial amount of attributable risk is associated with undiscovered alleles or when individual alleles are tested in an automatic fashion despite allelic heterogeneity. The use of markers, as opposed to genes, entails a possibly severe misclassification. Although it is possible to discover associations with markers and even for a marker to correspond coincidentally to an optimal contrast of alleles, the correct implication of a gene in disease etiology through an association test using markers requires a substantial amount of luck, making it a strategy more suitable to broad screening efforts than to hypothesis-driven research about specific candidate genes.

As we consider increasing numbers of alleles, there will come a point when the power of an association test is less than that of a linkage test. Additional power may be found in the joint testing of multiple genes or in the use of linkage studies more powerful than affected sib pairs. The latter might include studies of more-distant relatives or the detection of regions shared identically by descent outside of the known family.

Tests of joint effects of sets of candidate genes may remain feasible when the relative risk associated with individual loci is simply too small. The difficulty is of course that this approach requires an a priori hypothesis defining the collection of loci. Genes involved in common pathways might be hypothesized to contribute to a complex genetic etiology, but the relevant pathways may be large, and similar phenotypes might result from variation in proteins that play a key role in rather distantly related pathways. Linking the joint testing approach to data-driven methods for generating appropriate hypotheses might merit further methodological development.