On Rapid Simulation of P Values in Association Studies

To the Editor:

In the March issue of the Journal, Seaman and Müller-Myhsok (2005) proposed a method for rapid simulation of P values in association studies. The authors kindly discussed my article (Lin 2005), which was electronically published in September 2004. Unfortunately, their discussion is inaccurate. In particular, their assertion that the variance formula given in my article ignores the variation due to the estimation of nuisance parameters is untrue.

Both my article (Lin 2005) and that of Seaman and Müller-Myhsok (2005) are based on the simulation of the (same) joint distribution for a set of test statistics, although the actual simulation procedures are somewhat different. If a statistic is asymptotically normal, then it can be approximated by a sum of independent terms. Specifically, the statistic for testing the jth null hypothesis H_j:β_j=0 can be written as

up to an asymptotically negligible term, where U_ji involves only the data from the ith subject, and n is the sample size. Under H_j:β_j=0 (j=1,…,J), the set of statistics (U₁,…,U_J) is asymptotically multivariate zero-mean normal with covariance

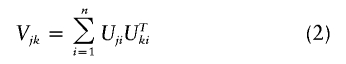between U_j and U_k (j,k=1,…,J). In my article, I proposed to simulate this joint distribution by

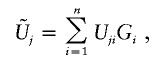where G₁,…,G_n are independent standard normal random variables, because 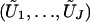has the same joint distribution as (U₁,…,U_J). Seaman and Müller-Myhsok proposed to fit a joint model that includes all β_j terms and to simulate the joint distribution of (U₁,…,U_J) by a multivariate normal random vector with mean 0 and with covariance matrix {V_jk;j,k=1,…,J}. The two proposals simulate from (essentially) the same joint distribution and are both very fast. In particular, my proposal involves the evaluation of the 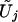terms, which is of the order nJ and which can be done in seconds or minutes, even for large values of n and J. One advantage of my proposal is that missing genotype data for one statistic do not affect any other statistics. (If the ith subject has no genotype data for calculating the jth statistic, then we simply set U_ji to 0. There is no need to impute missing data.) By contrast, the proposal of Seaman and Müller-Myhsok can include in the analysis only those subjects with complete genotype data on all the SNPs, unless all the missing genotypes are imputed. Imputation can adversely affect the type I error and power.

Seaman and Müller-Myhsok (2005) focused on the parametric statistics under generalized linear models, whereas my article (Lin 2005) covered all possible statistics, parametric or nonparametric. As described in the appendix of my article, all the commonly used association statistics can be written in the form of equation (1), in which U_ji is the ith subject’s efficient score function for β_j. In the special case of parametric statistics,

where S_βj,i and S_αj,i are the ith subject’s score functions for β_j and α_j, α_j is the set of nuisance parameters, and A_βjαj and A_αjαj are the appropriate submatrices of the limiting Fisher information matrix for β_j and α_j. As mentioned in the appendix of my article, this expression can be found in mathematical statistics texts, such as that by Bickel et al. (1993, p. 28). It was also given as equation (A1) of Lin and Zou (2004). In this case, 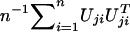converges to A_βjβj-A_βjαjA^-1_αjαjA_αjβj, the limiting covariance matrix of n^-1/2U_j, and the joint distribution of 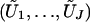indeed provides a valid approximation to that of (U₁,…,U_J). Thus, Seaman and Müller-Myhsok’s statement that my variance formula ignores the term A_βjαjA^-1_αjαjA_αjβj is simply untrue. Had I used the wrong variance formula, the numerical results presented in my article would not have been sensible.

Seaman and Müller-Myhsok (2005) might have been confusing score functions with efficient score functions. The score function for β_j involves the nuisance parameters α_j, which are replaced by 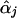, the maximum-likelihood estimators of α_j under H_j:β_j=0. To account for the extra variation caused by this estimation, we use the Taylor series expansion to express the score function for β_j (with α_j replaced by 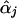) as a sum of independent terms, which is in the form of equation (1) with U_ji as given in equation (3), so that equation (2) provides the correct variance-covariance expression (Lin and Zou 2004). The efficient score functions U_ji involve the unknown parameters α_j. When α_j in U_ji is replaced by 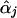, the resulting U_j, V_jj, and T_j are (essentially) the same as the U_β(l), V_β(l), and T_l given by Seaman and Müller-Myhsok (2005). Again, the framework of my article (Lin 2005) extends far beyond the parametric setting.

In fact, the parametric setting considered by Seaman and Müller-Myhsok (2005) does not demonstrate the full power of the simulation approach. In their setting, the calculation of each statistic is of the order n, so that the permutation test is very feasible, even for large values of n. There is a stronger case for the simulation approach when the calculation of each statistic is time consuming or when the null distribution cannot be properly generated by permutation, as discussed in my article (Lin 2005).

Incidentally, equation (2) in Seaman and Müller-Myhsok (2005) is confusing. The term in the middle is the score function for β, which is a function of α, whereas the term on the far right involves 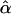instead.