Substituent effects on cation–π interactions: A quantitative study

Abstract

A synthetic supramolecular complex has been adapted to quantify cation–π interactions in chloroform by using chemical double-mutant cycles. The interaction of a pyridinium cation with the π-face of an aromatic ring is found to be very sensitive to the π-electron density. Electron-donating substituents lead to a strong attractive interaction (−8 kJ/mol⁻¹), but electron-withdrawing groups lead to a repulsive interaction (+2 kJ/mol⁻¹).

The interactions of cations with aromatic rings play an important role in a range of biological processes, including ion channels, membrane receptors, and enzyme substrate interactions (1–9). Supramolecular chemical model systems have been instrumental in establishing the basic properties of this important class of noncovalent interactions, but cation–π interactions are still poorly understood at a quantitative level, and it is difficult to predict substituent effects. Dougherty and coworkers (10) used the interaction between a synthetic aromatic host and a pyridinium guest to estimate a value of −10 kJ/mol⁻¹ for the interaction of a cation with four π-systems in water. This value agrees well with the value of −11 kJ/mol⁻¹ measured by using protein engineering for the interaction of S-methylmethionine with a cavity lined by three π-systems (11). Schneider et al. (12) obtained a value of −3 kJ/mol⁻¹ for a single cation–π interaction by using a positively charged lipophilic host and an aromatic guest in water.

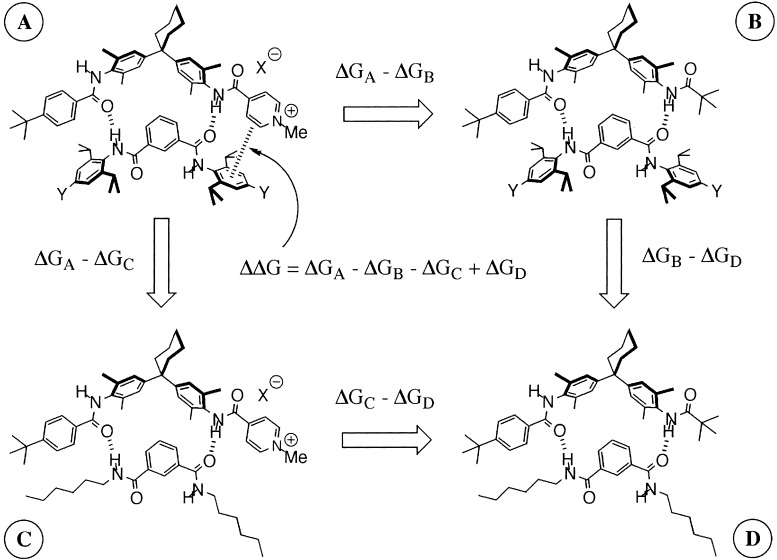
We have developed an approach to the quantitative measurement of noncovalent functional group interactions based on chemical double-mutant cycles. This approach has proved particularly valuable for investigating structure–activity relationships in edge-to-face aromatic interactions, providing new insight into the physical basis for substituent effects on the strengths of these interactions (13, 14). Here, we apply this approach to the cation–π interaction, or more specifically, to the interaction of a pyridinium cation with the π-face of functionalized aromatic rings. The double-mutant cycle is illustrated in Fig. 1. The difference between the stabilities of complexes A and B (ΔG_A-ΔG_B) provides an indication of the magnitude of the cation–π interaction in complex A, but the value is perturbed by changes in H-bond strength and other secondary interactions associated with the A→B mutation. The secondary effects can be quantified by using complexes C and D where there are no cation–π interactions, but the same chemical mutation is made. Thus, the difference ΔG_C-ΔG_D provides a direct measure of the changes in H-bond strength and secondary interactions associated with the A→B mutation, and it is possible to dissect out the thermodynamic contribution of the pyridinium-π interaction from all of the other interactions present in complex A (ΔΔG in Eq. 1).

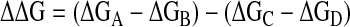1

Figure 1.

Chemical double-mutant cycle to quantify the cation–π interaction in complex A (Y = NO₂, H, NMe₂).

Methods

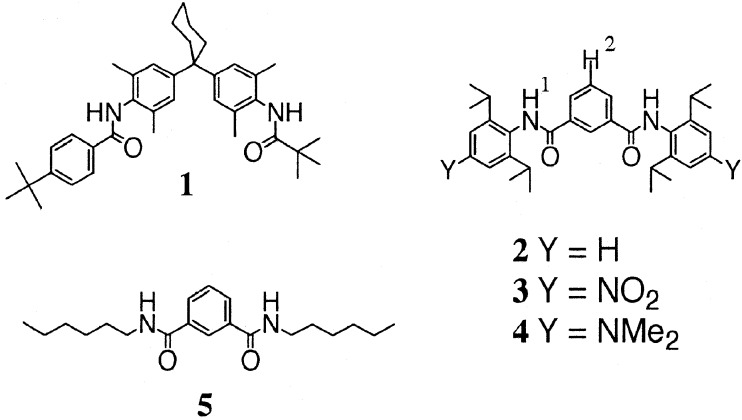
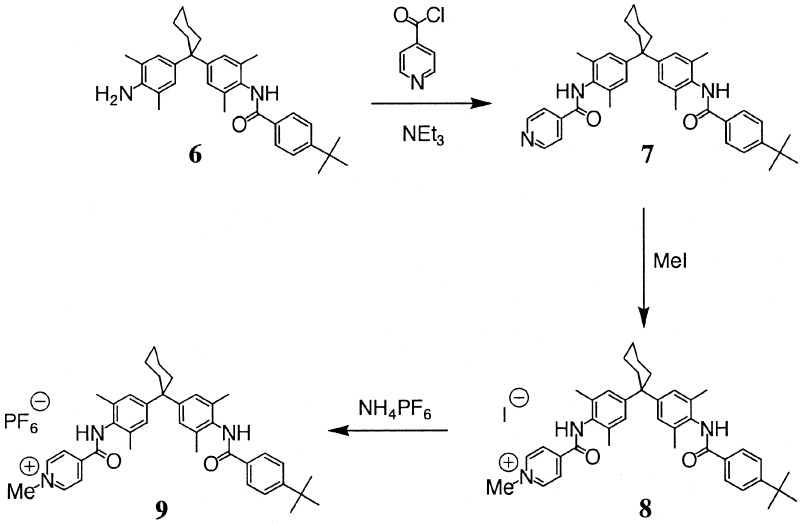
The synthesis of compounds 1-6 in Fig. 2 and Fig. 3 was described (15–18). Compound 9 was prepared from 6 according to Fig. 3.

Figure 2.

Compounds used in the double-mutant cycles.

Figure 3.

Synthesis of 9.

Synthesis of 7.

Nicotinyl chloride was prepared by suspending the nicotinic acid (1.18 g, 9.6 mmol) in dry CH₂Cl₂ (100 ml) under a nitrogen atmosphere. An excess of oxalyl chloride (2 ml, 20 mmol) was added with A few drops of dimethylformamide. The reaction mixture was stirred until all of the acid had dissolved (2 h). The CH₂Cl₂ and excess oxalyl chloride were removed under reduced pressure. The residue was dissolved in dry CH₂Cl₂ (100 ml), and a solution of 6 (3.1 g, 6.4 mmol) and triethylamine (1.5 ml) were added dropwise. The solution was stirred for 12 h before work-up with 1M HCl (2 × 50 ml), 1 M NaOH (2 × 50 ml), and brine (50 ml). After drying over anhydrous MgSO₄, the solvent was removed under reduced pressure. The product was isolated as a white solid (2.20 g, 60%) after purification by flash silica gel chromatography (ethyl acetate/petroleum ether 1:3). ¹H NMR (DMSO, 250 MHz, 293 K), δ(ppm) 9.95 (1H, s), 9.55 (1H, s), 8.80 (2H, d), 7.92–7.85 (4H, m), 7.52 (2h, d), 7.10 (2H, s), 7.08 (2H, s), 2.29 (4H, br m), 2.15 (6H, s), 1.60–1.40 (6H, br m), 1.33 (9H, s). FAB MS value found, 588 [MH]⁺; value calculated, 587 [M].

Synthesis of 8.

Compound 7 (0.117 g, 0.2 mmol) was dissolved in dry CHCl₃ (2 ml), methyl iodide (710 mg, 47 mmol) was added, and the mixture was stirred at room temperature for 72 h. The solvent was removed under reduced pressure, and the residue was purified by flash silica gel chromatography (CH₂Cl₂/MeOH 9:1). The product was isolated as a yellow solid (277 mg, 38 mmol, 80%). ¹H NMR (DMSO, 250 MHz, 293 K), δ(ppm) 9.90 (1H, s), 8.55 (2H, b), 8.05 (2H, bd), 7.70 (2H, J = 8 Hz d), 7.45 (1H, b), 7.42 (2H, J = 8 Hz d), 7.15 (4H, s), 3.52 (3H, m), 2.15 (6H, s), 1.30 (9H, s). +ve HRMS-FAB value found, 602.3762 [M-I]⁺ value calculated, 602.3747 [M-I]. −ve FAB MS value found, 127 [I]⁻; value calculated, 127 [I].

Synthesis of 9.

The iodide salt 8 (500 mg, 0.6 mmol) was dissolved in methanol (5 ml). Five milliliters of methanol saturated with ammonium hexafluorophosphate was added, and the solution was stirred for 1 h. The volume of solvent was reduced on a rotary evaporator to the minimum amount necessary to keep the product in solution, and then water was added. A pale yellow solid precipitated and was filtered and dried to yield 9 (450 mg, 89%). ¹H NMR (CDCl₃, 250 MHz, 293 K), δ(ppm) 8.74 (1H, s), 8.16 (2H, b), 7.98 (2H, bd), 7.68 (2H, J = 8 Hz d), 7.61 (1H, b), 7.42 (2H, J = 8 Hz d), 7.12 (2H, s), 7.03 (2H, s), 3.84 (3H, m), 2.15 (6H, s), 2.05 (6H, s), 1.33 (9H, s). +ve HRMS-FAB value found, 602.3779; [M-PF₆]⁺ value calculated, 602.3747 [M-PF₆]. −ve FAB MS value found, 145 [PF₆]⁻; value calculated, 145 [PF₆].

¹H NMR Dilution Experiments.

A sample of known concentration (of the order of 10–100 mM) in CDCl₃ was prepared. Aliquots of this solution were added successively to an NMR tube containing 0.5 ml of CDCl₃, the tube was shaken to mix the two solutions, and the ¹H NMR spectrum was recorded after each addition. The changes in chemical shift for each signal were recorded and analyzed with purpose-written software, NMRDil_IP, on an Apple Macintosh microcomputer. This program uses a Simplex procedure to fit the data to a binding isotherm that allows for ion pairing and dimerization of the ion pair. The fitting procedure yielded the two association constants (K_ip and K_d), the limiting chemical shifts of the free cation (δ_i), the ion pair (δ_ip), and the ion pair dimer (δ_d).

The method starts by assuming that [D] = 0, so that Eq. 2 can be solved exactly for [IP]. This value then is used to solve Eqs. 3 and 4 for [D]. At this point, [IP]+[I]+2[D] [C]₀, so the value of [D] from Eq. 4 is used in Eq. 2 to reevaluate [IP], and the procedure is carried out repetitively until [IP]+[I]+2[D] [C]₀. This procedure allows the set of simultaneous equations to be solved for the concentrations of all species present.

2

3

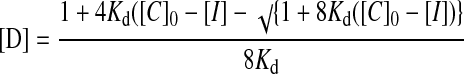4

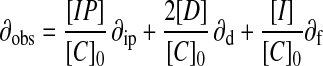5

where [IP] is the concentration of the ion pair, [C]₀ is the total concentration of the cation (and anion), [D] is the concentration of the ion pair dimer, and [I] is the concentration of the free cation (and anion). All experiments were performed at least twice. The association constant for a single run was calculated as the mean of the values obtained for each of the signals followed during the titration weighted by the observed changes in chemical shift. The association constants from different runs were then averaged. Errors are quoted at the 95% confidence limits (twice the SE). For a single run, the SE was determined by using the SD of the different association constants determined by following different signals. The curve fitting programs described above are available from the author on request.

¹H NMR Titration Experiments.

A 3.0 ml sample of host of known concentration (of the order of 1–10 mM) was prepared in CDCl₃. The concentration of the host was chosen so that the host was ion-paired but not significantly aggregated (determined from the dilution experiments). A portion (0.8 ml) of this solution was removed and a ¹H NMR spectrum was recorded. An accurately weighted sample of the guest then was dissolved in the remaining 2.2 ml of the host solution. This solution was almost saturated with guest to allow access to the top of the binding isotherm and contained host, so that the concentration of the host remained constant during the course of the titration. Aliquots of this solution were added successively to an NMR tube containing 0.5 ml of CDCl₃, the tube was shaken to mix the two solutions, and the ¹H NMR spectra was recorded after each addition. The changes in chemical shift for each signal were recorded and analyzed with purpose-written software, NMRTit_HG_HH_GG, on an Apple Macintosh microcomputer. This program uses a Simplex procedure to fit the data to a binding isotherm that allows for dimerization of the host and guest and yields the association constant for formation of the 1:1 complex from the host and guest monomers and the limiting chemical shifts of the fully bound complex (16).

Results and Discussion

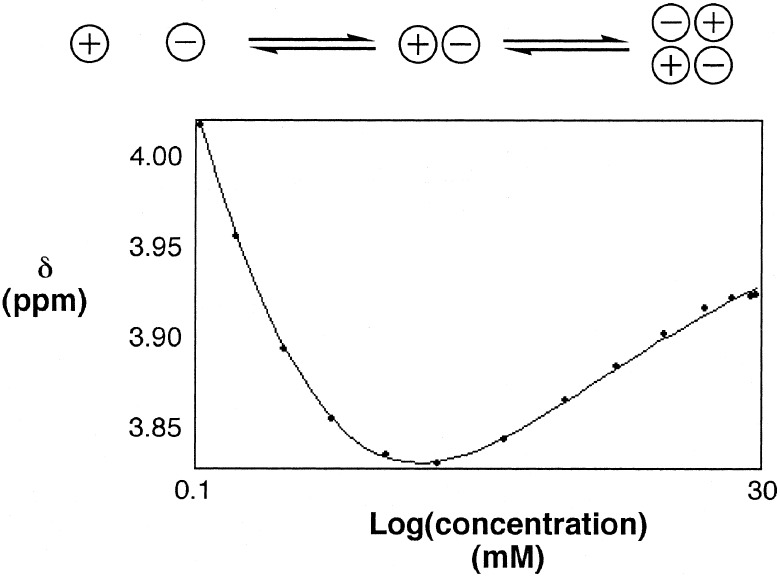
Initially, ¹H NMR titration experiments were carried out by using the iodide salt of the pyridinium cation (8), but the solubility of this compound is low, and the association constants for formation of 1:1 complexes with the isophthalic acid derivatives are small. This result is probably caused by H-bonding interactions between the iodide anion and the amide groups that compete with intermolecular complexation, and so, we exchanged the anion for hexafluorophosphate, which is a weaker H-bond acceptor. Compound 9 is more soluble than 8, but ¹H NMR dilution experiments revealed significant self-association in chloroform. A typical dilution curve is illustrated in Fig. 4. There are clearly two different processes taking place. The literature indicates that the process that takes place at low concentrations is dissociation of the ion pair, and the process at high concentrations is dimerization or aggregation of the ion pair (19, 20). The experimental data fit well to isotherms based on this model giving K_ip = 7.3 ± 0.5 × 10⁴ M⁻¹ and K_d = 7.6 ± 0.9 × 10² M⁻¹ (Fig. 4). The maximum concentration reached was 3 mM, and so the dimerization and aggregation models fit the data equally well (the principle mode of aggregation at this concentration is dimerization).

Figure 4.

¹H NMR dilution experiment showing the chemical shift of the signal caused by the pyridinium methyl group of 9 as a function of concentration in chloroform. The line represents the best fit to the three-state equilibrium illustrated.

¹H NMR titration experiments were carried out at mM concentrations; under these conditions, the ion pair is fully associated, and there is some further dimerization of the ion pair. The titration data were fit with a model that allowed for dimerization of the pyridinium salt by using the previously determined dimerization constants and limiting dimerization-induced changes in chemical shift, but ignored the possibility of dissociation of the ion pair. An attractive feature of the double-mutant cycle approach is that errors associated with minor competing equilibria cancel out in the thermodynamic analysis rather than propagate (21). The association constants for the formation of 1:1 complexes are listed in Table 1. The complexation-induced changes in chemical shift indicate that the structures of the core regions of all of the complexes are essentially identical (Table 1). Rotating-frame Overhauser effect spectroscopy experiments also show similar nuclear Overhauser effect patterns for all of the complexes, again suggesting that the chemical mutations do not have any significant conformational effects that might perturb the thermodynamic analysis.

Table 1.

¹H NMR titration data in chloroform at 298 K

Y	Complex	Ka (M−1)	G (kJ mol−1)	(H1)*	(H2)*
NO2	A 9⋅3	70  ± 8	−10.3  ± 0.3	+1.2	−0.8
NO2	B 1⋅3	79  ± 4	−10.7  ± 0.1	+1.6	−1.5
H	A 9⋅2	105  ± 11	−11.3  ± 0.3	+1.2	−1.8
H	B 1⋅2	17  ± 1	−6.9  ± 0.1	+1.4	−1.7
NMe2	A 9⋅4	404  ± 31	−14.6  ± 0.2	+1.4	−1.4
NMe2	B 1⋅4	8  ± 1	−4.9  ± 0.3	+1.0	−1.5
–	C 9⋅5	22  ± 1	−7.5  ± 0.1	+1.8	−1.1
–	D 1⋅5	10  ± 1	−5.6  ± 0.3	+1.0	−0.8

The results are average values from at least two experiments. Titration data for four to nine different signals were used to determine the association constant in each experiment. Errors are quoted as twice the SE from the weighted mean (based on the observed change in chemical shift). The values for complex C and D were reported and are common to all three double-mutant cycles (17). 

^*Limiting complexation-induced changes in chemical shift for formation of the 1:1 complex. See Fig. 2 for the proton labelling scheme. 

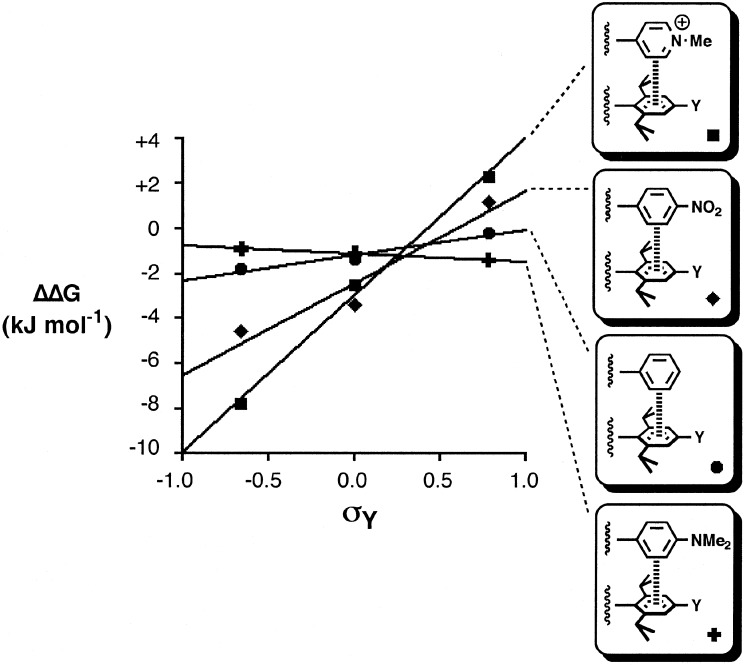
The data in Table 1 can be used to construct three different double-mutant cycles with Eq. 1. As discussed above, because we are working in the mM concentration range, the experiments probe intermolecular interactions with the ion pair rather than the naked pyridinium cation. ΔΔG is −7.8 kJ/mol⁻¹ for Y = NMe₂, −2.5 kJ/mol⁻¹ for Y = H, and +2.3 kJ/mol⁻¹ for Y = NO₂. Clearly, the cation–π interaction energies are highly sensitive to the electronic properties of the π-system. An electron-rich π-system gives rise to a very attractive interaction that is comparable in magnitude to a hydrogen-bond in chloroform. However, an electron-poor π-system can lead to an unfavorable repulsive interaction. Although interactions with the anion may play a role, these results strongly suggest that the electrostatics of the interaction of the cation with the π-electron density dominate in this system (4, 22, 23). Previously, we have found good correlations between edge-to-face aromatic interaction energies and Hammett substituent constant (14, 24); the Hammett plot for the cation–π interaction is shown in Fig. 5. The corresponding data for the edge-to-face aromatic interactions are included for comparison. Aromatic rings with electron-withdrawing substituents give a positive slope, i.e., stronger electrostatic interactions with the π-electron density on electron-rich aromatics. The plot for the cation–π interaction also shows a positive slope, but it is much steeper, i.e., these interactions are significantly more sensitive to substituent effects than aromatic interactions. This finding reflects stronger electrostatic interactions associated with the cation charge, although we are dealing with an ion pair that is neutral overall.

Figure 5.

The cation–π interaction in complex A plotted as a function of the Hammett substituent constant for the substituent Y ( ). The corresponding data for edge-to-face aromatic interactions are shown for comparison (14).

These experiments demonstrate the utility of simple synthetic supramolecular model systems for probing experimentally the fundamental nature of weak noncovalent interactions. Here, we have shown that the magnitude of the cation–π interaction is very sensitive to the electron density on the face of an aromatic ring and can be repulsive or attractive depending on the substituents. The principles derived from such studies can be applied to more complex systems where these interactions play a significant role (3), and the data generated by our experiments are being utilized in the development of molecular mechanics force-fields (25).