Nanoindentation: Toward the sensing of atomic interactions

Abstract

The mechanical properties of surfaces of layered materials (highly oriented pyrolytic graphite, InSe, and GaSe) and single-crystal ionic materials (NaCl, KBr, and KCl) have been investigated at the nanometer scale by using nanoindentations produced with an atomic force microscope with ultrasharp tips. Special attention has been devoted to the elastic response of the materials before the onset of plastic yield. A new model based on an equivalent spring constant that takes into account the changes in in-plane interactions on nanoindentation is proposed. The results of this model are well correlated with those obtained by using the Debye model of solid vibrations.

Tensile tests, usually performed on uniform cross-section rods, have been widely used to evaluate both the elastic and plastic response of bulk materials. In the elastic regime and for small strains ɛ Hooke's law applies (σ = E ɛ), where the applied stress σ is given by F/S, F and S standing for the applied force and the cross-sectional area, respectively, and E representing Young's modulus. Above a given critical stress, σ_Y, the so-called yield threshold, permanent plastic deformation is induced. Experimental full-scale tensile tests of materials are not simple because the sample preparation is rather involved, and the experiments must be done at temperatures not too far from the melting point to measure significant strains (1). A more convenient way to determine the mechanical properties of materials consists of measuring indentation hardness. A very hard indenter (i.e., a diamond pyramid in the Vickers test) exerts a plastic deformation (indentation) on the material surface under the action of a force F. The practice shows that, to a first approximation, permanent deformation is produced when the applied pressure p is about three times σ_Y (2).

More recently, indentation hardness has been used as a research tool for solids for identifying the various constituents of an alloy or to estimate the amount of deformation produced by a particular metal-working process, including creep properties (3, 4). For these purposes, the indentations must be small enough to resolve the examined features, and the corresponding measurements are known as microhardness measurements (3, 4). Typical loads lie between 0.1 and 10 N, with indentation diameters of about 10–100 μm, which are measured with sufficient accuracy by optical microscopy. A different approach is to measure the penetration depth of the indenter by using microdisplacement transducers of great accuracy (5). In this case, typical loads lie between 10⁻⁵ and 10⁻² N. At this level, microhardness measurements reveal that for metals, the hardness tends to increase as the size of the indenter is reduced (6); this is attributed to the limited range of dislocation movement available when very small volumes are involved. The plastic flow caused by the indentation on metals is known to be accompanied by the slip of atomic planes over one another. Thus, the smaller the indentation, the better the control over the local features that can be achieved. Indentation-induced surface defects can be studied by comparing the same area before and after indentation.

The study of the mechanical response of surfaces to forces at the nanonewton scale and nanometer penetration depth levels has become possible with the atomic force microscope (AFM) (7–9) and the interfacial force microscope (10, 11). Most of these studies have been focused on Au single crystals and thin films with indentation depths over 20 nm (12–14). More specifically, we have recently observed that at the first stages of cavity formation, steps along directions contained in the (111) plane originating around the cavity are created (P. F. M. Terán Arce, G. Andreu, P. Gorostiza and F.S., unpublished results). This nanometer depth scale is also appropriate to accurately study elastic deformation behavior before plastic deformation. The Hertz model (15) describes the deformation of isotropic materials through an increasing flat area of contact. When the penetration δ is negligible against the indenter radius R (δ ≪ R), the applied force F for a paraboloid indenting a plane follows the expression F = 4/3 E* R^1/2 δ^3/2 (16–18), where E* stands for the reduced Young's modulus. In the case of Au, the well-known Hertz model describes quite well the elastic region (14). However, using AFM cantilevers with ultrasharp tips (R < 10 nm), it is found in the elastic region that R ≈ δ, a situation outside the limits of applicability of the Hertz model. The contact area does not necessarily increase on application of an external force (19). In this way, a linear behavior of F against δ has been recently reported for suspended carbon (20) and polypyrrole nanotubes (21) when using an AFM cantilever loading perpendicularly to the tube axis, that is, these one-dimensional systems follow the simple Hooke's law.

Taking a more atomistic description, when forces are applied to a surface, they act directly on the surface atoms and are transmitted to the subsurface and bulk atoms via the network of bonds. The bonds thus play a crucial role in the mechanical response because of their strength and spatial distribution. When forces are uniformly applied on a sufficiently large surface, the atomic planes are homogeneously compressed along the direction of F. However, when the contact area is reduced, the deformation becomes local and, in an ideal case, only a few atoms would be involved. In this case, in-plane interactions on the indented surface are critical in how the surface is elastically deformed. To demonstrate the important role of in-plane interactions, we have studied two-dimensional layered materials and single-crystal ionic materials (alkali halides). Ionic single-crystal surfaces exhibit no ductility, that is, nanoindentations do not propagate surface modifications such as steps (22, 23). Moreover, nanoindentations allowed us to identify brittle failure with the yield threshold, because plastic modification of the surface is given by the discrete expulsion of atomic monolayers (24). We have recently performed nanoindentation experiments with ultrasharp tips on layered molecular organic materials dominated by van der Waals and hydrogen-bonding interactions, much weaker than the electrostatic and covalent bonding (25). In this case, the Hertz model fits well the experimental data despite the fact that R ≈ δ, because during penetration, the number of molecules in contact with the tip is continuously increasing.

Experimental Procedure

Nanoindentation experiments were performed with a Nanoscope III AFM (Digital Instruments, Santa Barbara, CA) either at ambient conditions or under argon flow (0% humidity) by using two types of cantilevers: stainless steel (spring constant k_c ≈ 194 Nm⁻¹) with a diamond tip (nominal radius R < 25 nm) from Digital Instruments or silicon microfabricated cantilevers with k_c ≈ 36 Nm⁻¹ and R < 10 nm (Nanosensors, Norderfriedrichskoog, Germany) and k_c ≈ 14 Nm⁻¹ and R < 10 nm (NT-MDT, Zelenograd, Moscow). The tip-to-sample approach velocity was set to 279 nm⋅s⁻¹. Applied forces F are given by F = k_c × Δ, where Δ is the cantilever deflection. The surface deformation or penetration is evaluated from δ = z − Δ, where z represents the piezo-scanner displacement.

Atomically flat defect-free regions away from steps were chosen for nanoindentations by imaging the surface using tapping-mode AFM. The amplitude of the oscillating cantilever was set to zero before every indentation experiment. The cantilever deflection Δ was calibrated by acquiring Δ vs. z curves on the surface of a clean diamond single crystal. Assuming that diamond remains undeformed on indentation, it follows that δ = 0 and thus Δ = z. To avoid nonlinearities and creep effects of the piezoscanner, indentation data were always calibrated with force curves having equal tip velocity and piezo ramp size. This experimental procedure is critical for a correct calibration. For a given material, the appropriate k_c has to be chosen (26, 27). Very soft cantilevers are insensitive to differences among hard materials, which leads to z ≈ Δ and, as a consequence, a large uncertainty in δ. On the other hand, if the cantilevers are too hard, the plastic onset is reached for small values of δ, implying insufficient statistics in the elastic region.

Results and Discussion

Layered Materials.

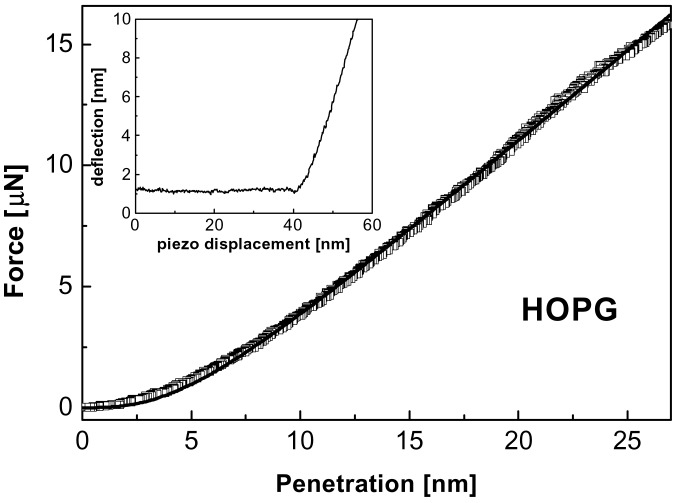
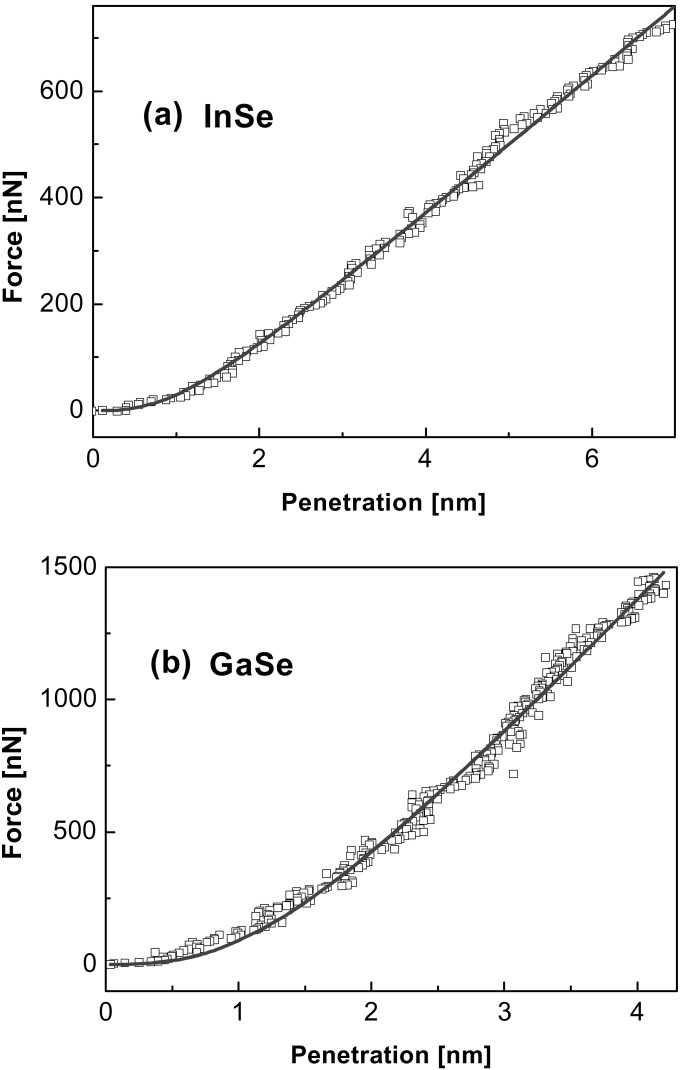
Fig. 1 represents the nanoindentation (F vs. δ) performed at ambient conditions by using a stainless steel cantilever with a diamond tip (k_c ≈ 194 Nm⁻¹, R< 25 nm) on a freshly cleaved highly oriented pyrolytic graphite (HOPG) surface. F is applied along the crystallographic c axis observing no adhesive contact on approaching the tip to the surface (see Fig. 1 Inset). From Fig. 1, we conclude that the plasticity yield threshold is not reached when forces as large as 16 μN are applied, so that a rather large elastic region is obtained, with the penetration at plastic yield δ_Y larger than 25 nm. The strong intraplanar C—C bonds (sp²) contained in the plane perpendicular to the c axis and the weak interplanar van der Waals interactions are at the origin of such large mechanical resistance. If it is assumed that the diamond tip does not deform, all deformation does arise from the HOPG surface. Fig. 1 also shows an asymptotic linear response for HOPG for larger penetrations. A similar behavior was obtained for the indentation of the layered III–VI semiconductors InSe and GaSe (Fig. 2), performed on freshly cleaved single-crystal surfaces under argon flow (microfabricated silicon cantilevers, k_c ≈ 36 Nm⁻¹, R < 10 nm).

Figure 1.

Nanoindentation curve obtained for HOPG at ambient conditions with a stainless steel cantilever (k_c ≈ 194 Nm⁻¹) with a diamond tip (R <25 nm). The continuous line corresponds to the fit to the proposed model (Eq. 1). Inset shows the deflection vs. piezo displacement curve evidencing negligible tip-surface adhesive contact.

Figure 2.

Nanoindentation curves performed with microfabricated silicon cantilevers (k_c ≈ 36 Nm⁻¹, R < 10 nm) on: (a) InSe and (b) GaSe. The continuous lines correspond to the fits to the proposed model (Eq. 1).

Proposed Model.

A model able to describe the force variation against penetration given in Figs. 1 and 2 has to take into account the fact that the tip-surface contact area remains essentially constant during penetration for δ values well above the tip-surface contact and below the onset of plastic deformation. If the size of the indenter is ideally reduced to a point (or an atom), then the affected area will be relatively large on the highly stressed surface (like in an elastic bed). Feynman developed a simple model relating the anion–cation interatomic interaction k_ac to elastic constants for small strains for NaCl-type crystals assuming central forces (28). In the harmonic limit, the interaction is described by a force constant k_T, which can be related to the long-wavelength transverse optical phonon frequency ω_T (or θ_T = ℏ ω_T/k_B) through the expression k_T = ½ μ ω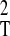, where μ stands for the anion-cation reduced mass (29). For the alkali halides k_T ≈ 10⁻¹² Nm⁻¹.

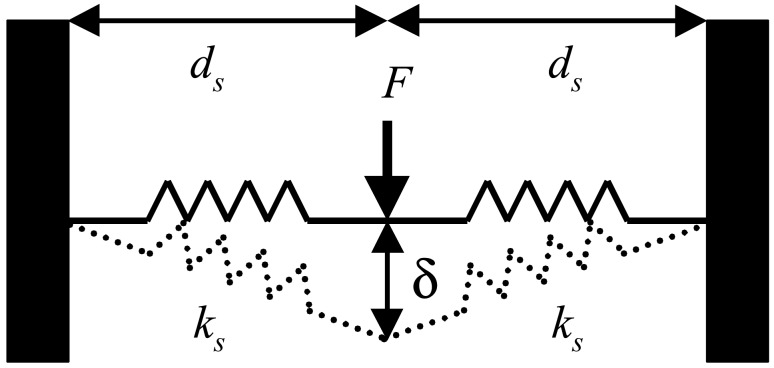
The simplest way to model the dynamics of the surface deformation is to consider the nanoindentation performed by a point force on a surface represented by a plane containing n interatomic interactions, which are represented by n-coupled springs sharing a common point where the force is applied and with the other ends fixed. For simplicity, we consider that the angle between two neighboring springs is 360/n degrees. Fig. 3 shows the model scheme for n = 2. The spring constants k_s and length d_s at zero elongation are assumed to be identical. The equation representing the induced perpendicular counterforce to the surface as a function of the deformation δ is:

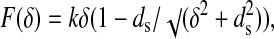1

where k = nk_s. The fits to Eq. 1 of the elastic parts of the nanoindentation curves of HOPG and InSe and GaSe are shown as continuous lines in Figs. 1 and 2, respectively (the fit parameters are given in Table 1). The experimental data are thus well described by Eq. 1.

Figure 3.

Schematic diagram of the F(δ) model described in the text.

Table 1.

Experimentally derived data for force constants (k, k_D, k_T, k_ac), lengths (d_s, δ_Y, Δ_Y) and values of the Debye temperatures (θ_D, θ_T) and elastic constants (c₁₁) discussed in text

	ds, nm	k, Nm−1	kD, Nm−1	θD, K	c11, GPa	k/ds	kT, Nm−1	θT, K	kac, Nm−1	δY, nm	ΔY, nm
HOPG			2,100	2,500
			300	950
Two springs	5.5  ± 1.0	700  ± 150
Three springs	11  ± 1.2	650  ± 160
		180  ± 40
GaSe	1.7  ± 0.5	540  ± 120
InSe	0.7  ± 0.3	140  ± 20
NaCl	0.9  ± 0.3	84  ± 13	86	321 (32)	48.7 (31)	46.7	12.0	245 (32)	6.6	2.5  ± 0.9	9.7  ± 3.0
KCl	0.8  ± 0.2	67  ± 9	65	246 (32)	40.5 (31)	41.9	12.3	215 (32)	8.5	2.5  ± 1.0	7.0  ± 2.1
KBr	0.9  ± 0.3	66  ± 20	51	173 (32)	34.6 (31)	36.7	10.5	166 (32)	7.9	2.4  ± 0.9	6.1  ± 3.2

Correlation to the Debye Model for Solids.

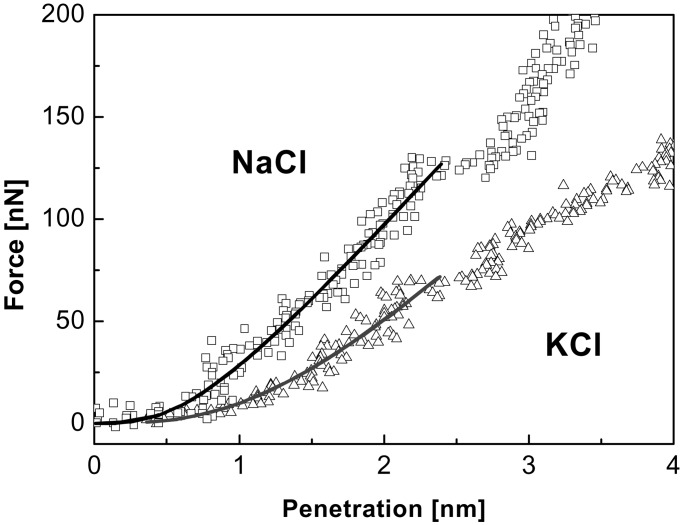
We have performed nanoindentation studies in ionic materials with fcc cubic structure because of the high symmetry of the crystal lattice and also the large amount of tabulated experimental data to compare with. The experimental results for NaCl (100) and KCl (100) are shown in Fig. 4. KBr (100) curves have been also measured but are not displayed here because they overlap with the KCl curves (see discussion below). The experiments were performed on freshly cleaved (100) alkali halides single-crystals surfaces under argon flow using microfabricated silicon cantilevers (k_c ≈ 14 Nm⁻¹ and R < 10 nm). Fits to the experimental data with Eq. 1 for δ ≤ 2.4 nm are represented in Fig. 4 by solid lines. Our model reproduces quite well the experimental points up to δ ≅ 2.4 nm, when plastic deformation sets in. Table 1 summarizes the values of k and d_s averaged for more than 20 independent fitted curves for each material.

Figure 4.

Nanoindentation curves obtained with microfabricated silicon cantilevers (k_c ≈ 14 Nm⁻¹, R < 10 nm) on: NaCl and KCl. The continuous lines correspond to the fits to the model represented by Eq. 1.

To understand the meaning of the fit parameters resulting from our model, we have compared them with those calculated by using the Debye model of vibrations in crystalline solids. We have calculated the mean spring constant, k_D, which is related to the debye frequency ω_D (or Debye temperature θ_D) through the expression k_D = m ω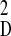 = m (k_B θ_D/ℏ)², where k_B and ℏ are the Boltzmann and normalized Planck constants, respectively, and m stands for the mean atomic mass. k_D can be considered as the stiffness of the crystal, because θ_D is a measure of the temperature above which all vibrational modes begin to be excited and below which modes begin to be frozen out (30). The calculated values of k_D are very close to the experimentally derived values of k, except for KBr, which exhibits a θ_D well below room temperature (Table 1). Nanoindentation thus reveals, at least for these cubic materials, the collective behavior of nanoscale volumes because many atoms are involved in the process (see discussion below). The calculated k/d_s ratios are also close to the tabulated values of c₁₁, the (1,1) component of the elastic tensor (31), independently of the actual radius of the tip and of Poisson's ratio. Thus, d_s represents an estimated linear dimension of the surface elastically perturbed by the nanoindentation process. The surface characterized by d_s does not necessarily correspond to the geometrical contact area, especially when in-plane interactions are strong. The systematic correspondence between k and k_D and between k/d_s and c₁₁ evidences that experimental artifacts associated with the AFM operation, such as nonlinearities, piezo-creep, or cantilever torsion, are not important (32). Using now the simple model of Feynman, it can be shown that k_ac < c₁₁ a/2, where a represents the lattice constant. If we transform to k_ac < (k/d_s) (a/2), we obtain k_ac < 13 Nm⁻¹, which is comparable to k_T.

In the case of HOPG, two Debye temperatures are tabulated, the higher value (2,500 K) corresponding to the in-plane hexagonal structure and the lower one (950 K) linked to the perpendicular direction. If k_D values are calculated by using the expression k_D = m (k_B θ_D/ℏ)² with m = 12 atomic mass units as an effective mass for both directions, the values 2,100 and 300 Nm⁻¹ are obtained (Table 1). A fit of the nanoindentation curve (Fig. 1) to Eq. 1 gives k = 700 ± 150 Nm⁻¹, which lies between 300 and 2,100 Nm⁻¹. As indentation is performed along the c axis, the contribution of the in-plane strong covalent C—C bonds is evident. If we consider an additional spring with a force constant k′ perpendicular to the two springs of Fig. 3 (the k′ spring aligned in the direction of the applied force), a fit gives k = 650 ± 160 Nm⁻¹, k′ = 180 ± 40 Nm⁻¹ and d_s = 11.0 ± 1.2 nm. The k values for both fits (with two and three springs, respectively) are quite similar, as expected, because of the stronger bonds on the lattice planes perpendicular to the c axis. If we correlate the ratio between these force constant values (k/k′) to the ratio of the squares of the Debye temperatures along the in-plane and c directions, the effective mass ratio would be ≈0.5, i.e., the effective mass associated with the c-axis direction (π-bonding) is about a factor 2 larger than the effective mass associated to the plane containing the strong σ-bonds.

In-plane interactions thus play a key role in nanoindentations performed with ultrasharp tips. Our experimental results also can help in the study of anisotropic materials. In this way, an interesting observation is that k(GaSe) > k(InSe) (Table 1), which again is a reasonable result because the in-plane Ga—Se covalent bond is stronger than the corresponding In—Se bond (the Ga—Se and In—Se bond lengths are 0.246 and 0.263 nm, respectively) (33, 34).

Elastic Energies.

We have further investigated the plastic yield threshold in the case of ionic single crystals. As observed in Table 1, all crystals show similar values of δ_Y. The force measured at the plastic yield threshold F_Y will be proportional to the energy required to break the layer bond, provided that the number of broken bonds in the ionic materials is similar. Neglecting repulsive forces, which account for the 10–20% compensation of the total electrostatic energy, the lattice energy U_c per ion pair of ionic crystals is given by the expression U_c = (e²/4πɛ₀)(z_az_c/d_ac) A (35), where z_a and z_c stand for the anion and cation charge, respectively, d_ac accounts for the anion–cation distance (= ½ a), A is the Madelung constant (= 1.7476 for the fcc crystals with rock salt structure), and e and ɛ₀ represent the elementary charge and the permissivity of vacuum, respectively. If we compare the singly charged ionic crystals NaCl and KCl, where d_ac is the only different parameter [d_ac(NaCl) = 0.282 nm and d_ac(KCl) = 0.315 nm], the slope of the indentation curve for NaCl should be larger than for KCl, which is experimentally confirmed in Fig. 4. The different repulsive interactions of the cations may account in this case for the difference between the experimental yield threshold ratio 120 nN/75 nN = 1.6 and the distances ratio 0.315 nm/0.282 nm = 1.1 (Na⁺ exhibits a larger charge density in comparison with K⁺). The indentation curves of KCl and KBr nearly overlap, because their anion–cation distances are very similar: 0.315 and 0.330 nm, respectively.

The number of ion pairs involved in the nanoindentation process can be estimated from U_c (e.g., for NaCl, U_c = 1.5 × 10⁻¹⁸ J) and from the estimated total elastic energy (E_e) at the yield threshold. E_e can be estimated, e.g., by integrating Eq. 1 from δ = 0 to δ_Y. For NaCl E_e ≈ 1.5 × 10⁻¹⁶ J, for KCl E_e ≈ 1.3 × 10⁻¹⁶ J and for KBr E_e ≈ 1.1 × 10⁻¹⁶ J. Another way to estimate E_e is by assuming that bonds are broken for strains ɛ = 0.3. For cubic systems, it can be shown that the energy density u = 9/2 B ɛ² (29), where B stands for the compression modulus (B = 1/3 [c₁₁ + 2 c₁₂]) and c₁₂ represents the (1,2) component of the elastic tensor. E_e ≈ uV, where V = π d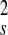 δ_Y. For NaCl E_e ≈ 2.5 × 10⁻¹⁶ J, for KCl E_e ≈ 1.8 ×10⁻¹⁶ J, and for KBr E_e ≈ 1.5 × 10⁻¹⁶ J. The number of ion pairs that may be broken is about 140 according to such estimations. Of course, only part of these bonds are broken in a mechanism of layer expulsion (23), part of the elastic energy being released. Above the first plastic yield threshold, elastic energy is again accumulated as the tip continues to indent the sample until the resulting surface reaches a second yield threshold.

Conclusion

In-plane interactions play a key role in the nanoindentation process performed with ultrasharp tips leading to a nonhertzian response of the elastic region of the nanoindentation curve. The proposed simple spring model takes into account the anisotropy created during the indentation process and reproduces quite well the experimental data.

Nanoindentation performed at the limit of tip radii tending to zero reveals, at least for cubic materials, the collective behavior of the nanoscale volumes involved. We believe that interatomic and intermolecular interactions in solids could be directly studied if undeformable tips with radius in the order of these interatomic distances could be produced.

Abbreviations

HOPG

highly oriented pyrolytic graphite

AFM

atomic force microscope