A structure-based method for derivation of all-atom potentials for protein folding

Abstract

A method for deriving all-atom protein folding potentials is presented and tested on a three-helix bundle protein, as well as on hairpin and helical sequences. The potentials obtained are composed of a contact term between pairs of atoms, and a local density term for each atom, mimicking solvent exposure preferences. Using this potential in an all-atom protein folding simulation, we repeatedly folded the three-helix bundle, with the lowest energy conformations having a C_α distance rms from the native structure of less than 2 Å. Similar results were obtained for the hairpin and helices by using different potentials. We derived potentials for several different proteins and found a high correlation between the derived parameters, suggesting that a potential of this form eventually could be found that folds multiple, unrelated proteins at the atomic level of detail.

The problem of deriving a potential to fold proteins has been fully solved only in simple lattice models (1, 2). Most off-lattice models that are presently used to obtain complete folding trajectories use a potential, known as a Gō potential, tailored to give lowest energy to the native state of a single protein (3). Because Gō potentials are actually potentials defined on structures rather than on sequences, one cannot use them to try to fold sequences of unknown structure or even to fold two different sequences by using the same parameters. Nevertheless, Gō potentials are useful for examining possible protein-folding pathways for a single protein (4–7) and for testing a particular model's computational feasibility.

In contrast, sequence-based potentials give a set of parameters that can be used to simulate any amino acid sequence. A sequence-based potential consists of an atom-typing scheme and a set of parameters giving the energetics of contacts between atom types. Given any amino acid sequence, the atom-typing scheme is used to assign a type to each atom of the sequence, and using the interaction parameters the simulation can then be performed. Recently, several groups have proposed off-lattice models using sequence-based potentials that can in principle be used to simulate any sequence (8–11). It is unclear at this time whether the simplified representation of proteins used in those models will eventually lead to correct folding of many proteins of various topologies to an acceptable level of accuracy.

In this article, we chose to work with a detailed representation that explicitly models all atoms other than hydrogen. All side-chain χ angles and backbone φ/ψ angles are free to rotate. At this level of detail, the basic problem of stabilizing the correct topology is further complicated by the conformational flexibility of the side chains, which can assume many different conformations consistent with a given backbone conformation (12–14). The advantages of this model are that (i) packing effects caused by diverse side-chain shapes are present (14), (ii) side-chain entropy is properly accounted for, and (iii) difficulties resulting from an oversimplified protein representation are largely eliminated, leaving only the underlying potential as a possible source of error. We have previously shown that simulations of this model using the structure-based Gō potential, starting from random coils, reach the native state by a cooperative transition in a reasonable amount of computational time (6).

Finding sequence-based potentials that fold even a single protein has proven to be a difficult problem. There is no consensus on which types of potentials should be investigated, and several papers have demonstrated that the problem has no solution for certain types of potentials (15, 16). It is therefore important to focus effort on potentials of the correct form. In the present article, we derive a sequence-based potential that repeatedly folds a single protein in the all-atom representation. The potential-derivation procedure is structure-based, that is, we find energetics tailored to fold a particular structure. The potential form, however, is sequence-based, and, unlike Gō parameters, the parameters we obtain can be used to simulate any sequence. Whether or not those same parameters would properly fold other sequences is a separate question, which we do not address here. We present data showing significant correlation between parameters derived for several different proteins, suggesting that a transferable potential of this form is likely to exist.

Methods

Density-Dependent Energy Term.

We defined two atoms, A and B, to be in contact if the distance between them was less than λ(r_A + r_B), where r_A and r_B are their respective van der Waals radii. We took λ = 1.8 and used radii as in previous work (6). Atomic hard sphere radii were taken to be 0.75 of their van der Waals sizes (6). To each atom type A, we assigned an ideal number of contacts, n_A, and a corresponding energy term penalizing deviations from this number: if an atom of type A makes n contacts, it receives an energy of E_A = |n − n_A|. The numbers n_A were determined by averaging the number of contacts, n, made by all atoms of type A in a given structure. If max(n) − min(n) >4 for a given atom type in a protein, it did not receive a density-dependent energy.

Contact Potential Derivation.

For each pair of atom types A and B in a given protein structure, we calculated N_AB and Ñ_AB, respectively the number of A−B pairs in contact and the number of A−B pairs not in contact. We assigned energy E_AB to an A−B contact as follows:

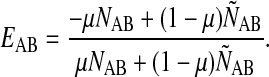1

Note that if N_AB = 0 for a pair of types, then E_AB = 1 regardless of μ. The parameter μ is needed because the number of pairs not in contact, Ñ_AB, is always far larger than the number of native contacts, N_AB. If we were to take μ = 0.5, E_AB would be an averaging of attractive native contacts, with a value −1, and repulsive non-native contacts, with a value of +1. Practically all values of E_AB were strongly repulsive under this μ = 0.5 scheme, so we had to give more weight (0.5 < μ< 1) to native contacts.

Combined Potential and Simulation.

The contact potential and density terms were combined as follows to give the protein folding potential, U:

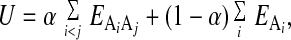2

where A_i is the atom type of atom i of the protein. We used α = 0.3, postponing systematic derivation of this parameter to future work. We turned off all side chain–backbone contacts, all local side chain–side chain contacts (up to i and i + 2), and all local backbone–backbone contacts (up to i and i + 3). All-atom protein representation and Monte Carlo simulation were taken from previous work (6). Simulations were run at Monte Carlo temperatures between 0.4 and 0.44, at which move acceptance rates in the native state were approximately 20%. The distance rms (drms) between two structures is given by (∑ (r_ij − R_ij)²)^1/2, where r_ij is the distance between atoms iand j of one structure (and correspondingly R_ij for the other structure). We computed drms values by using only C_α atoms.

Results and Discussion

Folding Helices: Interaction with Implicit Solvent.

Peptide backbones are comprised of four heavy atom types: the carbonyl carbon (C) and oxygen (O), the amide nitrogen (N), and the α-carbon (C_α). Because the i − i + 4 backbone hydrogen bonds are a distinct feature of α-helices, we thought that by introducing a strong hydrogen bonding-like interaction, we would be able to make an α-helical conformation the ground state for any peptide. A hydrogen bond would minimally require the N—O distance to be within 3.5 Å, and we initially thought that giving strong preference only to N—O contacts would result in a helical conformation. We quickly found, however, that this was not the case: many locally crumpled, nonhelical conformations were found that had lower energy than the helical conformation. O (and N) atoms in these nonhelical conformations made contacts with multiple N (and O) atoms. Given that the hydrogen bond is known to be strongly directional (17, 18), this naive contact potential appears to have failed because it lacked orientational specificity.

We found two ways of correcting this problem. The first method defined a potential based on four distances between backbone atoms: d_O−N, d_O−C, d_{C-amide H}, and d_{O−amide H}. The potential was tuned on a database of representative protein structures, including many β and α/β proteins (see Fig. 1B). Implementing only this hydrogen bonding potential, we were able to fold all peptides into helices. We were able to repeat this result by replacing some of the distances with angles (e.g., N—O—C), but opted for distances for reasons of computational efficiency. Using a potential parametrized by less than four distances led to nonhelical ground states, which is not surprising given that four independent spatial constraints are required to determine the orientation of two vectors.

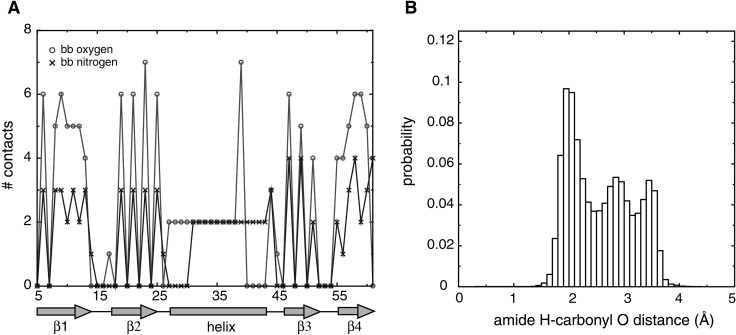
Figure 1.

Statistics for hydrogen-bonding potentials. (A) Number of backbone–backbone contacts made by backbone oxygen and nitrogen atoms at each position of protein G (Protein Data Bank code 1IGD). Local backbone contacts were turned off, so that contacts between residues i, i + 1, i + 2, and i + 3 were not included for all i. (B) Distribution of distances between backbone amide hydrogen and backbone carbonyl oxygen in proteins. The joint probabilities of observing a particular set of distances, p(d_O−N, d_O−C, d_{C−amide H}, d_{O−amide H}), were obtained from a database of representative protein structures. The database was comprised of one representative from each homologous family in the Families of Structurally Similar Proteins database (27), giving a total of ≈2,500 structures. Distances were recorded when the C—N distance was less than 5 Å. The distribution of O-amide H distances is shown here. The joint probabilities were converted to effective free energies by using the Boltzmann-like relation E = −ln(p). The energies obtained were then used as a potential to fold peptides.

While the resulting hydrogen bond is strongly directional, and emerges naturally from a knowledge-based procedure, it is computationally expensive, slowing down simulations by at least 50%. The second method we developed is less direct, but gives equally good helix formation, at low computational cost. We recorded the number of contacts made by each backbone atom of a given protein. In Fig. 1A, we plot the number of backbone contacts made by backbone nitrogen (N) and oxygen (O) atoms at each position in protein G. We see that the helical region of the protein shows a strong signal in the number of contacts made by backbone N and O atoms: each one makes exactly two contacts when present in the helix, whereas they can make between zero and seven contacts when present in strands or loops. Other proteins yielded similar data. We therefore introduced an energetic term, acting on each atom, which would penalize deviations from the ideal number of contacts made by that atom (see Methods). The ideal number of contacts depended on the atom type. We found that helices could be formed by simply setting the ideal number of contacts for O and N atoms to be two and adding an attractive contact interaction between O and N.

Both potentials give good helices because they introduce a directional hydrogen bond. The second method introduces directionality indirectly by restricting the local density around each atom. This prevents too many N atoms from crowding around a given O atom, and thus strongly destabilizes the decoy conformations that plagued the isotropic contact potential. We find this idea attractive because it has a nice physical interpretation as well: the local density term can be thought of as an implicit way of modeling interactions with solvent molecules, which are not present in our model. The density term controls the ideal degree of solvation for a given atom.

Folding a β-Hairpin: Deriving the Contact Potential.

To explore possible schemes for contact potential derivation, we started by looking at β-hairpin 2 from protein G, which is known to be partially stable in solution (19–22). Because this β-hairpin is relatively small and requires a balance between local and nonlocal interactions to fold properly, it is a good molecule for quickly testing out ideas about potentials.

To define the all-atom contact potential, we introduced an atom typing scheme in which each side-chain atom of each of the 20 amino acids is assigned a separate type. Atoms that are related by symmetry within a single amino acid are assigned the same type. Along with the four backbone atoms, we have a total of 84 atom types. The hairpin, containing a total of 130 atoms, has 44 different atom types by our scheme. Our sequence-based model of the hairpin contains ≈1/3 the number of atom types as the Gō model would, because in the Gō model each of the 130 atoms would constitute a separate type. Because the number of parameters in the model scales as the square of the number of types, the sequence model contains ≈1/9 the number of parameters as the Gō model. This is a very significant reduction in the number of parameters, and it is this reduction that makes the derivation of sequence-based potentials a challenging task. Because the hairpin contains five threonines, two valines, and two aspartic acid residues, there is a significant amount of reuse of the same atom types within this molecule. The problem becomes harder as the size of the protein increases, because its conformational space grows exponentially with length, while the number of types cannot exceed 84.

We used a simple guiding principle in deriving potential parameters: contacts formed in the native structure should be more favorable than contacts that are not seen. If two different atom types are always found to contact each other, we want to assign a strong attractive interaction between those two types. On the other hand, if a pair of atom types is never seen to contact, we introduce some repulsion between their types.

To implement this idea, we assigned an energy E_AB to contacts between atom types A and B, and computed E_AB as a function of the number of native A–B contacts made in a given protein structure (see Methods). If no native A–B contacts were present in the protein structure, we assigned E_AB = 1. A single parameter μ was introduced to control the distribution of energies E_AB for A–B pairs that made at least one native contact. For such pairs, when μ = 1, E_AB = −1, whereas lower values of μ introduce more repulsion and dispersion of energies.

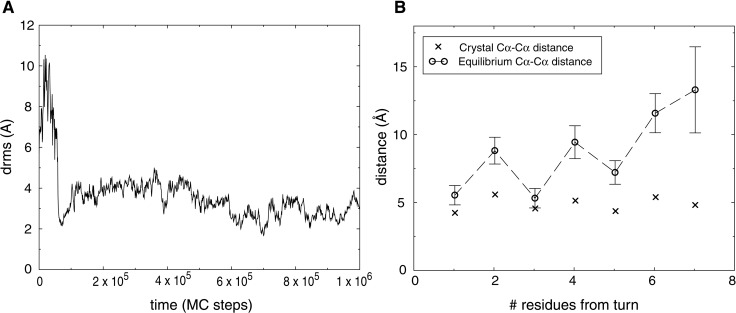
We were able to fold the hairpin repeatedly, as shown in Fig. 2A, by using values of μ between 0.8 and 0.96. The potential-derivation scheme thus identifies many potentials that can fold a single hairpin. Lowest energy conformations had low drms values, with a typical folded conformation having a drms of ≈2 Å. We found that the hairpin was often found in a frayed-end state, in which the turn was properly formed, but the two ends were somewhat free of each other. This behavior is shown in Fig. 2B. The average distance between hydrogen-bonded residues is plotted as a function of residue number, showing that residues far from the turn tend to be less constrained than residues closer to the turn. This is precisely what is seen in experimental studies of this hairpin (19). The peptide makes brief excursions to fully native hairpin conformations, having lowest energy, and then returns to the entropically more favorable frayed-end states.

Figure 2.

Folding of β-hairpin 2 from protein G. (A) A folding trajectory for the hairpin using a contact potential with μ = 0.93 at T = 0.4. The trajectory was started from a fully unfolded conformation. (B) The equilibrium Cα-Cα distances between hydrogen-bonded residues of the hairpin at T = 0.5. Average distances (○) were computed over uncorrelated conformations from a long simulation started at the native hairpin structure taken from protein G. The error bars indicate 1.5 SDs of the distance distribution. X-marks indicate the crystal structure Cα-Cα distances.

Folding a Protein: Putting the Pieces Together.

We applied our potential derivation method to the three-helix bundle protein consisting of the B domain of Staphylococcus aureus protein A, which has featured in both experimental (23, 24) and computational (4, 7, 11, 25, 26) studies. For each of the 61 atom types present in this protein, we determined the ideal local density (see Methods). We derived the contact potential for this protein by using a value of μ = 0.98. Because simulation time was considerably longer for this protein than for the helices and hairpin, we could not explore a range of μ values.

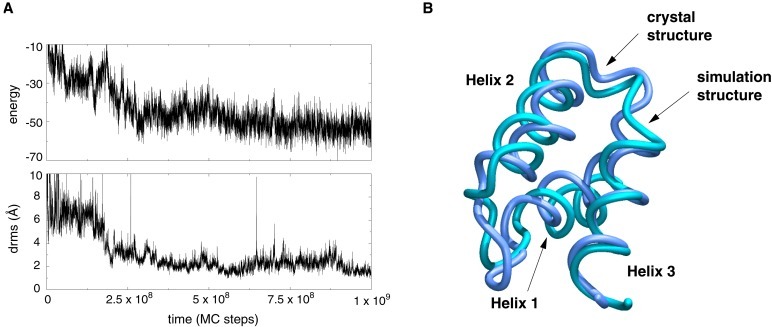
We ran 40 folding simulations, starting from completely random coils. Nineteen of these runs folded in the allotted simulation time. Average drms of the folded conformations from the native crystal structure was 2.5 Å. Low energy states always corresponded to low drms conformations, with native topology and secondary structure. A sample trajectory is shown in Fig. 3. The lowest-energy structure from one trajectory, with drms of 1.9 Å, is shown superimposed on the native conformation in Fig. 3.

Figure 3.

Folding of a three-helix bundle protein. (A) A folding trajectory started from a fully unfolded conformation of the three-helix bundle protein (B domain of Staphylococcus aureus protein A, Protein Data Bank code 1BDD) using the all-atom sequence-based potential described in the text. The plot shows the time course of both energy and drms from crystal structure. The trajectory reaches drms values as low as 1 Å. (B) The lowest-energy structure from a folding trajectory superimposed on the native crystal structure. The drms between the two structures is 1.9 Å.

We found that folding proceeded by several routes. The major pathway consisted of formation of a complex of helices 2 and 3, which formed a scaffold for subsequent formation of helix 1, consistent with previous Gō simulations in a different model (7). Another pathway consisted of formation of helices 1 and 3, in native orientation, followed by slow formation of helix 2. This pathway was necessarily somewhat slower because it is topologically more difficult for helix 2 to form once helices 1 and 3 are partially stable in their native orientation. A third, rare pathway consisted of formation of a complex of helices 1 and 2, followed by formation of helix 3.

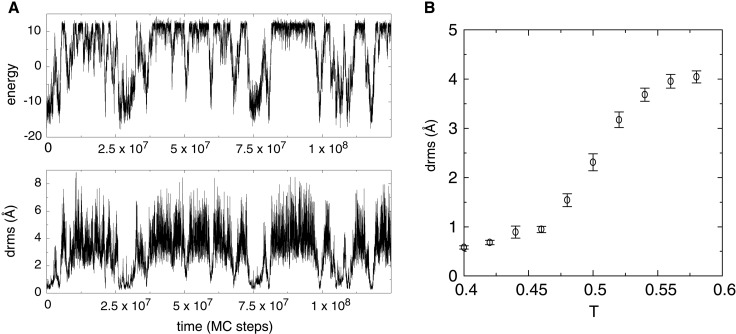
We measured the stabilities of each helix of the protein, by running equilibrium simulations for each one, using the same potential that was used to fold the entire protein. A plot of folding and unfolding transitions for helix 3 simulated at its transition temperature (T_f = 0.52) is given Fig. 4A. The thermodynamic curve is given in Fig. 4B. Because helix 2 had T_f = 0.58, and helix 3 had T_f = 0.44, we found that helices 2 and 3 were fully stable for the Monte Carlo temperature range of 0.4 to 0.44 at which simulations of the entire protein were run, whereas helix 1 was only marginally stable. Experiments have shown that, at room temperature, helix 3 is marginally stable, whereas the other two helices are unstable (24). Our Monte Carlo simulation temperature is therefore somewhat below the equivalent of room temperature, and helix stabilities need to be adjusted.

Figure 4.

Folding of the isolated helix 3 from the three-helix bundle protein. (A) A trajectory started from the native conformation of helix 3, run near the helix's transition temperature (T = 0.52). The same all-atom potential that was used to fold the entire protein is used here. Both energy and drms traces show that the helix repeatedly unfolds completely and refolds. (B) Average drms of helix 3 measured over long simulations at various temperatures. The average drms of fully unfolded conformations of the helix is ≈4 Å. Error bars indicate 1.5 SDs of the computed average.

Transferability of Potentials.

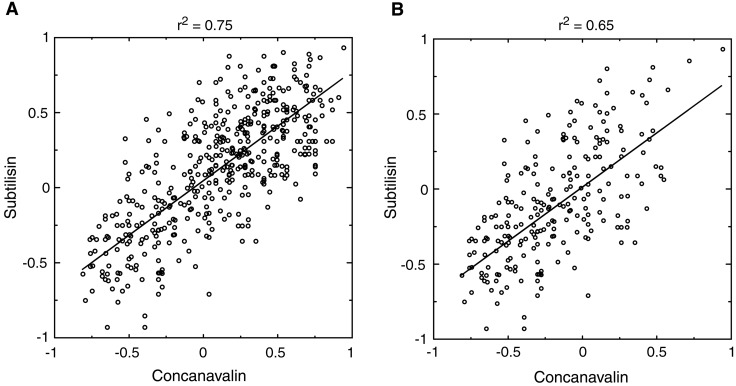
Having shown that a sequence-based potential can fold an all-atom protein model, the question of transferability remains: does a single potential of this form exist that can fold several different proteins? The method introduced here does, after all, rely on native structure information to derive the sequence-based potential. Although future work will investigate this question in full, we now give a partial answer by comparing the contact potentials derived with several different proteins. Fig. 5A shows the correlation between parameters of two contact potentials, obtained from the proteins concanavalin and subtilisin. While these proteins have completely different folds and secondary structure content, the contact potentials derived from them have high (r² = 0.75) correlation. Similar results were obtained over representatives of several other folds, such as Rossman and TIM-Barrel.

Figure 5.

Comparison of all-atom potentials derived from concanavalin (Protein Data Bank code 1NLS) and subtilisin (Protein Data Bank code 1GCI). (A) Each point represents the contact energy for a pair of atom types that were found to make contacts in both proteins. Contact energies were derived as described in Methods, using μ = 0.995 for concanavalin and μ = 0.993 for subtilisin. Note that the appropriate range of μ moves closer to 1 as protein size grows, because the number of pairs of atoms not in contact grows much faster than the number of pairs in contact. It is clear that these values of μ are not too close to 1 because we see a good dispersion of energies over both the x and y axes. We found good correlation between potentials over a large range of values of μ, indicating that the trend is not sensitive to errors in μ. (B) Same as A except side chain–backbone contacts were not included in plot. The best-fit lines are shown.

The high correlation is partially explained by the following observation. Side-chain atom types that are usually found on the surface will make fewer contacts with the backbone in all proteins, whereas hydrophobic side-chain atoms will make more contacts with the backbone. This results in lower variation of our derived side chain–backbone interactions across proteins. Nevertheless, when only side chain–side chain interactions are considered (Fig. 5B), we still obtain significant correlation between potentials (r² = 0.65). The potential we used to fold protein A also gave significant correlation with potentials from other proteins, but because of its small size, many contact types were not present in its structure. We therefore had to use larger proteins (Fig. 5) to have a meaningful comparison of potentials.

In this article we have shown that a sequence-based potential exists that folds a three-helix bundle protein in an all-atom representation. This finding is a marked departure from previous simulations in that we used a sequence-based potential that contains far fewer parameters than a Gō potential. Because of the parameter reduction, the energy landscape for sequence-based folding becomes rougher and less biased toward the native state than in the Gō model. Nevertheless, we showed that even in this rougher landscape, folding of a single protein is still possible. The next step is to develop methods that can derive a potential that stabilizes several protein structures simultaneously. The method given here explored a very small fraction of the total parameter space of potentials and was still able to find separate potentials for folding a hairpin, a helix, and an entire protein. Additionally, we found reasonable correlation between the contact potentials derived from different structures. These observations suggest that by searching a bigger piece of potential space in a well-chosen way one could obtain a transferable potential. This remains a major challenge for computational protein folding.

Abbreviation

drms

distance rms