Abstract
Characterization of the physical properties of protein surface hydration water is critical for understanding protein structure and folding. Here, using molecular dynamics simulation, we provide an explanation of recent x-ray and neutron solution scattering data that indicate that the density of water on the surface of lysozyme is significantly higher than that of bulk water. The simulation-derived scattering profiles are in excellent agreement with the experiment. In the simulation, the 3-Å-thick first hydration layer is 15% denser than bulk water. About two-thirds of this increase is the result of a geometric contribution that would also be present if the water was unperturbed from the bulk. The remaining third arises from modification of the water structure and dynamics, involving approximately equal contributions from shortening of the average water–water O–O distance and an increase in the coordination number. Variation in the first hydration shell density is shown to be determined by topographical and electrostatic properties of the protein surface. On average, denser water is found in depressions on the surface in which the water dipoles tend to be aligned parallel to each other by the electrostatic field generated by the protein atoms.
A characterization of protein hydration is essential for understanding protein structure, folding, and function. This characterization requires elucidating the effects of both the solvent on the protein and the protein on the solvent (1, 2). Concerning the latter effect, detailed information on ordering and dynamical properties of individual, highly perturbed, strongly bound water molecules has been furnished by high-resolution x-ray crystallography and NMR spectroscopy (3–10). However, to obtain the data required for a complete thermodynamic description of protein hydration it is necessary to obtain a more global picture in which the solvent is described in terms of probability distributions. Recent work in this direction has used molecular dynamics (MD) simulation (11–13) and novel crystallographic methods (6, 7, 14) to enable radial distribution functions of water molecules around protein groups in crystals and related quantities to be obtained.
It is of particular importance to determine how protein surface water is on average perturbed from the bulk. An intriguing result in this regard was reported by Svergun et al. (15), who combined small-angle scattering (SAS) of x-rays in H2O with that of neutrons in H2O and D2O to show that for lysozyme and other proteins the average density of the first hydration shell (0–3 Å from the surface) is significantly higher than that of bulk water. This finding is consistent with results from MD simulation (16) and the crystallographic work (14). The present article explains the physical origin of this effect. We use MD simulation of lysozyme in explicit water to determine the contributions to the hydration density profile. The MD allows detailed structural properties of the hydration water to be analyzed in the context of the SAS result and compared with bulk water. Excellent agreement is found between the SAS profiles calculated from the simulation and the experimental results. About two-thirds of the first-shell density increase of ≈15% is found to be caused by a geometric contribution that would also be present if the water was unperturbed from the bulk. The remaining one-third (5%) density increase involves significant changes in the average water structure.
We also address the question as to the physical origins of the first-shell density variations over the protein surface. Classically, protein hydration structure has often been discussed in terms of the hydrophobicity/hydrophilicity of the surface groups. However, recent work has emphasized the effect of protein surface topography (17–20). Here we demonstrate that both the topography of the protein surface and the electrostatic field generated by the protein atoms determine the density of the surface water layer. The relationship between these two effects is determined here and leads to a simple physical picture of the global surface density effect.
Methods
MD Simulations.
The MD simulations, which will be described in detail elsewhere, were performed with the CHARMM 27b1 program (21). The force field used was CHARMM22 (22), which treats all atoms explicitly. The TIP3P model was used for the water (23). The 1.33 Å resolution structure (193L) of hen egg-white lysozyme from the Protein Data Bank was used (24). For convergence in the scattering profile calculations, a sufficiently large amount of water is needed. To achieve this convergence the protein was embedded in a truncated octahedron containing 8,577 water molecules originating from a cubic box of side 84 Å. The system was simulated with periodic boundary conditions as an isothermal-isobaric (NPT = number, pressure, and temperature) ensemble at T = 300 K and P = 1 atmosphere (1 atm = 101.3 kPa) with particle mesh Ewald electrostatics. Nine chloride ions were included so as to neutralize the net charge on the lysozyme molecule. This effective ion concentration is similar to that used in the SAS experiments (15). A simulation performed without counterions gave the same results as that with counterions to within statistical errors. For analysis purposes the trajectory from 100 to 500 ps was used, and coordinates were saved every 0.2 ps. The average rms heavy-atom deviation of the lysozyme molecule from the crystal structure was 1.72 Å, comparable to the value for the corresponding rms deviation among lysozyme in different crystal forms (tetragonal, triclinic, and orthorhombic), which is 1.54 Å. The Cα B-factors agree with the experiment to within 15% on average.
SAS Profiles.
The details of the theory involved in the computation of the SAS profiles and the associated molecular envelope are given in a separate article (25). Here a very brief summary is given.
A technique was developed to efficiently calculate scattering profiles from many configurations of the explicit-atom protein/water system. To do this calculation, a model system was defined as a sphere containing one protein molecule surrounded by water molecules. The radius R of the sphere was chosen to be sufficiently large (32.4 Å) so that the time-averaged density of the water in the outer 4 Å shell of the sphere was homogeneous to that of the bulk water simulation. This homogeneity ensures that there is no artefactual excess scattering as a result of the finite size of the model scattering system. The excess scattering density I(q), where q is the scattering vector, was determined from all explicit atoms (i.e., protein and water) in the MD simulation within radius R. For the calculation of the scattering profiles (but not for performing the MD simulation, see above), the effect of the solvent outside radius R was modeled as a continuum. Multipole expansions were used for the scattering amplitudes (26), permitting evaluation of the spherically averaged scattering intensities in 1 day of central processing unit on a PC cluster, i.e., 50 times faster than using the direct method of spherically averaging the average of the square of the Fourier transforms of the coordinates. To calculate the scattering it is necessary to determine the excluded volume associated with each atom. The scattering profiles were evaluated for each set of coordinates generated in the simulated trajectory of the system and averaged to obtain the final profiles. The multipole expansions converged fully. The scattering profiles also converged as a function of simulation time.
Protein Surface.
To calculate densities and to determine surface topographic properties it is necessary to define a surface. To obtain a smooth analytical envelope around the protein each atom was approximated by a Gaussian sphere, 𝒢k whose volume is that of a uniform sphere of radius Rk and was taken from the excluded volumes in ref. 27. Spherical coordinates (R, θ, φ) were used with their origin at the center of mass of the protein. A mesh of points was constructed on the spherical surface, each point associated with a direction, ωi = (θi, φi). At each point along any radius vector ri the contribution from the protein and solvent atoms to the total volume density function was calculated. The protein and solvent contributions vary monotonically with the radius. Their intersection was considered to define locally the protein surface along the direction ωi, which we denote by SP(ωi). Expanding the surface points, ri over spherical harmonics Ylm(θ, φ) allows the protein surface to be represented as an analytical function of the radial angles θ and φ. The required angular integrations on the sphere were computed by using the Gaussian-like quadrature scheme due to Lebedev (28), applied with 1,202 grid points. The directions of the grid points and the associated weights were taken from ref. 29. To our knowledge, this is the finest-available grid for Lebedev integration. The grid was sufficiently fine that all of the quantities examined here had converged.
Pair Correlation Functions.
Protein–water pair correlation functions (PCFs, proximal pair correlation functions) were calculated according to the “proximity criterion” (30). To do this calculation, each solvent molecule was assigned to the protein atom to which it was closest and was represented by a Gaussian sphere of effective radius 1.5 Å (calculated from the excluded volume of the water molecule). The volume fraction of the shell around a given protein atom, required for the number density evaluation, was calculated with the Lebedev integration method, by distributing 1,202 Lebedev integration grid points over each spherical shell of radius r from the protein atom considered. At each grid point the volume density of the proximal water molecules was estimated by summing over the Gaussian spheres. If the volume density at the given grid point was greater than a value, α, then this grid point was chosen to contribute to the fractional volume. The value of α was 0.21, determined from the normalization condition that number density equals the bulk density for r > 6 Å. All other grid points were set to zero. Thus, the value of the PCF is the ratio between the number density ρ(r) obtained and the bulk density.
Surface Topographic Perturbation.
The surface topographic perturbation, h(Θ) was calculated as the difference between multipolar expansions of the protein surface at two different resolutions, h(Θ) = SL1 − SL2, (L1 > L2). For L2, a value of 3 was chosen. Cavities smaller in diameter than a water molecule (3.5 Å) were excluded. To do this calculation, we recall that at any given radius R the spatial resolution of the protein surface given by an Lth-order multipolar expansion is πR/L. Therefore, the multipolar expansion was truncated at L1 = 15 at R = 17 Å (the average radius of the protein surface).
Results
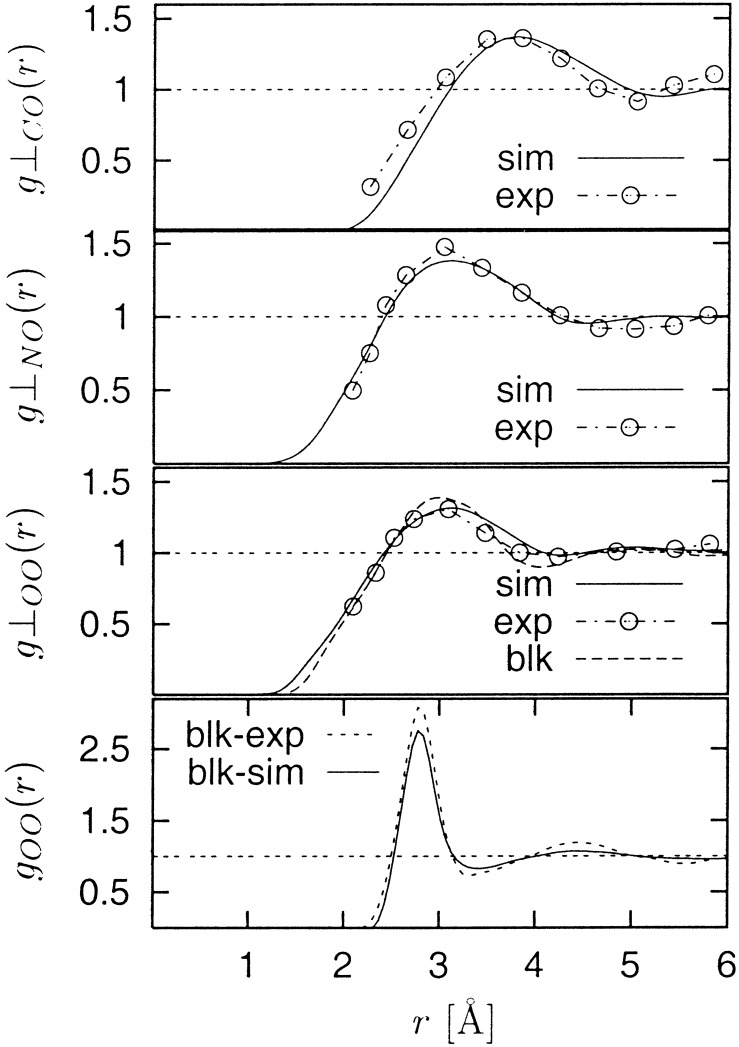
The PCFs, g⊥(r) between the water oxygen atoms and the protein surface C, N, and O atoms are shown in Fig. 1 together with the corresponding experimental results of ref. 14. The simulation-derived and experimental functions agree well. A control simulation was performed of pure water under the same conditions as for the solvated lysozyme simulation. The standard radial distribution function g(r) from this simulation is also shown in Fig. 1 and is also in good agreement with experiment (31).
Figure 1.
PCF, g⊥(r) between protein surface atoms (O, N, and C) and water oxygen atoms (solid curves, labeled as “sim”) calculated by using the “proximity criterion” as described in Methods, together with the corresponding experimental data (“exp”) from ref. 14, and that for the bulk water simulation (blk). Also shown is a comparison between experiment (blk-exp) and simulation (blk-sim) of g(r) for the bulk water oxygens, calculated as g(r) = 〈ρ(r)〉/〈ρ(∞)〉, where ρ(r) is the number density. The difference in the shape of the bulk water g(r) and the O–O g⊥(r) arises from the definition of the functions.
The calculated SAS intensities are compared with experiment in Fig.
2. χ values, a measure of the
similarity between the calculated and experimental profiles, are given
in Table 1 together with radii of
gyration, Rg, determined with the
low-q Guinier approximation, I(q)
≈ I0
exp(−q2R /3)
(32). The agreement between the simulation-derived and experimental
profiles and radii of gyration is found to be excellent, and the
differences between the three types of experiment (x-rays in
H2O, neutrons in D2O,
neutrons in H2O) are also well reproduced. To
examine the influence of explicit solvent, the profiles were computed
with the explicit solvent included (by including all protein and
solvent atoms in the scattering profile calculations) and with it not
included (including only the protein atoms, with the entire solvent
region modeled as bulk continuum). The χ values in Table 1 show that
for all three types of scattering the calculated profile is
significantly closer to experiment when the solvent molecules are
explicitly included. This result confirms previous studies indicating
that it is necessary to take into account hydration effects in SAS
studies (15, 33, 34).
/3)
(32). The agreement between the simulation-derived and experimental
profiles and radii of gyration is found to be excellent, and the
differences between the three types of experiment (x-rays in
H2O, neutrons in D2O,
neutrons in H2O) are also well reproduced. To
examine the influence of explicit solvent, the profiles were computed
with the explicit solvent included (by including all protein and
solvent atoms in the scattering profile calculations) and with it not
included (including only the protein atoms, with the entire solvent
region modeled as bulk continuum). The χ values in Table 1 show that
for all three types of scattering the calculated profile is
significantly closer to experiment when the solvent molecules are
explicitly included. This result confirms previous studies indicating
that it is necessary to take into account hydration effects in SAS
studies (15, 33, 34).
Figure 2.
Comparison of calculated (solid lines) with experimental x-ray and neutron SAS profiles (taken from ref. 15). In the main figure the y axis of different profiles is shifted for clarity. Inset shows calculated SAS intensities with common origin.
Table 1.
Comparison of experimental and simulation-derived scattering profiles
R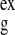 ,
Å ,
Å |
R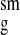 ,
Å ,
Å |
χ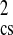
|
χ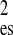
|
|
|---|---|---|---|---|
| X-ray | 15.4 ± 0.2 | 15.3 ± 0.2 | 0.90 | 0.61 |
| n/H2O | 13.8 ± 0.2 | 13.6 ± 0.2 | 2.88 | 2.77 |
| n/D2O | 12.4 ± 0.2 | 12.5 ± 0.2 | 2.09 | 1.91 |
The quality of the agreement is given by the χ function defined
as follows: χ2 = 1/(N −
1)∑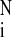 [Ism(qi)
−
Iex(qi)/σi]2,
where σi denotes the SD of the ith
experimental point. χ is given for calculations in which the solvent
molecules are included explicitly (χes) and when they are
represented by a continuum (χcs). The x-ray simulation
and experimental results are in significantly better agreement than the
neutron profiles, because of the improved statistical accuracy of the
experimental x-ray profile at high q. Radii of gyration were
obtained by fitting the profiles to the Guinier law in the range
qRg < 1. The differences of
Rg between the different types of scattering
originate in variations in the distribution of scattering lengths in
the systems as described in ref. 15. The geometric mass-weighted
Rg obtained from the MD simulation atomic
coordinates is 14.12 ± 0.10 Å, about 5% lower than the x-ray
and 5–10% higher than the neutron scattering values. The ±0.10 Å
fluctuation in the MD geometric Rg arises from
the internal protein dynamics.
[Ism(qi)
−
Iex(qi)/σi]2,
where σi denotes the SD of the ith
experimental point. χ is given for calculations in which the solvent
molecules are included explicitly (χes) and when they are
represented by a continuum (χcs). The x-ray simulation
and experimental results are in significantly better agreement than the
neutron profiles, because of the improved statistical accuracy of the
experimental x-ray profile at high q. Radii of gyration were
obtained by fitting the profiles to the Guinier law in the range
qRg < 1. The differences of
Rg between the different types of scattering
originate in variations in the distribution of scattering lengths in
the systems as described in ref. 15. The geometric mass-weighted
Rg obtained from the MD simulation atomic
coordinates is 14.12 ± 0.10 Å, about 5% lower than the x-ray
and 5–10% higher than the neutron scattering values. The ±0.10 Å
fluctuation in the MD geometric Rg arises from
the internal protein dynamics.
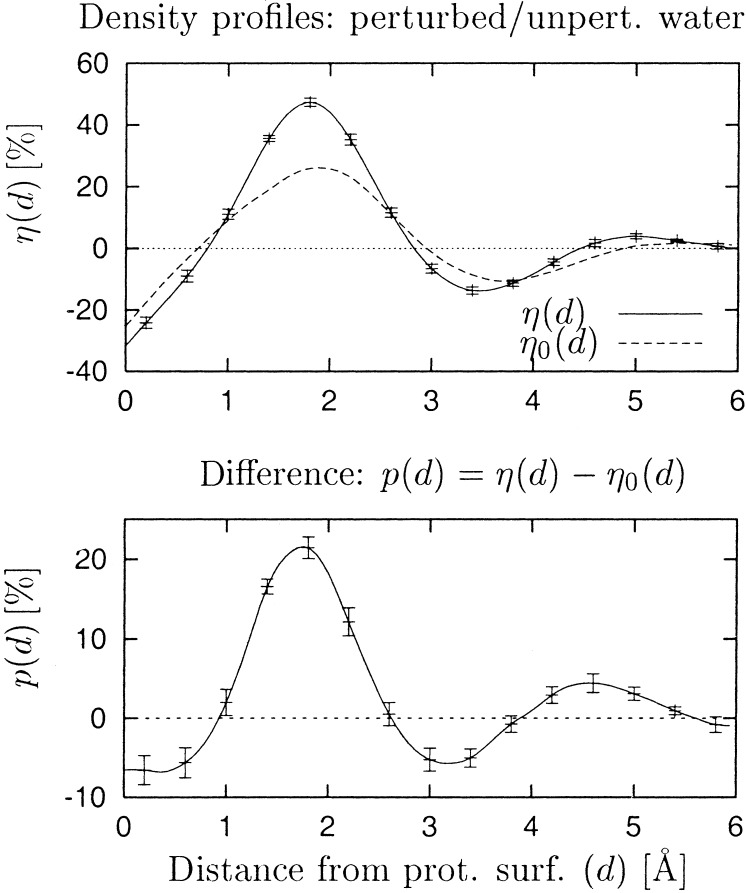
Fig. 3 shows the density profile, η(d), of the water around the protein, where d denotes the radial distance from the protein surface. A large peak is seen at ≈2 Å, at which the water density is nearly 50% higher than that of bulk water. Integration of η(d) between 0 and 3 Å (approximately the first hydration layer) gives a ≈15% density increase over the bulk.
Figure 3.
Relative water density η as a function of distance from the protein surface, d, expressed as percentage deviation from average bulk water density η(d) = 〈ρ(d)〉/〈ρ(∞)〉 − 1. Error bars denote the statistical error caused by dynamical fluctuations in the simulation. The surface, defined as a boundary of the protein, is separated on average by ≈1.3 Å from the protein surface atoms.
We now investigate to what extent the ≈15% increase of η(d) over the average bulk value is caused by perturbation of the water structure from that of bulk water. Even if the water structure was unperturbed there could be a pure “geometric” or “correlation” effect in the distribution of atoms that could lead to a nonuniform density distribution. This effect arises from the fact that the protein surface is defined to run between the two sets of atoms (water and protein) and therefore is at nonrandom distances from the water oxygens. Consequently, the structure of the bulk water radial distribution function may be partly reflected in η(d). To determine this “unperturbed water” effect the protein surface was superposed onto the results of a control simulation of pure water, and the water molecules inside the surface were denoted as fictitious “protein” atoms. The procedure of deriving the surface was then repeated for the fictitious protein, and the corresponding water density profile, η0(d), was calculated. η0(d), therefore, is the density profile expected if the water around the protein was structurally unperturbed from the bulk. Fig. 3 shows that, indeed, η0(d) does resemble η(d). However, the difference, η(d) − η0(d), which gives the perturbing effect of the protein on the water radial density distribution, is also significant (Fig. 3 Bottom). Integration of η(d) − η0(d) over d = 0–3 Å gives 5%. Therefore, of the 15% density increase over the bulk in the first hydration layer, about one-third originates from perturbation of the water structure from the bulk.
In Fig. 1 the radial density distribution g⊥00(r) for pure water (“blk”) is more sharply peaked than the distribution relative to the protein surface oxygens [g⊥00(r) “sim”]. In contrast, in Fig. 3 the water density distribution relative to the protein surface is sharper and narrower than that for pure water mapped relative to a fictitious surface separating a protein-sized and -shaped volume of water from the rest in a realistic water simulation. The explanation of this apparent paradox lies in the fact that that the layer of protein atoms in the protein surface is more densely packed than the corresponding layer of water molecules inside the fictitious water surface. Indeed, the ratio of the protein to water densities calculated in a layer between 3 and 4 Å inside the surfaces in the two simulations is 1.2.
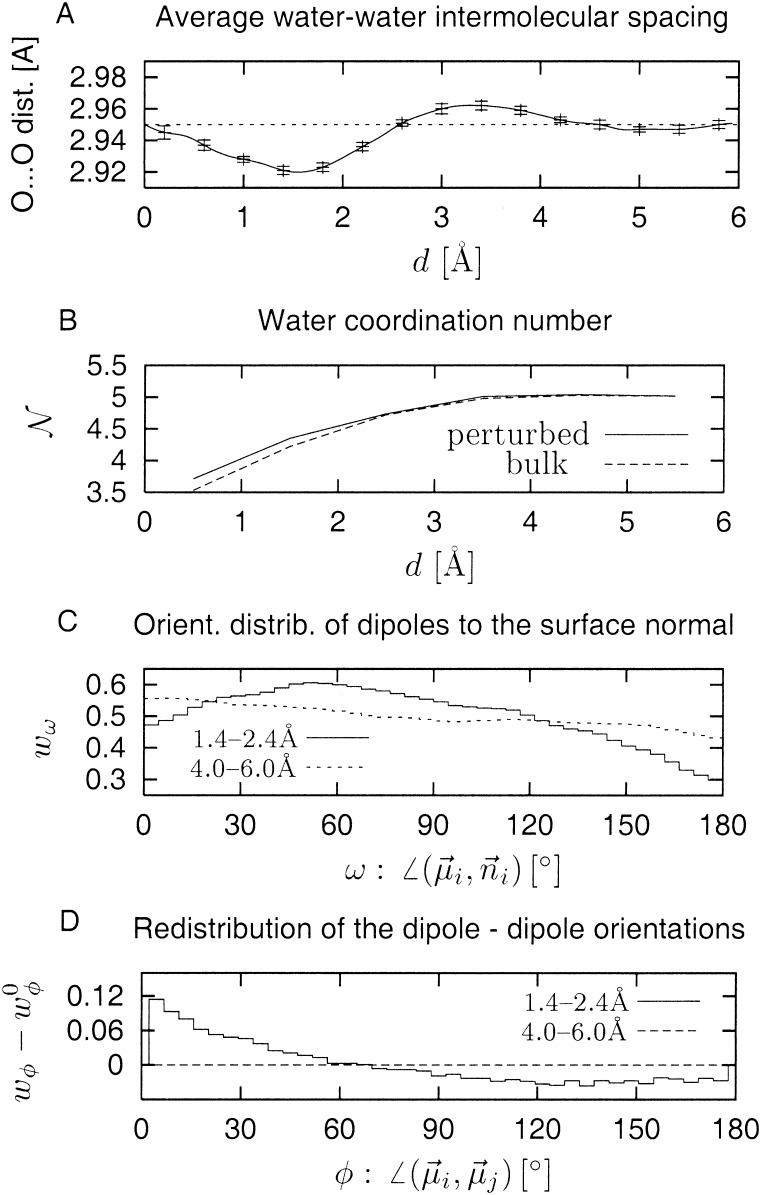
We next determine the change in average water structure associated with the density perturbation. There are two possible contributions to the density increase, one caused by an increase of the coordination number and the other caused by contraction of the O–O distance. Fig. 4A shows the average rO–O as a function of d. In the region below 3 Å a statistically significant contraction of ≈0.8% is seen, corresponding to a ≈2.4% volume reduction. As shown in Fig. 4B the coordination number also increases. Integration over the coordination number difference provides the remaining ≈2.6% of the volume reduction. The sum of these two effects is ≈5%, i.e., the same value as obtained with the alternative method [η(d) − η0(d)] described above.
Figure 4.
(A) Average water O–O distance as a function of
distance from the protein surface d. (B)
Average coordination number of water molecules as a function of
d for perturbed (solid line) and unperturbed (dashed
line) cases. (C) Distribution of angle ω of water
dipoles, μi, with respect to the surface
normal n⃗i.
(D) Difference between distributions of relative
orientations of neighboring water dipoles in perturbed
(wφ) and unperturbed
(w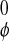 ) cases.
) cases.
The final question addressed concerns which aspects of the protein surface determine the water density variations. A series of calculations (not shown) showed no clear relationship between the hydration shell water density and the chemical characteristics of the surface atoms or residues, e.g., whether polar/nonpolar, hydrophobic/hydrophilic. The exception to this is groups with net charges, about which the density is increased. However, these charged groups make up only 5% of the protein surface and therefore have only a small effect on the average density profile properties.
In a simpler picture, the physical properties of the protein surface envelope can be considered to be determined by the envelope shape and its associated electrostatic properties. Therefore, we examined these and whether they are correlated with the density.
The average orientation of water dipoles with respect to the protein surface normal is shown in Fig. 4C. A completely unperturbed distribution, i.e., that of bulk water, is uniform with probability 1/2. The distribution at d = 4 − 6 Å shows a small preference for low angles over high angles. For the layer d = 1.4 − 2.4 Å the skew is considerable, in the form of a broad maximum centered at ≈45°. This result indicates a more perpendicular alignment of the water dipoles with respect to the normal vectors from the protein surface. A perturbation is also seen in the relative orientation of the dipoles of neighboring water molecules. This effect is shown in Fig. 4D, which demonstrates that as the protein surface is approached lower angles are more highly populated, i.e., the dipoles align more parallel with each other. Inspecting the dipole orientational distributions at sites on the protein surface of varying density (not shown) revealed that the dipole orientational perturbations are highly correlated with the water density, i.e., high-density regions are those with dipoles more parallel to each other and more perpendicular to the surface normal.
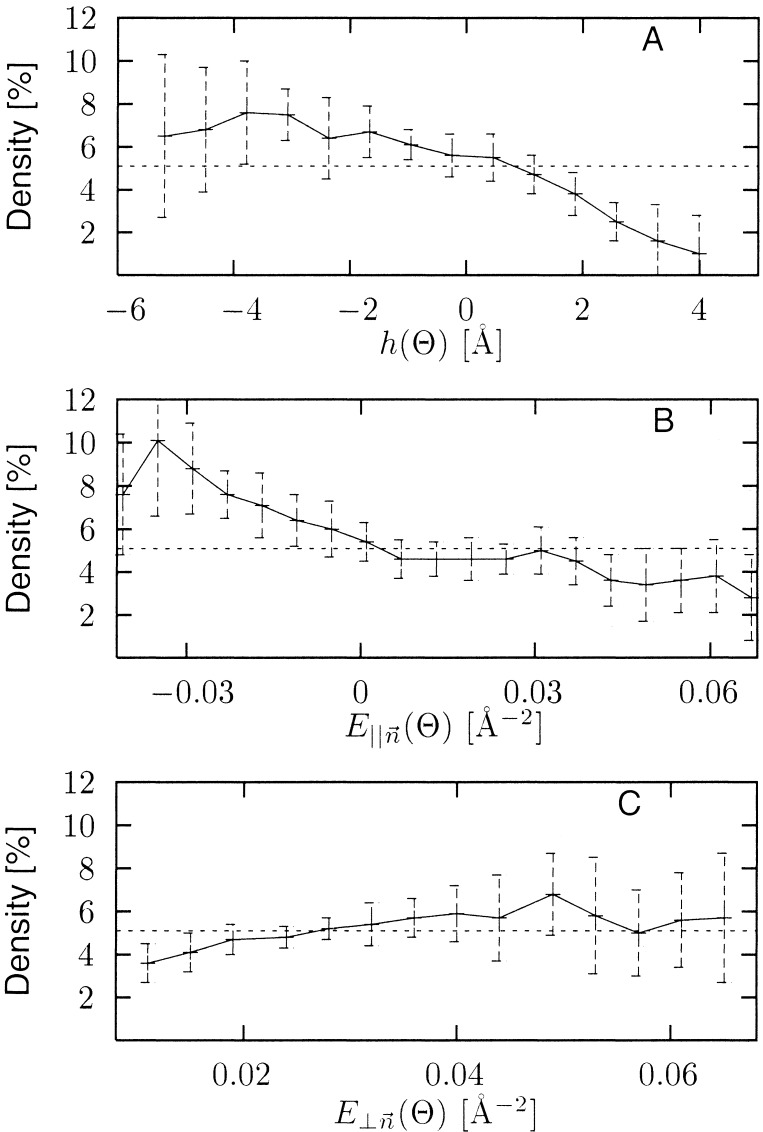
The variations with water density of topographic and electrostatic properties of the protein surface are plotted in Fig. 5. We define the surface topographic perturbation, h(Θ), as the difference between multipolar expansions of the protein surface at two different resolutions, one low (smooth) and one high (rough) (see Methods). This function is negative for depressions (grooves or cavities) in the surface and positive for protuberances, with the magnitude (in Å) determined by the depth of the depression or height of the protuberance. Fig. 5A shows that h(Θ) is clearly correlated with the local water density, the denser regions occurring in the surface depressions.
Figure 5.
Density increase in the 0–3 Å layer as a function of: (A) surface topographic perturbation, h(Θ); (B) component of electrostatic field parallel to the surface normal, E∥(Θ); and (C) component of electric field tangential to the surface, E⊥(Θ). Average increase in density is denoted by dashed line at 5.1%.
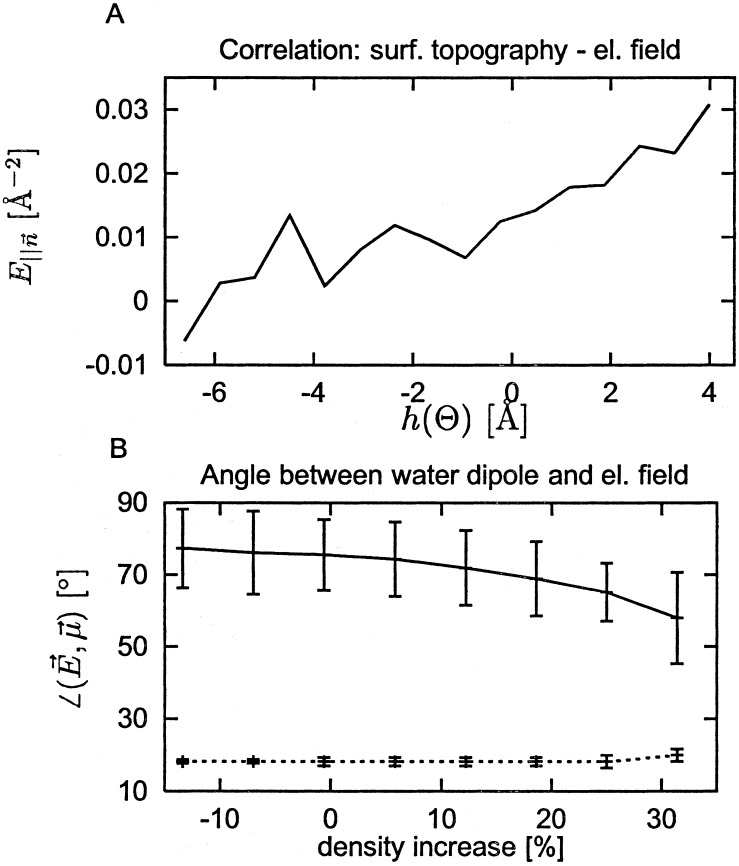
Fig. 5 B and C shows how the water density varies with the electrostatic field generated by the protein atom partial charges at 1.5 Å from the protein surface. Fig. 5B shows that high density occurs in fields for which the component parallel to the surface normal is negative. In this field the hydrogen atoms are closer to the surface than the oxygen atoms, an organization found to predominate in a neutron diffraction analysis of cubic insulin crystals (7). The strength of the field tangential to the surface is also correlated with the density over the most highly populated field values (0.005–0.03 Å−2), with higher tangential field strengths accompanying higher density (Fig. 5C). Finally, Fig. 6A shows that the strength of the parallel component of the electric field and the surface topographic perturbation are related: positive field strengths are found for positive values of h(Θ), i.e., for surface protuberances.
Figure 6.
(A) Correlation between E∥(Θ) and h(Θ). (B) Correlation of angle between water dipoles and electrostatic field with the density. Solid line: Electrostatic field calculated only from protein atoms. Dashed line: electrostatic field calculated from the entire system (protein and explicit water atoms).
The above results present a coherent picture of electrostatically driven protein surface water density effects. In depressions in the protein surface, water molecules are less exposed to the disorienting effect of bulk solvent. Therefore, they tend to orient themselves to follow the electrostatic field lines generated by the protein atoms. This effect is demonstrated further in Fig. 6B. When the electrostatic field is calculated including both the protein and water atom charges, then the resulting field vectors and the water dipoles are well aligned and independent of density. When only the protein partial charges are used, the alignment, although weak, is nonrandom (random would be 90°) and stronger in high-density regions.
Conclusions
The incentive for this work was to explain the increased density of the first hydration shell of lysozyme as indicated by low-resolution neutron and x-ray scattering measurements. Fig. 2 demonstrates that the computer simulation agrees with the low-resolution data. Furthermore, the present work reveals the physical origin of the high density of the hydration layer. About two-thirds of the observed density increase over bulk water arises from a geometrical effect caused by the definition of the surface. This contribution would arise even if the water density was not at all perturbed by the presence of the protein. On top of this effect, however, is a ≈5% density increase caused by perturbation of the average water structure from bulk water. About half of this density increase arises from shortening of the average water–water distances, and the other half arises from an increase in the coordination number. Although the nearest-neighbor water molecules are generally further from the protein atoms than they are from water atoms in bulk water, the higher density of protein atoms in the protein surface constrains the water density on the protein surface to be higher than in any comparable shell in pure water.
In harmony with the present work, in several recent studies (35–37) no clear relationship between first-shell water density variations and the hydrophobicity/hydrophilicity of chemical groups has been found. Moreover, in the present simulation, although the water oxygen:surface protein atom PCFs in Fig. 1 vary with the protein atom element concerned (C, N, or O), these differences do not persist in the corresponding surface density profiles (not shown). The reason for this effect stems from the fact that the surface shape is determined by the exclusion volume radii for the atoms. As a result the positions of the first peaks in the corresponding surface density profiles are shifted relative to the PCFs, approximately canceling out the differences seen in Fig. 1.
We do find clear density effects if a simple view of the protein surface is taken, in which it is considered to be an envelope with an associated electrostatic field generated by the protein atom partial charges. A relationship between peptide hydration structure and surface topography has been demonstrated in computer simulations of melittin in water (17, 18). Moreover, analysis of the corresponding densities of some crystallographically resolved water molecules revealed that concave cavity regions are of higher water density (19, 20). The present results are in agreement with refs. 19 and 20 in that surface topography is found to be strongly related to water density and depressions in the protein surface contain higher-density water. However, the present results generalize this effect to the whole protein:solvent interface rather than just a small proportion of crystallographically resolved solvent molecules, and, moreover, a clear electrostatic effect is demonstrated here. In depressions on the surface the water molecules have a stronger tendency to align with the electrostatic field generated by the protein atoms. This effect can be simply understood, as in a depression water molecules are less exposed to the randomizing, disorienting effect of neighboring water molecules. They align more tangentially to the surface than if they were unperturbed and more parallel to each other than in bulk water, leading to higher-density packing.
Further understanding of global hydration properties of proteins will require still more detailed decomposition of the various forces competing to determine surface water structure and dynamics. The effect of varying the potential functions used on the numerical values of the quantities obtained here will also be of interest, although the general trends revealed are not expected to be affected. Crystallographic structures of lysozyme exist in various crystal forms (10, 24, 38, 39). Comparison of the hydration structures derived by MD simulation of lysozyme in the crystalline state with experiment will provide a stringent test of the simulation methodology. Comparison with the present simulation will provide much information on the effect of crystalline environment on hydration structure. This work is in progress. Merging the structures of proteins in different crystal forms can provide an approximation to the hydration structure in solution (8). More generally, the present analysis demonstrates the usefulness of detailed simulation in the interpretation of experimental scattering results so as to obtain a simple physical picture of global protein hydration.
Acknowledgments
We thank Dr. Stefan Fischer and Prof. Don Caspar for stimulating discussions and useful suggestions. The Ministry for Science of Republic of Slovenia is gratefully acknowledged. F.M. received support from the Deutsches Zentrum fuer Luft- und Raumfahrt/Internationales Buero.
Abbreviations
- MD
molecular dynamics
- SAS
small-angle scattering
- PCF
proximal pair correlation function
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Teeter M M. Annu Rev Biophys Biophys Chem. 1991;20:577–600. doi: 10.1146/annurev.bb.20.060191.003045. [DOI] [PubMed] [Google Scholar]
- 2.Schoenborn B P, Garcia A, Knott R. Prog Biophys Mol Biol. 1995;64:105–119. doi: 10.1016/0079-6107(95)00012-7. [DOI] [PubMed] [Google Scholar]
- 3.Venu K, Svennson L A, Halle B. Biophys J. 1999;77:1074–1085. doi: 10.1016/s0006-3495(99)76957-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brunne R M, Liepinsh E, Otting G, Wuethrich K, van Gunsteren W F. J Mol Biol. 1993;231:1040–1048. doi: 10.1006/jmbi.1993.1350. [DOI] [PubMed] [Google Scholar]
- 5.Badger J. Biophys J. 1993;65:1656–1659. doi: 10.1016/S0006-3495(93)81220-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Badger J, Caspar D L D. Proc Natl Acad Sci USA. 1991;88:622–626. doi: 10.1073/pnas.88.2.622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Badger J, Kapulsky A, Caspar D L D, Korzun R. Nat Struct Biol. 1995;2:77–80. doi: 10.1038/nsb0195-77. [DOI] [PubMed] [Google Scholar]
- 8.Nakasako M. J Mol Biol. 1999;289:547–564. doi: 10.1006/jmbi.1999.2795. [DOI] [PubMed] [Google Scholar]
- 9.Bouquière J P, Finney J L, Savage H F J. Acta Crystallogr B. 1994;50:566–578. [Google Scholar]
- 10.Bon C, Lehmann M S, Wilkinson C. Acta Crystallogr D. 1999;55:978–987. doi: 10.1107/s0907444998018514. [DOI] [PubMed] [Google Scholar]
- 11.Pettitt B M, Makarov V A, Andrews B K. Curr Opin Struct Biol. 1998;8:218–221. doi: 10.1016/s0959-440x(98)80042-0. [DOI] [PubMed] [Google Scholar]
- 12.Phillips G N, Pettitt B M. Protein Sci. 1995;4:149–159. doi: 10.1002/pro.5560040202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marakov V A, Andrews B K, Smith P E, Pettitt B M. Biophys J. 2000;79:2966–2974. doi: 10.1016/S0006-3495(00)76533-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Burling F T, Weis W I, Flaherty K M, Brünger A T. Science. 1996;271:72–77. doi: 10.1126/science.271.5245.72. [DOI] [PubMed] [Google Scholar]
- 15.Svergun D, Richard S, Koch M H, Sayers Z, Kuprin S, Zaccai G. Proc Natl Acad Sci USA. 1998;95:2267–2272. doi: 10.1073/pnas.95.5.2267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Levitt M, Sharon R. Proc Natl Acad Sci USA. 1988;85:7557–7561. doi: 10.1073/pnas.85.20.7557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cheng Y K, Rossky P J. Nature (London) 1998;392:696–699. doi: 10.1038/33653. [DOI] [PubMed] [Google Scholar]
- 18.Cheng Y K, Sheu W S, Rossky P J. Biophys J. 1999;78:1734–1743. doi: 10.1016/S0006-3495(99)77335-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gerstein M, Chothia C. Proc Natl Acad Sci USA. 1996;93:10167–10172. doi: 10.1073/pnas.93.19.10167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Harpaz Y, Gerstein M, Chothia C. Structure (London) 1994;2:641–649. doi: 10.1016/s0969-2126(00)00065-4. [DOI] [PubMed] [Google Scholar]
- 21.Brooks B R, Bruccoleri R E, Olafson B D, States D J, Swaminathan S, Karplus M. J Comput Chem. 1983;4:187–217. [Google Scholar]
- 22.MacKerell A D, Bashford D, Bellott M, Dunbrack R L, Jr, Evenseck J, Field M J, Fischer S, Gao J, Guo H, Ha S, et al. J Phys Chem. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 23.Jorgensen W L, Chandrasekhar J, Madura J D. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 24.Vaney M C, Maignan S, RiesKautt M, Ducruix A. Acta Crystallogr D. 1996;52:505–517. doi: 10.1107/S090744499501674X. [DOI] [PubMed] [Google Scholar]
- 25.Merzel F, Smith J C. Acta Crystallogr D. 2002;58:242–249. doi: 10.1107/s0907444901019576. [DOI] [PubMed] [Google Scholar]
- 26.Svergun D, Barberato C, Koch M H J. J Appl Crystallogr. 1995;28:768–773. [Google Scholar]
- 27.Ibers J A, Hamilton W C, editors. International Tables for X-Ray Crystallography. Birmingham, AL: Kynoch; 1974. pp. 155–163. [Google Scholar]
- 28.Lebedev V I. Zh Vychisl Mat Fiziol. 1975;15:48–54. [Google Scholar]
- 29.Lebedev V I. Dokl Akad Nauk. 1994;338:454–456. [Google Scholar]
- 30.Lounnas V, Pettitt B M, Phillips G N. Biophys J. 1994;66:601–614. doi: 10.1016/s0006-3495(94)80835-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Soper A. J Chem Phys. 1994;101:6888–6901. [Google Scholar]
- 32.Guinier A. Ann Phys. 1939;12:161–237. [Google Scholar]
- 33.Hubbard S R, Hodgson K O, Doniach S. J Biol Chem. 1988;263:4151–4158. [PubMed] [Google Scholar]
- 34.Grossmann G, Abraham Z H L, Adman E T, Neu M, Eady R R, Smith B E, Hasnain S S. Biochemistry. 1993;32:7560–7366. doi: 10.1021/bi00080a005. [DOI] [PubMed] [Google Scholar]
- 35.Kovacs H, Mark A E, van Gunsteren W F. Proteins. 1997;27:395–404. doi: 10.1002/(sici)1097-0134(199703)27:3<395::aid-prot7>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- 36.Pertsemlidis A, Saxena A M, Soper A K, Head-Gordon T, Glaeser R M. Proc Natl Acad Sci USA. 1996;93:10769–10774. doi: 10.1073/pnas.93.20.10769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Turner J Z, Soper A K, Finney J L. J Chem Phys. 1995;102:5438–5443. [Google Scholar]
- 38.Berthou J, Lifchitz A, Artymiuk P, Jolles P. Proc R Soc London B Biol Sci. 1983;21:7471–7489. doi: 10.1098/rspb.1983.0021. [DOI] [PubMed] [Google Scholar]
- 39.Walsh M A, Schneider T R, Sieker L C, Dauter Z, Lamzin V S, Wilson K S. Acta Crystallogr D. 1998;54:522–546. doi: 10.1107/s0907444997013656. [DOI] [PubMed] [Google Scholar]