Changes in myosin S1 orientation and force induced by a temperature increase

Abstract

Force generation in myosin-based motile systems is thought to result from an angular displacement of the myosin subfragment 1 (S1) tail domain with respect to the actin filament axis. In muscle, raised temperature increases the force generated by S1, implying a greater change in tail domain angular displacement. We used time-resolved x-ray diffraction to investigate the structural corollary of this force increase by measuring M3 meridional reflection intensity during sinusoidal length oscillations. This technique allows definition of S1 orientation with respect to the myofilament axis. M3 intensity changes were approximately sinusoid at low temperatures but became increasingly distorted as temperature was elevated, with the formation of a double intensity peak at maximum shortening. This increased distortion could be accounted for by assuming a shift in orientation of the tail domain of actin-bound S1 toward the orientation at which M3 intensity is maximal, which is consistent with a tail domain rotation model of force generation in which the tail approaches a more perpendicular projection from the thin filament axis at higher temperatures. In power stroke simulations, the angle between S1 tail mean position during oscillations and the position at maximum intensity decreased by 4.7°, corresponding to a mean tail displacement toward the perpendicular of 0.73 nm for a temperature-induced force increase of 0.28 P₀ from 4 to 22°C. Our findings suggest that at least 62% of crossbridge compliance is associated with the tail domain.

Many intracellular processes depend on transduction of chemical free energy into mechanical work by isoforms of the myosin family of molecular motors. The subfragment 1 (S1) moiety of myosin, the myosin head, is divisible into a motor domain (bearing actin and ATP binding sites) and a tail domain [thought to produce force by rotation about the motor domain accompanied by ATP hydrolysis at the catalytic site (the power stroke); refs. 1 and 2]. The relation between tail orientation and S1 force is fundamental to our understanding of myosin motors. Modulation of force in motile systems is normally achieved through the recruitment or loss of working heads rather than by a change in S1 force and thus is unsuitable for relating force to tail orientation. However, in skeletal muscle, temperature elevation increases tension, not through recruitment of new heads (3, 4) but through increased S1 force, which implies a change in S1 tail orientation so as to extend series elasticity the required distance for the increased load (see Fig. 1). We have used x-ray diffraction by bundles of skeletal muscle cells to detect and measure this putative temperature-induced shift in S1 disposition and to relate it to S1 force.

Figure 1.

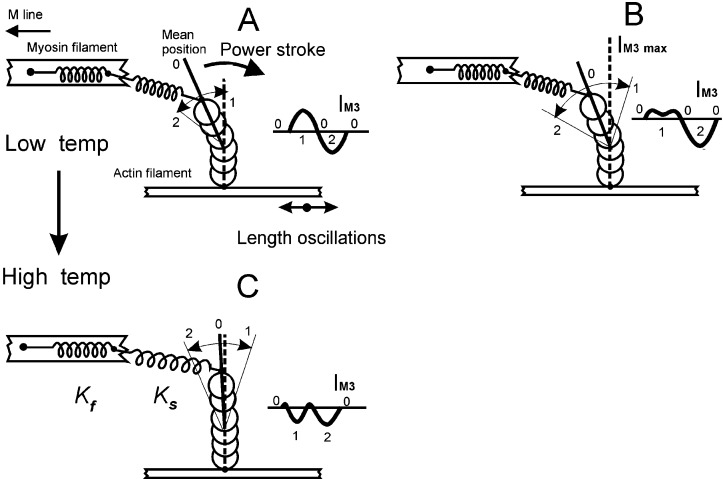
Schematic S1 used in simulations of I_M3 responses to oscillations. The Z line is located to the right of the figure. A and B show the effect of increased tail displacement. (Insets) The corresponding I_M3 changes. The horizontal line in each Inset indicates mean I_M3 during oscillations (point 0). The tail domain of S1 is represented by the top three spheres. The increased displacement in B (equivalent to an increase in oscillation amplitude or the enhanced quick recovery at lower oscillation frequency) carries the tail domain through the position at I_{M3 max} (vertical dashed line), causing intensity to fall again at the minimum fiber length (point 1) and produce a double peak at I_{M3 max} as described in ref. 7. Point 2 marks the maximum fiber length. A and C show the corresponding effects of temperature, shifting the mean position (point 0) closer to I_{M3 max} in C. Note that the intensity change during the release phase of oscillations between points 0 and 1 is now a decrease in intensity in C, whereas the corresponding phase in A caused a rise in intensity. This is the effect that reduces ΔI_M3 at the higher temperature.

The myosin II isoform in skeletal muscle offers a unique advantage for structural studies of S1 action; it is aggregated into highly structured, axially aligned filaments that overlap actin filaments within a hexagonal lattice to form an ordered, quasicrystalline structure, the sarcomere. This precise and repetitive positioning of myosin molecules permits dynamic structural data to be obtained in vivo by x-ray diffraction from a population of working S1s within a living cell. The meridional 14.5-nm x-ray reflection (M3), corresponding to the third harmonic of the myosin filament unit cell, samples S1 structure. Its intensity (I_M3) is highly sensitive to S1 tilt or distortion by length changes applied to tetanized muscle (5, 6), passing through an intensity maximum (I_{M3 max}) for releases >2 nm per half-sarcomere (hs). Recently we showed that I_M3 signals were distorted during small sinusoidal sarcomere length changes (≈4 nm per hs peak to peak, 4°C) at frequencies below 1 kHz (7) but were approximately sinusoidal at higher frequencies (8, 9). This distortion arises when S1 passes through its conformation at I_{M3 max} (in Fig. 1, this is a tail orientation perpendicular to the filament axis, shown as a vertical dashed line). At >1 kHz, we proposed that I_M3 signals arose chiefly from elastic displacement of the tail, which was insufficient to displace the tail to its I_{M3 max} position. At lower frequencies, additional tail displacement by the power stroke (too slow to occur appreciably >1 kHz) carried the tail through its I_{M3 max} orientation. A tail-rotation model of the power stroke would predict that a temperature-induced increase in S1 force should be accompanied by a change in tail domain tilt toward a higher force disposition. This change in tail tilt would alter its position relative to that at I_{M3 max} and thus might affect I_M3 distortion during sinusoidal oscillations. We therefore applied sinusoidal length changes to a fiber at 1 kHz, a frequency at the edge of the frequency range producing distortion at 4°C, to maximize sensitivity to any changes in distortion and monitored I_M3 at various temperatures between 3 and 24°C.

Methods

Small bundles of intact tibialis anterior muscle fibers (2–6 fibers from Rana temporaria) were mounted horizontally by using aluminum clips attached to the tendons to reduce series compliance. The preparation was exposed to x-ray synchrotron radiation (λ = 0.15 nm, beam dimensions 0.3 × 3 mm) from the Elettra SAXS Synchrotron beamline (Trieste, Italy) to obtain measurements of I_M3. Kapton x-ray windows (12.5 μm in thickness) were placed within 200 μm of the preparation to minimize solution scattering. Sarcomere length was monitored by laser diffraction. One first-order laser beam, diffracted by the preparation, struck a position-sensitive photodiode, the output of which was converted to real-time values of sarcomere length by an analogue computer circuit. Sarcomere length was adjusted to 2.2 μm. Bundles were stimulated tetanically by a pulsed electric field (0.5-ms duration pulses) applied at a frequency suitable to obtain a fused tetanus at the working temperature. Experimental chamber temperature was set by perfusion of its walls with a temperature-controlled water/ethylene glycol mixture.

We measured force, sarcomere length, and I_M3 signals during 1-kHz sinusoidal oscillations (5–6.6 nm per hs peak to peak amplitude) applied to bundles at temperatures between 4 and 24°C. Oscillations were generated by a precision function generator (HP 33120A, Hewlett–Packard), which drove a moving coil motor to which the fiber bundle was attached by one of its aluminum clips. Force was monitored by using a capacitance force transducer (resonance frequency 40 kHz, sensitivity 0.5 V⋅mN⁻¹). Meridional x-ray spectra were recorded on a one-dimensional delay line detector at 2.46 m from the preparation. At time 0, a 0.5–1-s tetanus (shorter tetani were used at higher temperatures) was triggered. At 200 ms, on the tetanic tension plateau (P₀), a fast local x-ray shutter opened (opening time ≈1 ms); 5 ms later a stream of 160–250 pulses at 2-ms intervals began, each triggering two cycles of 1.05 kHz length oscillations and collection of x-ray spectra at 47-μs intervals, providing 40 spectra sampled over two 1.05-kHz periods. This protocol was repeated every 180 s, and data were summed with previous tetani to maximize the counts in each 47-μs spectrum. Relaxed pattern quality was checked (100-ms exposure) between tetani. If I_M3 deteriorated by 50% or tetanic tension deteriorated by 25%, the experiment was terminated. Typically 10–20 tetani could be obtained. Summed tetanus data were averaged over just two oscillation periods, yielding 40 spectra containing summed counts over two 1.05-kHz cycles of oscillation. Meridional spectra were fitted by a background polynomial plus a Gaussian, using a Levenberg–Marquardt algorithm (7). Integrated intensity of I_M3 was obtained as the area of the Gaussian averaged over the two halves of each spectrum.

To examine the effects of different parameters on I_M3, we simulated force responses to oscillations. A small step-length change (<1% fiber length) applied to a tetanized, isometric muscle fiber is accompanied by an elastic change in load (3), which is a function of the number of attached S1s (crossbridges). These bridges undergo a synchronized power stroke to compensate for the load change, which partially or completely recovers the original force. This “quick recovery” of tension, the rate of which is temperature-dependent, resembles a viscoelasticity and tends to truncate the elastic load change. The simulated force response to measured sarcomere length oscillations (e.g., Fig. 3) of such a viscoelastic system is given by numerical integration of equations of the form

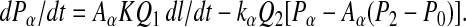1

The muscle force response resulting from a length change [l(t)] is well simulated by four such viscoelastic components, each decaying with its rate constant, k(l), which together provide an accurate representation of tension recovery (3). P₀ is the maximum tetanic tension, and P₂(l) is the final tension level reached if the quick recovery proceeded to completion, both normalized to their values at 4°C. P_α, P_β, P_γ, and P_δ are the fractional tension contributions from the four components, where P_α is the contribution from the process contributing a fraction A_α to the elastic tension transient [0.152, 0.335, 0.14, and 0.373 for components A_α–A, respectively (3)], decaying with rate constant k_α(l). K is the instantaneous stiffness of the preparation at 4°C [0.25P₀⋅(nm per hs)⁻¹]. Total force is found by summation of P₀, P_α(t), P_β(t), P_γ(t), and P_δ(t). The terms Q₁ and Q₂ are corrections for the effect of temperature on force and power stroke kinetics, respectively. Q₂ was calculated by using a Q₁₀ of 1.85 for power stroke kinetics (3); Q₁ values were measured experimentally (see Results). No attachment or detachment of bridges was assumed to occur during the period of simulation. Using these relations, we adjusted P₂(l) and k(l) values to the appropriate l(t) throughout an oscillation period. To avoid transient states at the start of oscillations, we allowed five full cycles of oscillation simulations before taking the steady-state tension response. To keep the S1 elastic contribution to I_M3 approximately constant, we maintained a constant force oscillation amplitude (approximately P₀ peak-to-peak amplitude at 4°C) by adjustment of length oscillation amplitude.

Figure 3.

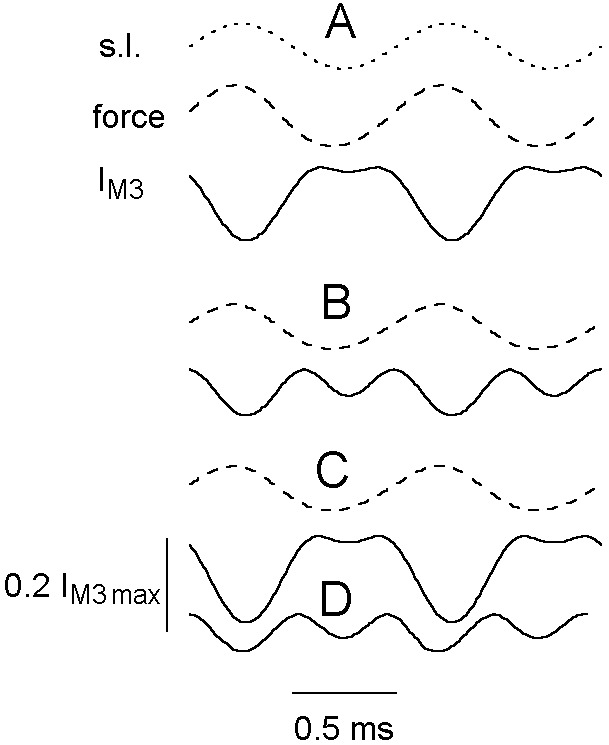
Simulated effects of temperature change on I_M3 (thick continuous lines); both kinetics and position variable at 4 (A) and 18°C (B) (comparable with experimental records in Fig. 2 B and D) or with 18°C power stroke kinetics but position restricted to that at 4°C (C), or with kinetics as at 4°C but position as at 18°C (D). Sarcomere length (s.l.; dots) and force (dashes) at 4°C (below A) and force (dashes) at 18°C (below B and C; force for D is as for C). Length and force scales are as described for Fig. 2.

The arrangement for simulation of I_M3 signals is shown in Fig. 1. S1 is represented as a column of six overlapping spheres (diameter 5 nm), of which the upper three represent the tail domain (7). The power stroke in this scheme is a clockwise rotation of the tail about its point of attachment to the motor domain (the lower three spheres), which produces an axial displacement of the tip of the tail, extending serial stiffnesses K_s and K_f, and causing force development or shortening. In addition to the active power stroke tail rotation, the tail also can be rotated passively by altering the series compliance load. In this case, the tail rotation is elastic, behaving as an elasticity associated with S1 and contributing to the aforementioned relation between muscle stiffness and crossbridge attachment. Movement of the tip of the tail during oscillations was determined from the sarcomere length signal minus the change in length of the Hookean series stiffness (K_s and K_f), deduced from the force response. The Fourier transform of each sphere was calculated, shifted axially to match tail tilt, and then summed to obtain the transform of the whole S1 moiety. The distribution of S1 along the thick filament was simulated by summing such transforms for 50 S1 moieties (half A-band length divided by the S1 spacing of 14.34 nm) on each side of the M line. Transforms on opposite sides of the M line were obtained from mirror images of the S1 structure (10) and multiplied by a shifting function equal to the M line half-width. The squared modulus of this transform was plotted as intensity.

Results

Typical force and sarcomere length signal from a tetanized fiber bundle subjected to 1-kHz length oscillations are shown in Fig. 2A. The averaged tension response to a stream of 200 double oscillations is shown as two periods of force oscillation at the tetanus plateau. Fig. 2 B–D shows representative records at 4, 12, and 18°C, respectively, for sarcomere length (top trace), force (middle trace), and I_M3 (bottom trace). At 4°C, I_M3 was approximately sinusoidal, with the minimum intensity coincident with maximum stretch. As temperature was increased, I_M3 became increasingly distorted at the peak of the release phase of the sinusoid (Fig. 2 C and D), resembling the distortion for low oscillation frequencies reported at 4°C (7); I_M3 developed an intensity minimum at maximum shortening, forming a double peak in intensity (see Fig. 1B Inset). The line through I_M3 points in Fig. 2 indicates a simulated I_M3 response obtained from the Fourier transform of the overlapping spheres we used to represent S1 mass.

Figure 2.

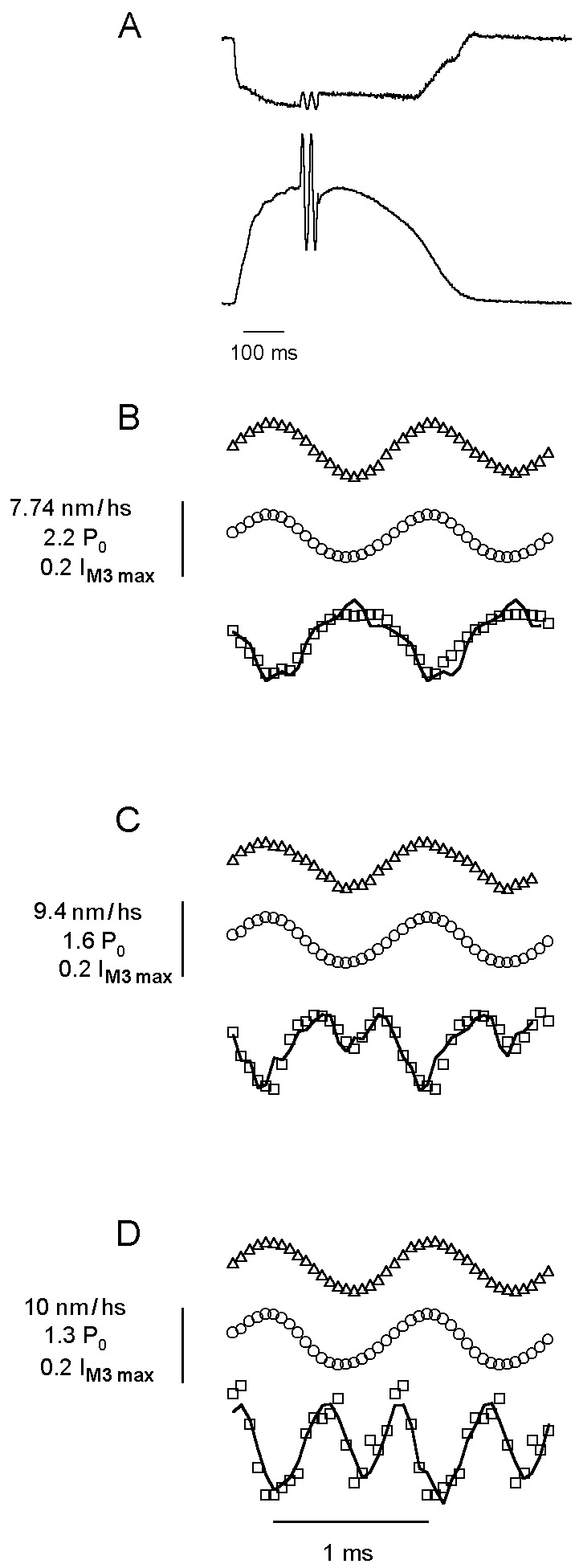
Force (○), sarcomere length (▵), and I_M3 (□) during 1-kHz sinusoidal length oscillations at 4 (B), 12 (C), and 18°C (D). (A) Sarcomere length (upper trace) and tetanic force with two oscillations representing the mean of all oscillations applied to the fiber (calibration bar: 5 ms for oscillations; 100 ms otherwise). The continuous line in I_M3 data represents the simulated I_M3 signal. Rate constants were recalculated for each t in the simulation (Eq. 1) by using kα = aα/t_1/2, where t_1/2 is the half time of the quick recovery to a step of amplitude l(t), obtained from t_1/2(l) = 1.1775 − 0.3514l(t)+ 0.05175l(t)² − 0.002862l(t)³ + 0.0000557l(t)⁴, which gave a good simulation of force responses to length steps. a values were 0.13, 0.47, 1.6, and 6.9 for components α to δ, respectively, taken from ref. 3. Similarly, the value of P₂(l) was recalculated at each t as 1.003664 + 0.019303l(t) + 0.0029374l(t)² + 0.0013382l(t)³ + 0.000062031l(t)⁴ − 0.003664 e^0.535l(t), based on the best fit to the relation of P₂(l) to l(t) for length steps.

To obtain these simulated I_M3 signals, axial tail displacement was calculated from sarcomere and force records (7), assuming compliance in series with the tail to be 2 nm per hs⋅P₀⁻¹ (11, 12) and total compliance to be 4 nm per hs⋅P₀⁻¹ (3) using P₀ measured at 4°C. Mean tail disposition was varied until the simulated I_M3 matched experimental records. The rotating tail power stroke model predicts that increased S1 force at higher temperatures would tilt its tail toward a plane normal to the filament axis corresponding to I_{M3 max} (13); this is because during a step release, which allows the S1 tail in Fig. 1A to rotate clockwise, I_M3 passes through I_{M3 max}, indicating that the isometric tail domain disposition must lie somewhat to the left of the perpendicular dashed line indicating I_{M3 max}. Increased active tension would require the tail to move closer to this dashed line to extend series elasticities K_s and K_f by the appropriate amounts; our simulations suggest this to be the case (Table 1).

Table 1.

Mean change in ΔI_M3 and tail displacement from I_M3 max during 1-kHz oscillations

Temperature, °C	ΔIM3, % IM3 max	Mean displacement from IM3 max, nm
4	20.6  ± 7.0	0.96  ± 0.16
12	25.9  ± 5.7	0.58  ± 0.06
22	18.7  ± 4.7	0.23  ± 0.11

ΔI_M3 measured at three temperature ranges ± standard deviation. Results from four (4°C), six (12°C), and five (22°C) bundles. ΔI_M3 at 12°C was significantly different from 22°C at the 5% level. 

If this tail shift were the sole effect of temperature, the peak-to-peak change in I_M3 during an oscillation period (ΔI_M3) should decrease at higher temperatures, which can be understood by comparing Fig. 1 A with C. When the tail is shifted toward its I_{M3 max} position at a high temperature (the vertical dashed line in Fig. 1C), the increase in intensity during release to point 1 in Fig. 1A is lost and replaced by a fall in intensity similar to that during stretch, which would cause ΔI_M3 at higher temperatures to tend toward 50% of its value at low temperature. We therefore measured ΔI_M3 during an oscillation period as a fraction of I_{M3 max} (Table 1). ΔI_M3 does fall significantly between 12 and 22°C but not between 4 and 12°C.

Acceleration of the power stroke by a rise in temperature might obscure a fall in ΔI_M3, because active displacement of the tail domain would proceed further during oscillations at higher temperatures, increasing tail movement and ΔI_M3 (compare Fig. 1 A with B). To examine this possibility, we tested the effects of tail disposition, isometric force change, and power stroke acceleration on I_M3 by using a temperature-sensitive simulation of force responses to sinusoidal oscillations, from which we then simulated the accompanying I_M3 response. First, we measured the dependence of isometric tetanic force on temperature in the range of 4–24°C. We found that force is well described by the function Q₁(T) = Q(0)+ 0.145(1 − e^−αT) +0.864(1 − e^−βT), where T is the temperature in °C, α is 0.392°C⁻¹, β is 0.019°C⁻¹, Q(0) is 0.837, and Q₁(T) is the ratio of tension at T relative to its value at 4°C used in Eq. 1. We simulated force oscillations and calculated an I_M3 response as described before, setting mean tail disposition to match I_M3 signals. Simulations at 4 and 18°C are shown in Fig. 3 A and B. Simulated ΔI_M3 decreased by 2 and 22% at 12 and 22°C, respectively, which is consistent with the relatively small ΔI_M3 changes in Table 1. Mean axial displacement during oscillations from I_{M3 max} in simulations was 0.95, 0.61, and 0.20 nm at 4, 12, and 22°C, respectively, similar to Table 1. Next we tested the effect of temperature-induced acceleration of power stroke kinetics by repeating the simulations but holding the mean S1 disposition at its 4°C value. ΔI_M3 now increased by 20 and 34% at 12 and 22°C (Fig. 3), respectively, in poor agreement with Table 1; the shape of the I_M3 signal was barely altered from the 4°C simulation (see Fig. 3C) with little distortion. This simulation shows that accelerated kinetics alone cannot account for I_M3 distortion. Finally, we repeated the simulations restricting power stroke kinetics to their values at 4°C, setting mean tail disposition to the displacement from I_M3 max obtained at high temperatures. ΔI_M3 decreased by 15 and 33% at 12 and 22°C, respectively (Fig. 3D), again in poor agreement with Table 1, and I_M3 continued to resemble Fig. 2D. Thus temperature-induced acceleration of power stroke kinetics alone increases ΔI_M3 but affects the shape of I_M3 only marginally. Instead, increased I_M3 distortion caused by a temperature increase arises chiefly from a shift in S1 disposition toward its structure at I_M3 max.

Fig. 4 shows the mean axial displacement of the S1 tail during oscillations from its position at I_{M3 max} (based on simulations such as those shown in Fig. 3) against the isometric tetanic tension developed by the preparation at various temperatures, normalized to P₀ at 4°C. A linear regression fit of these data yields a slope equivalent to a compliance of 2.94 nm per hs⋅P₀⁻¹.

Figure 4.

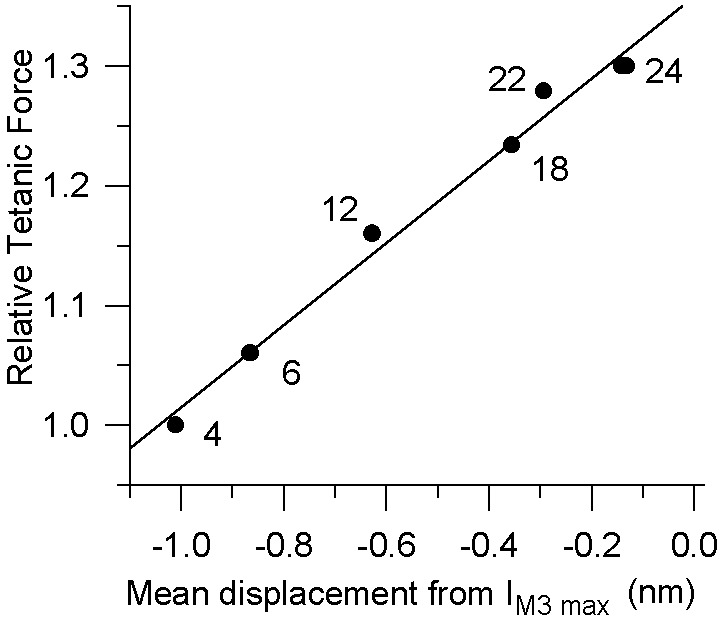
Isometric force and mean tail position from I_{M3 max} during oscillations as functions of temperature. The tail position was obtained by matching experimental data to simulated S1 distortion as described for Fig. 2. Data were fitted as a linear regression of force upon tail displacement from its I_{M3 max} position (i.e., the position at which the tail projects perpendicularly with respect to the axis of the actin filament; continuous line), giving a series compliance extension of 1 nm per hs per 0.34 P₀. Displacements are negative, because our simulations equate positive displacements of the tail domain with increases in S1 tension. The numbers adjacent to data points are the temperatures at which the data points were obtained.

In two bundles we also examined the effect of temperature on I_M3 in the relaxed and tetanized state without oscillations. Unlike rabbit psoas skinned muscle, where an increase in I_M3 occurs when temperature is elevated from 10 to 17°C in the relaxed state (14, 15), we found only a 2% increase in relaxed I_M3 on warming from 4 to 24°C. In the tetanized state, we found an 11–20% reduction in I_M3 on warming from 4 to 24°C. During oscillations, we also observed a fall in mean I_M3 at all temperatures (28.5 ± 12.0%) compared with its value at the isometric tetanus plateau. This fall showed some temperature dependence (4°C, 19%; 24°C, 36%; P = 0.04). There was no concomitant change in bundle stiffness during oscillations, suggesting that this fall in I_M3 is not related to attachment or detachment of crossbridges. Because there was no substantial change in mean oscillation tension indicative of a changed tail disposition, we think this fall in I_M3 may be disorder-related, similar to that which occurs during the rise of tetanic tension, and therefore would not affect our conclusions significantly.

Discussion

The myosin superfamily of molecular motors are actin-dependent transducers of chemical free energy into mechanical work. At least 17 classes of myosin exist, having similar motor domain structures but diverging extensively in other domains to reflect their differing functions (16). The similarity in motor domains suggests that the mechanism of all myosin motors is fundamentally identical. Myosin II, the myosin class responsible for contractility in muscle, possesses the unique advantage that in striated muscle cells it is aggregated into highly ordered filaments; this allows simultaneous collection of both structural and mechanical data from a population of working S1 moieties, which presently is impossible for other myosin classes. This property is of great importance, because the basis of a rotating tail power stroke model is a precise relation between tail orientation, ATP hydrolysis, and S1-generated force.

Since 1969, the proposed power stroke mechanism has been the generation of a torque by rotation of some portion of S1 about its point of attachment to actin, producing an unloaded filament sliding of ≈10 nm or an isometric force of 1–5 pN (1, 17–19). However, until recently, attempts to detect this rotation in situ have produced equivocal results. In 1993, the first crystal structure of S1 was obtained by using nucleotide-free chicken skeletal muscle myosin (1). In the intervening years, two further allosteric states of S1 have been crystallized, each showing a different angular tail disposition, depending on the ATP analogue occupancy of the active site (20). Recent fluorescence polarization (21) and electron microscopy data (22) from working myosins also point toward a tail rotation model for the power stroke.

The demonstration of a link between tail disposition and active S1 force is an essential element in the establishment of a tail rotation model of the power stroke. It is well known that myosin II force development increases with a rise in temperature (3, 4). We show here that this increased force is accompanied by a change in S1 structure, consistent with a tail rotation power stroke. Tail displacement from its position at I_{M3 max} at the different S1 forces developed at different temperatures were obtained by finding the mean tail position that yielded the best simulation of I_M3 changes during sinusoidal oscillations. This simulation is a simplification of S1 structural changes during oscillations; nevertheless, the appearance of a double peak in I_M3 signals at higher temperatures is not explained convincingly by other means such as lattice disorder. Therefore, we believe our findings provide a quantitative estimate of the change in tail orientation associated with an increase in S1 force based on noninvasive measurements in living cells and a rotating tail model of S1 action (1, 17–19).

ΔI_M3 values from simulations in Figs. 2 and 3 are significantly smaller than those measured experimentally. This difference may be because simulated ΔI_M3 depends on the diameter and number of spheres used to model the S1 tail, whereas measured ΔI_M3 is influenced by various structural factors (7); thus a precise match of absolute ΔI_M3 values is not to be expected. However, our simulations do represent accurately the shape of I_M3 signals as a function of oscillation frequency and amplitude and of ambient temperature. They show a mean tail disposition of 0.96 nm from its position at I_{M3 max} during 1-kHz oscillations at 4°C, similar to previous estimates (7, 13). At 22°C, the tip of the tail domain is tilted to 0.23 nm from I_{M3 max}, which gives a series compliance extension of 0.73 nm for a force increase of 0.28 P₀ between these temperatures, which would correspond to an angular tail displacement of ≈4.7°.

These values were obtained from simulations in which we chose a series compliance of 2 nm per hs⋅P₀⁻¹, consistent with x-ray (23, 24) and mechanical measurements (10, 11) of myofilament compliance. An estimate of compliance in series with the tail can be derived also without I_M3 simulation as follows: let applied oscillations produce a sarcomere length change of l_o peak to peak, total sarcomere instantaneous compliance be C_t, and total compliance in series with the tail domain C_a (equal to 1/K_f + 1/K_s in Fig. 1). Tail displacement is l_o minus the length change absorbed by C_a. If F is the peak-to-peak amplitude of the associated force oscillations, then l_o is FC_t, and tail displacement is F(C_t − C_a). The fraction of l_o that corresponds to the mean tail displacement from its position at I_{M3 max} is given by a coefficient α, where α is defined (assuming linearity between I_M3 and tail displacement and using the points on the Insets in Fig. 1) as 0.5[I_M3(2) − I_M3(1)]/[2I_{M3 max} − I_M3(1) − I_M3(2)]. The mean tail displacement from I_{M3 max} becomes α F(C_t − C_a). We now evaluate α and F at 4°C (α₁ and F₁), where I_M3(1) equals I_{M3 max} (Fig. 1A) and 22°C (α₂ and F₂), where I_M3(1) and I_M3(2), are almost equal, and errors from assuming linearity between I_M3 changes and tail displacement would be small (Fig. 1C). C_a and C_t are assumed to be temperature-insensitive. This change in temperature increases force by 0.22 P₀ (Fig. 4); therefore C_a compliance is extended by a further 0.22 P₀C_a beyond its length at 4°C, which provides us with the relation

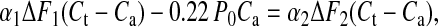2

from which we obtain

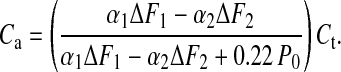3

The mean values of α₁ and α₂ were 0.5 and 0.03, respectively, and F₁ and F₂ were 1.057 and 0.958 P₀ (P₀ defined at 4°C), respectively. This yields C_a = 0.69 C_t, and because C_t is 4 nm per hs⋅P₀⁻¹, this gives a C_a of 2.76 nm per hs⋅P₀⁻¹, which is very close to the value measured in Fig. 4. If filament compliance (1/K_f) is 2 nm per hs⋅P₀⁻¹, then we have a residual compliance of 0.76 nm per hs⋅P₀⁻¹ in series with the tail domain.

The deviation of our total series compliance from filament compliance could result from a heavily damped M band and/or Z line compliance, which would not contribute to instantaneous stiffness (measured by fast length changes) but which would provide additional series compliance during force development. All crossbridge compliance then could be located in S1. Alternatively, crossbridge compliance may be located partially outside the tail domain, associated with the motor domain or the S2 myosin moiety. Agreement between a total compliance in series with the tail of 2.76 nm per hs⋅P₀⁻¹ and both filament and crossbridge compliances of 2 nm per hs⋅P₀⁻¹ (11, 12, 23, 24) can be obtained if the tail domain accounts for ≥62% of total crossbridge compliance.

The origin of the temperature-induced rise in force may be a temperature-sensitive endothermal isomerization step in the actomyosin ADP⋅P_i state, associated with no change (4) or a 20% increase in I_M3 (25) over a temperature jump from 5 to 17°C, according to temperature-jump studies in skinned fibers (26). In this case, a rise in temperature would displace the isomerization step toward a high force state. Our S1 simulations of a single state then would represent an average S1 orientation, which would cause us to underestimate the change in tail tilt for a rise in temperature because the increase in force between 4 and 22°C would result from only a small fraction of total bridges being displaced from low to high force states, each of which therefore would extend C_a by more than 0.22 P₀⋅C_a during the transition to the high force state. This effect would decrease C_a obtained from Eq. 3, causing it to approach the compliance of the myofilaments and thereby allocating a greater fraction of crossbridge compliance to the S1 tail domain. Alternatively, some pharmacological agents increase force exerted by each S1 moiety (27) rather than displacement of the equilibrium of an endothermic isomerization step. If temperature acted in this manner, the single state simulation used here would be appropriate. Our experiments do not allow us to distinguish between these possibilities. However, they do suggest that the temperature-induced rise in force in intact frog muscle fibers is not associated with an increase in I_M3. From a temperature-induced shift in tail disposition of 0.73 nm toward I_{M3 max}, an ≈10% increase in I_M3 would be expected based on data in Table 1. This increase probably is absent because of increased disordering of radial alignment of myofilaments during tetani at higher temperature. In temperature-jump experiments, where such disordering may not have time to develop, an increase in I_M3 has been observed (25). By determining tail disposition relative to a reference point (I_{M3 max}) using sinusoidal oscillations, we avoid such difficulties in defining S1 structure purely from static intensity and provide an alternative and powerful means of determination of tail orientation in different contractile states.

Abbreviations

S1

subfragment 1

hs

half-sarcomere