Long axial range 3D single-particle tracking using birefringent substrates

Abstract

3D single-particle tracking is a critical imaging technique for visualizing molecular motion in complex environments, including biological cells. Expanding the trackable depth of the 3D tracking technique to a greater range would broaden its applicability to larger biological samples. Most high-throughput 3D tracking techniques rely on the engineering of the point spread function of the optical system to precisely determine the 3D coordinate of the particle using spatial light modulators. Here, we report 3D single-particle tracking using a birefringent material, mica, as a substrate for mounting a sample. The spatial pattern of the fluorescence emitted by fluorescent nanoparticles captured at the image plane shows an axial position dependence over the tens of micrometers range due to the birefringent characteristic of the mica substrate, enabling us to localize the emitter with an accuracy better than 30 nm over an axial range of 30 µm. We demonstrate that our 3D tracking method can simultaneously track multiple particles separated by a 30 µm distance in the axial axis. We further validate our 3D tracking applicability in plant cells, which are significantly larger than animal cells. This work contributes to advancing single-particle 3D tracking using birefringent substrates with unique optical characteristics.

In this study, Nozue et al. reported a 3D single-particle tracking method through point spread function engineering using a birefringent mica substrate, achieving <30 nm precision over a 30 µm axial range without using a spatial light modulator.

Introduction

Three-dimensional (3D) single-particle tracking has been one of the essential imaging techniques for characterizing molecular motion in complex environments. Life science research, in particular, has greatly benefited from these techniques, as they enable direct characterization of the motion and associated functions of biological (macro) molecules and complexes in complex cellular environments. For instance, spatiotemporal dynamics of viruses^1–4, endosome⁵, exosomes, and nanoparticles^1,6, in live cells (e.g., cellular uptake^1,6, interactions³, transportation^2,7, and spatiotemporal heterogeneities in membranes⁸) have been investigated using 3D tracking⁷. Diffusion trajectories captured by 3D tracking have also provided invaluable insight into the size, conformation, and dynamics of diffusing molecules, together with interactions, such as dimerization, and with local environments^9–14.

Several key factors, including the axial range, multiplexing capability, and ease of use, define the performance of tracking techniques. While a greater axial range expands the applicability of 3D tracking to larger specimens, multiplexing tracking enables high throughput data acquisition; both contribute to a quantitative understanding of biological phenomena, particularly in biological specimens with a large individual variability that requires a large volume of data. Ease of use, especially the compatibility with standard fluorescence microscopes without customization, is a critical factor for the widespread utilization of the techniques.

3D tracking has been sorted into two major approaches; one uses active feedback for depth determination (Fig. 1a), and the other does not require feedback control (Fig. 1b, c)¹⁵. Although the adaptive approach is very effective in tracking individual particles in large 3D space (i.e., capable of obtaining longer trajectories) with high spatial and temporal resolution¹⁶, it is a low throughput method by definition. The feedback-free approach has been used more frequently for high-throughput 3D tracking. In this approach, optical components inserted in the detection path of a fluorescence signal modify the point spread function (PSF) of the optical system, giving axial position-dependent fluorescence patterns of the particles in the field of view, from which one can determine the 3D coordinates of the fluorescent emitter¹⁷. This approach enables accurate 3D localization of the emitter from a single wide-field 2D image. A spatial light modulator (SLM) has often been used for PSF engineering (Fig. 1b)^18,19. Other feedback-free approaches that cover relatively narrow axial ranges have also been reported, including multi-focus microscopy²⁰ and temporal phase self-interferometry²¹.

Fig. 1. Schematic illustrations of three different approaches of single-particle 3D tracking.

a Active adaptive tracking using feedback signal from the photodetector. b Wide-field microscopy-based feedback-free tracking using a spatial light modulator (SLM). Adapted with permission from ref. ¹⁷. Copyright 2017 American Chemical Society. c Wide-field microscopy-based feedback-free tracking using a birefringent substrate as a substrate to mount samples. EM-CCD: electron-multiplying charge-coupled device, PSF: point spread function, PC: personal computer.

3D tracking methods that utilize PSF engineering have enabled 3D tracking of single particles within a typical axial range of several microns^22–30. To date, the maximum reported axial range is 20 µm¹⁹. A critical factor impacting the performance of the 3D tracking is the size of the engineered PSF. Extending the axial tracking range often comes with an increased size of the PSF, particularly at the edges of the axial tracking range. This enlargement reduces the signal-to-background ratio because of the lower emission intensity density, which deteriorates the localization precision. Additionally, a larger spot size limits the total number of particles that can be tracked simultaneously in the field of view, thus reducing the throughput of the experiment. Together, a single-particle 3D tracking method with a larger axial range ( > 20 µm) while minimizing the PSF size and ideally operating on a standard fluorescence microscope without customization (i.e., without using SLM) would significantly broaden its applications.

Here, we report an approach to engineering the PSF for 3D single-particle tracking using a biaxial birefringent material, mica, as a substrate for mounting the sample (Fig. 1c). We found that the spatial pattern of the fluorescence emitted by fluorescent nanoparticles captured at the image plane showed an axial position dependence over tens of micrometers due to the birefringent characteristic of the mica substrate. Using a standard wide-field fluorescence microscope without SLM, we achieved localization precision higher than 30 nm over an axial range of 30 µm by optimizing experimental conditions (e.g., thickness and orientation of the mica substrate). Compared with other 3D tracking methods based on PSF engineering, the PSF in our method occupies a smaller area across the entire axial range, which is beneficial for localization precision and multiplex imaging. We examined the 3D tracking capability of the method in biological settings using plant cells. The experiment demonstrates that our tracking method could not only capture diffusion trajectories over 20 µm in depth but also quantify diffusion modes affected by local cellular environments. Our method holds great promise for the future development of single-particle 3D tracking methods based on birefringent materials.

Results

Birefringent characteristics of mica substrates

The critical factor for the performance of the feedback-free (i.e., scan-free) single-particle 3D tracking is PSF engineering because the 3D coordinates of the particle are determined by the axial-position dependent fluorescence pattern. Various PSF engineering methods covering different focal ranges have been reported³¹. Inserting an SLM in the detection optical path is the most common way to engineer the PSF. In theory, PSF engineering can also be done using optical materials with anisotropic optical characteristics as a substrate to mount microscope specimens.

Mica is an optically semi-transparent, birefringent material with potential applications in PSF engineering. While mica is commonly used as a substrate for atomic force microscopy measurements because it can provide an atomically flat surface, its application in optical microscopy has been limited³². This limitation arises from the complex optical properties of biaxial birefringence^33,34, which significantly alter fluorescence images captured through the substrate. To date, the effects of mica’s biaxial birefringence on image formation in optical microscopy have not been systematically explored. Consequently, mica substrates have not been utilized for PSF engineering. Biaxial birefringence is known for its unique optical effect of conical refraction, and in recent years, it has regained attention for applications in optical trapping, free-space optical communications, polarization metrology, super-resolution imaging, two-photon polymerization, and various laser applications³⁵.

Both excitation light (Fig. 2) and emitted fluorescence (Fig. 3) propagating through the mica plate are affected by its birefringence, characterized by an anisotropic refractive index. The mica usually comes in the form of a thin plate, with the surface being the (001) plane with crystal cleavage properties (Fig. 2a). It has a negative acute bisectrix of optical biaxial nearly matching the norm of cleavage surface with the shift of 3 to 5°^33,36. Therefore, the direction of the optical biradial of a thin mica substrate placed on a microscope aligns nearly coaxially with the optical axis of the microscope. Optical biaxial crystals can be described as three components of distinct refractive indices along the optic principal axis. The collimated light propagating through a thin mica substrate perpendicularly to the cleavage surface of (001) can be approximated using two effective reflective indices of n_β and n_γ (Fig. 2a). The differences between these refractive indices cause phase retardation between the light components vibrating along these principal optic axes. The intensities of two polarization components of the light transmitted through a thin mica plate are thus modulated with the rotation angle (θ) of the mica plate about the Z-axis (Fig. 2b, c). The effective birefringence of the mica plates in our experimental configuration $\left({\delta }_{\gamma -\beta }=n_{\gamma }-n_{\beta }\right)$ was determined by the mica substrate thickness-dependent retardation effect on the transmitting light (Fig. 2c, see Methods and Supplementary Methods for details). The effective birefringence of mica used in this study was determined to be δ_γ-β = 5.24 ×  10^-3 at 532 nm, the average of result from multiple mica plates with different thicknesses. The mica thickness-dependent retardation obtained from the δ_γ-β value is shown in Fig. 2d.

Fig. 2. Effect of the birefringence of the mica substrates on excitation light.

a Schematic illustration of the birefringent characteristics of mica. α, β, and γ represent the principal optic axes of mica with refractive indices of n_α, n_β, and n_γ, respectively. a, b, and c are crystallographic axes. b Schematic illustration of the optical path of an excitation laser in a wide-field fluorescence microscope. The mica substrate has a thickness of d. β and γ represent the principal optic axes of the mica substrate. θ is the rotational angle of the mica substrate. c Transmittance of the 532 nm light through the mica substrate with different thicknesses. The solid line shows the fitting of the data to Eq. 3. d Thickness-dependent retardance of the mica substrates. e Schematic illustration of the polarization states of the excitation light that passes through the mica substrates. A linearly polarized excitation light passes through the mica substrate with its polarization direction parallel (left) and non-parallel (right) to one of the optic axes of the mica substrate.

Fig. 3. Effect of the birefringence of the mica substrates on the image formation in wide-field fluorescence microscopy.

a Schematic illustration of the image formation of the fluorescence emitted by a fluorophore located close to the mica substrate. The mica substrate has a thickness of d. β and γ represent the principal optic axes of the mica substrate. b Experimentally obtained (top) and simulated (bottom) fluorescence images of the 60 nm fluorescent nanospheres captured at varied Z-axis positions through a glass substrate and the mica substrates with 110 µm, 170 µm, and 185 µm thickness. The Z-axis position of 0 µm was defined by the fluorescence image with the smallest spot size. PSF patterns obtained from three independent experiments were compared in each mica substrate thickness to ensure reproducibility. Scale bar = 10 µm. c Effect of the orientation of the mica substrate on the image formation. Fluorescence images of the 60 nm fluorescent nanospheres were captured through the mica substrate with its optic axes β and γ parallel (left) and non-parallel (right) to the X and Y axes of the imaging experiment. θ represents the angle between the optic axes of mica β and the X axis.

Because of the thickness- and wavelength-dependent retardation effect, a polarization state of the excitation light passing through mica substrates could be modified depending on its thickness or rotation (Fig. 2b). In order to unify the excitation conditions that are independent of the thickness of the mica substrate and the excitation wavelength, we used a linearly polarized light whose polarization direction aligned with one of the principal optic axes of mica (Fig. 2e). This excitation configuration guarantees the sample to be excited under the same linear polarization condition, regardless of the thickness of the mica substrates and the wavelength of the excitation laser.

PSF engineering using mica substrates

The birefringent characteristic of mica substrates also affects the image formation of the fluorescence emitted by a fluorophore located close to it (i.e., modification of the PSF, Fig. 3a). Fluorescence images of 60 nm fluorescent nanoparticles deposited on a 170 µm-thick glass coverslip captured at different axial positions through a high numerical aperture (NA) microscope objective lens clearly showed concentric patterns, whereas images of the same fluorescent nanoparticles captured through the mica substrates showed axial-position-dependent non-concentric patterns (Fig. 3b). We found that the mica substrates with different thicknesses exhibited axial-position-dependent pattern change over different axial axis ranges (Fig. 3b). Notably, the pattern change was observed over the 30 µm axial range (Fig. 3b and Supplementary Fig. 1). We note that the Z-axis position of 0 µm was defined by the fluorescence image with the smallest spot size (Supplementary Note 1). The mica substrate with 185 µm thickness gave the largest axial range with a relatively high signal-to-background ratio (Fig. 3b). We obtained similar axial-position-dependent pattern change for the 488, 532, and 640 nm excitation conditions (Supplementary Note 2). Since the magnification and NA of the objective lens also affect the PSF formed through the mica substrates (Supplementary Fig. 2), we conducted our imaging experiments with consistent conditions (i.e., an objective lens with 100× magnification and 1.49 NA).

The PSF along the XY plane obtained through the mica substrate is approximately half the size used in the 3D tracking method that covers the largest axial range reported previously over the entire axial range (Supplementary Figs. 3 and 4, Supplementary Table 1). In addition, the rotational orientation of the mica substrate (i.e., the orientation of optic axes) affects the orientation of the generated PSF (Fig. 3c). Thus, we adjusted the orientation of the two optic axes of the mica substrate to the X- and Y-axis of the imaging setup (Fig. 3c, Supplementary Note 3). We also confirmed that mica substrates with the same thicknesses (within 4% error³⁷) give virtually identical PSF (i.e., the same Z-position-dependent fluorescence pattern) and that the PSF generated through mica substrates are stable over an extended period of time under varying conditions (e.g., temperature and moisture, Supplementary Note 4). However, we note that mica substrates obtained from different origins might provide slightly different PSFs as muscovite mica is known to have a variation in optical properties (e.g., refractive index, absorbing spectrum³³, see below).

Simulation of the engineered PSF generated through mica substrates

To verify that the birefringent characteristic of the mica substrates causes the observed PSF modifications, we performed a simulation of the PSF and examined the effect of the biaxial birefringent substrates on the formation of the PSF. The PSF simulation was carried out by employing optical Fourier processing (see Methods and Supplementary Methods). The PSF calculated for the standard substrate (i.e., a glass substrate with 170 μm thickness) showed a diffraction-limited spot at the focal point, whereas concentric spatial patterns were observed at the Z-axis position 2 μm away from the focal point (Fig. 3b), consistent with the experimentally observed PSF. Next, we calculated PSF under the same conditions but replacing the standard substrate with a biaxial birefringent substrate with varied thickness. The optical axis of the microscope was aligned with the normal direction to the (001) plane (Fig. 2a), and the three refractive indices for each optic axis reported for muscovite mica were used for the simulation. The simulated PSF exhibited an axial position-dependent non-concentric pattern (Fig. 3b). Importantly, the simulated patterns agree excellently with the experimentally obtained patterns in the entire axial axis range. In addition, our simulation nicely reproduces the axial-position-dependent pattern change over different axial axis ranges observed for the mica substrates with different thicknesses (Fig. 3b). These results confirm that the modifications of the PSF originate from the biaxial-birefringent optical characteristic of mica.

Our simulation also indicated that the PSF modification by mica substrates might be sensitive to the value of three refractive indexes. We compared four different combinations of reported refractive indexes for muscovite mica from different origins³⁸. The PSF generated through the mica substrate is similar to the simulated PSF generated through muscovite mica obtained from different sources (Supplementary Fig. 5), suggesting that there is no need to experimentally measure the refractive indices of a mica substrate prior to the imaging experiment. The PSF simulation also suggests that the axial-position-dependent patterns generated through the mica substrates are almost identical in a thickness range of 165–185 μm (Supplementary Fig. 6), and thus, we arbitrarily chose the mica substrates within this thickness range for the experiments we reported in this study. We also simulated the PSF formation through the different optic axes of the mica substrate. The axial position-dependent patterns similar to the experimentally observed ones were obtained only when the optical axis of the microscope was aligned with the normal direction to the (001) plane (i.e., optical biradial of the substrate) in the simulation (Supplementary Fig. 7, Supplementary Note 5).

Single-particle 3D localization using the PSF

Using the axial position-dependent PSF imaged through the mica substrates, we determined the 3D coordinate of a single emitter. We recorded reference PSF images of a fluorescence nanoparticle at pre-defined axial positions. The 3D coordinates of the target nanoparticles were determined by finding the best-matched reference PSF images. This was done by performing a normalized 2D cross-correlation analysis (see Methods for details).

We experimentally determined the precision of 3D localization by localizing 60 nm fluorescent nanoparticles deposited on a mica substrate coated by poly(dimethylsiloxane) thin film (Fig. 4a; see Methods for the details). The localization precision was estimated by the standard deviation of the localized 3D coordinates. While the precision of the axial-position determination is limited by the z-axis interval distance of the reference PSF images, the precision of XY coordinates determination is restricted by the pixel size of the recorded images. The 3D localization precisions (i.e., standard deviations of the localizations) determined at different axial positions with the reference images captured at the 50 nm step size and the image pixel size of 83 nm are shown in Supplementary Fig. 8. The localization precisions along the X, Y, and Z coordinates obtained under these imaging conditions are better than 50 nm in the Z-axis range of 18 µm (Supplementary Fig. 8). The large axial position-dependent variation in the 3D localization precision was observed, indicating that the localization precisions are significantly affected by the z-axis interval distance of the reference PSF images and the pixel size.

Fig. 4. 3D localization precision of the birefringence-based point spread function engineering.

a A schematic illustration of the experimental configurations. 60 nm fluorescent nanospheres deposited on the mica substrate were embedded in a thin film of polydimethylsiloxane (PDMS). This experiment was conducted using a 185 µm-thick mica substrate. b A typical example of localized 3D coordinates (cyan) with projection to XY (black), XZ (blue), and YZ (red) planes. c Z-axis position-dependent 3D localization precision. The Z-axis position of 0 µm was defined by the fluorescence image with the smallest spot size.

We further conducted a similar 3D localization experiment with a smaller axial step size of the reference PSF images (10 nm interval) and sub-pixel localization in the XY directions (see Methods for the details). A typical 3D localization plot is displayed in Fig. 4b. The 3D localization precisions were greatly improved by reducing the axial interval distance and adapting sub-pixel localization, which gave the 3D localization precisions higher than 30 nm in the Z-axis range of 32 µm (Fig. 4c). Both the axial range (32 µm) and 3D localization precision (higher than 30 nm) achieved using our method surpass those reported in the literature (20 µm axial range with 50 nm theoretical localization precision)¹⁹.

Effect of the emitter-to-mica substrate distance on the axial position localization

We examined the effect of the distance between the emitters and the mica substrate on the formation of the PSF pattern and, therefore, the 3D localization accuracies for the emitters located at different axial positions from the mica surface. This was done by preparing a thin film sample with a wedge shape sandwiched between glass and mica substrates, on which fluorescent nanoparticles are deposited (Fig. 5). We first recorded fluorescence images of the nanoparticles deposited on both surfaces at different axial positions through the glass substrate (Fig. 5a, b). The axial positions of the two nanoparticles were determined by finding fluorescence images with minimum spot sizes from which the distance between the two nanoparticles on both surfaces was determined (Fig. 5b). Next, we flipped the sample and captured fluorescence images of the nanoparticles deposited on both surfaces at different axial positions through the mica substrate (Supplementary Fig. 9). The images were captured at different X-axis positions along the line region, which is the same as the one used in the imaging experiment through the glass substrate (Fig. 5c, d). The distances between the two surfaces were determined by finding the fluorescence patterns corresponding to the same axial positions (e.g., the images corresponding to 0 µm axial position, Fig. 5d). The distances between the two surfaces determined by the fluorescence patterns observed through the glass and mica substrates at different sample positions (i.e., different X-axis positions) are shown in Fig. 5e. The distance versus sample position plots (Fig. 5e) obtained from the images captured through the glass and mica substrates were fitted to a linear function with slopes of −1.36 (glass) and −1.43(mica). The nearly identical fitted lines for the two plots demonstrate that the gap distances between the two substrates, and, therefore, the axial positions of the fluorescent nanoparticles, are localized equally irrespective of the substrates (i.e., glass or mica) through which we captured fluorescence images. This result suggests that the accuracy of the 3D localization is not affected by the axial positions of the emitters with respect to the mica surface.

Fig. 5. Axial position localization accuracy of the 3D localization using the PSF generated through mica substrate.

a A schematic illustration of the experimental configurations. 60 nm fluorescent nanospheres deposited on the glass and mica substrates were embedded in a wedge-shaped thin film of polydimethylsiloxane (PDMS). This experiment was conducted using a 164 µm-thick mica substrate. Fluorescence images were captured through the glass substrate. b Representative images of the fluorescent nanospheres deposited on the mica surface (Particle 2 indicated by white arrowheads) and the glass surface (Particle 1 indicated by yellow arrowheads) captured at varied Z-axis positions. Scale bar = 5 µm. c A schematic illustration of the experimental configurations. The experimental configurations were identical to those in (a), except that fluorescence images were captured through the mica substrate. d Representative images of the fluorescent nanospheres deposited on the glass surface (Particle 1) and the mica surface (Particle 2) captured at varied Z-axis positions. Scale bar = 5 µm. e The gap distances between the nanospheres deposited on the mica and glass surfaces determined at different X positions. The gap distances were determined by capturing the images through the glass (blue) and mica (red) substrates. The solid lines show linear fits. Two sets of samples were prepared and tested to ensure data reproducibility. f A schematic illustration of the configurations for the PSF simulation. A point emitter is placed either on the surface of a 164 µm-thick mica substrate or in the water at a distance from the mica surface of d µm. g Simulated PSF of the point emitter placed on the mica surface (Particle 2) and in the water at a distance from the mica surface of d µm (Particle 1) at varied Z-axis positions.

The PSF simulation conducted under similar conditions (i.e., PSF simulation for the emitters located on the surface of the mica substrate and located d μm above the surface, Fig. 5f, g) reproduced the experimentally observed PSF (Fig. 5d), also confirming the negligible impact of the mica to emitter distance on the PSF formation through the mica substrates. Our simulation showed that the PSF formed through a 185 μm-thick mica substrate is not affected significantly by the substrate-to-emitter distance of at least up to 20 μm (Supplementary Fig. 10). A slight change in the PSF becomes visible at longer substrate-to-emitter distances, particularly at the substrate-to-emitter distance of 30 μm (Supplementary Fig. 10). The simulation also indicates that a refractive index matching between the medium surrounding the emitter and the immersion medium minimizes the substrate-to-emitter distance-dependent change in the PSF (Supplementary Fig. 11).

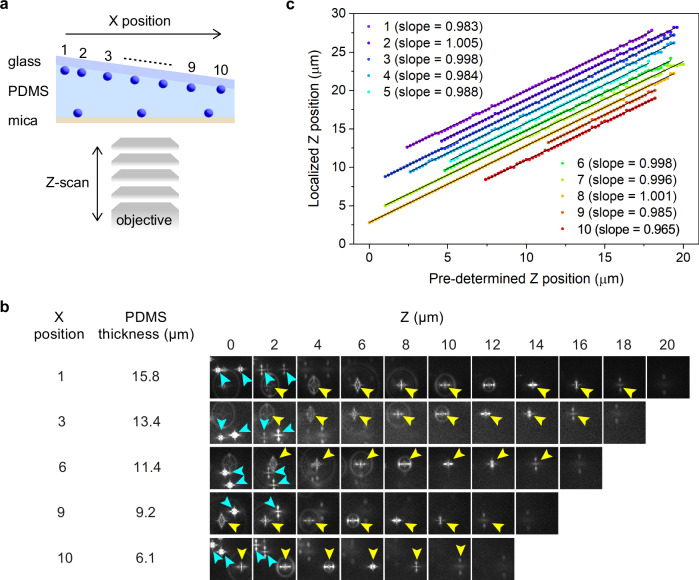
Next, we performed a 3D localization experiment of fluorescent nanoparticles using the same wedge-shaped sample with different pre-defined Z-axis positions (Fig. 6a, b and Supplementary Fig. 12). The axial positions of the nanoparticles determined by the 3D localization at different pre-defined Z-axis positions are shown in Fig. 6c. The plots obtained from all the nanoparticles were fitted nicely to a linear function with slopes of 0.97–1.01(r² = 0.99927–0.9999, Fig. 5j). This result demonstrates that the formation of the PSF pattern is unique to its axial position regardless of the emitter to mica distance, and the 3D localization accuracies of the emitters are not affected by their axial positions with respect to the mica surface.

Fig. 6. Effect of the emitter-to-mica substrate distance on the axial position localization.

a A schematic illustration of the experimental configurations. The sample configurations were identical to those in Fig. 5c. b Representative Z-axis position-dependent images of the fluorescent nanospheres deposited on both surfaces captured at ten different X positions. The fluorescence images obtained for the nanospheres deposited on the glass and mica surfaces are indicated by yellow and cyan arrowheads. c Localized Z-axis positions of the fluorescence nanospheres deposited on the glass substrate at pre-defined focal positions of the microscope objective determined at ten different X-positions. The solid lines show linear fits. The data are plotted with an offset for clarity. Two sets of samples were prepared and tested to ensure data reproducibility.

Long-range 3D tracking measurements and diffusion tracking

We tested the effective axial range of our 3D tracking method by localizing and tracking multiple freely diffusing 60 nm fluorescent polystyrene nanoparticles distributed across a wide depth range in a homogeneous solution (glycerol-water 4:1 mixture) (Fig. 7a and Supplementary Movie 1). Freely diffusing nanoparticles in the sealed chamber (Fig. 7a) located at different axial positions are captured in the time-lapse images shown in Fig. 7b (denoted by green, cyan, and red arrowheads). These nanoparticles were successfully localized in 3D space, generating 3D diffusion time trajectories displayed in Fig. 7c. Notably, the diffusion trajectories distribute across the axial range of 30 µm (Fig. 7c). This demonstrates the capability of our 3D tracking method to track fluorescence emitters with an axial range of at least 30 µm, which is 50% wider than 20 µm, the previously reported maximum localizable depth range with the PSF engineering methods¹⁹.

Fig. 7. Quantitative analysis of diffusional motion using the birefringence-based single-particle 3D tracking.

a Schematic illustrations of the sample configurations for the measurement of random diffusion using a sealed chamber (left) and directed diffusion using convection flow in an open chamber (right). This experiment was conducted using a 173 µm-thick mica substrate. b Representative time-lapse images of the 60 nm fluorescence nanoparticles freely diffusing in the sealed chamber. Three particles in the field of view are indicated by green, cyan, and blue arrowheads. The images were captured at a 1 Hz repetition rate with 100 ms exposure time. c Localized 3D diffusion trajectories of the three fluorescent nanospheres obtained from the time-lapse images in (b). d Mean square displacement (MSD) versus time lag plots obtained from the diffusion trajectories shown in (c) and (e). The dashed line shows the theoretically calculated MSD versus time lag plot of the nanospheres in a medium with 1 mPa s viscosity using the diffusion constant of the fluorescent nanospheres estimated by Eq. 7. The solid line shows fitting to the directed diffusion model (Eq. 6). Four sets of samples were prepared and tested to ensure data reproducibility. e Localized 3D diffusion trajectory of a fluorescent nanosphere obtained using the open chamber.

The applicability of our 3D tracking method to the quantitative characterization of diffusional motions was examined by mean square displacement analysis. Using the 3D diffusion trajectories (Fig. 7c) obtained in the sealed chamber, we calculated MSD versus time-lag plots for each trajectory (Fig. 7d). The MSD versus time lag plots can be fitted to a linear function (i.e., random diffusion, Fig. 7d). The diffusion constant (D) of the nanoparticles was estimated to be 0.0744 µm2 s^-1, calculated from the slope of the averaged MSD plot obtained from the three localized trajectories (Supplementary Fig. 13). This value agrees with the D value calculated by the Einstein-Stokes equation (D = 0.0783 µm2 s^-1; see Methods for the details)^39,40. The simulated MSD versus time lag plot with this calculated D value also agrees with the experimentally obtained MS plots (Fig. 7d). The linear MSD plot, together with the excellent agreement between the experimentally obtained and simulated MSD, indicate that our 3D tracking method can be used for the quantitative characterization of the 3D motion of the fluorescent nanoparticles. The MSD plot obtained from Trajectory 3 in Fig. 6c slightly deviates from a linear function (Fig. 7d), which could be attributed to the physical interaction between the nanoparticle and the mica surface.

Figure 7e shows a representative 3D diffusion trajectory of the nanoparticles captured in the open chamber (Fig. 7a and Supplementary Movie 2), where the directed diffusion caused by convection flow is clearly seen. The MSD versus time lag plot obtained from the diffusion trajectory (Fig. 7d) was fitted to the directed diffusion model, from which the diffusion constant (D = 0.0885 µm2 s^-1) and flow velocity (v = 0.305 µm s^-1) were estimated. The estimated D value is similar to that obtained for the random diffusion. The result also suggests the applicability of our 3D tracking method for the quantitative characterization of the 3D motion of the fluorescent nanoparticles.

Notably, we could record 3D diffusion trajectories over the 3500 image frames for over 11 min (Supplementary Fig. 14). This was possible because of the small PSF in the extended axial range, which allowed us to capture the fluorescence images with a high signal-to-background ratio at the reduced excitation power range, minimizing the photobleaching effect over the extended period of time.

3D tracking in plant cells

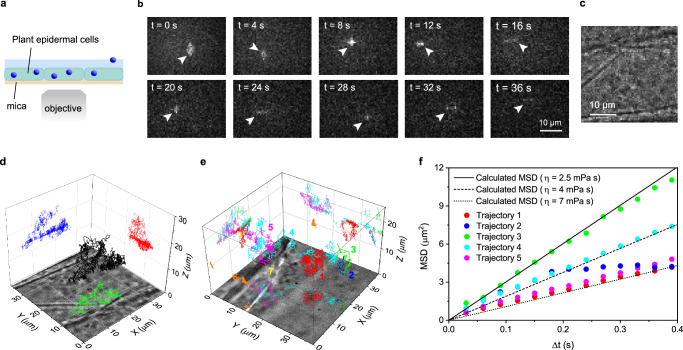
The applicability of our method to the 3D tracking in a biological sample was evaluated using live cells. We first applied our 3D tracking method to mammalian cells (see Methods for details of the sample preparation). As shown in Supplementary Fig. 15, 3D diffusion trajectories of the fluorescent nanospheres deposited on Chinese hamster ovary cells were tracked using our method, demonstrating the applicability of our method to 3D tracking in mammalian cells. Next, we applied our method to plant cells (Fig. 8a). Plant cells represent unique challenges for fluorescence microscopy, especially for single-particle 3D tracking, due to high autofluorescence, significant refractive index mismatches within cell structures (e.g., between the cytoplasm and cell wall), and their large size. Previously reported 3D tracking techniques have never been applied to tracking experiments in plant cells, partly due to these challenges. Using 3.5 nm size organic J-aggregate nanoparticles that emit bright fluorescence⁴¹, we conducted a 3D tracking experiment in onion (Allium cepa L.) epidermal cells, whose size is approximately 200 µm (length) × 50 µm (width) × 40 µm (height) (Fig. 8b and Supplementary Movie 3, see Methods for details of the sample preparation). Each image was recorded with a short exposure time of 6 ms and a time interval between the images of 30 ms to obtain sharp images of the rapidly moving nanoparticles (see Methods for experimental details). Bright-field images of the same sample region were also recorded (Fig. 8c). Notably, the mica substrate had a negligible effect on the quality of bright-field images (Fig. 8c). The time-lapse images obtained from a single fluorescent nanoparticle injected into the cells show that the fluorescence image of the nanoparticle and the time-dependent changes in its spatial pattern are clearly captured (Fig. 8b). We were able to capture more than 1500 frames of images of the tracked nanoparticle, from which we obtained the 3D diffusion trajectory of the nanoparticle in the plant cell (Fig. 8d). The result suggests that our 3D tracking method is applicable to biological samples, including challenging specimens for optical microscopy, such as plant cells.

Fig. 8. Birefringence-based single-particle 3D tracking in plant cells.

a A schematic illustration of the sample configurations for the 3D tracking experiment in plant cells. This experiment was conducted using a 170 µm-thick mica substrate. b Representative time-lapse fluorescent images of 3.5 nm size fluorescent nanoparticles injected into the plant cells. A particle in the field of view is indicated by arrowheads. c A bright-field transmitted microscopy image captured at the same sample position as the fluorescence imaging experiment shown in (b). d Localized 3D diffusion trajectory of a fluorescent nanoparticle in the cell obtained from the time-lapse images in (b). e Localized 3D diffusion trajectories of multiple fluorescent nanoparticles inside the cell. f Mean square displacement (MSD) versus time lag plots obtained from the five diffusion trajectories shown in (e). The solid, dashed, and dotted lines show the theoretically calculated MSD versus time lag plots of the nanoparticles in a medium with 2.5, 4, and 7 mPa·s viscosity using the diffusion constant of the fluorescent nanoparticles estimated by Eq. 7. Three sets of samples were prepared and tested to ensure data reproducibility.

Figure 8e shows an example of the 3D tracking of multiple fluorescence nanoparticles located at different axial positions in a plant cell. Seven trajectories distributed over a 20 µm axial range inside the cell were localized, demonstrating the multiplexing capability and large axial range of our 3D tracking method (Supplementary Note 6). The five nanoparticles (denoted by 1, 2, 3, 4, and 5 in Fig. 8e) exhibited 3D diffusional motion in the cell, and we characterized their motion by the MSD analysis (Fig. 8f). Two other nanoparticles (denoted by 6 and 7 in Fig. 8e) in the cell showed negligible motion throughout the imaging experiment, most likely due to anchoring to an inner surface of the cell. The MSD versus time lag plots obtained from these nanoparticles clearly show different slopes (i.e., distinct diffusion rates) and curvatures (i.e., distinct diffusion modes). While the MSD versus time lag plots obtained from trajectories 1, 3, 4, and 5 agree very well with the simulated MSD plot assuming a random diffusion of the particle in a homogenous medium with its viscosity slightly higher than that of water (2.5, 4, and 7 mPa s for trajectory 5, trajectory 4, and trajectories 1 and 3, respectively), the MSD plot obtained from trajectory 2 deviates significantly from the simulated random diffusion. These results demonstrate that our 3D tracking method can be used for the quantitative characterization of the velocity and modes of the motion of individual nanoparticles in biological samples, including plant cells.

Discussion

In this study, we developed a single particle 3D tracking method based on PSF engineering using the birefringent material, mica, as a substrate for mounting microscopy samples. The PSF was modified because of the birefringent characteristic of mica, from which we could precisely localize 3D coordinates of single fluorescent nanoparticles. We found that the axial range for the localization (i.e., the axial range over which the change of the spatial pattern of the PSF is observed) depends on the thickness of the mica substrates (Fig. 3b). The simulated PSF also supports this relation of the mica thickness and the axial range of the PSF formation (Fig. 3b). We used 185 µm-thick mica substrate for most of our 3D tracking experiments because the mica substrate with this thickness allowed us to localize the particles over the largest axial range, 30 µm, with the excellent localization precision of 30 nm throughout the range. Thinner mica substrates gave a narrower axial range for the localization (Fig. 3b). These substrates would, thus, be useful for 3D tracking experiments in relatively thin specimens. In addition, the smaller PSF sizes obtained for the thin mica substrates would be beneficial for 3D tracking experiments with less bright fluorescence emitter as a small PSF allows a high signal-to-background ratio imaging with a limited number of emitted photons.

The large axial range and the small PSF size obtained using the mica substrate are due to the existence of the extended focused region of the PSF along the Z axis, which can be seen in Supplementary Fig. 1 Y-Z plane panel. The axial position-dependent fluorescence patterns were observed in this focused region (i.e., each Z-axis position gives the distinct spatial pattern of fluorescence), enabling us to accurately determine the 3D coordinates of single particles. Our study demonstrated that the length of the focused region increased with the thickness of the mica substrate.

One of the advantages of feedback-free 3D tracking methods based on PSF engineering is that they can simultaneously track multiple particles (i.e., high multiplexing capability). A smaller size of the PSF is essential to avoid spatial overlapping of multiple particles and, thus, maximize the number of simultaneously localizable particles. Although previous studies indicated that multiple spatially overlapped PSFs can be localized by a software-based analysis^17,19, it is still challenging to process excessive numbers of overlapping PSFs. Over the entire axial range, the diameter of the PSF along the XY plane obtained in our 3D tracking method is nearly half that used in another 3D tracking method reported to cover the largest axial range (Supplementary Fig. 2)¹⁹. Since the area occupied by the PSF is proportional to the square of its diameter, our 3D tracking method can, in principle, localize single particles at up to four times the density of previous methods without spatial overlapping between them. Our method has a multiplex imaging capability that enables simultaneous 3D localization of up to 8 particles per 100 μm2 field of view without spatial overlap.

We demonstrated that our 3D tracking method can localize and track individual fluorescent particles over a 20 µm Z-axis range in the plant cells (Fig. 8e). The MSD analysis of the trajectories demonstrated spatial heterogeneity in the diffusion rate and mode (Fig. 8f), which could be interpreted by local environments in the plant cells. A previous study using fluorescence recovery after photobleaching (FRAP) technique indicated that the intracellular viscosity in the cytoplasm is 4-5 times higher than that of water⁴², whereas a recent fluorescence lifetime imaging (FLIM) study on the local viscosities in plant cells suggested the existence of subcellular level spatial heterogeneity⁴³. The results of the MSD analysis of the fluorescent nanoparticles in the plant cells obtained in our 3D tracking experiment are consistent with the observations in the previous study using FRAP and FLIM (Fig. 8f). In addition, we observed the distinct diffusion modes for each nanoparticle (i.e., each nanoparticle showed a different level of deviation from random diffusion, Fig. 8f). These results suggest that the subcellular structures also have a significant effect on the modes of motion (e.g., confined motion). All these observations demonstrate that our 3D tracking method provides a practicable means to characterize quantitatively sub-cellular level spatiotemporal dynamics in biological samples.

The simulation of the PSF was conducted by taking into consideration the three principal refractive indices of mica (Supplementary Fig. 5a). The excellent agreement of the simulated PSF with the experimentally obtained PSF demonstrated that the formation of the PSF with the extended focused region through the mica substrate originates from the biaxial-birefringent optical property of mica with a particular combination of the three refractive indices (Fig. 3b, and Supplementary Fig. 5). The PSF simulation showed that the modification of the PSF by the mica substrate significantly depends on the optic axes of mica through which the PSF is formed. Indeed, the PSF with the extended focused region with distinguishable patterns across the wide focal range, similar to the experimentally observed PSF, was obtained only when the optical axis of the microscope was aligned with the optical biradial of the substrate in the simulation (Supplementary Fig. 5b). The simulated PSF obtained through other optic axes of mica did not show the extended focused region with distinguishable patterns across the focal region (Supplementary Fig. 5b, c), indicating the essential role of the optical biradial in the observed PSF modification. This optical biradial axis is known to have a unique optical property of external conical refraction. Our results may indicate that the formation of the PSF with the extended focused region through the mica substrate could be related to the optical feature of external conical refraction, which is observed along the biradial axis of biaxial birefringent crystals³⁵. Hence, other biaxial birefringent materials with optical biradial orientation could also perform similarly, with the potential for PSF engineering and, thus, single-particle 3D tracking (Supplementary Note 7).

Mica is a naturally colored material (i.e., light is partly absorbed), which reduces the photon detection efficiency for imaging experiments (Supplementary Fig. 16). The 3D tracking method we developed in this study could be improved by using optically more transparent biaxial birefringent materials as a substrate for microscopy experiments. In addition, our 3D tracking method can easily be implemented without modifying a standard epi-illuminated wide-field fluorescence microscope. Moreover, the tracking range could be extended by combining with depth-enhanced high-throughput imaging methods⁴⁴. The ease of implementation compared with other 3D tracking methods based on PSF-engineering using SLM makes our method accessible to many users, which would lead to the widespread utilization of single-particle 3D tracking, one of the essential imaging techniques for visualizing molecular motion in complex environments, for life science research.

Methods

Birefringence measurement of mica substrates

Mica substrates used in this study were purchased from SPI supplies (Grade V-1 MICA sheets). The thickness of the mica was estimated by measuring the interference pattern observed in the non-absorbing spectrum region of the transmission spectrum, according to the procedure reported previously³⁷. Briefly, the transmittance spectrum was measured in the wavelength range of 700 to 760 nm. Then, the interference pattern on the measured spectra was fitted with the following equation,

$$T=T_0+A\sin \left(\omega \left(E-E_0\right)\right)$$ 1

where $\omega =4\pi nt/C$ and $C=1239.8\mathrm{eV}/\mathrm{nm}$. t and n represent the thickness of the substrate and the refractive index. The thicknesses of the substrates can be determined with an error of 4% using this method.

The thicknesses of the substrates were determined with an error of 4%.

The birefringence of the mica substrates was experimentally determined by recording the intensity of the transmitted light through the substrates. The transmittance of the light (T) through a wave retarder with retardation Γ placed in between two cross polarizers can be written as follows⁴⁵,

$$T={\sin }^2\left(\Gamma /2\right),$$ 2

where Γ can be described as Γ = 2πδd/λ₀ for the light with a wavelength of λ₀ propagating through a substrate with birefringence of δ and thickness of d. Therefore, T is described as

$$T={\sin }^2\left(\frac{\mathrm{\pi }\delta d}{{\mathrm{\lambda }}_0}\right).$$ 3

The T values were experimentally measured for the mica substrates with different thicknesses, from which we determined the birefringence δ by fitting the experimental data to the Eq. 3 (see Supplementary Methods for details of the experimental configurations in the T measurement).

Sample preparation

Fluorescent nanospheres used in this study were purchased from Bangs Laboratories (60 nm size Envy Green, aqueous suspension with 1% solid). 3.5 nm size J-aggregate nanodots were fabricated by the nanoprecipitation method⁴¹.

The glass (No. 1.5 coverslip from Menzel Gläser) and mica substrates were functionalized with 2% 3-aminopropyltriethoxysilane (Sigma-Aldrich) in acetone. A diluted solution of the nanospheres (the original suspension was diluted 4 × 10⁴ times into water) was dropped on the surface of the glass and mica substrates and washed with MilliQ water after incubating for 3 min. A PDMS solution was mixed with a curing agent and placed under a vacuum to remove air bubbles. A 5 µl of the PDMS solution was dropped over the mica substrate with the nanospheres on the surface. Then, the glass substrate with the nanospheres on the surface was placed on the PDMS solution. The sample was kept overnight at 30 °C for the curing of PDMS. Both plane and wedge-shaped samples were prepared in the same manner.

Open and sealed chambers were prepared using a fluidic chamber with a customizable bottom substrate (ibidi, sticky-Slide VI 0.4). The mica substrate was attached to the bottom of the sticky slide. A 50 µl of the aqueous suspension of the fluorescent nanospheres (60 nm size Envy Green, 4 × 10⁵ times dilution of the original suspension) was injected into the fluidic chamber. The inlet and outlet of the chamber were sealed by a plug attachment for the 3D tracking experiment with the sealed condition. The inlet and outlet were kept unsealed for the experiment under the open condition.

Chinese hamster ovary (CHO) cells were deposited on a mica substrate and incubated in a cell growth chamber (5% CO₂, 37 °C) for 24 to 48 h. Prior to depositing the CHO cells, the mica substrate was treated with oxygen plasma to enhance the growth of the adherent CHO cells, and polystyrene fluorescent nanospheres (Bangs Lab, Envy green, 60 nm) were deposited on the surface of the treated mica substrate and heated to 90 °C. Then, the cell medium was removed and the same fluorescent nanospheres diluted in DPBS were added to the top surface of the cell layer.

The onion (Allium cepa L.) epidermal cells layer sheet was removed from the onion by peeling it off and placing it onto the mica sheet with the torn side up. Silicon immersion oil for objectives (Olympus) was deposited between the mica and cells layer in order to prevent the nanodot solution from penetrating into the gap. Then, an aqueous solution containing the J-aggregate nanodots was dropped on the mounted cells, and the sample was incubated for approximately 1 to 3 min before rinsing with MiliQ water. A glass coverslip was placed on top to prevent the sample from drying.

Fluorescence microscopy experiments

Fluorescence imaging measurements were conducted by a home-assembled microscope system using an inverted microscope frame of Olympus IX71^46–48. A 532 nm (100 mW, Cobolt, Samba) or 523.5 nm (CNI Optoelectronics Technology, MLL-FN-523.5–300 mW) line of a continuous-wave laser was introduced into the microscope from the backport through a focusing lens (f = 300 mm). Excitation power was controlled with an acousto-optic tuneable filter (AOTF, AA Opto Electronics). The excitation light was reflected by a dichroic mirror (FF538-FDi01 or FF526-Di01, Semrock) and illuminated the samples through an objective lens (UAPON 100XOTIRF (100× NA = 1.49), UPLSAPO60XW (60× NA = 1.2), or UPLSAPO100XS (100× NA = 1.35)). Fluorescence emission was captured by the same objective lens, passed through an emission filter (FF01-596/83-25, FF01-542/20-25, or FF01-544/24-25, Semrock), and was detected by an EMCCD camera (iXon3 897, Andor Technology). A piezo nanopositioning Z-axis stage (Nano-Drive, Mad City Lab Inc.) was used to control the z-axis position of the microscope stage. An automatic focus drift correction (C-focus system, MCL Mad City Lab Inc.) was used in the microscopy imaging experiments at a single Z-axis position.

3D localization procedures

The 3D coordinates of the particles were determined by 2D cross-correlation analysis of the target and reference PSF images using MATLAB (R2021a Update 2 (9.10.01669831) script, see Supplementary Fig. 17). The reference images were recorded with a 10 nm step size. We calculated the normalized 2D cross-correlation of each target-reference combination, which gave Z position-dependent correlation values. The Z-position of the target particle was determined by finding the reference image that gave the highest correlation value. The original images (both reference and target images) were recorded with a pixel size of 83.3 nm. This reference image was then sub-pixelized to determine XY coordinates. Each pixel in the target and the reference images was divided into 10 pixels with the same width (i.e., 8.33 nm, Supplementary Fig. 18). We further applied a Gaussian blur filter with a two-standard deviation to the reference image. After these treatments, we calculated the normalized 2D cross-correlation of the target and reference images at different XY shifts between the two images. The XY-position of the target particle was determined by finding the XY shift between the target and reference image that gave the highest correlation value.

Mean square displacement analysis

Mean squared displacement (MSD) versus time lag (Δt) plots were calculated using the following formula,

$${MSD}_{3D}\left(\mathrm{\Delta }t\right)=⟨{\left[x\left(t+\mathrm{\Delta }t\right)-x\left(t\right)\right]}^2{+\left[y\left(t+\mathrm{\Delta }t\right)-y\left(t\right)\right]}^2+{\left[z\left(t+\mathrm{\Delta }t\right)-z\left(t\right)\right]}^2⟩,$$ 4

where x, y, and z are 3D coordinates of the diffusing particle at time points t and t + Δt. The obtained MSD plots were analyzed using either the random or directed diffusion models. The diffusion constant (D) of the particles in the random diffusion model was calculated by fitting the MSD plots to the following equation,

$${MSD}_{3D}=6D\mathrm{\Delta }t.$$ 5

The diffusion constant (D) of the particles and the flow velocity (v) in the directed diffusion model were calculated by fitting the MSD plots to the following equation,

$${MSD}_{3D}=6D\mathrm{\Delta }t+v^2{\mathrm{\Delta }t}^2.$$ 6

The theoretical MSD versus time lag plots for random diffusion were obtained by calculating the diffusion constant of the particles using the Einstein-Stokes equation,

$$D=\frac{kT}{6\pi \eta r},$$ 7

where η, r, k, and T are the viscosity of the solution, the radius of the particle, the Boltzmann constant, and the temperature (see Supplementary Methods for the calculation of the viscosity of the glycerol/water mixture).

Simulation of PSF image through mica substrate

To interpret our experimental findings, we developed a model based on Fourier processing⁴⁹, as schematically illustrated in Supplementary Fig. 19, and used it to numerically simulate the images. In our setup, a birefringent slab (Mica) of thickness d is placed between the water and the objective lens. The principal refractive indices of the birefringent material along its crystal axes are n_γ = 1.601 $n_{\beta }=1.596$ and $n_{\alpha }$ = 1.563⁵⁰. The z-axis is aligned with the propagation direction, and the crystal axes are rotated by angles γ, β and α, respectively. The incident field illuminates the sample and transmits through the slab, with transmission calculated via the transfer matrix method (see Supplementary Methods for details). The transmitted field leaving the slab at an angle $\theta <{\theta }_{\max }$ is collected by the high-NA objective lens with radius ${\rho }_{\max }=\sin \left({\theta }_{\max }\right)$, which rotates the polarization perpendicular to the propagation direction. Specifically, rays entering the objective at an inclination of θ exit parallel to the z-axis and enter the tube lens at a near-zero inclination angle ${\theta }_{\mathrm{tube}}\approx 0$. This configuration allows the application of the paraxial theory of Fourier optics. The intensity at the image plane can thus be related to the field at the back focal plane using the scaled Fourier transform (see Supplementary Methods for details). Finally, we recorded the image at the image plane by averaging the emanated field and plotted it on Cartesian coordinates using a simple coordinate transformation (see Supplementary Methods for details).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

S.N. and S.H. conceived the project. S.N. designed and conducted the experiments, and analyzed the data. R.A. and Y.W. conducted the simulation. S.N. and S.H. wrote the manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data supporting the findings of this study and the software developed in this study are available on Zenodo at 10.5281/zenodo.15583803.

Code availability

The codes for analysing the images and generating 3D trajectories are available on Zenodo at 10.5281/zenodo.15579597.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-025-61953-1.