Curvature of co-links uncovers hidden thematic layers in the World Wide Web

Abstract

Beyond the information stored in pages of the World Wide Web, novel types of “meta-information” are created when pages connect to each other. Such meta-information is a collective effect of independent agents writing and linking pages, hidden from the casual user. Accessing it and understanding the interrelation between connectivity and content in the World Wide Web is a challenging problem [Botafogo, R. A. & Shneiderman, B. (1991) in Proceedings of Hypertext (Assoc. Comput. Mach., New York), pp. 63–77 and Albert, R. & Barabási, A.-L. (2002) Rev. Mod. Phys. 74, 47–97]. We demonstrate here how thematic relationships can be located precisely by looking only at the graph of hyperlinks, gleaning content and context from the Web without having to read what is in the pages. We begin by noting that reciprocal links (co-links) between pages signal a mutual recognition of authors and then focus on triangles containing such links, because triangles indicate a transitive relation. The importance of triangles is quantified by the clustering coefficient [Watts, D. J. & Strogatz, S. H. (1999) Nature (London) 393, 440–442], which we interpret as a curvature [Bridson, M. R. & Haefliger, A. (1999) Metric Spaces of Non-Positive Curvature (Springer, Berlin)]. This curvature defines a World Wide Web landscape whose connected regions of high curvature characterize a common topic. We show experimentally that reciprocity and curvature, when combined, accurately capture this meta-information for a wide variety of topics. As an example of future directions we analyze the neural network of Caenorhabditis elegans, using the same methods.

The World Wide Web (WWW) is a graph (1, 2) that is continuously being expanded by an enormous number of independent agents. Millions of users add pages in an uncoordinated way, but in doing so they must obey clear rules on how to address other pages (3). Beyond the information placed by users directly in individual pages, their unified action creates a cooperative meta-information whose location is in the connectivity of the network. By meta-information we mean information that is based solely on the graph structure of the WWW, and which reveals strong contextual grouping. This type of information should be contrasted to that of a very informative but secluded page that is an archive of information (a “wise hermit”). Further on, we will compare our new meta-information to earlier work.

The billions of pages and links of the WWW create a maze of confusing and almost unmanageable complexity. To navigate through it and to find pages of interest, users rely on the help of search engines (4). These send out small, automated programs (robots) that roam the Web, retrieve links, and note keywords as they create a mirror image of the Web that can be stored within one room of storage data, ready for easy access. The Web remains intelligible to its human users precisely because it is constantly analyzed and monitored by these automatic agents. Robot activity dominates Web traffic and accounts for up to 70% of the total queries made at certain sites we studied.§ Because of the breadth of their search, robots obtain a clearer view of the Web than the common user.

It is therefore useful to adopt the perspective of robots, without having to define meaning or content, looking only at the identification tag of pages (URL addresses) and their links (5). To avoid the difficulty of having to know the complete Web graph, we use robots that explore some locally visible pieces that can be found by starting from a given page and progressing along its links. An analogy may be drawn with classical neurobiology (6), where a neuron takes up dye that then traces out its connections.

Defining a Curvature on the Web

Having defined our aim of revealing meta-information in the form of hidden thematic structures, we implement it by a novel combination of a number of key ideas: clustering, co-links, triangles, and curvature. The clustering regroups a “home” page with the pages in its subdirectories. The co-links are then the result of independent agents linking their pages. Triangles capture transitivity, which we measure by the associated notion of curvature. By using curvature, we show that practically all the connective information depends on co-links. Thus, our method reveals a new geometric view of the locus of information in networks, which is not “put there” but “happens” as a collective effect.

In detail, we proceed as follows: The first step of our method is clustering.¶ Once a certain number of pages have been found by our robot, we regroup them into a node by lumping together a “home” page with the pages in its subdirectories. This clustering is useful because (i) information within a given home site belongs to one contextual heading; (ii) the size of the graph is reduced by a factor of 10²-10³; and (iii) connective links that arise from physical proximity are eliminated, leaving the more relevant remote links.

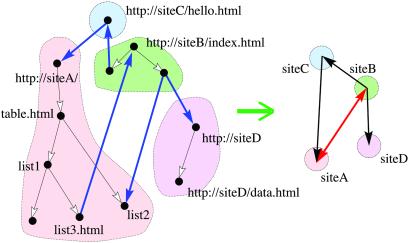
Working henceforth exclusively with the clustered graph (like the one on the right of Fig. 1), we introduce the pivotal notion of co-link for a reciprocal connection between two nodes, A and B (A points to B and B points to A, the red link in Fig. 1). They are then deemed to be “congruent” (friends, or members in the same interest group).

Figure 1.

The reduction of a set of pages and links by clustering. On the left, local links are black and remote links are blue. On the right, black links are one-way and the red one is a co-link. Clustering clarifies connectivity because it allows the links to go through different pages within the nodes.

Co-links are special because, whereas we can point to your page we cannot (in general) cause you to point to ours. Congruence therefore indicates an awareness by both nodes of the other's existence and content, and a recognition of the other's value to their own interests. Because congruence involves mutual recognition, we expect it to be a transitive property, i.e., if sites A and B are congruent and B and C are congruent, then A and C will be congruent with high probability, forming a triangle. Such triangles signal strong cooperative content, and would be extremely rare in any large random graph whose average number of links per node is bounded (7). To quantify the aggregation of triangles with congruent edges, we define the local curvature at a node n by c_n = 2t_n/((v_n − 1)v_n). This quantity was termed the clustering coefficient in ref. 8. Here, t_n is the number of triangles containing n as a corner, v_n is the number of links leaving n (the valence), and (v_n − 1)v_n/2 is the maximal number of possible triangles. We ignore in this the directionality of one-way links. If the graph is a tree, there are no triangles, and c_n = 0 everywhere, whereas for any complete graph (where all nodes are mutually connected), c_n = 1 everywhere.

To see that c_n is indeed a quantity that can be called a curvature, we regard the simple geometric picture of Fig. 2: One way to detect that we are on a curved surface by using local measurements is to walk a unit distance on a straight line in two different directions separated by a constant angle α. Connecting the two endpoints completes a triangle, and the length of the third edge is determined by the curvature. On surfaces this relation of triangles to curvature is a natural generalization of the law of cosines, relating the angle at the apex and the three sides. For general metric spaces, such as infinite graphs, this relation is the basis of a mathematical definition of curvature (9) obtained by comparing triangles in a continuous metric to their counterparts embedded in standard manifolds.

Figure 2.

Illustration of the law of cosines on a sphere (positive curvature) and a hyperboloid (negative curvature). The triangles have sides 1 and 1 and the same angle α, but the distances between the ends are different: d < d′.

The average number of triangles c_n at a node n is related to the average distance between any two of its nearest neighbors (say n′ and n"). This distance is measured by counting links in the shortest path from one node to another, namely n′ and n". Because for co-links this is either 1 (n′ and n" directly connected, triangle exists) or 2 (no triangle, need to go through node n), c_n = 2−〈r(n′,n")〉, where r is the distance. The average 〈⋅〉 is taken over all pairs of nearest neighbors so that the average triangle has sides 1, 1, 〈r〉. In principle, for one-way links the distance r may be a large number and can range all the way to infinity (no connection). Experimentally, we can measure triangles not only in the co-links but also in the one-way links. In that case, we ignore the direction of the link when measuring the distance r, and we shall still use c_n as measured by triangles to give us an upper bound on the connectivity.

We are not aware of a definition similar to the one of ref. 9 for finite graphs with discrete metric, but it is still useful to view c_n as the curvature of triangles with apex at n (though c_n is normalized to take values between 0 and 1),‖ with c_n being perhaps closer to a dimension measurement (10). Equipped with a metric (minimal number of hops between nodes) and a curvature, the graph of the WWW can be visualized geometrically. We shall say that it looks like a hyperboloid when it is tree-like, with exponential separation of branches that “fan out” (ref. 11; see Fig. 3). In contrast, a highly connected region looks more like a sphere that is “closed” on itself. Alternately, a random walk by the robot in the graph will tend to get trapped somewhat longer in highly curved regions.

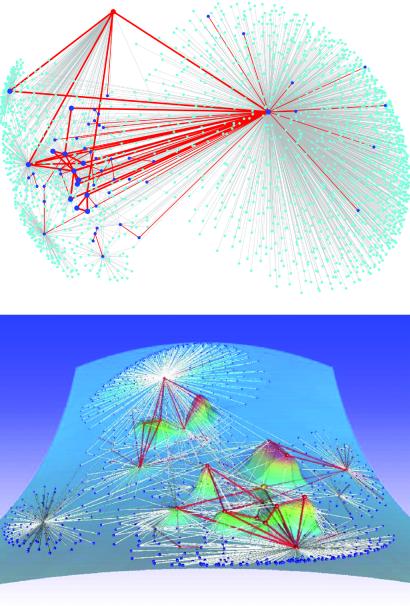
Figure 3.

(Top) The nodes (2,125) and links (2,755) of a site specializing in tango (specifically the music of Piazzolla). The co-links are shown in red, congruence triangles are enhanced, and one-way links are black. The anchor is red. The sparsity and high connectivity of the congruence graph are striking. (Bottom) A view of the curvature for the 947 nodes and the 1,307 links of a notorious Swiss revisionist (anti-Semitic) site. Height above the blue surface is proportional to curvature (of congruence triangles). The one-way graph is clearly less connected, its links are more likely to be dangling ends, and it is generally dominated by the appearance of hubs.

Triangles tend to aggregate, creating interest groups of widely varying size (in terms of the number of members), but of small diameter. In general, the border of interest groups is expected to be a sharp interface, but sometimes different interest groups will connect one to another, typically via a single link (e.g., the member of the “butterfly collection” interest group who also belongs to the “origami” interest group). Our definition of curvature implies that such connecting nodes tend to be hubs and are characterized by a low curvature.

The meta-information of the graph has been noted before (12) and has been used for data mining in the influential works (13, 14). These approaches view a link as conferring “authority” and search the WWW for “Authorities” and “Hubs” that point at them. Based on these ideas the successful search engine Google was designed; it also led to the notion of “Community” (15, 16). Similar investigations of the information content of linkages are common in other fields, such as studies of social (17) or paper citation (18) networks. Our approach, however, emphasizes different features. Indeed, note that “authorities” as defined above tend to have low curvature, because belonging to two interest groups basically halves the curvature for the connecting node. On the other hand, nodes that are mutually recognized by peers get high curvature. Thus, curvature captures contextual vicinity rather than notoriety of a set of pages.

Experimental Implementation

We tested our general ideas in several Web crawls, encompassing over 1 million URLs of which over 300,000 were actually accessed. The database is stored for offline analysis, whereas intermediate results are used to direct the further action of the robot. Large numbers of links in a page (indicating the page is a hub) tend to stall the crawl, and we followed at most 35 links per page (neither .cgi nor .jpg was explored). As an aside, we note that .com sites seem to make little contribution to “cooperative content” and connect badly to others.

As the crawl proceeds, clustering according to Fig. 1 is implemented. To that end, links are determined to be local or remote. A local link is basically one inside a given site and any other link is remote. This decision is usually made by looking at the URL and using the known conventions for naming of pages inside a home directory (details can be obtained from the authors at http://mpej.unige.ch/∼eckmann). The algorithm explores a page it encounters by following the local links down to depth d (and perhaps u upward, links like “back to home page”).

Crawls are initialized by choosing a first site (the anchor) and fetching it. The links in a fetched page are identified and entered into the database. Our robot then fetches all the pages to which these links point. After exhausting the search down and up, the database is clustered and the robot is sent out along the first remote link. It explores that node in a similar way, going down and up the newly found local links as before. Once that is done, the robot returns to the first node and follows the next remote link, until all remote links at distance r = 1 from the anchor have been followed. The robot can then be directed to explore r = 2 or sequentially larger distances, if needed.

The breadth of crawls is shown in Table 1, whereas results from specific crawls are shown in Fig. 4. The curvature was calculated for all nodes within a distance r = 1 of the anchor, and for three types of graphs. The “full” graph includes all links that were found in the crawl, the “congruence” graph is composed solely of co-links (the red link of Fig. 1), and the “one-way” subgraph is obtained from the full graph by removing all co-links (leaving only the black links).

Table 1.

Data collected in 5 experimental Web crawls

Anchor	URL encountered	URL read in	Clusters	Total links	Co-links
Shakespeare	277,114	69,982	1,560	3,730	321
Needlework	341,398	102,895	1,498	4,440	727
Revisionist	66,771	22,933	947	1,307	67
Piazzolla	47,978	20,404	2,125	2,577	70
Mol. Biol.	318,705	110,286	1,518	6,351	868

Our protocol ensures that nodes within distance r = 1 of the anchor are fully explored to a given depth d = 3. The crawls started at sites of literary studies of Shakespeare, instructions for needlework, a notorious Swiss revisionist (anti-Semitic) site, tango (specifically the music of Piazzolla), and a site for molecular biology (Mol. Biol.). A URL has been “read in” if our robot has fetched and analyzed the corresponding page. We deem a URL as “encountered” if it appeared in any page we have read in. The link counts are for the clustered graphs. 

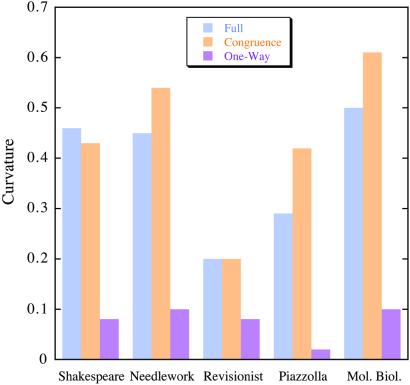
Figure 4.

Curvature for the data of Table 1. The quantities are the mean of the curvature of the anchor and its nearest neighbors. Full, all links, irrespective of direction; congruence, only triangles with three co-links; one-way, only triangles without co-links. Note that the curvature is carried basically only by triangles with at least one co-link.

Results

Our main result, shown in Fig. 4, is that the average curvatures of the congruence and full graphs are very similar, whereas that of the one-way graph is lower by a factor ranging between 2.5 and 21. This finding means that removal of the co-links results in a dramatic decrease of the curvature. The curvature of the full graph is carried predominantly by triangles containing at least one reciprocal side. This curvature is not produced by triangles with three co-links alone, because of their small relative number, but rather from triangles that have a combination of co- and one-way links. To put the results of Fig. 4 in perspective, we note that the density of triangles (and average curvature as well) of a random graph tends to zero with the size of the graph (7).

For all experiments, the distribution of curvatures c among the nodes of the full graphs obeys a power law, c = (2.0 ± 0.2)v⁻¹, where v is the valence of the node. Although the scaling is striking, we are not certain of its origin. It does cause highly connected nodes with high v such as hubs and authorities to have, on average, a low curvature. This finding agrees with our intuition that such nodes contribute perhaps to global connectivity but not to the local interest groups that curvature identifies.

Although we consistently avoided any reference to content of sites in the crawl itself, to check our method a separate, objective criterion was needed. We therefore checked manually whether the co-links reveal contextual linkages, by reading in 784 nodes from our crawls (in most cases checking the name of the node sufficed). Indeed, we found that no less than 75–100% of nodes congruent to the anchor relate to the same topic.

Extensions and Discussion

Going beyond the WWW, we examined the efficiency of curvature as a measure of thematic cohesion by studying three other networks. These are the neuronal network of the nematode Caenorhabditis elegans, the protein–protein interaction network of the yeast Saccharomyces cerevisiae, and the citation network of the mathematical physics archive (http://www.ma.utexas.edu/mp_arc). In each case we used an existing database to access and reconstruct the network, and as a control each had a separate, objective criterion by which related nodes were grouped into “themes.”

Our analysis of the neural network of the worm relies on classic work (19) that used about 8,000 electron microscopy sections to trace directed neuronal connections (R. Durbin, http://elegans.swmed.edu/parts/neurodata.txt). The control classification is the currently accepted association of neurons with organs found by both morphological and connective data (19, 20), where the existence of triangles was indeed noted, though only incidentally.

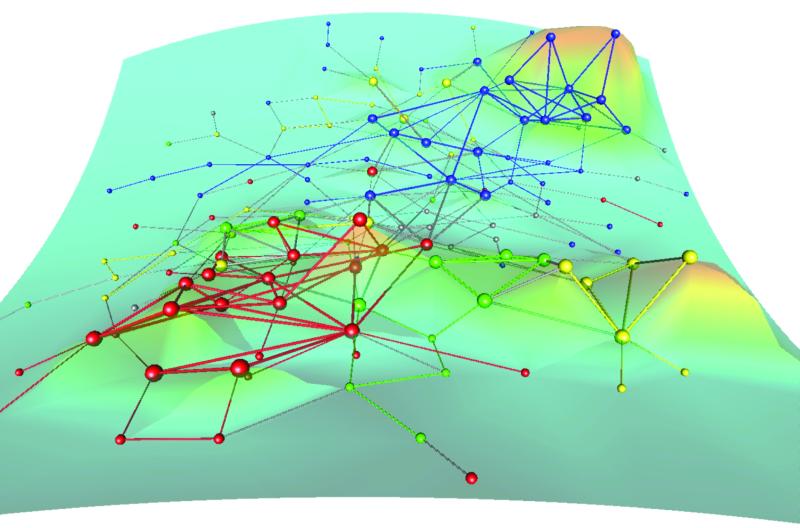
In Fig. 5 we present the network of the brain of the nematode. We immediately note three connected components of high curvature, color-coded to display the association with the major neural circuits or organs. The elevated groups are the amphids, the motor neurons of the nerve ring, and “other” sensory neurons of the head. The other circuits are either low-curvature (egg-laying and motor neurons of the ventral cord) or absent from the compilation (tail ganglia). The amphids and nerve ring are particularly well separated into connected components of the congruence graph. Furthermore, we find that interneurons [neurons that act like central processing units (CPU)] carry more curvature than sensory (input) or motor (output) neurons, which agrees with our intuition of how connections should distribute within the brain. Most co-links (61%) connect neurons that are within the same functional circuit (72% for co-links within triangles) whereas most of the one-way links (58%) connect between two different organs.

Figure 5.

The worm brain. The height is proportional to curvature. The red nodes are amphid cells, the yellow nodes are other sensory neurons of the head, and blue nodes are motor neurons of the nerve ring. Only co-links are shown, and triangles are enhanced.

For the protein–protein interactions of the yeast we took the protein–protein interaction database (http://dip.doe-mbi.ucla.edu/dip/Download.cgi), treating any interaction as a co-link (i.e., there are no one-way links). The control was taken from the functional classification given in the Yeast Protein Databank (YPD) (http://www.proteome.com/databases/YPD/YPDcategories/Functional_Categories.html). We found that proteins within the same connected groups of high curvature almost always (77% of the cases) belonged to the same functional grouping of the YPD. At c_n ≥ 0.15 there are 34 such groups, that include between 3 to 18 members, with an average of 5 proteins per group (data not shown; see supporting information, which is published on the PNAS web site, www.pnas.org).

In the case of the mathematical physics archive, we used the archive (http://www.ma.utexas.edu/mp_arc) to define a network of citations between authors in the same field. A co-link exists if author A cites author B (in any paper within the archive) and author B cites author A in any paper of his/hers, while co-authors are automatically co-linked. Note that our definition of co-links is fundamentally different from the co-citations defined in ref. 18, because there no reciprocal recognition exists. The control we used here was more problematic, relying on scanning manually all conference pages listed at the International Mathematical Physics Association homepage, and including an author in a group (e.g., “Quantum mechanics”, “Field theory” or “Statistical mechanics”) if she/he spoke under that topic in any of the conferences. However, we were able to classify only about 400 of the 1,700 authors (because not every author is talking at these conferences). As before, high curvature selected out the groups we found manually, with 5 of the 20 or so topic groups we defined very strongly represented and clearly identified (data not shown; see supporting information). Again, authorities, which in this case are very polyvalent scientists, have lower curvature than specialists in a small field and serve rather as hubs.

Conclusion

Our discovery opens a number of new possibilities for studying highly assembled complex structures in general, perhaps even the brain. First, the introduction of geometry frees us from the subjectivity of contextual concepts, such as meaning, content, and the like. The locality develops a different direction than global notions like scaling in the WWW and the “small-world” effect. Second, the concept of congruence shows the usefulness of combining geometry with selective action in probing sophisticated structures, including C. elegans. In particular, we have seen how a very simple dynamical rule—the search for congruence—radically changes our global view of the Web, replacing statistical aspects with unsuspected relations that can be found only by looking at combined, independently built pathways in the Web. Our approach can certainly be refined and extended in the Web but should prove useful in many other contexts.

Our study further shows that robots perceive the Web differently than the people who actually write and use the pages. Our robots go back and forth between various sites, gaining a more coherent view of their relations. We have shown that the geometric properties of the space in which they roam and the landscape that they reconstruct reveal new connective meta-information, hidden from the common user.

What can one expect in the future? Other forms of meta-information, not necessarily arising from connectivity, will certainly be found in the WWW and other complex networks. The dynamics of developing interest groups is also an important issue (21) that may involve rapid fusion processes (22). From a mathematical perspective, we have demonstrated the need for concepts of local curvature in graphs. Our definition of curvature seems a useful beginning to elicit Web properties and is easily generalized to balls of radius r = 2 (next-nearest neighbors) or more, as well as to simplices like tetrahedra. More advanced geometric concepts, however, such as measuring noncommutativity in the order of visiting sites, might be needed in the future.