Abstract
Accurate modeling of protein–protein complex structures is essential for understanding biological mechanisms. Hydrogen–deuterium exchange (HDX) experiments provide valuable insights into binding interfaces. Incorporating HDX data into protein complex modeling workflows offers a promising approach to improve prediction accuracy. Here, we developed HDXRank, a graph neural network (GNN)-based framework for candidate structure ranking utilizing alignment with HDX experimental data. Trained on a newly curated HDX data set, HDXRank captures nuanced local structural features critical for accurate HDX profile prediction. This versatile framework can be integrated with a variety of protein complex modeling tools, transforming the HDX profile alignment into a model quality metric. HDXRank demonstrates effectiveness at ranking models generated by rigid docking or AlphaFold, successfully prioritizing functionally relevant models and improving prediction quality across all tested protein targets. These findings underscore HDXRank’s potential to become a pivotal tool for understanding molecular recognition in complex biological systems.


Introduction
The interaction between proteins plays a crucial role in nearly all biological processes. There are approximately 500,000 binary contacts between proteins existing in humans, and those interactions support the essential cellular activities, such as signal transduction, metabolism, DNA/RNA/protein synthesis, etc. Gaining structural insights into these interactions at the molecular level is critical for understanding and modulation of protein functions, with direct implications on drug design and therapeutic strategies. While many high-resolution structures of protein complexes are available in the Protein Data Bank (PDB), a vast number of protein complex structures are not yet experimentally resolved. Experimental techniques, such as X-ray crystallography, nuclear magnetic resonance (NMR) spectroscopy, and cryogenic electron microscopy (cryo-EM), have elucidated many 3D protein complex structures. However, these methods are labor-intensive, time-consuming, and with specific limitations, such as constraints on protein size and required sample concentrations.
Development of computational prediction methods has enabled the rapid construction of atomic-scale protein models. Over the past 20–30 years, numerous protein–protein docking software packages and online tools have been developed to predict quaternary structure from the monomer structures, including ClusPro, HDOCK, ZDOCK, HADDOCK, and RosettaDock. , The protein–protein docking protocols typically consist of two steps: (1) docking configuration sampling; (2) produced decoy ranking. Predicting native structures (usually the complex structure defined by structural biology techniques) from monomers in a non-native state remains a significant challenge due to potential conformational changes and the vast binding pose search space. Recent advancements in AI-driven protein structure prediction have revolutionized the field. Deep learning-based methods like AlphaFold2 (AF2), AlphaFold3 (AF3), and RoseTTA-Fold2 achieved state-of-the-art accuracy in modeling quaternary structures directly from amino acid sequences. The quality of deep learning-based prediction heavily relies on the depth of multi-sequence alignment (MSA), which makes it challenging to predict structures for poorly characterized proteins. Alternatively, incorporating sparse structural experimental data, which is readily obtainable at relatively low cost and in a short time, can improve the prediction success rate by guiding the modeling process. For example, sparse structural information such as solvent accessibility, interface location and composition, distances and contacts, flexibility, and stoichiometry is typically insufficient on its own for accurate complex prediction. However, it can be utilized as restraints within modeling algorithms to reduce the search space and improve prediction quality. Several mass spectroscopy (MS)-based techniques, such as cross-linking (XL), − covalent labeling (CL), − ion mobility (IM), , and surface-induced dissociation (SID), have been successfully integrated into docking pipelines and AF2 workflows, leading to improved prediction performance.
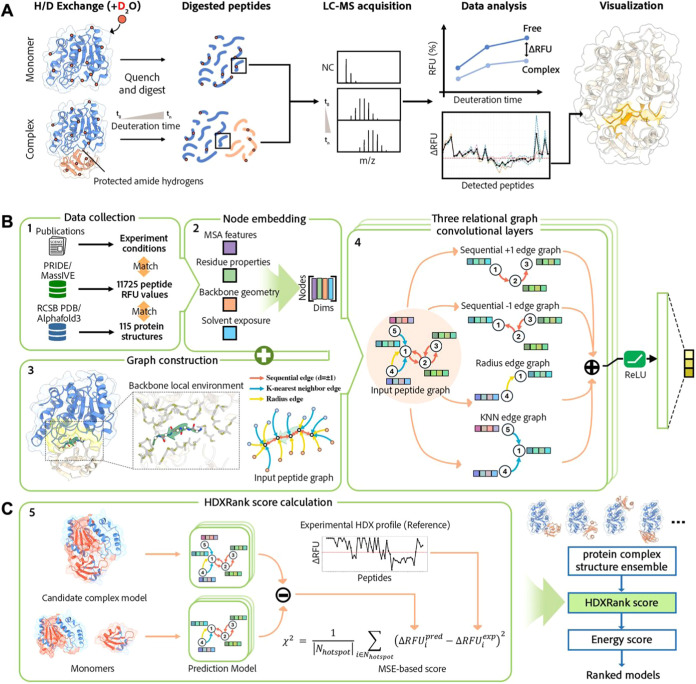
Hydrogen–deuterium exchange (HDX) is a nonspecific covalent labeling method, the combination of mass spectrometry makes it a widely used technique for probing protein backbone hydrogen accessibility and local flexibility. , In an HDX-MS experiment, proteins are exposed to a deuterated solvent, allowing exchange between amide hydrogens and deuterium, resulting in a detectable change in mass. After a specific exposure period, the protein is proteolyzed into peptide segments that are detected by mass spectrometry. Amide hydrogens that are more exposed to the solvent and not involved in strong interactions exchange more readily, while those in structured, buried, or hydrogen-bonded regions exchange more slowly. By comparing deuterium uptake patterns between free and bound states, HDX-MS provides insights into protein binding regions and structural changes upon complex formation (Figure A).
1.
Overview of the Principle of HDX experiment and the workflow of HDXRank. (A) Illustration of the mechanism for binding interface determination via HDX experiment. The receptor proteins (blue) in both free and ligand-bound states are exchanged with deuterium solution, the contacts between interface alter the solvent accessibility, resulting in a decreased deuterium uptake, which is captured by mass spectroscopy. The subsequent data analysis reveals the binding interface via calculating the differential relative fractional uptake (RFU) values among peptides. (B) HDXRank Workflow: Key steps involve data collection, node embedding, peptide graph construction, and model training. Peptides, annotated with experimental RFU values and structural information, are represented as expanded peptide-centered graphs to capture each peptide’s local structural and sequential environment. Sequential edges are limited to ± 1 distance for simplicity. Individual residues (nodes) are embedded using four distinct feature types. The constructed peptide graphs are processed by relational graph convolutional layers, generating RFU value predictions for three separate exposure-time clusters: short, medium, and long. (C) Workflow illustrating the two-step approach used in HDXRank for docking prediction refinement. Any computational docking algorithm can be used for the initial model ensemble generation. HDXRank score is calculated for each model based on its agreement with HDX experimental data. In the final step, energy-based scoring is used to further refine and prioritize near-native binding poses from the HDX-filtered models.
Currently, no standard integrative modeling protocol effectively utilizes HDX-MS information, and methods incorporating HDX-MS data into protein–protein docking vary across studies. These methods are generally exploited for sampling or model selection within traditional docking protocols. Accounting for HDX-MS data when sampling can provide a rough estimate for the complex interface and pinpoint binding hotspots. This can narrow down the search space during docking simulations, leading to more probable binding conformations. The second step, model selection, involves identifying near-native models from the ensemble of docking outputs. This remains a significant challenge for traditional docking protocols. Docking results are typically ranked using scoring functions that calculate a linear weighted sum of various energy terms. These weights are optimized on benchmark data sets to maximize ranking performance. − HDX-MS data can be used before the scoring process to filter out false-positive poses, as demonstrated in the docking of hUNG/UGI complex. In this approach, a predefined number of main-chain nitrogen atoms in the HDX-MS-detected peptides must be within 7 Å of any non-hydrogen atom in the contacting subunit. This filtering step enriches near-native decoys within the top predictions and improves the overall success rate. Simultaneously, an overly stringent interaction distance might exclude the correct configurations. Another strategy involves simulating HDX patterns for each model and quantitatively assessing their agreement with the experimental data. For instance, in the α-chymotrypsin/inhibitor eglin c docking case, HDX pattern was determined using phenomenological expression accounting only for hydrogen bonding and burial of amide groups. Comparing predicted with experimental patterns using a root-mean-square error (RMSE)-based metric effectively discriminated between near-native and incorrect binding poses. However, this approach is limited in its generalization due to incompleteness of predicted HDX behavior ,, and the use of scaling weights optimized on a limited set of globular proteins.
With the growing volume of HDX-MS data available in public mass spectroscopy databases like PRIDE and MassIVE, there is an emerging opportunity to apply deep learning to predict HDX patterns. Recently, Yu et al. have developed AI-HDX, a CNN-LSTM hybrid model for peptide-wise HDX relative fraction uptake (RFU) prediction. However, the AI-HDX model is trained on an apo protein data set, limiting its applicability to the ranking of protein complex predictions.
Here we present HDXRank, a graph neural network (GNN)-based scoring framework designed to rank predicted complex models according to their alignment with HDX experimental restraints. Our model was trained on a newly curated HDX-MS data set accounting for structural information from Protein Data Bank (PDB) and AF3 predictions. By representing protein structure as graph, HDXRank can predict HDX patterns for protein–protein complex across a diverse range of binding poses. This approach enables the calculation of an HDXRank score, a quantitative metric that evaluates how closely the HDX profile of a candidate model matches experimental data. Validation on four challenging protein docking tasks confirmed that this data-agreement-based scoring method can effectively distinguish near-native models from incorrect binding poses. Furthermore, the incorporation of the HDXRank score into general global docking workflows consistently improves prediction quality across all tested protein targets, addressing the limitations of traditional docking approaches. We also verified the effectiveness of HDXRank in prioritizing valid AF3 predictions for the SARS-CoV-2 spike protein/antibody complex. These results highlight HDXRank’s versatility for use with a variety of protein complex modeling tools and its ability to unify structural and experimental insights. HDXRank showcases its potential to accelerate therapeutic discovery and gain deeper insights into molecular recognition in complex biological systems.
Results
HDX-MS Database Curation
The primary obstacle in developing a deep learning model to predict protein HDX patterns, represented by peptide-wise Relative Fractional Uptake (RFU), is the limited availability of a well-curated HDX-MS data set paired with protein structural information. We address this by assembling a new data set from two public mass spectrometry databases, PRIDE and MassIVE, as of March 2024. To integrate structural information with the HDX-MS data, we mapped available crystal structures from the PDB to each protein in our data set. For instances without experimentally resolved structures, we generated prediction models using the AlphaFold3 server. The resulting data set includes 213 proteins from 13 species and 39 protein families, in free or bound states, comprising 21,799 peptides with their corresponding RFU values across time series (Figure S1).
We filtered the HDX-MS data set by selecting experiments conducted under standard conditions: pH 6.0–8.0, temperature 20–25 °C. To manage the variability in exposure times, we applied k-means clustering to the logarithm of peptide exposure durations. This resulted in three clusters representing short (log10(t) ≤ 1.35), medium (1.35 < log10(t) ≤ 2.85), and long exposure intervals (2.85 < log10(t)), with average RFU values of 27, 39, and 51%, respectively (Figure S2). Within each cluster, the RFU values for each peptide were averaged over grouped exposure times. Further analysis of RFU distribution relative to peptide length reveals that more than 85% of peptide fragments have RFU values between 0 and 0.7 and sequence length between 5 and 20 amino acids, indicating an imbalanced training data set (Figure S3).
HDXRank Framework
HDXRank is a biologically motivated framework for peptide RFU prediction based on the local environment, represented as a graph. HDX kinetics is highly dependent on peptide’s local unfolding equilibrium according to the general EX2 mechanism, reflecting the local stability influenced by different types of inter-residue interactions.
To capture this complexity of HDX patterns and reflect diverse geometric relationships, HDXRank encodes each protein structure as a residue-level relational graph, where each node corresponds to the α carbon atom of a residue. The graph incorporates three types of directed edges: radius edges, connecting residues within the spatial radius of 8 Å; K-nearest neighbor edges, linking the ten closest residues in 3D space; and sequential edges, consisting of five unique edges that connect residues with sequence distances of −2, −1, 0, 1, and 2, each treated as a separate edge type to capture specific sequential proximities. For each peptide segment detected in the HDX-MS experiment, the entire protein graph is divided into subgraphs centered on each containing residue nodes. The 1-hop neighboring nodes connected to the central nodes are included in each subgraph to represent the local environment (Figure B). The node representation was constructed from multiple encodings including multiple sequence alignment (MSA) against UniProt, residue properties, backbone geometry, and solvent exposure, forming a 56-dimensional vector, as described in the Materials and Methods section.
HDXRank is based on a GeomEtry-Aware Relational GNN (GearNet) model architecture for subgraph representation learning. In this architecture, a convolutional kernel matrix is shared across each edge type, allowing for efficient feature propagation specific to each relationship. The initial node representation is iteratively updated by aggregating features from neighboring nodes according to the edge type. After three relational convolutional graph layers, the aggregated graph representation is summed and passed through a linear transformation layer to output the final predictions (Figure B). Different from the original GearNet model, which is trained on entire protein graphs, the HDXRank model is based on peptide-centered subgraphs utilizing sequential and structural features tailored for RFU prediction. This adaptation allows HDXRank to accurately capture the local environment information relevant to the HDX-MS data.
We compared two model training strategies: training separate models for each of the three RFU exposure-time clusters individually versus training a single combined model to predict RFU values for all clusters simultaneously. The combined data set used for simultaneous training consisted of the intersection of peptides common to all three clusters, resulting in a total of 7785 peptides from 40 apo proteins and 25 protein complexes. For each category (apo proteins and complexes), 80% were assigned to the training set, and the remaining 20% were used for validation.
We trained five independent models for each strategy using different random seeds, with final predictions obtained by averaging the outputs from these models.
To validate HDXRank’s prediction accuracy, we conducted tests on an independent set of eight proteins selected from our HDX-MS data set. These test proteins, consisting of 1250 peptides from three apo proteins and five complex proteins, show no significant sequence similarity to the training data set (Figure S4). We assessed the model performance for each exposure-time cluster by using corresponding predictions from the combined model. The combined training approach exhibited improved RMSE and Spearman’s rank correlation (rho) for clusters 0 and 1 and comparable performance for cluster 2 (Figure S7).
For comparison, we also trained two additional graph-based models, graph attention neural network (GAT) and geometric vector perceptron (GVP). HDXRank consistently outperforms these models on the test set, achieving an average RMSE of 0.233 and a rho of 0.553 for cluster 1 (Figures B and S9 and Tables S1–S3). This highlights HDXRank’s superior strength to capture diverse geometric relationships important for accurate RFU prediction. Notably, while all models achieved a rho exceeding 0.60 on the training data set, this result also reflects a degree of overfitting (Figure S6), affecting the model’s generalization to new proteins. Additionally, the imbalanced training data set, characterized by a scarcity of RFU values above 0.7, introduces a bias toward lower RFU predictions (Figures A and S9).
2.
Evaluation of the HDXRank model performance. (A) Scatter plot depicting the true RFU value (x-axis) from cluster 1 against the prediction (y-axis) given by HDXRank for the training (orange) and test (blue) sets. The distance from each sample point to y = x represents the discrepancy between its predicted RFU and the real value. Marginal histograms along the top and right provide the distribution of true values and predicted values, respectively, for both data sets. See also Figure S9 for plots of baseline models. (B) Quantitative evaluation of model performance in terms of Spearman’s ranking correlation (rho) and root-mean-square error (RMSE) on the test set containing eight proteins. Boxes show interquartile ranges while the solid lines within each box represent the median, and the dashed line represents the mean. Whiskers cover up to 1.5 times the interquartile range, while circles represent outliers beyond that. See also Tables S1–S3.
Despite these limitations, HDXRank demonstrates sensitivity to structural context, effectively learning the underlying relationship between peptide local environments, node feature, and RFU values. We evaluated feature importance separately for each of the three RFU prediction by SHAP analysis. The results consistently identified the MSA-derived features as the most significant contributor across all predictions, followed by SASA and backbone dihedral angles (Figure S10). These top-ranked features capture key evolutional signals and reflect critical structural variations in the protein–protein binding poses. This enables HDXRank to transform diverse structure predictions into distinct HDX profiles for direct comparison. By integrating both sequence-derived and structure-sensitive features, HDXRank provides a biologically relevant framework for the HDX-informed ranking of protein complex models.
HDXRank Score-Integrated Docking Protocol Enhances the Prediction Quality
Protein–protein docking is a classical strategy to generate complex predictions, considering the steric and physicochemical complementarity at the protein–protein interface. We hypothesized that diverse docking poses could be differentiated by mapping them to distinct HDX patterns by using the trained HDXRank model. By subtracting the common native monomers’ HDX patterns from each docking pose’s HDX pattern, we generated a differential HDX (ΔRFU) pattern that highlights the binding interface. This ΔRFU pattern was compared to experimental data, enabling the calculation of an HDXRank score using a mean square error (MSE)-based metric for docking prediction ranking (Figure C).
To minimize interference from noninterface residues, we calculated the HDXRank score exclusively for HDX-identified hotspot residues. These were defined as residues within peptide segments where ΔRFU values were below the mean of all negative ΔRFU experimental data, as detailed in the Materials and Methods section. This hotspot filter step retains potential interface residues with significantly reduced RFU values. Notably, most of the hydrogen bond- or salt bridge-forming residues identified by the FIRST program , within the complex interface met our HDX hotspot criteria (Table S6: 1UGH: 85.7%; 6DJL: 57.4%; 8A0E: 60.5%; 8F7A: 78.3%), supporting the effectiveness of this approach.
We selected four protein complexes as docking targets, each with complete HDX-MS experimental data for both free and ligand-bound states, along with an elucidated complex crystal structure. The benchmark set includes the inhibitor bound uracil-DNA glycosylase (UGI/UDG, heterodimer, PDB ID: 1UGH), the Ras-related protein Rab-11a bound to SH3 domain-binding protein 5 (Rab11a/SH3BP5, heterodimer, PDB ID: 6DJL), eukaryotic translation factor 5A bound to deoxyhypusine synthase (elF5A/DHS, PDB ID: 8A0E), and GTP-binding nuclear protein GSP1 bound to importin-9 (IMP9/GSP1, PDB ID: 8F7A) (Table ). For each target, we first performed global docking with HDOCKlite to generate 4392 candidate structures. These were subsequently scored by HDOCKlite scoring function and clustered by 5 Å RMSD. The top 1000 decoys according to clustering were included in the global docking model set. To enrich near-native models, we perturbed each native complex structure with 5 Å translation and 15-degree rotations using RosettaDock protocol, resulting in an additional 1000 near-native models. The final model set contained 2000 predictions, spanning a wide range of model quality (Figure A).
1. Docking Conditions for Protein–Protein Complex Modeling.
| reference
complex |
starting receptor |
starting ligand |
||||||
|---|---|---|---|---|---|---|---|---|
| PDB ID | resolution (Å) | PDB ID | resolution (Å) | RMSD | PDB ID | resolution (Å) | RMSD | reference HDX exposure time (s) |
| 1UGH | 1.90 | 1AKZ | 1.57 | 0.293 | 1UGI | 1.55 | 0.553 | 1000 |
| 6DJL | 3.10 | 1OIX | 1.70 | 0.520 | 6IXE | 3.35 | 2.516 | 30 |
| 8A0E | 2.80 | chain A | chain B | 10,000 | ||||
| 8F7A | 3.78 | chain ABCD | chain E | 1000 | ||||
3.
HDXRank score-integrated docking protocol enhances the prediction quality. (A) Distribution of the ligand RMSD for near-native models (light orange) and global docking models (light blue). The bars are stacked to represent the total distribution. (B) Scatter plots of HDXRank score versus ligand RMSD, demonstrating a positive correlation. Models in the combined set are categorized into four quality groups according to DockQ evaluation: incorrect (blue), acceptable (teal green), medium (dark yellow), and high (rusty orange). See also Figures S11 and S12 for scatter plots of other scoring functions versus ligand RMSD for the global docking set and near-native set. (C) Violin plot showing the distribution of HDXRank scores for models within the four quality categories. The median HDXRank score increases as model quality decreases. See also Figure S13 for a comparison of hit discovery count across scoring functions. (D) Integration of the HDXRank score into the docking protocol improves prediction quality. 1000 global docking models were ranked by three energy-based scores, Rosetta energy (left), ZRank (middle), and ZRank2 (right), with and without HDX information. The ligand RMSD distributions for top 10-ranked models across four protein complexes (1UGH, 6DJL, 8A0E, and 8F7A) are shown. Blue dots represent results with HDXRank-based filtering, while orange dots represent results without HDX filtering.
We computed the HDXRank score for each model in the docking set and assessed its correlation with the ligand root-mean-square deviation (ligand RMSD, LRMS). For the reference experimental HDX data, we selected the exposure time that maximizes the ΔRFU signal, which highlights the binding interface (Table ). The HDXRank scores were calculated using model predictions corresponding to the relevant exposure-time cluster (short, medium, or long).
The results indicate a strong association between HDXRank score and model quality, as illustrated in Figure B. Specifically, two proteins (PDB ID: 1UGH and 8A0E) showed high correlations with rho above 0.75, while the other two proteins (PDB ID: 6DJL and 8F7A) displayed moderate correlations with rho above 0.50 (Table S7).
Docked models were then categorized into four quality groups based on DockQ score: incorrect (DockQ < 0.23), acceptable (0.23 ≤ DockQ < 0.49), medium (0.49 ≤ DockQ < 0.80), and high (DockQ > 0.80). The average HDXRank score was calculated for each quality category across the four protein docking sets. The high-quality class had the lowest average HDXRank score at 0.104, with scores increasing as model quality decreased (medium: 0.138, acceptable: 0.215, and incorrect: 0.496, Figure C). This trend shows that the HDX pattern gradually diverges from the native as model quality deteriorates. Particularly, models above the acceptable quality threshold had distinctly lower HDXRank scores compared to the ones with poor quality, indicating HDXRank’s strong discrimination ability.
The global docking prediction set exhibited a strong bias in the ligand RMSD distribution, with most models skewed toward incorrect poses and relatively few near-native solutions (Figure A). This bias indicates a reduced probability of identifying correct solutions among top-ranked models. Relying solely on global docking, the scarcity of acceptable or higher-quality models significantly hinders the performance of energy-based scoring functions. The state-of-the-art scoring functions, such as ZRank, ZRank2, and Rosetta energy, show decreased rho under these conditions (Figure S11 and Table S7).
In contrast, HDXRank provides an energy-free quality assessment, accounting for structural variations in different binding poses and translating them into the simulated HDX pattern. A close match between the simulated and experimental HDX profiles suggests spatial alignment between the docked and actual ligand positions. We hypothesized that the HDXRank score-based selection could prioritize certain energetically unfavored poses when the ligand is positioned close to the binding region. We examined the top 5 models ranked by HDXRank score from 1000 global docking predictions, and compared them to the top 5 models ranked by other state-of-the-art scoring functions (ZRank, ZRank2, and Rosetta energy) (Figure ). Generally, HDX-identified hotspot residues roughly align with the interface residues in the native crystal structures. Since HDX-MS is a low-resolution technique that provides information solely at the peptide level, additional noninterface residues within the same hotspot peptide segment may be potentially included, broadening the identified hotspot region, as noted in Table S6. Despite this coarse-grained binding region information, HDX-guided selection narrowed the binding poses. The top 5 predictions ranked by HDXRank score consistently aggregated around the binding site in three proteins (Figure B: 1UGH, 6DJL, and 8F7A). In contrast, energy-based scoring functions, ZRank, ZRank2, and Rosetta energy, prioritized more diverse binding poses spread across the receptor surface (Figure C–E).
4.
Visualization of top 5 ranked docking models according to different scoring functions. (A) HDX-MS-identified hotspot regions are mapped onto the crystal structures, with receptor regions highlighted in blue and ligand regions in red. These hotspot regions align with the interface in the native crystal structures. For protein 8A0E, the same hotspot residues within two identical subunits are colored blue and purple, respectively, forming an interfacial binding pocket. (B–E) Comparison of the top 5 models (from a pool of 1000 global docking models) ranked by (B) HDXRank score, and the top 5 models ranked by other scoring functions: (C) Rosetta energy, (D) ZRank, and (E) ZRank2. The HDXRank score-ranked top 5 poses cluster near the binding interface, while the top 5 poses ranked by other scoring functions are more dispersed across the receptor surface.
To leverage the strengths of both evaluation methods, we implemented a two-step approach for model selection, where the HDXRank score is applied as a prefilter before classical energy scoring functions (Figure C). By assessing the compatibility of each model with HDX experimental data, HDXRank score ensures that functional-relevant models are retained for subsequent energy-based evaluation. We applied this strategy on four docking instances, where the top 100 models ranked by the HDXRank score were further reranked using three different energy scoring methods. We examined the top 10 predictions with and without HDXRank score-based prefiltering. In almost all cases, HDX-assisted ranking achieved a lower average ligand RMSD compared with methods relying solely on energy scores (Figure D). These findings highlight the effectiveness of integrating HDX data into protein–protein docking workflows, resulting in a more accurate near-native model identification.
HDXRank Prioritizes Functionally Relevant AF Models of SARS-CoV-2 Spike Protein/IcoHu23 Complex
Encouraged by the successful validation of HDXRank on docking tasks, we evaluated its capacity for ranking predictions from other sources. The recent advent of AI-driven protein structure prediction, particularly AlphaFold, has revolutionized the field by achieving unprecedented prediction accuracy. The latest version, AlphaFold3 (AF3), has achieved significant advance in predicting antigen/antibody complexes, with over 60% success rate reaching acceptable quality (DockQ score > 0.23) when sampling 1000 random seeds. However, the application of this strategy comes at a substantial computational cost. Furthermore, the ipTM confidence metric, which is an alignment-based measure of interface accuracy, was found to be less effective within the range of 0.6–0.8, leading to ambiguity in model selection. We hypothesized that integrating an HDX-assisted ranking process could efficiently identify acceptable models from predictions generated with a reduced number of seeds.
The spike protein of the SARS-CoV-2 virus plays a crucial role in mediating viral entry into human cells. This trimeric protein, composed of three identical chains, consisted of two primary subunits: S1 and S2. The S1 subunit contains the receptor-binding domain (RBD, R319–F541), which is responsible for recognizing and binding to the host cell receptor. The S2 subunit facilitates the fusion of viral and cellular membranes. A recently identified antibody, icoHu23, discovered by Hermet et al., exhibits capacity to bind to the SARS-CoV-2 spike protein. HDX data were collected for the spike protein in both the apo and antibody-bound state. We used this instance to test HDXRank ability to refine AF3-generated predictions for the complex of the SARS-CoV-2 spike protein/Fragment antigen binding region (Fab) of icoHu23.
We generated 50 AF3 predictions utilizing 10 random seeds for sampling initialization; following that, using ligand RMSD, we grouped candidate models into seven distinct clusters (Figure S14). The clustering results revealed highly distributed binding epitopes (Figure A). Among the identified epitopes, the majority of antibodies were predicted to bind to the fusion peptide (FP, I788-L806) and heptapeptide repeat sequence 1 (HR1, T912-L984) regions within the S2 subunit (Cluster 5–7). In contrast, other antibodies were shown to bind to the RBD regions across three chains (Clusters 1 and 3) or to the central hole formed by the triple RBD contact (Cluster 4).
5.
Ranking of AF predictions of the SARS-CoV-2 spike protein and Fab icoHu23 complex. (A) Structural representation of the SARS-CoV-2 spike protein and Fab-bound models predicted by AF3. The left panel overlays the predicted antibody models on the apo SARS-CoV-2 spike protein, while the right panel depicts the whole spike protein structure. The antibodies are colored according to their respective clusters in (B). Key contact regions in the spike protein are indicated by different colors, including the N-terminal domain (NTD, light blue), receptor-binding domain (RBD, red), fusion peptide (FP, purple), and heptapeptide repeat sequence 1 (HR1, dark green). Additionally, HDX-identified epitopes (C432-Y449, T470-V510, S514-L533) are highlighted in blue. (B) Hierarchical clustering of 50 AlphaFold3 (AF) predicted models generate seven clusters based on ligand RMSD, see also Figure S14. Each model is labeled as “Seed X_Model Y” (e.g., S1_M0) and scored using HDXRank. The mean HDXRank scores for each cluster show a correlation with the mean DockQ scores, as illustrated in the scatter plot. Cluster 3 highlighted by star shape exhibits the highest DockQ score. (C) Superimposing of RBD region of AF3 model S5_M1 (light gray) and crystal structure (PDB: 8ELJ, gray), HDX-identified hotspots are labeled in blue in crystal structure. Structural inspection reveals a crucial polar interaction network present in both the Fab crystal structure (cyan, PDB: 8ELJ) and the Fab AF3 prediction (orange, S5_M1).
The HDXRank framework was used to assign scores to each AF3 prediction by comparing their predicted RFU profiles to HDX-MS data collected at a 60 s exposure time. Each binding mode was evaluated by averaging the HDXRank scores within the same cluster. The results revealed a remarkably strong correlation between the averaged HDXRank score and the averaged DockQ score (Figure B). This result demonstrates the effectiveness of HDXRank in transforming the HDX profile alignment into a meaningful model quality metric. On the other hand, the ipTM values of spike protein/Fab icoHu23 models fell within a narrow and ambiguous range between 0.72 and 0.75 (Figure A). The mean ipTM values of acceptable models (DockQ score > = 0.23) and inaccurate models (DockQ < 0.23) were 0.738 and 0.735, respectively, demonstrating inability to discriminate the correct binding mode.
Further inspection of the two models from the top-ranked Cluster 3 reveals a conserved interfacial polar interaction network, observed in both models S5_M1 (DockQ:0.35, Figure C) and S5_M2 (DockQ: 0.28). These interactions, involving key residues E484 in RBD interacting with Y33 and N52 in the Fab VH chain, are also present in the reference crystal structure (PDB: 8ELJ). This conserved network plays a central role in the binding of the icoHu23 antibody and explains the loss of affinity to the Omicron variant, which contains the function-disruptive E484A mutation. It should be noted that the S5_M1 model has slightly shifted positions of Y33 and N52, indicating a modified polar contact network. This subtle deviation suggests that further refinement of the binding interface may be necessary to more accurately capture the molecular interactions in detail.
Overall, our results demonstrate that HDX experimental data can be effectively integrated as restraints to enhance the quality of protein complex predictions from various sources, including docking and deep learning-based methods. The energy-free, experimentally informed HDXRank scoring function exhibits robust performance across diverse ranking tasks, establishing itself as a flexible and reliable framework for integrative protein modeling. By leveraging HDX data to prioritize biologically relevant protein complex models, we have the potential to reduce computational demands while maintaining high-quality predictions.
Discussion
Various experimental restraints have been successfully incorporated into computational modeling workflows to improve protein complex prediction accuracy. For example, 1v1 and MvN types of distance restraints from XL-MS have been integrated into the ColabDock with AF2 predictions. Unlike the precise distance restraints from XL-MS that detect specific residues or peptide pairs, HDX-MS offers broader, more ambiguous restraints at the protein complex binding interface. The fast and straightforward HDX-MS protocol enables high-throughput detection of protein complexes in their native state, with deuterium labeling exerting minimal perturbation of the structural conformation. This gives HDX-MS a unique advantage when preserving the native state is essential.
Previous integrative docking protocols utilizing sparse HDX-MS data lack a standardized framework applicable to different proteins as well as a comprehensive simulation of HDX behaviors. To address this gap, we developed HDXRank, a GNN-based scoring framework that incorporates HDX-MS experimental restraints into protein complex modeling workflows. A newly curated data set, combining HDX-MS experimental data with protein structural information, enabled us to create an HDX pattern prediction model. We demonstrated that the experimentally informed HDXRank score can efficiently discriminate near-native models from decoys. Incorporating the HDXRank score filtering step into general global docking protocols enriched near-native models within top predictions for all test protein targets. HDXRank supports arbitrary model ensembles from classical docking methods such as FFT (fast Fourier transformation)-based − and MCMC (Markov Chain Monte Carlo) based docking method, , as well as deep learning-based protein structure prediction models. Correct ranking of AF3-predicted models for spike protein/antibody complexes demonstrates the versatility and effectiveness of HDXRank.
The false-negative results, where energetically unfavorable poses are discarded despite their proximity to the correct binding position, are common issues in rigid-body docking. These errors often arise when significant conformation changes occur upon complex formation or when inaccurate side chain packing is present in starting models. Such side chain inaccuracies are particularly notable in AF predictions, where 7–20% of side chains in models with pLDDT scores above 70 are incompatible with experimental data. For these cases, interface modeling errors hinder the performance of energy-based scoring functions. HDXRank score is a new alternative for handling these instances. For example, in the docking case of Rab11a/SH3BP5 (PDB ID: 6DJL), the ligand SH3BP5 (PDB ID: 6IXE) exhibited an RMSD of 2.516 Å from the bound state. This discrepancy led to incorrect evaluation of global docking predictions by energy-based scoring functions (Figure S11). HDX-MS data for Rab11a/SH3BP5 suggest potential binding regions of T32-I64, Y80-L89, and N101-E108 on Rab11a, as well as V41-L77 and Q233-M252 on SH3BP5. These experimentally derived restraints, incorporated into HDXRank, prioritize experimentally supported binding modes when conventional energy-based scoring functions prove insufficient (Figure A: 6DJL).
An exception was the complex elF5A/DHS (PDB: 8A0E), where the HDXRank score-based ranking proved challenging. In this case, the receptor protein DHS comprises four identical protomers symmetrically arranged to form four binding interfaces between protomers. While three of these binding pockets in the complex elF5A/DHS structure are naturally blocked by N-terminal helix motifs (A11–V17) within each subunit, the remaining pocket is accessible for elF5A binding. HDX-MS data reveal HDX reductions in the elF5A binding pocket of DHS (T104–Y118, V129–L183, I266–M278, and G282–L295) and the active site loop (I306–S344). However, HDX-MS cannot discriminate peptides from identical chains, resulting in all binding pockets being identified as hotspots across the subunit surfaces (Figure B: 8A0E). This ambiguity in HDX-MS data made it difficult for the HDXRank score to correctly differentiate between the predictions.
Currently, HDXRank is designed for ranking protein–protein complex models, as the limited availability of HDX-MS data for protein-nucleic acid (NA) or protein-small-molecule interactions restricts its applicability to these systems. Expanding the HDX-MS data set to encompass a wider range of molecular interactions could pave the way for adaptations of HDXRank to diverse biological systems. Moreover, the HDXRank framework, which integrates sparse protein structural information into protein modeling workflows, can account for data from other experimental techniques such as Nuclear magnetic resonance (NMR), cryo-electron microscopy (Cryo-EM), and small-angle X-ray scattering (SAXS). Incorporating multisource experimental measurements into the protein complex modeling process has the potential to establish a unified integrative modeling framework. When combined with high-throughput wet-lab techniques, such a framework could accelerate therapeutic biomolecule design and verification, significantly advancing drug discovery and development efforts.
While HDXRank demonstrates strong potential for protein complex model selection by integrating HDX-MS data, several limitations should be acknowledged. One key limitation is that HDX-MS typically provides data at the peptide level, which constrains HDXRank’s ability to discern subtle differences among near-native models. Various analytical techniques have been developed to enhance HDX-MS resolution to the residue level. , Additionally, tandem MS with peptide fragmentation techniques, such as electron capture dissociation (ECD) or electron transfer dissociation (ETD), can produce more detailed deuterium uptake maps. Alternatively, Nuclear Magnetic Resonance (NMR) can detect chemical shifts of backbone amide groups in different chemical environments, allowing residue-resolved measurements of HDX rates. However, backbone NMR is typically restricted to small proteins due to challenges in spectral resolution and signal sensitivity in larger systems. Another limitation lies in the interpretation of differential HDX-MS signals, which may reflect allosteric effects rather than direct binding interactions. Allosteric conformational changes can influence HDX behavior in regions that are distant from the binding interface. Reducing HDX labeling time to the millisecond range may help suppress allosteric effects and improve interface specificity for detecting the true interface contacts.
Although not explored in this study, HDX data could also be used to assess the biological relevance of interfaces in crystal structures, by comparing HDX-identified contact regions with those observed in the resolved structures, complementing existing computational methods. ,
While HDXRank has demonstrated strong performance in ranking protein complexes based on RFU profiles, predicting RFU values at arbitrary time points remains difficult due to the time-dependent nature of the measurement. An alternative approach could be to model protection factors, which are time-independent and reflect intrinsic exchange rates corrected for structural and sequence context. Predicting protection factors may provide a more general and robust strategy for modeling HDX behavior across different experimental setups.
Materials and Methods
Data Set
The HDX-MS data utilized in this study were sourced from public databases, PRIDE (https://www.ebi.ac.uk/pride/) and MassIVE (https://massive.ucsd.edu/ProteoSAFe/static/massive.jsp) up to March 2024. A comprehensive data set comprising 105 proteins from 61 experiments was compiled. The included proteins were distributed across 19 species and 154 known protein families (Figure S1). Each result table contains the experimental HDX rates for individual peptides generated from HDX-MS. The database was trimmed by eliminating duplicate entries for the same protein across different HDX experiments, the data set with higher sequence coverage was retained. We gathered detailed experimental conditions including protein states, reaction pH, reaction temperature, and deuterium concentration from published studies for each HDX-MS experiment, and linked this metadata to each HDX-MS entry. As experiment pH and temperature will influence the HDX rate, we filtered the database that is out of the standard experiment condition (pH 6–8, temperature 20–25 °C).
We directly use the data from the original literature utilizing Relative fractional uptake (RFU) values; otherwise, we estimate the RFU value from the experiment condition and a back-exchange correction factor of 0.7 according to eq . The back-exchange ratio should not exceed 50% in a well-conducted conventional state-of-the-art bottom-up HDX-MS workflow, and we take a value of 30% same as in the previous work.
| 1 |
where U(t) is the deuterium uptake of the peptide M at specific time point t, c D is the final concentration of deuterium in solution, N(M) is the exchangeable number of amide hydrogens in peptide M which equals the residue numbers excluding the first residue at N-terminal and prolines, and F is the back-exchange correction factor.
The relative fractional uptake (RFU) data is usually obtained at several different time points ranging from seconds to hours, to eliminate the variance in collected data, we clustered all experimental RFU values according to the peptide exposure time based on the k-means clustering method (Figure S2), It resulted in three clusters that represent the short, medium, and long exposure intervals in our HDX-MS data set, containing 7478, 9361, and 7904 unique peptide segments, respectively. The final RFU values were averaged over different exposure time points within the same group. The respective data group shows clearly divergence in RFU distribution, with a mean RFU of 27, 39, and 51% for groups 1, 2, and 3. These three RFU clusters showed an increasing trend in mean RFU value when the peptides were exposed to deuterium solution for a longer time. We use the second cluster with middle deuterium exposure time ranging from 0.5 to 10 min for model training and evaluation, as this cluster contains the largest number of RFU values.
Protein Structure Modeling
The protection level of amide proton in protein backbone is closely associated with the protein’s structure and dynamics. To extract additional insights, we matched each protein in the data set with either crystal structure or AlphaFold3 (AF3) prediction. For experimental structures, we used the structures explicitly referenced in the original HDX publications. In cases in which no structure was mentioned, we retrieved available PDB entries using the corresponding UniProt ID and selected the structure with the highest sequence coverage and best available resolution to ensure reliable mapping of HDX data. Among the generated AF3 models, the top-ranked model was chosen as the representative structure, assuming that it reflects the most confident backbone prediction. To ensure structural plausibility, all AF3-predicted structures were screened to confirm the absence of atomic clashes before inclusion in the training set. The source of each structural model used in this study is documented in the Supporting Information.
The protein structure models were subsequently matched with peptides from the HDX-MS data set. Peptides were excluded if their sequences did not align with the structure models or if the structure was discontinuous in the corresponding region. This approach ensures the generation of a well-aligned HDX-MS data set and structure model, facilitating accurate protein representation feature extraction and enabling effective training of deep learning models.
Protein Representation
Proteins were represented by a feature matrix comprising 4 types of scalar value: multi-sequence alignment (MSA) encoding, residue properties, solvent exposure features, and backbone geometry features, as outlined in Table . Protein primary sequences were sourced from UniProt and then aligned against the UniProt Reference Clusters (UniRef30_2020_06) using HHblits, producing a 30-dimensional encoding for each residue that captures evolutionary similarities.
2. Features Used in Graph Node Embedding.
| feature type | residue properties | solvent exposure | MSA encoding | backbone geometry |
|---|---|---|---|---|
| feature name | HDMD | SASA | Hhblits | dihedrals |
| charge | HSE | orientations | ||
| polarity | ||||
| dimensions | 10 | 4 | 30 | 12 |
Solvent exposure information was derived from solvent accessible surface area (SASA) and half-solvent exposure (HSE) values extracted from protein structures. Residue properties were encoded with high-dimensional molecular data (HDMD), and dimensionality was reduced to five using principal component analysis as described in previous work. Residue charge is represented by the net charge for each amino acid type, while residue polarity was encoded using one-hot encoding across four categories: negatively charged, positively charged, nonpolar, and polar.
In addition, we incorporated a structural backbone representation, as utilized in the GVP model. Consecutive dihedral angles of the protein backbone, along with residue orientations, were embedded together with the other features to create a comprehensive protein embedding matrix with dimensions [N, 56], where N represents the protein sequence length.
Protein Graph Construction
We adapt the protein graph representation from GearNet which constructs a residue-level relational graph , where and denote the set of nodes and edges, respectively, and R is the set of edge types. Each node in the protein graph represents the α carbon of a residue with the embedding matrix of all nodes , the coordinates for all nodes were noted as . Three sets of directed edges are incorporated into protein graphs: sequential edges, radius edges, and k-nearest neighbor (KNN) edges. Specifically,
| 2 |
| 3 |
| 4 |
| 5 |
where dseq = 3 defines the sequential distance threshold, referring to residues that are sequentially neighboring within 3 positions along the protein chain. d radius = 8Å defines the spatial distance threshold, and knn(i) indicates the K-nearest neighbors of node i with k = 10. For sequential edges, edges with different sequential distances are treated as different types. For radius edges, we tested three different cutoffs of 5, 8, and 10 Å and determined 8 Å as the most well-performing cutoff in our data set (Figure S5). In total, 7 different edges were included in protein graph, which capture a comprehensive geometry relationship in protein structure.
Definition of Peptide-Level Microenvironment
The microenvironment of a peptide describes its surrounding chemical and geometric features based on the sequential and structural contexts. Formally, let be a protein graph corresponding to the entire protein structure. For peptide M identified by HDX-MS experiment, let represent the set of residues constituting this peptide. We define the microenvironment E M of peptide M as the -centered subgraph of the protein graph with its node set defined as
| 6 |
and the edge set defined as
| 7 |
Graph Neural Network (GNN) Model for HDX Prediction
HDXRank framework leverages a Graph Neural Network (GNN) to predict HDX patterns by modeling protein structures as relational graphs. Given the protein graph , where and denote the set of nodes and edges, respectively, and R is the set of edge types. Each node is assigned an initial vector h v that encodes residue features, including multi-sequence alignment (MSA) encoding, residue properties, solvent exposure features, and backbone geometry features.
For the general GNN framework, the model aims to learn a representation of input graph. They exploit the message-passing mechanism in which each node updates its representation by aggregating information on its 1-hop neighboring nodes. For each layer l, the hidden states of node v, denoted h v , are updated as follows:
| 8 |
| 9 |
where N(v) represents the neighbors of node v, Aggregate is a message function that aggregates information among neighboring nodes and passes to the Update function to generate the updated hidden state h v .
For specific implementation, we applied relational graph convolutional layer to learn a representation of the subgraph for each peptide. A convolutional kernel matrix is shared within each edge type, and there are |R| different kernel matrices in total. Aggregate and Update functions in the relational graph convolutional layer are defined as
| 10 |
| 11 |
where denotes the neighborhood of node v with the edge type r, and W r denotes the learnable convolutional kernel matrix for edge type r. BN denotes a batch normalization layer, and σ is the nonlinear activation ReLU function.
After L layers of message passing, the final node representations for each node v are formed by concatenating its hidden states across all layers. The resulting concatenated vectors are then summed to form the graph level representation h G that summarizes the peptide information:
| 12 |
| 13 |
This graph representation h G is then passed through a linear layer and a sigmoid activation function to predict the RFU value for peptide M.
Model and Evaluation
The model consists of 3 layers of relational graph convolutional layers, and the dropout rate was set to 0.5 for preventing overfitting. The training of this model uses the binary cross-entropy loss function, optimized with the Adam optimizer set at a learning rate of 5 × 10–4 and a weight decay of 5 × 10–4. To improve training stability and generalization, we applied a cosine learning rate scheduler, which gradually decreased the learning rate from 5 × 10–4 to 1 × 10–6 over 100 training epochs.
The HDX-MS data set was clustered based on exposure time into three groups. To train a unified model across all three exposure-time clusters, we constructed a combined training set by taking the intersection of peptides shared across all of the clusters. This combined data set was randomly split into a training set (80%) and a validation set (20%). The model was trained to predict three RFU values simultaneously, corresponding to the short, medium, and long exposure clusters. To ensure robustness, each training setup was repeated five times using different random seeds, and the final prediction was obtained by averaging results across all five models.
HDXRank Score
The binding region can be identified based on HDX reduction defined by ΔRFU. ΔRFU is calculated by taking the difference between RFU in complex and RFU in apo:
| 14 |
HDXRank score (χ2) evaluates the difference between the experimental ΔRFU and HDXRank prediction. It is determined as follows:
| 15 |
where N hotspot = {i|ΔRFU i < mean(ΔRFU j |ΔRFU j < 0)} is defined as a set of peptides with the experimental ΔRFU values below the mean of all negative ΔRFU values. This hotspot criterion filters out residue sites that do not belong to the binding interface.
Generation of Protein Complex Docking Set and Energy-Based Scoring
To generate a comprehensive docking set containing models with diverse quality, we applied both rigid-body global docking and local docking. To produce models with a different range of binding modes, we exploited FFT-based rigid-body docking program HDOCKlite. Utilizing a 15° angle interval for rotational sampling and a 1.2 Å grid spacing for translational sampling, we produced approximately 4,392 binding modes per run. For each rotation, the top 10 translations with the best shape complementarity are further refined by using iterative knowledge-based scoring functions. Binding modes are clustered with a 5 Å RMSD cutoff. Highest-scoring modes within each cluster are retained. The top 1000 predictions were selected as the blind docking set.
To produce near-native models, we utilized local docking only. It was performed using the Monte Carlo-based RosettaDock protocol. , Initial orientations were generated by superimposing the receptor and ligand on the native crystal structure, followed by local docking with random perturbations. Perturbations were controlled using the -dock_pert flag: 5 Å translation and 15° rotation for targets 1UGH, 6DJL, and 8A0E, and 1 Å translation and 15° rotation for target 8F7A. This produced a 1000 near-native model set.
To rank the generated docking models, we applied three energy-based scores, each model was evaluated using ZRank, ZRank2, and Rosetta energy score (REF15), which assesses the stability of binding poses accounting for van der Waals forces, electrostatic interactions, and hydrogen bonding. Hydrogen atoms were added to protein structures before scoring by HBPLUS v.3.06 software.
Docking Models Evaluation
The quality of the docking models was quantitatively assessed using ligand root-mean-square deviation (LRMS), interface root-mean-square deviation (iRMS), and the fraction of native interactions (Fnat) relative to the native crystal structure, calculated for each model using the DockQ Python package. LRMS measures the root-mean-square deviation of the backbone atoms of the shorter chain (ligand) after superposition onto the longer chain (receptor) in the model. iRMS evaluates the root-mean-square deviation of the backbone atoms of the interface residues relative to their equivalents in the predicted complex. Fnat represents the fraction of native interfacial contacts preserved within the predicted interface.
Shapley Value-Based Feature Importance
Shapley values are a widely used approach from cooperative game theory to explain machine learning models by fairly allocating credit for the output, f(x), among its input features. The Shapley value for a feature j is calculated as the average marginal contribution relative to all possible coalitions of features. Mathematically, the Shapley value ϕ j for feature j is defined as
| 16 |
where S is a subset of the input features, j is the feature under consideration (j = 1,···,p). val(S) represents the model prediction for the feature subset S, with the contributions of features not included in set S marginalized.
For this analysis, Shapley values were computed for 2000 randomly selected graphs from the training set. The global mean of each feature across the data set was used to estimate the expected model output when marginalized over the remaining features. It is important to note that while Shapley values provide a quantitative measure of feature contribution to model predictions, they do not explain the causal relationship between features and the truth.
Supplementary Material
Acknowledgments
The authors thank Dr. Francois Berenger for the helpful discussions regarding the article.
All original code has been deposited at Github at https://github.com/tsudalab/HDXRank.git and is publicly available as of the date of publication. The collected HDX-MS data set has been deposited on Zenodo and can be accessed at 10.5281/zenodo.14625492. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.5c00175.
Analysis of proteins in HDX-MS data set (Figure S1); distribution of relative fractional uptake (RFU) across clusters based on HDX exposure time (Figure S2); co-distribution of peptide sequence length and graph node count with RFU values in the HDX-MS data set (Figure S3); sequence similarity analysis of HDX-MS data set (Figure S4); impact of radius edge cutoff on HDXRank model performance on the test set (Figure S5); per-residue pLDDT distribution of Alphafold3 predictions (Figure S6); training progress of the model across eight different data sets (Figure S7); scatter plots comparing predicted and true values (Figure S8); model predictions on training and test sets across baseline models (Figure S9); SHAP value analysis of model input features (Figure S10); evaluation of ranking ability for four scoring functions (HDXRank score, Rosetta energy, ZRank, and ZRank2) across four protein targets (1UGH, 6DJL, 8A0E, and 8F7A) on global docking set (Figure S11); evaluation of ranking ability for four scoring functions (HDXRank score, Rosetta energy, ZRank, and ZRank2) across four protein targets (1UGH, 6DJL, 8A0E, and 8F7A) on near-native set (Figure S12); comparison of hit discovery across four scoring functions for different protein targets (1UGH, 6DJL, 8A0E, and 8F7A) (Figure S13); hierarchical clustering of AF predictions of SARS-CoV-2 spike protein and Fab icoHu23 complex (Figure S14); models performance on test set (cluster 0–2) (Tables S1–S3); comparison of HDXRank Model performance after applying pLDDT-based filtering (Tables S4 and S5); contact residues in cocrystal structures and HDX-MS-identified hotspots (Table S6); Spearman correlation across different scoring functions (HDXRank score, ZRank, ZRank2, and Rosetta energy) for ranking three docking model sets (Table S7) (PDF)
HDX-MS data set, PDB source, and UniProt ID mapping (XLSX)
L.W. conceptualized the framework and performed the research. L.W., A.T., A.S., and S.D. designed experiments and interpreted results. L.W. wrote the initial manuscript draft. L.W., A.T., A.S., and K.T. reviewed and edited the manuscript. K.T. and A.S. contributed to supervision and project administration. K.T. acquired funding. All authors read and approved the final manuscript.
The authors declare no competing financial interest.
References
- Mitra K., Carvunis A.-R., Ramesh S. K., Ideker T.. Integrative approaches for finding modular structure in biological networks. Nat. Rev. Genet. 2013;14:719–732. doi: 10.1038/nrg3552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sliwoski G., Kothiwale S., Meiler J., Lowe J.. Computational Methods in Drug Discovery. Pharmacol. Rev. 2014;66:334. doi: 10.1124/pr.112.007336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seffernick J. T., Lindert S.. Hybrid methods for combined experimental and computational determination of protein structure. J. Chem. Phys. 2020;153:240901. doi: 10.1063/5.0026025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeau S. R., Gatchell D. W., Vajda S., Camacho C. J.. ClusPro: a fully automated algorithm for protein-protein docking. Nucleic Acids Res. 2004;32:W96–W99. doi: 10.1093/nar/gkh354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan Y., Zhang D., Zhou P., Li B., Huang S.-Y.. HDOCK: a web server for protein–protein and protein–DNA/RNA docking based on a hybrid strategy. Nucleic Acids Res. 2017;45:W365. doi: 10.1093/nar/gkx407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce B. G., Wiehe K., Hwang H., Kim B.-H., Vreven T., Weng Z.. ZDOCK server: interactive docking prediction of protein–protein complexes and symmetric multimers. Bioinformatics. 2014;30:1771–1773. doi: 10.1093/bioinformatics/btu097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Vries S. J., van Dijk M., Bonvin A. M. J. J.. The HADDOCK web server for data-driven biomolecular docking. Nat. Protoc. 2010;5:883–897. doi: 10.1038/nprot.2010.32. [DOI] [PubMed] [Google Scholar]
- Marze N. A., Roy Burman S. S., Sheffler W., Gray J. J.. Efficient flexible backbone protein–protein docking for challenging targets. Bioinformatics. 2018;34:3461–3469. doi: 10.1093/bioinformatics/bty355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray J. J., Moughon S., Wang C., Schueler-Furman O., Kuhlman B., Rohl C. A., Baker D.. Protein–Protein Docking with Simultaneous Optimization of Rigid-body Displacement and Side-chain Conformations. J. Mol. Biol. 2003;331:281–299. doi: 10.1016/S0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
- Tran M. H., Schoeder C. T., Schey K. L., Meiler J.. Computational Structure Prediction for Antibody-Antigen Complexes From Hydrogen-Deuterium Exchange Mass Spectrometry: Challenges and Outlook. Front. Immunol. 2022;13:859964. doi: 10.3389/fimmu.2022.859964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jumper J., Evans R., Pritzel A., Green T., Figurnov M., Ronneberger O., Tunyasuvunakool K., Bates R., Žídek A., Potapenko A.. et al. Highly accurate protein structure prediction with AlphaFold. Nature. 2021;596:583–589. doi: 10.1038/s41586-021-03819-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abramson J., Adler J., Dunger J., Evans R., Green T., Pritzel A., Ronneberger O., Willmore L., Ballard A. J., Bambrick J.. et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature. 2024;630:493–500. doi: 10.1038/s41586-024-07487-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek M., DiMaio F., Anishchenko I., Dauparas J., Ovchinnikov S., Lee G. R., Wang J., Cong Q., Kinch L. N., Schaeffer R. D.. et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science. 2021;373:871–876. doi: 10.1126/science.abj8754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng S., Chen Z., Zhang C., Xie Y., Ovchinnikov S., Gao Y. Q., Liu S.. Integrated structure prediction of protein–protein docking with experimental restraints using ColabDock. Nat. Mach. Intell. 2024;6:924–935. doi: 10.1038/s42256-024-00873-z. [DOI] [Google Scholar]
- Hauri S., Khakzad H., Happonen L., Teleman J., Malmström J., Malmström L.. Rapid determination of quaternary protein structures in complex biological samples. Nat. Commun. 2019;10:192. doi: 10.1038/s41467-018-07986-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarpe V., Rafiei A., Hepburn M., Ostan N., Schryvers A. B., Schriemer D. C.. High Sensitivity Crosslink Detection Coupled With Integrative Structure Modeling in the Mass Spec Studio. Mol. Cell. Proteomics. 2016;15:3071. doi: 10.1074/mcp.O116.058685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahraman A., Herzog F., Leitner A., Rosenberger G., Aebersold R., Malmström L.. Cross-Link Guided Molecular Modeling with ROSETTA. PLoS One. 2013;8:e73411. doi: 10.1371/journal.pone.0073411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biehn S. E., Lindert S.. Accurate protein structure prediction with hydroxyl radical protein footprinting data. Nat. Commun. 2021;12:341. doi: 10.1038/s41467-020-20549-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake Z. C., Seffernick J. T., Lindert S.. Protein complex prediction using Rosetta, AlphaFold, and mass spectrometry covalent labeling. Nat. Commun. 2022;13:7846. doi: 10.1038/s41467-022-35593-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borysik A. J.. Simulated Isotope Exchange Patterns Enable Protein Structure Determination. Angew. Chem., Int. Ed. 2017;56:9396–9399. doi: 10.1002/anie.201704604. [DOI] [PubMed] [Google Scholar]
- Eschweiler J. D., Farrugia M. A., Dixit S. M., Hausinger R. P., Ruotolo B. T.. A Structural Model of the Urease Activation Complex Derived from Ion Mobility-Mass Spectrometry and Integrative Modeling. Structure. 2018;26:599–606. doi: 10.1016/j.str.2018.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eschweiler J. D., Frank A. T., Ruotolo B. T.. Coming to Grips with Ambiguity: Ion Mobility-Mass Spectrometry for Protein Quaternary Structure Assignment. J. Am. Soc. Mass Spectrom. 2017;28:1991–2000. doi: 10.1007/s13361-017-1757-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seffernick J. T., Harvey S. R., Wysocki V. H., Lindert S.. Predicting Protein Complex Structure from Surface-Induced Dissociation Mass Spectrometry Data. ACS Cent. Sci. 2019;5:1330–1341. doi: 10.1021/acscentsci.8b00912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James E. I., Murphree T. A., Vorauer C., Engen J. R., Guttman M.. Advances in Hydrogen/Deuterium Exchange Mass Spectrometry and the Pursuit of Challenging Biological Systems. Chem. Rev. 2022;122:7562–7623. doi: 10.1021/acs.chemrev.1c00279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandit D., Tuske S. J., Coales S. J., E S. Y., Liu A., Lee J. E., Morrow J. A., Nemeth J. F., Hamuro Y.. Mapping of discontinuous conformational epitopes by amide hydrogen/deuterium exchange mass spectrometry and computational docking. J. Mol. Recognit. 2012;25:114–124. doi: 10.1002/jmr.1169. [DOI] [PubMed] [Google Scholar]
- Pierce B., Weng Z.. ZRANK: Reranking protein docking predictions with an optimized energy function. Proteins. 2007;67:1078–1086. doi: 10.1002/prot.21373. [DOI] [PubMed] [Google Scholar]
- Pierce B., Weng Z.. A Combination of Rescoring and Refinement Significantly Improves Protein Docking Performance. Proteins. 2008;72:270–279. doi: 10.1002/prot.21920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alford R. F., Leaver-Fay A., Jeliazkov J. R., O’Meara M. J., DiMaio F. P., Park H., Shapovalov M. V., Renfrew P. D., Mulligan V. K., Kappel K.. et al. The Rosetta all-atom energy function for macromolecular modeling and design. J. Chem. Theory Comput. 2017;13:3031–3048. doi: 10.1021/acs.jctc.7b00125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts V. A., Pique M. E., Hsu S., Li S.. Combining H/D Exchange Mass Spectrometry and Computational Docking To Derive the Structure of Protein–Protein Complexes. Biochemistry. 2017;56:6329–6342. doi: 10.1021/acs.biochem.7b00643. [DOI] [PubMed] [Google Scholar]
- Vendruscolo M., Paci E., Dobson C. M., Karplus M.. Rare Fluctuations of Native Proteins Sampled by Equilibrium Hydrogen Exchange. J. Am. Chem. Soc. 2003;125:15686–15687. doi: 10.1021/ja036523z. [DOI] [PubMed] [Google Scholar]
- Devaurs D., Antunes D. A., Borysik A. J.. Computational Modeling of Molecular Structures Guided by Hydrogen-Exchange Data. J. Am. Soc. Mass Spectrom. 2022;33:215–237. doi: 10.1021/jasms.1c00328. [DOI] [PubMed] [Google Scholar]
- Park I.-H., Venable J. D., Steckler C., Cellitti S. E., Lesley S. A., Spraggon G., Brock A.. Estimation of Hydrogen-Exchange Protection Factors from MD Simulation Based on Amide Hydrogen Bonding Analysis. J. Chem. Inf. Model. 2015;55:1914–1925. doi: 10.1021/acs.jcim.5b00185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Riverol Y., Csordas A., Bai J., Bernal-Llinares M., Hewapathirana S., Kundu D. J., Inuganti A., Griss J., Mayer G., Eisenacher M.. et al. The PRIDE database and related tools and resources in 2019: improving support for quantification data. Nucleic Acids Res. 2019;47:D442–D450. doi: 10.1093/nar/gky1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M., Wang J., Carver J., Pullman B. S., Cha S. W., Bandeira N.. Assembling the Community-Scale Discoverable Human Proteome. Cell Syst. 2018;7:412–421. doi: 10.1016/j.cels.2018.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J., Uzuner U., Long B., Wang Z., Yuan J. S., Dai S. Y.. Artificial intelligence-based HDX (AI-HDX) prediction reveals fundamental characteristics to protein dynamics: Mechanisms on SARS-CoV-2 immune escape. iScience. 2023;26:106282. doi: 10.1016/j.isci.2023.106282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H. M., Westbrook J., Feng Z., Gilliland G., Bhat T. N., Weissig H., Shindyalov I. N., Bourne P. E.. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gromiha M. M., Selvaraj S.. Inter-residue interactions in protein folding and stability. Prog. Biophys. Mol. Biol. 2004;86:235–277. doi: 10.1016/j.pbiomolbio.2003.09.003. [DOI] [PubMed] [Google Scholar]
- Martin M. J., Orchard S.. et al. UniProt: the universal protein knowledgebase in 2021. Nucleic Acids Res. 2021;49:D480–D489. doi: 10.1093/nar/gkaa1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Z. ; Xu, M. ; Jamasb, A. ; Chenthamarakshan, V. ; Lozano, A. ; Das, P. ; Tang, J. In Protein Representation Learning by Geometric Structure Pretraining, International Conference on Learning Representations, 2023. [Google Scholar]
- Jing, B. ; Eismann, S. ; Suriana, P. ; Townshend, R. J. L. ; Dror, R. In Learning from Protein Structure with Geometric Vector Perceptrons, International Conference on Learning Representations, 2021. [Google Scholar]
- Lundberg, S. M. ; Lee, S.-I. . A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17; Curran Associates Inc., 2017; pp 4768–4777. [Google Scholar]
- Sljoka, A. Structural and Functional Analysis of Proteins Using Rigidity Theory. In Sublinear Computation Paradigm: Algorithmic Revolution in the Big Data Era; Katoh, N. ; Higashikawa, Y. ; Ito, H. ; Nagao, A. ; Shibuya, T. ; Sljoka, A. ; Tanaka, K. ; Uno, Y. , Eds.; Springer, 2022; pp 337–367. [Google Scholar]
- Jacobs D. J., Rader Aj., Kuhn L. A., Thorpe Mf.. Protein flexibility predictions using graph theory. Proteins. 2001;44:150–165. doi: 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
- Jenkins M. L., Margaria J. P., Stariha J. T. B., Hoffmann R. M., McPhail J. A., Hamelin D. J., Boulanger M. J., Hirsch E., Burke J. E.. Structural determinants of Rab11 activation by the guanine nucleotide exchange factor SH3BP5. Nat. Commun. 2018;9:3772. doi: 10.1038/s41467-018-06196-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wątor E., Wilk P., Biela A., Rawski M., Zak K. M., Steinchen W., Bange G., Glatt S., Grudnik P.. Cryo-EM structure of human eIF5A-DHS complex reveals the molecular basis of hypusination-associated neurodegenerative disorders. Nat. Commun. 2023;14:1698. doi: 10.1038/s41467-023-37305-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaffer J. M., Jiou J., Tripathi K., Olaluwoye O. S., Fung H. Y. J., Chook Y. M., D’Arcy S.. Molecular basis of RanGTP-activated release of Histones H2A-H2B from Importin-9. Structure. 2023;31:903–911. doi: 10.1016/j.str.2023.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirabello C., Wallner B.. DockQ v2: improved automatic quality measure for protein multimers, nucleic acids, and small molecules. Bioinformatics. 2024;40:btae586. doi: 10.1093/bioinformatics/btae586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abramson J., Adler J., Dunger J., Evans R., Green T., Pritzel A., Ronneberger O., Willmore L., Ballard A. J., Bambrick J.. et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature. 2024;630:493–500. doi: 10.1038/s41586-024-07487-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans, R. ; O’Neill, M. ; Pritzel, A. ; Antropova, N. ; Senior, A. ; Green, T. ; Žídek, A. ; Bates, R. ; Blackwell, S. ; Yim, J. . et al. Protein complex prediction with AlphaFold-Multimer, 2022. 10.1101/2021.10.04.463034. [DOI]
- Huang Y., Yang C., Xu X., Xu W., Liu S.. Structural and functional properties of SARS-CoV-2 spike protein: potential antivirus drug development for COVID-19. Acta Pharmacol. Sin. 2020;41:1141–1149. doi: 10.1038/s41401-020-0485-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermet P., Delache B., Herate C., Wolf E., Kivi G., Juronen E., Mumm K., Žusinaite E., Kainov D., Sankovski E.. et al. Broadly neutralizing humanized SARS-CoV-2 antibody binds to a conserved epitope on Spike and provides antiviral protection through inhalation-based delivery in non-human primates. PLoS Pathog. 2023;19:e1011532. doi: 10.1371/journal.ppat.1011532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terwilliger T. C., Liebschner D., Croll T. I., Williams C. J., McCoy A. J., Poon B. K., Afonine P. V., Oeffner R. D., Richardson J. S., Read R. J., Adams P. D.. AlphaFold predictions are valuable hypotheses and accelerate but do not replace experimental structure determination. Nat. Methods. 2024;21:110–116. doi: 10.1038/s41592-023-02087-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smit J. H., Krishnamurthy S., Srinivasu B. Y., Parakra R., Karamanou S., Economou A.. Probing Universal Protein Dynamics Using Hydrogen–Deuterium Exchange Mass Spectrometry-Derived Residue-Level Gibbs Free Energy. Anal. Chem. 2021;93:12840–12847. doi: 10.1021/acs.analchem.1c02155. [DOI] [PubMed] [Google Scholar]
- Salmas R. E., Borysik A. J.. HDXmodeller: an online webserver for high-resolution HDX-MS with auto-validation. Commun. Biol. 2021;4:199. doi: 10.1038/s42003-021-01709-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng B., Zhu S., Macklin A. M., Xu J., Lento C., Sljoka A., Wilson D. J.. Suppressing allostery in epitope mapping experiments using millisecond hydrogen/deuterium exchange mass spectrometry. mAbs. 2017;9:1327–1336. doi: 10.1080/19420862.2017.1379641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra P., Pal D.. Combining Bayes classification and point group symmetry under Boolean framework for enhanced protein quaternary structure inference. Structure. 2011;19:304–312. doi: 10.1016/j.str.2011.01.009. [DOI] [PubMed] [Google Scholar]
- Bliven S., Lafita A., Parker A., Capitani G., Duarte J. M.. Automated evaluation of quaternary structures from protein crystals. PLoS Comput. Biol. 2018;14:e1006104. doi: 10.1371/journal.pcbi.1006104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masson G. R., Burke J. E., Ahn N. G., Anand G. S., Borchers C., Brier S., Bou-Assaf G. M., Engen J. R., Englander S. W., Faber J.. et al. Recommendations for performing, interpreting and reporting hydrogen deuterium exchange mass spectrometry (HDX-MS) experiments. Nat. Methods. 2019;16:595–602. doi: 10.1038/s41592-019-0459-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remmert M., Biegert A., Hauser A., Söding J.. HHblits: lightning-fast iterative protein sequence searching by HMM-HMM alignment. Nat. Methods. 2012;9:173–175. doi: 10.1038/nmeth.1818. [DOI] [PubMed] [Google Scholar]
- Atchley W. R., Zhao J., Fernandes A. D., Drüke T.. Solving the protein sequence metric problem. Proc. Natl. Acad. Sci. U.S.A. 2005;102:6395–6400. doi: 10.1073/pnas.0408677102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald I. K., Thornton J. M.. Satisfying hydrogen bonding potential in proteins. J. Mol. Biol. 1994;238:777–793. doi: 10.1006/jmbi.1994.1334. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All original code has been deposited at Github at https://github.com/tsudalab/HDXRank.git and is publicly available as of the date of publication. The collected HDX-MS data set has been deposited on Zenodo and can be accessed at 10.5281/zenodo.14625492. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.