Abstract
Kinesin is a motor protein that transports organelles along a microtubule toward its plus end by using the energy of ATP hydrolysis. To clarify the nucleotide-dependent binding mode, we measured the unbinding force for one-headed kinesin heterodimers in addition to conventional two-headed kinesin homodimers under several nucleotide states. We found that both a weak and a strong binding state exist in each head of kinesin corresponding to a small and a large unbinding force, respectively; that is, weak for the ADP state and strong for the nucleotide-free and adenosine 5′-[β,γ-imido]triphosphate states. Model analysis showed that (i) the two binding modes in each head could be explained by a difference in the binding energy and (ii) the directional instability of binding, i.e., dependence of unbinding force on loading direction, could be explained by a difference in the characteristic distance for the kinesin–microtubule interaction during plus- and minus-end-directed loading. Both these factors must play an important role in the molecular mechanism of kinesin motility.
Kinesin is a processive molecular motor that is essential for the transport of vesicles and organelles along a microtubule in various cells. Kinesin's processive movement has been explained by a mechanism that involves alternating between single- and double-headed bindings to a microtubule (1–5). Adjacent tubulin dimers of 8-nm length form consecutive binding sites (6), such that kinesin takes hundreds of 8-nm steps down a microtubule (7–10). Our recent single-molecule analysis of unbinding force (11) showed that conventional two-headed kinesin is involved in single-headed binding, both in the absence of nucleotides (nucleotide-free state) and in the coexistence of ADP and adenosine 5′-[β,γ-imido]triphosphate (AMP-PNP) (ATP analogue), and double-headed binding in the presence of AMP-PNP (AMP-PNP state), which is consistent with the putative mechanism of kinesin motility.
In the present study, we have measured the unbinding force of a single kinesin⋅microtubule complex under an optical microscope equipped with optical tweezers as was reported (11). To clarify the binding mode, we used one-headed kinesin heterodimers (12) in addition to conventional two-headed kinesin homodimers. Conventional two-headed homodimers or one-headed heterodimers of kinesin molecules were attached to a polystyrene bead such that single kinesin binds to a single bead, and each bead was manipulated with optical tweezers on a microtubule that was adsorbed onto a coverslip (1, 9). An external load was imposed on the attached kinesin molecule by moving the bead toward the plus or the minus end of the microtubule. Here, we found that the two binding states exist in each head of kinesin depending on the nucleotide state. Also, we found that the dependence of the unbinding force on loading direction (where the unbinding force is smaller for the plus-end loading than for the minus-end loading) was independent of nucleotide states.
We have analyzed the results for a weak and a strong binding of each head according to a simple model, where the detachment of the kinesin–microtubule complex is assumed to occur according to the load (F)-dependent lifetime (τ) expressed by τ(F) = τ(0) exp(−Fd/kBT). τ(0), the lifetime in the absence of external load, is 1 s for the ADP state and 150 s for the AMP-PNP and nucleotide-free states; d is the characteristic distance, kB, the Boltzmann constant, and T, the absolute temperature.
Materials and Methods
Proteins.
Conventional two-headed kinesin homodimers and tubulin were prepared from bovine (9) and porcine (13) brains, respectively. One-headed kinesin heterodimers were engineered and purified as described (12). This construct includes the neck, rod, and tail domains but lacks one head domain. Polarity-marked microtubules labeled with tetramethyl-rhodamine succinimidyl ester (Molecular Probes) were prepared according to Hyman (14) except that N-ethylmaleimide-treated tubulin was not used; thus, polymerization at the minus end was not inhibited (compare figure 2A in ref. 11).
Unbinding Force Measurement.
Kinesin-coated beads were prepared according to the established procedure (9) except for fluorescent polystyrene beads (1.0 μm in diameter, carboxylate-modified latex; yellow-green, Molecular Probes). The average number of functional kinesin molecules on a bead was estimated by statistical methods (1, 9). The polarity-marked fluorescent microtubules in an assay buffer (2 mM MgCl2/80 mM Pipes, pH 6.8/1 mM EGTA) were introduced into a flow cell and incubated for 2 min to allow binding to the glass surface. The solvent was exchanged three times with an assay buffer containing 0.7 mg/ml filtered casein to coat the glass surface with casein. The flow cell was then filled with an assay buffer containing the kinesin-coated beads, filtered casein, and an oxygen-scavenging enzyme system. The final solvent condition was ≈0.1 pM kinesin-coated beads/2 mM MgCl2/80 mM Pipes, pH 6.8/1 mM EGTA/0.7 mg/ml filtered casein/10 μM Taxol/10 mM DTT/4.5 mg/ml glucose/0.22 mg/ml glucose oxidase/0.036 mg/ml catalase/1 unit/ml apyrase (nucleotide-free state) or 1 mM AMP-PNP (AMP-PNP state) or 1 mM ADP containing 1 unit/ml hexokinase (ADP state). We were able to measure the unbinding force repeatedly on the same beads and hence, presumably, the same kinesin molecules. The proportion of beads that underwent the binding and unbinding cycle was about 40% of those examined. Among them the proportion for which unbinding did not occur even at the largest external load (about 20 pN) was less than 5%. The remaining beads (about 60%) did not bind even after three trials of unbinding experiments.
Model Analysis.
For the model analysis, in which equilibrium between attached and detached states of one-headed kinesin is assumed to exist, the time dependence of the proportion of attached kinesin, N(t), was calculated by using Mathematica for Windows. Here, the value of N(t), was obtained by solving the kinetic equation dN(t)/dt = −N(t)/τ(F). The load (F) dependence of the lifetime (τ) of the attached state of kinesin was expressed as τ(F) = τ(0) exp(−Fd/kBT), where T is the absolute temperature (300 K), kB is the Boltzmann constant, and d is a characteristic distance. This relationship was obtained for the F-actin-HMM rigor complex (15). In the present study, F was linearly increased at a constant rate, α, such that F = αt. Accordingly, τ(F) became a function of t as expressed by τ(t) = τ(0) exp(−dαt/kBT), such that we obtained N(t) = exp[kBT(1 − exp(dαt/kBT))/τ(0)αd] as a solution for the differential equation above. The unbinding force distribution, P(F)ΔF as a function of F or P(t)Δt as a function of t, was thus obtained by (dN(t)/dt)Δt.
Apparatus.
Microscopy system equipped with optical tweezers as described (16); the stiffness of the optical trap was estimated to be 0.050 pN/nm. Because the spatial resolution of our system is estimated to be a few nanometers at this stiffness of optical trap, the resolution of the force measurements made is considered to be ±0.2 pN.
Results and Discussion
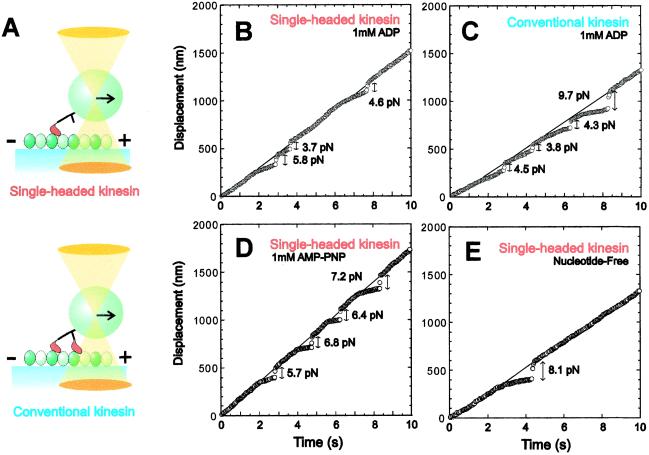
A polystyrene bead, to which either a single one- or two-headed kinesin molecule was attached, was trapped with optical tweezers and placed in contact with a microtubule for 20–30 s (Fig. 1A). Then, the unbinding force was measured by pulling the kinesin-coated bead along the microtubule at constant velocity. Typical data are shown in Fig. 1 B–E, where thin lines and circles, respectively, show the time course of the trap center and the bead center. As the bead began to deviate from the trap center, an external load was gradually applied to the kinesin–microtubule complex. When kinesin was detached from the microtubule, the bead quickly returned to the trap center. The unbinding force was estimated by multiplying the magnitude of the abrupt displacement of the bead at the moment of detachment by the stiffness of the optical tweezers (0.050 pN/nm). Considering that the length of kinesin is 60 nm and the radius of the bead is 500 nm (for this geometry, see ref. 1), the angle between the tail of kinesin and the microtubule is estimated to be about 60° for plus-end loading, whereas about 120° for minus-end loading when the external load is imposed (11).
Figure 1.
Measurement of unbinding force. (A) Schematic illustration showing the method of application of external load to one-headed or two-headed kinesin-coated bead by using optical tweezers. The relative size of the bead to kinesin is reduced to about 1/10 of the actual scale. In this illustration, the load is applied toward the plus-end of a microtubule. (B and C) Examples in the ADP state showing the time course of movement of the trap center (thin lines) and the bead (circles) on which one-headed (B) or conventional two-headed (C) kinesin was attached. The trap center was moved at a constant rate toward the plus-end of a microtubule. The unbinding force was estimated from the abrupt displacement of the bead. (D and E) Examples showing the behavior of the bead in the AMP-PNP state (D) or in the nucleotide-free state (E). In all examples, the load was applied toward the plus end.
Regardless of whether kinesin was one- or two-headed, binding and unbinding events occurred repeatedly when the bead was kept moving along a microtubule in both the ADP state (Fig. 1 B and C) and the AMP-PNP state (Fig. 1D). In the nucleotide-free state (Fig. 1E), however, unbinding occurred only once and subsequent binding and unbinding events were not repeated as described (11), suggesting a low binding-rate constant. The external load could be applied not only toward the plus end but also toward the minus end of a microtubule.
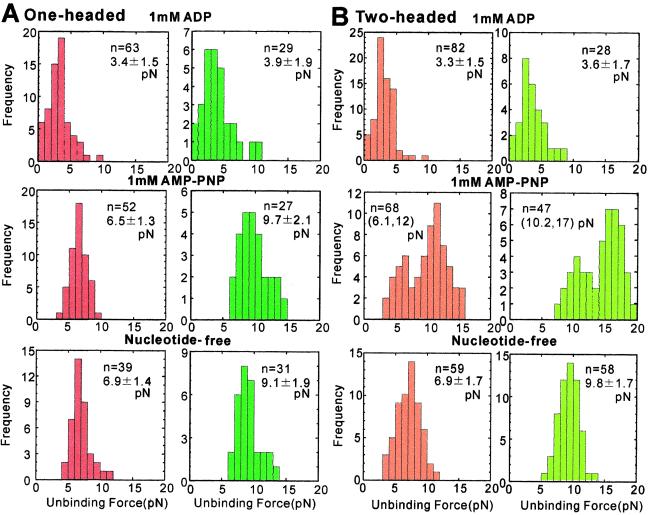
The unbinding force distributions thus obtained in the presence of 1 mM ADP or 1 mM AMP-PNP, and in the absence of nucleotides are summarized in Fig. 2. We found that the main difference between the behavior of one-headed and two-headed kinesin molecules was that the distribution is bimodal for two-headed kinesin in the AMP-PNP state (compare Fig. 2 A and B). This result strongly supports the conclusion (11) that the smaller and larger values for the unbinding force represent single- and double-headed binding, respectively. We confirmed that the average unbinding force for minus-end loading was about 45% greater than that for plus-end loading in both the nucleotide-free and AMP-PNP states (11), both for one- and two-headed kinesin molecules.
Figure 2.
Unbinding-force distribution for (A) one-headed kinesin and (B) conventional two-headed kinesin. External load was applied at a constant rate (5.0 ± 1.68 pN/s, n = 583) at several nucleotide states toward either the plus-end (red for A and orange for B) or the minus-end (dark green for A and light green for B) of the microtubule. The average unbinding force (pN) with SD is shown in each panel except in the presence of AMP-PNP (B), where only the average unbinding force of each peak is shown in the parentheses. The boundary between two peaks was determined by the junction of two Gaussian distributions that simulated two peaks.
An important finding in the present study is that the average unbinding force measured in the ADP state was smaller than both that in the nucleotide-free state and that for single-headed binding in the AMP-PNP state (Fig. 2). For plus-end loading, the values of the unbinding force were 3.3–3.4 pN for the ADP state, but 6.1–6.9 pN for the latter two states. On the other hand, for minus-end loading, the corresponding values obtained were 3.6–3.9 pN and 9.1–10 pN, respectively. Here, it should be noted that the dependence of the unbinding force distribution on loading direction in the ADP state was not as significant as in the latter two states. Moreover, we could not find any difference between the unbinding force distributions of one-headed and two-headed kinesin molecules, which implies that conventional two-headed kinesin binds single-headedly in the ADP state. The tail of the unbinding force distribution observed at higher than 5 pN (top row in Fig. 2 A and B) may be attributed to those heads that were nucleotide-free at the time of unbinding.
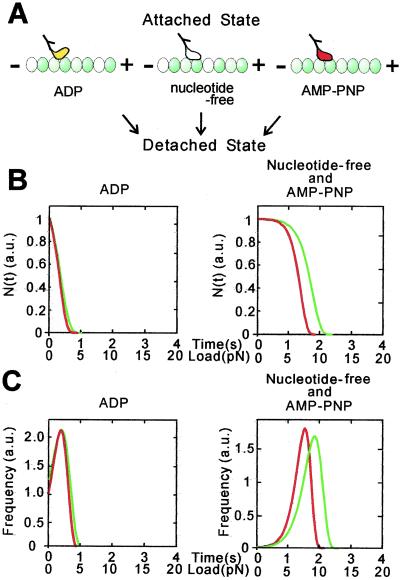
We have analyzed the results above according to a simple scheme illustrated in Fig. 3A. Here, the parameters to be determined are τ(0), the average lifetime of the kinesin–microtubule complex in the absence of external load, and d, a characteristic distance of kinesin-microtubule interaction. The most important result of this analysis is that, if the d value is assumed to be common to all of the nucleotide states, the small unbinding force in the ADP state could be explained by a short lifetime of the complex (i.e., large unbinding rate constant), τ(0) of 1 s, and the large unbinding force in the nucleotide-free and AMP-PNP states by a longer lifetime (i.e., smaller unbinding rate constant), τ(0) of 150 s, both of which are consistent with experimentally determined values (17). The loading-direction dependence of the unbinding force distribution, that is, the directional instability of binding, was attributable to the difference in the value of d, being 4.0 and 3.0 nm, respectively, for plus- and minus-end loading, regardless of the nucleotide state (Fig. 3). This implies that the effective load needed to induce unbinding is smaller for plus-end loading, which may be due to the asymmetrical geometry of the peptide chain through which the external load is applied.
Figure 3.
Model analysis of unbinding-force distribution for one-headed kinesin in three nucleotide states. (A) Schematic illustration of two binding modes, i.e., weak binding in the ADP state and strong binding in the nucleotide-free and AMP-PNP states. (B and C) Total number of binding (B) and the frequency of unbinding events (C) depending on the loading time (s) and the unbinding force (pN) for plus-end (red) and minus-end (green) loading in the presence of ADP (Left) and in the absence of nucleotide or in the presence of AMP-PNP (Right). The loading rate α was assumed to be 5 pN/s (see Materials and Methods). In B, N(0), the proportion of attached kinesin at time 0, is defined as 1. In C, the frequency of unbinding events was obtained by differentiating N(t) in B with respect to t (see text). The value of d was chosen as 4.0 and 3.0 nm, respectively, for plus-end (red) and minus-end (green) loading regardless of nucleotide state. The value of τ(0) at the ADP state was defined as 1 s while that at the nucleotide-free and AMP-PNP states was chosen as 150 s.
Given that τ(0) is related to the binding energy, the result above suggests that two types of microtubule-binding sites exist in each head of kinesin. Amino acid sequence analysis also suggests that at least two binding regions exist in each head of kinesin, located at loop 12, and loop 7 or 8 (18–20). Furthermore, cryo-electron microscopy (21, 22) shows that the angle of the attached head against the microtubule in the ADP state is different from those in the nucleotide-free and AMP-PNP states. Recent polarization measurements of fluorophores rigidly attached to the kinesin heads have shown broad orientational distribution in the ADP state (23, 24), which suggests weak binding to the microtubule. The present results describing single molecular mechanics together with model analysis support this result, and indicate that weak binding in the ADP state and strong binding in the nucleotide-free and AMP-PNP states can be attributed to a small and large binding energy, respectively.
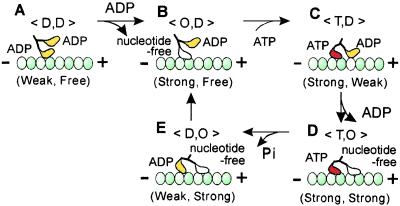
Taking into account the present results, a mechanistic model of kinesin motility proposed to date (2–7, 11) is summarized as illustrated in Fig. 4. Although 〈T,D〉 and 〈D,O〉 states in Fig. 4 C and E, respectively, have not been identified by the present method, we assume that these states exist as intermediates in the ATPase cycle. The present results suggest that the leading and the trailing ADP-bound heads in these states are in a weak-binding state.
Figure 4.
Summary of the present results in relation to the walking model of kinesin motility. Upon weak attachment of one of two ADP-bound heads of kinesin to the microtubule (A, 〈D,D〉 state), the bound ADP immediately detaches, resulting in nucleotide-free strong binding of the attached head (B, 〈O,D〉 state). Due to the binding of ATP to the attached head, zippering of the neck linker of the ATP-bound head is expected to occur so that the free ADP-bound head tends to move forward, resulting in weak binding (C, 〈T,D〉 state). The bound ADP immediately detaches, so that the leading head assumes the strong binding state similar to that of the trailing head (D, 〈T,O〉 state). This double-headed binding state is the most stable in a single cycle of the present walking model. This 〈T,O〉 state is the only state in which double-headed binding was demonstrated by the present unbinding force measurements. ATP on the trailing head is then hydrolyzed into ADP and inorganic phosphate (Pi), so that the ADP-Pi-bound trailing head or the ADP-bound trailing head after Pi release becomes unstable (E, 〈D,O〉 state), resulting in its immediate detachment from the microtubule. As a result, the molecule takes an 8-nm step forward (the size of a tubulin heterodimer) that accompanies ATP hydrolysis. Note that the existence of states 〈T,D〉 and 〈D,O〉 have not yet been confirmed by the present method, but are assumed to exist as intermediates.
Furthermore, it is inferred that the probability of detachment of the trailing head during double-headed binding is higher than that of the leading head by exp[F′(4.0–3.0 nm)/kBT], where F′ is the internal stress between the two attached heads. Here, if F′ is assumed to be 4 pN, the unbinding force we obtained, at room temperature, the trailing head will detach more readily by a factor of about 3. Thus, such a difference in stability of the attachment of the leading and trailing heads to the microtubule caused by mechanical properties (vectorial stress and strain imposed on motor domain) coupled with enzymatic properties (binding of ATP and its hydrolytic products), can be seen to be essential to the mechanism of directional motility of processive molecular motors.
Acknowledgments
We thank Mr. Mark Chee of Duke University and Mr. Charles V. Sindelar of University of California, San Francisco, for critical reading of the manuscript and colleagues at Waseda University and Japan Science and Technology Corporation (CREST) for encouragement and support. This research was partly supported by Grants-in-Aid for Scientific Research, for Scientific Research on Priority Areas, and for the Bio-venture Project from the Ministry of Education, Culture, Sports, Science and Technology of Japan, and by Grants-in-Aid from CREST and the Mitsubishi Foundation.
Abbreviation
- AMP-PNP
adenosine 5′-[β,γ-imido]triphosphate
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Svoboda K, Block S M. Cell. 1994;77:773–784. doi: 10.1016/0092-8674(94)90060-4. [DOI] [PubMed] [Google Scholar]
- 2.Hackney D D. Proc Natl Acad Sci USA. 1994;91:6865–6869. doi: 10.1073/pnas.91.15.6865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cross R A. J Muscle Res Cell Motil. 1995;16:91–94. doi: 10.1007/BF00122526. [DOI] [PubMed] [Google Scholar]
- 4.Rice S, Lin A W, Safer D, Hart C L, Naber N, Carragher B O, Cain S M, Pechatnikova E, Wilson-Kubalek E M, Whittaker M, et al. Nature (London) 1999;402:778–784. doi: 10.1038/45483. [DOI] [PubMed] [Google Scholar]
- 5.Vale R D, Milligan R A. Science. 2000;288:88–95. doi: 10.1126/science.288.5463.88. [DOI] [PubMed] [Google Scholar]
- 6.Lockhart A, Crevel I M, Cross R A. J Mol Biol. 1995;249:763–771. doi: 10.1006/jmbi.1995.0335. [DOI] [PubMed] [Google Scholar]
- 7.Howard J. Annu Rev Physiol. 1996;58:703–729. doi: 10.1146/annurev.ph.58.030196.003415. [DOI] [PubMed] [Google Scholar]
- 8.Vale R D, Funatsu T, Pierce D W, Romberg L, Harada Y, Yanagida T. Nature (London) 1996;380:451–453. doi: 10.1038/380451a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kojima H, Muto E, Higuchi H, Yanagida T. Biophys J. 1997;73:2012–2022. doi: 10.1016/S0006-3495(97)78231-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Svoboda K, Schmidt C F, Schnapp B J, Block S M. Nature (London) 1993;365:721–727. doi: 10.1038/365721a0. [DOI] [PubMed] [Google Scholar]
- 11.Kawaguchi K, Ishiwata S. Science. 2001;291:667–669. doi: 10.1126/science.291.5504.667. [DOI] [PubMed] [Google Scholar]
- 12.Hancock W O, Howard J. J Cell Biol. 1998;140:1395–1405. doi: 10.1083/jcb.140.6.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weingarten M D, Lockwood A H, Hwo S Y, Kirschner M W. Proc Natl Acad Sci USA. 1975;72:1858–1862. doi: 10.1073/pnas.72.5.1858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hyman A A. J Cell Sci. 1991;s14:125–127. doi: 10.1242/jcs.1991.supplement_14.25. [DOI] [PubMed] [Google Scholar]
- 15.Nishizaka T, Seo R, Tadakuma H, Kinosita K, Jr, Ishiwata S. Biophys J. 2000;79:962–974. doi: 10.1016/S0006-3495(00)76350-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nishizaka T, Miyata H, Yoshikawa H, Ishiwata S, Kinosita K., Jr Nature (London) 1995;377:251–254. doi: 10.1038/377251a0. [DOI] [PubMed] [Google Scholar]
- 17.Hancock W O, Howard J. Proc Natl Acad Sci USA. 1999;96:13147–13152. doi: 10.1073/pnas.96.23.13147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Woehlke G, Ruby A K, Hart C L, Ly B, Hom-Booher N, Vale R D. Cell. 1997;90:207–216. doi: 10.1016/s0092-8674(00)80329-3. [DOI] [PubMed] [Google Scholar]
- 19.Alonso M C, van Damme J, Vandekerckhove J, Cross R. EMBO J. 1998;17:945–951. doi: 10.1093/emboj/17.4.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kikkawa M, Okada Y, Hirokawa N. Cell. 2000;100:241–252. doi: 10.1016/s0092-8674(00)81562-7. [DOI] [PubMed] [Google Scholar]
- 21.Hirose K, Lockhart A, Cross R A, Amos L A. Nature (London) 1995;376:277–279. doi: 10.1038/376277a0. [DOI] [PubMed] [Google Scholar]
- 22.Kikkawa M, Sablin E P, Okada Y, Yajima H, Fletterick R J, Hirokawa N. Nature (London) 2001;411:439–445. doi: 10.1038/35078000. [DOI] [PubMed] [Google Scholar]
- 23.Quinlan M E, Forkey J N, Goldman Y E. Nat Struct Biol. 2001;8:478–480. doi: 10.1038/88522. [DOI] [PubMed] [Google Scholar]
- 24.Sosa H, Peterman E J, Moerner W E, Goldstein L S. Nat Struct Biol. 2001;8:540–544. doi: 10.1038/88611. [DOI] [PubMed] [Google Scholar]