Abstract
Myosin, similar to many molecular motors, is a two-headed dimer held together by a coiled-coiled rod. The stability of the coiled coil has implications for head–head interactions, force generation, and possibly regulation. Here we used two different resonance energy transfer techniques to measure the distances between probes placed in the regulatory light chain of each head of a skeletal heavy meromyosin, near the head–rod junction (positions 2, 73, and 94). Our results indicate that the rod largely does not uncoil when myosin is free in solution, and at least beyond the first heptad, the subfragment 2 rod remains relatively intact even under the relatively large strain of two-headed myosin (rigor) binding to actin. We infer that uncoiling of the rod likely does not play a role in myosin II motility. To keep the head–rod junction intact, a distortion must occur within the myosin heads. This distortion may lead to different orientations of the light-chain domains within the myosin dimer when both heads are attached to actin, which would explain previously puzzling observations and require reinterpretation of others. In addition, by comparing resonance energy transfer techniques sensitive to different dynamical time scales, we find that the N terminus of the regulatory light chain is highly flexible, with possible implications for regulation. An intact rod may be a general property of molecular motors, because a similar conclusion has been reached recently for kinesin, although whether the rod remains intact will depend on the relative stiffness of the coiled coil and the head in different motors.
Myosin II is involved in muscle contraction and cellular and intracellular motility. Similar to many other molecular motors, myosin II is a dimer consisting of two heads (myosin subfragments 1, S1s) held together by a coiled-coiled subfragment 2 (S2) rod. Why myosin is dimeric and how or if the two heads are functionally coupled together is still poorly understood. This coupling is in part determined by whether or not the S2 rod remains coiled or unfolds. Resolving the conformation of S2, particularly while myosin is interacting with actin, has important implications for the interpretation of a large number of experiments and for understanding force generation by actomyosin and possibly other molecular motors. Several studies have been interpreted to indicate that S2 likely uncoils (ref. 1 and references therein), although one study indicates that S2 likely remains intact at least part of the time (2). However, these experiments are indirect measurements.
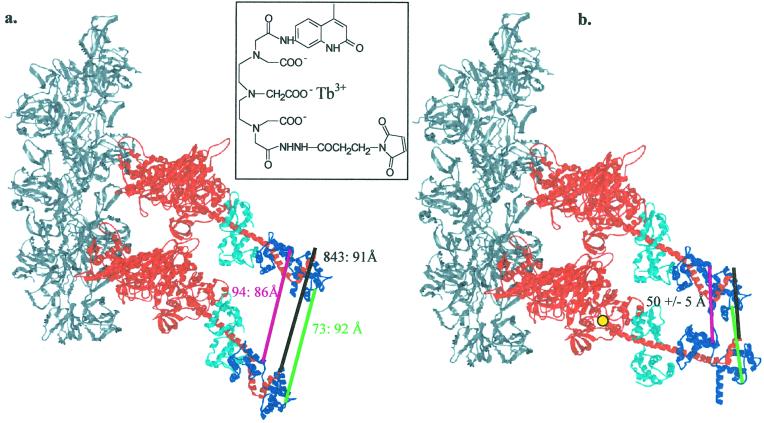
To study S2 uncoiling, we have measured distances between probes placed on the regulatory light chain (RLC) of each head, near the head–rod junction, under “rigor” conditions where both myosin heads are bound to actin (Fig. 1). This condition is expected to exert maximal strain on S2 and hence provide a robust test whether S2 uncoils under physiological conditions. If the two heads bind without distortion, then S2 must uncoil, and distances of ≈90 Å are expected (Fig. 1a); if S2 remains intact, then distances of ≈50 Å or less are expected (Fig. 1b). This large difference, combined with a relatively direct measure of distances, therefore provides a robust test of S2 uncoiling.
Figure 1.
Model of two-headed myosin binding to actin and position of probes with the LC domains undistorted, implying an uncoiling of S2 (a), or distorted to fit our observed distances, implying a largely coiled S2 (b). Two S1 myosin heads were docked to F-actin (gray) according to the model of Rayment, Holmes, and coworkers (23) with each head following an undistorted actin helix, leading to distances of ≈90 Å (a). With the catalytic regions remaining rigidly in this conformation, the LC domain of the leading (Lower) head was moved to decrease the distance to the trailing (Upper) LC domain, the position of which was not changed. The orientation of the myosin LC domain was rotated about amino acid 770 (yellow; ref. 31), and distances were measured between the two RLCs, residues 94 to 94 or 73 to 73. In addition, the distance between the two C-terminal ends of the heavy chains, i.e., amino acid 843, was measured also to ascertain the degree of unfolding required in S2. When the bottom head was distorted by rotating its LC domain by 25° from the actin axis (axial angle) and a change in the azimuthal angle by 15°, the three distances all decreased to ≈50 Å (b). The myosin heavy chains are shown in red. The essential LCs (cyan) and RLCs (blue) are shown, as are the distances between Cys-94s (pink), Cys-73s (green), and residues 843 (black), where S2 begins. Cys-2 of the RLC is not visible in the crystal structure. (Inset) The structure of the lanthanide chelate donor, terbium diethylenetriaminepentacetate-carbostyril 124-maleimidopropionic hydrazide (Tb-DTPA-cs124-EMPH), is shown.
For distance measurements, we have used two related spectroscopic techniques: fluorescence (FRET) and luminescence (LRET) resonance energy transfer (refs. 3 and 4 and references therein), in which a donor fluorophore transfers energy in a distance-dependent fashion to an acceptor fluorophore. Both are capable of measuring biologically relevant distances (≈20–100 Å) under physiological conditions. LRET, which uses a luminescent lanthanide chelate as donor (Fig. 1a Inset), has a number of technical advantages over FRET (4). Nevertheless, FRET and LRET are complimentary, because FRET uses a donor with nanosecond lifetime, whereas LRET uses a donor with millisecond lifetime. Consequently, they can yield different energy transfer efficiencies if the donor-acceptor distance fluctuates (e.g., because of protein dynamics) on a time scale longer than nanoseconds but shorter than milliseconds.
We find RLC-to-RLC distances (residues Cys-73 and Cys-94) are in the 50-Å range, with a subpopulation that can be within 35 Å in the millisecond time scale. These residues are near and on either side of amino acid 843 of the heavy chain, generally defined as the head-rod junction (Fig. 1). Consequently, distances from 73 to 73 and 94 to 94 are good indicators of the structure of S2 at the head–rod junction. These distances are found under conditions where maximal strain on S2 is expected, i.e., when both heads are bound to an actin filament. Significant uncoiling therefore is not likely to be required for myosin II motility, although limited uncoiling in the first heptad of S2 may occur to prevent steric clashes between the two RLCs. An intact rod also implies a distortion elsewhere in the myosin, which has implications for the interpretation of many previous experiments and helps explain some previously puzzling results. In addition to these static structural conclusions, a comparison between FRET and LRET measurements for probes placed near the N terminus of the RLC (Cys-2) indicates that this region is highly flexible, which may be important for myosin regulation.
Methods
Protein Preparation.
Single Cys mutants of chicken skeletal myosin RLC (P2C, S73C, and P94C with the endogenous Cys-126 and Cys-155 changed to Ala) were cloned, expressed, and purified (ref. 5; Fig. 1; position of Cys-2 not shown). Heavy meromyosin (HMM) and F-actin were purified, and LCs were labeled with 5-tetramethylrhodamineiodoacetamide (TMRIA), fluorescein iodoacetamide (FIA), or Tb-DTPA-cs124-EMPH and exchanged into HMM as described (6) with minor modification. The efficiency of exchange of labeled RLC onto HMM was 70–80% for all three mutant RLCs. Control experiments mixing RLC with HMM without heating confirmed that there was no detectable nonspecific binding of RLC to HMM (6).
FRET, LRET, and Anisotropy Measurements.
The amount of energy transfer (E) and hence distance (R) between donor and acceptor on the same HMM was determined by steady-state FRET, donor-lifetime FRET, and lifetime LRET. In all cases, distances were determined by R = Ro(1 − 1/E)1/6, where E is the efficiency of energy transfer and Ro is a constant depending on the dyes used. Ro was calculated to be 55 Å for FIA to TMRIA and 53–56 Å for Tb-DTPA-cs124-EMPH to TMRIA, with the exact value depending on donor lifetime in each mutant. For steady-state FRET, the average E was determined by comparing the acceptor fluorescence caused by energy transfer (i.e., sensitized emission, Iad) to the residual donor fluorescence on a donor-acceptor-labeled sample (Ida) according to refs. 7 and 8: E = (Iad/Qa)/(Ida/Qd + Iad/Qa), where QI, the quantum yield for donor or acceptor, is measured by intensity or lifetime comparisons to standards. In steady-state FRET, the average E must be corrected for incomplete labeling (i.e., donor-only or acceptor-only HMMs). E was corrected by determining the stoichiometry of labeling and exchange via lifetime donor measurements or via absorbance measurements and assuming a binomial distribution of labels on HMM.
For lifetime measurements, E for both FRET and LRET was calculated from the lifetimes of donor luminescence, E = 1 − (τda/τd), where τda and τd are the donor's excited-state lifetime in the presence and absence of the acceptor, respectively. For LRET, E was calculated also from the acceptor's sensitized emission lifetimes, E = 1 − (τad/τd), where τad is the (μsec-msec) lifetime of the sensitized emission of the acceptor. Lifetime FRET measurements were carried out by using the phase-modulation method, and the donor lifetime was fit to a multiexponential decay. The residuals showed no structure with χ2 ranging between 0.1 and 3.0. The donor-only lifetime was typically either single or biexponential for the FIA donor (typically 85% 4.0 nsec and 15% 1.4 nsec, respectively), and the average lifetime was used. The donor lifetime in the donor- and acceptor-labeled HMM was fit to a sum of donor-only signal plus two additional exponential terms and the average lifetime of the latter exponentials used as τda. LRET donor lifetimes (at 546 nm) and sensitized emission lifetimes (at 570 nm, where the acceptor emits but the donor is silent) was measured via pulsed methods (9) and curve-fit to multiexponential decays. Steady-state anisotropies of donor and acceptor exchanged into HMM were measured according to standard procedures.
HMM concentrations were typically 0.1–0.3 μM; F-actin, when present, was in 10–15-fold excess over HMM. E was independent of protein concentration, therefore verifying that E reflects intra-HMM energy transfer and not inter-HMM energy transfer. The buffer used for spectroscopy measurements was 150 mM NaCl/5 mM MgCl2/1–2 mM DTT/25 mM Mops, pH 7.0.
Actin Binding.
Two-headed binding of myosin to actin was confirmed under rigor conditions by a slight modification of the procedure of Greene (10). Briefly, labeled HMM was titrated into a buffer containing F-actin (1–2 μM) at an HMM/actin ratio from 0 to >5, and the mixture was spun in an airfuge (36–48 min, 87,000 × g), causing precipitation of the bound HMM and actin. The ratio of bound HMM/actin was determined from absorption and/or fluorescence measurements on the supernatant. The ratio increased linearly and then reached a plateau at 0.4–0.6 for all mutants, indicating two-headed binding of HMM on actin. A single-headed myosin (S1) control reached a plateau near unity. At the actin concentrations used in spectroscopy (typically 2–4 μM, always <8 μM), essentially all the myosin is bound via two heads to the same actin filament (11). Both our own results based on myosin quenching of pyrene-labeled actin (data not shown) as well as those in the literature (11) indicate that both heads are bound strongly.
Results
Myosin RLCs were labeled and exchanged into HMM as described in Methods. FRET and LRET then were measured for free HMM and HMM bound to actin. Conditions were chosen as described above so that HMM was bound by both of its heads to the same actin filament. Fig. 2 presents steady-state FRET, lifetime FRET, and lifetime LRET between probes from Cys-73 to Cys-73. Results for Cys-94 were similar. All three techniques indicate that Cys-73 and Cys-94 on one head are relatively close to the identical residue on the opposite head, with or without actin. These results imply that S2 remains largely intact even when HMM is bound via two heads to an actin filament. One measurement on Cys-73 to Cys-94 also indicated close proximity (data not shown). Fig. 3 shows data for Cys-2, which is qualitatively different from the Cys-73 and Cys-94 mutants, showing no significant steady-state or lifetime FRET, yet significant LRET. Comparing the FRET and LRET data on Cys-2 implies that distances can come close on the millisecond time scale but on average are far apart (see below). The results for the three mutants, plus and minus actin, are summarized in Table 1. A more detailed analysis of the data are now presented.
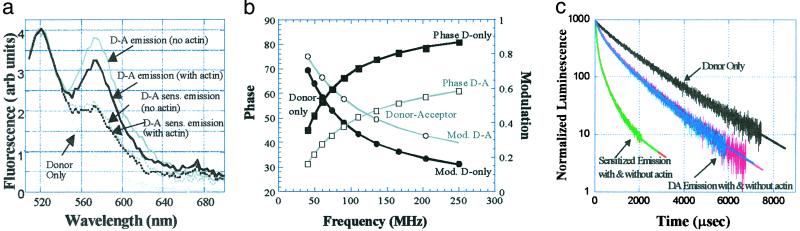
Figure 2.
(a) Steady-state FRET on probes at Cys-73 with and without actin. Donor-acceptor (D-A) emission includes donor emission and acceptor emission arising from direct excitation and sensitized emission. Subtracting off the direct acceptor emission leaves donor emission plus sensitized emission of acceptor (D-A sens. emission). Significant sensitized emission is evident, indicating energy transfer and relatively close proximity between a donor on one head and an acceptor on the other head of HMM. For this data set, distances are 49.3 and 48.7 Å with and without actin, respectively. For more details see text. Black curves, HMM with actin; gray curves, HMM without actin. (b) Lifetime FRET on the Cys-73 mutant. The data shown are without actin. Lifetimes with actin are very similar (data not shown for clarity of presentation). Donor (D) only = 100% 4.02 nsec, χ2 = 0.2 (4.0 nsec with actin). Donor-acceptor (D-A) without actin fit to 20% donor only + 52% 1.59 nsec + 28% 0.36 nsec, χ2 = 0.6: average E = 72% for those donors with acceptors, corresponding to R = 47 Å. With actin, donor-acceptor fit to 21% donor only + 79% 0.98 nsec (χ2 = 3.3), or E = 76%, R = 46 Å. These results indicate the probes at Cys-73 remain in close proximity when HMM is free or bound to actin. (c) Lifetime LRET on the Cys-73 mutant. The data are shown for both with and without actin, although in all cases decays with and without actin were very similar and showed significant energy transfer. The donor-only curve (black) with and without actin was indistinguishable and fit to a two-exponential decay: τd = 38%exp(−t/725) + 62%exp(−t/1823), χ2 = 1.03, 〈τd〉 = 1,401 μsec. Donor-acceptor (DA) emissions are measured at the terbium emission peak at 546 nm (pink curve is without actin; blue curve is with actin). For the donor-acceptor fit at 545 nm (without actin), we have 21% donor only + 41% 217 μsec + 39% 963 μsec (χ2 = 1.06, 〈τda〉 = 581 μsec), where the latter two time constants correspond to τda, which implies that 80% of the donors are paired with acceptors, and these donors undergo an 〈E〉 of 59%, corresponding to a donor-acceptor distance of 53 Å. For the donor-acceptor fit with actin we have 22% donor only + 40% 205 μsec + 37% 894 μsec (χ2 = 0.97, 〈τda〉 = 536 μsec). E calculated from 〈τda〉 equals 62%, corresponding to a distance of 52 Å. Donor-acceptor-sensitized emission measured at 570 nm (τad) without actin (red curve) fit to 2.4% donor only (because of donor leakage into sensitized emission channel) + 79% 64 μsec + 19% 338 μsec, χ2 = 1.48. Converting the amplitudes into populations (12) yields a 〈τad〉 = 232 μsec and 〈E〉 = 83.4%, corresponding to an average distance of 43 Å. With actin, the donor-acceptor-sensitized emission measured at 570 nm (green curve) fit to 2.4% donor only + 80% 63 μsec + 18% 343 μsec, χ2 = 1.40; a 〈τad〉 = 231.5 μsec, 〈E〉 = 83.5%, corresponding to an average distance of 43 Å. The multiexponential nature of the decays is discussed further in the text.
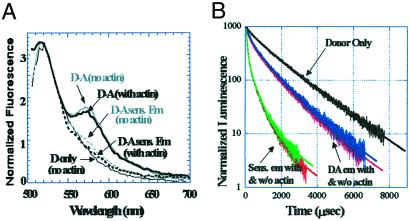
Figure 3.
Steady-state FRET (a) and lifetime LRET (b) on Cys-2. Steady-state FRET shows almost no sensitized emission, indicating probes are on average far apart. LRET measurements show significant donor-lifetime shortening and sensitized emission; hence probes can come close on the submillisecond time scale. For b, the same color scheme as that described for Fig. 2c is used. From donor-acceptor (D-A) emission, the average distance is 53 Å with actin and 52 Å without actin. From sensitized emission, the distances are 44 Å with actin and 45 Å without actin.
Table 1.
Summary of FRET (steady-state and lifetime FRET), and LRET measurements
| Sample | Steady-state FRET | Lifetime FRET | LRET*
|
|
|---|---|---|---|---|
| τda | τad | |||
| Cys-73 | ||||
| Without actin | ||||
| % ET | 65.8 ± 0.5% | 69.0 ± 6.7% | 66.4 ± 8.6% | 85.0 ± 1.8% |
| Distance | 48.5 ± 0.2A | 47.3 ± 2.4A | 50.0 ± 3.3A | 42.0 ± 1.0A |
| n = 2 | n = 3 | n = 2 | n = 2 | |
| With actin | ||||
| % ET | 59.6 ± 4.3% | 67.8 ± 6.2% | 59.4 ± 1.7% | 86.5 ± 3.3% |
| Distance | 50.7 ± 1.4A | 48.4 ± 3.1A | 52.6 ± 1.8A | 40.7 ± 2.2A |
| n = 2 | n = 2 | n = 2 | n = 2 | |
| Cys-94 | ||||
| Without actin | ||||
| % ET | 57.2 ± 9.3% | 47.1 ± 0.1% | 66.8 ± 2.8% | 88.0 ± 2.4% |
| Distance | 54.7 ± 3.3A | 56.1 ± 0.04A | 47.2 ± 1.0A | 38.0 ± 1.5A |
| n = 5 | n = 3 | n = 2 | n = 2 | |
| With actin | ||||
| % ET | 59.8 ± 9.5% | 43.1 ± 0.2% | 69.2 ± 4.5% | 86.4 ± 2.8% |
| Distance | 51.1 ± 4.1A | 57.6 ± 0.09 | 46.4 ± 1.7A | 39.0 ± 1.6A |
| n = 4 | n = 2 | n = 2 | n = 2 | |
| Cys-2 | ||||
| Without actin | ||||
| % ET | 7.5 ± 1.7% | No detectable ET | 50.7 ± 9.5% | 81.2 ± 1.4% |
| Distance | 75 ± 2A | 55.9 ± 3.6A | 43.5 ± 1.1A | |
| n = 2 | n = 2 | n = 2 | ||
| With actin | ||||
| % ET | 6.1 ± 0.3% | No detectable ET | 57.1 ± 2.3% | 76.5 ± 4.9% |
| Distance | 79 ± 1A | 53.7 ± 1.0A | 46.1 ± 2.3A | |
| n = 2 | n = 2 | n = 2 | ||
The energy transfer (ET) and distance from residues 73 to 73, 94 to 94, and 2 to 2 are shown with and without actin.
τda indicates donor lifetime in the presence of acceptor. τad indicates sensitized emission lifetime (see FRET, LRET, and Anisotropy Measurements.
Fig. 2a shows steady-state FRET between FIA and TMRIA on Cys-73 with and without actin. Significant sensitized emission, and hence energy transfer, is observed. The average E, which includes donor-acceptor pairs and donor-only pairs because of incomplete exchange, was 42% with actin and 43% without actin (see also Table 1). Assuming binomial statistics, these results correspond to energy transfer efficiencies of 64 and 65% with and without actin, respectively, for the donor-acceptor pairs, which yields distances of 49.3 and 48.7 Å with and without actin, respectively. The distances measured when HMM is bound to actin clearly are much less than the ≈90 Å expected if myosin heads bind in an unconstrained orientation (Fig. 1a), which would require S2 to uncoil. Indeed, it implies that some force must be exerted to keep the two RLCs together, and the only source of such a force is a largely coiled S2 (Fig. 1b).
Fig. 2b shows lifetime FRET on the Cys-73 mutant. The donor-only lifetime is 4.0 nsec. The lifetime decreases in the presence of acceptor, indicative of energy transfer and relatively close proximity of the probes. The lifetime measurement on the HMM labeled with donor and acceptor is fit to the sum of a donor-only lifetime and a one- or two-exponential decay arising from donors in the presence of acceptor. The average lifetime, energy transfer efficiency, and distance from this decay are 1.16 nsec, 72%, and 47 Å without actin and 0.98 nsec, 76%, and 46 Å with actin, respectively, which is consistent with the steady-state FRET measurements (see also Table 1). Again, these distances imply that S2 need not uncoil significantly when HMM binds to actin, except perhaps in the first heptad (see Discussion). This distance is not consistent with S2 uncoiling.
Fig. 2c shows lifetime LRET data on the Cys-73 mutant with and without actin. The donor-acceptor curve decays faster than the donor-only curve, implying significant energy transfer. There is also a sizable sensitized emission signal, which also is relatively rapidly decaying, again implying significant energy transfer. LRET with and without actin are very similar, leading to distances that differ by less than 1 Å. The decays are not single exponentials, implying a distribution of species, although for our purposes of differentiating between coiling and uncoiling of S2, taking average lifetimes suffices (although see the next paragraph). The average lifetime of the donor-only is 1.40 msec both with and without actin (see the Fig. 2c legend for detailed curve fits). The donor decay in the presence of acceptor has an average lifetime of 536 μsec and 581 μsec, or 62% and 59% energy transfer without and with actin, respectively, which corresponds to an average donor-acceptor distance of 53 Å without actin and 52 Å with actin. The sensitized emission is predominantly biexponential (with a third exponential of 2.4% population, corresponding to spectral leakage of donor emission into the sensitized emission channel). The population-weighted (12) average sensitized-emission lifetime is 228 μsec, which corresponds to 83% energy transfer or 43 Å both with and without actin. The LRET data therefore also support the notion that probes on the RLC are relatively close together even when myosin is bound via both heads to actin.
As mentioned, LRET lifetimes are multiexponential. Because the donor-only is multiexponential, interpreting each component in a donor-acceptor decay as distinct populations becomes difficult. Nevertheless, it is likely that there is a population of donor-acceptor distances, some of which are quite close. For example, for a donor on myosin that also has an acceptor, there is a rapidly decaying component of the donor lifetime, corresponding to a distance of 43 Å (Fig. 2c, D-A decay). Via sensitized emission, there is a component corresponding to 34 Å. These close distances further support the notion of S2 remaining intact, although the distribution implies that there may be flexibility in this region as well. Finally, why there is a difference between distances determined via donor decay and sensitized emission decay is unclear. It may arise from a distribution of probe–probe distances or from dynamics, because the sensitized-emission signal is weighted toward strongly transferring species, whereas the donor-emission signal is weighted toward weakly interacting species (12). These differences, however, do not affect the conclusion regarding S2 coiling.
Fig. 3 shows LRET and FRET data for Cys-2. Steady-state FRET shows very little energy transfer (<10%), and energy transfer was undetectably small via lifetime FRET (data not shown). In contrast, LRET displays significant energy transfer (an average of 60% by donor emission and 80% by sensitized emission), with a population that can undergo as much as 94% energy transfer measured by sensitized emission. Taken together, these measured energy transfer efficiencies indicate that the probes are far apart (>70 Å) on average but can approach each other occasionally (≈50 Å and as short as ≈35 Å) on the millisecond time scale. A quantitative dynamical theory supports this possibility and will be presented elsewhere (W. Peng, T.C., M.X., P. M. Goldbart, and P.R.S., unpublished results). Further discussion about the origin of this flexibility is presented below.
Finally, the anisotropy of donor and acceptor fluorophores were measured. The values with and without actin were the same. FIA and TMRIA had an anisotropy of 0.16 and 0.26 at Cys-2, 0.22 and 0.29 at Cys-94, and 0.18 and 0.31 at Cys-73, respectively. Terbium emission is inherently unpolarized, which was verified previously on Tb-DTPA-cs124-EMPH attached to RLC-HMM (6). These results indicate that while nonzero, errors in distances caused by the dependence of energy transfer on dye orientation are very unlikely to alter the conclusions based on the distances we calculate assuming random orientation; this is particularly true for LRET, which has very little orientation dependence (4). Even with FRET, microsecond rotational motion of our probes, as has been seen with similar probes (13), tends to decrease the energy transfer dependence on orientation. Furthermore, we have measured several distances (73 to 73, 73 to 94, and 94 to 94), all of which lead to the same conclusion, and any systematic effect of orientation is very unlikely to alter the distances in the same manner for these different sites.
Discussion
The dimeric nature of myosin has presented a puzzle since its discovery. HMM, a two-headed myosin species, will bind to a single actin filament with both of its heads. A model of the resulting structure demonstrates that considerable distortion must occur at some point in this protein complex to accommodate the binding of both heads. The nature of this structure throws light on possible molecular distortions that can occur in these proteins, distortions that also may play a role in force generation. The results from structural and biochemical studies lead to two general classes of models for the acto–HMM complex. In one class, the two strands of the coiled-coil rod separate and possibly unfold, allowing the two heads of HMM to bind to actin in a rigid and undistorted fashion (model 1; see Fig. 1a). In the second class, the coiled coil remains intact, keeping the positions of the two head–rod junctions close to one another, and distortions occur within the myosin head or within the actin filament to produce the required strain (model 2; Fig. 1b). A combination of these models involving partial rod separation and myosin or actin distortion also is possible. The measurements described here differentiate between these models, because they predict very different distances between pairs of RLCs. The relatively short distances measured between the two RLCs of HMM bound to actin are not consistent with the first class of models discussed above in which the two myosin heads bind in identical orientations following the actin helix. In such a structure the distances would have been in the range of 80–90 Å, clearly outside the range of distances observed here. If the two RLCs of an HMM remain in close proximity in the actin–HMM complex, some force must be exerted to distort the proteins, which only can come from S2. Thus the above measurements are most compatible with an S2 rod, which remains largely coiled when the two heads of HMM bind to actin. We note that it is likely that S2 uncoils a small amount (in the first heptad) to avoid steric clashes between the RLCs.
To accommodate the strain required to keep the two RLCs in the ≈50-Å range while maintaining two-headed binding to the actin filament, a distortion presumably could occur in a variety of locations within the acto–HMM complex. Likely candidates include (i) a distortion of the actin helix, (ii) a distortion of the orientation of the myosin catalytic domain relative to the actin filament, (iii) a distortion of the myosin LC domain relative to the catalytic domain, and (iv) a distortion within the LC domain. The first two possibilities seem unlikely, because paramagnetic and fluorescent probes placed on the catalytic domain have shown that this domain has the same orientation relative to the fiber filament axis for S1, HMM, or rigor muscle fibers, and that furthermore this orientation remains unchanged after the application of large forces (14–16). These results suggest that the interface between actin and the catalytic domain is undistorted. Thus, although other sources are not ruled out completely, the most likely region of distortion is in the orientation and conformation of the LC domain.
In addition to this static structural picture, by comparing the FRET and LRET measurements dynamic information can be deduced. If LRET gives significantly more energy transfer than FRET, it is likely that RLCs are moving in the submillisecond time regime. The observation that the mean distances measured by FRET and LRET are similar for probes on Cys-73 and Cys-94 shows that dynamics likely do not play a dominant factor for the LC domain as a whole. However, at Cys-2 LRET gives significantly more energy transfer than FRET (Fig. 3). These results imply that the Cys-2s on the two RLCs of myosin generally are far apart but can move in close proximity on the millisecond time scale, which indicates that the LC domain of skeletal myosin near Cys-2, the N terminus, has significant flexibility. The FRET observation that the two Cys-2s are far apart implies that Cys-2 may be docked in a position that is far from the two other sites that were used, which can be achieved if the N-terminal 18 aa are aligned on myosin toward the actin filament.
Relation to Other Studies.
Our results are supported by several previous investigations. Distortion within the myosin heads has been observed in electron micrographs of single HMMs interacting with an actin filament and in insect flight muscles in rigor (17). These distortions, occurring largely in the LC domain, could be capable of allowing the two RLCs to remain in close proximity while potentially keeping S2 intact. For example, the two RLCs of scallop myosin in rigor myofibrils (18) and smooth muscle acto–HMM (2) can be cross-linked to each other, demonstrating that the two RLCs do approach each other. However, cross-linking is not an unambiguous measure of structure and can be the result of infrequent fluctuations in protein structures.
Our conclusions would also seem to be at odds with some previous observations. (i) Spectroscopic studies of the orientation of the LC domain, measured by using paramagnetic (19) or fluorescent (15) probes, have found that the orientation of the LC domains were similar when S1 or HMM were bound to oriented actin, and both were similar to rigor fibers. These results led to the conclusion that the myosin heads are not distorted by binding to actin. However, interpretation of these spectra are complicated by the fact that the spectroscopic probes contain a principal axis, which is unlikely to be aligned for maximal sensitivity to the change in orientation of the LC domain, and by the substantial disorder (20–40°) in the LC domains. Hence, these studies likely would not have detected a change in angle of between 15 and 25° occurring in half of the LC domains of the sample, as we find here (Fig. 1). (ii) Older FRET measurements (18), along with antibody labeling visualized by electron microscopy (20), found the RLCs to be relatively far apart (>50 Å); however, suboptimal probe location in the FRET studies and sample handling artifacts in the EM studies may have led to erroneous conclusions. (iii) Trybus and coworkers found that truncated rods do not coil readily, which they interpreted as implying limited S2 stability (ref. 1 and references therein). This observation might lead to the conclusion that S2 uncoils after two-headed binding. However, the inability of truncated rods to form a coil may be caused by the absence of a “trigger sequence” required to initiate proper folding (1), and our results support the latter possibility. Trybus and coworkers also added a high melting temperature zipper at the head–rod junction, which likely prevented S2 uncoiling. This construct did not inhibit the velocity of actin observed in gliding assays (1) but did affect the displacement generated by single molecules. Our present results suggest that unfolding is not required in the active cycle, and that the inhibition of single molecule displacements is caused by some other effect caused by the addition of the leucine zipper, perhaps involving regulation.
The flexibility we find in the N terminus of the RLC is consistent with previous, more indirect measurements. These include a comparison of cross-linking to FRET (ref. 18 and references therein), disorder found in the first 19 residues of the N terminus of RLC under crystallization (21), and mutagenesis analysis that indicated a flexible hinge in the RLC (22). For smooth muscle myosin, this flexibility may play a role in phosphorylation-mediated regulation (22).
Molecular Models of the Acto–HMM Complex.
We have developed models of the structure of the actomyosin complex to understand the magnitude of the distortions needed to bring the two heads at the head–rod junctions in close proximity. Two S1s were aligned on two actin monomers that are adjacent to each other in the long-pitch helix of an undistorted actin filament (Fig. 1). The S1 closer to the z band, i.e., the minus end of the actin filament, is termed the leading head and the other the trailing head. Both heads were aligned initially in a putative rigor conformation (ref. 23; Fig. 1a). Distances between three pairs of amino acids were measured as described for Fig. 1. Initially, all these distances were in the range of 85–92 Å, implying an uncoiling of S2, which is not consistent with our current results.
The orientation of the LC domain of the leading S1 then was moved manually, avoiding steric clashes between proteins (Fig. 1). Distances in the range of 50 Å, consistent with our measurements, could be achieved for all three (73, 94, and 843) pairs of amino acids by a change in the axial angle of 25° or by simultaneously changing the axial angle by 15° and the azimuthal angle by 25°. If the orientations of the LC domain of the trailing head also were allowed to move, the angular changes of each LC domain could be smaller, approximately one half of the values shown. Because the two head–rod junctions are also found to be ≈50 Å apart, a small portion of S2, approximately one heptad, likely unfolds to prevent steric clashes between the RLCs. Indeed, the sequence of this first heptad indicates that the stability of a coiled coil in this region is likely low.
We can roughly estimate the energy required to distort the LC domain roughly, keeping the S2 largely coiled, and then compare it to an estimate of the energy needed to uncoil S2. We find an ≈4-nm distortion of the head–rod junction (9 nm undistorted, 5 nm distorted; Fig. 1), which represents 40–80% of the distance traversed in the power stroke, which can be estimated to involve ≈8–30 kJ/mol of free energy. We estimate that S2 uncoiling requires 5–6 kJ/mol per residue, based on values for small coiled-coiled proteins (24). Hence, distorting the LC domain as we have proposed would require somewhat less energy than uncoiling 10 residues of S2.
Our conclusions regarding S2 uncoiling are reached from data obtained from the HMM bound to actin. In the absence of actin, the two heads are likely under little strain, and short distances do not a priori give information about the structure of S2. [In one case where head–head interaction was found in the absence of actin, RLC-to-RLC distances remained short (25).] However, if the S2 remains largely coiled when bound to actin, it likely remains coiled in the absence of actin, where forces tending to uncoil S2 are insignificant.
Conclusions and Implications
Our model in which HMM binds to actin with distorted LC domains and a relatively intact S2 has implications for the interpretation of a wide range of structural and mechanical measurements. Previously, two-headed binding of myosin to actin in the absence of nucleotide (the rigor state) has been taken as a “gold standard,” representing the end of the power stroke. Yet this rigor state represents the end of the power stroke only if S2 uncoils. If S2 remains mostly coiled, then the two heads are not at the same orientation, with one or both heads or distorted from the end of the power stroke. Thus our results imply that spectra taken in the rigor state cannot be used as a post-power stroke reference to interpret other states, e.g., active, etc. In addition, if the two heads are not in the same orientation, when a rigor fiber is pulled the spectral response will be complex, with different angular changes occurring in leading and trailing heads. For instance, the application of a length step in a rigor fiber causes a surprisingly small change in the orientation of fluorescent probes on the RLC (15, 26). This result can be explained if the LC domains are at different angles; one probe might move toward the perpendicular, whereas the other would move away from it, yielding a small average change. The stiffness of rigor fibers, which has been used widely to estimate the fraction of attached myosin heads, will also not be interpreted easily, because the stiffness of two distorted heads will not be related easily to that of one head attached in a power stroke (27). Furthermore, models of the rigor state derived from x-ray diffraction studies will not reflect the end of the power stroke accurately (28, 29). On the other hand, the conclusion that the two head–rod junctions are within 50 Å provides a constraint that can be used in modeling probe spectra, x-ray intensities, or electron micrographs. Distortion of one of the heads would be expected to influence the energetics of binding, and indeed, differential binding of the two heads of HMM to actin has been observed (11).
The S2 rod in myosin is homologous to the coiled-coiled rods in other dimeric motor proteins such as kinesin. Recent evidence indicates that an unfolding of this part of kinesin is not required for motility (30). Other myosins such as myosin VI have what are likely a much weaker S2. Further studies will be necessary to determine the general role of S2 in different motor proteins.
Acknowledgments
We thank Dr. Susan Lowey for the gift of cDNA of RLCs. This work was supported by National Institutes of Health Grant AR44420 (to P.R.S.) and AR42895 (to R.C.).
Abbreviations
- S1 and S2
myosin subfragments 1 and 2
- RLC
regulatory light chain
- LC
light chain
- FRET
fluorescence resonance energy transfer
- LRET
luminescence- or lanthanide-based resonance energy transfer
- HMM
heavy meromyosin
- Tb-DTPA-cs124-EMPH
terbium diethylenetriaminepentacetate-carbostyril 124-maleimidopropionic hydrazide
- TMRIA
5-tetramethylrhodamineiodoacetamide
- FIA
fluorescein iodoacetamide
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Lauzon A M, Fagnant P M, Warshaw D M, Trybus K M. Biophys J. 2001;80:1900–1904. doi: 10.1016/S0006-3495(01)76159-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wu X, Clack B A, Zhi G, Stull J T, Cremo C R. J Biol Chem. 1999;274:20328–20335. doi: 10.1074/jbc.274.29.20328. [DOI] [PubMed] [Google Scholar]
- 3.Xiao M, Li H, Snyder G E, Cooke R, G, Yount R, Selvin P R. Proc Natl Acad Sci USA. 1998;95:15309–15314. doi: 10.1073/pnas.95.26.15309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Selvin P R. Nat Struct Biol. 2000;7:730–734. doi: 10.1038/78948. [DOI] [PubMed] [Google Scholar]
- 5.Saraswat L D, Lowey S. J Biol Chem. 1991;266:19777–19785. [PubMed] [Google Scholar]
- 6.Burmeister-Getz E, Cooke R, Selvin P R. Biophys J. 1998;75:2451–2458. doi: 10.1016/s0006-3495(98)77953-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Clegg R M, Murchie A I, Zechel A, Lilley D M. Proc Natl Acad Sci USA. 1993;90:2994–2998. doi: 10.1073/pnas.90.7.2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Selvin P R. IEEE J Quantum Electron. 1996;2:1077–1087. [Google Scholar]
- 9.Xiao M, Selvin P R. Rev Sci Instrum. 1999;70:3877–3881. [Google Scholar]
- 10.Greene L. Biochemistry. 1981;20:2120–2126. doi: 10.1021/bi00511a008. [DOI] [PubMed] [Google Scholar]
- 11.Conibear P B, Geeves M A. Biophys J. 1998;75:926–937. doi: 10.1016/S0006-3495(98)77581-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Heyduk T, Heyduk E. Anal Biochem. 2001;289:60–67. doi: 10.1006/abio.2000.4925. [DOI] [PubMed] [Google Scholar]
- 13.Roopnarine O, Szent-Gyorgyi A G, Thomas D D. Biochemistry. 1998;37:14428–14436. doi: 10.1021/bi9808363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cooke R. Nature (London) 1981;294:570–571. doi: 10.1038/294570a0. [DOI] [PubMed] [Google Scholar]
- 15.Corrie J, Brandmeier B, Ferguson R, Trentham D, Kendrick-Jones J, Hopkins S, van der Heide U, Goldman Y, Sabido-David C, Dale R, Criddle S, Irving M. Nature (London) 1999;400:425–430. doi: 10.1038/22704. [DOI] [PubMed] [Google Scholar]
- 16.Cooke R. Physiol Rev. 1997;77:671–697. doi: 10.1152/physrev.1997.77.3.671. [DOI] [PubMed] [Google Scholar]
- 17.Schmitz H, Reedy M C, Reedy M K, Tregear R T, Winkler H, Taylor K A. J Mol Biol. 1996;264:279–301. doi: 10.1006/jmbi.1996.0641. [DOI] [PubMed] [Google Scholar]
- 18.Chantler P D, Tao T, Stafford W F d. Biophys J. 1991;59:1242–1250. doi: 10.1016/S0006-3495(91)82339-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhao L, Gollub J, Cooke R. Biochemistry. 1996;35:10158–10165. doi: 10.1021/bi960505v. [DOI] [PubMed] [Google Scholar]
- 20.Knight P J. J Mol Biol. 1996;255:269–274. doi: 10.1006/jmbi.1996.0022. [DOI] [PubMed] [Google Scholar]
- 21.Rayment I, Rypniewski W R, Schmidt-Base K, Smith R, Tomchick D R, Benning M M, Winkelmann D A, Wesenberg G, Holden H M. Science. 1993;261:50–57. doi: 10.1126/science.8316857. [DOI] [PubMed] [Google Scholar]
- 22.Ikebe M, Kambara T, Stafford W F, Sata M, Katayama E, Ikebe R. J Biol Chem. 1998;273:17702–17707. doi: 10.1074/jbc.273.28.17702. [DOI] [PubMed] [Google Scholar]
- 23.Rayment I, Holden H M, Whittaker M, Yohn C B, Lorenz M, Holmes K C, Milligan R A. Science. 1993;261:58–65. doi: 10.1126/science.8316858. [DOI] [PubMed] [Google Scholar]
- 24.Durr E, Jelesarov I. Biochemistry. 2000;39:4472–4482. doi: 10.1021/bi992948f. [DOI] [PubMed] [Google Scholar]
- 25.Wendt T, Taylor D, Trybus K M, Taylor K. Proc Natl Acad Sci USA. 2001;98:4361–4366. doi: 10.1073/pnas.071051098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hopkins S C, Sabido-David C, Corrie J E, Irving M, Goldman Y E. Biophys J. 1998;74:3093–3110. doi: 10.1016/S0006-3495(98)78016-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Linari M, Dobbie I, Reconditi M, Koubassova N, Irving M, Piazzesi G, Lombardi V. Biophys J. 1998;74:2459–2473. doi: 10.1016/S0006-3495(98)77954-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bershitsky S Y, Tsaturyan A K, Bershitskaya O N, Mashanov G I, Brown P, Burns R, Ferenczi M A. Nature (London) 1997;388:186–190. doi: 10.1038/40651. [DOI] [PubMed] [Google Scholar]
- 29.Huxley H E, Faruqu A R. Annu Rev Biophys Bioeng. 1983;12:381–417. doi: 10.1146/annurev.bb.12.060183.002121. [DOI] [PubMed] [Google Scholar]
- 30.Tomishige M, Vale R D. J Cell Biol. 2000;151:1081–1092. doi: 10.1083/jcb.151.5.1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Uyeda T Q, Abramson P D, Spudich J A. Proc Natl Acad Sci USA. 1996;93:4459–4464. doi: 10.1073/pnas.93.9.4459. [DOI] [PMC free article] [PubMed] [Google Scholar]