Chromatic aberration (Cc) corrected cryo-EM: The structure of pseudorabies virus (PRV) using both zero-loss and energy loss electrons

Highlight

• •1 Application of Cc-correction in cryo-EM was explored.
• •2 Energy-loss electrons were used for single particle reconstruction.
• •3 Datasets of zero-loss and energy-loss electrons were compared.

Abstract

Here we have investigated the potential improvement in imaging vitrified biological specimens with the help of a chromatic aberration (Cc)-corrector. Using a newly developed chromatic aberration-corrected electron cryomicroscope (cryo-EM), the phase contrast micrographs comprising signals from both the zero loss and low energy loss (1-100 eV) channels were used to determine the structure of a pseudorabies virus (PRV). Using an energy selecting, electron energy loss spectrometer after the Cc corrector, datasets were collected separately yet sequentially on the same specimen to allow quantification of the signal in each of the respective channels. Both zero-loss first and low-loss first datasets were acquired. For further comparison, datasets from non-Cc-corrected cryo-EM were also collected. 3D reconstructions of the virus from all 4 above datasets are presented including two maps reconstructed only from electrons having lost 18-28 eV of energy whilst transiting the specimen. Although the amplitude contrast of the signals in the low-loss micrographs is opposite in sign to that of typical defocused images using only elastically scattered electrons, we show that the inelastic maps also contain detailed structural information which can be recovered using Cc correction. This can be verified by comparing the maps from each of the channels. Interestingly, the resolution of the reconstructed volume from the low-loss electrons decreases with defocus independently of the purely elastic electron images taken from the same specimen, which is consistent with previous theoretical predictions and experimental measurements of specimen induced decoherence using room temperature test specimens. Together, these results indicate that the inelastically scattered electrons do indeed contain useful phase contrast signals, particularly for thick specimens, but their recovery requires imaging as close to in-focus as possible. Combing the optical correction demonstrated here, with a lossless phase plate for in focus imaging, may offer the most straightforward way to achieve this in the future.

1. Introduction

Chromatic aberration correction has enabled major advances in electron microscope performance [1,2], particularly in the sub-angstrom range on metallic and two-dimensional specimens that are insensitive to radiation damage. It can significantly improve the information limit and reduce the focus spread caused by energy loss and is ultimately limited by Johnson noise rather than the traditional temporal coherence envelope function that limits standard transmission electron microscopes [3,4]. Haider et al. [5] demonstrated a significantly improved linear contrast transfer from a Cc-corrected electron microscope operated at 80 kV, for which the information limit increased from 0.16 nm to below 0.1 nm for an amorphous carbon film. Furthermore, it was shown that Cc correction offered significant improvements in both signal and resolution when imaging thick specimens: e.g. gold nanoparticles on 500 nm thick SiN [6] and in-situ atomic-level resolution imaging of colloidal Pt nano-crystal in a liquid cell [7].

In the context of biological specimens, it was recently shown that Cc correction offers potential improvement in the signal from thick biological specimens [8,9]. These advantages of a Cc corrector motivated us to commission the construction of a Cc corrected cryo-EM with all the standard features of a typical high-end transmission electron-microscope like automated specimen loading and data collection, and a high-speed, high-efficiency detector (Falcon 4/Gatan K3, etc.) but with the addition of a Cc-corrector optimized for stability and reliability in this context. Its use for in situ cryo-EM studies of biological specimens, in which the structure and distribution of the molecules can be obtained in their native cellular environment, is of particular interest [[10], [11], [12]]. In situ studies often employ electron tomography, where specimens are routinely tilted to ±70 degrees. At 70 degrees tilt, the specimen becomes three times as thick as it was 0 degrees. With thicker specimens, the fraction of inelastically scattered electrons increases dramatically; these are then incorrectly focused when using conventional electron cryomicroscopes due to chromatic-aberration of the objective lens, which is 2-3 mm in a typical 300 keV electron cryomicroscope designed for biology. Filtering out these inelastically scattered electrons reduces noise in an image but cannot recover the signal lost to these electrons. So, the Cc-corrector is expected to make use of some of these electrons and boost the signal in images of thick specimens (∼100-500 nm thick). However, whether the inelastically scattered electrons can contribute positively to the phase contrast of cryo-EM micrographs by Cc-corrector has not before now, been demonstrated.

The inelastic scattering process changes both the energy and direction of the entry electrons. Partial spatial coherence is preserved, which can be demonstrated by high-resolution energy filtered transmission electron microscope (EFTEM) imaging [2,13,14] and electron holography [[15], [16], [17]]. A Cc-corrector can significantly improve the EFTEM resolution from typically worse than 4 Å [18] to 1.35 Å resolution imaged using Si L_2,3 edge [14]. Kraus et al. also [13] employed the Cc correction on an energy-filtered STEM image and obtained an atomic-scale elemental distribution map. The spatial coherence was further quantitatively investigated using energy-filtered holography and to successfully predict fringe contrast as a function of energy loss [19].

Inelastically scattered electrons have an increased angular distribution, and therefore phase contrast carried by these electrons is more strongly focus dependent and generally reduced compared to zero-loss electrons. Two recent papers [8,9] have explored the potential applications of inelastic scattering in in situ cryo-EM for thick specimens. Experiments were carried out on gold nanoparticles using a Cc-corrected electron microscope operated at 200 kV to measure the phase contrast changing with defocus and spatial frequency, and the results fit well with the numerical studies. Conclusions were drawn that inelastically scattered electrons can enhance the signal from thick biological specimens close to focus with the help of a Cc-corrector, but the degree of enhancement will be defocus dependent. However, direct experiments using single particle analysis or electron tomography on vitrified biological specimens are still urgently needed. This study aims to provide a first glimpse of the potential of Cc-corrected imaging of biological specimens by single particle cryo-EM of a vitrified virus specimen using both zero-loss and inelastically scattered electrons. We employed highly symmetrical icosahedral (60-fold) deactivated Pseudorabies virus (PRV) virions as an experimental sample, with a diameter of around 120 nm that can generate enough inelastic signals for subsequent 3D refinement.

2. Materials and methods

2.1. Specimens preparation

Virus production and purification: Mature and infective Pseudorabies virus (PRV) virions were handled in BSL2 facilities at Cryo-Electron Microscopy Center, Southern University of Science and Technology, and at College of Animal Veterinary Medicine, Henan Agricultural University. A PRV strain isolated in the field was incubated in monolayers Vero Cells (ATCC CCL-81) at an approximate multiplicity of infection (MOI) of 0.01 for 30 min to allow viruses to bind and enter into the vero cells. The supernatant was removed and replaced with a fresh culture medium (DMEM with 2 % FBS and 1 % PS). PRV was proliferated in 10 T225 culture flasks and harvested 40 h postinfection. The cell debris of the supernatant was removed at 10,000 × g for 1 h (Sorvall LYNX 6000 Superspeed Centrifuge). The PRV particles were concentrated by centrifuging at 80,000 × g for 1.5 h in Ultracentrifuge (Beckman Optima XPN-100) with a type 45 Ti rotor at 4 °C. After soaking in 30 mL phosphate-buffered saline (PBS, pH 7.4) for 4 h, the virus suspension was initially purified via a 20 % (w/v) sucrose cushion at 80,000 × g for 1.5h in a type SW32 Ti rotor at 4 °C. The virus pellet was gently resuspended in 2 mL PBS buffer for 4h and loaded onto a linear 20 %–50 % (w/v) sucrose density gradient at 100,000× g for 2 h in an SW41 Ti rotor at 4 °C. The light scattering band corresponding to the virus was collected and resuspended in PBS. The integrity and purity of the PRV particles were examined by SDS-PAGE and mass spectrometry, and by negative-stain electron microscopy prior to preparing cryo-EM grids.

For vitrified specimen preparation, a 2.5-μL aliquot of PRV was pipetted onto glow-discharged holy carbon grids (Quantifoil Au R2/1, 200 mesh) and then blotted for 5 s using a Vitrobot Mark IV (Thermo Fisher Scientific, TFS) at 4 °C with 100 % humidity. Grids were stored in liquid nitrogen until examination.

2.2. Electron cryomicroscopes

Two types of electron cryomicroscopes were used in this study: 1) A Cc/Cs-corrected Titan Krios G4 (subsequently referred to as Cc-corrected cryo-EM) equipped with a Selectris energy filter and Falcon 4 direct electron detector (Thermo Fisher Scientific, TFS); 2) A Cs-corrected TFS Titan Krios G3i (subsequently referred to as non-Cc-corrected cryo-EM) equipped with Gatan Continuum 1069 energy filter and a K3 summit direct detector. Supplementary Fig. S1 shows photographs of the Cc-corrected cryo-electron microscope with its box closed and open. The Cc/Cs corrector is 890 mm tall and 310 mm in diameter, and is located in the column of the microscope immediately below the objective lens and above the projection chamber and energy filter. Both electron guns were X-FEGs and the microscopes were operated at 300kV and liquid nitrogen temperature. Images were collected during multiple microscope sessions, so before image collection began, the Cs value of each microscope was tuned to 5 ± 2 um and Cc value of the Cc-corrected microscope was tuned to 0±1 um to keep consistency. We note that during the commissioning and testing of the Cc-corrected microscope, a number of technical problems were encountered, which were difficult to address due to practical limitations during the COVID pandemic. Two in particular that were difficult to diagnose and address were stage vibrations caused by bubbling from a defect in a nitrogen dewar and interment image shifts in a corrector transfer lens likely due to an interment connection to one of the lenses. Both were intermittent and manifested as a loss of resolution (damping of Thon rings) along two similar but slightly distinct directions in the image plane. All these were eventually resolved with the help of many from CEOS GmBH and ThermoFisher Scientific.

2.3. Pseudorabies virus imaging

The energy filter was used to select a particular range of energy loss electrons (zero-loss electrons and low-loss electrons) and were used to form EFTEM images. In this study, the zero-loss images were from the zero-loss peak (ZLP), where the slit center is at 0 eV and the slit width is 10 eV (energy offset ΔE = 0 eV, width of energy window ΔW = 10 eV). For the purposes of collecting low-loss peak (LLP) images, the slit center was set to 23 eV and the slit width is set to 10 eV (ΔE = 23 eV, ΔW = 10 eV). Zero-loss electrons constitute approximately 55 % of the total dose, while low-loss electrons (18–28 eV energy loss) account for about 12 % of the total dose.

For Cc-corrected cryo-EM, dataset Cc-A and dataset Cc-B were collected, and the detailed information are shown in supplementary Table 1. For dataset Cc-A, the same region of interest was imaged first for zero-loss elastic image (Cc-A-ZLP1) and followed by a low-loss image (Cc-A-LLP2). For dataset Cc-B, the low-loss images (Cc-B-LLP1) were taken before zero-loss images (Cc-B-ZLP2). The data was collected in an automated way using SerialEM [20] with a nominal magnification of 53000x resulting in a pixel size of 1.7 Å. All raw image frames were stored in EER format. The overall defocus range was set from −0.3 to −3 μm. A total of 7535 positions were collected for Cc-corrected cryo-EM.

For non-Cc-corrected cryo-EM, dataset Non-Cc-C and dataset Non-Cc-D were also collected using SerialEM software with a nominal magnification of 64,000x resulting in a pixel size of 1.9 Å. The simplified experimental conditions were presented in Table 1 and detailed information was shown in Supplementary Table 2. The same region of interest was imaged first for zero-loss image in dataset Non-Cc-C, whereas for dataset Non-Cc-D, the low-loss image was taken first. Image stacks were collected in super-resolution mode with a preset defocus range from −0.3 to −3 μm. Due to the significant difference of dose rates on the detector while collecting zero-loss and low-loss electrons, all the movies were collected on the condition of gain unnormalized and were subsequently normalized during processing. A total of 6868 positions were collected for non-Cc-corrected cryo-EM. Gain references with different dose rates compatible with elastic and inelastic images were collected separately for both cryo-EMs and applied when conducting motion correction.

Table 1.

Experimental conditions for 4 datasets. First image and second image were taken on the same region.

	Dataset Cc-A	Dataset Cc-B	Dataset Non-Cc-C	Dataset Non-Cc-D
Microscope	Cc-corrected	Cc-corrected	Non-Cc-corrected	Non-Cc-corrected
First image	Cc-A-ZLP1	Cc-B-LLP1	Non-Cc-C-ZLP1	Non-Cc-D-LLP1
	ΔE=0 eV,	ΔE=23 eV,	ΔE=0 eV,	ΔE=23 eV,
	ΔW=10 eV	ΔW=10 eV	ΔW=10 eV	ΔW=10 eV
Second image	Cc-A-LLP2	Cc-B-ZLP2	Non-Cc-C-LLP2	Non-Cc-D-ZLP2
	ΔE=23 eV,	ΔE=0 eV,	ΔE=23 eV,	ΔE=0 eV,
	ΔW=10 eV	ΔW=10 eV	ΔW=10 eV	ΔW=10 eV

2.4. Single particle reconstruction process

For zero-loss images, the single particle reconstruction was conducted following the standard procedures outlined in Relion 4.0 [21]. Motion corrections of the movies was performed using MotionCorr2 [22]. Contrast transfer function (CTF) estimation was carried out using both CTFFIND4 [23] and Gctf [24] and each result manually evaluated for accuracy. The CTF parameters for images that were too close to focus for automatic fitting were adjusted manually. Particles were picked from each image by template matching and then extracted, summed. The CTF images of the particles were used for manual fitting. Particles picking from each image was also performed using Gautomatch, followed by extraction summation. After CTF estimation, the two-dimensional (2D) classification and three-dimensional (3D) auto-refinement of PRV particles were executed in Relion 4.0 [21]. An initial model based on a herpesvirus capsid structure (EMD-6907) was built up, with I1 symmetry applied.

For low-loss images, reconstructing the 3D volume density of particles using only these images is very challenging due to the weak signal. Therefore, the poses (position and angles) of particles were initially determined using corresponding zero-loss particles. The motion in the low-loss movies was corrected using MotionCorr2 [22]. To minimize drift between zero-loss and low-loss images from the same region, frames from the previous were aligned with the last frame of their respective movies. Additionally, the translational motion between the resulting two sets of images was also corrected using EMAN2 [25]. Particles from low-loss images were then extracted based on coordinates and poses derived from zero-loss particles, after which both zero-loss and low-loss particles were combined for a final round of 3D local refinement. Following 3D refinement, zero-loss and low-loss particles from different datasets were separated and used for individual 3D reconstructions without further refinement. To investigate the impact of defocus on the resolution of reconstructed volume density from low-loss images, particles were categorised further by defocus values within specific ranges (Fig. 6). For 3D reconstructions of low-loss particles using negative amplitude contrast, Relion 4.0 was modified to permit the application of negative amplitude contrast to low-loss particle images, a feature not supported in the standard version.

Fig. 6.

(a-d) The low-loss EM density volume reconstructed from combined dataset Cc-A-LLP2 and Cc-B-LLP1 with various defocus range: (a) 0-3500 Å defocus range with 9.7 Å resolution; (b) 3500-7000 Å defocus range with 9.5 Å resolution; (c) 7000-13000 Å defocus range with 9.8 Å resolution; (d) 13000-30000 Å defocus range with 11.0 Å resolution. Each subset contains 10,000 particles; (e) The resolution change with different defocus range using different FSC criterions for estimation of resolution.

2.6. Amplitude contrast measurement

The amplitude contrast of the PRV particles was estimated based on the method described in reference [26]. Subsequent pairs of raw movies were acquired from the same region of interest, using slit widths of 10eV and 60eV respectively, with the slit center set at 0eV (ΔE = 0 eV) and varying value of over-focus. The raw movies underwent motion-corrected using MotionCorr2 [22], defocus estimation was conducted with CTFFIND4 [23], and particle picking and extraction were performed using Relion 4.0. To determine the amplitude contrast, the azimuthal average of the 2D Fast Fourier Transform (FFT) of the particles was calculated in Gatan Digital Micrograph. The first cross-over point of the Contrast Transfer Function (CTF) curve was identified, from which the amplitude contrast value was subsequently derived.

3. Results and discussion

3.1. Inelastic image of PRV particles and its 3D reconstruction

In a Young’s double slit experiment [27] using a gold-on-carbon cross grating grid (Fig. 1a), shows that the information limit was extends to 1 Å in all directions following the tunning of the Cc-corrector. For investigating the defocus spread, a carbon film (Quantifoil) was used and zero-loss and low-loss images with different defocus values were captured at the same position. For Cc-corrected microscope defocus shift was -1.5±5.3 nm. In contrast, an identical experiment conducted on the non-Cc-corrected microscope resulted in defocus shift of -292 ± 20 nm for 23 eV energy shift (Fig. 1b). This indicates that the Cc-corrector effectively eliminates defocus spread caused by energy shifts.

Fig. 1.

Performance tests of the Cc corrected cryomicroscope at 300 keV. A Young’s double slit experiment using a gold on carbon cross grating grid is shown in (a). The fringes extend to 1 Å in all directions, with one axis slightly weaker as indicated by the arrow. In (b) the difference in measured defocus between the zero-loss and low-loss electrons vs. defocus, measured from the CTF fits in each case, is plotted for a Cc/Cs corrected and a Cs corrected microscope. The oscillations about zero are a result of errors in the fits which increase close to zero defocus.

At first glance, the raw zero-loss and low-loss electron micrographs exhibit markedly different appearance. Fig. 2 illustrates pseudorabies virus as dark particles against a bright vitrified ice background in the conventional elastic image, while the virus particles appear bright in the relatively dark background in the inelastic image. Both Cc-corrected and non-Cc-corrected images consistently display this characteristic. Magnified views of the low-loss image reveal that the Cc-corrected low-loss image exhibits significantly stronger contrast and more detailed features compared to its non-Cc-corrected images. Typical images from dataset Cc-A and dataset Cc-B are shown in Supplementary Fig. S2 and Supplementary Fig. S3. The selected reference-free 2D class averages of PRV using only elastically scattered electrons from dataset Cc-A-ZLP1 are shown in Supplementary Fig. S4. The observed difference in contrast is attributed to variations in the amplitude contrast term of the CTF. To clarity this phenomenon, Fig. 3(a) presents a comparison of the 2D power spectra of zero-loss signals and low loss signals from a carbon film (Quantifoil) using Cc-corrected cryo-EM. While the positions of the Thon rings in the ZLP and LLP power spectra are nearly identical, higher spatial resolution signals are more strongly in the ZLP image compared to the LLP image. Fig. 3(b) compares the rotationally averaged one-dimensional power spectra. The first minimum in the LLP power spectrum appears slightly to the right of the ZLP power spectrum, which aligns with the CTF curve with an opposing amplitude contrast. The CTF of LLP signals exhibits a small positive value for amplitude contrast (y-intercept of the CTF function) as opposed to the typical negative found for ZLP images. At higher frequencies, the positions of maxima and minima are quite similar, yet the signal decay in the LLP is noticeably faster than in the ZLP. The phase shift due to changes in amplitude contrast primarily affects in the low-frequency part comparing to the elastic electrons and is not significantly different at high spatial frequencies. Therefore, the CTF correction used for elastic signals remains valid for inelastic signals used for high spatial frequency reconstruction. In the current 3D local refinement process of LLP signals, the CTF correction is applied only after first peak (In Relion 3D auto-refine options, set Do CTF-correction and Ignore CTFs until first peak to yes).

Fig. 2.

PRV in vitrified ice imaged using cryo-EM: (a) Cc-corrected zero-loss image (top left, from dataset Cc-A-ZLP1) and low-loss image (top right, from dataset Cc-A-LLP2) from the same region. Part of the low-loss image was magnified and shown in the bottom for more details. (b) Non-Cc-corrected zero-loss image (top left, Non-Cc-C-ZLP1) and low-loss image (top right, Non-Cc-C-LLP2) from the same region. Magnified low-loss image is also shown on the bottom.

Fig. 3.

(a) 2D power spectrums from ZLP image (ΔE=0 eV, ΔW=10 eV) and LLP image (ΔE=60 eV, ΔW=100 eV taken at same defocus value of about -280 nm. The upper half includes the simulated (upper left) and experimental (upper right) power spectra from the ZLP image, while the lower half displays the simulated (lower left) and experimental (lower right) power spectra from the LLP image; (b) 1D rotational averaged power spectrums show the first minima of LLP curve appears slightly to the right comparing to ZLP curve at low spatial frequency.

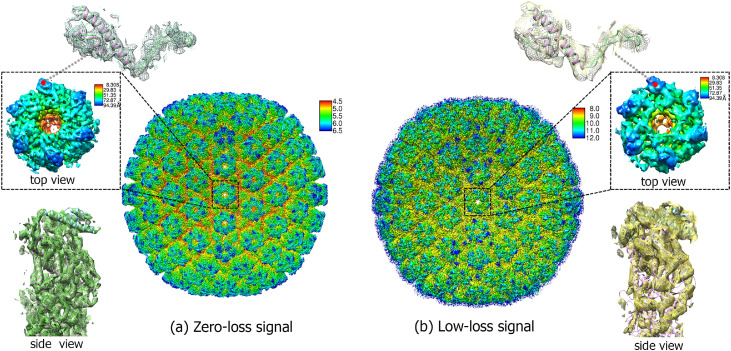
Sections through the 3D reconstructed maps are presented in Fig. 4. The related Fourier Shell Correlation (FSC) plots [28] are shown in Supplementary Fig. S5 and Fig. S6. The zero-loss reconstructions from the Cc-corrected and non-Cc-corrected microscopes (Fig. 4a and c) had a resolution of 4.9 Å and 7.2 Å respectively. These maps were consistent given the resolution and number of particles. In contrast, the low-loss map from the Cc-corrected cryo-EM (Fig. 4b) shows more detail and better resolution compared to that from the non-Cc-corrected cryo-EM (Fig. 4d). With Cc-correction, the cross-section in Fig. 4b resembles the one from the zero-loss maps, albeit at lower resolution. However, without the Cc-correction, there are barely any distinctive features and only a vague shape can be obtained (Fig. 4d). The comparison of radially coloured PRV particles reconstructed from elastic and inelastic signals was also shown in Fig. 5. The volume density from both reconstructions shows similarity in general. However, the inelastic reconstruction shows poorer resolution and appears noisier. The top view of the low-loss reconstruction exhibits a higher density comparing to the side view, where the density in the side view appears discontinuous. This suggests that the surface of the low-loss reconstruction has a stronger density comparing to the inside density which might be associated with signals from surface plasma. The discontinuous in density is due to insuggicient signals relative to the zero-loss signals and requires more particle mumber for reconstruction.

Fig. 4.

The central cross section of the reconstructed density volume of the PRV using Cc-corrected cryo-EM (a, b) and Non-Cc-corrected cryo-EM (c, d). (a) Volume densities were reconstructed from zero-loss images from dataset Cc-A-ZLP1 under standard CTF correction (23194 particles); (b) low-loss reconstruction from random subset of dataset Cc-A-LLP2 and Cc-B-LLP1 (17,536 particles, specific particle numbers were chosen to maintain consistency with Fig. 4d). The CTF of the LLP particles was corrected only after the first peak to minimize the effect of reversal amplitude contrast; (c) Volume densities were reconstructed from the zero-loss image of dataset Non-Cc-C-ZLP1 under standard CTF correction (7565 particles); (d) Low-loss reconstruction from the combined dataset Non-Cc-C-LLP2 and Non-Cc-D-LLP1, with CTF correction applied after the first peak (17,536 particles).

Fig. 5.

(a) PRV particle reconstructed from zero-loss electron images using Cc-corrected cryo-EM colored with local resolution. The radially colored magnified subarea contains top view of small capsid proteins (SCPs) on the surface and major capsid proteins (MCPs) on the bottom. The segmented density map (mesh) and corresponding atomic models of SCP are also indicated. The side view of the SCPs and MCPs were shown in the bottom left; (b) PRV particle reconstructed from low-loss electron images using Cc-corrected cryo-EM and its corresponding magnified subarea are shown.

3.2. The inversed amplitude contrast of PRV particles in inelastic images

The opposite amplitude contrast raised issues in CTF correction only for inelastic electrons. The conventional CTF correction is based on the simulated CTF curve for zero-loss electrons and does not apply well for the energy-loss electrons. To understand the change in the contrast in quantitative way, we now consider how the standard CTF used in cryo-EM reconstructions has to be modified to correctly interpret images using only low-loss electrons.

The contrast transfer function omitting the envelope function is [26]

$$\text{CTF}=\text{sin}\left(2\pi \left(\frac{1}{4}{\mathrm{C}}_{\mathrm{s}}·{\lambda }^3·{\mathrm{k}}^4-\frac{1}{2}\Delta \mathrm{z}·\lambda ·{\mathrm{k}}^2\right)-\text{arcsin}\left[\mathrm{Q}\left(\mathrm{k}\right)\right]\right)$$ (1)

Where $\mathrm{Q}\left(\mathrm{k}\right)$ is the ratio of the attenuation term to the total contrast, which is defined as amplitude contrast, $\lambda$ is the electron wavelength, $\Delta \mathrm{z}$ is the defocus and $\mathrm{k}$ is the spatial frequency. Aside from a loss of spatial coherence, electrons in the low loss regime (<100 eV) encode the same information as the primary beam (as discussed in Refs [8,9]). Therefore, the contrast transfer function is still valid once the electron wavelength and the amplitude contrast value are appropriately adjusted. It is possible that future work may improve the analytical description of the CTF for energy loss electrons but Fig. 3b shows that Eq. (1) is good enough for now. It is possible to estimate the amplitude contrast of vitrified specimens in various ways [29,30,26], e.g. from the position of the zero-crossover point at low spatial frequency and the amount of defocus using an over-focused elastic micrograph [26]. However, the inelastic images and the corresponding FFT images have very limited signal due to dose limitation of vitrified biological sample, meaning we were unable to conduct the measurement of the amplitude contrast directly. In this study, the PRV particles were imaged using zero-loss peaks with slit widths of 10 eV and 60 eV separately to compare the difference in amplitude contrasts (Fig. S7). The findings align with existing literature, which indicates the amplitude contrast of vitrified specimens is typically negative, ranging from a few to ten percent [26,29,30]. A narrower slit width results in a higher absolute value of amplitude contrast. This suggests that inelastically scattered electrons possess an opposite sign of amplitude contrast compared to elastically scattered electrons, consequently reducing the low-frequency contrast of PRV particles. This phenomenon explains why filtering out energy-loss electrons can enhance amplitude contrast in traditional cryo-EM [26]. Unfortunately, Fig. S7 does not supply the amplitude values for low-loss signals. Therefore, a range of amplitude values were directly applied in the reconstruction of low-loss signals to determine if any meaningful insights could be obtained. As illustrated in Fig. S8, the optimal reconstructions (with a flat background) occurred within the range of 0.02 to 0.04, indicating an expected amplitude contrast value of approximately 0.03 for low-loss PRV particles.

3.3. The effect of defocus range on the reconstructed resolution

The measurements conducted by Dickerson et al. [8] on gold nanoparticles deposited on carbon film revealed that there is a strong defocus dependent signal loss in the phase contrast within the energy loss channels due to the specimen induced incoherence. To investigate this phenomenon further in virus datasets that include inelastically scattered electrons, we divided the Cc-corrected low-loss datasets into groups based on different defocus ranges and carried out reconstructions from each group, along with corresponding Fourier Shell Correlation (FSC) plots to evaluate resolution as a function of defocus. The central slices of the reconstructed volume at different defocus values are illustrated in Fig. 6. Fig. 6a shows a structure close to in-focus, achieving a resolution of 9.7 Å. The structure exhibits fine features but suffers from low contrast, potentially due to the very low contrast for particle refinement and inaccuracies in defocus measurement. A defocus near zero significantly reduces the phase contrast for both elastic and inelastic images, complicating 3D reconstruction process. Fig. 6b–d illustrate increasingly coarser structures with higher defocus values, resulting in progressively poorer resolutions. The finest structures are observed in Fig. 6b. Fig. 6e compares the resolutions of LLP volumes within different defocus ranges using various FSC cutoffs, all of which show a consistent trend. The corresponding FSC curves are presented in Supplementary Fig. S9. Finer defocus ranges were also assessed, however, resolution criteria based on a FSC = 0.143 value is not valid due to the zero crossing on the CTF curve significantly affecting the information recovery. Nonetheless, the FSC curves of both zero-loss and low-loss reconstruction are displayed in Supplementary Fig. S10.

Fig. 7 illustrates the Rosenthal B-factor of LLP reconstructions using FSC 0.143 criterion corresponding to various defocus ranges displayed in Fig. 6. No clear trend was observed in the B factors. For instance, the highest resolution was obtained within the defocus range of 3500-7000 Å, while the highest B factor of 193 Ų was also in this range, which theoretically corresponds to the lowest resolution. The intrinsic reason for this inconsistency remains unclear. However, one possible explanation is that contrast decay rates of signals at different spatial frequencies are different. At the same defocus value, the contrast of signals at low spatial frequency are significantly higher compared to the contrast of signals at higher spatial frequency. Consequently, for reaching lower spatial resolution, the B factor may be smaller. In contrast, for higher spatial resolution signal, the B factor is larger. When comparing the particle number and the resolution, the defocus range 3500-7000 Å has the highest resolution. Also, the B factor of 193 Ų for defocus range of 3500-7000 Å is colesly with the overall B factor of 225 Ų for the whole dataset, as shown in Fig. 8.

Fig. 7.

Rosenthal-Henderson plots of LLP volumes reconstructed using particles within different defocus range.

Fig. 8.

Rosenthal plot [31] for reconstructions of PRV virus under different imaging conditions. Cc-corrected low-loss electron reconstruction combines dataset Cc-A-LLP2 and Cc-B-LLP1; Cc-corrected zero-loss reconstruction originated from dataset Cc-A- ZLP1. Non-Cc-corrected low-loss reconstruction combines dataset Non-Cc-C-LLP2 and Non-Cc-D-LLP1; Non-Cc-corrected zero-loss reconstruction originated from dataset Non-Cc-C-ZLP1.

3.4. The comparison of B factors for different imaging conditions

Fig. 8 presents the Rosenthal plot [31] for reconstructions of PRV virus under various imaging conditions. The Cc-corrected elastic reconstruction without pre-exposure exhibits the lowest B-factor of 78±3 Ų, which is significantly better than the non-Cc-corrected elastic reconstruction with a B-factor of 128±8 Ų. The Cc-corrected inelastic reconstruction has a higher B-factor (225±12 Ų) compared to both elastic reconstruction, which is consistent with faster contrast decay off LLP signals at higher resolution comparing to ZLP signals (Fig. 3b). Among all the reconstructions, the non-Cc-corrected LLP volume has the largest B factor.

Our findings here demonstrate the potential of using all the inelastically scattered electrons for imaging biological specimens, most of which are typically lost in standard electron cryomicroscopy of thick specimens. It is evident that a significant amount of signal encoded in the inelastically scattered electrons which are usually discarded in the cryo-EM of thick specimens. Moreover, a Cc-corrector can recover these signals, subject to two important considerations. 1. The CTF for inelastically scattered electrons is distinct in amplitude contrast (i.e. opposite) from that of elastically scattered electrons. 2. The extent of signal recovery by Cc-correction is defocus dependent, with lower defocus values being the more favorable. This requirement, in turn, makes it more difficult to determine the CTF accurately in an individual micrograph, necessitating methods like those proposed in [32] and [33] to improve CTF fitting at low-defocus values. Additionally, combination of Cc-correction with in-focus imaging using a phase plate, as demonstrated by the group at Berkley [34] may offer the best opportunity to recover all the phase information from the inelastically scattered electrons. Both the Cc-corrector and the phase plate require imaging as close to focus as possible to maximize information transfer over the special frequencies relevant for biological studies. However, in-focus imaging presents substantial challenges for data collection and processing as both single-particle methods and in-situ/tomographic imaging demand precise measurement of the contrast transfer function for each micrograph. Therefore, it would make sense to eventually integrate these two elements in a single instrument and addressing the in-focus imaging challenge could provide combined benefit for imaging molecules in cells and large biological specimens.

4. Conclusion

As increasing research interest has grown on in-situ cryo-EM, hardware improvements aimed at imaging thicker specimens has become urgently needed. This paper has explored the possibility of preserving the signal from inelastically scattered electrons by correctly focusing them with a Cc-corrector. For the first time, single-particle reconstructions from inelastic electrons with a range of energies were carried out using a vitrified pseudorabies virus and a 9.3 Å resolution volume density was obtained with the help of a Cc-corrector. More work is needed to quantify the true potential of Cc correction at minimal defocus values but the potential for biological imaging with phase contrast from inelastically scattered electrons is now increasingly clear.

CRediT authorship contribution statement

J. Wu: Writing – original draft, Validation, Investigation, Formal analysis, Data curation. C. Liu: Resources, Methodology, Formal analysis. A.J. Wang: Resources. Y.Z. Gao: Software, Data curation. L.T. Fu: Methodology, Data curation. Z. Liu: Resources. J.L. Dickerson: Formal analysis, Data curation. C.J. Russo: Writing – review & editing, Validation, Methodology, Formal analysis, Conceptualization. P. Wang: Writing – review & editing, Validation, Supervision, Resources, Methodology, Funding acquisition, Formal analysis, Data curation, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.