Difference in Network Effects of Pulsatile and Galvanic Stimulation

Abstract

Biphasic pulsatile stimulation is the present standard for neural prosthetic use, and it is used to understand connectivity and functionality of the brain in brain mapping studies. While pulses have been shown to drive behavioral changes, such as biasing decision making, they have deficits. For example, cochlear implants restore hearing but lack the ability to restore pitch perception. Recent work shows that pulses produce artificial synchrony in networks of neurons and non-linear changes in firing rate with pulse amplitude. Studies also show galvanic stimulation, delivery of current for extended periods of time, produces more naturalistic behavioral responses than pulses. In this paper, we use a winner-take-all decision-making network model to investigate differences between pulsatile and galvanic stimulation at the single neuron and network level while accurately modeling the effects of pulses on neurons for the first time. Results show pulses bias spike timing and make neurons more resistive to natural network inputs than galvanic stimulation at an equivalent current amplitude.

I. Introduction

Biphasic pulsatile stimulation (PS) is the present standard for safe long-term electrical stimulation of the brain. As a result, single sub-millisecond pulses or sequences of pulses are commonly used to excite areas of the brain to understand connectivity and functionality of the brain, through brain mapping studies[1]–[3]. Additionally, clinically, pulses are used for stimulation in neural prosthetic treatments[4], or pre-resection surgeries for drug-resistant epilepsy[5]. While pulses are clearly capable of inducing sensations (as relied on for sensory neural prosthetics)[4] and have been experimentally used to bias decision making[6] or trigger arm movements[7], there are numerous observed limitations to their ability to drive perception with the same spectrum of experience as natural sensation[8] or to induce movements with the precision and control observed naturally[9].

Investigations of the source of these deficits seem to point to a lack of naturalistic firing induction throughout processing networks being interacted with electrically. In the case of the cochlear implants, deficits include a lack of ability to distinguish hearing in noise, which points to an inability to trigger top-down network effects[10]. Additionally, in the vestibular system, pulsatile stimulation has been found to drive neural firing with unnatural regularity (timing closely aligned to the timing of pulse delivery) across thousands of neurons in the population; this unnatural synchrony has been hypothesized to cause adaptation of higher order areas and reduced effectiveness of electrical stimulation at behavior over time[11]. These effects have not been thoroughly investigated in vivo or in silico.

Galvanic stimulation (GS), extended periods of current delivery with no restriction to balance negative or positive charge, has re-emerged as an alternative form of stimulation, due to the recent development of novel, implantable galvanic stimulation devices[12]. GS causes larger, more naturalistic vestibulo-ocular reflex (VOR) eye responses to vestibular stimulation[13], and it modulates single neuron firing rates up and down while preserving natural firing statistics and without producing unnatural synchrony[14], [15]. Detailed biophysical modeling predicts that GS has these effects because it modulates axonal sensitivity to incoming inputs[15]. As a result, GS is predicted to cause any neuron within the field to experience the same directional modulation, so neurons will modulate firing rate up or down together, with modulation proportional to the distance from the electrode[15].

In contrast, recent investigations of the single neuron effects of pulsatile stimulation reveal that the source of limited recovery of function for neural prosthetics could be non-linear relationships between pulse parameters (pulse rate and pulse amplitude) and the induced firing rate of neurons[16], [17]. Pulses were shown to produce unnatural activations of voltage-gated channels that result in facilitation or inhibition of firing, depending on pulse parameters and the level of natural activity (i.e., EPSCs arriving at the axon). These findings suggest that neighboring neurons with on-going activity will not experience the same induced firing rate and that as distance from the electrode increases mixed effects will be observed throughout the population[17]. Importantly, GS has been shown to produce more naturalistic behavioral responses than PS[13], suggesting that these differences in single neuron stimulation may lead to differences in network effects of the two paradigms.

The effects on single neurons described above lead to strong predictions about how populations of neurons and therefore network activity may be altered by PS versus GS. However, existing models have not included these recently uncovered effects of pulses on single neurons[17]. Typically, the leaky-integrate-and-fire (LIF) model, a simplified channel model, has been used to create simulations with hundreds of neurons for computational efficiency. Thus, past models of electrical stimulation of a behavioral network have not accounted for the complexities of PS mentioned above [18]–[20]. This study aims to answer the question of how pulses induce coherent behavior in networks of neurons, while producing complex population-level firing patterns that are different from the natural ones. Additionally, this study investigates whether GS has different network-level firing behaviors compared to natural and pulsatile. We also observe how these differences in firing patterns in response to each stimulus type may lead to differences in experimentally testable behavioral responses.

To study these different response patterns, we introduced both forms of stimulation in silico to a winner-take-all (WTA) decision-making network[21] and compared the effects on individual neuron spiking, mean firing rates of motion-selective populations, and network-level decisions (Figure 1). The experimental paradigm was based on a classic decision making experiment in which pulsatile microstimulation of a population of neurons associated with one choice was shown to shift the accuracy versus coherence curve [6], [22]. To ensure equivalence in stimulation amplitude, PS and GS were parameterized to change the average firing rate of the biased population (P1) by 3 spikes per second (spk/s) across ten simulated “brains” with different sensitivities to electrical stimulation. Despite the apparent equivalence in electrical stimulation inputs, we observed that PS directly affected more neurons than GS and induced highly regular synchronous firing that quickly propagated through the network. At the population level, pulses maintained unnaturally elevated firing rates in the stimulated population, even when the stimulated population lost the trial. This resulted in PS inducing a greater bias in decision making than GS for the same population-level firing rate change in this firing-rate-dependent network. Together, these effects show several ways in which both paradigms interact with networks of neurons that should cause differences at the behavioral and neural computation levels.

Figure 1.

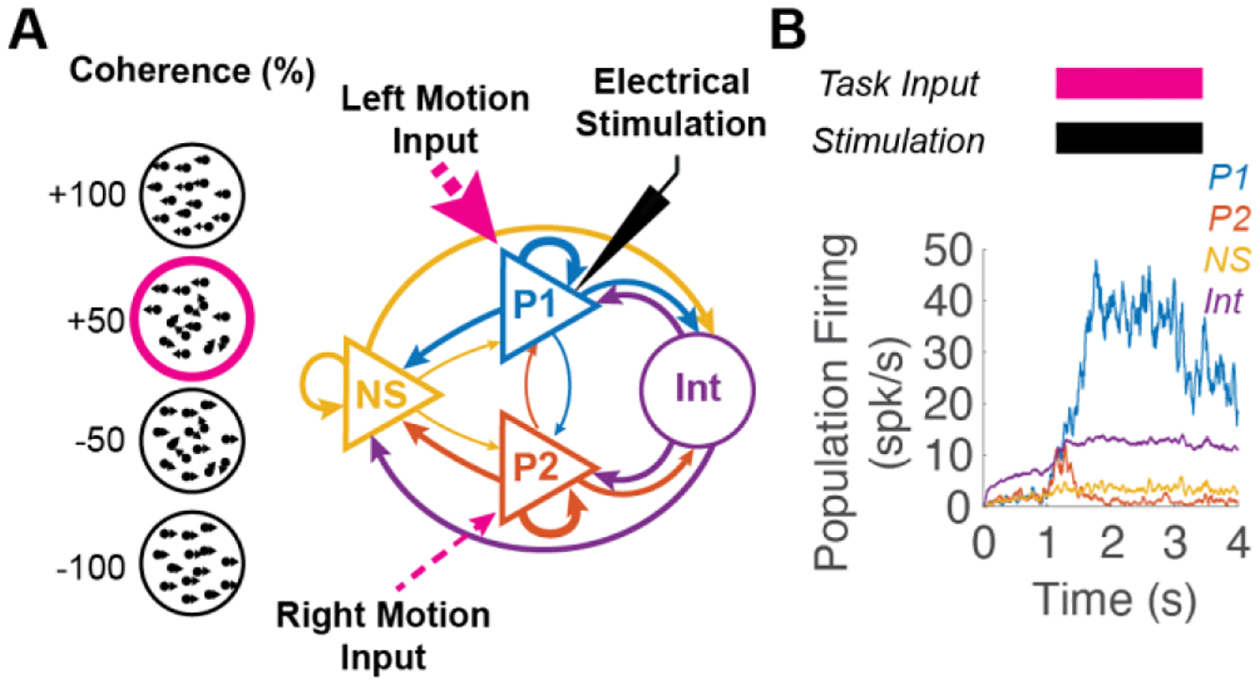
Experimental Design. (A) Model consists of two subpopulations (P1 and P2) responsive to leftward and rightward motion, non-selective pyramidal neurons (NS) and inhibitory interneurons (Int). Neurons are connected with strong, medium, and weak connections (thickness proportional to strength). During a trial, all neurons receive background input. From 1–3s, P1 receives input proportional to coherence of left versus rightward motion. Stronger input to P1 shown for +50% leftward coherence in magenta. P1 also receives electrical stimulation from 1–3s (black) to bias the network. (B) Mean population firing rates of P1 (blue), P2 (red), NS (yellow) and Int (purple) in a representative pulsatile stimulation trial. Stimulation and take input timing shown above.

II. Materials and Methods

A. Perceptual Decision-making Task

A random dot motion task was simulated at coherence levels from fully leftward (+100%) to fully rightward (−100%) coherence (Figure 1A circles). 36 trials were run at each coherence level under three conditions: pulsatile, galvanic, and control. Throughout the 4-second trial, all neurons received 2400 Hz background Poisson inputs that triggered AMPA EPSCs. This caused neurons in the network to fire spontaneously at 2–3 spk/s (Figure 1B). At t = 1 s, neurons in populations P1 (blue) and P2 (red) received task-related input proportional to coherence (c):

$$I_{\mathit{\text{task}}}=40c+40$$ (1)

where if motion is in the opposite direction c is negative [21] (Figure 1A–B, magenta). To bias the network, all neurons in P1 also received electrical stimulation (black) concurrent with task input (Figure 1). At t = 3 s, task-related inputs and stimulation ceased, and P1 or P2 kept a high firing rate if a decision was made favoring that population. Decision making experiments show a sigmoidal relationship between coherence and accuracy. To capture this relationship, coherences were sampled logarithmically (in 5 steps) around the empirically determined center of the sigmoid for each stimulation condition. For control stimulation, this was 0% [21][22]. For pulsatile and galvanic stimulation, the center coherences were estimated as −72.4% and −36.2% respectively.

B. Biophysical Attractor Model

The biophysical model used was based on a well-established decision-making network described in [21]. The model simulates a two alternative forced choice task with P1 (blue) and P2 (red) encoding task input (strength of moving dot leftward versus rightward motion). A non-selective (NS) population (yellow) and inhibitory interneuron (Int) population (purple) are also included for a winner-take-all network construction (Figure 1A). The network model consisted of N neurons (80% pyramidal neurons and 20% inhibitory interneurons), connected with weights

$$w_s=1.7,w_m=1,w_w=0.8765$$

for strong, medium, and weak connections respectively (Figure 1 strength shown with line thickness). Importantly, all neurons in this model were connected with one of these three weights. The model simulated neurons with leaky-integrate-and-fire (LIF) dynamics and synaptic currents from AMPA, NMDA, and GABA receptors. For our simulations, N = 1000 neurons and a time step of dt = 0.05ms were used. The model was modified to include more accurate effects of pulsatile stimulation.

C. Realistic Intracortical Microstimulation

Three electrical stimulation conditions were simulated in the model: pulsatile, galvanic, and control.

Pulsatile stimulation parameters were selected based on [22]: 10 μA, 300 μs/phase, 200 pulse/s. Because the decision network relied on population firing rate, galvanic stimulation amplitude (28 nA) was chosen such that the average firing rate increase in P1 matched that of pulsatile stimulation for disconnected neurons (~3 spk/s, Figure 3C). In the control condition, no electrical stimulation was delivered. In all three conditions, the background and task-related inputs and neuron-electrode distances were the same, allowing a control counterfactual comparison.

Figure 3.

Effects of pulsatile (red), galvanic (green) and control (black) stimulation on individual P1 neural firing rates. Subjects with disconnected (A-C) and connected (D-F) neurons are investigated. Each neuron’s start-of-task firing rate (t=1.0–1.1s) is shown as a function of its distance to the stimulation electrode (A: full P1, B: closest 20% of P1). Bar graphs (C and F) depict each brain’s population-averaged change in firing rate relative to control. For all trials, task-related input was equal for P1 and P2 (coherence = 0%). The effect of pulses on change in start-of-task firing rate was significantly stronger than galvanic (p<0.00001,****).

Current was assumed to spread through a uniform resistivity medium from the electrode to the neuron. This resulted in an internal current inversely dependent on the square of the distance:

$$I_{\mathit{\text{internal}}}=-\frac{I_{\mathit{\text{electrode}}}\times A_{\mathit{\text{axon}}}}{4\pi r^2},$$ (2)

where A_axon is the surface area of a typical axon segment (100 μm²). Our recent simulation work [17] showed that when biphasic pulsatile stimulation (PS) is introduced to neurons exhibiting spontaneous firing, a variety of interactions can occur that deviate from the classical assumption that every pulse produces an action potential (AP). For example, pulses can block subsequent spontaneous APs, spontaneous APs can block subsequent pulses, and pulses can block subsequent pulses. These refractory effects are amplitude-dependent, with higher-amplitude pulses causing longer blocking periods. Here, we adapted these effects[17] to the neural dynamics of LIF neurons in our decision-making network [21]. Using the blocking times from Steinhardt et al. [17] (0–132 ms) scaled to the range of pulse amplitudes relevant for LIF dynamics (0–278 nA), we reproduced the non-monotonic, amplitude dependent relationship between pulse rate and firing rate.

D. Simulating Distinct Virtual Subjects

In physical pulsatile microstimulation experiments, monkeys show high variability in their responsiveness to the pulse input[6], [22], [23], likely due to variability in the placement of the stimulation electrode relative to target neurons. To simulate this effect, for each subject, neurons in P1 were placed randomly from 10 μm to 2 mm away from the stimulation electrode based on geometry of the putative decision-making microcircuit[24], [25]. This gave each virtual subject a slightly different sensitivity to electrical stimulation inputs.

E. Decision Data Analyses

Instantaneous neuron firing rates were calculated in 5 ms bins, followed by a 50 ms moving average. Population firing rates were then taken as the average instantaneous firing rate of all the neurons in a given subpopulation. Decisions were recorded at the end of the 4-second trial, if the final average firing rate of one of the two neural subpopulations (P1 or P2) exceeded 15 spk/s, while the other did not. In such cases, the subpopulation whose firing rate exceeded 15spk/s was deemed the “winner” of the trial. This threshold was chosen based on [21]. Decision data were then analyzed using logistic regression as in [22]. The time at which the winning subpopulation exceeded 15 spk/s after the start of task stimulation (t = 1 s) was considered the decision time.

Comparisons of decision-making metrics between the three stimulation conditions were assessed for significance by 1-way ANOVA. Activation of neurons was determined by whether stimulation caused a change in firing rate three standard deviations from control levels. Phase-locking of neurons to the pulse stimuli was assessed by measuring the percentage of APs occurring during pulse presentations for each neuron. If the percentage differed from control levels by three standard deviations or more, that neuron was determined to be significantly phase-locked to the pulses. Regularity of spiking was assessed using coefficient of variation (CV). Synchrony of firing between pairs of neurons was quantified by measuring the percentage of coincident APs, normalized to the neuron with the higher overall firing rate. To facilitate comparison with phase-locking, APs were deemed coincident if they occurred within one pulse phase (300μs) of each other. If the percentage of coincident APs was greater than the maximum value achieved in the control condition (3.7% for disconnected networks, 6.7% for connected), that neuron pair was determined to be significantly synchronized. Comparisons of changes in end-of-task and start-of-task firing rates between galvanic and pulsatile stimulation were assessed for significance by unpaired t-tests. Distributions of single-neuron firing rates were also investigated, and comparisons were assessed for significance by Kolmogorov-Smirnov tests.

III. Results

The effects of pulsatile and galvanic electrical stimulation were assessed on networks of neurons in this study by exposing a well-established attractor model [21] of decision making to both paradigms. To ensure a fair comparison between the two stimulation modalities, we selected stimulation amplitudes such that both produced the same average increase in firing rates in the stimulated population (+2.78±0.18spk/s for galvanic, +2.83±0.04spk/s for pulsatile). Since network-level decisions in the model only depend on population-averaged firing rates, we expected this to equalize the effects of galvanic and pulsatile stimulation. Despite this apparent equivalence, differences in behavioral, neuron-level, and population-level effects were observed.

A. Behavioral Differences

The behavioral effects of PS and GS were measured by the change in the percentage of trials the stimulated population (P1) won and the decision time. Although both paradigms changed the firing rate of disconnected neurons by only ~3 spk/s, they significantly biased the decision making of the network toward choosing P1 (p<0.00001 by 1-way ANOVA). PS caused a significantly larger shift in the coherence curve (p<0.00001 by 1-way ANOVA), shifting the curve by 66.44% (red), while GS shifted it by 38.31% (Figure 2A green).

Figure 2:

Effects on decision making and decision time. The decision metrics across subjects at the same coherence levels for pulsatile (red), galvanic (green) and control (black) conditions. (A) The percentage of trials in which the stimulated population (P1) wins the decision-making process. (B) The time it takes for the winning population to clear the decision threshold (15 spk/s). Bold error bars depict mean and standard error at each coherence level.

Both stimulation paradigms also significantly reduced decision times (p<0.00001 by 1-way ANOVA) and shifted the coherence curve left so that peak decision time was at a more negative coherence (Figure 2B, p<0.00001 by 1-way ANOVA). PS reduced overall decision-time by 0.3528 s and shifted peak decision time by 75.92% (Figure 2B red), while GS reduced overall decision times by 0.2452 s and shifted peak decision time by 39.74% (Figure 2B green).

The changes in decision making elicited by PS in our model are consistent with those observed in behavioral studies[22]: coherence vs. accuracy curves are shifted such that stronger task-related input is required to make decisions against the stimulated population (P1); decision times decreased when task-related input and stimulation both favor P1 (e.g. at +25.6% coherence) but increased when task-related input and stimulation battle over control of the network (e.g. at −100% coherence) (Figure 2). GS showed these same interactions. However, for the same change in firing rate, the magnitude of shift and reduction in decision time were less. These behavioral differences suggested differences in how both forms of stimulation interact with networks of neurons.

B. Differences in Spatial Spread of Neuronal Activation

We observed a variety of differences between the effect of PS and GS on the distributions of neural firing rates, the regularity and synchrony of spike timing, and their interactions with networks of connected neurons.

As expected from single neuron studies, in the disconnected network, where the average population firing rate was equalized for GS and PS, the distributions of firing rates are significantly different (p=0.0363 by Kolmogorov-Smirnov test, Figure 3A). Due to the refractory effects of high-amplitude pulses, the neurons closest to the pulsatile stimulation electrode (<40 μm) are blocked, producing firing rates below baseline. The neurons farther away (40–250 μm) get excited, but because of pulse-pulse blocking effects, they never achieve firing rates over 100 spk/s (Figure 3A–B red). In contrast, the neurons closest to the galvanic stimulation electrode (<100 μm) are strongly excited with firing rates up to 300 spk/s, and none are blocked (Figure 3A green). As a result, for the same change in population firing rate in the disconnected network (Figure 3C), pulses activated more neurons (14.00%) than galvanic stimulation (5.83%, Figure 3A–B dashed line). Only 40.5% of the neurons affected by pulses were affected by GS. In this network, where average firing rate is important and all neurons are connected, this was not a detriment, but in a sparser network, this difference could also cause significant differences in network effects.

When the neurons were connected, they became subject to feedback inhibition, which decreased spontaneous neural firing rates from ~25 spk/s to 2–3 spk/s (Figure 3D–E black). Neurons directly affected by electrical stimulation, however, are largely resistant to feedback inhibition. The neurons closest to the GS electrode still achieve firing rates up to 300 spk/s (Figure 3D green) and the neurons a moderate distance away from the PS electrode (55–85 μm) still fire at ~70 spk/s (Figure 3D–E red). Since PS directly affects more neurons than GS, its effects are more resistant to the balancing effect of feedback inhibition. As a result, not only do pulses and GS have significantly different distributions of activation (p<0.00001 by Kolmogorov-Smirnov test, Figure 3D–E), but also they induce significantly different increases of average firing rate in connected neurons (p<0.00001 by unpaired t-test). Compared to control conditions in the connected network, pulses increased firing rates by 5.31±0.06 spk/s. Meanwhile, GS only increased firing rates by 3.07±0.24 spk/s (Figure 3F). The relatively larger effect of pulses in the connected network is likely one cause of the downstream differences in behavioral outcomes.

C. Differences in Spike-timing

Single neuron studies also predict differences in spike timing in response to PS and GS[16,18]. PS transiently depolarizes neuron membrane potentials at a fixed interval, and, if the membrane potential is sufficiently depolarized, they induce action potentials (APs). Even if they do not elicit APs, pulses generate brief amplitude-dependent refractory periods, which prevent natural EPSCs from triggering APs immediately after pulses. As a result, neurons directly affected by PS have highly regular, synchronized spike trains with APs phase-locked to the timing of the pulse. This phenomenon is visible in raster plots of individual spike trains (Figure 4A red). On the other hand, GS provides a constant current input that effectively sets the resting membrane potential closer to the AP threshold, so neurons fire for more of the incoming EPSCs. This essentially increases the likelihood of firing with timing dependent on natural inputs[16]. We also see these effects in the raster, with corresponding GS neurons firing in a desynchronized, irregular fashion, similar to control (Figure 4A green).

Figure 4.

Spike timing differences in P1 neurons among stimulation conditions (Pulsatile, red; Galvanic, green; and Control, black). (A) Rasters are plotted for the three P1 neurons with highest firing rates in the pulsatile condition, along with the times of each pulse (grey). Corresponding neurons receiving identical natural inputs are plotted for galvanic and control conditions. (B) The percent of each neuron’s action potentials that occur during a pulse presentation for the end-of-task (t=2.5–3s) period is shown as a function of its distance to the stimulation electrode for connected (triangles) and disconnected (circles) cases. (C) Each neuron’s end-of-task coefficient of variation (CV) is shown as a function of its distance to the stimulation electrode for connected (triangles) and disconnected (circles) cases. (D) Heat map of the percent of action potentials from a neuron that are synchronized to another neuron as a function of distance from the stimulation electrode for connected (top) and disconnected (bottom) cases. Self-synchrony was undefined (N/A, blue). For all trials, task-related input was equal for P1 and P2 (coherence = 0%). For connected simulations, only trials in which P1 won were included.

Firing regularity, phase-locking, and spike synchrony were quantified across trials by analyzing responses at the end of the stimulation window when effects would likely be maximized (2.5–3 s). Once the neurons were connected, the effects of PS were reassessed. Neurons that received PS were significantly more regular than control or galvanic stimulation as measured with CV (p<0.00001 by 1-way ANOVA), but GS also induced more regular firing than control (p<0.00001 by 1-way ANOVA, Figure 4C). PS induces regular firing in all effected neurons due to regular pulse presentation, but GS can also cause regular firing in neurons when the amplitude is large enough to directly drive firing. This only occurs in a subset of highly depolarized neurons. In the pulse condition 26.8% of neurons up to 671 μm away from the electrode were significantly phase-locked in P1 to pulses. The maximum phase-locking was found to be 100%. When the network was connected, there was no significant difference in phase-locking compared to when it was disconnected (p=0.1623 by unpaired t-test, Figure 4B). There was no significant phase-locking in the GS or control condition in stimulated neurons (Figure 4B).

Spike synchrony was also measured independent of pulse timing and showed that PS induces significantly more synchrony than GS compared to control (p<0.00001 by unpaired t-test for all comparisons). When P1 was exposed to PS, 249±2 neuron pairs up to 684μm away from the electrode became significantly synchronized (more synchronous than the most synchronized control neuron pair). 26.8±0.4% of neurons had between 1 and 28 significantly synchronized connections with synchrony values ranging from 3.7% to 93.5% (Figure 4D Disconnected Pulsatile). Only 5.6±0.3 neuron pairs exposed to GS became significantly synchronized, and these pairs only achieved synchrony values between 3.7% and 7.0% (Figure 4D Disconnected Galvanic).

An overwhelming 98.6±0.2% of synchronized pairs consisted of only neurons phase-locked to pulses, suggesting that phase-locking is the primary driver of this effect. Connections among neurons phase-locked to pulses were significantly more synchronous than GS or control conditions (p<0.00001 by 1-way ANOVA), but synchrony among neurons not phase-locked did not significantly differ from control or GS levels (p=0.95 by 1-way ANOVA). When the network was connected, synchrony significantly increased in all conditions (p<0.00001 by 2-way ANOVA, Figure 4D Connected) by 1.12±0.02% on average. In this model, which has homogenous connectivity and responds to average population firing rates, these nuanced spike-timing effects do not dramatically alter decision-making function. They may nevertheless be relevant in biological circuits that have been shown to depend heavily on precise spike timing [26], [27]. In addition, the tendency of PS to override the natural timing of the network may contribute to the resistance of P1 to feedback inhibition and excitation under pulsatile stimulation.

D. Population-level Differences

In addition to differences in spatial spread of activation and spike timing, PS and GS also had different effects at the population level, depending on the decision outcome of the network. When the population receiving the stimulation (P1) won the trial, the population firing rate of P1 was greater in response to GS (+4.21±0.27 spk/s) than PS (+2.18±0.08 spk/s) relative to control (p<0.00001 by unpaired t-test, Figure 5A–C). However, when the population not receiving stimulation (P2) won the trial, the average firing rate of P1 remained more elevated in the pulsatile condition (+2.09±0.06 spk/s) than galvanic (+0.93±0.04 spk/s) compared to control (p<0.00001 by unpaired t-test, Figure 5D–F). This suggests that neurons undergoing PS are less sensitive to network-level effects (feedback inhibition and recurrent excitation) than neurons undergoing GS. For PS, neurons in P1 were less excited when P1 wins and less suppressed when P1 loses. As discussed earlier, this effect may derive from two sources. One is that PS directly affects more neurons, and, in consequence, PS has a greater effect on decision making than GS. The other may be that during pulse delivery, the refractory effects may be blocking incoming input from other neurons.

Figure 5.

Effects of stimulation on P1 firing rates for different network-level outcomes. Trials in which (A-C) P1 wins (coherence=+25.6%) and (D-F) P1 loses (coherence=−100%). Average P1 firing rates for all 3 stimulation conditions (Pulsatile, red; Galvanic, green; and Control, black) are shown for the full trial (A and D) and during the end of task period (B and E, t=2.9–3s highlighted yellow in A and D). Bar graphs (C and F) depict each brain’s population-averaged change in end-of-task firing rate relative to control in all trials in which P1 wins (C) and P1 loses (F). Significance of effect (p<0.00001) is indicated by ****.

IV. Discussion

The central finding of this work is that when the non-linear stimulation effects of biphasic pulses are applied to a decision-making network, they affect the network more dramatically than GS, even when both are parameterized to elicit the same effects on average neural firing rates. This difference occurs because pulses affect more neurons than GS and the pulse effect is synchronized across the network. As a result, neurons experiencing pulse inputs are less sensitive to network effects, such as feedback inhibition. Feedback inhibition is a crucial component of the decision-making network, and disruptions to its operation have been shown to impair the decision-making process[28]. Similarly, synchrony effects are important in a variety of cognitive processes [26] and disease states such as epilepsy[27]. Therefore, although electrical pulses are clearly an effective way to alter decision-making circuits and, more broadly, to interface with the nervous system at large, they may struggle to replicate nuanced interactions that depend on precise spike timing or on-going network activity. GS may preserve neural spike timing and respect feedback inhibition, but it has its own set of challenges, including safe implementation in implanted devices.

One limitation of this study is that the effect of PS on decision making in the model is much larger than the effect in vivo with the same stimulation parameters[22], but similar studies with lower pulse amplitude (5 μA) can achieve an equivalent effect on decision making[23]. Additionally, in this work, we only considered one type of equivalence between pulsatile and galvanic stimulation: equivalent average firing rate increase. However, many other types of equivalence exist, such as equivalent proportion of neurons affected, and these should be explored in future work. Finally, due to the lack of blocking effects, GS can drive firing rates very high (>200 spk/s) for a few neurons very close to the electrode. These high firing rates may not be achievable in real cortical neurons with spontaneous activity, so more realistic neuron models may be needed.

V. Conclusion

In this paper, we considered the non-linear effects of pulsatile stimulation on an established decision-making network compared to the effects of galvanic stimulation. We found that pulsatile stimulation biased decision making significantly more, largely due to it affecting more neurons and causing them to have a greater insensitivity to feedback inhibition than natural inputs or galvanic stimulation. This effect may partially be caused by an artificial synchronizing of spike timing. This synchronization likely causes other consequences for networks that rely on spike-timing specific signaling.

Clinical Relevance—

This establishes that pulsatile stimulation may disrupt natural spike timing and network-level interactions while certain parameterizations of galvanic stimulation avoid these effects and can drive network firing more naturally.