Abstract
Ultracold atoms and molecules provide an unprecedented view into the role of quantum effects in chemical reactions. However, these same quantum effects make ultracold chemical reactions notoriously difficult to simulate. Contrary to conventional wisdom that ultracold systems necessitate quantum approaches, with classical mechanics offering a rough approximation at best, the past three decades have seen an explosion in classical, quasiclassical, and semiclassical approaches that yield near-exact results for ultracold systemsincluding in cases where today’s quantum methods would be computationally intractable. This review illustrates the power of these approaches with 30 years’ worth of numerical and experimental evidence. The review provides a comprehensive account of the successes of universal classical post-threshold laws for low-energy atomic and molecular scattering systems, as well as the cutting edge in quasiclassical approaches that unravel the ongoing controversy surrounding long-lived collision complex lifetimes in ultracold collisions. Special attention is placed on atomic systems where classical scaling laws hold directly at zero Kelvin, which underline the predictive power classical methods can offer even in the most extreme quantum chemical environments. The review culminates with a discussion of broader implications for classically inspired approaches to prototypically quantum chemistry in the second quantum revolution.


1. Introduction
In 2012, when Chemical Reviews published its Special Issue on ultracold molecules, − the field of ultracold chemistry was at its outset. The Special Issue placed a special focus on the preparation of molecules in the cold regime (below 1 K) − and the ultracold regime (below 1 mK). − Provisions were made for future applications for condensed matter theory and aspirations toward quantum chemistry. At the time, evidence of ultracold chemical reactions was restricted to reactant lossas in the groundbreaking measurement of molecular density decay in the ultracold 40K87Rb dimer reaction at just 300 nK by Ospelkaus, Ni et al. In the intervening years, there has been a “quantum leap” in ultracold chemistry.
A surprising outcome of such recent developments in ultracold chemistry − is classical, semiclassical, and quasiclassical mechanics is sufficient to simulate aspects of a wide range of cold and ultracold chemical reactions nearly exactly. This advancement provides an opportunity to develop computational tools that vastly reduce the cost of cold and ultracold simulations and aid interpretation of fundamental nonreactive and reactive collision processes. Section provides a comprehensive account of the numerical and experimental evidence in the past 25 years, including the ubiquitous ability of classical and semiclassical mechanics to closely reproduce quantum cross sections for atom–ion collisions at collision energies as low as 10 nK, the capability of classical Langevin capture theory to yield accurate reactive rate coefficients for triatomic collisions at collision energies as low as 10 nK, and the power of semiclassical mechanics to evidence a quasiuniversal quantum-to-classical crossover in dipolar collisions at collision energies as low as 7 pK. Note the lowest of these temperatures is 12 orders of magnitude colder than the interstellar medium. These findings go beyond theoretical results. Classical and semiclassical mechanics have been seen to closely agree, for example, with experimentally obtained cross sections on the order of 10 μK for Li + Ba+ collisions, 10 mK for H2 + HD collisions, and 0.1 K for H2 + He collisionsthe latter with a relative error of just 1%.
Recent rationales explain how semiclassical and classical mechanics can retain such accuracy in such a counterintuitive regime. Competing theories are detailed in Section , beginning with the foundational work of Gribakin and Flambaum, who found that semiclassical cross sections can hold when not a single oscillation of the scattering wave function fits in the potential well. − This argument is compared with the semiclassical Wentzel-Kramers-Brillouin (WKB) criterion furthered by Julienne and Mies in 1989, Côté et al. in 1996, and Mody et al. in 2001 to pinpoint the onset of the quantum effects of quantum reflection and quantum suppression. Ultracold inferno theory, introduced in 2018, is also presented as a conceptual framework to indicate when not just semiclassical, but also classical treatment is expected to hold: namely, in the absence of quantum reflection and quantum interference. , These methods are placed in light of the controversy surrounding the true applicability of the WKB criterion and the related quantality condition and the question of whether these points of reference are sufficient to determine the “source” of quantum reflection effects. ,
The observation and justification of classical, semiclassical, and quasiclassical treatment of cold and ultracold collisions opens the door wide to applications throughout the field of chemistry. Section details how such advancements enable the derivation of novel semiclassical scaling laws for cross sections and rate coefficients, such as the semiclassical eikonal scaling laws of Bohn et al. for dipolar collisions currently underway in the laboratory, , as well as the development of techniques to rigorously extend existing quantum and classical cross section scaling laws to cover the whole of the collision energy region, as in the quantum threshold model of Quéméner and Bohn − and the quantum Langevin model of Gao. − Additionally, the review generalizes the semiclassical analogue of the Fermi golden rule approach of Mody et al. to derive semiclassical laws that apply to two-body collisions in not just three-dimensional, but reduced-dimensional collisions relevant to reactions in optical traps. ,− Section covers the novel perspective that rationales for classical and semiclassical behaviors in ultracold collisions offer on the origin of quantum-classical correspondence in scaling laws directly at zero collision energy in the renowned three-dimensional Coulomb potential and Wannier double ionization system, with implications for multiple ionization − and atomic fragmentation. , Section collects these universal scaling lawsspanning one- to N-dimensions and short-range to long-range potentialsto highlight and facilitate prediction of where classical and semiclassical predictions are expected to hold in a yet wider range of cold and ultracold collisions.
Section considers “sticky collisions”the mysterious disappearance of reactants even in ultracold collisions with no energetically accessible products. − Here a quasiclassical strategy based on the Rice–Ramsperger–Kassel–Marcus (RRKM) theory of unimolecular dissociation rates − has emerged as the method of choice. − This method has succeeded not least of all because simulation of such collision complexes with exact quantum mechanics ranges from highly computationally intensive for three-atom systems to computationally intractable for just four atoms. There remains a conundrumwhereas the quasiclassical and experimental collision-complex lifetimes for the 40K 87Rb + 40K 87Rb collision differ by a factor of just 2, , quasiclassical and experimental collision-complex lifetimes for 40K87Rb + 87Rb differ by 5 orders of magnitude ,, namely, a key area for further study.
Section provides an outlook for the future of classical, semiclassical, and quasiclassical methods in cold and ultracold molecules. The ability of classical mechanics to reap near-exact results opens the door to simulations of systems that are computationally intractable today, which includes systems of four atoms. Rigorous criteria for quantum-classical correspondence facilitate identification of not only where classical mechanics applies, but also where quantum treatment is essential, which is especially relevant today given the importance of accurate simulation of ultracold molecules proposed for quantum sensing − and quantum computing − technologies central to the second quantum revolution. Results at cold and ultracold temperatures also have implications for room-temperature chemistrythe exponential improvement in computational cost of classical simulations relative to quantum calculations provides a valuable complement to state-of-the-art data-science approaches to quantum mechanics, as well as the means to readily visualize detailed reaction mechanisms in terms of classical particles. And, the insight these findings offer into the border between quantum and classical worlds has implications for the wider field of near-threshold phenomena throughout chemistry and physics. We have moved far beyond the ultracold chemistry of 25 years ago, and this review provides a vision of what may be in store for the next 25 years.
2. Universal Classical and Semiclassical Scaling Laws in Ultracold Molecular Systems
2.1. Evidence of Quantum-to-Classical Crossover in the Cold and Ultracold Regime
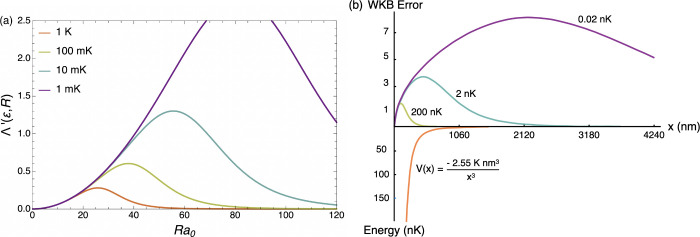
To begin, some of the strongest support for classical treatment of ultracold collisions comes in the form of universal classical and semiclassical scalings near threshold in cold and ultracold scattering cross sections. ,− ,− Modern scattering calculations ,− ,− ,− ,− and experiments − ,,,,− confirm the prototypical picture of low-energy atomic and molecular cross sections: In the absence of resonances and bound states, − the Bethe–Wigner quantum threshold law , operates at the threshold of energetic accessibility (see Table ). , As the energy increases, a quantum-to-classical crossover appears. And, at the highest energies, the cross section asymptotically obeys (semi)classical post-threshold laws such as the classical capture theory laws of Langevin and Gorin , (modulo oscillations and resonances, see Table ). A schematic of this behavior is given in Figure .
1. Wigner Threshold Laws for Universal Scalings of Collision Cross Sections σ(k) as a Function of the Wavenumber k for Two-Body Collisions in Three Dimensions .
| Inelastic |
||||
|---|---|---|---|---|
| lim r→∞ V(r) | Endothermic | Exothermic | Depolarization | Elastic |
| 0 | ||||
| Ze2/r | exp(−2πμZe 2/(ℏ2 k)) | k–2 exp(−2πμZe 2/(ℏ2 k)) | k–2 exp(−4πμZe 2/(ℏ2 k)) | k –2 |
| –Ze 2/r | 1 | k –2 | k –2 | k –2 |
Scalings are shown for elastic collisions and inelastic collisions with positive threshold energy (endothermic reactions), negative threshold energy (exothermic reactions), and changes in angular momentum (depolarization events) and are given for short-range (lim r→∞ V(r)) and long-range (attractive Coulombic lim r→∞ V(r) = −Ze 2/r and repulsive Coulombic lim r→∞ V(r) = −Ze 2/r) potentials. Expressions are provided in terms of the reduced mass μ, charge number product Z, and initial and final angular momentum quantum numbers of the collision partners, where e is the electron charge and ℏ is reduced Planck’s constant.
2. Summary of Classical Langevin and Gorin , Laws for Scalings of the Capture Cross Sections σ L (E) with the Collision Energy E for van der Waals Potentials C n r –n of Order n .
| n | 3 | 4 | 6 |
|---|---|---|---|
| σ L (E) |
The universal form of the scattering cross section, including its constant multiplicative factor, at low energy is provided. Reproduced table with permission from Robin Côté and Ionel Simbotin, Physical Review Letters, 121, 17, 173401, 2018. Copyright 2018 by the American Physical Society.
1.
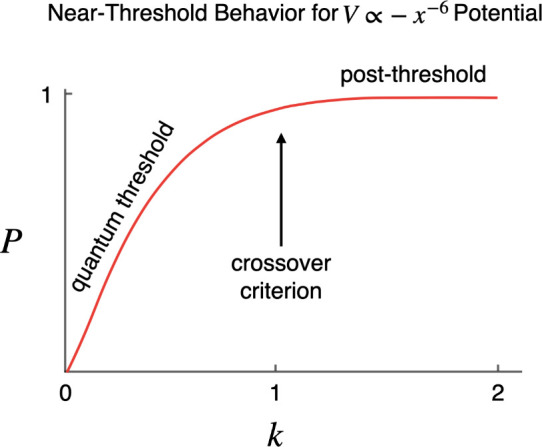
Prototypical framework for near-threshold cross sections as exemplified by numerical calculation of the transmission probability P in a one-dimensional V(x) ∝ – x –6 potential as a function of the wavenumber k. The transmission probability follows the quantum threshold law P ∝ k at threshold (k → 0) and crosses over (k ≈ 1) to the classical post-threshold law P = 1 at higher wavenumber (k → 1).
Numerical and experimental results show the quantum-to-classical crossover frequently appears in the cold to ultracold regime in molecular collisions. ,− ,,,− ,− Such low-energy quantum-to-classical crossovers imply that classical post-threshold laws for cross section and rate coefficient scalings are also highly accurate at extremely low collision energies. Several of the lowest-energy numerical examples of ultracold quantum-to-classical crossover and operation of classical post-threshold laws in the cold and ultracold regime are depicted in Figures –, with experimental counterparts in Figures – and additional details and related work below.
2.

Numerical evidence of quantum-to-classical crossover at ultracold energies approximately on the order of 10 nK in the averaged diffusion cross section ⟨σ d ⟩ (black line) and diffusion coefficient D (red line) for Na + Na+ collisions. Reprinted from Advances in Atomic, Molecular, and Optical Physics, 65, R. Côté, Ultracold atom–ion collisions, 67, Copyright 2016, with permission from Elsevier, based on reproduced figures with permission from R. Côté and A. Dalgarno, Physical Review A, 62, 1, 012709, 2000. Copyright 2000 by the American Physical Society.
7.
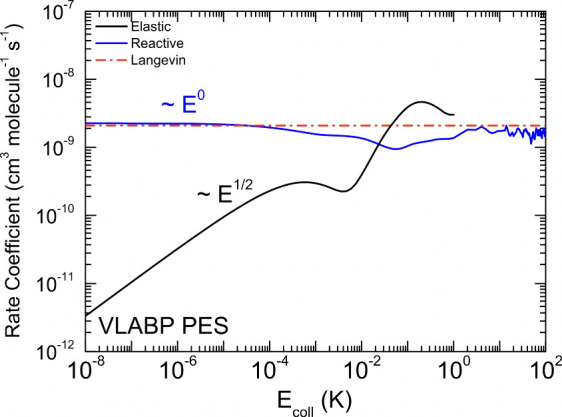
Comparison of the reactive (blue) and elastic (black) rate coefficients to the classical Langevin rate coefficient (dashed-dotted red line) for D+ + H2 (v = 0, j = 0) indicates the reactive rate coefficient obeys the classical Langevin scaling down to the ultracold regime on the order of 10 nK. Reproduced from M. Lara and P. G. Jambrina, Cold and ultracold dynamics of the barrierless D+ + H2 reaction: Quantum reactive calculations for ∼R –4 long-range interaction potentials, Journal of Chemical Physics, 143 (2015) 204305, with the permission of AIP Publishing.
8.

Agreement between experimental total cross section measured at 30 μK (circles) with the classical Langevin (black line), scaled classical Langevin (thin dashed lines), quantum (colorful solid lines), and quantum thermalized (thick dashed lines) cross sections for (left) Li(2S 1/2) + Ba+ (5D 5/2) and (right) Li(2S 1/2) + Ba+ (5D 3/2). Quantum results are shown for competing nonradiative charge exchange (NRCE, yellow), nonradiative quenching (NRQ, red), and fine-structure quenching (FSQ, green) processes. Reproduced with permission from ref by Xing et al. CC BY 2024 IOP Publishing.
13.

Experimental evidence of cold quantum-to-classical crossover in He(23 P 2)/para-H2 (j = 0) collisions. The measured reaction rate constant (black points) obeys the classical Langevin post-threshold law (red dashed line) at collision energies as low as 0.8 K, with a quantum-to-classical crossover at energies on the order of 1 K for HD (j = 0) (gray points), compared to the p-wave barrier height (vertical dashed line). Reproduced figure with permission from Y. Shagam, A. Klein, W. Skomorowski, R. Yun, V. Akerbukh, C. P. Koch, and E. Narevicius, Molecular hydrogen interacts more strongly when rotationally excited at low temperatures leading to faster reactions, Nature Chemistry, 7, 921–926, 2015, Springer Nature. Reproduced with permission from SNCSC.
2.1.1. Numerical Evidence
2.1.1.1. Atom–Ion Collisions
A number of authors have numerically identified quantum-to-classical crossover in hybrid atom–ion systems at collision energies well below 1 K. ,− ,,,, In 2000, Côté and Dalgarno identified a quantum-to-classical crossover at extremely low energies, as low as 10 nK, for collisions of Na + Na+. , As shown in Figures and , computed cross sections indicated that semiclassical treatment accurately modeled the quantum results at energies as low as 10–12 au (300 nK) for elastic and charge-transfer cross sections, with classical treatment accurately reproducing quantum results at energies as low as 10 nK for charge exchange cross sections. Côté and Dalgarno determined cross sections for ab initio potential energy surfaces and , with the potential approximated at short distances by an exponential wall and the potential approximated at long distances as V g,u (R) ∼ V disp (R) ∓ V exch (R) for dispersion term V disp (R) and exchange term V disp (R). Quantum scattering cross sections were determined from phase shifts calculated from the regular solutions of the corresponding partial wave equation. The quantum scattering cross sections were compared to both the classical Langevin formula and Massey and Mohr’s high angular momentum limit of Jeffrey’s semiclassical approximation. − Côté and Dalgarno recognized the underlying calculation strategies rest only on the neutral atom’s polarizability and mass, and thus are equally applicable to other alkali-metal hybrid atom–ion systemsand therefore low-energy quantum-to-classical crossover in atom–ion systems is expected to be widespread.
3.
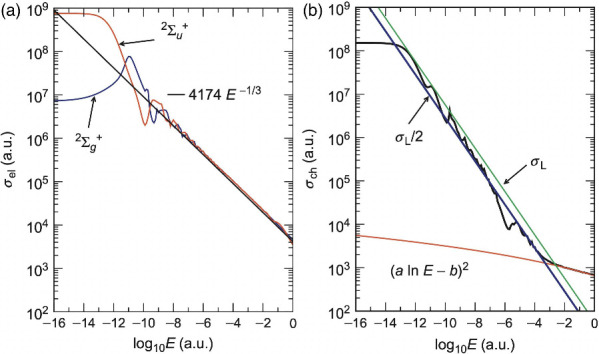
Numerical evidence of quantum-to-classical crossover at ultracold energies approximately on the order of 10–12 au (300 nK) in (a) the elastic cross section of the state (blue line) and state (red line, semiclassical formula shown in black) and (b) the charge exchange cross section (black line, Langevin σ L shown in green, σ L /2 shown in blue, and higher-energy prediction in red) for Na + Na+ collisions. Reproduced from Advances in Atomic, Molecular, and Optical Physics, 65, R. Côté, Ultracold atom–ion collisions, 67, Copyright 2016, with permission from Elsevier, based on reproduced figures with permission from R. Côté and A. Dalgarno, Physical Review A, 62, 1, 012709, 2000. Copyright 2000 by the American Physical Society.
In 2001, Siska supported this finding, similarly identifying a quantum-to-classical crossover by collision energies of 10 μK in spin–orbit relaxation of Ne+ + He. Calculations were performed on an empirical potential energy surface based on spectroscopic measurements for the molecular ion and ab initio theory. Siska recognized that the required potential energy surface shares the form of an atom–homonuclear model potential, which facilitates rigorous quantum treatment according to the formalism of Reid, Arthurs, and Dalgarno. − The resulting coupled radial equations were then integrated numerically according to a variable step-size modified log-derivative method specifically for 4He + 20Ne+. Although the magnitude of the cross section usually remained <0.1% of the magnitude predicted by Langevin for the polarizability considered, the quantum scaling was seen to closely agree with the classical Langevin scaling down to collision energies in the quantum Wigner threshold regime less than 10 μK, well within the ultracold regime.
Likewise, in 2020, Pandey et al. demonstrated that total cross sections for the 7Li+ – 7Li collision agree with semiclassical and classical scalings at collision energies just above the ultracold regime. Pandey et al. developed ab initio potential energy curves for the Li2 electronic ground state X 2Σ g and first-excited state A 2Σ g according to the multireference configuration interaction (MRCI) method, which were used to determine the cross section quantum mechanically via direct numerical solution of the radial Schrödinger equation for individual partial waves and semiclassically according to the work of Côté and Dalgarno. The scattering cross sections for for all computed potential energy curves agreed with the semiclassical, classical Langevin, or scaled classical Langevin cross sections at collision energies at or greater than on the order of 10 mK.
In line with these results, in 2009, Zhang et al. identified quantum-to-classical crossover at 10 mK to 1 μK for inelastic and elastic 6Li + 7Li+ → 6Li+ + 7Li collisions, respectively. Zhang et al. considered cross sections computed for Born–Oppenheimer potentials with nonadiabatic couplings via the multiconfiguration self-consistent field (MCSCF) theory and multireference configuration interaction (MRCI) calculations. A comparison of quantum scattering cross sections and the semiclassical Langevin charge exchange model of Côté and Dalgarno , again demonstrated quantum-to-classical crossover from Wigner’s quantum threshold law beginning at 10–10 eV (1 μK), with semiclassical mechanics yielding accurate elastic scattering cross sections at energies higher than 10–6 eV (10 mK).
And, in 2011, Zhang et al. further showed that semiclassical mechanics reproduces quantum scattering cross sections at lower energy for charge exchange in atom–ion Be2 collisions. Zhang et al. again calculated ab initio quantum scattering cross sections on Born–Oppenheimer potentials with nonadiabatic couplings and compared the results to Côté and Dalgarno’s semiclassical Langevin charge model. Here, quantum-to-classical crossovers were identified in these results at 0.1 K to 0.1 mK.
Côté and Simbotin further extended the use of semiclassical mechanics to accurately predict ultracold atom–ion collision cross sections to temperatures up to 10 orders of magnitude colder (just above fK) in 2018, as shown in Figure . Côté and Simbotin published findings on quantum-to-classical crossover in the ultracold regime for resonant charge transfer of Yb + Yb+, spin flip of Na + Ca+ and 85Rb + 87Rb, and excitation exchange of – the last well below 1 pK. For Yb2 , quantum results were considered for V g /u potentials’ and states; for Na + Ca+, singlet A 1Σ+ and triplet a 3Σ+ states; , for 85Rb + 87Rb, for singlet X 1Σ g and triplet a 3Σ u states; and for Cs+ + Cs* (6p), for two Σ g/u and two Π g/u states. , van der Waals potentials of order four, four, six, and three approximated the asymptotic potentials, respectively. Semiclassical Wentzel–Kramers–Brillouin (WKB) treatment − of the cross section for third-, fourth-, and sixth-order van der Waals potentials were directly related to the classical Langevin cross section to the expression for s-wave scattering; which yielded a modified Langevin scaling law for excitation exchange that incorporates the impact of quantum s-wave scattering above the prototypical Wigner quantum regime. This semiclassical modified Langevin scaling was again found to hold above a quantum-to-classical crossover that appears at energies on the order of approximately sub-mK to mK for spin-flip collisions of A Rb + B Rb for A = 85, 87 and B = 85, 87; μK to nK for resonant charge transfer in A Yb + A Yb+ for A = 168, 170, 172, 173, 174, 176; μK to nK for spin-flip collisions of Na + A Ca+ for A = 40, 42, 43, 44; and pK to fK in excitation exchange in A Cs + A Cs+ for A = 133, 132.75. These results, which encompass hybrid atom–ion systems for a variety of species of differing isotopes, both predict that quantum s-wave signatures are accessible experimentally via measurement of the semiclassical modified Langevin cross section and fulfill Côté and Dalgarno’s projection two decades prior , that their semiclassical treatment again applies broadly to alkali-metal hybrid atom–ion systems.
4.

Numerical example in which quantum-to-classical crossover appears at energies between on the order of 1 fK and 1 pK in excitation exchange in (a) and (b) in the same system with a rescaled fictitious mass m Cs = 132.75 that models an isotope effect. Images directly compare quantum numerical results (solid black line) with the classical Langevin cross section σ L (blue dot-dashed line), s-wave contribution (black dashed line), Langevin cross section s-wave contribution σ L sin2Δδ0 (solid blue line), and the s-wave-scattering-modulated Langevin cross section = . Reproduced figure with permission from Robin Côté and Ionel Simbotin, Physical Review Letters, 121, 17, 173401, 2018. Copyright 2018 by the American Physical Society.
In 2021, Hirzler and Pérez-Ríos demonstrated that quasiclassical and classical mechanics is also sufficient to accurately simulate another type of atom–ion collision processcharge exchange cross sections for low-energy Rydberg atom–ion collisions of Li* – Li+ and Li* – Cs+. Hirzler and Pérez-Ríos considered the interaction between the ionic cores and the Rydberg electron in resonant charge exchange according to two models: (i) a Coulomb potential and (ii) a pseudopotential that consists of a screened Coulomb interaction term and Rydberg electron–core electron interaction term. Scattering cross sections were determined quasiclassically according to a quasiclassical trajectory (QCT) approach ,− that treated nuclear dynamics classically and related the trajectories’ initial conditions and final positions to individual quantum states semiclassically. In order to examine the regions of parameter space well described by QCT and classical Langevin scaling, the number of partial waves required for accurate simulation of cross sections was determined, with the result that QCT remains accurate to energies as low as on the order of 1 K, and a classical Langevin framework holds to energies as low as on the order of that associated with Bose-Einstein condensation, namely, 100 nK.
2.1.1.2. Molecule–Molecule Collisions
In 2009, Bohn, Cavagnero, and Ticknor found quasiuniversal quantum-to-classical crossover behavior also holds for dipolar collisions in the ultracold regime, of particular interest today given ongoing ultracold dipolar collision experiments. − ,,− In order to generate a widely applicable formulation for scattering cross sections, Bohn, Cavagnero, and Ticknor considered a potential dictated solely by two-body dipole–dipole interactions, with short-range physics and internal structure of the dipole neglected, as supported by previous work by Ticknor. , The resulting scattering cross section thus encompassed dipolar collisions in general, with the identity of the molecules of interest imparting on the resulting scattering cross sections only a length scale D = M⟨μ1⟩⟨μ2⟩/ℏ2 and energy scale E D = ℏ6/M 3 ⟨μ1⟩2 ⟨μ2⟩2, where M is the reduced mass and μ1 and μ2 are the dipoles. (Note that since both scales are dependent on the dipole moment, they are also dependent on the strength of any applied electric field.) Close-coupling results for this dipolar collision system were compared to the quantum Born approximation and the semiclassical eikonal approximation.
Semiclassical mechanics was found to be accurate throughout the cold collision regime to energies on the order of the energy scale E D , usually nK to μK. A quantum-to-classical crossover is therefore expected at 445 nK for OH, 83 nK for KRb, and 7 pK for LiCs for fully polarized molecules, as shown in Figure well within the ultracold regime. Bohn, Cavagnero, and Ticknor additionally recognized that in the quantum-to-classical crossover regime, universality falters and the cross section rests on lengths shorter than the length scale D, such that examination of the relevant energy regime may facilitate exploration of short-range physics and the intermolecular potential energy surface.
5.
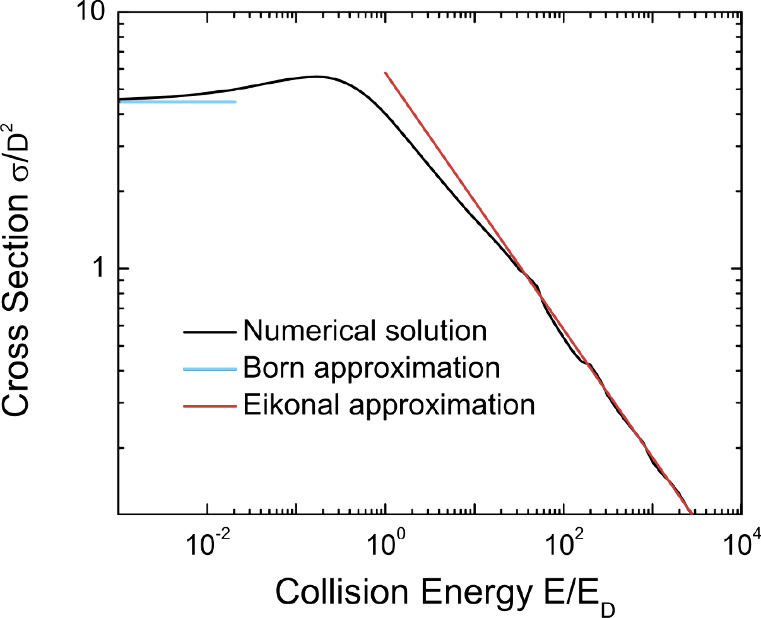
Quantum-to-classical crossover of the total scattering cross section (black line) from the quantum Born approximation scaling (blue line) to the semiclassical eikonal approximation scaling (red line) occurs at characteristic energy E D = ℏ6/M 3 ⟨μ1⟩2 ⟨μ2⟩2 in distinguishable dipolar molecules, which corresponds to ultracold temperatures of 7 pK for LiCs, 83 nK in KRb, and 445 pK in OH. Reproduced with permission from ref by Bohn, Cavagnero, and Ticknor. CC BY 2009 IOP Publishing.
Dashevskaya et al. likewise showed that complex formation rates for a wide range of diatomic-diatomic/polyatomic ion collisions are amenable to quasiclassical treatment at temperatures above on the order of 1 to 10 mK in 2005and further showed that this behavior is expected to be widespread for molecular ion-neutral ion collisions. Dashevskaya et al. considered an asymptotic diatomic-ion interaction potential given by a sum of terms for an isotropic charge-induced dipole and an anisotropic charge-induced dipole with a charge-induced quadrupole. The total capture rate coefficient was determined in the zero-energy limit according to the quantum Bethe expression of Eltschka, Moritz, and Friedrich; in the intermediate energy range by direct solution of quantum coupled equations and the adiabatic channel classical (ACCl) approximation; , and in the high-energy limit by the classical Langevin rate. Quasiuniversal behavior of the capture cross section was observed, as shown in Figure , in which the total capture rate coefficient transitioned to its classical Langevin value at temperatures above T VLT, the characteristic temperature (termed Very Low Temperature) at which the de Broglie wavelength of relative motion equals the Langevin capture radius. This characteristic temperature was found to appear at T VLT = 1.49 · 10–4 K for collisions of diatomic nitrogen N2 with an ion X+ of mass 10 amu, and in the range 1.43 to 17.2 mK for a wide array of collisions of diatomic hydrogen isotopologues with molecular ions, as shown in Table . In 2016, Dashevskaya et al. confirmed accurate quantum capture rate coefficients for H2 (j = 0, 1) + H2 collisions approach the classical Langevin value on the order of 1 to 10 mK. These findings point to a broad ability of quasiclassical simulations to accurately model cold collisions of diatomic-molecular ion collisions in the cold regime below 1 K.
6.
Comparison of the total capture rate coefficient scaled to the classical Langevin rate for H2 (j = 0) collisions with any ionic partner indicate close agreement between the quantum (χ j=0 = k j=0/k L, solid line), ACCl (Χ j=0 , dashed line), quantum mechanically amplified ACCl (open circles), and Langevin rates (1.0) above the characteristic temperature TVLT. See ref for additional details. Adapted from E. I. Dashevskaya and I. Litvin, Rates of complex formation in collisions of rotationally excited homonuclear diatoms with ions at very low temperatures: Application to hydrogen isotopes and hydrogen-containing ions, Journal of Chemical Physics, 122 (2005) 184311, with the permission of AIP Publishing.
3. Characteristic Temperature T VLT for Transition to the Classical Langevin Capture Rate in Collisions of Diatomic Hydrogen Isotopologues with Selected Diatomic and Polyatomic Isotopologues .
| Molecular Ion | Neutral Molecule | TVLT [mK] |
|---|---|---|
| H2 | H2 | 17.2 |
| HD | 12.0 | |
| D2 | 9.70 | |
| HD+ | H2 | 12.0 |
| HD | 7.65 | |
| D2 | 5.86 | |
| D2 | H2 | 9.70 |
| HD | 5.86 | |
| D2 | 4.30 | |
| H3 | H2 | 12.0 |
| HD | 7.65 | |
| D2 | 5.86 | |
| H2D+ | H2 | 9.70 |
| HD | 5.86 | |
| D2 | 4.30 | |
| HD2 | H2 | 8.43 |
| HD | 4.90 | |
| D2 | 3.48 | |
| D3 | H2 | 7.65 |
| HD | 4.30 | |
| D2 | 3.00 | |
| CH3 | H2 | 5.53 |
| HD | 2.75 | |
| D2 | 1.73 | |
| C2H2 | H2 | 5.00 |
| HD | 2.38 | |
| D2 | 1.43 |
Note all temperatures considered occur in the cold regime well below 1 K. Adapted from E. I. Dashevskaya and I. Litvin, Rates of complex formation in collisions of rotationally excited homonuclear diatoms with ions at very low temperatures: Application to hydrogen isotopes and hydrogen-containing ions, Journal of Chemical Physics, 122 (2005) 184311, with the permission of AIP Publishing.
2.1.1.3. Atom–Molecule and Ion–Molecule Collisions
Likewise, numerous authors have identified ultracold quantum-to-classical crossover in triatomic collisions, including those relevant to experiments on three-body recombination (see refs , , , , , , , , , − , − ). In 2015, Lara et al. recognized that the classical Langevin scaling law accurately yields the reactive rate coefficient in the triatomic D+ + H2 (v = 0, j = 0) reaction in the ultracold regime as low as 10 nK, see Figure . Here, quantum calculations were performed according to the quantum reactive scattering method of Launey and Dourneuf on the potential energy surfaces of Velilla et al. and Aguado et al. Classical calculations were performed according to the classical Langevin model for long-range fourth-order van der Waals potentials both in its standard form and according to a numerical-capture statistical model that incorporates numerical values for centrifugal barrier heights to capture short-range behaviors, discrete summation over partial wave components, and a statistical factor to model the probability a collision complex decomposes into products. In its standard form, the classical Langevin model agrees with the quantum Wigner threshold law for long-range fourth-order van der Waals potentials, such that the classical Langevin model was found to accurately predict the E 0 scaling of the reactive cross section for D+ + H2 (v = 0, j = 0) collisions both in the low-energy and high-energy limits. Moreover, not only do the scalings agree, but the values of the cross sections also agree for this collision system (with the quantum result only 10% larger than the classical value), such that the cross section is predicted to vary by a multiplicative factor of just <10 from the classical value throughout the ultracold regime and extending beyond 10 orders of magnitude in energy.
In 2024, Karpa and Dulieu underlined the ubiquity of classical behavior in ultracold ion–molecule collisions according to a semiclassical Langevin scattering model. , The characteristic length and energy scales of s-wave collisions, defined by the position R * of the centrifugal barrier maximum E * associated with p-wave collisions in the absence of a Langer correction, were considered for an ion-neutral system with reduced mass μ and fourth-order van der Waals coefficient C 4
| 1 |
| 2 |
With the permanent electric dipole moments and static dipole polarizabilities of Vexiau et al., the characteristic scales were computed for collisions of 138Ba+ with bialkali molecules currently of interest in ultracold molecular experiments, revealing characteristic energies on the order of pK to nK, as shown in Table . Karpa and Dulieu suggested that this implies that even at the coldest temperatures at which molecular experiments have been performed as of 2024 (on the order of 10 nK), − ion–molecule collisions involving the species in Table would behave according to the classical Langevin capture model.
4. Characteristic Semiclassical Langevin Energy E * and Length R * Scales of the s-Wave Regime in 138Ba+ Ion-Neutral Rovibronic Ground-State Molecule Collisions, with Ion–Atom Collisions for Reference .
| Molecule | R* [10–6 m] | E* [nK] |
|---|---|---|
| LiCs | 25.9 | 0.00521 |
| NaCs | 40.1 | 0.00206 |
| LiRb | 16.2 | 0.0165 |
| LiK | 10.0 | 0.0703 |
| NaRb | 23.6 | 0.00711 |
| NaK | 14.2 | 0.0281 |
| KCs | 22.2 | 0.00644 |
| RbCs | 21.6 | 0.00614 |
| KRb | 6.21 | 0.0952 |
| LiNa | 1.12 | 7.86 |
| Rb | 0.295 | 52.3 |
| Li | 0.0694 | 8760. |
For all systems considered, the characteristic energy falls in the ultracold regime. Reproduced with permission from ref by Karpa and Dulieu. CC BY 2025 arXiv.
A great number of numerical studies have found classical, semiclassical, and quasiclassical mechanics are sufficient to accurately predict many triatomic scattering cross sections at energies above 0.1 mK in triatomic collisions (see refs , , , , , , , , , − , ). In 2000, Dashevskaya and Nikitin demonstrated that quasiclassical mechanics can be used to accurately determine s-wave vibrational relaxation cross sections for H2 (ν = 1, j = 0) + 4He → H2 (ν = 0, j = 0) + 4He in the ultracold regime above 0.1 mK. Dashevskaya and Nikitin expanded the Landau–Lifshitz method to determine quasiclassical matrix elements , to apply to states that are quasiclassical only in that their asymptotics obey the WKB approximation. This generalized Landau–Lifshitz method was applied to an exponential repulsive interaction and a Morse potential model and the results were compared to close-coupling cross sections. Quasiclassical results for the exponential repulsive interaction and for the Morse interaction closely agreed with quantum results just above 10–8 eV (0.1 mK) with the inclusion of quantum suppression effects. Dashevskaya et al. subsequently identified quantum-to-classical crossover in ion–molecule capture of H2 (j = 1) + Ar+ on the order of 0.1 mK and N2 (j = 1) + He+ on the order of 1 mK in 2004. Dashevskaya et al. treated the ion–molecule capture process in terms of a closed-state, structureless atomic ion and a rigid rotor molecule and found close agreement between rate coefficients computed with accurate quantum mechanics and the adiabatic channel classical approximation. , This agreement allowed for the accurate analysis of the capture process via classical treatment of the relative motion of the collision partners under an assumption of conserved intrinsic angular momentum projected onto the collision axis.
Similarly, in 2005, Quéméner et al. found that quenching rates in ultracold K + K2 collisions obey the classical Langevin model at energies higher than 0.1 mK. , An ab initio potential energy surface was generated for the potassium trimer 14 A 2 state via single-reference restricted open-shell coupled-cluster with single, double, and noniterative triple excitations [RCCSD(T)] − and employed the resulting surface in quantum close-coupling calculations with a body-frame democratic hyperspherical coordinate formalism at short atom–diatom distances , and the Arthurs–Dalgarno formalism at long atom–diatom distances. The resulting quantum total quenching rate coefficients reached their classical Langevin capture model values semiquantitatively past 0.1 mK. In 2017, Croft et al. also calculated elastic cross sections for s-wave K2 (v = 0, j = 0) + Rb collisions that exhibited a quantum-to-classical crossover on the order of 0.1 mK. Croft et al. evaluated quantum cross sections according to the atom–diatom scattering method of Pack et al. , and observed a large number of fine resonances appearing above approximately 10 mK. Although not explicitly discussed with reference to the classical post-threshold law in the work, resonances are visible beyond the energy at which the cross section begins to deviate from the threshold regime associated with E 0 quantum scaling in the energy range beyond 0.1 mK.
And, likewise, in 2016, Stoecklin et al. found that quantum vibrational quenching cross sections agree with the classical Langevin capture scaling at collision energies above 1 mK for the collision of Ca and BaCl+. Stoecklin et al. created an analytic potential energy surface for the electronic ground state 1 A′ via ab initio calculation at the coupled cluster singles, doubles, and perturbative triples [CCSD(T)] level of theory and employed both the close-coupling method and quantum defect theory − to determine the cross section quantum mechanically. The classical Langevin rate was computed and used to determine a statistical capture rate constant according to the method of Lara et al. Additionally, results were compared to the experimental data of Campbell et al. on the order of 10 to 100 mK. Both the experimental and quantum close-coupling vibrational quenching rate coefficients were found to obey the classical Langevin scaling on the order of 10 to 100 mK. Likewise, quantum defect theory universal loss rate coefficients were found to agree closely with the classical Langevin law (modulo oscillations) at energies on the order of 10 nK and above, and despite discrepancies at energies below one mK, was consistent with the experimental data and close-coupling calculations at energies above one mK.
Additional studies identify triatomic collisions in which classical post-threshold laws operate at collision energies above 10 mK. ,, In 2005, Cvitaš et al. found that classical post-threshold laws hold for the total inelastic rate coefficient of Li + Li2 collisions above 10 mK. Cvitaš et al. considered an ab initio global potential energy surface for Li3 computed via all-electron coupled-cluster theory. To determine scattering cross sections, the scattering S matrix was determined through wave function matching at the boundary of an inner region, where the wave function is determined through propagation of coupled equations in a diabatic-by-sector basis, and an outer region, where the wave function is determined according to the Arthurs–Dalgarno formalism. Comparison of the resulting quenching rates to the classical Langevin rate coefficient for vibrational quantum numbers v = 1, 2 indicated semiquantitative agreement for bosonic and fermionic Li. It was noted that the same Langevin rate coefficient holds for other spin-polarized state alkali atom–diatom inelastic rates in the post-threshold regime, which Cvitaš et al. predict to occur at or above 6.86 mK for Na, 1.89 mK for K, 0.537 mK for Rb, and 0.235 mK for Cs. In a similar spirit, in 2023, Morita et al. demonstrated that numerical quantum reactive and elastic cross sections obey classical post-threshold laws above 10 mK for Li + NaLi(ν = 0, j = 0) → Li2 + Na. Morita et al. considered an ab initio potential energy surface for the 14 A′ state of NaLi2 calculated according to the multireference configuration interaction (MRCI) method , and performed accurate quantum reactive scattering calculations with the adiabatically adjusting principal-axis frame hyperspherical (APH) coordinates method of Pack et al. , Examination of the reactive and elastic cross sections as a function of the collision energy evidence a rate law change consistent with quantum-to-classical crossover on the order of 10 mK and below for quantum numbers J = 0, 1 for both even and odd parity.
Beyond classical and semiclassical mechanics, beginning in 2019 Pérez-Ríos et al. also identified that QCT was valid for the determination of vibrational quenching cross sections of BaRb+(v) + Rb at energies above 1 mK. ,, In 2019, Pérez-Ríos considered interaction of spin-polarized Rb atoms in terms of Strauss et al.’s empirical triplet a Σ u potential and interaction of Ba+ – Rb according to a generalized Lennard-Jones potential that behaves asymptotically as a fourth-order van der Waals potential. QCT was again calculated with nuclear dynamics treated according to classical mechanics with initialization of trajectories and identification of final trajectories as individual quantum states treated according to the semiclassical quantization rule. The scaling of the vibrational quenching cross section was found to be consistent with the classical Langevin capture model scaling where the molecule was initialized in vibrational states v = 187–195 with angular momentum j = 0 for collision energies at and above 1 mK, with discrepancies for higher initial vibrational states. In 2021, Mohammadi et al. subsequently found that quasiclassical mechanics agrees with the classical Langevin value for BaRb+ (v)+ Rb for (2)1 Σ+ and (1)3 Σ+ vibrational relaxation cross sections. Mohammadi et al. employed QCT to simulate the collision, as in Pérez-Ríos’ 2019 approach, using a pairwise additive ground-state potential with a Rb2 interaction given by Strauss et al. and generalized Lennard-Jones potentials for both Ba+ – Rb and Ba – Rb+. The vibrational relaxation cross section from QCT was shown to be near the Langevin value for vibrational quantum numbers v = 5–16 for all collision energies studied, namely in the range of 1 to 100 mK. And, in 2024, Koots and Pérez-Ríos revisited the RbBa+ + Rb collision, now with the use of a Lennard-Jones potential to represent the triplet a Σ u state of Rb2 with QCT performed with their Python Quasi-Classical Atom-Molecule Scattering (PyQCAMS) package. These results confirmed quenching cross sections in agreement with the classical Langevin capture model at 20 and 100 mK for v = 187–195, with closest agreement for the lower vibrational quantum numbers. Over the years 2014 to 2021, Pérez-Ríos et al. have further employed a classical model based on a dynamical Langevin approach to determine classical ultracold threshold laws in a wide array of literature on three-body recombination ,,,, for which Dieterle et al. have experimentally confirmed the presence of Langevin capture dynamics for inelastic three-body collisions of individual ionic impurities in high-density rubidium Bose–Einstein condensates and Stevenson et al. have experimentally observed close agreement between NaCs three-body loss rates for varied field detunings and Rabi couplings across temperatures of 100 to 500 nK. ,,
2.1.2. Experimental Evidence
The aforementioned numerical evidence predicts quantum-to-classical crossover in the cold to ultracold regime for a broad range of atom–atom, atom–ion, molecule–molecule, and atom–molecule collisions. ,,,,,− ,− ,, Fortunately, in the past 15 years, experiment has supported these numerical predictions with flying colors. − ,,,− ,,,− A wide variety of experimental setups, including optical and/or radio-frequency traps ,,,,,, and merged supersonic beams, ,,, have reliably produced observations in keeping with classical and semiclassical predictions for disparate atomic and molecular processes including quenching, , charge exchange, ,, photofragmentation, , and atom–ion/molecule capture. ,,,
2.1.2.1. Atom–Atom and Atom–Ion Collisions
In 2024, Xing et al. found that total cross sections for Li(2S 1/2) + Ba+ (5D 5/2) and Li(2S 1/2) + Ba+ (5D 3/2) at 30 μK are consistent with scaled classical Langevin cross sections both in experiment and quantum numerics, as shown in Figure . This finding further supports the ability of classical mechanics to accurately describe many atom–ion collisions in the ultracold regime. To measure the cross sections experimentally, Xing et al. employed a combined all-in-one-spot ultracold atom apparatus with a segmented linear Paul trap. , 138Ba+ atoms were cooled to approximately the Doppler temperature of ∼354 μK and prepared in their 5 D 3/2 or 5 D 5/2 electronic state and 6Li atoms were cooled to approximately quantum degeneracy and prepared in their |f = 1/2, m f = −1/2⟩ state. The survival probability of Ba+ (52 D 3/2) or Ba+ (52 D 5/2) was recorded after various interaction durations, as well as the proportion of fine-structure quenching (FSQ), nonradiative charge exchange (NRCE), and nonradiative quenching (NRQ) events associated with distinct radial, spin–orbit, and rotational energy level transitions. Numerically, calculations were performed for LiBa+ potential energy curves computed via the CIPSI (configuration interaction by perturbation of a multiconfiguration wave function selected iteratively) package − with spin–orbit couplings computed via a quasidiabatic method. − Quantum cross sections were calculated in space-fixed frame according to two models: (i) a four-channel quantum scattering (FCQS) model of states in body-fixed frame with total electronic angular momentum Ω = 0+: 11Σ+ of Li(2s) + Ba+ (6s), 21Σ+ of Li+ + Ba(6s 2 1 S), and 31Σ+ and 13Π of Li(2s) + Ba+ (5d) (with coupling between atomic internal angular momentum and relative motional angular momentum neglected) and (ii) a multichannel quantum scattering (MCQS) model that additionally included Ω = 0–, 1 for 13Σ+ of Li(2s) + Ba+ (6s), as well as Ω = 0–, 1 for 23Σ+, Ω– = 0–, 1, 2 for 13Π, Ω = 1 for 11Π, Ω = 1, 2, 3 for 13Δ, and Ω = 2 for 11Δ of Li(2s) + Ba+ (5s). Results were thermalized according to a Maxwell–Boltzmann velocity distribution. For the FCQS model, the classical Langevin cross sections provided an upper bound for quantum cross sections. For MCQD, classical Langevin cross sections no longer serve as an upper bound for quantum cross sections locally due to the impact of shape resonances, but qualitatively provide an energy scaling of the quantum cross sections for FSQ, NRCE, and NRQ processes, often at energies well below 10 mK. Xing et al. found that experimental NRCE and NRQ cross sections at 30 μK, normalized to the computed classical Langevin rate, agree with both quantum calculations and the classical partial Langevin rate coefficient. Note quantum numerics suggest that elastic contributions are significant in the collision and are greater than the total Langevin rate coefficient, which suggests that the full capture assumption of the standard classical Langevin model does not hold.
In 2009, Grier et al. demonstrated agreement between experimental and classical Langevin rate coefficients also extends to multiple isotope combinations of resonant charge exchange for Yb+ + Yb at collision energies as low as 3 μeV (35 mK). Grier et al. employed a double-trap setup , in which neutral and singly charged atoms were trapped with a magneto-optical trap (MOT) and surface planar Paul trap, respectively, in a shared spatial volume. Isotope-selective ion fluorescence was used to measure signatures of charge-exchange collisions of αYb+ + βYb →αYb + βYb+ via tracking of αYb population decay. A pair of charge-coupled device (CCD) cameras were used to image the local atomic density n(r), which informed computation of the average atomic density colocated with the ions ⟨n⟩ = ∫p(r)n(r) dr for normalized ion distribution p(r) and subsequently the elastic rate coefficient K via a linear fit of the average atomic density ⟨n⟩ as a function of the measured ion decay rate constant Γ = 1/τ. For comparison, the semiclassical Langevin cross section was determined for an ab initio polarizability for the atomic ground state. , The rate coefficients were found to agree closely with the semiclassical Langevin value for collisions examined (172Yb+ + 174Yb, 172Yb+ + 171Yb, and 174Yb+ + 172Yb). The agreement extended from 3.1 μeV (36 mK) to 4 meV (46 K), namely over more than 3 orders of magnitude in energy. At 100 μeV (1.2 K) the semiclassical prediction was 5.8 · 10–10 cm3 s–1 with an experimental measurement of 6 · 10–10 cm3 s–1an absolute difference of just O(10–11 cm3 s–1).
And, in 2021, Ben-shlomi et al. identified classical Langevin scaling of quenching cross sections in 88Sr+ – Rb collisions at collision energies in the ultracold and cold regime as well. Ben-shlomi et al. measured the quenching cross section for the atom–ion collision with fine energy resolution on the order of 100 μK via the passage of optical-lattice-trapped Rb atoms across a radio-frequency-trapped 88Sr+ ion. Measured total quenching, electronic-excitation-exchange, and spin–orbit-change cross sections closely agreed with the Langevin cross section for all energies measured, which appeared in the domain of [0.2, 12] mK. In 2017, Saito et al. also experimentally measured classical Langevin scaling in cross sections for cold 6Li and 40Ca+ collisions. Saito et al. experimentally measured charge-exchange collision cross sections for the atom–ion mixture by trapping and cooling the two collision partners in distinct areas of a vacuum chamber and transporting the optically trapped atoms with an optical tweezer to be mixed with the radio-frequency-trapped ions. The resulting products of the collision were probed via measurement of the ions in their S 1/2, P 1/2, D 3/2, and D 5/2 states. The charge-exchange collision cross sections for the ions in a S 1/2, P 1/2, and D 3/2 mixture; the D 3/2 state alone; and the D 5/2 state alone agreed with the classical Langevin cross section for all energies measured, namely on the order of 1 mK to 1 K.
The extremely high accuracy possible with classical and quasiclassical treatment of cold molecules is especially evident in Kondov, Majewska et al.’s 2018 Sr2 photofragmentation experiments. , Kondov, Majewska et al. answered a decades-old quandary in the field of photodissociation − by experimentally observing and theoretically confirming a quantum-to-quasiclassical crossover at temperatures on the order of mK in photofragment angular distributions of diatomic strontium. , Above this crossover, at collision energies on the order of 0.1 to 1 mK, experiment, quantum, and semiclassical photofragmentation distributions were often nearly visually indistinguishable, as shown in Figure . In particular, there was near complete agreement between fully quantum, semiclassical WKB, and quasiclassical axial recoil limit photofragment distributions for the 0 u (−2,1,0) and 1 u (−2,1,0) states at just 48 mK, as is readily visible in Figure (right column center and bottom)a finding that evidences the ability of semiclassical and quasiclassical mechanics to accurately model not only collision cross sections, but photofragment distributions at cold temperatures for suitable molecular systems.
9.
Comparison of measured, quantum numerical, and semiclassical WKB numerical photofragment angular distributions of cold and ultracold strontium for initial 0 u (left column) and 1 u (right column top) states at energies 13 MHz (0.6 mK), 33 MHz (1.6 mK), 53 MHz (2.5 mK), 100 MHz (4.8 mK), and 300 MHz (14.4 mK) where each pair of rows corresponds to experiment (top) and quantum theory (bottom) with the exception of the final semiclassical WKB row. Strong agreement is also visible between between quantum theory, the semiclassical WKB approximation, and the quasiclassical axial recoil limit results at 1000 MHz (48 mK) for 0 u (right column center) and 1 u (right column bottom), and between quantum theory (solid lines) and the semiclassical WKB approximation (dashed line) for R (thick red line) and cos δ (thin blue line) above energies of approximately 1 mK (bottom center). Additional details in refs , . Reproduced figures with permission from I. Majewska, S. S. Kondov, C.-H. Lee, M. McDonald, B. H. McGuyer, R. Moszynski, and T. Zelevensky, 98, 4, 043404, 2018, Copyright 2018 by the American Physical Society, and from S. S. Kondov, C.-H. Lee, M. McDonald, B. H. McGuyer, I. Majewska, R. Moszynski, and T. Zelevensky, 121, 14, 143401, 2018, Copyright 2018 by the American Physical Society.
To identify this agreement, 88Sr atoms were cooled and photoassociated to produce Sr2 molecules with a temperature on the order of μK in a one-dimensional optical lattice trap, and photodissociation light pulses with a duration of 10 to 20 μs were employed, leading to a time-of-flight of 20 to 800 μs and an imaging pulse of 10 to 20 μs. The inverse Abel transform was used to convert the time-of-flight images to cross sections, which were subsequently averaged radially to produce the angular photofragment density. To identify the quantum-to-quasiclassical crossover, the photodissociation cross sections were simulated fully quantum mechanically according to Fermi’s golden rule on ab initio potentials, , semiclassically according to the WKB approximation, and semiclassically via an alternative model that treats molecular rotation classically. A quasiclassical model was also used to predict the angular distribution as a function of the initial molecular orientation probability density and the angular probability density of electric-dipole light absorption. ,, The quantum approach was found to accurately determine the cross sections at all energies considered (modulo potential energy surface corrections).
The quasiclassical model accurately yielded the angular distribution for 0 u (v = −4, J i = 1, M i = 0) molecules with parallelly polarized photodissociation light (P = 0) at the axial recoil limitthe energy above all potential energy barriers at which the photodissociation speed greatly surpasses rotation speeds, such that molecular fragments exit on the molecular axis, here just 14 mK. Likewise, the energy evolution of the amplitude R of photofragments in the J i – 1 angular momentum state and the phase difference δ obeyed the quasiclassical axial recoil limit R ≈ 1/2 above 5 mK and reached the semiclassical WKB (as well as semiclassical model) values at ≳ 1 mK, as depicted in Figure . Note quantum nuclear spin statistics and selection rules still can lead to discrepancies relative to quasiclassical results even at high energies, as Kondov, Majewska et al. observed, for example, for 1 u (−1,1,0) molecules subject to a projection quantum number selection rule ΔM = ±1 for perpendicular polarization that disallows odd angular momenta J. ,
Significant literature also points to the ability of classical and semiclassical approaches to reproduce quantum mechanical and experimental results for cold and ultracold atom–atom and atom–ion collisions in the presence of electromagnetic fields. ,− Initial demonstrations in the late 1980s and 1990s ,− indicated agreement between (semi)classical, quantum, and experimental analyses of atomic loss in optical traps with molecular states subject to laser-field dressing at collision energies on the order of 100 μK. − In the late 2000s and 2010s, classical and semiclassical methods to simulate cooling and trapping in radio frequency ion traps were found to be consistent with experiments. ,,− Notable among these advancements include Monte Carlo simulations based on classical time-evolution matrices by Devoe and classical trajectory simulations based on hard-sphere collisions and the polarization method of Cetina, Grier, and Vuletić by Meir et al. Devoe’s simulations closely reproduced experimental trapped ion lifetimes in noble buffer gases, including those of 136Ba+ in argon (theoretical value, 45 s; experimental value, 50 to 100 s) and krypton or xenon (theoretical value, < 0.1 s; experimental value, <5 s). ,, Likewise, Meir et al.’s simulations closely reproduced experimental values for the dependence of the ion temperature in the range of approximately 0.5 to 3 mK on the number of Langevin collisions for an 88Sr+ ion in a linear segmented Paul trap with ∼5 μK 87Rb in a cross dipole trap. Furthermore, all of Meir et al.’s classically simulated data points for the collision-number dependence of the ion temperature were found to be within one-sigma confidence bounds of the experimental mean. Contemporaneously, Wright et al. further supported the ability of (semi)classical mechanics to accurately model experimental loss rates of ultracold ions in traps with pulsed, frequency-chirped light close to resonance, ,− as their hybrid Landau–Zener excitation and Monte Carlo calculation based on classical atomic dynamics produced qualitative agreement with both experiment and fully quantum simulations. There are also studies in the literature that examine these systems from the perspective of semiclassical catastrophes and rainbows, , alternative classical models of cooling in electromagnetic traps, − and semiclassical models of quantum beats, which are interesting to watch as additional examples.
2.1.2.2. Molecule–Molecule Collisions
Just as predicted by quantum theory, Höveler et al. likewise experimentally observed classical capture rate coefficients on the order of 10 mK for molecular collisions of H2 + HD and on the order of 1 K for molecular collisions of H2 + D2, H2 + H2, and HD+ + HD, as shown in Figures , , and . ,, This finding represents classical behavior well within and on the cusp of the cold regime in molecule-cation collisions of a family of diatomic hydrogen molecule isotopologues, as presaged by Dashevskaya et al. The collision was studied experimentally via a merged supersonic beam setup: ,, Höveler et al. prepared ground rotational state J = 0 molecules (GS) in two pulsed supersonic beams, excited one beam’s molecules to a low-field seeking Rydberg–Stark state (Rg) with a rovibronic ground state ion core of a given principal quantum number, and merged the beams with a relative mean velocity of v rel = v Rg – v GS. The product ions were then measured with a time-of-flight mass spectrometer. The resulting relative total reaction cross section and rate coefficients for all collisions were compared to the classical Langevin capture model scaling, with H2 + H2, H2 + D2, and HD+ + HD collisions additionally compared against the theoretical rate coefficients of Dashevskaya et al. with appropriate mass scaling for isotopologues as required. ,,
10.
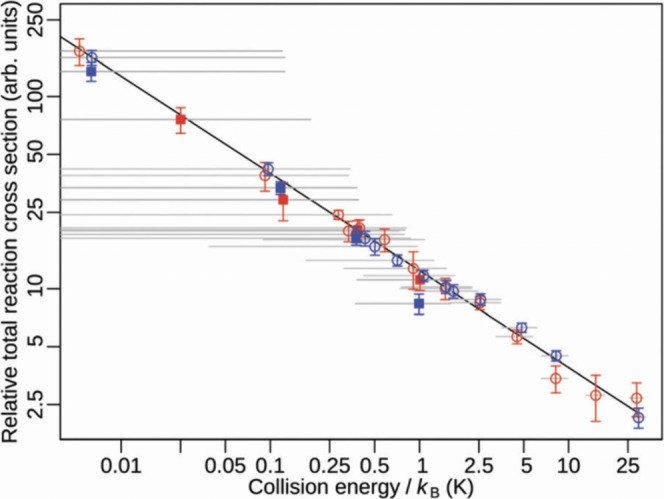
Close agreement between the classical Langevin law [exponent 0.5] and experiment [exponent – 0.505(14) from linear regression, black line] for the relative total reaction cross section in the H2 + HD collision. Experimental data are shown for time-of-flight windows of 5 μs (blue points) and 6 μs (red points), with vertical and horizontal gray bars indicating standard deviation of single data points and extent of probed collision energies, respectively. Used with permission of the Royal Society of Chemistry from The H2 + HD reaction at low collision energies: H3/H2D+ branching ratio and product-kinetic-energy distributions, K. Höveler, J. Deiglmayr, J. A. Agner, H. Schmutz, and F. Merkt, 23, 4 2021; permission conveyed through Copyright Clearance Center, Inc.
11.

Quantum-to-classical crossover apparent in the cold regime for (top) and (bottom) . Gray points indicate individual measurements and black points measurements averaged within collision-energy ranges delineated with gray vertical lines, where vertical bars indicate one standard deviation and dashed lines indicate theoretical predictions. A transition is evident below 1 K between the quantum threshold value [blue arrow] and the classical Langevin capture model limit [red solid horizontal line]. Figure used with permission from Höveler, Deiglmayr, and Merkt from ref , CC BY 2021 Taylor & Francis.
12.
Cold quantum-to-classical crossover below 1 K visible in experimental rate coefficients for (a–c) H2 + H2 collisions [with para H2 (J = 0):ortho-H2 (J = 1) ratios of (a) 25:75, (b) 59(1):41(1), and (c) 80(1):20(1)] and (d) HD+ + HD collisions with 4.25% H2 and 4.25% D2 by volume. Theoretically computed contributions of individual molecules/molecular states are shown in color ([a–c]: ortho-H2 (J = 1) in red, para-H2 (J = 0) in blue, [d]: HD (J = 0) in blue, HD (J = 1) in red, H2 in green, D2 in orange), with experimental data and classical Langevin values presented as in Figure . Figure used with permission from Katharina Höveler, Johannes Deiglmayr, Josef A. Agner, Raphaël Hahn, Valentina Zhelyazkova, and Frédéric Merkt, Physical Review A, 106, 5, 052806, 2022, Copyright 2022 by the American Physical Society.
These experimental results showed clear agreement with classical Langevin capture model predictions both in terms of reaction cross sections and rate coefficients. ,, The experimental relative total reaction cross section for H2 + HD agreed with the classical Langevin capture law for all collision energies E coll measured50 mK to 30 K, encompassing 3 orders of magnitudewith a linear regression slope −0.505(14) in agreement with Langevin capture E coll with an absolute difference of O(10–3) (i.e., a relative discrepancy of just 1%). The experimental rate coefficients for H2 + H2 and H2 + D2 agreed with the classical Langevin capture scaling at higher energies above 3 K. Moreover, analysis of the deviation from classical Langevin behavior in the quantum limit below 1 K supported the theoretical prediction that a lower reduced mass would be associated with a wider collision energy range associated with deviations from Langevin behavior. , Namely, quantum theory predicts a 3.0 enhancement factor in the threshold rate coefficient’s rise between H2 and D2 (due to a product of the relative proportion of ortho and para spin isomers in the natural molecules and the reduced mass ratio for D2 and H2, ), which was supported by the experimental finding of an enhancement factor of 2.8(3), a difference of 7%. Additionally, the experimental branching ratio of H2 + D2 into H2D+ + D and HD2 + H products at 10 K of η = 0.341(15) and 1 – η agreed with the quasiclassical prediction of 0.3 at 0.01 meV (1.2 K), an absolute prediction error of O(10–2). Experimental rate coefficients for H2 + H2 and HD+ + HD were both consistent with reaching the classical Langevin capture model scaling by a collision energy on the order of 1 mK and consistent with Vogt and Wannier’s prediction over half a century prior: that ion-atom/molecule capture is enhanced by a factor of 2 at the quantum limit with respect to the Langevin rate. Finer collision-energy resolution remains a need to verify the precise enhancement factor.
2.1.2.3. Atom–Background Gas Collisions
In the same vein, for glancing and diffractive collisions of optically and magnetically trapped atoms and background gases, a wide array of authors have found close agreement between classical and semiclassical formulas ,,− and experimental data. , In 1988, Bjorkholm built on the classical small-angle scattering formula ,− to model trap loss due to elastic collisions of cold atoms with ambient background gas molecules as occurring due to the transfer of sufficient energy to expel the atom from the trap (namely, where the scattering angle exceeds the associated threshold). ,, This classical ejection rate yielded lifetimes that closely matched experimental values for sodium in varied conditions: 500 mK magnetic-molasses optical traps at pressure p (theoretical value, 2.2 · 10–8 s/p; experimental value, 2.0 · 10–8 s/p), 17 mK magnetic traps at pressure 10–8 Torr (theoretical value, 1.1 s; experimental value 0.83 s), and ∼5 mK optical traps at pressure 4 · 10–9 Torr (theoretical value, 2.2 s; experimental ∼ 1 s). Likewise, Arpornthip, Sackett, and Hughes’ 2012 classical loss rate for atoms in 1 K traps colliding with 300 K ambient gases closely agreed with experiment for sodium in hydrogen gas (theoretical value, 5.3 · 107 Torr–1 s–1; experimental value, 5 · 107 Torr–1 s–1), as well as for rubidium in argon gas (theoretical value, 2.3 · 107 Torr–1 s–1; experimental values 2.2 · 107 Torr–1 s–1 and 1.6 · 107 Torr–1 s–1). , Arpornthip, Sackett, and Hughes’ classical formula additionally concurred with the experimentally observed behavior of reduced dependence of the loss rate on the trap depth in the range [0.5, 2] K , with deviations observed for shallower traps where the classical approximation fails. ,,,
In the 2010s, Booth, Shen, Krems, and Madison similarly developed a semiclassical approach to trapped atom–background gas collisions that agrees with both quantum calculations and ultracold experiments to high accuracy. Booth, Shen, Krems, and Madison employed the minimum angle leading to trapped atom ejection and the total collision rate expression for a Maxwell–Boltzmann distribution to produce a semiclassical loss rate Γloss = n⟨σtot v⟩(1 – p QDU) as a function of the gas density n, total cross section σtot, collision velocity v, and a novel probability of atomic retention in the trap p QDU. This probability p QDU was found to constitute a law of quantum diffraction universality in terms of the trap depth U, in which the coefficients β j and characteristic quantum diffractive energy U d are entirely independent of the van der Waals coefficient, mass, and dipole (ultimately leading to a universal formula for the gas pressure P = nk B T = Γloss (U)k B T/⟨σloss (U)v⟩ that has led to a search extending into the 2020s to establish the use of cold trapped atoms as pressure sensors ,− ,− ).
Booth, Shen, Krems, and Madison’s semiclassically predicted pressure agreed with experiment for magnetically trapped 87Rb atoms at <0.5 mK with helium, xenon, argon, molecular hydrogen, nitrogen, and carbon dioxide. In particular, in the case of nitrogen, the associated pressure measurement reached as high as 0.5%-level agreement with the value for an ionization gauge calibrated by the National Institute for Standards and Technology (NIST). Similarly, in 2023, Kłos and Tiesinga further found agreement between quantum scattering results and the semiclassical small-angle approximation to the thermalized total elastic rate coefficient to within 10% for ultracold 7Li and 87Rb with 4He, 20Ne, 40Ar, 84Kr, 132Xe, and 14N2; ,− and, in 2024, Booth and Madison identified agreement between the quantum scattering results of Medvedev et al. and Kłos and Tiesinga and a semiclassical formula based on the Jeffreys–Born approximation for accurate total rate coefficients for collisions of cold 87Rb and 7Li with higher-mass background gases, in the case of trapped 7Li, with an error of less than 2% for krypton or xenon background gas and with an error less than the uncertainty range for argon or nitrogen background gas. These results for diffractive and glancing collisions thus support the use of semiclassical and classical methods to produce near-exact results in the cold and ultracold regimes for a wide array of atomic and molecular systems.
2.1.2.4. Atom–Molecule Collisions
We see the same high level of correspondence between (semi)classical methods and experiment in cold and ultracold atom–molecule collisions. With less than 1% error from classical predictions, Shagam et al. found in merged supersonic beam experiments that the rate constants for reaction of para-H2 (j = 0) and HD with He(23 P 2) obey the classical Langevin law to temperatures as low as on the order of 0.1 K, as shown in Figure further evidence of classical behavior in cold collisions of atoms with hydrogen molecule isotopologues. The experiment prepared supersonic beams of H2 or HD and He, excited He to the desired collision partner state, and employed a magnetic quadrupole guide to merge the resulting beams. The resulting beams were collided in a time-of-flight mass spectrometer such that the reaction rate could be found via detection of the atom at a microchannel plate. − For comparison, the scaling of the respective classical Langevin/Gorin scaling law was determined according to the order of the long-range van der Waals interaction, with the rate itself determined according to an estimated van der Waals coefficient. For collision of para-H2 with He(23 P 2), which features an asymptotic sixth-order van der Waals interaction, the sixth-order van der Waals coefficient was determined according to the H2 dipole polarizability of Bishop and Pipin and the sum-over-states expression for He(23 P 2) polarizability, dipole moments and transitions were calculated according to multireference configuration interaction calculations with single and double excitations (MRCISD), and potential energy surfaces were produced with the MOLPRO and DALTON packages. For collisions of He(23 P 2) with para-H2, the reaction rate constant scaled according to classical Langevin (Gorin) scaling to energies as low as 0.8 K, namely, in the unitary “black hole” limit in which reactants capable of surpassing the centrifugal energy barrier formed products with (near-)unit probability and the rate depended solely on the long-range interaction. The energy dependence of the reaction rate constant for collisions of He(23 P 2) with the HD isotopologue was also found to be consistent with the same classical Langevin scaling. Shagam et al. noted that the scaling law is independent of collision partner for a given specific van der Waals interaction, and suggested that the conformity of experimental reaction rates with universal Langevin scaling laws allows such laws to be used to probe long-range forces in cold collisions, including those that pertain to astrochemistry.
2.2. Rationales for the Accuracy of Classical and Semiclassical Approaches in the Cold and Ultracold Regime
Recent theoretical and experimental work (refs , , , , , , , , and − ) suggests a variety of rationales for why classical behavior of near-threshold physical and chemical systems is so ubiquitous beyond the classical limit of ℏ→0, high energy, and large quantum numbers ,,− ,,,, and how to predict what new ultracold molecular systems are expected to be accurately simulable with computationally efficient classical, semiclassical, and quantum-classical methods in the future.
2.2.1. Approach of Gribakin and Flambaum
Since 2020, a plurality of studies (see refs , , , , , − , − , − , − , − , − ) relate semiclassical behavior in cold and ultracold atomic and molecular collisions to the 1993 work of Gribakin and Flambaum, who discovered that semiclassical mechanics is often sufficient to accurately determine cross sections even for low collision energies typically associated with quantum mechanics. ,
Initially, Gribakin and Flambaum argued similarly that the semiclassical WKB approximation is expected to be accurate for scattering at low collision energies as long as there exist deep potential wells that permit the wave function to have a short oscillation period. This argument permits direct determination of the scattering length from the connection of the semiclassical wave function in the interior region to the quantum mechanical wave function in the exterior region at the region boundary. Specifically, Gribakin and Flambaum first assumed the semiclassical WKB solution holds in the interior beyond the classical turning point
| 3 |
and a quantum superposition state of Bessel and Neumann functions holds in the exterior asymptotic region. Matching the semiclassical WKB solution to the approximate analytic solution for an n th order asymptotic van der Waals potential U(R) ≃ −α/R n at a radius R = R * at which the semiclassical interior and quantum exterior solutions agree yielded the near-threshold scattering length in terms of the mean scattering length a̅
| 4 |
| 5 |
| 6 |
for the zero-energy semiclassical phase between the classical turning point and infinity Φ and the derived constant . As predicted by the rationale that semiclassics holds for deep potential wells, the hybrid semiclassical-quantum method gave a scattering length that agrees closely with the quantum result (namely, the extrapolation of the quantum result to zero Kelvin), as well as experimental data, for scattering from the deep Cs–Cs3Σ u potential (see Table )
| 7 |
| 8 |
| 9 |
where the potential is given by the sum of an exchange repulsion term (parametrized by B, α, and β) and a series of van der Waals terms (parametrized by C 6, C 8, and C 10 and modulated by a cutoff potential f c (R) that removes the van der Waals terms’ R = 0 divergence via imposition of a cutoff radius R c ). This scattering length in turn yielded a high-accuracy s-wave phase shift δ0 = −ak at wavenumber k, as well as the near-threshold scattering cross section σ = 4πa 2. Their subsequent development of a hybrid semiclassical-quantum formula for the effective range r e in terms of the aforementioned γ and ν = 1/(n – 2) along the same lines continued to support this initial deep potential well argument. Based on the same argument that the wave function can be determined by matching the semiclassical wave function in the interior region and the quantum wave function in the exterior region at the region boundary, Flambaum and Gribakin found that the semiclassical equation for the effective range r e
| 10 |
| 11 |
| 12 |
| 13 |
produced values of the effective range r e for the deep potentials of Li2, Na2, and Cs2 that agreed with quantum results with less than 1% error, again based on zero-energy semiclassical and quantum solutions. Note the special case result for n = 6 was simultaneously developed by Gao in the context of quantum defect theory. This effective range in turn gave high-accuracy s-wave phase shifts according to the definition of the standard effective range expansion
| 14 |
5. Gribakin and Flambaum’s Semiclassical Scattering Length a class (eq ) Closely Agrees with the Fully Quantum Mechanical Scattering Length a quant with Low Relative Error for Various Parametrizations of the Cs2 3Σ u Potential (eq ) .
| R c [au] | Rmin [au] | Umin [10–3 au] | aclass [au] | aquant [au] | Relative Error |
|---|---|---|---|---|---|
| 23.215 | 11.93 | –1.273 | 376 | 352.5 | 6.7% |
| 23.190 | 11.91 | –1.286 | 140 | 144.2 | 2.9% |
| 23.165 | 11.88 | –1.300 | 65 | 68.0 | 4.4% |
| 23.140 | 11.86 | –1.313 | –69 | –67.7 | 1.9% |
| 23.115 | 11.83 | –1.327 | 467 | 485.3 | 3.8% |
Results are shown for parameters B = 0.0016, α = 5.53, β = 1.072, C 6 = 6.5, C 8 = 1.1 · 106, and C 10 = 1.7 · 108 from ref , with stated cutoff radii R c resulting in shifted potential minima (R min, U min). The quantum result follows from extrapolation of the s-wave phase shift at k = 0.005 au (12 μK) to k = 0 au (zero Kelvin). Reproduced table with permission from G. F. Gribakin and V. V. Flambaum, Physical Review A, 48, 1, 546, 1993. Copyright 1993 by the American Physical Society.
The combination of these successes at first led Gribakin and Flambaum to first formally state that the scattering phase shift for deep potentials with asymptotic behavior U (R) ≃ −α/R n depends only on the derived constant γ and the semiclassical phase Φ where the potential well depth is much greater than the scattering energy. This implies the scattering phase shift in such cases is independent of energy, which they connect to the fact that deep in the potential well the potential may be substituted with a boundary condition that is independent of the energy.
However, what most closely relates to recent measurement of semiclassical behavior in cold and ultracold collisions is that Gribakin and Flambaum subsequently identified that, beyond their deep well hypothesis, their semiclassical method also succeeds for determination of the scattering length for a shallow H2 3Σ u potential. Gribakin and Flambaum rationalized the close agreement between semiclassical and quantum results for this shallow potential in terms of their derived formula and noted that the scattering length a for the system is significantly smaller than the average scattering length a̅, which ensures the scattering length is determined nearly entirely by the semiclassical phase Φ between the classical turning point and infinite radius. This finding points to a potentially much broader range of applicability of semiclassical mechanics near threshold in modern studies than originally theorized in which the semiclassical approximation can provide accurate results for shallow potentials, including potentials that support no wave function oscillations.
2.2.2. WKB Criterion
The WKB approximation has also been used to explain quantum-to-classical crossovers in the cold and ultracold regimes. These rationales, introduced by Julienne and Mies in 1989, Côté et al. in 1996, and Mody et al. in 2001, continue to be actively cited nearly three decades on (see refs , , , , − , − , , , − , , , , , , , , , − ).
Specifically, Julienne and Mies proposed that one may identify a broad range of energies at which semiclassical methods are accurate near threshold via careful consideration of the energies for which WKB holds at all interatomic distances. Building on prior work, − Julienne and Mies began with considering the deep connection between WKB and multichannel quantum defect theory (MQDT), which revealed that MQDT reference wave functions approach WKB wave functions at energies sufficiently beyond threshold, as follows: In MQDT, the fully quantum MQDT reference functions in the interior potential for the analytic matrix Y(E) at energy E, wavenumber k, and radius R assume the WKB-like form
| 15 |
| 16 |
| 17 |
| 18 |
for an uncoupled channel reference potential U 0 and channel state β; and quantum mechanically the reference wave functions for the scattering matrix S(E) assume the form
| 19 |
| 20 |
for relative angular momentum of the collision partners l and scattering phase shift ξ. Julienne and Mies noted that for great enough collision kinetic energy ε, the MQDT reference functions f and g become equal to s and c, respectively. Moving past the deep-well theorem, Julienne and Mies clarified that the criterion for this agreement is that the WKB approximation holds for all radii: namely, that the local de Broglie wavelength Λ(E,R) varies slowly as
| 21 |
To identify the range of energies at which this approach applies, Julienne and Mies introduced a graphical approach, thereafter adapted by others, , which plots the criterion Λ′ as a function of the radii R for varying collision energies ε/k B (see Figure ). The energy at which semiclassical mechanics breaks down and a quantum-to-classical crossover occurs is then approximated as the energy at which the criterion rises above a benchmark value at any radius. Below this energy, Julienne and Mies attributed the breakdown of semiclassical treatment and appearance of quantum effects as arising from the loss of a smooth WKB connection between the WKB-like solution in the inner region and the asymptotic wave function. Above this energy, the WKB approximation is expected to closely approximate the quantum wave function at all radii and to thereby yield an accurate depiction of the associated scattering processeven in cases where the energy satisfying the WKB criterion falls in the cold or ultracold regime.
14.
WKB criterion for the (a) collision and (b) neon impinging on a semi-infinite SiN slab indicating the accuracy of semiclassical methods to energies as low as approximately 1 K and 200 nK, respectively. Adapted with permission from ref . Copyright Optical Society of America and from A. Mody, M. Haggerty, J. M. Doyle, and E. J. Heller, Physical Review B, 64, 8, 085418, 2001. Copyright 2001 by the American Physical Society.
Note Julienne and Mies’ argument suggests that semiclassical mechanics is expected to be accurate well within the ultracold regime for a number of atomic collisions for ground and metastable state species, as summarized in Table . To approximate the characteristic quantum threshold energy ε Q below which semiclassical treatment breaks down within a given range of radii, Julienne and Mies identified the maximum WKB criterion for an asymptotic potential V 0 (R) → −C n /R n for n ≥ 3
| 22 |
at radius
| 23 |
which yields the energy at which the WKB criterion begins to rise above the arbitrary maximum WKB criterion Λmax = 1/2
| 24 |
at effective temperature T Q = ε Q /k B. Although strongly dependent on the force power n, reduced mass μ, and van der Waals constant C n , this quantum threshold energy formula indicates semiclassical treatment of rate coefficients can remain accurate at ultracold temperatures of T > 300 μK for ground-state Cs collisions or T > 1 nK for and ground-state Na collisions, as detailed in Table . This finding confirmed their prior calculation showing semiclassical and quantal agreement in the computed spectrum for at 1 mK, work further expanded into the 2010s. − It is important to note that ε Q is considered to be the upper bound of the quantum-to-classical crossover, as the crossover varies in response to the energy of the highest-energy bound vibrational state, with key considerations with reference to inelastic scattering collisions, as discussed by Siska in 2001. Siska showed that these caveats in fact allow the quantum-to-classical crossover to appear at orders of magnitude lower energy than even ε Q for Ne+ + He. 15 years later, DeMille, Glenn, and Petricka would go on to show that this analysis predicts semiclassical behavior of SrO collisions in standing-wave electromagnetic-field microwave traps at temperatures above 200 fKor, where the upper bound of s-wave collisions is instead held as a benchmark, 30 fK.
6. Characteristic Quantum Threshold Temperatures T Q above which Semiclassical Methods Hold, as Derived by Julienne and Mies for Collisions of Species in Specified States Subject to van der Waals Potentials of Force Power n .
| Species | State | n | T Q |
|---|---|---|---|
| H + H | 6 | 20 K | |
| 6 | 100 mK | ||
| Cs + Cs | 6 | 300 μK | |
| Na + Na | 6 | 10 mK | |
| 1 u | 5 | 740 μK | |
| 0 u | 3 | 1 nK |
Note T Q occurs in the ultracold regime for collisions of Cs + Cs, , and and in the cold regime for and Na + Na. Reproduced with permission from ref . Copyright Optical Society of America.
Subsequent work on cold–atom collisions and atom–surface sticking , tied Julienne and Mies’ wide-ranging agreement between semiclassical and quantal results in the ultracold regime to a physical origin: the loss of quantum reflection. ,,,− These works considered that the WKB approximation holds to first approximation where the WKB criterion is satisfied, stated in terms of the de Broglie wavelength λ(x), momentum , or potential V (x) as
| 25 |
| 26 |
| 27 |
for mass m and energy E. What distinguished their rationale is an explicit link between the failure of WKB and quantum reflection, which as Mody et al. stated in 2001 concerns the quantum effect “that quantum mechanically the amplitude is reflected back without penetrating the interaction region, analogous to the elementary case of reflection from the edge of a step-down potential in one dimension while attempting to go over the edge.” An illustrative example of such quantum reflection from 2018 , is given in Figure for context, specifically scattering from the attractive V(q) = 2tanh[q/5]-2 step potential. In the quantum regime, semiclassical and quantum amplitudes differ, with the wave function reflected backward to have higher amplitude at right due to quantum reflection. As the collision energy increases, the quantum wave function passes through increasingly, until semiclassical and quantum amplitudes agree for energies at which the WKB criterion is satisfied at all positions such that semiclassical mechanics accurately describes the system. (As an aside, it bears mentioning that this quantum interference effect has an acoustic analog: for example, a trumpet bell is shaped to cause wavelength-dependent sound wave reflection ever further toward the end of the bell with decreasing wavelength, thus providing a much needed realignment of the harmonic structure of the instrument.)
15.
Illustration of quantum reflection in the absence of a barrier at increasing collision energies (in arbitrary units) in the V(q) = 2tanh[q/5]-2 step potential. At the lowest energy (top left), the quantum wave function (thin black line) is reflected from the step potential (thick black line), leading to greater amplitude at right than the semiclassical WKB result (dashed line). As the energy increases (left to right, top to bottom), the quantum amplitude approaches the semiclassical amplitude until quantum-classical correspondence is reached. Used with permission of Princeton University Press from The Semiclassical Way to Dynamics and Spectroscopy, E. J. Heller, 2018; permission conveyed through Copyright Clearance Center, Inc.
Côté et al. further recognized in 1996 that near-threshold quantum reflection is intimately tied to near-threshold quantum suppression, a topic that continues to be of active interest in ultracold scattering. ,,,,− ,,, Côté et al. showed that near-threshold reflection suppresses the exterior amplitude of the quantum scattering wave function relative to semiclassical and classical predictions. This led the authors to both demonstrate that the WKB criterion (which they term the WKB error) acts as a harbinger of quantum suppression and to derive a quantum suppression factor that corrects the WKB approximation to the quantum cross section, which allows semiclassical mechanics to be used to accurately determine quantities such as dipole matrix elements yet closer to threshold. This method enabled accurate determination of dipole matrix elements for singlet and triplet 7Li2 transitions deep in the ultracold regime, as shown in Figure , which further supports the ability of semiclassical mechanics to accurately simulate aspects of s-wave atom–atom scattering systems close to threshold. Note the corrected results remain accurate to ultracold energies as low as O(10 au) [O(1 μK)].
16.

7Li2 dipole matrix elements |D v (E)|2 for the ν = 68 (a) singlet and (b) triplet transitions computed exactly (solid line), semiclassically (dotted line), and semiclassically with a correction factor (dashed line), which indicate strong agreement between the quantum result and the hybrid quantum-semiclassical result deep in the ultracold regime. Approximate agreement exists between exact and corrected semiclassical results at energies as low as O(10–11 au) [O(1 μK)]. Reproduced figure with permission from R. Côté, E. J. Heller, and A. Dalgarno, Physical Review A, 53, 1, 234, 1996. Copyright 1996 by the American Physical Society.
2.2.3. Beyond the WKB Criterion
Modern semiclassical and quantum theory has increasingly brought into question whether the WKB criterion alone is sufficient to identify the onset of quantum behaviors and the breakdown of semiclassical approaches. ,,, In 2004 to 2017, Friedrich and Trost recognized that not only the WKB criterion, but also the quantality ,, or badlands function
| 28 |
| 29 |
must also be small to ensure the WKB solution to the Schrödinger equation simultaneously fulfills both the Schrödinger equation
| 30 |
and the equation for the second derivative of the WKB wave function
| 31 |
In 2021 and 2023, this badlands function was also been capitalized on in ultracold chemistry in the form of a WKB potential to reduce anomalous reflection in complex absorbing potential simulations and to investigate bound states in the continuum, reflectionless scattering modes, and parity-time reversal symmetry with Bose–Einstein condensates.
More recently, both the WKB criterion and the quantality have become the source of controversy as an indication of the “source” of quantum reflection. , In 2017, Miret-Artés, Petersen, and Pollak indicated that the nonlocality of quantum scattering means that the region of large quantality (the “badlands region”) is not solely responsible for quantum reflection and that the full potential must be considered. As evidence, Mirét-Artes and Pollak demonstrated that numerically exact close-coupling calculations of quantum reflection probabilities and diffraction patterns agree with experimental results for helium scattering from a microstructured grating only when the full potential region is considered. They further recall that the potential V(x) = −sech2 (x) features no quantum reflection at any energy, − despite the presence of a badlands region at low energies. Likewise, Petersen, Pollak, and Miret-Artés performed time-dependent calculations that demonstrate that at the lowest energies a quantum wavepacket impinging on a Morse potential reaches its maximal density at a position orders of magnitude greater than the maximum magnitude of the badlands function (see Figure ). For this reason, the authors argue that quantum reflection is better considered as a result of not local high quantality but reduced density caused by nonlocal destructive interference. It is important to note that this caveat on the quantality, which is consistent with prior theorems concerning the applicability of semiclassical methods close to threshold, serves as a reminder of the need for care in WKB criterion and quantality analyses, in particular to recognize that destructive interference, not the magnitude of the quantality, indicates where quantum reflection occursan essential ingredient in the quest to accurately identify cases in which ultracold molecular collisions are amenable to semiclassical study.
17.
Quantum (top row) and classical Wigner (bottom row) propagation (color heat map) of a coherent state initialized with energy E init = 5 · 10–9 in Morse potential V(z) = e–2z – 2e–z over time t indicates that a quantum wavepacket features negligible magnitude relative to its classical counterpart at positions up to ∼1000 times greater than the location of the maximum badlands function magnitude z BF ≈ 20.7 (vertical dotted blue line). Right column images magnify short-time dynamics. Reproduced figure with permission from J. Petersen, E. Pollak, and S. Miret-Artés, Physical Review A, 97, 4, 042102, 2018. Copyright 2018 by the American Physical Society.
In 2018, ref further emphasized that quantum results in the ultracold regime may in fact agree with not only semiclassical but also classical mechanics for aspects of systems near threshold in what was termed “ultracold inferno theory” due to the reliance of the semiclassical propagator on classical quantities. The authors considered that the semiclassical Van Vleck–Morette–Gutzwiller propagator −
| 32 |
assumes the general form of the semiclassical amplitude
| 33 |
where S k is the classical action and ν k is the Maslov index of classical path z and the intersection of finite-width position-space regions q and q′ (t) where the sum is taken over each classical path j. In the absence of quantum reflection, the semiclassical amplitude agrees with the quantum amplitude, as argued in previous rationales. What this form emphasizes is that in the additional absence of quantum interference, semiclassical and classical results also agree, and there exists a full quantum-classical correspondence.
To provide an example of the impact of quantum interference detailed in ref , this review considers two fundamental nonrelativistic scattering systems: Mott and Rutherford scattering (see Figure ). Recall that in three-dimensional nonrelativistic Mott scattering, an α particle and a helium nucleus approach each other with equal and opposite velocities. , Upon collision, the α particle deflects by an angle ∠ACD = θ. Although only this path brings the α particle to point D, an additional contribution to the differential scattering cross section must be considered: the deflection of the indistinguishable helium nucleus by an angle ∠BCD = π – θ. Since the two scattered bodies are indistinguishable, a detector situated at point D cannot distinguish between the two paths ACD and BCD, such that the paths interfere and there exists no quantum-classical correspondence. In contrast, in three-dimensional Rutherford scattering, , an α particle of a given initial momentum and impact factor deflects off a gold atom to reach a specific angle with a given final momentum in a fixed amount of time. Here trajectories that lead the gold atom to be deflected into the same final angle do not contribute to the scattering cross section as the two colliding bodies are distinguishable. Since the particles are distinguishable, the system is free of quantum interference and quantum-classical correspondence exists in the absence of quantum reflection. In fact, classical and quantum results for the cross section agree for Rutherford scattering at all energiesa special case of quantum-classical correspondence at threshold related to atomic fragmentation with possible future ramifications for ultracold atomic systems.
18.
Schematic of classical pathways contributing to the semiclassical amplitude and possible quantum-classical correspondence in two fundamental scattering systems: (a) nonrelativisitic Mott scattering, in which an α particle A scatters off a Helium nucleus B toward detectors D and E and (b) Rutherford scattering, , in which an α particle (solid lines) scatters off a gold atom (solid point, example trajectory of a gold atom scattering off an α particle shown with a dashed line). Adapted from J. M. Rost and E. J. Heller, Semiclassical scattering of charged particles, Journal of Physics B, 27, 7, 1387–1395. Copyright IOP Publishing. Reproduced with permission. All rights reserved.
2.3. Semiclassical Scaling Laws and Holistic Quantum Models
In the midst of this classical renaissance; new developments are also being made to use classical, semiclassical, and quasiclassical techniques to accurately simulate a wider range of chemical systems. A wide variety of authors have developed novel semiclassical scaling laws to describe the post-threshold regime in a wider range of atomic and molecular systems. ,,,,− ,, Quéméner, Gao, Bohn et al. have established holistic quantum-to-semiclassical models that closely model atomic and molecular collision cross sections throughout not only the classical Langevin regime, but the entirety of the collision energy domain. − And, others have revived attention on unique atomic systems in which the quantum-to-classical crossover not only appears in the ultracold regime, but in fact directly at zero Kelvin, which entails classical and semiclassical scaling laws that hold at all collision energies, as confirmed by both simulation and experiment. ,,,,,,− ,,,−
2.3.1. Kinematic Derivations
Today’s derivations of semiclassical scaling laws and holistic quantum models for ultracold collisions can largely be divided into two strategies: kinematic derivations, , which consider the geometry of phase space, and dynamical derivations, ,,, which consider the fate of individual particles.
Today’s kinematic derivations of semiclassical and classical post-threshold laws , build on the foundation laid by Wigner over 75 years ago in his original quantum threshold law: the idea that it is possible to derive (quasi)universal laws for cross section scaling using only the form of the long-range potential and the system’s dimensionalityall with no knowledge of the exact short-range forces between collision partners.
A prime example is the derivation of a quasiuniversal post-threshold law for cold and ultracold dipolar scattering of Bohn, Cavagnero, and Ticknor in 2009. Based on prior kinematic quantum threshold law derivations ,− and the theoretical low-energy molecular collision studies of Kajita; ,− DeMille, Glenn, and Petricka; and Roudnev and Cavagnero; , Bohn, Cavagnero, and Ticknor employed a kinematic approach to develop a quasiuniversal post-threshold law for cold and ultracold dipolar scattering based on the eikonal approximation. This derivation rested on calculation of the total scattering cross section arising from an approximate eikonal wave function in a dipole–dipole potential in the presence of an applied field. They assumed that the wave function amplitude in the interaction region varies slowly and is therefore amenable to the cylindrical-coordinate phase-amplitude Ansatz
| 34 |
for initial, final, and average wavenumber k⃗ i, k⃗ f, and k⃗ avg = (k⃗ i + k⃗ f)/2, respectively. For a dipole–dipole potential
| 35 |
in an applied field
| 36 |
| 37 |
they derived the eikonal integral scattering amplitude as
| 38 |
Consideration of the optical theorem and averaging over initial wavevectors then gave the quasiuniversal semiclassical post-threshold law for dipolar scattering
| 39 |
where D = Mμ 2/ℏ 2 is the dipole length as a function of the reduced mass M and dipole moment μ of the dipole in question.
Concurrently, Hudson employed the same strategy to develop an eikonal approximation to the total elastic scattering cross section for molecular ion collisions of velocity v subject to an interaction potential of the form −C 4/r 4
| 40 |
and Ticknor developed an eikonal approximation to the total cross section for dipolar molecules confined to two dimensions ,
| 41 |
In 2024, Wang and Bohn followed with a similarly eikonal approximation to the total cross section for microwave-shielded collisions of distinguishable dipoles
| 42 |
for dipole length a d . This eikonal scaling derivation resulted in complete agreement with Bohn, Cavagnero, and Ticknor’s prior point-dipole universal semiclassical scaling law.
2.3.2. Dynamical Derivations
A greater number of recent universal semiclassical scaling laws ,,, pull from the dynamical tradition founded by Langevin and Gorin: − ,, that scaling laws for classical capture can be wholly determined by whether classical particles of interest would have sufficient radial momentum to surmount interposing centrifugal barriers.
In the early 2010s, Quéméner and Bohn − and Gao − recognized that the dynamical classical capture approach holds post-threshold for ultracold collisions. This insight served as the basis for their development of holistic quantum models based on classical input that reproduce the expected scaling laws in both the threshold and post-threshold regimes. Quéméner and Bohn developed the quantum threshold model, which replicates both threshold and post-threshold scaling behavior by assuming the quenching probability follows the Bethe–Wigner threshold law below the barrier and the Langevin (post-threshold) model at or above the barrier − ,
| 43 |
Meanwhile, Gao developed the quantum Langevin model, , which assumes the submatrix S̃ eff of the S matrix in multichannel quantum defect theory is approximately zeronamely, it is unlikely for molecules to exit their initial configurations upon close approachin agreement with the Langevin assumption in a quantum context. The dynamical Langevin classical capture approach has also been used for purposes beyond cross section determination for derived scaling laws that have been shown to hold in a cold and ultracold atomic and molecular context, such as Pinkas et al.’s 2023 use of classical Langevin capture to determine the probability of Langevin collisions relevant to the generation of 88Sr+ – 87Rb ion–atom molecules in a linear Paul trap and Kłos and Tiesinga’s 2023 use of a semiclassical approximation to determine both semiclassical glancing rate coefficients and thermalized total elastic rate coefficients, the latter to within ∼10 to 20% accuracy of quantum mechanics for ultracold 7Li and 87Rb collisions with room-temperature H2, 4He, 20Ne, 14N2, 40Ar, 84Kr, and 132Xe.
In 2018, ref presented ultracold inferno theory as another approach to dynamically determine classical post-threshold laws in ultracold chemistry. Ref argued that classical phase-space counting is sufficient to determine the post-threshold law for collision complex decay in a simple, two-dimensional model of ultracold chemical reactions as long as there is no quantum interference and the reaction is sufficiently exothermic to preclude quantum reflection along the reaction coordinate. Derivation of the post-threshold law then boils down to determination of a phase-space bottleneck: the minimum radial momentum at a given radius that leads to collision complex decay, beyond which any additional angular momentum leads to reformation of the collision complex. Based on this phase-space bottleneck insight, the law was determined for nonpolar homonuclear diatomic point particles subject to a central van der Waals potential
| 44 |
with dispersion coefficient C 6, parametrization constants α and β, and chaotic motion modeled by energy-preserving phase-space kicks within radius r ≤ R. ,, In direct analogy to classical capture, the approach indicated that a classical particle of mass m that surmounts the effective potential energy maximum
| 45 |
at critical radius
| 46 |
and the critical momenta
| 47 |
| 48 |
will pass unimpeded to r → ∞ and lead to collision complex decay. In contrast, particles that cannot reach the critical radius r crit can pass no further than the classical turning point radius
| 49 |
Alternatively, in Birkhoff coordinates (s,p s ) defined at a fixed-radius annulus r = R Birk around the origin, the critical momentum normal to the annulus is
| 50 |
such that the phase-space bottleneck and angle of acceptance is simply
| 51 |
According to (semi)classical phase-space counting, the ergodic rate given by the ratio of the volume flux for escaping particles to the total phase-space volume of nonescaping particles is then
| 52 |
| 53 |
as a function of the turning-point radius R turn. The resulting rate scales as k(E) ∝ E 2/3, in close agreement with the results of classical trajectory simulations.
2.3.3. (Semi)classical Analog of Fermi’s Golden Rule
In light of these classical successes, it is worthwhile to reconsider Mody et al.’s 2001 approach to derive (semi)classical post-threshold laws for today’s ultracold atomic and molecular collisions in alternative (e.g., reduced) dimensionalities. Mody et al.’s approach, which can be interpreted both kinematically and dynamically, recognized that where accurate semiclassical wave functions can be used to approximate the wavenumber dependence of the transition rate Γ ij according to a Fermi’s golden rule approach ,
| 54 |
given a semiclassical density of states ρ(E f ) and matrix element V fi . The post-threshold rate law then reduces to knowledge of the scalings of the probability density and the density of states as a function of the collision energy E f . Originally introduced by Mody et al. in 2001 to describe three-dimensional two-body collisions, in the presentation that follows, this review generalizes the approach to N dimensions in order to enable the technique to describe both the full-dimensional and reduced-dimensional two-body ultracold collisions currently underway experimentally, as follows: According to the semiclassical Weyl law , and kinematics, the number of states accessible in a given region of phase space Ω at energy E for a Hamiltonian in N dimensions is
| 55 |
| 56 |
where the Heaviside step function is
| 57 |
and the momentum p(E) is approximated as ℏk in the asymptotic region. The gradient of the number of states with respect to energy then yields the semiclassical density of states in the absence of an electromagnetic field interaction
| 58 |
In the absence of tunneling, the squared average overlap which determines the wavenumber-dependence of the average matrix element squared V fi , is proportional to the particle probability densities |ψ i |2 and |ψ f |2. The probability density of the incoming wave |i⟩ scales as k, according to unit flux normalization. However, the probability density of the scattered wave |f⟩ is not as straightforward: Here, the classical particle probability density is inversely proportional to the allowed volume in phase space. To illustrate, the amount of phase space accessible in the inner region at a given energy is pictured in Figure . As the dimensionality increases, the amount of accessible phase space also increases, which leads to a drop in the particle probability density. The semiclassical Weyl law gives the scaling of this reduction as
| 59 |
19.

Classical particle probability density |ψ(x)|2 eq declines as the dimension of the system increases due to a concomitant increase in the extent of energetically accessible phase space, as depicted for a Lennard-Jones potential in one dimension (|ψ(x)|2 ∝ k –1), two dimensions (|ψ(x,y)|2 ∝ k 0), and three dimensions (|ψ(x,y,z)|2 ∝ k 1).
When multiplied with the expression for the density of states, the density of states and matrix element wavenumber dependence combine to yield the semiclassical post-threshold law
| 60 |
| 61 |
This universal semiclassical scaling law has an intuitive universal, classical interpretation in line with a dynamical classical capture theory approach: in the absence of dynamical barriers, particles with sufficient energy to surmount any intervening potential barriers separate.
2.4. Classical Behavior at Zero Kelvin
Authors have identified two key classes of systems that exhibit classical scaling laws directly at zero Kelvin: scattering from attractive Coulomb potentials in three dimensions ,,,,,,− and multiple ionization. ,,− Arguments for this extreme classical behavior at infinite wavelength pull from both the semiclassical Wentzel–Kramers–Brillouin criterion , or the Van Vleck–Morette–Gutzwiller propagator, , as outlined below.
2.4.1. Scattering from Attractive Coulomb Potentials in Three Dimensions
Modern inquiry into scattering from attractive Coulomb potentials in an ultracold atomic context arose from a controversy surrounding atom–surface sticking coefficients and atom–grating reflection (refs , , − , − , , and − ): whether the low-energy limit of the sticking coefficient for hydrogen atoms on superfluid 4He follows the expected quantum threshold law s(T) ∝ T 1/2, reaches a constant value reminiscent of the classical result s(T) ∝ 1, and/or succumbs to decoherence and resonance effects that alter the threshold law. A lasting legacy of this inquiry has been the recognition that classical and semiclassical mechanics yield not only approximate, but exact quantum scattering cross sections for three-dimensional attractive Coulomb potentials at all energies.
Several arguments explain the origin of this all-energy quantum-classical correspondence. ,,, The early argument of Clougherty and Kohn in 1992 recognized that the sticking coefficient for attractive Coulomb tails z –1 scales as the s(E) ∝ α, as initially observed in atom–surface sticking experiments, in contrast to the standard quantum threshold law s(E) ∝ E 1/2 identified for attractive z –3 potential tails identified by Böheim, Brenig, and Stutzki. Clougherty and Kohn attributed the discrepancy to the fact that Coulomb potentials always satisfy the semiclassical WKB criterion for sufficiently large radii z where van der Waals potentials of order β > 2 do not, as follows: where the WKB criterion for a van der Waals potentials of the form U(z) = C β /z β is
| 62 |
| 63 |
where k 2 (z) ≡ k 2 + U(z), Clougherty and Kohn recognized that for short-range potential with van der Waals component β > 2, semiclassical results never hold as z → ∞. As an example, they demonstrated that β = 3 satisfies the WKB criterion taken as an equality when
| 64 |
| 65 |
In this case, , quantum reflection appears at arbitrarily distant radii z** ∼ γk –1 for γ ≪ 1, and semiclassical and quantum results do not agree. In contrast, Clougherty and Kohn demonstrated that the Coulomb potential β = 1 satisfies the WKB criterion taken as an equality when
| 66 |
| 67 |
| 68 |
The WKB criterion then holds for all k for sufficiently large radii z > z**, z** ≫ z* (0) has no k-dependence, and semiclassical and quantum results agree.
In 2001, Mody et al. also put forward a WKB argument for the semiclassical nature of attractive Coulomb potential scattering. This WKB argument relied on showing that, although the maximal WKB criterion diverges in the threshold limit for van der Waals potentials of order n > 2, the maximal WKB criterion remains small near threshold for van der Waals potentials of lower order n ≤ 2 in the asymptotic regime. Mody et al. recognized that the WKB criterion
| 69 |
is maximal where
| 70 |
They determined that the maximum WKB criterion for a van der Waals potential V(x) = −c n /x n for n > 2 scales as
| 71 |
which approaches infinity as k → 0indicative of WKB failure. Mody et al. then showed that, in contrast, the maximal WKB criterion remains small at all radii sufficiently far from the origin for van der Waals potential n ≤ 2: the WKB approximation then holds at sufficiently large radii for Coulomb potentials, in direct agreement with Clougherty and Kohn.
Yet, in arguments laid out from 2004 to 2017, Friedrich and Trost noted several properties that raise concerns with such WKB arguments. ,,, Although the WKB approximation holds at sufficiently large radii for attractive Coulomb potentials, the WKB approximation still fails close to the origin. Arguments based on the WKB approximation also do not contend with the fact that, although quantum and classical scattering cross sections agree in three-dimensional Coulomb potentials, they do not agree in two-dimensional Coulomb potentials, as identified independently by Barton in 1983 and Lin in 1997. Finally, the focus on specific radii associated with transitions in quantum reflection behavior (such as z *) also appear counter to the Coulomb potential’s property of mechanical similarity for dimension d = −1 and scaling factor a
| 72 |
In such mechanically similar systems, for any classical path r(t) of energy E in a Coulomb potential, there must be a valid classical path ar(r 3/2 t) of energy E/a. Thus, each radius is in a loose sense on an equal footing.
An argument based on the Van Vleck–Morette–Gutzwiller propagator, introduced in 1994 and revisited in light of Friedrich and Trost’s findings in 2019, avoids these pitfalls by recognizing that a three-dimensional attractive Coulomb potential obeys a classical scaling law because of a hidden equivalence to another system known to behave classically: , a regularization followed by a canonical transformation metamorphosizes a three-dimensional Coulomb potential into a collection of independent harmonic oscillators. In detail, the Hamiltonian for a three-dimensional Coulomb potential
| 73 |
upon Kustaanheimo–Stiefel regularization with positions and momenta
| 74 |
| 75 |
| 76 |
| 77 |
| 78 |
| 79 |
| 80 |
yields the Hamiltonian
| 81 |
which is none other than a system of four uncoupled harmonic oscillators. Note the kinetic energy operator remains unchanged such that no changes are needed to ensure position and momenta remain canonical coordinates. The quantum Hamiltonian then follows directly as
| 82 |
and the quantum scattering amplitude may be determined via the pseudotime quantum propagator. What remains is to show agreement between the pseudotime quantum propagator and the classical propagator. Since the classical action of harmonic oscillators is quadratic, the propagator is semiclassically exact. And, since the system features no quantum interference, semiclassical and classical results agree. Thus, attractive Coulomb scattering in three dimensions features quantum-classical correspondence at all energiesincluding directly at zero Kelvin. ,
2.4.2. Wannier Threshold Law, Multiple Ionization, Atomic Fragmentation, and Implications for Ultracold Chemistry
Advancements in atomic and molecular cooling have also led to a return to ,,,,, Wannier’s threshold laws for double and multiple , ionizationspecifically regarding the source of the renowned ability of the Wannier threshold law for double ionization to hold directly at zero Kelvin, as has been confirmed semiclassically, − quantum mechanically, − ,− and experimentally to at least three digits in the argument of the exponential. − (Note some dissent in favor of a linear scaling law in recent years, , as well as the presence of a high-profile, fully quantum dynamics study of the system, which has no reference to Wannier.)
In 2019, it was put forward that a possible explanation of why classical mechanics is sufficient to predict the threshold law for double atomic ionization follows from a generalization of the aforementioned Van Vleck–Morette–Gutzwiller argument given for the accuracy of classical threshold laws in attractive three-dimensional Coulomb potentials. Analysis of the potential energy associated with two electrons escaping a central atom
| 83 |
indicates that the potential energy for double ionization reduces to a single Coulomb potential in the limit of double electron escape r 1 = – r 2, r 12 → ∞, which implies that the Kustaanheimo-Stiefel regularization again allows the Hamiltonian to be expressed as a set of harmonic oscillators in the asymptotic limit. The pseudotime propagator is then semiclassically exact and semiclassical and quantum cross sections agree. Likewise, as in Rutherford scattering, only one path between initial and final states contributes to double ionization, such that there is no quantum interference and semiclassical and classical cross sections agree. Quantum and classical cross sections then agree at all energies, including zero Kelvin.
The same work introduces an important caveat: although the Hamiltonian for double ionization can be expressed as a sum over harmonic oscillators in the asymptotic region, in the inner region, interaction between the electrons obviates such an expression. This distinction can be readily confirmed by analysis of the form of the transformed potential energy away from asymtopia, with the collinear case as an example. In the collinear case, − the regularized Hamiltonian, given by two Kustaanheimo-Stiefel and one Levi-Civita − regularizations, is
| 84 |
This expression contains nonquadratic terms, such that the propagator is not expected to be semiclassically exact in the inner region.
Although not recently discussed in the field of ultracold atomic and molecular collisions, the success of Wannier’s classical threshold law gave rise to classical scaling laws for multiple (n-fold) ionization that has continued to attract some interest in near-threshold physics in recent years. ,− Wannier put forward a classical approach to determine the threshold law for multiple ionization in a half-page article in Physical Review, which Geltmann confirmed quantum mechanically: the threshold laws for ionization by electrons and photons are σ(E) ∝ E n and σ(E) ∝ E n–1, respectively. Subsequent generalizations of Wannier’s threshold law include development and verification of threshold laws for triple ionization, ,− ,− quadruple ionization, quintuple ionization, and generic multiple ionization − and atomic fragmentation, , which inspire investigation of such behaviors in an ultracold context.
2.5. Summary of Universal (Semi)classical Near-Threshold Scaling Laws
In order to highlight where (semi)classical post-threshold laws are expected to be accurate in cold and ultracold collisionsand where classical mechanics is expected to give accurate cross section and rate scalings for all energiesthis review briefly summarizes key universal quantum threshold and classical post-threshold laws in one place, Table . These universal scaling laws are expected to apply regardless of the species of the scatterers in question, including in reduced dimensional scattering systems which are gaining in interest since 2010. ,− However, as reflected in recent work, ,− ,− cross section scalings may deviate from expected scalings. Newly open channels may lead to Wigner cusps. ,− Bound states or resonances may abbreviate or alter the s-wave quantum threshold regime, as studied in-depth in recent years by Macri, Barrachina et al. − and Simbotin, Côté, and Ghosal. , And, other near-threshold phenomena may intervene, affecting the near-threshold scaling laws, including threshold resonances, proximity resonances, ,, the Thomas effect, − the Efimov effect, ,− ,− Borromean binding, and Brunnian binding. − Nonetheless, the independence of the laws on the short-range form of the potentialand the exact strength of the asymptotic potentialsuggest the quantum-classical correspondences predicted therein are expected to be even more widespread. ,
7. Summary of Universal (Semi)classical Scaling Laws for Two-Body s-Wave Endothermic Collisions Subject to Short-Range Potentials in Varied Dimensionality (1D to ND), the Attractive Coulomb Potential in Three Dimensions (Coulomb), and the Wannier Double Ionization System in Full Dimensionality (Wannier) .
Both (semi)classical (class) and quantum (quant) scalings are provided for the probability density |ψ|2, cross section σ, and rate in terms of the wavenumber k, with (semi)classical scalings also provided for the density of states ρ class. The semiclassical 1D-ND and Coulomb scaling laws are determined according to the classical analogue of the Fermi Golden Rule, , with classical scaling laws determined for the Wannier system according to phase-space counting. Quantum threshold laws (quant) are included for direct comparison, with instances of quantum-classical correspondence bolded and emphasized in blue.
3. Classical and Quasiclassical Methods for Ultracold Molecular Collision Complex Decay
Classical and quasiclassical methods have now taken center stage in what has been termed the ultracold “sticky mystery”: In the 2010s, ground-state alkali metal dimer collision experiments observed reactant loss not only for exothermic ultracold chemical reactions, where disappearance of reactants is expected, but also for nonreactive ultracold collisions, where no products are energetically favorable to form. − Mayle et al. hypothesized this reactant loss was not due to product formation, but instead the formation of long-lived (namely, “sticky”) collision complexesa hypothesis that was confirmed experimentally for the ultracold KRb dimer reaction via the direct measurement of the collision complex by Hu et al.
The question then remained: just how long-lived are such collision complexes? Investigation of such collision complexes remains computationally intractable with today’s exact quantum dynamical methods. The low energies of product moleculesat times on the order of 100 nKare associated with extremely long wavelengths, which necessitate simulation of broad swaths of position space. As Bause et al. stated in 2023, formation of the collision complex can be energetically favorable by on the order of 1000 K, such that on the order of 10,000 rotational states may be required to represent just one dimer molecule alone. And, treatment of a four-atom alkali metal dimer collision complex constitutes a six-dimensional problem, which lies at the upper limit of the dimensionality amenable to standard grid-based quantum dynamics methods for relatively light atoms at high temperatures. Croft, Balakrishnan, and Kendrick put this cost into context in 2017:
Quantum-scattering calculations for collisions of ultracold molecules are extremely computationally expensive. Even...for only total angular momentum J = 0, even exchange symmetry and parity, [and without inclusion of] spin or field effects...calculations [of scattering cross sections in the ultracold K2 + Rb collision] still required over 300,000 hours of CPU time. It is possible that numerically exact quantum scattering calculations including all the effects omitted in these calculation will never be computationally tractable.
This extreme computational cost led to the development of computationally tractable alternatives based on classical, semiclassical, and quasiclassical mechanics. −
3.1. Quantum Rice–Ramsperger–Kassel–Marcus Theory Approach
In 2012 and 2013, Mayle et al. , laid the foundations for classical approaches to collision complexes in ultracold collisions when they recognized that long-lived collision complexes correspond to both high numbers of Fano-Feshbach resonances associated with rovibrational states quantum mechanically and winding trajectories that ergodically sample phase space classically, such that the collision complex lifetime can be determined classically or quasiclassically notwithstanding the ultracold temperature of the initial scattering partners (see Figure ). This statistical behavior allowed the collision complex to be determined according to Rice–Ramsperger–Kassel–Marcus (RRKM) theory, − which models unimolecular dissociation as a process in which energy passes throughout all degrees of freedom until it concentrates on a single mode driving dissociation. Calculation of the collision complex lifetime according to RRKM theory
| 85 |
then requires knowledge of only the number of open scattering channels N o and the collision complex density of states ρ. In 2012 and 2013, Mayle et al. , estimated the required density of states quantum mechanically by calculating the bound state energies E α of an approximate potential energy surface to determine the short-range resonances for vibrational quantum number α, offsetting the short-range resonances by asymptotic rovibrational channel (v,n) threshold energies to determine the rovibrational channel short-range resonance states E α = E α + E v ,n , analyzing the E α spectrum to determine the mean level spacing d, and employing the mean level spacing to determine the rovibrational density of states ρrv = 1/d. Mayle et al. found that quantum RRKM theory yielded collision complex lifetimes for both atom–diatom and diatom–diatom collisions that were consistent with the “sticky mystery” observation of reactant loss in both reactive and nonreactive ultracold collisions. In addition, Mayle et al. estimated semiclassically the likelihood of hyperfine state changes during the collision process, and noted that the density of states is unaffected by the number of nuclear spin states N nuc, as N o and ρ scale according to the same multiplicative factor τ = 2πℏρ/N o = 2πℏ(ρrv N nuc)/(N o N nuc) = 2πℏρrv. This approach has been yet further extended by Croft, Bohn, and Quéméner in the early 2020s via the incorporation of transition-state-theory and optical model corrections that improve the magnitude, if not the energy scaling, of the predicted time dependence of the relative population of the collision complex. ,
20.
Current picture of sticky ultracold metal dimer collisions, in which (bottom left) an initial state of molecules with a kinetic-energy distribution of temperature T passes through a centrifugal collision threshold to form (bottom center) a collision complex that supports a large density of states. The collision complex behaves like (top left) a classical particle that samples phase space ergodically until reaching a configuration compatible with formation of the product dimers, either via (top right) photoexcitation to the excited complex and spontaneous emission or predissociation or an unknown process leading to (bottom right) molecule loss. Reproduced from ref . Copyright 2023 American Chemical Society.
3.2. Classical Trajectory Approach
In 2014, Croft and Bohn recognized that classical trajectories can also yield collision complex lifetimes on par with quantum RRKM theory. Croft and Bohn simulated classical homonuclear atom–diatom collision trajectories and recorded the time required in each trajectory for the atom to reach a distance from the diatom R ∞ with sufficient momentum to escape irreversibly. The fraction of atoms remaining in the complex at time t followed an exponential distribution
| 86 |
as expected for ergodic trajectories, which supported the underlying ergodicity assumption of prior RRKM treatments. Moreover, the collision complex lifetimes τ̅ ct agreed to within an order of magnitude of quantum RRKM theory lifetimes for Li + Li2, K + K2, and Cs + Cs2 (see Table ), which opened the door to subsequent quasiclassical treatment of collision complex lifetimes. Classical trajectory results for lifetimes in agreement with RRKM theory were also obtained for K + K + Rb by Lide in 2021 and for NaK + K, NaK + NaK, and RbCs + RbCs, by Man, Groenenboom, and Karman in 2022, with additional collision complex lifetimes determined by Kłos et al. in 2021 with quasiclassical trajectories for 23Na87Rb + 23Na87Rb collisions evidencing roaming trajectories. Beyond collision complex lifetime prediction, Croft and Bohn also demonstrated that classical trajectories enabled investigation into the onset of chaos via calculation of the fractal dimension, which set the path to later identification of classical fractals in dipolar collisions by Yang, Pérez-Ríos, and Robicheaux in 2017.
8. Comparison of Collision Complex Lifetimes Determined via Quantum RRKM Theory τ quant and Classical Trajectory Simulations τ̅ ct for Triatomic Collision Systems .
| System | τquant [ns] | τ̅ct [ns] |
|---|---|---|
| Li + Li2 | 2.4 | 12 ± 1 |
| K + K2 | 146 | 303 ± 36 |
| Cs + Cs2 | 2746 | 2871 ± 328 |
The quantum and classical lifetimes agree to within one standard deviation for Cs + Cs2, with greater deviation observed for Li + Li2 and Cs + Cs2. Adapted table with permission from James F. E. Croft and John L. Bohn, Physical Review A, 89, 1, 012714, 2014. Copyright 2014 by the American Physical Society.
It is worthwhile to note that such classical trajectory approaches to ultracold collisions extend beyond sticky collisions. Classical trajectories have also been used to examine the possible formation of collision complexes in buffer gas cooling of low-energy complex hydrocarbons in 2012 and 2014 , and to identify the role of quasiresonant vibration–rotation energy transfer in low-energy atom–diatom collisions by Forrey et al. in 1999 and 2001. , For example, in quasiresonant transfer, a collision time that exceeds the rotational period can lead to a surprising specificity in the transfer of energy between vibrational and rotational degrees of freedom: namely, adiabaticity of the action I leads to dominance of a highly specific set of collisions that satisfy
| 87 |
where Δv and Δj are the changes in the vibrational and rotational quantum numbers, respectively, and where n v and n j satisfy the quasiresonant condition
| 88 |
where ω v and ω j are the classical vibrational and rotational frequencies, respectively. In 1999, Forrey et al. employed classical trajectories to investigate whether classical quasiresonant transfer extends into the cold regime, and showed that ultracold 4He – H2 collisions of collision energy E i = 10–6 au (0.32 K) with initial quantum numbers (v i , j i ) = (2,21) hewed closely to Δj = −2Δv and a quasiresonant condition ω v /ω j ≈ 2.079.
3.3. Quasiclassical Rice–Ramsperger–Kassel–Marcus Theory Approach
In 2019, Christianen, Karman, and Groenenboom built on these results to demonstrate that quasiclassical RRKM theory also allows for accurate determination of collision complex lifetimes. This advancement was essential to overcome difficulties extending previous quantum RRKM theory approaches to collision complex lifetimes beyond isotropic, bond-length-independent potentials. Christianen, Karman, and Groenenboom employed a quasiclassical phase-space counting approach to determine the density of states, and thereby the RRKM rate eq : they approximated the number of quantum states supported by an N-atom collision complex of N i indistinguishable particles of identity i with total angular momentum J 0 at energies up to E
| 89 |
where Θ(E) is the Heaviside function, and evaluated the density of states as
| 90 |
The density of space for specific quantum numbers of the total angular momentum J, its projection M J , and parity p is then given by
| 91 |
where g NJp is the proportion of classical phase space for quantum numbers N and J associated with parity p. Christianen, Karman, and Groenenboom subsequently employed analytic integration over the momentum coordinates to yield the three-atom AB + C field-free density of states
| 92 |
where the degeneracy factor is g ABC = ∏ i N i !, the three-body reduced mass is μ = (m A + m B)m C /(m A + m B + m C), and the diatom reduced mass is μAB = (m A m B) /(m A + m B + m C); as well as the four-atom AB + CD density of states
| 93 |
| 94 |
| 95 |
| 96 |
where is the inertial tensor, ε jlm is the Levi-Civita tensor, and (bf) refers to body-fixed frame. Christianen, Karman, and Groenenboom also considered the case of external fields. Given an external field sufficient to cause nonconservation of the angular momentum quantum number J, the density of states becomes
| 97 |
where represents the rotationally averaged . A second external field can also lead to nonconservation of the angular momentum quantum number M. The density of states then becomes
| 98 |
A comparison of these quasiclassical density of states for field-free K2 + Rb and NaK + NaK collisions indicated close agreement between quasiclassical and quantum results, as shown in Figure , which further supported quasiclassical treatment of the collision complex in the ultracold scattering systems. Given quasiclassical RRKM theory’s accuracy and versatility, quasiclassical RRKM theory is currently the state-of-the-art benchmark for experimental results, as exemplified by the work of authors such as Gregory et al., Liu et al., Bause et al., Gersema et al., and Nichols et al.
21.
Quantum (crosses) and quasiclassical (lines) density of states for ultracold metal dimer collisions closely agree, as demonstrated for K2 + Rb (left) and NaK + NaK (right) both with (bottom) and without (top) applied fields. Dashed lines of slopes 3, 2.5, and 1.5 (left) and 5, 4.5, and 3.5 (right) indicate power-law scaling of the density of states, and dashed-dotted lines indicate quantum density of states for realistic potential energy surfaces not amenable to treatment with previous quantum RRKM theory approaches. Reproduced figure with permission from Arthur Christianen, Tijs Karman, and Gerrit C. Groenenboom, Physical Review A, 100, 3, 032708, 2019. Copyright 2019 by the American Physical Society.
Comparison between quasiclassical RRKM theory and experimental collision complex lifetimes in these works, as summarized in Table , reveals that quasiclassical RRKM theory successfully predicts collision complex lifetimes to within an order of magnitude in both the 87Rb133Cs + 87Rb133Cs and 40K87Rb + 40K87Rb collisions. ,, However, for 23Na40K + 23Na40K, 23Na87Rb + 23Na87Rb, 23Na39K + 23Na39K, and 40K87Rb + 87Rb collisions, quasiclassical and experimental lifetimes differ by up to 5 orders of magnitude. ,, The source of this discrepancy remains an open question as of the writing of this review, with hypotheses ranging from the influence of conical intersections to the role of coupling between nuclear spin states.
9. Comparison of Quasiclassical τ class and Experimental τ exp Collision Complex Lifetimes of Ground-Hyperfine-State Alkali Metal Dimers/Atoms in Terms of an Order-of-Magnitude Multiplicative Factor .
Systems for which the quasiclassical and experimental lifetimes are of the same order of magnitude are emphasized in blue (see references [Refs.] and ref for additional details).
4. Outlook
The ongoing success of classical, semiclassical, and quasiclassical approaches to ultracold molecular collisions offers classical methods a position at the forefront of today’s quantum revolution. Of the variety of rationales given to explain the applicability of classical methods beyond the classical limit ℏ → 1, all can be applied to highlight the ability of classical, semiclassical, and quasiclassical mechanics to describe aspects of a wide variety of molecular systems deep in the prototypically quantum regime. ,,− ,,,, The rationales underline three key elements shared by ultracold molecular collisions amenable to such approaches: the presence of deep potential wells introduced by Bethe and formalized and extended to lower energies by Gribakin and Flambaum , (as in highly energetically favorable transition-state collision complexes); the satisfaction of the WKB criterion of Julienne and Mies, Gribakin and Flambaum, , Mody et al., and Côté et al. (as in many two-body ultracold molecular scattering processes, ranging from exothermic product formation to excitation exchange), and/or the absence of quantum reflection and quantum interference in ultracold inferno theory. Theoretical and experimental evidence in the past decade − ,,,− ,− supports the use of classical, semiclassical, and quasiclassical methods to simulate these systems, not only approximately, but nearly exactlyespecially important in cases where exact quantum mechanical approaches are computationally intractable today. This accuracy has the capacitywith careful considerationto enable simulation of aspects of a broad range of cold and ultracold molecular collisions within experimental accuracy that would be otherwise inaccessible.
Rationales for classical, semiclassical, and quasiclassical approaches to ultracold molecular collisions also provide a benchmark of where quantum effects are in fact essential. Quantum reflection and quantum interference determine the limitations of straightforward classical approaches. , However, both of these points are often correctable. Quantum reflection effects can be incorporated in terms of quantum suppression factors, , and quantum interference can be accounted for semiclassically via Van Vleck–Morette–Gutzwiller propagator/Green’s function, ,, Gutzwiller trace formula, , and wavepacket propagation methods. − Quantum resonances are also amenable to accurate semiclassical treatment, as exemplified by Roudnev and Cavagnero’s accurate semiclassical prediction of resonance positions in ultracold dipolar collisions in applied electric fields according to the WKB/Bohr-Sommerfeld quantization condition. , At times, classical calculations may be cumbersome. For example, the common assumption that collision partners may be represented as point particles may belie the importance of internal motion and its quantization, ,− and the assumption of ergodicity in RRKM-based calculation of collision complex lifetimes − may entail careful consideration of the true manifold on which classical trajectories are ergodic or alternative approaches to ameliorate nonergodicity in the considered range of phase space.
What is not addressed in this review and is not possible to simulate efficiently classically with modern methods is entanglement. This lacuna opens an opportunity for quantum computers of interest for the simulation of entanglement in chemistry; a topic that is especially important given leading-edge research into entanglement in ultracold molecules for reaction control, quantum sensing, and quantum computing, ,,− including in the presence of electromagnetic fields. ,
Theoretical prediction of quantum-to-classical crossover in the ultracold regime by a wide variety of authors (see refs − , , , , , , , , , , , − ) throws down the gauntlet for the wider experimental measurement of classical behaviors in the sub-mK regime. The novel picture of near-threshold cross sections given by recent classical and semiclassical approaches points to a key observable, namely the factor k scaling change in the cross section from the quantum threshold to the classical post-threshold law. A search is also underway for how to incorporate quantum effects and nonstatistical behavior into quasiclassical RRKM ,,,− and classical trajectory ,,, approaches in order to compute quantitative collision complex lifetimes. In particular, the hunt is on for a solution to unravel the mystery of why quasiclassical collision complex lifetimes accurate for certain ultracold collisions yield 5 orders of magnitude of discrepancy for others, with recent focus placed on examination of the role of conical intersections by Bause et al. and nuclear spin state coupling by Jachymski, Gronowski, and Tomza. Additionally, the longstanding predictions surrounding classical scattering cross sections for three-dimensional Coulomb potentials, multiple ionization, and atomic fragmentation invite a search for ultracold analogs beyond traditional atom–surface sticking systems in order to identify the extreme limits of quantum-classical correspondence to probe the nature of the interface between quantum and classical mechanics.
An additional theoretical area that remains to be further explored is how to address the severe impact that small variations in potential energy surfaces frequently have on scattering observables. Here, a 1% change in the potential (less than the uncertainty of contemporary ab initio methods) can exact a change of almost 10 orders of magnitude on the scattering cross section. − This means that even where classical, semiclassical, and quasiclassical approaches to cold and ultracold collisions are highly accurate, the result may still be wildly inaccurate. Since the days of Gribakin and Flambaum, ,− there has been significant work to illustrate this problem via a potential scaling technique ,,,,,− and to leverage this problem to probe potentials in terms of their quantum resonances − and Ramsauer-Townsend minima. Recently, statistical methods have been developed in an effort to ameliorate this problem. In 2015, Cui, Li, and Krems − instituted a Gaussian process model capable of producing the relationship between desired observables and potential and control parameters to high accuracy with few training points. For example, the Gaussian process model produced collision lifetimes of near-threshold C6H6 – Ar with a scaled root-mean-square error of just 5.09% for 40 classical-trajectory-derived training points. Likewise, in 2019 and 2020, Morita, Kłos, Krems, and Tscherbul , established a technique to capture observable variation by performing an ensemble of quantum scattering observables for potentials of varying strength to yield cumulative probability distributions for desired observables. These distributions exhibited universal behavior independent of the basis set and low-cost convergence with maximum quantum number N as low as N max = 5 for Li – CaH collisions. These advancements point toward a continued role of data science and classical machine learning approaches to take full advantage of the limited knowledge of short-range potential energy surfaces and to peer into the mechanisms driving the cold and ultracold potential sensitivity.
The ongoing successes of classical, semiclassical, and quasiclassical approaches in the prototypically quantum regime encourage their resurgence at the standard chemistry occurring at higher temperatures. Chemistry stands to benefit at two levels: Computationally, given that the cost grows exponentially with the number of degrees of freedom quantum mechanically, classical approaches offer an exponential cost reduction. This reduction in cost suggests that the methods employed for ultracold molecules detailed here, as well as as quasiclassical trajectories and mixed/quantum classical dynamics − and additional semiclassical and path integral methods ,− may be further applied to bring accurate dynamics and scattering within reach for wide ranger of systems, thereby offering a tool complementary to current multiconfiguration time-dependent Hartree − and tensor-network methods. − Analytically, given that quantum approaches may necessitate visualization of molecular processes in terms of highly multidimensional wavepackets, classical approaches allow the envisionment of molecular processes in terms of readily interpretable particles, which facilitates elucidation of scattering and reaction mechanisms. This is especially relevant today given the current interest in simulation of molecules in the prototypical quantum regime to be the basis of molecular qubits − and quantum sensors. −
Finally, it is worth noting that the rationales put forward for classical, semiclassical, and quasiclassical approaches to ultracold molecular collisions make no assumption on the underlying particles in question. Thus, the same phenomenaclassical post-threshold laws, ,,,,− (quasi)classical collision complex decay times, − etc.are expected to have a parallel life in near-threshold systems of other fields. Consider quantum threshold laws as a historical example. First developed in nuclear physics via the continuity approach of Bethe, Wigner R-matrix theory, and effective range theory; , the same quantum threshold laws have since been rederived in atomic physics via quantum defect theory , and multichannel quantum defect theory ,, and its advancements ,,,,− (a theory that is in fact mathematically equivalent to nuclear R-matrix theory , ). The classical post-threshold laws described here are therefore expected to follow in fields including positron and positronium collisions, ,,,− pion and hadron atom collisions, , plasma science, − and astrophysics and astrochemistry. − This universality of classical behavior close to threshold hints at a possible widespread impact of the ongoing molecular classical revival in today’s quantum era.
Acknowledgments
This work was financially supported by the Office of the Vice Chancellor for Research and Graduate Education at the University of Wisconsin-Madison with funding from the Wisconsin Alumni Research Foundation, the National Science Foundation grant number DGE-1144152, and the Blue Waters Graduate Research Fellowship. This research is part of the Blue Waters sustained-petascale computing project (National Science Foundation awards OCI-0725070 and ACI-1238893), the State of Illinois, and as of December 2019, the National Geospatial-Intelligence Agency. Blue Waters is a joint effort of the University of Illinois at Urbana–Champaign and its National Center for Supercomputing Applications. The authors are grateful for discussions with V. S. Batista and E. T. J. Nibbering.
Biographies
Micheline B. Soley is an assistant professor in the Department of Chemistry at the University of Wisconsin–Madison, where she is affiliate of the Department of Physics and Data Science Institute as well as a member of the Wisconsin Quantum Institute and Chicago Quantum Exchange. Before her appointment as an assistant professor, she was a Yale Quantum Institute Postdoctoral Fellow at Yale University and a National Center for Supercomputing Applications Blue Waters Fellow, Harvard Merit/Graduate Society Term-time Research Fellow, and National Science Foundation Graduate Research Fellow at Harvard University. She was also a Fulbright Fellow at the Max Born Institute for Nonlinear Optics and Short Pulse Spectroscopy. In 2023, Micheline B. Soley was awarded the American Chemical Society Kavli Emerging Leader Award for her work to harness the power of data science in chemistry, based on her work on computing and chemistry deep in the quantum regime with an emphasis on ultracold collisions, quantum control, and parity-time reversal symmetry and the intersection of quantum computing and tensor-network methods.
Eric J. Heller is the Abbott and James Lawrence Professor of Chemistry and Professor of Physics at Harvard University, where he first joined as director of the Institute for Theoretical Atomic, Molecular, and Optical Physics (ITAMP) and Center for Astrophysics (CfA) in 1993. His current research on wave phenomena spans from chemistry to oceanography, with current research foci on time-dependent quantum mechanics, semiclassical physics, and classical-quantum correspondence in devices and molecular systems. In 2013, Eric J. Heller published Why You Hear What You Hear: An Experiential Approach to Sound, Music, and Psychoacoustics at Princeton University Press, the first textbook for nonspecialists on the physics of acoustics and psychoacoustics. In 2018, he followed this text with The Semiclassical Way to Dynamics and Spectroscopy to provide a holistic view into a semiclassical approach to quantum mechanics in molecular systems. For his discoveries, Eric J. Heller has been elected to numerous societies, including the American Academy of Arts and Sciences, the American Philosophical Society, and the National Academy of Science.
The authors declare no competing financial interest.
References
- Jin D. S., Ye J.. Introduction to ultracold molecules: new frontiers in quantum and chemical physics. Chem. Rev. 2012;112:4801–4802. doi: 10.1021/cr300342x. [DOI] [PubMed] [Google Scholar]
- Hutzler N. R., Lu H.-I., Doyle J. M.. The buffer gas beam: An intense, cold, and slow source for atoms and molecules. Chem. Rev. 2012;112:4803–4827. doi: 10.1021/cr200362u. [DOI] [PubMed] [Google Scholar]
- van de Meerakker S. Y., Bethlem H. L., Vanhaecke N., Meijer G.. Manipulation and control of molecular beams. Chem. Rev. 2012;112:4828–4878. doi: 10.1021/cr200349r. [DOI] [PubMed] [Google Scholar]
- Narevicius E., Raizen M. G.. Toward cold chemistry with magnetically decelerated supersonic beams. Chem. Rev. 2012;112:4879–4889. doi: 10.1021/cr2004597. [DOI] [PubMed] [Google Scholar]
- Ulmanis J., Deiglmayr J., Repp M., Wester R., Weidemüller M.. Ultracold Molecules Formed by Photoassociation: Heteronuclear Dimers, Inelastic Collisions, and Interactions with Ultrashort Laser Pulses. Chem. Rev. 2012;112:4890–4927. doi: 10.1021/cr300215h. [DOI] [PubMed] [Google Scholar]
- Koch C. P., Shapiro M.. Coherent Control of Ultracold Photoassociation. Chem. Rev. 2012;112:4928–2948. doi: 10.1021/cr2003882. [DOI] [PubMed] [Google Scholar]
- Quemener G., Julienne P. S.. Ultracold molecules under control! Chem. Rev. 2012;112:4949–5011. doi: 10.1021/cr300092g. [DOI] [PubMed] [Google Scholar]
- Baranov M. A., Dalmonte M., Pupillo G., Zoller P.. Condensed matter theory of dipolar quantum gases. Chem. Rev. 2012;112:5012–5061. doi: 10.1021/cr2003568. [DOI] [PubMed] [Google Scholar]
- Nesbitt D. J.. Toward State-to-State Dynamics in Ultracold Collisions: Lessons from High-Resolution Spectroscopy of Weakly Bound Molecular Complexes. Chem. Rev. 2012;112:5062–5072. doi: 10.1021/cr300208b. [DOI] [PubMed] [Google Scholar]
- Ospelkaus S., Ni K.-K., Wang D., de Miranda M. H. G., Neyenhuis B., Quéméner G., Julienne P. S., Bohn J. L., Jin D. S., Ye J.. Quantum-State Controlled Chemical Reactions of Ultracold Potassium-Rubidium Molecules. Science. 2010;327:853–857. doi: 10.1126/science.1184121. [DOI] [PubMed] [Google Scholar]
- Takekoshi T., Reichsöllner L., Schindewolf A., Hutson J. M., Le Sueur C. R., Dulieu O., Ferlaino F., Grimm R., Nägerl H.-C.. Ultracold dense samples of dipolar RbCs molecules in the rovibrational and hyperfine ground state. Phys. Rev. Lett. 2014;113:205301. doi: 10.1103/PhysRevLett.113.205301. [DOI] [PubMed] [Google Scholar]
- Park J. W., Will S. A., Zwierlein M. W.. Ultracold dipolar gas of fermionic 23Na40K molecules in their absolute ground state. Phys. Rev. Lett. 2015;114:205302. doi: 10.1103/PhysRevLett.114.205302. [DOI] [PubMed] [Google Scholar]
- Ye X., Guo M., González-Martínez M. L., Quéméner G., Wang D.. Collisions of ultracold 23Na87Rb molecules with controlled chemical reactivities. Sci. Adv. 2018;4:eaaq0083. doi: 10.1126/sciadv.aaq0083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo M., Ye X., He J., González-Martínez M. L., Vexiau R., Quéméner G., Wang D.. Dipolar collisions of ultracold ground-state bosonic molecules. Phys. Rev. X. 2018;8:041044. doi: 10.1103/PhysRevX.8.041044. [DOI] [Google Scholar]
- Hu M.-G., Liu Y., Grimes D. D., Lin Y.-W., Gheorghe A. H., Vexiau R., Bouloufa-Maafa N., Dulieu O., Rosenband T., Ni K.-K.. Direct observation of bimolecular reactions of ultracold KRb molecules. Science. 2019;366:1111–1115. doi: 10.1126/science.aay9531. [DOI] [PubMed] [Google Scholar]
- Liu Y., Hu M.-G., Nichols M. A., Yang D., Xie D., Guo H., Ni K.-K.. Precision test of statistical dynamics with state-to-state ultracold chemistry. Nature. 2021;593:379–384. doi: 10.1038/s41586-021-03459-6. [DOI] [PubMed] [Google Scholar]
- Park J. J., Lu Y.-K., Jamison A. O., Tscherbul T. V., Ketterle W.. A Feshbach resonance in collisions between triplet ground-state molecules. Nature. 2023;614:54–58. doi: 10.1038/s41586-022-05635-8. [DOI] [PubMed] [Google Scholar]
- Côté R., Dalgarno A.. Ultracold atom-ion collisions. Phys. Rev. A. 2000;62:012709. doi: 10.1103/PhysRevA.62.012709. [DOI] [Google Scholar]
- Lara M., Jambrina P., Aoiz F., Launay J.-M.. Cold and ultracold dynamics of the barrierless D+ + H2 reaction: Quantum reactive calculations for R –4 long range interaction potentials. J. Chem. Phys. 2015;143:204305. doi: 10.1063/1.4936144. [DOI] [PubMed] [Google Scholar]
- Bohn J. L., Cavagnero M., Ticknor C.. Quasi-universal dipolar scattering in cold and ultracold gases. New J. Phys. 2009;11:055039. doi: 10.1088/1367-2630/11/5/055039. [DOI] [Google Scholar]
- Xing X., Weckesser P., Thielemann F., Jónás T., Vexiau R., Bouloufa-Maafa N., Luc-Koenig E., Madison K. W., Orbán A., Xie T.. et al. Competing excitation quenching and charge exchange in ultracold Li-Ba+ collisions. J. Phys. B. 2024;57:245201. doi: 10.1088/1361-6455/ad8a35. [DOI] [Google Scholar]
- Höveler K., Deiglmayr J., Agner J. A., Schmutz H., Merkt F.. The H2 + + HD reaction at low collision energies: H3 +/H2D+ branching ratio and product-kinetic-energy distributions. Phys. Chem. Chem. Phys. 2021;23:2676–2685. doi: 10.1039/D0CP06107G. [DOI] [PubMed] [Google Scholar]
- Shagam Y., Klein A., Skomorowski W., Yun R., Averbukh V., Koch C. P., Narevicius E.. Molecular hydrogen interacts more strongly when rotationally excited at low temperatures leading to faster reactions. Nat. Chem. 2015;7:921–926. doi: 10.1038/nchem.2359. [DOI] [PubMed] [Google Scholar]
- Gribakin G. F., Flambaum V. V.. Calculation of the scattering length in atomic collisions using the semiclassical approximation. Phys. Rev. A. 1993;48:546–553. doi: 10.1103/PhysRevA.48.546. [DOI] [PubMed] [Google Scholar]
- Gribakin G. F., Kuchiev M. Y.. Multiphoton detachment of electrons from negative ions. Phys. Rev. A. 1997;55:3760–3771. doi: 10.1103/PhysRevA.55.3760. [DOI] [Google Scholar]
- Flambaum V. V., Gribakin G. F., Harabati C.. Analytical calculation of cold-atom scattering. Phys. Rev. A. 1999;59:1998–2005. doi: 10.1103/PhysRevA.59.1998. [DOI] [Google Scholar]
- Julienne P. S., Mies F. H.. Collisions of ultracold trapped atoms. J. Opt. Soc. Am. B. 1989;6:2257–2269. doi: 10.1364/JOSAB.6.002257. [DOI] [Google Scholar]
- Côté R., Heller E. J., Dalgarno A.. Quantum suppression of cold atom collisions. Phys. Rev. A. 1996;53:234–241. doi: 10.1103/PhysRevA.53.234. [DOI] [PubMed] [Google Scholar]
- Mody A., Haggerty M., Doyle J. M., Heller E. J.. No-sticking effect and quantum reflection in ultracold collisions. Phys. Rev. B. 2001;64:085418. doi: 10.1103/PhysRevB.64.085418. [DOI] [Google Scholar]
- Soley M. B., Heller E. J.. Classical approach to collision complexes in ultracold chemical reactions. Phys. Rev. A. 2018;98:052702. doi: 10.1103/PhysRevA.98.052702. [DOI] [Google Scholar]
- Soley, M. B. Escaping from an Ultracold Inferno: Classical and Semiclassical Mechanics Near Threshold. PhD Thesis, Harvard University, Cambridge, MA, 2019. [Google Scholar]
- Miret-Artes S., Pollak E.. Scattering of He atoms from a microstructured grating: quantum reflection probabilities and diffraction patterns. J. Phys. Chem. Lett. 2017;8:1009–1013. doi: 10.1021/acs.jpclett.6b02991. [DOI] [PubMed] [Google Scholar]
- Petersen J., Pollak E., Miret-Artes S.. Quantum threshold reflection is not a consequence of a region of the long-range attractive potential with rapidly varying de Broglie wavelength. Phys. Rev. A. 2018;97:042102. doi: 10.1103/PhysRevA.97.042102. [DOI] [Google Scholar]
- Wang R. R., Bohn J. L.. Prospects for thermalization of microwave-shielded ultracold molecules. Phys. Rev. Res. 2024;6:L022033. doi: 10.1103/PhysRevResearch.6.L022033. [DOI] [Google Scholar]
- Quéméner G., Bohn J. L.. Electric field suppression of ultracold confined chemical reactions. Phys. Rev. A. 2010;81:060701(R) doi: 10.1103/PhysRevA.81.060701. [DOI] [Google Scholar]
- Quéméner G., Bohn J. L.. Strong dependence of ultracold chemical rates on electric dipole moments. Phys. Rev. A. 2010;81:022702. doi: 10.1103/PhysRevA.81.022702. [DOI] [Google Scholar]
- Ni K.-K., Ospelkaus S., Wang D., Quéméner G., de Miranda M. H. G., Bohn J. L., Ye J., Jin D. S.. Dipolar collisions of polar molecules in the quantum regime. Nature. 2010;464:1324–1328. doi: 10.1038/nature08953. [DOI] [PubMed] [Google Scholar]
- Quéméner G., Bohn J. L., Petrov A., Kotochigova S.. Universalities in ultracold reactions of alkali-metal polar molecules. Phys. Rev. A. 2011;84:062703. doi: 10.1103/PhysRevA.84.062703. [DOI] [Google Scholar]
- Gao B.. Quantum-defect theory of atomic collisions and molecular vibration spectra. Phys. Rev. A. 1998;58:4222–4225. doi: 10.1103/PhysRevA.58.4222. [DOI] [Google Scholar]
- Gao B.. Universal Model for Exoergic Bimolecular Reactions and Inelastic Processes. Phys. Rev. Lett. 2010;105:263203. doi: 10.1103/PhysRevLett.105.263203. [DOI] [PubMed] [Google Scholar]
- Gao B.. Quantum Langevin model for exoergic ion–molecule reactions and inelastic processes. Phys. Rev. A. 2011;83:062712. doi: 10.1103/PhysRevA.83.062712. [DOI] [PubMed] [Google Scholar]
- Ticknor C.. Quasi-two-dimensional dipolar scattering. Phys. Rev. A. 2010;81:042708. doi: 10.1103/PhysRevA.81.042708. [DOI] [Google Scholar]
- Micheli A., Idziaszek Z., Pupillo G., Baranov M. A., Zoller P., Julienne P. S.. Universal Rates for Reactive Ultracold Polar Molecules in Reduced Dimensions. Phys. Rev. Lett. 2010;105:073202. doi: 10.1103/PhysRevLett.105.073202. [DOI] [PubMed] [Google Scholar]
- D’Incao J. P., Greene C. H.. Collisional aspects of bosonic and fermionic dipoles in quasi-two-dimensional confining geometries. Phys. Rev. A. 2011;83:030702. doi: 10.1103/PhysRevA.83.030702. [DOI] [Google Scholar]
- Julienne P. S., Hanna T. M., Idziaszek Z.. Universal ultracold collision rates for polar molecules of two alkali-metal atoms. Phys. Chem. Chem. Phys. 2011;13:19114–19124. doi: 10.1039/c1cp21270b. [DOI] [PubMed] [Google Scholar]
- de Miranda M. H. G., Chotia A., Neyenhuis B., Wang D., Quéméner G., Ospelkaus S., Bohn J. L., Ye J., Jin D. S.. Controlling the quantum stereodynamics of ultracold bimolecular reactions. Nat. Phys. 2011;7:502–507. doi: 10.1038/nphys1939. [DOI] [Google Scholar]
- Zhu B., Quéméner G., Rey A. M., Holland M. J.. Evaporative cooling of reactive polar molecules confined in a two-dimensional geometry. Phys. Rev. A. 2013;88:063405. doi: 10.1103/PhysRevA.88.063405. [DOI] [Google Scholar]
- Zhu B., Gadway B., Foss-Feig M., Schachenmayer J., Wall M. L., Hazzard K. R. A., Yan B., Moses S. A., Covey J. P., Jin D. S.. et al. Suppressing the Loss of Ultracold Molecules Via the Continuous Quantum Zeno Effect. Phys. Rev. Lett. 2014;112:070404. doi: 10.1103/PhysRevLett.112.070404. [DOI] [PubMed] [Google Scholar]
- D’Incao J. P., Esry B. D.. Adiabatic hyperspherical representation for the three-body problem in two dimensions. Phys. Rev. A. 2014;90:042707. doi: 10.1103/PhysRevA.90.042707. [DOI] [Google Scholar]
- Idziaszek Z., Jachymski K., Julienne P. S.. Reactive collisions in confined geometries. New J. Phys. 2015;17:035007. doi: 10.1088/1367-2630/17/3/035007. [DOI] [Google Scholar]
- Simoni A., Srinivasan S., Launay J.-M., Jachymski K., Idziaszek Z., Julienne P. S.. Polar molecule reactive collisions in quasi-1D systems. New J. Phys. 2015;17:013020. doi: 10.1088/1367-2630/17/1/013020. [DOI] [Google Scholar]
- Wannier G. H.. The Threshold Law for Single Ionization of Atoms or Ions by Electrons. Phys. Rev. 1953;90:817–825. doi: 10.1103/PhysRev.90.817. [DOI] [Google Scholar]
- Wannier G. H.. Threshold Law for Multiple Ionization. Phys. Rev. 1955;100:1180–1180. doi: 10.1103/PhysRev.100.1180. [DOI] [Google Scholar]
- Geltman S.. Theory of Threshold Energy Dependence of Photodetachment of Diatomic Molecular Negative Ions. Phys. Rev. 1958;112:176–178. doi: 10.1103/PhysRev.112.176. [DOI] [Google Scholar]
- Koslowski H. R., Binder J., Huber B. A., Wiesemann K.. Multiple ionization of Ar atoms by single-electron impact at energies near threshold. J. Phys. B. 1987;20:5903–5915. doi: 10.1088/0022-3700/20/21/032. [DOI] [Google Scholar]
- Pattard T., Rost J. M.. Degenerate Wannier Theory for Multiple Ionization. Phys. Rev. Lett. 1998;80:5081–5084. doi: 10.1103/PhysRevLett.80.5081. [DOI] [Google Scholar]
- Pattard T., Rost J. M.. Erratum: Degenerate Wannier Theory for Multiple Ionization [Phys. Rev. Lett. 80, 5081 (1998)] Phys. Rev. Lett. 1998;81:2618. doi: 10.1103/PhysRevLett.81.2618. [DOI] [Google Scholar]
- Pattard T., Rost J. M.. Cross Sections for (Multiple) Ionization of Ions in Collisions with Electrons. Phys. Scr. 1999;T80:295. doi: 10.1238/Physica.Topical.080a00295. [DOI] [Google Scholar]
- Ostrovsky V. N., Rost J. M.. Wannier-Type Threshold Laws for Multifragmentation and Thomson’s Problem. Few-Body Systems. 2006;38:153–160. doi: 10.1007/s00601-005-0126-y. [DOI] [Google Scholar]
- Emmanouilidou A., Wang P., Rost J. M.. Initial State Dependence in Multielectron Threshold Ionization of Atoms. Phys. Rev. Lett. 2008;100:063002. doi: 10.1103/PhysRevLett.100.063002. [DOI] [PubMed] [Google Scholar]
- Kuchiev M. Y., Ostrovsky V. N.. Threshold laws for the break-up of atomic particles into several charged fragments. Phys. Rev. A. 1998;58:321–335. doi: 10.1103/PhysRevA.58.321. [DOI] [Google Scholar]
- Rost J.-M.. Semiclassical S-matrix theory for atomic fragmentation. Phys. Rep. 1998;297:271–344. doi: 10.1016/S0370-1573(97)00079-3. [DOI] [Google Scholar]
- Bause R., Christianen A., Schindewolf A., Bloch I., Luo X.-Y.. Ultracold sticky collisions: Theoretical and experimental status. J. Phys. Chem. A. 2023;127:729–741. doi: 10.1021/acs.jpca.2c08095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice O. K., Ramsperger H. C.. Theories of Unimolecular Gas Reactions at Low Pressures. J. Am. Chem. Soc. 1927;49:1617–1629. doi: 10.1021/ja01406a001. [DOI] [Google Scholar]
- Kassel L. S.. Studies in Homogeneous Gas Reactions. I. J. Phys. Chem. 1928;32:225–242. doi: 10.1021/j150284a007. [DOI] [Google Scholar]
- Marcus R. A., Rice O. K.. The Kinetics of the Recombination of Methyl Radicals and Iodine Atoms. J. Phys. Chem. 1951;55:894–908. doi: 10.1021/j150489a013. [DOI] [Google Scholar]
- Marcus R. A.. Unimolecular Dissociations and Free Radical Recombination Reactions. J. Chem. Phys. 1952;20:359. doi: 10.1063/1.1700424. [DOI] [Google Scholar]
- Marcus R. A.. On the Analytical Mechanics of Chemical Reactions. Quantum Mechanics of Linear Collisions. J. Chem. Phys. 1966;45:4493. doi: 10.1063/1.1727528. [DOI] [Google Scholar]
- Marcus R. A.. Energy Distributions in Unimolecular Reactions. Ber. Bunsenges. 1977;81:190–197. doi: 10.1002/bbpc.19770810226. [DOI] [Google Scholar]
- Mayle M., Ruzic B. P., Bohn J. L.. Statistical aspects of ultracold resonant scattering. Phys. Rev. A. 2012;85:062712. doi: 10.1103/PhysRevA.85.062712. [DOI] [Google Scholar]
- Mayle M., Quéméner G., Ruzic B. P., Bohn J. L.. Scattering of ultracold molecules in the highly resonant regime. Phys. Rev. A. 2013;87:012709. doi: 10.1103/PhysRevA.87.012709. [DOI] [Google Scholar]
- Croft J. F. E., Bohn J. L.. Long-lived complexes and chaos in ultracold molecular collisions. Phys. Rev. A. 2014;89:012714. doi: 10.1103/PhysRevA.89.012714. [DOI] [Google Scholar]
- Christianen A., Karman T., Groenenboom G. C.. Quasiclassical method for calculating the density of states of ultracold collision complexes. Phys. Rev. A. 2019;100:032708. doi: 10.1103/PhysRevA.100.032708. [DOI] [Google Scholar]
- Croft, J. F. , Bohn, J. L. , Quéméner, G. . Anomalous Lifetimes of Ultracold Complexes Decaying into a Single Channel: What’s Taking So Long in There? arXiv preprint arXiv:2111.09956 2021, 10.48550/arXiv.2111.09956. [DOI] [Google Scholar]
- Croft J. F., Bohn J. L., Quéméner G.. Anomalous lifetimes of ultracold complexes decaying into a single channel. Phys. Rev. A. 2023;107:023304. doi: 10.1103/PhysRevA.107.023304. [DOI] [Google Scholar]
- Croft J. F. E., Makrides C., Li M., Petrov A., Kendrick B. K., Balakrishnan N., Kotochigova S.. Universality and chaoticity in ultracold K+KRb chemical reactions. Nat. Commun. 2017;8:15897. doi: 10.1038/ncomms15897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Hu M.-G., Nichols M. A., Grimes D. D., Karman T., Guo H., Ni K.-K.. Photo-excitation of long-lived transient intermediates in ultracold reactions. Nat. Phys. 2020;16:1132–1136. doi: 10.1038/s41567-020-0968-8. [DOI] [Google Scholar]
- Christianen A., Zwierlein M. W., Groenenboom G. C., Karman T.. Photoinduced two-body loss of ultracold molecules. Phys. Rev. Lett. 2019;123:123402. doi: 10.1103/PhysRevLett.123.123402. [DOI] [PubMed] [Google Scholar]
- Nichols M. A., Liu Y.-X., Zhu L., Hu M.-G., Liu Y., Ni K.-K.. Detection of long-lived complexes in ultracold atom-molecule collisions. Phys. Rev. X. 2022;12:011049. doi: 10.1103/PhysRevX.12.011049. [DOI] [Google Scholar]
- Safronova M., Budker D., DeMille D., Kimball D. F. J., Derevianko A., Clark C. W.. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018;90:025008. doi: 10.1103/RevModPhys.90.025008. [DOI] [Google Scholar]
- Safronova M. S.. The search for variation of fundamental constants with clocks. Ann. Phys. 2019;531:1800364. doi: 10.1002/andp.201800364. [DOI] [Google Scholar]
- Leung K., Iritani B., Tiberi E., Majewska I., Borkowski M., Moszynski R., Zelevinsky T.. Terahertz Vibrational Molecular Clock with Systematic Uncertainty at the 10–14 Level. Phys. Rev. X. 2023;13:011047. doi: 10.1103/PhysRevX.13.011047. [DOI] [Google Scholar]
- DeMille D., Hutzler N. R., Rey A. M., Zelevinsky T.. Quantum sensing and metrology for fundamental physics with molecules. Nat. Phys. 2024;20:741–749. doi: 10.1038/s41567-024-02499-9. [DOI] [Google Scholar]
- DeMille D.. Quantum Computation with Trapped Polar Molecules. Phys. Rev. Lett. 2002;88:067901. doi: 10.1103/PhysRevLett.88.067901. [DOI] [PubMed] [Google Scholar]
- Yelin S., Kirby K., Côté R.. Schemes for robust quantum computation with polar molecules. Phys. Rev. A. 2006;74:050301. doi: 10.1103/PhysRevA.74.050301. [DOI] [Google Scholar]
- Yelin, S. F. , DeMille, D. , Côté, R. . Quantum information processing with ultracold polar molecules. In Cold Molecules; CRC Press, 2009; pp 661–680. [Google Scholar]
- Friedman J. F., Miller T. M., Schaffer L. C., Viggiano A. A., Fabrikant I. I.. Electron attachment to Cl2 from 300 to 1100 K: Experiment and theory. Phys. Rev. A. 2009;79:032707. doi: 10.1103/PhysRevA.79.032707. [DOI] [Google Scholar]
- Pellegrini P., Vranckx S., Desouter-Lecomte M.. Implementing quantum algorithms in hyperfine levels of ultracold polar molecules by optimal control. Phys. Chem. Chem. Phys. 2011;13:18864–18871. doi: 10.1039/c1cp21184f. [DOI] [PubMed] [Google Scholar]
- Vranckx S., Pellegrini P., Desouter-Lecomte M.. Implementing quantum algorithms in hyperfine levels of ultracold polar molecules. J. Phys.: Conf. Ser. 2012;388:112010. doi: 10.1088/1742-6596/388/11/112010. [DOI] [PubMed] [Google Scholar]
- Vranckx S., Jaouadi A., Pellegrini P., Bomble L., Vaeck N., Desouter-Lecomte M.. Implementing quantum gates and algorithms in ultracold polar molecules. Architecture and Design of Molecule Logic Gates and Atom Circuits: Proceedings of the 2nd AtMol European Workshop. 2013:279–290. doi: 10.1007/978-3-642-33137-4_21. [DOI] [Google Scholar]
- Côté R.. Ultracold molecules: Their formation and application to quantum computing. Quantum Information and Computation for Chemistry. 2014:403–448. doi: 10.1002/9781118742631.ch14. [DOI] [Google Scholar]
- Herrera F., Cao Y., Kais S., Whaley K. B.. Infrared-dressed entanglement of cold open-shell polar molecules for universal matchgate quantum computing. New J. Phys. 2014;16:075001. doi: 10.1088/1367-2630/16/7/075001. [DOI] [Google Scholar]
- Karra M., Sharma K., Friedrich B., Kais S., Herschbach D.. Prospects for quantum computing with an array of ultracold polar paramagnetic molecules. J. Chem. Phys. 2016;144:094301. doi: 10.1063/1.4942928. [DOI] [PubMed] [Google Scholar]
- Blackmore J. A., Caldwell L., Gregory P. D., Bridge E. M., Sawant R., Aldegunde J., Mur-Petit J., Jaksch D., Hutson J. M., Sauer B.. et al. Ultracold molecules for quantum simulation: rotational coherences in CaF and RbCs. Quantum Sci. Technol. 2019;4:014010. doi: 10.1088/2058-9565/aaee35. [DOI] [Google Scholar]
- Ni K.-K., Rosenband T., Grimes D. D.. Dipolar exchange quantum logic gate with polar molecules. Chem. Sci. 2018;9:6830–6838. doi: 10.1039/C8SC02355G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu P., Cheuk L. W., Kozyryev I., Doyle J. M.. A scalable quantum computing platform using symmetric-top molecules. New J. Phys. 2019;21:093049. doi: 10.1088/1367-2630/ab428d. [DOI] [Google Scholar]
- Sawant R., Blackmore J. A., Gregory P. D., Mur-Petit J., Jaksch D., Aldegunde J., Hutson J. M., Tarbutt M. R., Cornish S. L.. Ultracold polar molecules as qudits. New J. Phys. 2020;22:013027. doi: 10.1088/1367-2630/ab60f4. [DOI] [Google Scholar]
- Zhang Z.-Y., Liu J.-M., Hu Z., Wang Y.. Implementation of three-qubit quantum computation with pendular states of polar molecules by optimal control. J. Chem. Phys. 2020;152:044303. doi: 10.1063/1.5139688. [DOI] [PubMed] [Google Scholar]
- Gregory P. D., Blackmore J. A., Bromley S. L., Hutson J. M., Cornish S. L.. Robust storage qubits in ultracold polar molecules. Nat. Phys. 2021;17:1149–1153. doi: 10.1038/s41567-021-01328-7. [DOI] [Google Scholar]
- Kaufman A. M., Ni K.-K.. Quantum science with optical tweezer arrays of ultracold atoms and molecules. Nat. Phys. 2021;17:1324–1333. doi: 10.1038/s41567-021-01357-2. [DOI] [Google Scholar]
- Wang K., Williams C. P., Picard L. R., Yao N. Y., Ni K.-K.. Enriching the quantum toolbox of ultracold molecules with Rydberg atoms. PRX Quantum. 2022;3:030339. doi: 10.1103/PRXQuantum.3.030339. [DOI] [Google Scholar]
- Zhang C., Tarbutt M.. Quantum computation in a hybrid array of molecules and Rydberg atoms. PRX Quantum. 2022;3:030340. doi: 10.1103/PRXQuantum.3.030340. [DOI] [Google Scholar]
- Asnaashari K., Krems R.. Quantum annealing with pairs of 2Σ molecules as qubits. Phys. Rev. A. 2022;106:022801. doi: 10.1103/PhysRevA.106.022801. [DOI] [Google Scholar]
- Softley T. P.. Cold and ultracold molecules in the twenties. Proceedings of the Royal Society A. 2023;479:20220806. doi: 10.1098/rspa.2022.0806. [DOI] [Google Scholar]
- Asnaashari K., Krems R. V., Tscherbul T. V.. General classification of qubit encodings in ultracold diatomic molecules. J. Phys. Chem. A. 2023;127:6593–6602. doi: 10.1021/acs.jpca.3c02835. [DOI] [PubMed] [Google Scholar]
- Tscherbul T. V., Ye J., Rey A. M.. Robust nuclear spin entanglement via dipolar interactions in polar molecules. Phys. Rev. Lett. 2023;130:143002. doi: 10.1103/PhysRevLett.130.143002. [DOI] [PubMed] [Google Scholar]
- Ruttley D. K., Guttridge A., Hepworth T. R., Cornish S. L.. Enhanced quantum control of individual ultracold molecules using optical tweezer arrays. PRX Quantum. 2024;5:020333. doi: 10.1103/PRXQuantum.5.020333. [DOI] [Google Scholar]
- Cornish S. L., Tarbutt M. R., Hazzard K. R.. Quantum computation and quantum simulation with ultracold molecules. Nat. Phys. 2024;20:730–740. doi: 10.1038/s41567-024-02453-9. [DOI] [Google Scholar]
- Kosloff R.. Quantum Molecular Devices. ACS Phys. Chem. Au. 2024;4:226–231. doi: 10.1021/acsphyschemau.3c00077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siska P.. Cold and ultracold ion-neutral inelastic collisions: Spin-orbit relaxation in He+Ne+ . J. Chem. Phys. 2001;115:4527–4533. doi: 10.1063/1.1394938. [DOI] [Google Scholar]
- Zhang P., Bodo E., Dalgarno A.. Near Resonance Charge Exchange in Ion-Atom Collisions of Lithium Isotopes. J. Phys. Chem. A. 2009;113:15085–15091. doi: 10.1021/jp905184a. [DOI] [PubMed] [Google Scholar]
- Zhang P., Dalgarno A., Côté R., Bodo E.. Charge exchange in collisions of beryllium with its ion. Phys. Chem. Chem. Phys. 2011;13:19026–19035. doi: 10.1039/c1cp21494b. [DOI] [PubMed] [Google Scholar]
- Pérez-Ríos J., Ragole S., Wang J., Greene C. H.. Comparison of classical and quantal calculations of helium three-body recombination. J. Chem. Phys. 2014;140:044307. doi: 10.1063/1.4861851. [DOI] [PubMed] [Google Scholar]
- Pérez-Ríos J., Greene C. H.. Communication: Classical threshold law for ion-neutral-neutral three-body recombination. J. Chem. Phys. 2015;143:041105. doi: 10.1063/1.4927702. [DOI] [PubMed] [Google Scholar]
- Côté, R. Ultracold hybrid atom-ion systems. In Advances in Atomic, Molecular, and Optical Physics; Elsevier, 2016; Vol. 65; pp 67–126. [Google Scholar]
- Stoecklin T., Halvick P., Gannouni M. A., Hochlaf M., Kotochigova S., Hudson E. R.. Explanation of efficient quenching of molecular ion vibrational motion by ultracold atoms. Nat. Commun. 2016;7:11234. doi: 10.1038/ncomms11234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croft J. F. E., Balakrishnan N., Kendrick B. K.. Long-lived complexes and signatures of chaos in ultracold K2 + Rb collisions. Phys. Rev. A. 2017;96:062707. doi: 10.1103/PhysRevA.96.062707. [DOI] [Google Scholar]
- Côté R., Simbotin I.. Signature of the s-wave regime high above ultralow temperatures. Phys. Rev. Lett. 2018;121:173401. doi: 10.1103/PhysRevLett.121.173401. [DOI] [PubMed] [Google Scholar]
- Majewska I., Kondov S. S., Lee C.-H., McDonald M., McGuyer B. H., Moszynski R., Zelevinsky T.. Experimental and theoretical investigation of the crossover from the ultracold to the quasiclassical regime of photodissociation. Phys. Rev. A. 2018;98:043404. doi: 10.1103/PhysRevA.98.043404. [DOI] [PubMed] [Google Scholar]
- Kondov S. S., Lee C.-H., McDonald M., McGuyer B. H., Majewska I., Moszynski R., Zelevinsky T.. Crossover from the Ultracold to the Quasiclassical Regime in State-Selected Photodissociation. Phys. Rev. Lett. 2018;121:143401. doi: 10.1103/PhysRevLett.121.143401. [DOI] [PubMed] [Google Scholar]
- Pérez-Ríos J.. Vibrational quenching and reactive processes of weakly bound molecular ions colliding with atoms at cold temperatures. Phys. Rev. A. 2019;99:022707. doi: 10.1103/PhysRevA.99.022707. [DOI] [Google Scholar]
- Pandey A., Niranjan M., Joshi N., Rangwala S., Vexiau R., Dulieu O.. Interaction potentials and ultracold scattering cross sections for the 7Li+ - 7Li ion-atom system. Phys. Rev. A. 2020;101:052702. doi: 10.1103/PhysRevA.101.052702. [DOI] [Google Scholar]
- Pérez Ríos, J. Few-Body Processes Involving Ions and Neutrals at Cold Temperatures. In An Introduction to Cold and Ultracold Chemistry: Atoms, Molecules, Ions and Rydbergs; Springer, 2020; pp 193–214. [Google Scholar]
- Dieterle T., Berngruber M., Hölzl C., Löw R., Jachymski K., Pfau T., Meinert F.. Inelastic collision dynamics of a single cold ion immersed in a Bose–Einstein condensate. Phys. Rev. A. 2020;102:041301. doi: 10.1103/PhysRevA.102.041301. [DOI] [PubMed] [Google Scholar]
- Hirzler H., Pérez-Ríos J.. Rydberg atom-ion collisions in cold environments. Phys. Rev. A. 2021;103:043323. doi: 10.1103/PhysRevA.103.043323. [DOI] [Google Scholar]
- Mohammadi A., Krükow A., Mahdian A., Deiß M., Pérez-Ríos J., da Silva H. Jr, Raoult M., Dulieu O., Hecker Denschlag J.. Life and death of a cold BaRb+ molecule inside an ultracold cloud of Rb atoms. Phys. Rev. Res. 2021;3:013196. doi: 10.1103/PhysRevResearch.3.013196. [DOI] [Google Scholar]
- Pérez-Ríos J.. Cold chemistry: a few-body perspective on impurity physics of a single ion in an ultracold bath. Mol. Phys. 2021;119:e1881637. doi: 10.1080/00268976.2021.1881637. [DOI] [Google Scholar]
- Ben-shlomi R., Pinkas M., Meir Z., Sikorsky T., Katz O., Akerman N., Ozeri R.. High-energy-resolution measurements of an ultracold-atom-ion collisional cross section. Phys. Rev. A. 2021;103:032805. doi: 10.1103/PhysRevA.103.032805. [DOI] [Google Scholar]
- Höveler K., Deiglmayr J., Merkt F.. Deviation of the rate of the H2 + + D2 reaction from Langevin behaviour below 1 K, branching ratios for the HD2 + + H and H2D+ + D product channels, and product-kinetic-energy distributions. Mol. Phys. 2021;119:e1954708. doi: 10.1080/00268976.2021.1954708. [DOI] [Google Scholar]
- Höveler K., Deiglmayr J., Agner J. A., Hahn R., Zhelyazkova V., Merkt F.. Observation of quantum capture in an ion–molecule reaction. Phys. Rev. A. 2022;106:052806. doi: 10.1103/PhysRevA.106.052806. [DOI] [Google Scholar]
- Morita M., Kendrick B. K., Kłos J., Kotochigova S., Brumer P., Tscherbul T. V.. Signatures of Non-universal Quantum Dynamics of Ultracold Chemical Reactions of Polar Alkali Dimer Molecules with Alkali Metal Atoms: Li(2S) + NaLi(a 3Σ+) → Na(2S) + Li2(a 3Σ u +) J. Phys. Chem. Lett. 2023;14:3413–3421. doi: 10.1021/acs.jpclett.3c00159. [DOI] [PubMed] [Google Scholar]
- Koots R., Pérez-Ríos J.. PyQCAMS: Python Quasi-Classical Atom-Molecule Scattering. Atoms. 2024;12:29. doi: 10.3390/atoms12050029. [DOI] [Google Scholar]
- Karpa, L. , Dulieu, O. . Ultracold Interactions between Ions and Polar Molecules. arXiv preprint arXiv:2409.16833 2024, 10.48550/arXiv.2409.16833. [DOI] [Google Scholar]
- Senn P.. Threshold anomalies in one-dimensional scattering. Am. J. Phys. 1988;56:916–921. doi: 10.1119/1.15359. [DOI] [Google Scholar]
- Macri P., Barrachina R. O.. Extracting low-energy electron-atom scattering parameters from ionic measurements. Nucl. Instrum. Methods Phys. Res. B. 2003;205:543–545. doi: 10.1016/S0168-583X(02)02062-1. [DOI] [Google Scholar]
- Macri P. A., Plastic F. S., Barrachina R. O.. Jost function description of elastic and few-body resonances. Radiat. Phys. Chem. 2007;76:504–507. doi: 10.1016/j.radphyschem.2005.11.036. [DOI] [Google Scholar]
- Barrachina R. O., Fiol J., Macri P.. Threshold effects in the ionization of atoms by positron impact. Nucl. Instrum. Methods Phys. Res. B. 2008;266:402–406. doi: 10.1016/j.nimb.2007.12.040. [DOI] [Google Scholar]
- Macri P. A., Barrachina R. O.. Extraction of interaction parameters from near threshold positron experiments. Nucl. Instrum. Methods Phys. Res. B. 2009;267:254–256. doi: 10.1016/j.nimb.2008.10.015. [DOI] [Google Scholar]
- Macri P. A., Barrachina R. O.. Inverse scattering for inelastic atomic processes at thresholds. J. Phys. Conf. Ser. 2012;397:012005. doi: 10.1088/1742-6596/397/1/012005. [DOI] [Google Scholar]
- Macri P. A., Barrachina R. O.. A Jost function description of zero-energy resonance and transparency effects in elastic collisions. J. Phys. B. 2013;46:065202. doi: 10.1088/0953-4075/46/6/065202. [DOI] [Google Scholar]
- Simbotin I., Ghosal S., Côté R.. Threshold resonance effects in reactive processes. Phys. Rev. A. 2014;89:040701(R) doi: 10.1103/PhysRevA.89.040701. [DOI] [Google Scholar]
- Simbotin I., Côté R.. Jost function description of near threshold resonances for coupled-channel scattering. Chem. Phys. 2015;462:79–93. doi: 10.1016/j.chemphys.2015.06.009. [DOI] [Google Scholar]
- Bethe H. A.. Theory of Disintegration of Nuclei by Neutrons. Phys. Rev. 1935;47:747. doi: 10.1103/PhysRev.47.747. [DOI] [Google Scholar]
- Wigner E. P.. On the Behavior of Cross Sections Near Thresholds. Phys. Rev. 1948;73:1002. doi: 10.1103/PhysRev.73.1002. [DOI] [Google Scholar]
- Langevin M. P.. Une formule fondamentale de théorie cinétique. Ann. Chim. Phys. 1905;5:245–288. [Google Scholar]
- Gorin E.. The Primary Process in the Photo-Decomposition of Aldehydes and Ketones. Acta Physicochimica. 1938;8:513. [Google Scholar]
- Gorin E.. Photolysis of Aldehydes and Ketones in the Presence of Iodine Vapor. J. Chem. Phys. 1939;7:256–264. doi: 10.1063/1.1750427. [DOI] [Google Scholar]
- Grier A. T., Cetina M., Oručević F., Vuletić V.. Observation of cold collisions between trapped ions and trapped atoms. Phys. Rev. Lett. 2009;102:223201. doi: 10.1103/PhysRevLett.102.223201. [DOI] [PubMed] [Google Scholar]
- Gregory P. D., Blackmore J. A., Bromley S. L., Cornish S. L.. Loss of ultracold 87Rb133Cs molecules via optical excitation of long-lived two-body collision complexes. Phys. Rev. Lett. 2020;124:163402. doi: 10.1103/PhysRevLett.124.163402. [DOI] [PubMed] [Google Scholar]
- Gersema P., Voges K. K., Meyer zum Alten Borgloh M., Koch L., Hartmann T., Zenesini A., Ospelkaus S., Lin J., He J., Wang D.. Probing Photoinduced Two-Body Loss of Ultracold Nonreactive Bosonic 23Na87Rb and 23Na39K Molecules. Phys. Rev. Lett. 2021;127:163401. doi: 10.1103/PhysRevLett.127.163401. [DOI] [PubMed] [Google Scholar]
- Bause R., Schindewolf A., Tao R., Duda M., Chen X.-Y., Quéméner G., Karman T., Christianen A., Bloch I., Luo X.-Y.. Collisions of ultracold molecules in bright and dark optical dipole traps. Phys. Rev. Res. 2021;3:033013. doi: 10.1103/PhysRevResearch.3.033013. [DOI] [Google Scholar]
- Sardar D., Bohn J. L.. Sticking lifetime of ultracold CaF molecules in triplet interactions. J. Phys. Chem. A. 2023;127:4815–4821. doi: 10.1021/acs.jpca.3c01676. [DOI] [PubMed] [Google Scholar]
- Magnier, S. Détermination des états électroniques excités des molécules Na2 et K2: application aux collisions entre atomes excités par laser. Ph.D. thesis, Université Paris-Sud, 1993. [Google Scholar]
- McDaniel, E. W. Collision phenomena in ionized cases; Wiley, 1964. [Google Scholar]
- Massey H., Mohr C.. Free paths and transport phenomena in gases and the quantum theory of collisions. II. The determination of the laws of force between atoms and molecules. Proc. Roy. Soc. A. 1934;144:188–205. [Google Scholar]
- Langer R. E.. On the Connection Formulas and the Solutions of the Wave Equation. Phys. Rev. 1937;51:669–676. doi: 10.1103/PhysRev.51.669. [DOI] [Google Scholar]
- Dalgarno A., McDowell M. C., Williams A.. The mobilities of ions in unlike gases. Philos. Trans. R. Soc. A. 1958;250:411–425. doi: 10.1098/rsta.1958.0002. [DOI] [Google Scholar]
- Falcetta M., Dorko M., Siska P.. Ab initio/spectroscopic interaction potential for He + Ne+ . J. Chem. Phys. 2000;113:11044–11054. doi: 10.1063/1.1327267. [DOI] [Google Scholar]
- Seong J., Janda K. C., McGrath M. P., Halberstadt N.. HeNe+: resolution of an apparent disagreement between experiment and theory. Chem. Phys. Lett. 1999;314:501–507. doi: 10.1016/S0009-2614(99)01179-3. [DOI] [Google Scholar]
- Arthurs A., Dalgarno A.. The theory of scattering by a rigid rotator. Proc. Roy. Soc. A. 1960;256:540–551. doi: 10.1098/rspa.1960.0125. [DOI] [Google Scholar]
- Reid R., Dalgarno A.. Fine-structure transitions and shape resonances. Phys. Rev. Lett. 1969;22:1029. doi: 10.1103/PhysRevLett.22.1029. [DOI] [Google Scholar]
- Reid R.. Transitions among the 3p2P states of sodium induced by collisions with helium. J. Phys. B. 1973;6:2018. doi: 10.1088/0022-3700/6/10/018. [DOI] [Google Scholar]
- Manolopoulos D.. An improved log derivative method for inelastic scattering. J. Chem. Phys. 1986;85:6425–6429. doi: 10.1063/1.451472. [DOI] [Google Scholar]
- Werner H.-J., Knowles P. J.. A second order multiconfiguration SCF procedure with optimum convergence. J. Chem. Phys. 1985;82:5053–5063. doi: 10.1063/1.448627. [DOI] [Google Scholar]
- Werner H.-J., Knowles P. J.. An efficient internally contracted multiconfiguration-reference configuration interaction method. J. Chem. Phys. 1988;89:5803–5814. doi: 10.1063/1.455556. [DOI] [Google Scholar]
- Zhang P., Dalgarno A., Côté R.. Scattering of Yb and Yb+ . Phys. Rev. A. 2009;80:030703. doi: 10.1103/PhysRevA.80.030703. [DOI] [Google Scholar]
- Makarov O. P., Côté R., Michels H., Smith W.. Radiative charge-transfer lifetime of the excited state of (NaCa)+ . Phys. Rev. A. 2003;67:042705. doi: 10.1103/PhysRevA.67.042705. [DOI] [Google Scholar]
- Gacesa M., Montgomery J. A. Jr, Michels H. H., Côté R.. Production of NaCa+ molecular ions in the ground state from cold atom-ion mixtures by photoassociation via an intermediate state. Phys. Rev. A. 2016;94:013407. doi: 10.1103/PhysRevA.94.013407. [DOI] [Google Scholar]
- Li Z., Singh S., Tscherbul T., Madison K.. Feshbach resonances in ultracold 85Rb -87Rb and 6Li -87Rb mixtures. Phys. Rev. A. 2008;78:022710. doi: 10.1103/PhysRevA.78.022710. [DOI] [Google Scholar]
- Bouledroua M., Dalgarno A., Côté R.. Diffusion and excitation transfer of excited alkali-metal atoms. Phys. Rev. A. 2001;65:012701. doi: 10.1103/PhysRevA.65.012701. [DOI] [Google Scholar]
- Jraij A., Allouche A.-R., Korek M., Aubert-Frécon M.. Theoretical electronic structure including spin-orbit effects of the alkali dimer cation Cs2 + . Chem. Phys. 2005;310:145–151. doi: 10.1016/j.chemphys.2004.10.023. [DOI] [Google Scholar]
- Wentzel G.. Eine Verallgemeinerung der Quantenbedingung für eine Zwecke der Wellenmechanik. Z. Phys. 1926;38:518–529. doi: 10.1007/BF01397171. [DOI] [Google Scholar]
- Wentzel G.. Zwei Bemerkungen über die Zerstreuung korpuskularer Strahlen als Beugungserscheinung. Z. Phys. 1926;40:590–593. doi: 10.1007/BF01390457. [DOI] [Google Scholar]
- Kramers H. A.. Wellenmechanik und halbzahlige Quantisierung. Z. Phys. 1926;39:828–840. doi: 10.1007/BF01451751. [DOI] [Google Scholar]
- Kramers H. A.. Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions. Physica. 1940;7:284–304. doi: 10.1016/S0031-8914(40)90098-2. [DOI] [Google Scholar]
- Brillouin L.. La Mécanique Ondulatoire de Schrödinger une Method Générale de Resolution par Approximations Successives. C. R. Acad. Hebd. Séances Acad. Sci. 1926;183:24–26. [Google Scholar]
- Brillouin L.. Remarques sur la Mécanique Ondulatoire. J. Phys. Radium. 1926;7:353–368. doi: 10.1051/jphysrad:01926007012035300. [DOI] [Google Scholar]
- Marinescu M., Sadeghpour H. R., Dalgarno A.. Dispersion coefficients for alkali-metal dimers. Phys. Rev. A. 1994;49:982–988. doi: 10.1103/PhysRevA.49.982. [DOI] [PubMed] [Google Scholar]
- Truhlar, D. G. , Muckerman, J. T. . Reactive scattering cross sections III: Quasiclassical and semiclassical methods. In Atom-Molecule Collision Theory: A Guide for the Experimentalist; Springer, 1979; pp 505–566. [Google Scholar]
- Levine, R. D. , Bernstein, R. B. . Molecular reaction dynamics and chemical reactivity; Oxford, 1987. [Google Scholar]
- Pérez-Ríos, J. An Introduction to Cold and Ultracold Chemistry; Springer, 2020. [Google Scholar]
- Ticknor C.. Energy dependence of scattering ground-state polar molecules. Phys. Rev. A. 2007;76:052703. doi: 10.1103/PhysRevA.76.052703. [DOI] [Google Scholar]
- Ticknor C.. Collisional control of ground state polar molecules and universal dipolar scattering. Phys. Rev. Lett. 2008;100:133202. doi: 10.1103/PhysRevLett.100.133202. [DOI] [PubMed] [Google Scholar]
- Dashevskaya E. I., Litvin I., Nikitin E., Troe J.. Rates of complex formation in collisions of rotationally excited homonuclear diatoms with ions at very low temperatures: Application to hydrogen isotopes and hydrogen-containing ions. J. Chem. Phys. 2005;122:184311. doi: 10.1063/1.1889425. [DOI] [PubMed] [Google Scholar]
- Eltschka C., Moritz M. J., Friedrich H.. Near-threshold quantization and scattering for deep potentials with attractive tails. J. Phys. B. 2000;33:4033. doi: 10.1088/0953-4075/33/19/315. [DOI] [Google Scholar]
- Dashevskaya E. I., Litvin I., Nikitin E. E., Troe J.. Quantum scattering and adiabatic channel treatment of the low-energy and low-temperature capture of a rotating quadrupolar molecule by an ion. J. Chem. Phys. 2004;120:9989–9997. doi: 10.1063/1.1724822. [DOI] [PubMed] [Google Scholar]
- Smith S. C., Troe J.. Statistical modeling of ion–molecule electrostatic capture. J. Chem. Phys. 1992;97:5451–5464. doi: 10.1063/1.463804. [DOI] [Google Scholar]
- Nikitin E., Troe J.. Quantum and classical calculations of adiabatic and nonadiabatic capture rates for anisotropic interactions. Ber. Bunsenges. Phys. Chem. 1997;101:445–458. doi: 10.1002/bbpc.19971010317. [DOI] [Google Scholar]
- Maergoiz A., Nikitin E., Troe J., Ushakov V.. Classical trajectory and adiabatic channel study of the transition from adiabatic to sudden capture dynamics. II. Ion-quadrupole capture. J. Chem. Phys. 1996;105:6270–6276. doi: 10.1063/1.472468. [DOI] [Google Scholar]
- Dashevskaya E. I., Litvin I., Nikitin E., Troe J.. Relocking of intrinsic angular momenta in collisions of diatoms with ions: Capture of H2(j = 0, 1) by H2 + . J. Chem. Phys. 2016;145:244315. doi: 10.1063/1.4972129. [DOI] [PubMed] [Google Scholar]
- Dashevskaya E. I., Nikitin E. E.. Quantum suppression and enhancement of the quasiclassical Landau-Lifshitz matrix elements: Application to the inelastic H2 - He scattering at ultralow energies. Phys. Rev. A. 2000;63:012711. doi: 10.1103/PhysRevA.63.012711. [DOI] [Google Scholar]
- Quéméner G., Honvault P., Launay J.-M., Soldán P., Potter D. E., Hutson J. M.. Ultracold quantum dynamics: Spin-polarized K + K2 collisions with three identical bosons or fermions. Phys. Rev. A. 2005;71:032722. doi: 10.1103/PhysRevA.71.032722. [DOI] [Google Scholar]
- Cvitaš M. T., Soldán P., Hutson J. M., Honvault P., Launay J.-M.. Ultracold Li + Li2 Collisions: Bosonic and Fermionic Cases. Phys. Rev. Lett. 2005;94:033201. doi: 10.1103/PhysRevLett.94.033201. [DOI] [PubMed] [Google Scholar]
- Hutson J. M., Soldán P.. Molecule formation in ultracold atomic gases. Int. Rev. Phys. Chem. 2006;25:497. doi: 10.1080/01442350600921772. [DOI] [Google Scholar]
- Launay J.M., Le Dourneuf M.. Quantum-mechanical calculation of integral cross sections for the reaction F+H2 (ν = 0,j = 0)→FH(ν′ j′)+H by the hyperspherical method. Chem. Phys. Lett. 1990;169:473–481. doi: 10.1016/0009-2614(90)85634-O. [DOI] [Google Scholar]
- Velilla L., Lepetit B., Aguado A., Beswick J. A., Paniagua M.. The H3 + rovibrational spectrum revisited with a global electronic potential energy surface. J. Chem. Phys. 2008;129:084307. doi: 10.1063/1.2973629. [DOI] [PubMed] [Google Scholar]
- Aguado A., Roncero O., Tablero C., Sanz C., Paniagua M.. Global potential energy surfaces for the H3 + system. Analytical representation of the adiabatic ground-state 1 A′ potential. J. Chem. Phys. 2000;112:1240–1254. doi: 10.1063/1.480539. [DOI] [Google Scholar]
- Metcalf, H. J. , Van der Straten, P. . Laser cooling and trapping; Springer Science & Business Media, 1999. [Google Scholar]
- Vexiau R., Borsalino D., Lepers M., Orbán A., Aymar M., Dulieu O., Bouloufa-Maafa N.. Dynamic dipole polarizabilities of heteronuclear alkali dimers: optical response, trapping and control of ultracold molecules. Int. Rev. Phys. Chem. 2017;36:709–750. doi: 10.1080/0144235X.2017.1351821. [DOI] [Google Scholar]
- Valtolina G., Matsuda K., Tobias W. G., Li J.-R., De Marco L., Ye J.. Dipolar evaporation of reactive molecules to below the Fermi temperature. Nature. 2020;588:239–243. doi: 10.1038/s41586-020-2980-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindewolf A., Bause R., Chen X.-Y., Duda M., Karman T., Bloch I., Luo X.-Y.. Evaporation of microwave-shielded polar molecules to quantum degeneracy. Nature. 2022;607:677–681. doi: 10.1038/s41586-022-04900-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bigagli N., Yuan W., Zhang S., Bulatovic B., Karman T., Stevenson I., Will S.. Observation of Bose–Einstein condensation of dipolar molecules. Nature. 2024;631:289. doi: 10.1038/s41586-024-07492-z. [DOI] [PubMed] [Google Scholar]
- Cvitanović, P. , Artuso, R. , Mainieri, R. , Tanner, G. , Vattay, G. . Chaos: Classical and Quantum; Niels Bohr Inst.: Copenhagen, 2016. [Google Scholar]
- Landau L. D.. Zur theorie der Energieübertragung I. Phys. Z. Sowjetunion. 1932;1:88. [Google Scholar]
- Landau, L. D. , Lifshitz, E. M. . Quantum Mechanics: Non-relativisitic Theory, 2nd ed.; Pergamon: New York, 1965; Vol. 3. [Google Scholar]
- Balakrishnan N., Forrey R. C., Dalgarno A.. Quenching of H2 Vibrations in Ultracold 3He and 4He Collisions. Phys. Rev. Lett. 1998;80:3224–3227. doi: 10.1103/PhysRevLett.80.3224. [DOI] [Google Scholar]
- Čížek J.. On the correlation problem in atomic and molecular systems. Calculation of wavefunction components in Ursell-type expansion using quantum-field theoretical methods. J. Chem. Phys. 1966;45:4256–4266. doi: 10.1063/1.1727484. [DOI] [Google Scholar]
- Knowles P. J., Hampel C., Werner H.-J.. Coupled cluster theory for high spin, open shell reference wave functions. J. Chem. Phys. 1993;99:5219–5227. doi: 10.1063/1.465990. [DOI] [Google Scholar]
- Knowles P. J., Hampel C., Werner H.-J.. Erratum: “Coupled cluster theory for high spin, open shell reference wave functions” [J. Chem. Phys. 99, 5219 (1993)] J. Chem. Phys. 2000;112:3106–3107. doi: 10.1063/1.480886. [DOI] [Google Scholar]
- Launay J.-M., Le Dourneuf M.. Hyperspherical close-coupling calculation of integral cross sections for the reaction H + H2 → H2 + H. Chem. Phys. Lett. 1989;163:178–188. doi: 10.1016/0009-2614(89)80031-4. [DOI] [Google Scholar]
- Honvault, P. , Launay, J.-M. . Quantum dynamics of insertion reactions. In Theory of Chemical Reaction Dynamics; Springer, 2004; pp 187–215. [Google Scholar]
- Pack R. T., Parker G. A.. Quantum reactive scattering in three dimensions using hyperspherical (APH) coordinates. Theory. J. Chem. Phys. 1987;87:3888. doi: 10.1063/1.452944. [DOI] [Google Scholar]
- Kendrick B. K., Pack R. T., Walker R. B., Hayes E. F.. Hyperspherical surface functions for nonzero total angular momentum. I. Eckart singularities. J. Chem. Phys. 1999;110:6673. doi: 10.1063/1.478574. [DOI] [Google Scholar]
- Seaton M. J.. Quantum Defect Theory. I. General formulation. Proc. Phys. Soc. London. 1966;88:801–814. doi: 10.1088/0370-1328/88/4/302. [DOI] [Google Scholar]
- Seaton M. J.. Quantum defect theory. Rep. Prog. Phys. 1983;46:167–257. doi: 10.1088/0034-4885/46/2/002. [DOI] [Google Scholar]
- Idziaszek Z., Julienne P. S.. Universal Rate Constants for Reactive Collisions of Ultracold Molecules. Phys. Rev. Lett. 2010;104:113202. doi: 10.1103/PhysRevLett.104.113202. [DOI] [PubMed] [Google Scholar]
- Kotochigova S.. Dispersion interactions and reactive collisions of ultracold polar molecules. New J. Phys. 2010;12:073041. doi: 10.1088/1367-2630/12/7/073041. [DOI] [Google Scholar]
- Gao B.. Quantum-defect theory for −1/r 4-type interactions. Phys. Rev. A. 2013;88:022701. doi: 10.1103/PhysRevA.88.022701. [DOI] [Google Scholar]
- Campbell W. C., Groenenboom G. C., Lu H.-I., Tsikata E., Doyle J. M.. Time-domain measurement of spontaneous vibrational decay of magnetically trapped NH. Phys. Rev. Lett. 2008;100:083003. doi: 10.1103/PhysRevLett.100.083003. [DOI] [PubMed] [Google Scholar]
- Knowles P. J., Werner H.-J.. An efficient method for the evaluation of coupling coefficients in configuration interaction calculations. Chem. Phys. Lett. 1988;145:514–522. doi: 10.1016/0009-2614(88)87412-8. [DOI] [Google Scholar]
- Strauss C., Takekoshi T., Lang F., Winkler K., Grimm R., Denschlag J. H., Tiemann E.. Hyperfine, rotational, and vibrational structure of the a 3 Σ u + state of 87Rb2 . Phys. Rev. A. 2010;82:052514. doi: 10.1103/PhysRevA.82.052514. [DOI] [Google Scholar]
- Krükow A., Mohammadi A., Härter A., Denschlag J. H., Pérez-Ríos J., Greene C. H.. Energy scaling of cold atom-atom-ion three-body recombination. Phys. Rev. Lett. 2016;116:193201. doi: 10.1103/PhysRevLett.116.193201. [DOI] [PubMed] [Google Scholar]
- Stevenson I., Singh S., Elkamshishy A., Bigagli N., Yuan W., Zhang S., Greene C. H., Will S.. Three-Body Recombination of Ultracold Microwave-Shielded Polar Molecules. Phys. Rev. Lett. 2024;133:263402. doi: 10.1103/PhysRevLett.133.263402. [DOI] [PubMed] [Google Scholar]
- Beijerinck H.. Rigorous calculation of heating in alkali-metal traps by background gas collisions. Phys. Rev. A. 2000;61:033606. doi: 10.1103/PhysRevA.61.033606. [DOI] [Google Scholar]
- DeMille D., Glenn D. R., Petricka J.. Microwave traps for cold polar molecules. Eur. Phys. J. D. 2004;31:375–384. doi: 10.1140/epjd/e2004-00163-6. [DOI] [Google Scholar]
- Fagnan D. E., Wang J., Zhu C., Djuricanin P., Klappauf B. G., Booth J. L., Madison K. W.. Observation of quantum diffractive collisions using shallow atomic traps. Phys. Rev. A. 2009;80:022712. doi: 10.1103/PhysRevA.80.022712. [DOI] [Google Scholar]
- Van Dongen J., Zhu C., Clement D., Dufour G., Booth J., Madison K.. Trap-depth determination from residual gas collisions. Phys. Rev. A. 2011;84:022708. doi: 10.1103/PhysRevA.84.022708. [DOI] [Google Scholar]
- Meir Z., Sikorsky T., Ben-Shlomi R., Akerman N., Dallal Y., Ozeri R.. Dynamics of a ground-state cooled ion colliding with ultracold atoms. Phys. Rev. Lett. 2016;117:243401. doi: 10.1103/PhysRevLett.117.243401. [DOI] [PubMed] [Google Scholar]
- Booth J. L., Shen P., Krems R. V., Madison K. W.. Universality of quantum diffractive collisions and the quantum pressure standard. New J. Phys. 2019;21:102001. doi: 10.1088/1367-2630/ab452a. [DOI] [Google Scholar]
- Saito R., Haze S., Sasakawa M., Nakai R., Raoult M., Da Silva H. Jr, Dulieu O., Mukaiyama T.. Characterization of charge-exchange collisions between ultracold 6Li atoms and 40Ca+ ions. Phys. Rev. A. 2017;95:032709. doi: 10.1103/PhysRevA.95.032709. [DOI] [Google Scholar]
- Weckesser P., Thielemann F., Wiater D., Wojciechowska A., Karpa L., Jachymski K., Tomza M., Walker T., Schaetz T.. Observation of Feshbach resonances between a single ion and ultracold atoms. Nature. 2021;600:429–433. doi: 10.1038/s41586-021-04112-y. [DOI] [PubMed] [Google Scholar]
- Weckesser P., Thielemann F., Hoenig D., Lambrecht A., Karpa L., Schaetz T.. Trapping, shaping, and isolating of an ion Coulomb crystal via state-selective optical potentials. Phys. Rev. A. 2021;103:013112. doi: 10.1103/PhysRevA.103.013112. [DOI] [Google Scholar]
- Huron B., Malrieu J., Rancurel P.. Iterative perturbation calculations of ground and excited state energies from multiconfigurational zeroth-order wavefunctions. J. Chem. Phys. 1973;58:5745–5759. doi: 10.1063/1.1679199. [DOI] [Google Scholar]
- Aymar M., Dulieu O.. Calculation of accurate permanent dipole moments of the lowest 1,3Σ+ states of heteronuclear alkali dimers using extended basis sets. J. Chem. Phys. 2005;122:204302. doi: 10.1063/1.1903944. [DOI] [PubMed] [Google Scholar]
- Aymar M., Dulieu O.. The electronic structure of the alkaline-earth-atom (Ca, Sr, Ba) hydride molecular ions. J. Phys. B. 2012;45:215103. doi: 10.1088/0953-4075/45/21/215103. [DOI] [Google Scholar]
- Xing X., da Silva H. Jr, Vexiau R., Bouloufa-Maafa N., Willitsch S., Dulieu O.. Ion-loss events in a hybrid trap of cold Rb-Ca+: Photodissociation, blackbody radiation, and nonradiative charge exchange. Phys. Rev. A. 2022;106:062809. doi: 10.1103/PhysRevA.106.062809. [DOI] [Google Scholar]
- Cimiraglia R., Malrieu J.-P., Persico M., Spiegelmann F.. Quasi-diabatic states and dynamical couplings from ab initio CI calculations: A new proposal. J. Phys. B. 1985;18:3073. doi: 10.1088/0022-3700/18/15/014. [DOI] [Google Scholar]
- Angeli C., Persico M.. Quasi-diabatic and adiabatic states and potential energy curves for Na-Cd collisions and excimer formation. Chem. Phys. 1996;204:57–64. doi: 10.1016/0301-0104(95)00436-X. [DOI] [Google Scholar]
- Szczepkowski J., Grochola A., Jastrzebski W., Kowalczyk P., Vexiau R., Bouloufa-Maafa N., Dulieu O.. Study of excited electronic states of the 39KCs molecule correlated with the K (42S) + Cs (52D) asymptote: experiment and theory. J. Quant. Spectrosc. Ra. 2022;291:108330. doi: 10.1016/j.jqsrt.2022.108330. [DOI] [Google Scholar]
- Smith W. W., Makarov O. P., Lin J.. Cold ion-neutral collisions in a hybrid trap. J. Mod. Opt. 2005;52:2253–2260. doi: 10.1080/09500340500275850. [DOI] [Google Scholar]
- Cetina M., Grier A., Campbell J., Chuang I., Vuletić V.. Bright source of cold ions for surface-electrode traps. Phys. Rev. A. 2007;76:041401. doi: 10.1103/PhysRevA.76.041401. [DOI] [Google Scholar]
- Zhang P., Dalgarno A.. Static dipole polarizability of ytterbium. J. Phys. Chem. A. 2007;111:12471–12476. doi: 10.1021/jp0750856. [DOI] [PubMed] [Google Scholar]
- Meir Z., Sikorsky T., Ben-shlomi R., Akerman N., Pinkas M., Dallal Y., Ozeri R.. Experimental apparatus for overlapping a ground-state cooled ion with ultracold atoms. J. Mod. Opt. 2018;65:501–519. doi: 10.1080/09500340.2017.1397217. [DOI] [Google Scholar]
- Zare R. N., Herschbach D. R.. Doppler line shape of atomic fluorescence excited by molecular photodissociation. Proc. IEEE. 1963;51:173–182. doi: 10.1109/PROC.1963.1676. [DOI] [Google Scholar]
- Zare R. N.. Photoejection dynamics. Mol. Photochem. 1972;4:1–37. [Google Scholar]
- Choi S. E., Bernstein R. B.. Theory of oriented symmetric-top molecule beams: Precession, degree of orientation, and photofragmentation of rotationally state-selected molecules. J. Chem. Phys. 1986;85:150–161. doi: 10.1063/1.451821. [DOI] [Google Scholar]
- Zare R. N.. Photofragment angular distributions from oriented symmetric-top precursor molecules. Chem. Phys. Lett. 1989;156:1–6. doi: 10.1016/0009-2614(89)87070-8. [DOI] [Google Scholar]
- Taatjes C. A., Janssen M. H., Stolte S.. Dynamical information in angular distributions of fragments from photolysis of oriented molecules. Chem. Phys. Lett. 1993;203:363–370. doi: 10.1016/0009-2614(93)85582-9. [DOI] [Google Scholar]
- Baugh D. A., Kim D. Y., Cho V. A., Pipes L. C., Petteway J. C., Fuglesang C. D.. Production of a pure, single ro-vibrational quantum-state molecular beam. Chem. Phys. Lett. 1994;219:207–213. doi: 10.1016/0009-2614(94)87046-2. [DOI] [Google Scholar]
- Seideman T.. The analysis of magnetic-state-selected angular distributions: a quantum mechanical form and an asymptotic approximation. Chem. Phys. Lett. 1996;253:279–285. doi: 10.1016/0009-2614(96)00201-1. [DOI] [Google Scholar]
- Bazalgette G., White R., Trénec G., Audouard E., Büchner M., Vigué J.. Photodissociation of ICl molecule oriented by an intense electric field: experiment and theoretical analysis. J. Phys. Chem. A. 1998;102:1098–1105. doi: 10.1021/jp972074b. [DOI] [Google Scholar]
- Beswick J. A., Zare R. N.. On the quantum and quasiclassical angular distributions of photofragments. J. Chem. Phys. 2008;129:164315. doi: 10.1063/1.3000581. [DOI] [PubMed] [Google Scholar]
- McDonald M., McGuyer B., Apfelbeck F., Lee C.-H., Majewska I., Moszynski R., Zelevinsky T.. Photodissociation of ultracold diatomic strontium molecules with quantum state control. Nature. 2016;535:122–126. doi: 10.1038/nature18314. [DOI] [PubMed] [Google Scholar]
- Chandler D. W.. Quantum control of light-induced reactions. Nature. 2016;535:42–44. doi: 10.1038/535042a. [DOI] [PubMed] [Google Scholar]
- Reinaudi G., Osborn C., McDonald M., Kotochigova S., Zelevinsky T.. Optical production of stable ultracold 88Sr2 molecules. Phys. Rev. Lett. 2012;109:115303. doi: 10.1103/PhysRevLett.109.115303. [DOI] [PubMed] [Google Scholar]
- Skomorowski W., Pawłowski F., Koch C. P., Moszynski R.. Rovibrational dynamics of the strontium molecule in the A1Σ u +, c 3Π u , and a 3Σ u + manifold from state-of-the-art ab initio calculations. J. Chem. Phys. 2012;136:194306. doi: 10.1063/1.4713939. [DOI] [PubMed] [Google Scholar]
- Borkowski M., Morzyński P., Ciuryło R., Julienne P. S., Yan M., DeSalvo B. J., Killian T.. Mass scaling and nonadiabatic effects in photoassociation spectroscopy of ultracold strontium atoms. Phys. Rev. A. 2014;90:032713. doi: 10.1103/PhysRevA.90.032713. [DOI] [Google Scholar]
- Holland M., Suominen K.-A., Burnett K.. Cold collisions in a laser field: Quantum Monte Carlo treatment of radiative heating. Phys. Rev. A. 1994;50:1513. doi: 10.1103/PhysRevA.50.1513. [DOI] [PubMed] [Google Scholar]
- Boesten H. J., Verhaar B.. Simple quantum-mechanical picture of cold optical collisions. Phys. Rev. A. 1994;49:4240. doi: 10.1103/PhysRevA.49.4240. [DOI] [PubMed] [Google Scholar]
- Marcassa L., Muniz S., De Queiroz E., Zilio S., Bagnato V., Weiner J., Julienne P., Suominen K.-A.. Optical suppression of photoassociative ionization in a magneto-optical trap. Phys. Rev. Lett. 1994;73:1911. doi: 10.1103/PhysRevLett.73.1911. [DOI] [PubMed] [Google Scholar]
- Band Y., Tuvi I., Suominen K.-A., Burnett K., Julienne P.. Loss from magneto-optical traps in strong laser fields. Phys. Rev. A. 1994;50:R2826. doi: 10.1103/PhysRevA.50.R2826. [DOI] [PubMed] [Google Scholar]
- Suominen K.-A., Holland M. J., Burnett K., Julienne P.. Optical shielding of cold collisions. Phys. Rev. A. 1995;51:1446. doi: 10.1103/PhysRevA.51.1446. [DOI] [PubMed] [Google Scholar]
- Wright M., Pechkis J., Carini J., Gould P.. Probing ultracold collisional dynamics with frequency-chirped pulses. Phys. Rev. A. 2006;74:063402. doi: 10.1103/PhysRevA.74.063402. [DOI] [Google Scholar]
- DeVoe R. G.. Power-law distributions for a trapped ion interacting with a classical buffer gas. Phys. Rev. Lett. 2009;102:063001. doi: 10.1103/PhysRevLett.102.063001. [DOI] [PubMed] [Google Scholar]
- Gallagher A., Pritchard D. E.. Exoergic collisions of cold Na* - Na. Phys. Rev. Lett. 1989;63:957. doi: 10.1103/PhysRevLett.63.957. [DOI] [PubMed] [Google Scholar]
- Sesko D., Walker T., Monroe C., Gallagher A., Wieman C.. Collisional losses from a light-force atom trap. Phys. Rev. Lett. 1989;63:961. doi: 10.1103/PhysRevLett.63.961. [DOI] [PubMed] [Google Scholar]
- Julienne P. S., Vigué J.. Cold collisions of ground-and excited-state alkali-metal atoms. Phys. Rev. A. 1991;44:4464. doi: 10.1103/PhysRevA.44.4464. [DOI] [PubMed] [Google Scholar]
- Band Y. B., Julienne P. S.. Optical-Bloch-equation method for cold-atom collisions: Cs loss from optical traps. Phys. Rev. A. 1992;46:330. doi: 10.1103/PhysRevA.46.330. [DOI] [PubMed] [Google Scholar]
- Boesten H., Verhaar B., Tiesinga E.. Quantum suppression of collisional loss rates in optical traps. Phys. Rev. A. 1993;48:1428. doi: 10.1103/PhysRevA.48.1428. [DOI] [PubMed] [Google Scholar]
- Julienne P. S., Suominen K.-A., Band Y.. Complex-potential model of collisions of laser-cooled atoms. Phys. Rev. A. 1994;49:3890. doi: 10.1103/PhysRevA.49.3890. [DOI] [PubMed] [Google Scholar]
- Sanchez-Villicana V., Gensemer S., Tan K., Kumarakrishnan A., Dinneen T., Süptitz W., Gould P.. Suppression of ultracold ground-state hyperfine-changing collisions with laser light. Phys. Rev. Lett. 1995;74:4619. doi: 10.1103/PhysRevLett.74.4619. [DOI] [PubMed] [Google Scholar]
- Zipkes C., Palzer S., Sias C., Köhl M.. A trapped single ion inside a Bose–Einstein condensate. Nature. 2010;464:388–391. doi: 10.1038/nature08865. [DOI] [PubMed] [Google Scholar]
- Schmid S., Härter A., Denschlag J. H.. Dynamics of a cold trapped ion in a Bose–Einstein condensate. Phys. Rev. Lett. 2010;105:133202. doi: 10.1103/PhysRevLett.105.133202. [DOI] [PubMed] [Google Scholar]
- Cetina M., Grier A. T., Vuletić V.. Micromotion-induced limit to atom-ion sympathetic cooling in Paul traps. Phys. Rev. Lett. 2012;109:253201. doi: 10.1103/PhysRevLett.109.253201. [DOI] [PubMed] [Google Scholar]
- Nguyên L. H., Kalev A., Barrett M. D., Englert B.-G.. Micromotion in trapped atom-ion systems. Phys. Rev. A. 2012;85:052718. doi: 10.1103/PhysRevA.85.052718. [DOI] [Google Scholar]
- Höltkemeier B., Weckesser P., López-Carrera H., Weidemüller M.. Buffer-gas cooling of a single ion in a multipole radio frequency trap beyond the critical mass ratio. Phys. Rev. Lett. 2016;116:233003. doi: 10.1103/PhysRevLett.116.233003. [DOI] [PubMed] [Google Scholar]
- Secker T., Ewald N., Joger J., Fürst H., Feldker T., Gerritsma R.. Trapped ions in Rydberg-dressed atomic gases. Phys. Rev. Lett. 2017;118:263201. doi: 10.1103/PhysRevLett.118.263201. [DOI] [PubMed] [Google Scholar]
- Green M., Wodin J., DeVoe R., Fierlinger P., Flatt B., Gratta G., LePort F., Montero Díez M., Neilson R., O’Sullivan K.. et al. Observation of single collisionally cooled trapped ions in a buffer gas. Phys. Rev. A. 2007;76:023404. doi: 10.1103/PhysRevA.76.023404. [DOI] [Google Scholar]
- Flatt B., Green M., Wodin J., DeVoe R., Fierlinger P., Gratta G., LePort F., Díez M. M., Neilson R., O’Sullivan K.. et al. A linear RFQ ion trap for the Enriched Xenon Observatory. Nucl. Instrum. Methods Phys. Res. A. 2007;578:399–408. doi: 10.1016/j.nima.2007.05.123. [DOI] [Google Scholar]
- Wright M. J., Gensemer S., Vala J., Kosloff R., Gould P.. Control of ultracold collisions with frequency-chirped light. Phys. Rev. Lett. 2005;95:063001. doi: 10.1103/PhysRevLett.95.063001. [DOI] [PubMed] [Google Scholar]
- Wright M., Pechkis J., Carini J., Kallush S., Kosloff R., Gould P.. Coherent control of ultracold collisions with chirped light: Direction matters. Phys. Rev. A. 2007;75:051401. doi: 10.1103/PhysRevA.75.051401. [DOI] [Google Scholar]
- Wight M. J.. Semi-classical calculations of ultracold and cold collisions with frequency-chirped light. Eur. Phys. J. D. 2015;69:1–6. doi: 10.1140/epjd/e2014-50433-7. [DOI] [Google Scholar]
- Moore F., Robinson J., Bharucha C., Sundaram B., Raizen M.. Atom optics realization of the quantum δ-kicked rotor. Phys. Rev. Lett. 1995;75:4598. doi: 10.1103/PhysRevLett.75.4598. [DOI] [PubMed] [Google Scholar]
- Averbukh I. S., Arvieu R.. Angular focusing, squeezing, and rainbow formation in a strongly driven quantum rotor. Phys. Rev. Lett. 2001;87:163601. doi: 10.1103/PhysRevLett.87.163601. [DOI] [PubMed] [Google Scholar]
- Bird, G. A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Oxford University Press: New York, 1994. [Google Scholar]
- Davis K. B., Mewes M. O., Ketterle W.. An analytical model for evaporative cooling of atoms. Appl. Phys. B. 1995;60:155–159. doi: 10.1007/BF01135857. [DOI] [Google Scholar]
- Luiten O., Reynolds M., Walraven J.. Kinetic theory of the evaporative cooling of a trapped gas. Phys. Rev. A. 1996;53:381. doi: 10.1103/PhysRevA.53.381. [DOI] [PubMed] [Google Scholar]
- Holland M., Williams J., Coakley K., Cooper J.. Trajectory simulation of kinetic equations for classical systems. Quantum Semiclass. Opt.: J. Eur. Opt. Soc. B. 1996;8:571. doi: 10.1088/1355-5111/8/3/019. [DOI] [Google Scholar]
- Wu H., Foot C. J.. Direct simulation of evaporative cooling. J. Phys. B. 1996;29:L321. doi: 10.1088/0953-4075/29/8/003. [DOI] [Google Scholar]
- Wu H., Arimondo E., Foot C. J.. Dynamics of evaporative cooling for Bose–Einstein condensation. Phys. Rev. A. 1997;56:560. doi: 10.1103/PhysRevA.56.560. [DOI] [Google Scholar]
- Anderlini M., Courtade E., Cristiani M., Cossart D., Ciampini D., Sias C., Morsch O., Arimondo E.. Sympathetic cooling and collisional properties of a Rb-Cs mixture. Phys. Rev. A. 2005;71:061401. doi: 10.1103/PhysRevA.71.061401. [DOI] [Google Scholar]
- Barletta P., Tennyson J., Barker P.. Direct Monte Carlo simulation of the sympathetic cooling of trapped molecules by ultracold argon atoms. New J. Phys. 2010;12:113002. doi: 10.1088/1367-2630/12/11/113002. [DOI] [Google Scholar]
- Garraway B., Suominen K.-A.. Wave-packet dynamics and quantum beats. Phys. Rev. A. 1998;58:440. doi: 10.1103/PhysRevA.58.440. [DOI] [Google Scholar]
- Allmendinger P., Deiglmayr J., Schullian O., Höveler K., Agner J. A., Schmutz H., Merkt F.. New method to study ion–molecule reactions at low temperatures and application to the reaction. ChemPhysChem. 2016;17:3596–3608. doi: 10.1002/cphc.201600828. [DOI] [PubMed] [Google Scholar]
- Vogt E., Wannier G. H.. Scattering of Ions by Polarization Forces. Phys. Rev. 1954;95:1190–1198. doi: 10.1103/PhysRev.95.1190. [DOI] [Google Scholar]
- Bjorkholm J.. Collision-limited lifetimes of atom traps. Phys. Rev. A. 1988;38:1599. doi: 10.1103/PhysRevA.38.1599. [DOI] [PubMed] [Google Scholar]
- Bali S., O’Hara K., Gehm M., Granade S., Thomas J.. Quantum-diffractive background gas collisions in atom-trap heating and loss. Phys. Rev. A. 1999;60:R29. doi: 10.1103/PhysRevA.60.R29. [DOI] [Google Scholar]
- Arpornthip T., Sackett C., Hughes K.. Vacuum-pressure measurement using a magneto-optical trap. Phys. Rev. A. 2012;85:033420. doi: 10.1103/PhysRevA.85.033420. [DOI] [Google Scholar]
- Shen P., Madison K. W., Booth J. L.. Realization of a universal quantum pressure standard. Metrologia. 2020;57:025015. doi: 10.1088/1681-7575/ab7170. [DOI] [Google Scholar]
- Shen P., Madison K. W., Booth J. L.. Refining the cold atom pressure standard. Metrologia. 2021;58:022101. doi: 10.1088/1681-7575/abe02f. [DOI] [Google Scholar]
- Booth J. L., Madison K. W.. Revising the universality hypothesis for room-temperature collisions. Phys. Rev. A. 2024;110:052802. doi: 10.1103/PhysRevA.110.052802. [DOI] [Google Scholar]
- Eckel S. P., Barker D. S., Fedchak J. A., Scherschligt J., Kłos J., Tiesinga E.. Effect of glancing collisions in the cold-atom vacuum standard. Phys. Rev. A. 2025;111:023317. doi: 10.1103/PhysRevA.111.023317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massey H., Mohr C.. Free paths and transport phenomena gases and the quantum theory of collisions. I. The rigid sphere model. Proc. Roy. Soc. A. 1933;141:434–453. doi: 10.1098/rspa.1933.0128. [DOI] [Google Scholar]
- Kennard, E. H. Kinetic theory of gases; McGraw-Hill: New York, 1938. [Google Scholar]
- Schiff L.. Approximation method for high-energy potential scattering. Phys. Rev. 1956;103:443. doi: 10.1103/PhysRev.103.443. [DOI] [Google Scholar]
- Mason E., Vanderslice J., Raw C.. Quantum Effects in Small-Angle Molecular-Beam Scattering. J. Chem. Phys. 1964;40:2153–2164. doi: 10.1063/1.1725488. [DOI] [Google Scholar]
- Helbing R., Pauly H.. Differentielle Streuquerschnitte bei der Wechselwirkung neutraler Moleküle Messungen der Kleinwinkelstreuung. Z. Phys. 1964;179:16–37. doi: 10.1007/BF01379211. [DOI] [Google Scholar]
- Anderson R. W.. Quantum correction factors for classical small angle scattering by inverse power potentials. J. Chem. Phys. 1974;60:2680–2683. doi: 10.1063/1.1681427. [DOI] [Google Scholar]
- Beijerinck H., van der Kam P., Thijssen W., Verster N.. Semiclassical description of the small angle differential cross section for elastic atom-atom scattering. Chem. Phys. 1980;45:225–247. doi: 10.1016/0301-0104(80)85070-1. [DOI] [Google Scholar]
- Cornell, E. A. , Ensher, J. R. , Wieman, C. E. . Experiments in dilute atomic Bose–Einstein condensation. In Bose–Einstein Condensation in Atomic Gases; IOS Press, 1999; pp 15–66. [Google Scholar]
- Prentiss M., Cable A., Bjorkholm J., Chu S., Raab E., Pritchard D.. Atomic-density-dependent losses in an optical trap. Opt. Lett. 1988;13:452–454. doi: 10.1364/OL.13.000452. [DOI] [PubMed] [Google Scholar]
- Migdall A. L., Prodan J. V., Phillips W. D., Bergeman T. H., Metcalf H. J.. First observation of magnetically trapped neutral atoms. Phys. Rev. Lett. 1985;54:2596. doi: 10.1103/PhysRevLett.54.2596. [DOI] [PubMed] [Google Scholar]
- Chu S., Bjorkholm J., Ashkin A., Cable A.. Experimental observation of optically trapped atoms. Phys. Rev. Lett. 1986;57:314. doi: 10.1103/PhysRevLett.57.314. [DOI] [PubMed] [Google Scholar]
- Gensemer S., Sanchez-Villicana V., Tan K., Grove T., Gould P.. Trap-loss collisions of 85Rb and 87Rb: Dependence on trap parameters. Phys. Rev. A. 1997;56:4055. doi: 10.1103/PhysRevA.56.4055. [DOI] [Google Scholar]
- Yuan J.-P., Ji Z.-H., Zhao Y.-T., Chang X.-F., Xiao L.-T., Jia S.-T.. Simple, reliable, and nondestructive method for the measurement of vacuum pressure without specialized equipment. Appl. Opt. 2013;52:6195–6200. doi: 10.1364/AO.52.006195. [DOI] [PubMed] [Google Scholar]
- Booth, J. L. , Fagnan, D. E. , Klappauf, B. G. , Madison, K. W. , Wang, J. . Method and device for accurately measuring the incident flux of ambient particles in a high or ultra-high vacuum environment. US Patent 8,803,072, 2014.
- Makhalov V., Martiyanov K., Turlapov A.. Primary vacuometer based on an ultracold gas in a shallow optical dipole trap. Metrologia. 2016;53:1287. doi: 10.1088/0026-1394/53/6/1287. [DOI] [Google Scholar]
- Stewart R. A., Shen P., Booth J. L., Madison K. W.. Measurement of Rb-Rb van der Waals coefficient via quantum diffractive universality. Phys. Rev. A. 2022;106:052812. doi: 10.1103/PhysRevA.106.052812. [DOI] [Google Scholar]
- Shen P., Frieling E., Herperger K. R., Uhland D., Stewart R. A., Deshmukh A., Krems R. V., Booth J. L., Madison K. W.. Cross-calibration of atomic pressure sensors and deviation from quantum diffractive collision universality for light particles. New J. Phys. 2023;25:053018. doi: 10.1088/1367-2630/acd46e. [DOI] [Google Scholar]
- Barker, D. S. , Fedchak, J. A. , Kłos, J. , Scherschligt, J. , Sheikh, A. A. , Tiesinga, E. , Eckel, S. P. . Accurate measurement of the loss rate of cold atoms due to background gas collisions for the quantum-based cold atom vacuum standard. AVS Quantum Sci. 2023, 5. 10.1116/5.0147686 [DOI] [Google Scholar]
- Guo X., Madison K. W., Booth J. L., Krems R. V.. Boundaries of universality of thermal collisions for atom-atom scattering. Phys. Rev. A. 2024;110:063317. doi: 10.1103/PhysRevA.110.063317. [DOI] [Google Scholar]
- Kłos J., Tiesinga E.. Elastic and glancing-angle rate coefficients for heating of ultracold Li and Rb atoms by collisions with room-temperature noble gases, H2, and N2 . J. Chem. Phys. 2023;158:014308. doi: 10.1063/5.0124062. [DOI] [PubMed] [Google Scholar]
- Child, M. S. Molecular Collision Theory; Academic Press: New York, 1974. [Google Scholar]
- Makrides C., Barker D. S., Fedchak J. A., Scherschligt J., Eckel S., Tiesinga E.. Elastic rate coefficients for Li+H2 collisions in the calibration of a cold-atom vacuum standard. Phys. Rev. A. 2019;99:042704. doi: 10.1103/PhysRevA.99.042704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makrides C., Barker D. S., Fedchak J. A., Scherschligt J., Eckel S., Tiesinga E.. Erratum: Elastic rate coefficients for Li+H2 collisions in the calibration of a cold-atom vacuum standard [Phys. Rev. A 99, 042704 (2019)] Phys. Rev. A. 2022;105:039903. doi: 10.1103/PhysRevA.105.039903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makrides C., Barker D. S., Fedchak J. A., Scherschligt J., Eckel S., Tiesinga E.. Collisions of room-temperature helium with ultracold lithium and the van der Waals bound state of HeLi. Phys. Rev. A. 2020;101:012702. doi: 10.1103/PhysRevA.101.012702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makrides C., Barker D. S., Fedchak J. A., Scherschligt J., Eckel S., Tiesinga E.. Erratum: Collisions of room-temperature helium with ultracold lithium and the van der Waals bound state of HeLi [Phys. Rev. A 101, 012702 (2020)] Phys. Rev. A. 2022;105:029902. doi: 10.1103/PhysRevA.105.029902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medvedev A. A., Meshkov V. V., Stolyarov A. V., Heaven M. C.. Ab initio interatomic potentials and transport properties of alkali metal (M = Rb and Cs)-rare gas (Rg = He, Ne, Ar, Kr, and Xe) media. Phys. Chem. Chem. Phys. 2018;20:25974–25982. doi: 10.1039/C8CP04397C. [DOI] [PubMed] [Google Scholar]
- Henson A. B., Gersten S., Shagam Y., Narevicius J., Narevicius E.. Observation of Resonances in Penning Ionization Reactions at Sub-Kelvin Temperatures in Merged Beams. Science. 2012;338:234–238. doi: 10.1126/science.1229141. [DOI] [PubMed] [Google Scholar]
- Shagam Y., Narevicius E.. Sub-Kelvin collision temperatures in merged neutral beams by correlation in phase-space. J. Phys. Chem. C. 2013;117:22454–22461. doi: 10.1021/jp4045868. [DOI] [Google Scholar]
- Lavert-Ofir E., Shagam Y., Henson A. B., Gersten S., Kłos J., Zuchowski P. S., Narevicius J., Narevicius E.. Observation of the isotope effect in sub-kelvin reactions. Nat. Chem. 2014;6:332–335. doi: 10.1038/nchem.1857. [DOI] [PubMed] [Google Scholar]
- Bishop D. M., Pipin J.. Dipole, quadrupole, octupole, and dipole-octupole polarizabilities at real and imaginary frequencies for H, He, and H2 and the dispersion-energy coefficients for interactions between them. Int. J. Quantum Chem. 1993;45:349–361. doi: 10.1002/qua.560450403. [DOI] [Google Scholar]
- Werner H.-J., Knowles P. J., Knizia G., Manby F. R., Schütz M.. Molpro: a general-purpose quantum chemistry program package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012;2:242–253. doi: 10.1002/wcms.82. [DOI] [Google Scholar]
- Aidas K., Angeli C., Bak K. L., Bakken V., Bast R., Boman L., Christiansen O., Cimiraglia R., Coriani S., Dahle P.. et al. The Dalton quantum chemistry program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014;4:269–284. doi: 10.1002/wcms.1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balakrishnan N., Dalgarno A.. Chemistry at ultracold temperatures. Chem. Phys. Lett. 2001;341:652–656. doi: 10.1016/S0009-2614(01)00515-2. [DOI] [Google Scholar]
- Bodo E., Gianturco F. A., Dalgarno A.. F+D2 reaction at ultracold temperatures. J. Chem. Phys. 2002;116:9222–9227. doi: 10.1063/1.1472515. [DOI] [Google Scholar]
- Friedrich H., Jacoby G., Meister C. G.. Quantum reflection by Casimir-van der Waals potential tails. Phys. Rev. A. 2002;65:032902. doi: 10.1103/PhysRevA.65.032902. [DOI] [Google Scholar]
- Côté R., Segev B.. Quantum reflection engineering: The bichromatic evanescent-wave mirror. Phys. Rev. A. 2003;67:041604. doi: 10.1103/PhysRevA.67.041604. [DOI] [Google Scholar]
- Friedrich H., Jurisch A.. Quantum Reflection for Attractive Potential Tails. Phys. Rev. Lett. 2004;92:103202. doi: 10.1103/PhysRevLett.92.103202. [DOI] [PubMed] [Google Scholar]
- Crubellier A., Luc-Koenig E.. Threshold effects in the photoassociation of cold atoms: R –6 model in the Milne formalism. J. Phys. B. 2006;39:1417–1446. doi: 10.1088/0953-4075/39/6/013. [DOI] [Google Scholar]
- Bodo E., Gianturco F. A.. Collisional quenching of molecular ro-vibrational energy by He buffer loading at ultralow energies. Int. Rev. Phys. Chem. 2006;25:313–351. doi: 10.1080/01442350600772928. [DOI] [Google Scholar]
- González-Sánchez L., Marinetti F., Bodo E., Gianturco F. A.. OH–(X1Σ+) collisions with 4He(1S) at vanishing energies: a quantum analysis of rotational quenching efficiency. J. Phys. B. 2006;39:S1203–S1213. doi: 10.1088/0953-4075/39/19/S27. [DOI] [Google Scholar]
- Bovino S., Bodo E., Gianturco F. A.. Collisional quenching at ultralow energies: Controlling efficiency with internal state selection. J. Chem. Phys. 2007;127:224303. doi: 10.1063/1.2800658. [DOI] [PubMed] [Google Scholar]
- Krems R. V.. Cold controlled chemistry. Phys. Chem. Chem. Phys. 2008;10:4079–4092. doi: 10.1039/b802322k. [DOI] [PubMed] [Google Scholar]
- Saeidian S., Melezhik V. S., Schmelcher P.. Multichannel atomic scattering and confinement-induced resonances in waveguides. Phys. Rev. A. 2008;77:042721. doi: 10.1103/PhysRevA.77.042721. [DOI] [Google Scholar]
- Jachymski K., Krych M., Julienne P. S., Idziaszek Z.. Quantum-defect model of a reactive collision at finite temperature. Phys. Rev. A. 2014;90:042705. doi: 10.1103/PhysRevA.90.042705. [DOI] [Google Scholar]
- Cui J., Li Z., Krems R. V.. Collision lifetimes of polyatomic molecules at low temperatures: Benzene-benzene vs benzene-rare gas atom collisions. J. Chem. Phys. 2014;141:164315. doi: 10.1063/1.4898796. [DOI] [PubMed] [Google Scholar]
- Pires R., Repp M., Ulmanis J., Kuhnle E. D., Weidemüller M., Tiecke T. G., Greene C. H., Ruzic B. P., Bohn J. L., Tiemann E.. Analyzing Feshbach resonances: A 6Li -133Cs case study. Phys. Rev. A. 2014;90:012710. doi: 10.1103/PhysRevA.90.012710. [DOI] [Google Scholar]
- Jankunas J., Bertsche B., Jachymski K., Hapka M., Osterwalder A.. Dynamics of gas phase Ne*+NH3 and Ne*+ ND3 Penning ionisation at low temperatures. J. Chem. Phys. 2014;140:244302. doi: 10.1063/1.4883517. [DOI] [PubMed] [Google Scholar]
- Dufour G., Guérout R., Lambrecht A., Reynaud S.. Liouville transformations and quantum reflection. J. Phys. B. 2015;48:155002. doi: 10.1088/0953-4075/48/15/155002. [DOI] [Google Scholar]
- Lepers M., Quéméner G., Luc-Koenig E., Dulieu O.. Four-body long-range interactions between ultracold weakly-bound diatomic molecules. J. Phys. B. 2016;49:014004. doi: 10.1088/0953-4075/49/1/014004. [DOI] [Google Scholar]
- Dulieu O., Ayouz M., Raoult M., Robert J., Kokoouline V.. Could the H3-ion exist in interstellar medium? Computational Methods in Sciences and Engineering 2010 (ICCMSE-2010) 2015;1642:366–369. [Google Scholar]
- Tscherbul T. V., Buchachenko A. A.. Adiabatic channel capture theory applied to cold atom-molecule reactions: Li + CaH → LiH + Ca at 1K. New J. Phys. 2015;17:035010. doi: 10.1088/1367-2630/17/3/035010. [DOI] [Google Scholar]
- Burdick N. Q., Baumann K., Tang Y., Lu M., Lev B. L.. Fermionic suppression of dipolar relaxation. Phys. Rev. Lett. 2015;114:023201. doi: 10.1103/PhysRevLett.114.023201. [DOI] [PubMed] [Google Scholar]
- Frye M. D., Julienne P. S., Hutson J. M.. Cold atomic and molecular collisions: approaching the universal loss regime. New J. Phys. 2015;17:045019. doi: 10.1088/1367-2630/17/4/045019. [DOI] [Google Scholar]
- Wang Y., Julienne P., Greene C. H.. Few-body physics of ultracold atoms and molecules with long-range interactions. Annu. Rev. Cold Atoms Mol. 2015;3:77–134. doi: 10.1142/9789814667746_0002. [DOI] [Google Scholar]
- Zhao B. S., Zhang W., Schöllkopf W.. Universal diffraction of atoms and molecules from a quantum reflection grating. Sci. Adv. 2016;2:e1500901. doi: 10.1126/sciadv.1500901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prepelita O.. Spontaneous decay in cold dense atomic systems: caloric effect and spectrum of emitted light. Can. J. Phys. 2016;94:1–12. doi: 10.1139/cjp-2016-0098. [DOI] [Google Scholar]
- Zhang W., Lee J. H., Kim H. A., Jin B. G., Kim B. J., Kim L. Y., Zhao B. S., Schöllkopf W.. Universal Diffraction of Atomic and Molecular Matter-Waves: A Comparison of He and D2 Quantum Reflected from a Grating. ChemPhysChem. 2016;17:3670–3676. doi: 10.1002/cphc.201600965. [DOI] [PubMed] [Google Scholar]
- Flores A., Vassen W., Knoop S.. Quantum-state-controlled Penning-ionization reactions between ultracold alkali-metal and metastable helium atoms. Phys. Rev. A. 2016;94:050701. doi: 10.1103/PhysRevA.94.050701. [DOI] [Google Scholar]
- Fabrikant I. I., Kadyrov A. S., Bray I., Charlton M.. Low-energy l-mixing collisions of excited positronium with protons and antiprotons. J. Phys. B. 2017;50:134001. doi: 10.1088/1361-6455/aa743c. [DOI] [Google Scholar]
- Nassar, A. B. , Miret-Artés, S. , Nassar, A. B. , Miret-Artés, S. . Bohmian Stochastic Trajectories; Springer, 2017; pp 125–180. [Google Scholar]
- Friedrich, H. Special Topics; Springer, 2017; pp 403–560. [Google Scholar]
- He P., Tengdin P. M., Anderson D. Z., Rey A. M., Holland M.. Sub-Doppler laser cooling using electromagnetically induced transparency. Phys. Rev. A. 2017;95:053403. doi: 10.1103/PhysRevA.95.053403. [DOI] [Google Scholar]
- Kadyrov A. S., Bray I., Charlton M., Fabrikant I. I.. Quantum suppression of anti hydrogen formation in positronium-antiproton scattering. Nat. Commun. 2017;8:1544. doi: 10.1038/s41467-017-01721-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scribano Y., Parlant G., Poirier B.. Communication: Adiabatic quantum trajectory capture for cold and ultra-cold chemical reactions. J. Chem. Phys. 2018;149:021101. doi: 10.1063/1.5041091. [DOI] [PubMed] [Google Scholar]
- Kadyrov A. S., Rawlins C. M., Charlton M., Fabrikant I. I., Bray I.. Antihydrogen formation in low-energy antiproton collisions with excited-state positronium atoms. Hyperfine Interact. 2018;239:42. doi: 10.1007/s10751-018-1519-x. [DOI] [Google Scholar]
- Cop C., Walser R.. Two-body loss rates for reactive collisions of cold atoms. Phys. Rev. A. 2018;97:012704. doi: 10.1103/PhysRevA.97.012704. [DOI] [Google Scholar]
- McGrew W., Zhang X., Fasano R., Schäffer S., Beloy K., Nicolodi D., Brown R., Hinkley N., Milani G., Schioppo M.. et al. Atomic clock performance enabling geodesy below the centimetre level. Nature. 2018;564:87–90. doi: 10.1038/s41586-018-0738-2. [DOI] [PubMed] [Google Scholar]
- Cocks D. G., Whittingham I. B., Peach G.. Ultracold homonuclear and heteronuclear collisions in metastable helium. Phys. Rev. A. 2019;99:062712. doi: 10.1103/PhysRevA.99.062712. [DOI] [Google Scholar]
- Lee J. H., Kim L. Y., Kim Y.-T., Lee C. Y., Schöllkopf W., Zhao B. S.. Matter-wave diffraction from a periodic array of half planes. Phys. Rev. Lett. 2019;122:040401. doi: 10.1103/PhysRevLett.122.040401. [DOI] [PubMed] [Google Scholar]
- Bai Y.-P., Li J.-L., Wang G.-R., Cong S.-L.. Model for investigating quantum reflection and quantum coherence in ultracold molecular collisions. Phys. Rev. A. 2019;100:012705. doi: 10.1103/PhysRevA.100.012705. [DOI] [Google Scholar]
- Puri P., Mills M., Simbotin I., Montgomery J. A. Jr, Côté R., Schneider C., Suits A. G., Hudson E. R.. Reaction blockading in a reaction between an excited atom and a charged molecule at low collision energy. Nat. Chem. 2019;11:615–621. doi: 10.1038/s41557-019-0264-3. [DOI] [PubMed] [Google Scholar]
- Simbotin I., Shu D., Côté R.. Phase-amplitude formalism for ultranarrow shape resonances. Phys. Rev. A. 2019;99:022709. doi: 10.1103/PhysRevA.99.022709. [DOI] [Google Scholar]
- Mills M., Puri P., Li M., Schowalter S. J., Dunning A., Schneider C., Kotochigova S., Hudson E. R.. Engineering excited-state interactions at ultracold temperatures. Phys. Rev. Lett. 2019;122:233401. doi: 10.1103/PhysRevLett.122.233401. [DOI] [PubMed] [Google Scholar]
- Szmytkowski R.. Analytical calculations of scattering lengths for a class of long-range potentials of interest for atomic physics. J. Math. Phys. 2020;61:012103. doi: 10.1063/1.5140726. [DOI] [Google Scholar]
- Schwarzer M., Toennies J. P.. An accurate semiempirical potential energy curve for the a 3Σ+-state of KRb. J. Chem. Phys. 2020;153:114303. doi: 10.1063/5.0019223. [DOI] [PubMed] [Google Scholar]
- Yang D., Huang J., Hu X., Xie D., Guo H.. Statistical quantum mechanical approach to diatom-diatom capture dynamics and application to ultracold KRb+KRb reaction. J. Chem. Phys. 2020;152:241103. doi: 10.1063/5.0014805. [DOI] [PubMed] [Google Scholar]
- Hu Q., Xiao H., Su J., Sun R., Zhang Y.. Elastic Scattering Properties of Ultracold Potassium Atoms in the Triplet State. J. Low Temp. Phys. 2020;198:18–25. doi: 10.1007/s10909-019-02241-3. [DOI] [Google Scholar]
- Frye M. D., Cornish S. L., Hutson J. M.. Prospects of forming high-spin polar molecules from ultracold atoms. Phys. Rev. X. 2020;10:041005. doi: 10.1103/PhysRevX.10.041005. [DOI] [Google Scholar]
- Sardar, D. , Rakshit, A. , Naskar, S. , Deb, B. . Calculation of d-wave Feshbach resonance in 87Rb -85Rb cold collisions by a multichannel computational method. arXiv preprint arXiv:2004.09091 2020, 10.48550/arXiv.2004.09091. [DOI] [Google Scholar]
- Thomas K., Ross J., Henson B., Shin D., Baldwin K., Hodgman S., Truscott A.. Direct Measurement of the Forbidden 23 S 1 → 33 S 1 Atomic Transition in Helium. Phys. Rev. Lett. 2020;125:013002. doi: 10.1103/PhysRevLett.125.013002. [DOI] [PubMed] [Google Scholar]
- Croft J. F., Bohn J. L., Quéméner G.. Unified model of ultracold molecular collisions. Phys. Rev. A. 2020;102:033306. doi: 10.1103/PhysRevA.102.033306. [DOI] [Google Scholar]
- Frye M. D., Hutson J. M.. Complexes formed in collisions between ultracold alkali-metal diatomic molecules and atoms. New J. Phys. 2021;23:125008. doi: 10.1088/1367-2630/ac3ff8. [DOI] [Google Scholar]
- Ahmed-Braun D. J., Jackson K. G., Smale S., Dale C. J., Olsen B. A., Kokkelmans S. J., Julienne P. S., Thywissen J. H.. Probing open-and closed-channel p-wave resonances. Phys. Rev. Res. 2021;3:033269. doi: 10.1103/PhysRevResearch.3.033269. [DOI] [Google Scholar]
- Jurgilas S., Chakraborty A., Rich C., Caldwell L., Williams H., Fitch N., Sauer B., Frye M. D., Hutson J. M., Tarbutt M.. Collisions between ultracold molecules and atoms in a magnetic trap. Phys. Rev. Lett. 2021;126:153401. doi: 10.1103/PhysRevLett.126.153401. [DOI] [PubMed] [Google Scholar]
- Kao W., Li K.-Y., Lin K.-Y., Gopalakrishnan S., Lev B. L.. Topological pumping of a 1D dipolar gas into strongly correlated prethermal states. Science. 2021;371:296–300. doi: 10.1126/science.abb4928. [DOI] [PubMed] [Google Scholar]
- Cikojević V., Poli E., Ancilotto F., Vranješ-Markić L., Boronat J.. Dilute quantum liquid in a K-Rb Bose mixture. Phys. Rev. A. 2021;104:033319. doi: 10.1103/PhysRevA.104.033319. [DOI] [Google Scholar]
- Augustovičová L. D., Špirko V.. Relating Binding Energy and Scattering Length of Weakly Bound Dimers of Strontium. Ann. Phys. 2021;533:2000588. doi: 10.1002/andp.202000588. [DOI] [Google Scholar]
- Visentin G., Buchachenko A. A., Tecmer P.. Reexamination of the ground-state Born-Oppenheimer Yb2 potential. Phys. Rev. A. 2021;104:052807. doi: 10.1103/PhysRevA.104.052807. [DOI] [Google Scholar]
- Schwarzer M., Toennies J. P.. Accurate semiempirical potential energy curves for the a 3Σ+-state of NaCs, KCs, and RbCs. J. Chem. Phys. 2021;154:154304. doi: 10.1063/5.0046194. [DOI] [PubMed] [Google Scholar]
- Soley M. B., Avanaki K. N., Heller E. J.. Reducing anomalous reflection from complex absorbing potentials: A semiclassical approach. Phys. Rev. A. 2021;103:L041301. doi: 10.1103/PhysRevA.103.L041301. [DOI] [Google Scholar]
- Kim L. Y., Lee J. H., Kim Y.-T., Park S., Lee C. Y., Schöllkopf W., Zhao B. S.. Experimental test of Babinet’s principle in matter-wave diffraction. Phys. Chem. Chem. Phys. 2021;23:8030–8036. doi: 10.1039/D0CP05694D. [DOI] [PubMed] [Google Scholar]
- Schöllkopf, W. Grating Diffraction of Molecular Beams: Present Day Implementations of Otto Stern’s Concept. In Molecular Beams in Physics and Chemistry: From Otto Stern’s Pioneering Exploits to Present-Day Feats; Springer International Publishing: Cham, 2021; pp 575–593. [Google Scholar]
- Charlton M., Ambalampitiya H., Fabrikant I., Fursa D., Kadyrov A., Bray I.. Collisions of antiprotons with excited positronium atoms. Phys. Rev. A. 2021;104:L060803. doi: 10.1103/PhysRevA.104.L060803. [DOI] [Google Scholar]
- Liu Y., Luo L.. Molecular collisions: From near-cold to ultra-cold. Front. Phys. 2021;16:42300. doi: 10.1007/s11467-020-1037-6. [DOI] [Google Scholar]
- Yamaguchi T., Akamatsu D., Kanamoto R.. Low-energy scattering of ultracold atoms by a dielectric nanosphere. Phys. Rev. Res. 2021;3:043214. doi: 10.1103/PhysRevResearch.3.043214. [DOI] [Google Scholar]
- Ciamei A., Finelli S., Trenkwalder A., Inguscio M., Simoni A., Zaccanti M.. Exploring ultracold collisions in 6Li -53Cr Fermi mixtures: Feshbach resonances and scattering properties of a novel alkali-transition metal system. Phys. Rev. Lett. 2022;129:093402. doi: 10.1103/PhysRevLett.129.093402. [DOI] [PubMed] [Google Scholar]
- Brookes S. G., Hutson J. M.. Interaction potential for NaCs for ultracold scattering and spectroscopy. J. Phys. Chem. A. 2022;126:3987–4001. doi: 10.1021/acs.jpca.2c01810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishikawa K.. Noble-gas atoms characterized by hyperfine frequency shift of lithium atom. J. Chem. Phys. 2022;156:144301. doi: 10.1063/5.0085859. [DOI] [PubMed] [Google Scholar]
- Kim L. Y., Park S., Lee C. Y., Schöllkopf W., Zhao B. S.. Enhanced elastic scattering of He2 and He3 from solids by multiple-edge diffraction. Phys. Chem. Chem. Phys. 2022;24:21593–21600. doi: 10.1039/D2CP02641D. [DOI] [PubMed] [Google Scholar]
- Son H., Park J. J., Lu Y.-K., Jamison A. O., Karman T., Ketterle W.. Control of reactive collisions by quantum interference. Science. 2022;375:1006–1010. doi: 10.1126/science.abl7257. [DOI] [PubMed] [Google Scholar]
- Mukherjee B., Frye M. D., Hutson J. M.. Feshbach resonances and molecule formation in ultracold mixtures of Rb and Yb (3P) atoms. Phys. Rev. A. 2022;105:023306. doi: 10.1103/PhysRevA.105.023306. [DOI] [Google Scholar]
- Guo Z., Jia F., Zhu B., Li L., Hutson J. M., Wang D.. Improved characterization of Feshbach resonances and interaction potentials between 23Na and 87Rb atoms. Phys. Rev. A. 2022;105:023313. doi: 10.1103/PhysRevA.105.023313. [DOI] [Google Scholar]
- Sheng X., Li M., Tang K.. An accurate potential model for the a 3Σ u + state of the lithium dimer. Phys. Chem. Chem. Phys. 2022;24:13325–13334. doi: 10.1039/D2CP01490D. [DOI] [PubMed] [Google Scholar]
- Katz O., Pinkas M., Akerman N., Ozeri R.. Quantum suppression of cold reactions far from the quantum regime. Nat. Phys. 2022;18:533. doi: 10.1038/s41567-022-01517-y. [DOI] [Google Scholar]
- Margulis B., Paliwal P., Skomorowski W., Pawlak M., Zuchowski P. S., Narevicius E.. Observation of the p-wave shape resonance in atom-molecule collisions. Phys. Rev. Res. 2022;4:043042. doi: 10.1103/PhysRevResearch.4.043042. [DOI] [Google Scholar]
- Ajaleen A. A. A., Sandouqa A. S., Ghassib H. B.. The transition from the classical to the quantum regime for rubidium-87 (87Rb) vapor in terms of the second virial coefficient and the scattering length. Can. J. Phys. 2022;100:334–343. doi: 10.1139/cjp-2021-0335. [DOI] [Google Scholar]
- Patscheider A., Chomaz L., Natale G., Petter D., Mark M. J., Baier S., Yang B., Wang R., Bohn J. L., Ferlaino F.. Determination of the scattering length of erbium atoms. Phys. Rev. A. 2022;105:063307. doi: 10.1103/PhysRevA.105.063307. [DOI] [Google Scholar]
- Soley M. B., Bender C. M., Stone A. D.. Experimentally realizable PT phase transitions in reflectionless quantum scattering. Phys. Rev. Lett. 2023;130:250404. doi: 10.1103/PhysRevLett.130.250404. [DOI] [PubMed] [Google Scholar]
- Ambalampitiya H., Stallbaumer J., Fabrikant I. I., Kalinkin I., Fursa D., Kadyrov A., Bray I.. Near-threshold collisional dynamics in the e – e + p system. Phys. Rev. A. 2023;108:032808. doi: 10.1103/PhysRevA.108.032808. [DOI] [Google Scholar]
- Harris, A. Controlling Atom-Surface Scattering with Laser Assisted Quantum Reflection. arXiv preprint arXiv:2311.15357 2023, 10.48550/arXiv.2311.15357. [DOI] [Google Scholar]
- Etrych J., Martirosyan G., Cao A., Glidden J. A., Dogra L. H., Hutson J. M., Hadzibabic Z., Eigen C.. Pinpointing Feshbach resonances and testing Efimov universalities in 39K. Phys. Rev. Res. 2023;5:013174. doi: 10.1103/PhysRevResearch.5.013174. [DOI] [Google Scholar]
- Mukherjee B., Frye M. D., Hutson J. M.. Magnetic Feshbach resonances between atoms in 2S and 3P0 states: Mechanisms and dependence on atomic properties. Phys. Rev. Res. 2023;5:013102. doi: 10.1103/PhysRevResearch.5.013102. [DOI] [Google Scholar]
- Kiefer Y., Hachmann M., Hemmerich A.. Ultracold Feshbach molecules in an orbital optical lattice. Nat. Phys. 2023;19:794–799. doi: 10.1038/s41567-023-01994-9. [DOI] [Google Scholar]
- Bird R. C., Tarbutt M. R., Hutson J. M.. Tunable Feshbach resonances in collisions of ultracold molecules in 2Σ states with alkali-metal atoms. Physical Review Research. 2023;5:023184. doi: 10.1103/PhysRevResearch.5.023184. [DOI] [Google Scholar]
- Borkowski M.. Analytic approximations to the strengths of near-threshold optical Feshbach resonances. Phys. Rev. A. 2023;107:063101. doi: 10.1103/PhysRevA.107.063101. [DOI] [Google Scholar]
- Zuchowski, P. S. , Madajczyk, K. . Potential energy surface of Li-O2 system for cold collisions. In Adv. Quantum Chem.; Elsevier, 2023; Vol. 87; pp 209–229. [Google Scholar]
- Tempest K.-M., Jonsell S.. Multichannel hyperspherical model for Efimov physics with van der Waals interactions controlled by a Feshbach resonance. Phys. Rev. A. 2023;107:053319. doi: 10.1103/PhysRevA.107.053319. [DOI] [Google Scholar]
- Lara M., Jambrina P., Aoiz F.. Universal behavior in complex-mediated reactions: Dynamics of S(1 D) + o - D2 → D + SD at low collision energies. J. Chem. Phys. 2023;158:184303. doi: 10.1063/5.0147182. [DOI] [PubMed] [Google Scholar]
- Rost, J.-M. Classical, Quantal and Semiclassical Propagators and Applications to Elastic Scattering. In Springer Handbook of Atomic, Molecular, and Optical Physics; Springer, 2023; pp 685–711. [Google Scholar]
- Frye M. D., Hutson J. M.. Long-range states and Feshbach resonances in collisions between ultracold alkali-metal diatomic molecules and atoms. Phys. Rev. Res. 2023;5:023001. doi: 10.1103/PhysRevResearch.5.023001. [DOI] [Google Scholar]
- Oi K., Naidon P., Endo S.. Universality of Efimov states in highly mass-imbalanced cold-atom mixtures with van der Waals and dipole interactions. Phys. Rev. A. 2024;110:033305. doi: 10.1103/PhysRevA.110.033305. [DOI] [Google Scholar]
- Kilianski R., Bennett R.. Designer quantum reflection from a micropore. Phys. Rev. A. 2024;109:032812. doi: 10.1103/PhysRevA.109.032812. [DOI] [Google Scholar]
- Modak S., Das P., Mishra C., Panigrahi P. K.. Chemical oscillation in ultracold chemistry. Europhys. Lett. 2024;145:32003. doi: 10.1209/0295-5075/ad259e. [DOI] [Google Scholar]
- Barshilia, L. , Sk, R. , Panigrahi, P. K. , Khare, A. . Neutral-atom qubits in atom-molecular BEC. arXiv preprint arXiv:2406.01177 2024, 10.48550/arXiv.2406.01177. [DOI] [Google Scholar]
- Barshilia, L. , Sk, R. , Panigrahi, P. K. , Khare, A. . Quantum droplets and Schrödinger’s cat states in atomic-molecular Bose–Einstein condensates. arXiv preprint arXiv:2411.16529 2024, 10.48550/arXiv.2411.16529. [DOI] [Google Scholar]
- Chowdhury S., Perez-Ríos J.. Ion solvation in atomic baths: from snowballs to polarons. Nat. Sci. 2024;4:e20240006. doi: 10.1002/ntls.20240006. [DOI] [Google Scholar]
- Johansen C. H., Frank B., Lang J.. Spectral functions of the strongly interacting three-dimensional Fermi gas. Phys. Rev. A. 2024;109:023324. doi: 10.1103/PhysRevA.109.023324. [DOI] [Google Scholar]
- He J., Pasquiou B., Escudero R. G., Zhou S., Borkowski M., Schreck F.. Coherent three-photon excitation of the strontium clock transition. Phys. Rev. Res. 2025;7:L012050. doi: 10.1103/PhysRevResearch.7.L012050. [DOI] [Google Scholar]
- Frye M. D., Zuchowski P. S., Tomza M.. Spin-spin interaction and magnetic Feshbach resonances in collisions of high-spin atoms with closed-shell atoms. Phys. Rev. Res. 2024;6:023254. doi: 10.1103/PhysRevResearch.6.023254. [DOI] [Google Scholar]
- Bohn J. L., Wang R. R.. Probability distributions of atomic scattering lengths. Can. J. Phys. 2025;103:81–88. doi: 10.1139/cjp-2023-0263. [DOI] [Google Scholar]
- Mukherjee B., Hutson J. M., Hazzard K. R.. SU(N) magnetism with ultracold molecules. New J. Phys. 2025;27:013013. doi: 10.1088/1367-2630/ad89f2. [DOI] [Google Scholar]
- Friedrich H., Trost J.. Working with WKB waves far from the semiclassical limit. Phys. Rep. 2004;397:359–449. doi: 10.1016/j.physrep.2004.04.001. [DOI] [Google Scholar]
- Friedrich H., Trost J.. Corrigendum to “Working with WKB waves far from the semiclassical limit” [Phys. Rep. 397 (2004) 359–449] Phys. Rep. 2007;451:234–235. doi: 10.1016/j.physrep.2007.07.004. [DOI] [Google Scholar]
- Monroe C., Cornell E. A., Sackett C., Myatt C., Wieman C.. Measurement of Cs-Cs elastic scattering at T = 30 μK. Phys. Rev. Lett. 1993;70:414. doi: 10.1103/PhysRevLett.70.414. [DOI] [PubMed] [Google Scholar]
- Radtsig, A. A. , Smirnov, B. M. . Parameters of Atoms and Atmic Ions Handbook; Energoatomizdat, 1986. [Google Scholar]
- Notermans R., Vassen W.. High-Precision Spectroscopy of the Forbidden 23 S 1 → 21 P 1 Transition in Quantum Degenerate Metastable Helium. Phys. Rev. Lett. 2014;112:253002. doi: 10.1103/PhysRevLett.112.253002. [DOI] [PubMed] [Google Scholar]
- Kotochigova S.. Controlling interactions between highly magnetic atoms with Feshbach resonances. Rep. Prog. Phys. 2014;77:093901. doi: 10.1088/0034-4885/77/9/093901. [DOI] [PubMed] [Google Scholar]
- Fano U., Theodosiou C. E., Dehmer J. L.. Electron-optical properties of atomic fields. Rev. Mod. Phys. 1976;48:49–68. doi: 10.1103/RevModPhys.48.49. [DOI] [Google Scholar]
- Mies F. H.. A multichannel quantum defect analysis of diatomic predissociation and inelastic atomic scattering. J. Chem. Phys. 1984;80:2514–2525. doi: 10.1063/1.447000. [DOI] [Google Scholar]
- Mies F. H., Julienne P. S.. A multichannel quantum defect analysis of two-state couplings in diatomic molecules. J. Chem. Phys. 1984;80:2526–2535. doi: 10.1063/1.447046. [DOI] [Google Scholar]
- Julienne, P. , Pan, S. , Thorsheim, H. , Weiner, J. . Theory of collision-induced optical trap loss. AIP Conf. Proc. 1988; pp 308–310. [Google Scholar]
- Julienne P. S., Smith A. M., Burnett K.. Theory of Collisions Between Laser Cooled Atoms. Advances In Atomic, Molecular, and Optical Physics. 1992;30:141–198. doi: 10.1016/S1049-250X(08)60175-5. [DOI] [Google Scholar]
- Julienne P. S.. Cold Binary Atomic Collisions in a Light Field. J. Res. Natl. Inst. Stand. Technol. 1996;101:487–503. doi: 10.6028/jres.101.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner J., Bagnato V. S., Zilio S., Julienne P. S.. Experiments and theory in cold and ultracold collisions. Rev. Mod. Phys. 1999;71:1–85. doi: 10.1103/RevModPhys.71.1. [DOI] [Google Scholar]
- Orzel C., Walhout M., Sterr U., Julienne P. S., Rolston S. L.. Spin polarization and quantum-statistical effects in ultracold ionizing collisions. Phys. Rev. A. 1999;59:1926–1935. doi: 10.1103/PhysRevA.59.1926. [DOI] [Google Scholar]
- Julienne, P. S. In Cold Molecules: Theory, Experiment, Applications; Krems, R. V. , Stwalley, W. C. , Friedrich, B. , Eds.; CRC: Boca Raton, FL, 2009; Chapter 6. Molecular States Near a Collision Threshold, pp 221–244. [Google Scholar]
- Idziaszek Z., Simoni A., Calarco T., Julienne P. S.. Multichannel quantum-defect theory for ultracold atom-ion collisions. New J. Phys. 2011;13:083005. doi: 10.1088/1367-2630/13/8/083005. [DOI] [Google Scholar]
- Kohn W.. Quantum Mechanics of Sticking. Surf. Rev. Lett. 1994;1:129–132. doi: 10.1142/S0218625X94000151. [DOI] [Google Scholar]
- Carraro C., Cole M. W.. Quantum reflection. Z. Phys. B. 1995;98:319–321. doi: 10.1007/BF01338397. [DOI] [Google Scholar]
- Lennard-Jones J. E., Devonshire A. F.. The Interaction of Atoms and Molecules with Solid Surfaces. III. The Condensation and Evaporation of Atoms and Molecules. Proc. Roy. Soc. A. 1936;156:6–28. doi: 10.1098/rspa.1936.0131. [DOI] [Google Scholar]
- Lennard-Jones J. E., Devonshire A. F.. The Interaction of Atoms and Molecules with Solid Surfaces. V. The Diffraction and Reflexion of Molecular Rays. Proc. Roy. Soc. A. 1936;156:37–44. [Google Scholar]
- Böheim J., Brenig W., Stutzki J.. On the Low Energy Limit of Reflection and Sticking Coefficients. Z. Phys. B. 1982;48:43–49. doi: 10.1007/BF02026427. [DOI] [Google Scholar]
- Nayak V. U., Edwards D. O., Masuhara N.. Scattering of 4He Atoms Grazing the Liquid-4He Surface. Phys. Rev. Lett. 1983;50:990–992. doi: 10.1103/PhysRevLett.50.990. [DOI] [Google Scholar]
- Berkhout J., Luiten O., Setija I., Hijmans T., Mizusaki T., Walraven J.. Quantum reflection: Focusing of hydrogen atoms with a concave mirror. Phys. Rev. Lett. 1989;63:1689. doi: 10.1103/PhysRevLett.63.1689. [DOI] [PubMed] [Google Scholar]
- Yu I. A., Doyle J. M., Sandberg J. C., Cesar C. L., Kleppner D., Greytak T. J.. Evidence for Universal Quantum Reflection of Hydrogen from Liquid 4He. Phys. Rev. Lett. 1993;71:1589–1592. doi: 10.1103/PhysRevLett.71.1589. [DOI] [PubMed] [Google Scholar]
- Shimizu F.. Specular Reflection of Very Slow Metastable Neon Atoms from a Solid Surface. Phys. Rev. Lett. 2001;86:987–990. doi: 10.1103/PhysRevLett.86.987. [DOI] [PubMed] [Google Scholar]
- Pasquini T. A., Shin Y., Sanner C., Saba M., Schirotzek A., Pritchard D. E., Ketterle W.. Quantum reflection from a solid surface at normal incidence. Phys. Rev. Lett. 2004;93:223201. doi: 10.1103/PhysRevLett.93.223201. [DOI] [PubMed] [Google Scholar]
- Heller, E. J. The Semiclassical Way to Dynamics and Spectroscopy; Princeton University Press: Princeton, NJ, 2018. [Google Scholar]
- Friedrich, H. Theoretical Atomic Physics, 4th ed.; Graduate Texts in Physics; Springer: New York, 2017. [Google Scholar]
- Zhao B. S., Schulz S. A., Meek S. A., Meijer G., Schöllkopf W.. Quantum reflection of helium atom beams from a microstructured grating. Phys. Rev. A. 2008;78:010902. doi: 10.1103/PhysRevA.78.010902. [DOI] [Google Scholar]
- Epstein P. S.. Reflection of waves in an inhomogeneous absorbing medium. Proc. Natl. Acad. Sci. U. S. A. 1930;16:627–637. doi: 10.1073/pnas.16.10.627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckart C.. The penetration of a potential barrier by electrons. Phys. Rev. 1930;35:1303. doi: 10.1103/PhysRev.35.1303. [DOI] [Google Scholar]
- Crandall R.. Exact propagator for reflectionless potentials. J. Phys. A. 1983;16:3005. doi: 10.1088/0305-4470/16/13/023. [DOI] [Google Scholar]
- Van Vleck J. H.. The Correspondence Principle in the Statistical Interpretation of Quantum Mechanics. Proc. Natl. Acad. Sci. U. S. A. 1928;14:178–188. doi: 10.1073/pnas.14.2.178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morette C.. On the definition and approximation of Feynman path integrals. Phys. Rev. 1951;81:848–852. doi: 10.1103/PhysRev.81.848. [DOI] [Google Scholar]
- Gutzwiller M. C.. Phase-Integral Approximation in Momentum Space and the Bound States of an Atom. J. Math. Phys. 1967;8:1979–2000. doi: 10.1063/1.1705112. [DOI] [Google Scholar]
- Gutzwiller M. C.. Periodic Orbits and Classical Quantization Conditions. J. Math. Phys. 1971;12:343. doi: 10.1063/1.1665596. [DOI] [Google Scholar]
- Mott N. F.. The Solution of the Wave Function for the Scattering of Particles by a Coulombian Centre of Force. Proc. Roy. Soc. A. 1928;118:542–549. doi: 10.1098/rspa.1928.0067. [DOI] [Google Scholar]
- Chadwick J.. The Scattering of α-Particles in Helium. Proc. Roy. Soc. A. 1930;128:114–122. [Google Scholar]
- Rutherford E.. The Scattering of α and β Particles by Matter and the Structure of the Atom. Philos. Mag. 1911;21:669–688. doi: 10.1080/14786440508637080. [DOI] [Google Scholar]
- Rost J. M., Heller E. J.. Semiclassical scattering of charged particles. J. Phys. B. 1994;27:1387–1395. doi: 10.1088/0953-4075/27/7/014. [DOI] [Google Scholar]
- Mott N. F.. The Collision between Two Electrons. Proc. Roy. Soc. A. 1930;126:259–267. doi: 10.1098/rspa.1930.0006. [DOI] [Google Scholar]
- Pinkas M., Katz O., Wengrowicz J., Akerman N., Ozeri R.. Trap-assisted formation of atom-ion bound states. Nat. Phys. 2023;19:1573–1578. doi: 10.1038/s41567-023-02158-5. [DOI] [Google Scholar]
- Barton G.. Rutherford scattering in two dimensions. Am. J. Phys. 1983;51:420–422. doi: 10.1119/1.13228. [DOI] [Google Scholar]
- Anderson A., Haroche S., Hinds E., Jhe W., Meschede D., Moi L.. Reflection of thermal Cs atoms grazing a polished glass surface. Phys. Rev. A. 1986;34:3513. doi: 10.1103/PhysRevA.34.3513. [DOI] [PubMed] [Google Scholar]
- Doyle J. M., Sandberg J. C., Yu I. A., Cesar C. L., Kleppner D., Greytak T. J.. Hydrogen in the submillikelvin regime: Sticking probability on superfluid 4He. Phys. Rev. Lett. 1991;67:603. doi: 10.1103/PhysRevLett.67.603. [DOI] [PubMed] [Google Scholar]
- Carraro C., Cole M. W.. H atom sticking to He and He films. Phys. Rev. Lett. 1992;68:412. doi: 10.1103/PhysRevLett.68.412. [DOI] [PubMed] [Google Scholar]
- Carraro C., Cole M. W.. Role of long-range forces in H sticking to liquid He. Phys. Rev. B. 1992;45:12930. doi: 10.1103/PhysRevB.45.12930. [DOI] [PubMed] [Google Scholar]
- Clougherty D. P., Kohn W.. Quantum theory of sticking. Phys. Rev. B. 1992;46:4921–4937. doi: 10.1103/PhysRevB.46.4921. [DOI] [PubMed] [Google Scholar]
- Hijmans T., Walraven J., Shlyapnikov G.. Influence of the substrate on the low-temperature limit of the sticking probability of hydrogen atoms on He films. Phys. Rev. B. 1992;45:2561. doi: 10.1103/PhysRevB.45.2561. [DOI] [PubMed] [Google Scholar]
- Lin Q.-g.. Scattering by a Coulomb field in two dimensions. Am. J. Phys. 1997;65:1007–1009. doi: 10.1119/1.18694. [DOI] [Google Scholar]
- Shimizu F., Fujita J.-i.. Reflection-type hologram for atoms. Phys. Rev. Lett. 2002;88:123201. doi: 10.1103/PhysRevLett.88.123201. [DOI] [PubMed] [Google Scholar]
- Druzhinina V., DeKieviet M.. Experimental observation of quantum reflection far from threshold. Phys. Rev. Lett. 2003;91:193202. doi: 10.1103/PhysRevLett.91.193202. [DOI] [PubMed] [Google Scholar]
- Zhao B. S., Meijer G., Schöllkopf W.. Quantum reflection of He2 several nanometers above a grating surface. Science. 2011;331:892–894. doi: 10.1126/science.1200911. [DOI] [PubMed] [Google Scholar]
- Zhao B. S., Zhang W., Schöllkopf W.. Non-destructive quantum reflection of helium dimers and trimers from a plane ruled grating. Mol. Phys. 2013;111:1772–1780. doi: 10.1080/00268976.2013.787150. [DOI] [Google Scholar]
- Friedrich, H. Scattering Theory; Lecture Notes in Physics 872; Springer: New York, 2013. [Google Scholar]
- Tsikritea A., Diprose J. A., Softley T. P., Heazlewood B. R.. Capture theory models: An overview of their development, experimental verification, and applications to ion–molecule reactions. J. Chem. Phys. 2022;157:060901. doi: 10.1063/5.0098552. [DOI] [PubMed] [Google Scholar]
- Blatt J. M., Jackson J. D.. On the Interpretation of Neutron-Proton Scattering Data by the Schwinger Variational Method. Phys. Rev. 1949;76:18–37. doi: 10.1103/PhysRev.76.18. [DOI] [Google Scholar]
- Bethe H. A.. Theory of the Effective Range in Nuclear Scattering. Phys. Rev. 1949;76:38–50. doi: 10.1103/PhysRev.76.38. [DOI] [Google Scholar]
- Delves L. M.. Effective range expansion of the scattering matrix. Nucl. Phys. 1958;8:358–373. doi: 10.1016/0029-5582(58)90162-7. [DOI] [Google Scholar]
- Heller E. J., Yamani H. A.. J-Matrix Method - Application to s-Wave Electron-Hydrogen Scattering. Phys. Rev. A. 1974;9:1209–1214. doi: 10.1103/PhysRevA.9.1209. [DOI] [Google Scholar]
- Heller E. J., Yamani H. A.. New L 2 Approach to Quantum Scattering: Theory. Phys. Rev. A. 1974;9:1201–1208. doi: 10.1103/PhysRevA.9.1201. [DOI] [Google Scholar]
- Yamani H. A., Fishman L.. J-matrix Method: Extension to Arbitrary Angular Momentum and to Coulomb Scattering. J. Math. Phys. 1975;16:410–420. doi: 10.1063/1.522516. [DOI] [Google Scholar]
- Alhaidari, A. D. , Heller, E. J. , Yamani, H. A. , Abdelmonem, M. S. , Eds. The J-Matrix Method; Springer, 2008. [Google Scholar]
- Burke, P. G. R-Matrix Theory of Atomic Collisions; Springer Series on Atomic, Optical, and Plasma Physics; Springer, 2011; Vol. 61. [Google Scholar]
- Kajita M.. Collisions between electrostatically confined linear polar molecules. Eur. Phys. J. D. 2002;20:55–59. doi: 10.1140/epjd/e2002-00104-5. [DOI] [Google Scholar]
- Kajita M.. Collisions between molecules in the J = 0 state. Eur. Phys. J. D. 2004;31:39–43. doi: 10.1140/epjd/e2004-00120-5. [DOI] [Google Scholar]
- Roudnev V., Cavagnero M.. Resonance phenomena in ultracold dipole-dipole scattering. J. Phys. B. 2009;42:044017. doi: 10.1088/0953-4075/42/4/044017. [DOI] [Google Scholar]
- Roudnev V., Cavagnero M.. Universal resonant ultracold molecular scattering. Phys. Rev. A. 2009;79:014701. doi: 10.1103/PhysRevA.79.014701. [DOI] [Google Scholar]
- Hudson E. R.. Method for producing ultracold molecular ions. Phys. Rev. A. 2009;79:032716. doi: 10.1103/PhysRevA.79.032716. [DOI] [Google Scholar]
- Ticknor C.. Two-dimensional dipolar scattering. Phys. Rev. A. 2009;80:052702. doi: 10.1103/PhysRevA.80.052702. [DOI] [Google Scholar]
- Gonzalez Montoya F., Wiggins S.. Phase space structure and escape time dynamics in a Van der Waals model for exothermic reactions. Phys. Rev. E. 2020;102:062203. doi: 10.1103/PhysRevE.102.062203. [DOI] [PubMed] [Google Scholar]
- Gonzalez Montoya F.. The Classical Action as a Tool to Visualise the Phase Space of Hamiltonian Systems. Dynamics. 2023;3:678–694. doi: 10.3390/dynamics3040036. [DOI] [Google Scholar]
- Birkhoff G. D.. On the periodic motions of dynamical systems. Acta Math. 1927;50:359–379. doi: 10.1007/BF02421325. [DOI] [Google Scholar]
- Dirac P. A. M.. The quantum theory of the emission and absorption of radiation. Proc. Roy. Soc. A. 1927;114:243–265. doi: 10.1098/rspa.1927.0039. [DOI] [Google Scholar]
- Fermi, E. Nucl. Phys.; University of Chicago: Chicago, 1950. [Google Scholar]
- Weyl H.. Über die Randwertaufgabe der Strahlungstheorie und asymptotische Spektralgesetze. J. Reine Angew. Math. 1913;143:177–202. doi: 10.1515/crll.1913.143.177. [DOI] [Google Scholar]
- Berry M. V.. The Bakerian Lecture, 1987. Quantum chaology. Proc. Roy. Soc. A. 1987;413:183–198. doi: 10.1098/rspa.1987.0109. [DOI] [Google Scholar]
- Wehlitz R., Pattard T., Huang M.-T., Sellin I. A., Burgdörfer J., Azuma Y.. Near-threshold triple-photoionization cross section of lithium. Phys. Rev. A. 2000;61:030704. doi: 10.1103/PhysRevA.61.030704. [DOI] [Google Scholar]
- Bartlett P. L., Stelbovics A. T.. Threshold Behavior of e-H Ionizing Collisions. Phys. Rev. Lett. 2004;93:233201. doi: 10.1103/PhysRevLett.93.233201. [DOI] [PubMed] [Google Scholar]
- Bartlett, P. L. Complete numerical solution of electron-hydrogen collisions. Ph.D. thesis, Murdoch University, Perth, Australia, 2005. [Google Scholar]
- Bartlett P. L.. A complete numerical approach to electron-hydrogen collisions. J. Phys. B. 2006;39:R379–R424. doi: 10.1088/0953-4075/39/22/R01. [DOI] [Google Scholar]
- Emmanouilidou A., Rost J. M.. The Coulomb four-body problem in a classical framework: triple photoionization of lithium. J. Phys. B. 2006;39:4037–4048. doi: 10.1088/0953-4075/39/20/003. [DOI] [Google Scholar]
- Emmanouilidou A., Rost J. M.. Triple photoionization of lithium near threshold. J. Phys. B. 2006;39:L99–L103. doi: 10.1088/0953-4075/39/5/L04. [DOI] [Google Scholar]
- Emmanouilidou A., Rost J. M.. Attosecond-time-scale multielectron collisions in the Coulomb four-body problem: Traces in classical probability densities. Phys. Rev. A. 2007;75:022712. doi: 10.1103/PhysRevA.75.022712. [DOI] [Google Scholar]
- Kustaanheimo P., Davenport H., Stiefel E.. Perturbation theory of Kepler motion based on spinor regularization. J. Reine Angew. Math. 1965;218:204–219. doi: 10.1515/crll.1965.218.204. [DOI] [Google Scholar]
- Sadeghpour H. R., Bohn J. L., Cavagnero M. J., Esry B. D., Fabrikant I. I., Macek J. H., Rau A. R. P.. Collisions near threshold in atomic and molecular physics. J. Phys. B. 2000;33:R93–R140. doi: 10.1088/0953-4075/33/5/201. [DOI] [Google Scholar]
- Mirahmadi M., Pérez-Ríos J.. Three-body recombination in physical chemistry. Int. Rev. Phys. Chem. 2022;41:233–267. doi: 10.1080/0144235X.2023.2237300. [DOI] [PubMed] [Google Scholar]
- Peterkop R.. WKB approximation and threshold law for electron-atom ionization. J. Phys. B. 1971;4:513. doi: 10.1088/0022-3700/4/4/013. [DOI] [Google Scholar]
- Crothers D. S. F.. Quantal threshold ionisation. J. Phys. B. 1986;19:463–483. doi: 10.1088/0022-3700/19/4/013. [DOI] [Google Scholar]
- Rost J.-M.. Two-electron escape near threshold: A classical process? Phys. Rev. Lett. 1994;72:1998–2001. doi: 10.1103/PhysRevLett.72.1998. [DOI] [PubMed] [Google Scholar]
- Rost J. M., Heller E. J.. Ionization of hydrogen by positron impact near the fragmentation threshold. Phys. Rev. A. 1994;49:R4289–R2492. doi: 10.1103/PhysRevA.49.R4289. [DOI] [PubMed] [Google Scholar]
- Rau A. R. P.. Two Electrons in a Coulomb Potential. Double-Continuum Wave Functions and Threshold Law for Electron-Atom Ionization. Phys. Rev. A. 1971;4:207. doi: 10.1103/PhysRevA.4.207. [DOI] [Google Scholar]
- Roth T. A.. Threshold Law for Double Photoionization and Related Processes with L = 1 Final States. Phys. Rev. A. 1972;5:476–478. doi: 10.1103/PhysRevA.5.476. [DOI] [Google Scholar]
- Greene C. H., Rau A. R. P.. Double Escape of Two Electrons at Threshold: Dependence on L, S, and π . Phys. Rev. Lett. 1982;48:533–537. doi: 10.1103/PhysRevLett.48.533. [DOI] [Google Scholar]
- Altick P. L.. Use of a long-range correlation factor in describing triply differential electron impact ionization cross sections. J. Phys. B. 1985;18:1841–1846. doi: 10.1088/0022-3700/18/9/017. [DOI] [Google Scholar]
- Kato D., Watanabe S.. Fully quantal treatment of the ionization threshold law: e + H with frozen angular degrees of freedom. J. Phys. B. 1996;29:L779–L785. doi: 10.1088/0953-4075/29/22/001. [DOI] [Google Scholar]
- Scott M. P., Burke P. G., Bartschat K., Bray I.. Near-threshold electron impact ionization of atomic hydrogen. J. Phys. B. 1997;30:L309–L315. doi: 10.1088/0953-4075/30/9/004. [DOI] [Google Scholar]
- Kato D., Watanabe S.. Ab initio study of interelectronic correlations in electron-impact ionization of hydrogen. Phys. Rev. A. 1997;56:3687–3700. doi: 10.1103/PhysRevA.56.3687. [DOI] [Google Scholar]
- Cvejanović S., Read F. H.. Studies of the threshold electron impact ionization of helium. J. Phys. B. 1974;7:1841. doi: 10.1088/0022-3700/7/14/008. [DOI] [Google Scholar]
- Donahue J. B., Gram P. A. M., Hynes M. V., Hamm R. W., Frost C. A., Bryant H. C., Butterfield K. B., Clark D. A., Smith W. W.. Observation of Two-Electron Photoionization of the H– Ion near Threshold. Phys. Rev. Lett. 1982;48:1538–1541. doi: 10.1103/PhysRevLett.48.1538. [DOI] [Google Scholar]
- Hippler R., Klar H., Saeed K., McGregor I., Duncan A., Kleinpoppen H.. Threshold behaviour of Ar K and Xe L3 ionisation by electron impact. J. Phys. B. 1983;16:L617. doi: 10.1088/0022-3700/16/20/004. [DOI] [Google Scholar]
- Kossmann H., Schmidt V., Andersen T.. Test of Wannier threshold laws: Double-photoionization cross section in helium. Phys. Rev. Lett. 1988;60:1266. doi: 10.1103/PhysRevLett.60.1266. [DOI] [PubMed] [Google Scholar]
- Dunn, G. Electron-ion ionization. In Electron Impact Ionization; Springer, 1985; pp 277–319. [Google Scholar]
- Winkler C., Märk T.. Experimental investigation of the electron impact ionization cross-section behaviour near threshold. Int. J. Mass Spectrom. Ion Processes. 1994;133:157–164. doi: 10.1016/0168-1176(94)03955-0. [DOI] [Google Scholar]
- Rescigno T. N., Baertschy M., Isaacs W. A., McCurdy C. W.. Collisional Breakup in a Quantum System of Three Charged Particles. Science. 1999;286:2474–2479. doi: 10.1126/science.286.5449.2474. [DOI] [PubMed] [Google Scholar]
- Aarseth S. J., Zare K.. A regularization of the three-body problem. Celest. Mech. 1974;10:185–205. doi: 10.1007/BF01227619. [DOI] [Google Scholar]
- Richter K., Wintgen D.. Analysis of classical motion on the Wannier ridge. J. Phys. B. 1990;23:L197–L201. doi: 10.1088/0953-4075/23/11/002. [DOI] [Google Scholar]
- Tanner G., Richter K., Rost J.-M.. The theory of two-electron atoms: between ground state and complete fragmentation. Rev. Mod. Phys. 2000;72:497–544. doi: 10.1103/RevModPhys.72.497. [DOI] [Google Scholar]
- Levi-Civita T.. Sur les trajectoires singuilières du problème restreint des trois corps. C. R. Hebd. Séances Acad. Sci. 1903;136:82–84. [Google Scholar]
- Levi-Civita T.. Condition du choc dans le problème restreint des trois corps. C. R. Hebd. Séances Acad. Sci. 1903;136:221–223. [Google Scholar]
- Levi-Civita T.. Traiettorie singolari ed urti nel problema ristretto dei tre corpi. Ann. Mat. Pura Appl. 1904;9:1–32. doi: 10.1007/BF02419867. [DOI] [Google Scholar]
- Klar H., Schlecht W.. Threshold multiple ionization of atoms. Energy dependence for double and triple escape. J. Phys. B. 1976;9:1699–1711. doi: 10.1088/0022-3700/9/10/015. [DOI] [Google Scholar]
- Samson J. A. R., Angel G. C.. Test of the Threshold Law for Triple Photoionization in Atomic Oxygen and Neon. Phys. Rev. Lett. 1988;61:1584–1586. doi: 10.1103/PhysRevLett.61.1584. [DOI] [PubMed] [Google Scholar]
- Malcherek A. W., Rost J. M., Briggs J. S.. Complete photo fragmentation of the lithium atom. Phys. Rev. A. 1997;55:R3979–R3982. doi: 10.1103/PhysRevA.55.R3979. [DOI] [Google Scholar]
- Wehlitz R., Huang M.-T., DePaola B. D., Levin J. C., Sellin I. A., Nagata T., Cooper J. W., Azuma Y.. Triple Photoionization of Lithium. Phys. Rev. Lett. 1998;81:1813–1816. doi: 10.1103/PhysRevLett.81.1813. [DOI] [Google Scholar]
- Grujić P.. The fourfold escape threshold law. Phys. Lett. A. 1983;96:233–235. doi: 10.1016/0375-9601(83)90340-7. [DOI] [Google Scholar]
- Dimitrijević M. S., Grujić P., Simonović N.. Fourfold ionization by electrons near the threshold. Z. Phys. D. 1990;15:203–209. doi: 10.1007/BF01437181. [DOI] [Google Scholar]
- Li S., Heller E. J.. Quantum multiple scattering: Eigenmode expansion and its applications to proximity resonance. Phys. Rev. A. 2003;67:032712. doi: 10.1103/PhysRevA.67.032712. [DOI] [Google Scholar]
- D’Incao J. P., Esry B. D.. Scattering Length Scaling Laws for Ultracold Three-Body Collisions. Phys. Rev. Lett. 2005;94:213201. doi: 10.1103/PhysRevLett.94.213201. [DOI] [PubMed] [Google Scholar]
- Yamashita M. T., Fedorov D. V., Jensen A. S.. Universality of Brunnian (N-body Borromean) four and five-body systems. Phys. Rev. A. 2010;81:063607. doi: 10.1103/PhysRevA.81.063607. [DOI] [Google Scholar]
- Yamashita M. T., Fedorov D. V., Jensen A. S.. Brunnian and Efimov N-Body States. Few-Body Systems. 2011;51:135–151. doi: 10.1007/s00601-011-0228-7. [DOI] [Google Scholar]
- Baas N. A.. New states of matter suggested by new topological structures. Int. J. Gen. Sys. 2013;42:137–169. doi: 10.1080/03081079.2012.728403. [DOI] [Google Scholar]
- Baas N. A., Fedorov D. V., Jensen A. S., Riisager K., Volosniev A. G., Zinner N. T.. Higher-order Brunnian structures and possible physical realizations. Phys. At. Nucl. 2014;77:336–343. doi: 10.1134/S1063778814030028. [DOI] [Google Scholar]
- Chen Y.-H., Greene C. H.. Efimov physics implications at p-wave fermionic unitarity. Phys. Rev. A. 2022;105:013308. doi: 10.1103/PhysRevA.105.013308. [DOI] [Google Scholar]
- Higgins M. D., Greene C. H.. Three and four identical fermions near the unitary limit. Phys. Rev. A. 2022;106:023304. doi: 10.1103/PhysRevA.106.023304. [DOI] [Google Scholar]
- Chen Y.-H., Greene C. H.. P-wave Efimov physics implications at unitarity. Phys. Rev. A. 2023;107:033329. doi: 10.1103/PhysRevA.107.033329. [DOI] [Google Scholar]
- Baz’ A. I.. The energy dependence of a scattering cross section near the threshold of a reaction. J. Exp. Theor. Phys. 1957;33:923–928. [Google Scholar]
- Baz’ A. I.. The energy dependence of a scattering cross section near the threshold of a reaction. Sov. Phys. J. Exp. Theor. Phys. 1958;6:709–713. [Google Scholar]
- Breit G.. Energy Dependence of Reactions at Thresholds. Phys. Rev. 1957;107:1612–1615. doi: 10.1103/PhysRev.107.1612. [DOI] [Google Scholar]
- Newton R. G.. Inelastic Scattering. Ann. Phys. 1958;4:29–56. doi: 10.1016/0003-4916(58)90036-8. [DOI] [Google Scholar]
- Newton R. G.. Threshold Properties of Scattering and Reaction Cross Sections. Phys. Rev. 1959;114:1611–1618. doi: 10.1103/PhysRev.114.1611. [DOI] [Google Scholar]
- Hodgson P. E.. Wigner cusps in nuclear reactions. Nature. 1976;259:364–365. doi: 10.1038/259364a0. [DOI] [Google Scholar]
- Hersch J. S., Heller E. J.. Threshold resonances in a double well system. Phys. Lett. A. 1999;254:72–78. doi: 10.1016/S0375-9601(99)00047-X. [DOI] [Google Scholar]
- Heller E. J.. Quantum Proximity Resonances. Phys. Rev. Lett. 1996;77:4122. doi: 10.1103/PhysRevLett.77.4122. [DOI] [PubMed] [Google Scholar]
- Hersch J. S., Heller E. J.. Observation of Proximity Resonances in a Parallel-Plate Waveguide. Phys. Rev. Lett. 1998;81:3059. doi: 10.1103/PhysRevLett.81.3059. [DOI] [Google Scholar]
- Thomas L. H.. The Interaction Between a Neutron and a Proton and the Structure of H3 . Phys. Rev. 1935;47:903–909. doi: 10.1103/PhysRev.47.903. [DOI] [Google Scholar]
- Danilov G. S.. On the three-body problem with short-range forces. Sov. Phys. J. Exp. Theor. Phys. 1961;13:349–355. [Google Scholar]
- Danilov G. S.. On the three-body problem with short-range forces. J. Exp. Theor. Phys. 1961;40:498–507. [Google Scholar]
- Efimov V. N.. Weakly-bound states of three resonantly-interacting particles. Yad. Fiz. 1970;12:1080–1091. [Google Scholar]
- Efimov V.. Energy levels arising from resonant two-body forces in a three-body system. Phys. Lett. B. 1970;33:563–564. doi: 10.1016/0370-2693(70)90349-7. [DOI] [Google Scholar]
- Efimov V. N.. Weakly-bound states of three resonantly-interacting particles. Sov. J. Nucl. Phys. 1971;12:589–595. [Google Scholar]
- Efimov V.. Level spectrum of three resonantly interacting particles. Sov. Phys. J. Exp. Theor. Phys. Lett. 1972;16:34–37. [Google Scholar]
- Efimov V.. Level spectrum of three resonantly interacting particles. ZhETF Pis’ma Redaktsiiu. 1972;16:50–54. [Google Scholar]
- Amado R. D., Noble J. V.. Efimov’s Effect: A New Pathology of Three-Particle-Systems. II. Phys. Rev. D. 1972;5:1992–2002. doi: 10.1103/PhysRevD.5.1992. [DOI] [Google Scholar]
- Efimov V.. Energy levels of three resonantly interacting particles. Nucl. Phys. A. 1973;210:157–188. doi: 10.1016/0375-9474(73)90510-1. [DOI] [PubMed] [Google Scholar]
- Zhukov M. V., Danilin B. V., Fedorov D. V., Bang J. M., Thompson I. J., Vaagen J. S.. Bound state properties of Borromean halo nuclei: 6He and 11Li. Phys. Rep. 1993;231:151–199. doi: 10.1016/0370-1573(93)90141-Y. [DOI] [Google Scholar]
- Lide, M. Classical Simulations of Ultracold Chemical Reactions. Bachelor’s Thesis, Trinity University, 2021. [Google Scholar]
- Man M. P., Groenenboom G. C., Karman T.. Symmetry breaking in sticky collisions between ultracold molecules. Phys. Rev. Lett. 2022;129:243401. doi: 10.1103/PhysRevLett.129.243401. [DOI] [PubMed] [Google Scholar]
- Kłos J., Guan Q., Li H., Li M., Tiesinga E., Kotochigova S.. Roaming pathways and survival probability in real-time collisional dynamics of cold and controlled bialkali molecules. Sci. Rep. 2021;11:10598. doi: 10.1038/s41598-021-90004-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang B. C., Pérez-Ríos J., Robicheaux F.. Classical Fractals and Quantum Chaos in Ultracold Dipolar Collisions. Phys. Rev. Lett. 2017;118:154101. doi: 10.1103/PhysRevLett.118.154101. [DOI] [PubMed] [Google Scholar]
- Li Z., Heller E. J.. Cold collisions of complex polyatomic molecules. J. Chem. Phys. 2012;136:054306. doi: 10.1063/1.3682982. [DOI] [PubMed] [Google Scholar]
- Li Z., Krems R. V., Heller E. J.. Collision dynamics of polyatomic molecules containing carbon rings at low temperatures. J. Chem. Phys. 2014;141:104317. doi: 10.1063/1.4894793. [DOI] [PubMed] [Google Scholar]
- Forrey R. C., Balakrishnan N., Dalgarno A., Haggerty M. R., Heller E. J.. Quasiresonant Energy Transfer in Ultracold Atom-Diatom Collisions. Phys. Rev. Lett. 1999;82:2657. doi: 10.1103/PhysRevLett.82.2657. [DOI] [Google Scholar]
- Forrey R. C., Balakrishnan N., Dalgarno A., Haggerty M. R., Heller E. J.. Effect of quasiresonant dynamics on the predissociation of van der Waals molecules. Phys. Rev. A. 2001;64:022706. doi: 10.1103/PhysRevA.64.022706. [DOI] [Google Scholar]
- Jachymski K., Gronowski M., Tomza M.. Collisional losses of ultracold molecules due to intermediate complex formation. Phys. Rev. A. 2022;106:L041301. doi: 10.1103/PhysRevA.106.L041301. [DOI] [Google Scholar]
- Gutzwiller, M. C. Chaos in Classical and Quantum Mechanics; Interdisciplinary Applied Mathematics; Springer: New York, 1990. [Google Scholar]
- Heller E. J.. Time-dependent approach to semiclassical dynamics. J. Chem. Phys. 1975;62:1544. doi: 10.1063/1.430620. [DOI] [Google Scholar]
- Heller E. J.. Classical S-matrix limit of wave packet dynamics. J. Chem. Phys. 1976;65:4979–4989. doi: 10.1063/1.432974. [DOI] [Google Scholar]
- Herman M. F., Kluk E.. A semiclassical justification for the use of non-spreading wavepackets in dynamics calculations. Chem. Phys. 1984;91:27–34. doi: 10.1016/0301-0104(84)80039-7. [DOI] [Google Scholar]
- Herman M. F.. Time reversal and unitarity in the frozen Gaussian approximation for semiclassical scattering. J. Chem. Phys. 1986;85:2069–2076. doi: 10.1063/1.451150. [DOI] [Google Scholar]
- Kay K. G.. The Herman-Kluk approximation: Derivation and semiclassical corrections. Chem. Phys. 2006;322:3–12. doi: 10.1016/j.chemphys.2005.06.019. [DOI] [Google Scholar]
- Huber D., Heller E. J.. Generalized Gaussian wave packet dynamics. J. Chem. Phys. 1987;87:5302–5311. doi: 10.1063/1.453647. [DOI] [Google Scholar]
- Huber D., Heller E. J., Littlejohn R. G.. Generalized Gaussian wave packet dynamics, Schrödinger equation, and stationary phase approximation. J. Chem. Phys. 1988;89:2003–2014. doi: 10.1063/1.455714. [DOI] [Google Scholar]
- Miller W. H.. Classical S matrix: Numerical application to inelastic collisions. J. Chem. Phys. 1970;53:3578–3587. doi: 10.1063/1.1674535. [DOI] [Google Scholar]
- Miller W. H.. The semiclassical initial value representation: A potentially practical way for adding quantum effects to classical molecular dynamics simulations. J. Phys. Chem. A. 2001;105:2942–2955. doi: 10.1021/jp003712k. [DOI] [Google Scholar]
- Heller E. J.. Cellular dynamics: a new semiclassical approach to time-dependent quantum mechanics. J. Chem. Phys. 1991;94:2723. doi: 10.1063/1.459848. [DOI] [Google Scholar]
- Tomsovic S., Heller E. J.. Semiclassical dynamics of chaotic motion: unexpected long-time accuracy. Phys. Rev. Lett. 1991;67:664. doi: 10.1103/PhysRevLett.67.664. [DOI] [PubMed] [Google Scholar]
- O’Connor P. W., Tomsovic S., Heller E. J.. Accuracy of semiclassical dynamics in the presence of chaos. J. Stat. Phys. 1992;68:131. doi: 10.1007/BF01048839. [DOI] [Google Scholar]
- Sepulveda M. A., Tomsovic S., Heller E. J.. Semiclassical propagation: how long can it last? Phys. Rev. Lett. 1992;69:402. doi: 10.1103/PhysRevLett.69.402. [DOI] [PubMed] [Google Scholar]
- Tomsovic S., Heller E. J.. Long-time semiclassical dynamics of chaos: the stadium billiard. Phys. Rev. E. 1993;47:282. doi: 10.1103/PhysRevE.47.282. [DOI] [PubMed] [Google Scholar]
- Sawada S.-I., Heather R., Jackson B., Metiu H.. A strategy for time dependent quantum mechanical calculations using a Gaussian wave packet representation of the wave function. J. Chem. Phys. 1985;83:3009–3027. doi: 10.1063/1.449204. [DOI] [Google Scholar]
- Ben-Nun M., Quenneville J., Martínez T. J.. Ab initio multiple spawning: Photochemistry from first principles quantum molecular dynamics. J. Phys. Chem. A. 2000;104:5161–5175. doi: 10.1021/jp994174i. [DOI] [Google Scholar]
- Ben-Nun, M. , Martínez, T. J. . Ab initio quantum molecular dynamics; John Wiley and Sons, 2002; Vol. 121; pp 439–512. [Google Scholar]
- Kais, S. , Whaley, K. , Dinner, A. , Rice, S. . Quantum Information and Computation for Chemistry, Vol. 154; Advances in Chemical Physics; Wiley: Hoboken, NJ, 2014. [Google Scholar]
- Gong J., Shapiro M., Brumer P.. Entanglement-assisted coherent control in nonreactive diatom-diatom scattering. J. Chem. Phys. 2003;118:2626–2636. doi: 10.1063/1.1535428. [DOI] [Google Scholar]
- Lin Y., Leibrandt D. R., Leibfried D., Chou C.-w.. Quantum entanglement between an atom and a molecule. Nature. 2020;581:273–277. doi: 10.1038/s41586-020-2257-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu M.-G., Liu Y., Nichols M. A., Zhu L., Quéméner G., Dulieu O., Ni K.-K.. Nuclear spin conservation enables state-to-state control of ultracold molecular reactions. Nat. Chem. 2021;13:435–440. doi: 10.1038/s41557-020-00610-0. [DOI] [PubMed] [Google Scholar]
- Luke J., Zhu L., Liu Y.-X., Ni K.-K.. Reaction interferometry with ultracold molecules. Faraday Discuss. 2024;251:63–75. doi: 10.1039/D3FD00175J. [DOI] [PubMed] [Google Scholar]
- Zhang Z.-Y., Sun Z., Duan T., Ding Y.-K., Huang X., Liu J.-M.. Entanglement generation of polar molecules via deep reinforcement learning. J. Chem. Theory Comput. 2024;20:1811–1820. doi: 10.1021/acs.jctc.3c01214. [DOI] [PubMed] [Google Scholar]
- Ruttley D. K., Hepworth T. R., Guttridge A., Cornish S. L.. Long-lived entanglement of molecules in magic-wavelength optical tweezers. Nature. 2025;637:827–832. doi: 10.1038/s41586-024-08365-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devolder, A. , Tscherbul, T. , Brumer, P. . Leveraging Reactant Entanglement in the Coherent Control of Ultracold Bimolecular Chemical Reactions. arXiv preprint arXiv:2505.10684 2025, 10.48550/arXiv.2505.10684. [DOI] [Google Scholar]
- Lemeshko M., Krems R. V., Doyle J. M., Kais S.. Manipulation of molecules with electromagnetic fields. Mol. Phys. 2013;111:1648–1682. doi: 10.1080/00268976.2013.813595. [DOI] [Google Scholar]
- Krems, R. V. Molecules in electromagnetic fields: from ultracold physics to controlled chemistry; John Wiley & Sons: Hoboken, NJ, 2018. [Google Scholar]
- Wallis A. O., Longdon E. J., Zuchowski P. S., Hutson J. M.. The prospects of sympathetic cooling of NH molecules with Li atoms. Eur. Phys. J. D. 2011;65:151–160. doi: 10.1140/epjd/e2011-20025-4. [DOI] [Google Scholar]
- Morita M., Krems R. V., Tscherbul T. V.. Universal probability distributions of scattering observables in ultracold molecular collisions. Phys. Rev. Lett. 2019;123:013401. doi: 10.1103/PhysRevLett.123.013401. [DOI] [PubMed] [Google Scholar]
- Morita M., Kłos J., Tscherbul T. V.. Full-dimensional quantum scattering calculations on ultracold atom-molecule collisions in magnetic fields: The role of molecular vibrations. Phys. Rev. Res. 2020;2:043294. doi: 10.1103/PhysRevResearch.2.043294. [DOI] [Google Scholar]
- Côté R., Jamieson M., Yan Z., Geum N., Jeung G.-H., Dalgarno A.. Enhanced cooling of hydrogen atoms by lithium atoms. Phys. Rev. Lett. 2000;84:2806. doi: 10.1103/PhysRevLett.84.2806. [DOI] [PubMed] [Google Scholar]
- Gadéa F., Leininger T., Dickinson A.. Accurate calculation of the scattering length for the cooling of hydrogen atoms by lithium atoms. Eur. Phys. J. D. 2001;15:251–255. doi: 10.1007/s100530170173. [DOI] [Google Scholar]
- Soldán P., Cvitaš M. T., Hutson J. M., Honvault P., Launay J.-M.. Quantum Dynamics of Ultracold Na + Na2 Collisions. Phys. Rev. Lett. 2002;89:153201. doi: 10.1103/PhysRevLett.89.153201. [DOI] [PubMed] [Google Scholar]
- Dickinson A., Gadéa F., Leininger T.. Scattering lengths for spin-polarized metastable helium-3 and helium-4. J. Phys. B. 2004;37:587. doi: 10.1088/0953-4075/37/3/005. [DOI] [Google Scholar]
- Quéméner G., Honvault P., Launay J.-M.. Sensitivity of the dynamics of Na + Na2 collisions on the three-body interaction at ultralow energies. Eur. Phys. J. D. 2004;30:201–207. doi: 10.1140/epjd/e2004-00078-2. [DOI] [Google Scholar]
- Cvitaš M. T., Soldán P., Hutson J. M., Honvault P., Launay J.-M.. Interactions and dynamics in Li + Li2 ultracold collisions. J. Chem. Phys. 2007;127:074302. doi: 10.1063/1.2752162. [DOI] [PubMed] [Google Scholar]
- Wallis A. O., Hutson J. M.. Production of ultracold NH molecules by sympathetic cooling with Mg. Phys. Rev. Lett. 2009;103:183201. doi: 10.1103/PhysRevLett.103.183201. [DOI] [PubMed] [Google Scholar]
- Zuchowski P. S., Hutson J. M.. Low-energy collisions of NH3 and ND3 with ultracold Rb atoms. Phys. Rev. A. 2009;79:062708. doi: 10.1103/PhysRevA.79.062708. [DOI] [Google Scholar]
- Zuchowski P. S., Hutson J. M.. Cold collisions of N (4 S) and NH (3Σ) molecules in magnetic fields. Phys. Chem. Chem. Phys. 2011;13:3669–3680. doi: 10.1039/C0CP01447H. [DOI] [PubMed] [Google Scholar]
- Janssen L. M., Zuchowski P. S., van der Avoird A., Groenenboom G. C., Hutson J. M.. Cold and ultracold NH-NH collisions in magnetic fields. Phys. Rev. A. 2011;83:022713. doi: 10.1103/PhysRevA.83.022713. [DOI] [PubMed] [Google Scholar]
- Janssen L. M. C., Zuchowski P. S., van der Avoird A., Hutson J. M., Groenenboom G. C.. Cold and ultracold NH-NH collisions: The field-free case. J. Chem. Phys. 2011;134:124309. doi: 10.1063/1.3570596. [DOI] [PubMed] [Google Scholar]
- Janssen L. M. C., van der Avoird A., Groenenboom G. C.. Quantum Reactive Scattering of Ultracold NH(X 3Σ–) Radicals in a Magnetic Trap. Phys. Rev. Lett. 2013;110:063201. doi: 10.1103/PhysRevLett.110.063201. [DOI] [PubMed] [Google Scholar]
- Frye M. D., Hutson J. M.. Collision cross sections for the thermalization of cold gases. Phys. Rev. A. 2014;89:052705. doi: 10.1103/PhysRevA.89.052705. [DOI] [Google Scholar]
- Suleimanov Y. V., Tscherbul T. V.. Cold NH-NH collisions in a magnetic field: Basis set convergence versus sensitivity to the interaction potential. J. Phys. B. 2016;49:204002. doi: 10.1088/0953-4075/49/20/204002. [DOI] [Google Scholar]
- Chefdeville S., Kalugina Y., van de Meerakker S. Y., Naulin C., Lique F., Costes M.. Observation of partial wave resonances in low-energy O2-H2 inelastic collisions. Science. 2013;341:1094–1096. doi: 10.1126/science.1241395. [DOI] [PubMed] [Google Scholar]
- Vogels S. N., Onvlee J., Chefdeville S., van der Avoird A., Groenenboom G. C., van de Meerakker S. Y.. Imaging resonances in low-energy NO-He inelastic collisions. Science. 2015;350:787–790. doi: 10.1126/science.aad2356. [DOI] [PubMed] [Google Scholar]
- Bergeat A., Onvlee J., Naulin C., Van Der Avoird A., Costes M.. Quantum dynamical resonances in low-energy CO(j = 0) + He inelastic collisions. Nat. Chem. 2015;7:349–353. doi: 10.1038/nchem.2204. [DOI] [PubMed] [Google Scholar]
- Costes M., Naulin C.. Observation of quantum dynamical resonances in near cold inelastic collisions of astrophysical molecules. Chem. Sci. 2016;7:2462–2469. doi: 10.1039/C5SC04557F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein A., Shagam Y., Skomorowski W., Zuchowski P. S., Pawlak M., Janssen L. M., Moiseyev N., Van De Meerakker S. Y., Van Der Avoird A., Koch C. P.. et al. Directly probing anisotropy in atom-molecule collisions through quantum scattering resonances. Nat. Phys. 2017;13:35–38. doi: 10.1038/nphys3904. [DOI] [Google Scholar]
- Vogels S. N., Karman T., Kłos J., Besemer M., Onvlee J., van der Avoird A., Groenenboom G. C., van de Meerakker S. Y.. Scattering resonances in bimolecular collisions between NO radicals and H2 challenge the theoretical gold standard. Nat. Chem. 2018;10:435–440. doi: 10.1038/s41557-018-0001-3. [DOI] [PubMed] [Google Scholar]
- Bodo E., Gianturco F. A., Balakrishnan N., Dalgarno A.. Chemical reactions in the limit of zero kinetic energy: virtual states and Ramsauer minima in F + H2 → HF + H. J. Phys. B. 2004;37:3641–3648. doi: 10.1088/0953-4075/37/18/007. [DOI] [Google Scholar]
- Cui J., Krems R. V.. Gaussian process model for collision dynamics of complex molecules. Phys. Rev. Lett. 2015;115:073202. doi: 10.1103/PhysRevLett.115.073202. [DOI] [PubMed] [Google Scholar]
- Cui J., Li Z., Krems R. V.. Gaussian process model for extrapolation of scattering observables for complex molecules: From benzene to benzonitrile. J. Chem. Phys. 2015;143:154101. doi: 10.1063/1.4933137. [DOI] [PubMed] [Google Scholar]
- Balakrishnan N.. Perspective: Ultracold molecules and the dawn of cold controlled chemistry. J. Chem. Phys. 2016;145:150901. doi: 10.1063/1.4964096. [DOI] [PubMed] [Google Scholar]
- Paranjothy M., Sun R., Zhuang Y., Hase W. L.. Direct chemical dynamics simulations: coupling of classical and quasiclassical trajectories with electronic structure theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013;3:296–316. doi: 10.1002/wcms.1132. [DOI] [Google Scholar]
- Bowman J. M.. Roaming. Mol. Phys. 2014;112:2516–2528. doi: 10.1080/00268976.2014.897395. [DOI] [Google Scholar]
- Crespo-Otero R., Barbatti M.. Recent advances and perspectives on nonadiabatic mixed quantum-classical dynamics. Chem. Rev. 2018;118:7026–7068. doi: 10.1021/acs.chemrev.7b00577. [DOI] [PubMed] [Google Scholar]
- Babikov D., Semenov A.. Recent advances in development and applications of the mixed quantum/classical theory for inelastic scattering. J. Phys. Chem. A. 2016;120:319–331. doi: 10.1021/acs.jpca.5b09569. [DOI] [PubMed] [Google Scholar]
- Littlejohn R. G.. The semiclassical evolution of wave packets. Phys. Rep. 1986;138:193–291. doi: 10.1016/0370-1573(86)90103-1. [DOI] [Google Scholar]
- Lubich, C. From Quantum to Classical Molecular Dynamics: Reduced Models and Numerical Analysis; Zurich Lectures in Advanced Mathematics; European Mathematical Society, 2008. [Google Scholar]
- Makri N.. Numerical path integral techniques for long time dynamics of quantum dissipative systems. J. Math. Phys. 1995;36:2430–2457. doi: 10.1063/1.531046. [DOI] [Google Scholar]
- Sepúlveda M. A., Grossmann F.. Time-Dependent Semiclassical Mechanics. Adv. Chem. Phys. 1996;96:191–304. doi: 10.1002/9780470141557.ch4. [DOI] [Google Scholar]
- Makri N.. Quantum dissipative dynamics: A numerically exact methodology. J. Phys. Chem. A. 1998;102:4414–4427. doi: 10.1021/jp980359y. [DOI] [Google Scholar]
- Miller W. H., Zhao Y., Ceotto M., Yang S.. Quantum instanton approximation for thermal rate constants of chemical reactions. J. Chem. Phys. 2003;119:1329–1342. doi: 10.1063/1.1580110. [DOI] [Google Scholar]
- Shi Q., Geva E.. A semiclassical generalized quantum master equation for an arbitrary system-bath coupling. J. Chem. Phys. 2004;120:10647–10658. doi: 10.1063/1.1738109. [DOI] [PubMed] [Google Scholar]
- Ceotto M., Atahan S., Shim S., Tantardini G. F., Aspuru-Guzik A.. First-principles semiclassical initial value representation molecular dynamics. Phys. Chem. Chem. Phys. 2009;11:3861–3867. doi: 10.1039/b820785b. [DOI] [PubMed] [Google Scholar]
- Ceotto M., Atahan S., Tantardini G. F., Aspuru-Guzik A.. Multiple coherent states for first-principles semiclassical initial value representation molecular dynamics. J. Chem. Phys. 2009;130:234113. doi: 10.1063/1.3155062. [DOI] [PubMed] [Google Scholar]
- Richings G. W., Polyak I., Spinlove K. E., Worth G. A., Burghardt I., Lasorne B.. Quantum dynamics simulations using Gaussian wavepackets: the vMCG method. Int. Rev. Phys. Chem. 2015;34:269–308. doi: 10.1080/0144235X.2015.1051354. [DOI] [Google Scholar]
- Richardson J. O.. Perspective: Ring-polymer instanton theory. J. Chem. Phys. 2018;148:200901. doi: 10.1063/1.5028352. [DOI] [PubMed] [Google Scholar]
- Meyer H.-D., Manthe U., Cederbaum L. S.. The multi-configurational time-dependent Hartree approach. Chem. Phys. Lett. 1990;165:73–78. doi: 10.1016/0009-2614(90)87014-I. [DOI] [Google Scholar]
- Beck M. H., Jäckle A., Worth G. A., Meyer H.-D.. The multiconfiguration time-dependent Hartree (MCTDH) method: a highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000;324:1–105. doi: 10.1016/S0370-1573(99)00047-2. [DOI] [Google Scholar]
- Wang H., Thoss M.. Multilayer formulation of the multiconfiguration time-dependent Hartree theory. J. Chem. Phys. 2003;119:1289–1299. doi: 10.1063/1.1580111. [DOI] [Google Scholar]
- Schollwöck U.. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011;326:96–192. doi: 10.1016/j.aop.2010.09.012. [DOI] [Google Scholar]
- Thomas P. S., Carrington T. Jr. Using nested contractions and a hierarchical tensor format to compute vibrational spectra of molecules with seven atoms. J. Phys. Chem. A. 2015;119:13074–13091. doi: 10.1021/acs.jpca.5b10015. [DOI] [PubMed] [Google Scholar]
- Greene S. M., Batista V. S.. Tensor-Train Split-Operator Fourier Transform (TT-SOFT) Method: Multidimensional Nonadiabatic Quantum Dynamics. J. Chem. Theory Comput. 2017;13:4034–4042. doi: 10.1021/acs.jctc.7b00608. [DOI] [PubMed] [Google Scholar]
- Borrelli R., Gelin M. F.. Finite temperature quantum dynamics of complex systems: Integrating thermo-field theories and tensor-train methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021;11:e1539. doi: 10.1002/wcms.1539. [DOI] [Google Scholar]
- Gelin M. F., Borrelli R.. Simulation of nonlinear femtosecond signals at finite temperature via a thermo field dynamics-tensor train method: General theory and application to time-and frequency-resolved fluorescence of the Fenna-Matthews-Olson complex. J. Chem. Theory Comput. 2021;17:4316–4331. doi: 10.1021/acs.jctc.1c00158. [DOI] [PubMed] [Google Scholar]
- Soley M. B., Bergold P., Gorodetsky A. A., Batista V. S.. Functional tensor-train Chebyshev method for multidimensional quantum dynamics simulations. J. Chem. Theory Comput. 2022;18:25–36. doi: 10.1021/acs.jctc.1c00941. [DOI] [PubMed] [Google Scholar]
- Soley M. B., Videla P. E., Nibbering E. T., Batista V. S.. Ultrafast Charge Relocation Dynamics in Enol-Keto Tautomerization Monitored with a Local Soft-X-ray Probe. J. Phys. Chem. Lett. 2022;13:8254–8263. doi: 10.1021/acs.jpclett.2c02037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu N., Soley M. B., Batista V. S.. Tensor-train split-operator KSL (TT-SOKSL) method for quantum dynamics simulations. J. Chem. Theory Comput. 2022;18:3327–3346. doi: 10.1021/acs.jctc.2c00209. [DOI] [PubMed] [Google Scholar]
- Lyu N., Mulvihill E., Soley M. B., Geva E., Batista V. S.. Tensor-train thermo-field memory kernels for generalized quantum master equations. J. Chem. Theory Comput. 2023;19:1111–1129. doi: 10.1021/acs.jctc.2c00892. [DOI] [PubMed] [Google Scholar]
- Ross M. H., Shaw G. L.. Multichannel effective range theory. Ann. Phys. 1961;13:147–186. doi: 10.1016/0003-4916(61)90078-1. [DOI] [Google Scholar]
- Greene C. H., Rau A. R. P., Fano U.. General form of the quantum-defect theory. II. Phys. Rev. A. 1982;26:2441–2459. doi: 10.1103/PhysRevA.26.2441. [DOI] [Google Scholar]
- Gao B.. Theory of slow-atom collisions. Phys. Rev. A. 1996;54:2022–2039. doi: 10.1103/PhysRevA.54.2022. [DOI] [PubMed] [Google Scholar]
- Burke J. P. Jr, Greene C. H., Bohn J. L.. Multichannel Cold Collisions: Simple Dependences on Energy and Magnetic Field. Phys. Rev. Lett. 1998;81:3355–3358. doi: 10.1103/PhysRevLett.81.3355. [DOI] [Google Scholar]
- Bohn J. L., Julienne P. S.. Semianalytic theory of laser-assisted resonant cold collisions. Phys. Rev. A. 1999;60:414–425. doi: 10.1103/PhysRevA.60.414. [DOI] [Google Scholar]
- Mies F. H., Raoult M.. Analysis of threshold effects in ultracold atomic collisions. Phys. Rev. A. 2000;62:012708. doi: 10.1103/PhysRevA.62.012708. [DOI] [Google Scholar]
- Idziaszek Z., Quéméner G., Bohn J. L., Julienne P. S.. Simple quantum model of ultracold polar molecule collisions. Phys. Rev. A. 2010;82:020703(R) doi: 10.1103/PhysRevA.82.020703. [DOI] [Google Scholar]
- Jachymski K., Krych M., Julienne P. S., Idziaszek Z.. Quantum Theory of Reactive Collisions for 1/r n Potentials. Phys. Rev. Lett. 2013;110:213202. doi: 10.1103/PhysRevLett.110.213202. [DOI] [PubMed] [Google Scholar]
- Li M., Gao B.. Proton-hydrogen collisions at low temperature. Phys. Rev. A. 2015;91:032702. doi: 10.1103/PhysRevA.91.032702. [DOI] [Google Scholar]
- Li H., Li M., Makrides C., Petrov A., Kotochigova S.. Universal Scattering of Ultracold Atoms and Molecules in Optical Potentials. Atoms. 2019;7:36. doi: 10.3390/atoms7010036. [DOI] [Google Scholar]
- Lane A. M.. The application of Wigner’s R-matrix theory to atomic physics. J. Phys. B. 1986;19:253–257. doi: 10.1088/0022-3700/19/2/014. [DOI] [Google Scholar]
- Hategan C., Ionescu R.-A.. Multichannel quantum defect and reduced R-matrix. Proc. Rom. Acad. A. 2007;8:107–110. [Google Scholar]
- Sabin Del Valle J., Bodo E., Gianturco F. A.. Rotational cooling of molecular gases by positron impact at vanishing collision energies. J. Phys. B. 2005;38:2069–2077. doi: 10.1088/0953-4075/38/13/001. [DOI] [Google Scholar]
- Kadyrov A. S., Bray I., Stelbovics A. T.. Near-Threshold Positron-Impact Ionization of Atomic Hydrogen. Phys. Rev. Lett. 2007;98:263202. doi: 10.1103/PhysRevLett.98.263202. [DOI] [PubMed] [Google Scholar]
- Yamashita T., Kino Y., Hiyama E., Jonsell S., Froelich P.. Near-threshold production of antihydrogen positive ion in positronium-antihydrogen collision. New J. Phys. 2021;23:012001. doi: 10.1088/1367-2630/abd682. [DOI] [Google Scholar]
- Kadyrov A. S., Lugovskoy A. V., Utamuratov R., Bray I.. Benchmark calculation of hydrogen (antihydrogen) formation at rest in positronium-proton (-antiproton) scattering. Phys. Rev. A. 2013;87:060701. doi: 10.1103/PhysRevA.87.060701. [DOI] [Google Scholar]
- Lugovskoy A. V., Utamuratov R., Kadyrov A. S., Stelbovics A. T., Bray I.. Threshold behavior of positronium formation in positron-alkali-metal scattering. Phys. Rev. A. 2013;87:042708. doi: 10.1103/PhysRevA.87.042708. [DOI] [Google Scholar]
- Kadyrov A. S., Rawlins C. M., Stelbovics A. T., Bray I., Charlton M.. Antihydrogen Formation via Antiproton Scattering with Excited Positronium. Phys. Rev. Lett. 2015;114:183201. doi: 10.1103/PhysRevLett.114.183201. [DOI] [PubMed] [Google Scholar]
- Rawlins C. M., Kadyrov A. S., Stelbovics A. T., Bray I., Charlton M.. Calculation of antihydrogen formation via antiproton scattering with excited positronium. Phys. Rev. A. 2016;93:012709. doi: 10.1103/PhysRevA.93.012709. [DOI] [PubMed] [Google Scholar]
- Fabrikant I. I., Bray A. W., Kadyrov A. S., Bray I.. Near-threshold behavior of positronium-antiproton scattering. Phys. Rev. A. 2016;94:012701. doi: 10.1103/PhysRevA.94.012701. [DOI] [Google Scholar]
- Higgins M. D., Daily K. M., Greene C. H.. Low-energy scattering properties of ground-state and excited-state positronium collisions. Phys. Rev. A. 2019;100:012711. doi: 10.1103/PhysRevA.100.012711. [DOI] [Google Scholar]
- Danielson J., Gribakin G., Arthur-Baidoo E., Surko C.. Similarity of near-threshold energy dependence of positronium formation and photoionization in molecules. Phys. Rev. Lett. 2024;133:123001. doi: 10.1103/PhysRevLett.133.123001. [DOI] [PubMed] [Google Scholar]
- Pomerantsev V. N., Popov V. P.. Coulomb deexcitation of pionic hydrogen within the close-coupling method. Phys. Rev. A. 2006;73:040501. doi: 10.1103/PhysRevA.73.040501. [DOI] [Google Scholar]
- Popov V. P., Pomerantsev V. N.. Collision-induced absorption and annihilation in hadronic atoms within a close-coupling approach. Phys. Rev. A. 2012;86:052520. doi: 10.1103/PhysRevA.86.052520. [DOI] [Google Scholar]
- Qi Y. Y., Wang J. G., Janev R. K.. Dynamics of photoionization of hydrogenlike ions in Debye plasmas. Phys. Rev. A. 2009;80:063404. doi: 10.1103/PhysRevA.80.063404. [DOI] [Google Scholar]
- Qi Y.-Y., Ning L.-N.. Dynamic processes and polarizability of sodium atom in Debye plasmas. Phys. Plasmas. 2014;21:033301. doi: 10.1063/1.4867060. [DOI] [Google Scholar]
- Xie L. Y., Wang J. G., Janev R. K.. Relativistic effects in the photoionization of hydrogen-like ions with screened Coulomb interaction. Phys. Plasmas. 2014;21:063304. doi: 10.1063/1.4882244. [DOI] [Google Scholar]
- Qi Y. Y., Wang J. G., Janev R. K.. Photoionization of hydrogen-like ions in dense quantum plasmas. Phys. Plasmas. 2017;24:0621. doi: 10.1063/1.4985658. [DOI] [Google Scholar]
- Zhao G. P., Xie L. Y., Liu L., Wang J. G., Janev R. K.. Photoionization of C5+ ion in warm dense plasmas. Phys. Plasmas. 2018;25:083302. doi: 10.1063/1.5042295. [DOI] [Google Scholar]
- Lu S., Zhou F., Xie L., Ma Y., Zhao G., Gao X., Wu Y., Wang J.. Photoionization process of the hydrogenlike carbon ion embedded in warm and hot dense plasmas. Phys. Rev. E. 2024;109:055205. doi: 10.1103/PhysRevE.109.055205. [DOI] [PubMed] [Google Scholar]
- Yang B., Perera H., Balakrishnan N., Forrey R. C., Stancil P. C.. Quenching of rotationally excited CO in cold and ultracold collisions with H, He, and H2 . J. Phys. B. 2006;39:S1229–S1239. doi: 10.1088/0953-4075/39/19/S29. [DOI] [PubMed] [Google Scholar]
- Yang B., Stancil P. C.. Close-coupling study of rotational energy transfer and differential scattering in H2O collisions with He atoms. J. Chem. Phys. 2007;126:154306. doi: 10.1063/1.2720390. [DOI] [PubMed] [Google Scholar]
- Yanga B. H., Stancil P. C.. Rotational excitation of CH4 by He atoms. Eur. Phys. J. D. 2008;49:317–324. doi: 10.1140/epjd/e2008-00167-2. [DOI] [Google Scholar]
- Yang B. H., Stancil P. C.. Rotational excitation of NH3 and ND3 due to He atom collisions. Eur. Phys. J. D. 2008;47:351–358. doi: 10.1140/epjd/e2008-00061-y. [DOI] [Google Scholar]
- Yang B., Stancil P. C.. Rotational quenching of CO2 by collision with He atoms. J. Chem. Phys. 2009;130:134319. doi: 10.1063/1.3108998. [DOI] [PubMed] [Google Scholar]
- Fonseca dos Santos S., Balakrishnan N., Forrey R. C., Stancil P. C.. Vibration-vibration and vibration-translation energy transfer in H2-H2 collisions: A critical test of experiment with full-dimensional quantum dynamics. J. Chem. Phys. 2013;138:14302. doi: 10.1063/1.4793472. [DOI] [PubMed] [Google Scholar]
- Yang B., Stancil P. C., Balakrishnan N., Forrey R. C., Bowman J. M.. Quantum calculation of inelastic CO collisions with H. I. rotational quenching of low-lying rotational levels. Astrophys. J. 2013;771:49. doi: 10.1088/0004-637X/771/1/49. [DOI] [Google Scholar]
- Yang B., Stancil P. C.. Quenching of highly rotationally excited HCl in Collisions with He. Astrophys. J. 2014;783:92. doi: 10.1088/0004-637X/783/2/92. [DOI] [Google Scholar]
- Yang B., Walker K. M., Forrey R. C., Stancil P. C., Balakrishnan N.. Collisional quenching of highly rotationally excited HF* . Astron. Astrophys. 2015;578:A65. doi: 10.1051/0004-6361/201525799. [DOI] [Google Scholar]
- Yang B., Balakrishnan N., Zhang P., Wang X., Bowman J. M., Forrey R. C., Stancil P. C.. Full-dimensional quantum dynamics of CO in collision with H2 . J. Chem. Phys. 2016;145:034308. doi: 10.1063/1.4958951. [DOI] [PubMed] [Google Scholar]
- Jóźwiak H., Thibault F., Viel A., Wcisło P., Lique F.. Revisiting the rovibrational (de-)excitation of molecular hydrogen by helium. Astron. Astrophys. 2024;685:A113. doi: 10.1051/0004-6361/202348645. [DOI] [Google Scholar]
- Ashworth E. K., Bull J. N.. Photoelectron spectroscopy of deprotonated benzonitrile. J. Chem. Phys. 2024;161:114302. doi: 10.1063/5.0231206. [DOI] [PubMed] [Google Scholar]