An atmospheric pCO₂ reconstruction across the Cretaceous-Tertiary boundary from leaf megafossils

Abstract

The end-Cretaceous mass extinctions, 65 million years ago, profoundly influenced the course of biotic evolution. These extinctions coincided with a major extraterrestrial impact event and massive volcanism in India. Determining the relative importance of each event as a driver of environmental and biotic change across the Cretaceous-Tertiary boundary (KTB) crucially depends on constraining the mass of CO₂ injected into the atmospheric carbon reservoir. Using the inverse relationship between atmospheric CO₂ and the stomatal index of land plant leaves, we reconstruct Late Cretaceous-Early Tertiary atmospheric CO₂ concentration (pCO₂) levels with special emphasis on providing a pCO₂ estimate directly above the KTB. Our record shows stable Late Cretaceous/Early Tertiary background pCO₂ levels of 350–500 ppm by volume, but with a marked increase to at least 2,300 ppm by volume within 10,000 years of the KTB. Numerical simulations with a global biogeochemical carbon cycle model indicate that CO₂ outgassing during the eruption of the Deccan Trap basalts fails to fully account for the inferred pCO₂ increase. Instead, we calculate that the postboundary pCO₂ rise is most consistent with the instantaneous transfer of ≈4,600 Gt C from the lithic to the atmospheric reservoir by a large extraterrestrial bolide impact. A resultant climatic forcing of +12 W⋅m⁻² would have been sufficient to warm the Earth's surface by ≈7.5°C, in the absence of counter forcing by sulfate aerosols. This finding reinforces previous evidence for major climatic warming after the KTB impact and implies that severe and abrupt global warming during the earliest Paleocene was an important factor in biotic extinction at the KTB.

The end-Cretaceous period, 65 million years (Myr) ago, was marked by one of the five largest mass extinction events in Earth's history and had major evolutionary consequences for the surviving biota (1, 2). Severe extinctions of marine (≈80 families) and continental (≈100 families) organisms (2) within a few tens of thousands of years of the Cretaceous-Tertiary boundary (KTB) indicate the abrupt imposition of an environmental stress to which they were poorly adapted (1). Two long-competing hypotheses to explain this biotic crisis attribute marked “greenhouse” warming to either volcanic degassing of mantle volatiles (especially CO₂) during the eruption of the Deccan Traps in India (3, 4) or CO₂ release by a substantial extraterrestrial impact event (5). The bolide impact is widely accepted to have formed the ≈100-km diameter Chicxulub crater in the Yucatan Peninsula, Mexico (6). Because the target rock was a carbonate-rich marine sedimentary terrace, massive amounts of CO₂ are hypothesized to have been instantaneously (<30 s) transferred from the lithic to the atmospheric carbon reservoir, leading to enhanced greenhouse warming (7). Determining the actual shift in the atmospheric CO₂ concentration (pCO₂) has proved elusive, however, and this uncertainty limits our ability to propose causal mechanisms for the abrupt KTB mass extinctions shown by the marine and terrestrial fossil records.

Here we address this issue by using a palaeobotanical method of pCO₂ estimation based on the inverse relationship between the stomatal index (SI, proportion of epidermal cells that are stomatal pores) of land plant leaves and atmospheric CO₂ concentration (8). This approach offers the best temporal resolution of all palaeo-CO₂ proxies (several months to 10² years) (8) and is therefore most suitable for the detection of a multimillennial pCO₂ perturbation so far back in the geological record. We use the SI method with leaf megafossils of Ginkgo adiantoides to establish baseline pCO₂ levels for the latest Cretaceous/earliest Tertiary (66 Myr to 63 Myr ago). Atmospheric CO₂ levels immediately above the KTB were estimated by using SI measurements on cuticles of the extinct fossil fern aff. Stenochlaena, a taxon that became widespread and abundant in the Western Interior of North America immediately above the KT claystone layer (9, 10). In an attempt to decipher our paleo-CO₂ record, we used a global biogeochemical model of the carbon cycle (after ref. 11) to investigate the potential for either KTB volcanism and/or an impact event to force atmospheric CO₂ levels in a manner consistent with the pCO₂ reconstruction.

Materials and Methods

Fossil Leaves.

SI determinations were made on cuticles derived from leaf megafossils of G. adiantoides from seven stratigraphically well-dated sites in North America and one in Spitsbergen, an island in the high Arctic (Table 1). Identity with G. adiantoides was established on the basis of foliar architecture, and in particular the pattern of leaf lobation and number of veins per lobe. SI determinations also were made on cuticles derived from isolated leaflets of the fern aff. Stenochlaena from the Clear Creek South KTB locality in the Raton Basin, New Mexico, collected 5–25 cm above the iridium-rich KTB claystone layer that contains shocked quartz (9, 10, 12) (Table 1). The Clear Creek South fern megafossils occur immediately above the KTB coal, a thin coal bed that overlies the KTB clay in many sections from the Raton Basin, in a carbonaceous shale bed that contains both the fern spore abundance anomaly (or “fern spike”) and the overlying phase of vegetational recovery where woody angiosperms were returning to dominance in regional vegetation after mass mortality at the KTB. Identity of the Clear Creek South materials with Stenochlaena was established on the basis of morphological similarity with the leaflets of fern fronds that occur at stratigraphically equivalent localities in the Raton Basin, and which together are identical to the living genus Stenochlaena in terms of frond architecture, leaflet venation, tooth architecture, and peculiarities of stomatal anatomy.

Table 1.

Source, age and stomatal characteristics of fossil plants used to reconstruct Late Cretaceous to Early Tertiary changes in atmospheric CO₂

Site	Formation	Estimated age, Myr	Species	Life form	No. of leaves	SI, %	Atmospheric CO2 (ppm) ± 95% cls
1.  DMNH 571 (North Dakota)	Hell Creek formation	65.9  ± 0.2*	Ginkgo adiantoides	Deciduous tree	1	7.0  ± 0.5	554  ± 192
2.  DMNH 572 (North Dakota)	Hell Creek formation	65.8  ± 0.2*	G. adiantoides	Deciduous tree	2	7.1  ± 0.3	527  ± 105
3.  DMNH 566 (North Dakota)	Hell Creek formation	65.5  ± 0.2*	G. adiantoides	Deciduous tree	31	8.3  ± 0.1	384  ± 8
4.  DMNH 1489 (North Dakota)	Hell Creek formation	65.4  ± 0.2*	G. adiantoides	Deciduous tree	2	8.4  ± 0.3	361  ± 31
5.  Raton Basin (Colorado)	Raton formation	64.9†	aff. Stenochlaena	Evergreen fern	13	14.8  ± 0.1	>2,300
Clear Creek South	Vegetation phase II
6.  LJH 7423 (Montana)	Fort Union formation	64.5  ± 0.5‡	G. adiantoides	Deciduous tree	5	9.5  ± 0.2	338  ± 16
7.  LJH 7659 (Wyoming)	Fort Union formation	64.5  ± 0.5‡	G. adiantoides	Deciduous tree	15	9.3  ± 0.1	343  ± 10
8.  DMNH 2360 (Colorado)	Dawson formation	64.1  ± 0.2§	G. adiantoides	Deciduous tree	5	9.9  ± 0.3	329  ± 16
9.  South-central Spitsbergen	Firkanten formation	64.0  ± 1.0¶	G. spitsbergensis	Deciduous tree	8	9.4  ± 0.2	340  ± 13

^*Based on palaeomagnetic data and linear interpolation assuming the KTB = 65 Myr ago (37). 

^† Based on radiometric and some paleomagnetic data summarized in ref. 9. 

^‡ Sites are ∼5 m above the Lance/Fort Union formation contact (KTB) and are assigned a Puercan age (38). 

^§ Radiometric ⁴⁰Ar/³⁹Ar dating of a single sanidine crystal from an ash stratigraphically just below the fossil plant site (39). 

^¶ Site lies 20 cm above an unconformable surface, dividing an upper Cretaceous sandstone and the Tertiary Firkanten formation. Dinoflagellate and mollusc biostratigraphy suggest a Danian age for the Firkanten formation (40). The assigned age and errors are approximate only. Note that G. spitsbergensis is considered conspecific with G. adiantoides (41). 

Leaf cuticles were prepared from the fossils, and stomatal counts were made, following standard procedures (13, 14), with replication as given in Table 1. Site details, geologic formations, and approximate ages are given in Table 1.

Paleo-CO₂ Estimation.

Atmospheric pCO₂ levels were reconstructed from fossil Ginkgo cuticle SIs [SI(f)] by using a species-specific inverse regression function (15) given by:

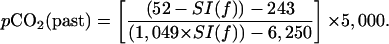1

Eq. 1 was derived from a combination of measurement on historical archives of G. biloba leaves collected during the anthropogenic CO₂ increases of the past 200 years and greenhouse CO₂ enrichment experiments (15, 16).

Measurements of fossil fern SIs were calibrated by developing a modern training set with the extant species Stenochlaena palustris, identified on the basis of foliar architecture, as one of its nearest living relatives (10). SI measurements were made on herbarium fronds of S. palustris from Indo-Pacific plants collected over the past two centuries of CO₂ increase. We supplemented these data with a series of controlled environment plant growth experiments, in which the growth pCO₂ level ranged from Late Cretaceous to Early Tertiary values (350–700 ppm by volume) and included an additional very high concentration (2,300 ppm). In the experiments, individual plants (n = 8 per atmospheric CO₂ concentration) were grown in controlled environment chambers under standard conditions (day/night temperatures 25/20°C, 350 μmol⋅m⁻²⋅s⁻¹ photosynthetically active radiation and a vapor pressure deficit of 1.2–1.4 kPa) at three different atmospheric CO₂ concentrations (350, 700, and 2,300 ppmv for 6 weeks). SI was determined on newly developed fronds from stomatal and epidermal cell counts made under light microscopy on acetate impressions of the leaf surface (n = two leaves per plant).

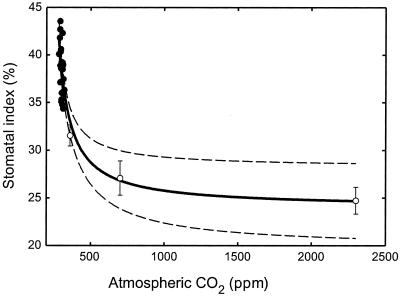
The resulting calibration function (Fig. 1) shows that as atmospheric pCO₂ increased from 280 to 330 ppmv between 1837 and 1964 AD SI declined linearly by 15%, confirming that the stomata of S. palustris are sensitive to atmospheric CO₂ (Fig. 1). At growth CO₂ concentrations >350 ppm, the SI response was nonlinear, as seen in experiments with a range of woody angiosperm trees, shrubs, and herbs (16). Nonetheless, SI continued to exhibit a decline between CO₂ concentrations of 700 and 2,300 ppm, establishing that the stomata of this taxon respond to very high atmospheric CO₂ concentrations (Fig. 1).

Figure 1.

Response of frond SI of the subtropical fern S. palustris to historical increases in atmospheric CO₂ (●) between 1837 AD and 1964 AD, and to different experimental growth CO₂ concentrations (○). The solid black line represents the nonlinear regression curve fitted to the experimental data {r² = 0.76, P < 0.0001; SI = (24.8996 × [CO₂ concentration, ppmv] − 4053.26)/([CO₂ concentration, ppm]) − 211.504}. Broken curves indicate ± the 95% confidence limits. Values are means ± 1 SE.

Global Carbon Cycle Modeling.

All of the simulations described here used a modified version of the carbon cycle model described in ref. 11. This global biogeochemical carbon cycle model emphasizes the roles of ocean chemistry and chemical weathering of carbonate and silicate rocks in regulating the concentration of atmospheric CO₂ in the long term (11). In the model, the decadal to millennial scale response to a large addition of CO₂ to the atmosphere is dominated by oceanic uptake, but this sink is limited by the relatively small buffering capacity of dissolved CO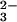. Seafloor dissolution of CaCO₃ provides additional buffering. As CO 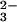is depleted the calcium-carbonate compensation depth shallows, exposing more seafloor to undersaturated, corrosive waters. But after ≈10⁵ yr only weathering provides a sink for the remaining, additional CO₂. Weathering of both limestone and silicate rock involves the neutralization of atmospheric CO₂ in soil waters and the transport of cations and bicarbonate to the ocean. The ocean accumulates this alkalinity, resaturates, then begins to deposit CaCO₃ as fast as Ca²⁺ and HCO 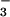are delivered to the ocean. Thus, at this stage only silicate weathering and CaCO₃ deposition provide a net sink, and these restore the atmosphere to its original state only over 10⁵- to 10⁶-year time scales.

Most of the model specifications are as in ref. 11 including the separation of the ocean into subreservoirs (boxes), the parameterization of ocean mixing rates as transfers between these reservoirs (tuned to the modern), and the treatment of the controls on lysocline depth (including a specification of the modern hypsometric curve). Weathering rates were scaled to an estimate for the present day (11). For these short-interval runs, land area, evolutionary, and tectonic correction factors (17) were held constant, and only the climate sensitivity of chemical weathering was factored into the weathering calculation. This “correction factor” was specified to be a function of the CO₂ greenhouse effect (as it controls runoff and global temperatures) according to the climate weathering factor (f_wr) (18):

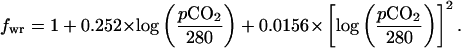Alternative formulations could be used (17, 19), and these would change somewhat the rate at which the CO₂ pulse was removed from the atmosphere. In the simulations described below, use of the formulation in refs. 17 and 19 leads to faster drawdown of the CO₂ pulse, meaning that larger amounts of CO₂ have to be injected to sustain a particular pCO₂ at some point in time after the event.

The rate of organic carbon burial was specified to be a constant proportion (0.24) of the weathering input of carbon, and the remainder was removed as carbonate carbon. No attempt was made to mimic the carbon isotopic record of the Early Tertiary. However, it has been argued (20) that the isotopic response indicates only a small (10%) reduction in organic carbon burial rates in the earliest Tertiary. A steady-state value of ≈400 ppmv CO₂ in the atmosphere was achieved by arbitrarily increasing the volcanic CO₂ input for the latest Cretaceous by 20% compared with the modern-day rate.

Results and Discussion

Atmospheric pCO₂ Reconstruction.

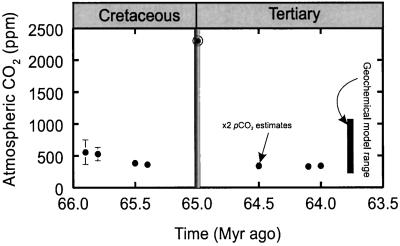
The calibrated fossil leaf cuticular records yield background pCO₂ values of around 350–540 ppm between the Late Cretaceous and the Early Tertiary. The record exhibits strong self-consistency with Ginkgo leaves of the same age, but derived from different sites, yielding similar pCO₂ estimates (Fig. 2). Although SI determinations were made on fewer than five leaves for three of the Late Cretaceous sites, we have included them here because of the relative paucity of proxy CO₂ data for this interval (8). Our stomatal-derived paleo-CO₂ values for the latest Cretaceous and earliest Tertiary all lie within the ranges predicted by long-term geochemical carbon cycle modeling (17) and reconstructed from pedogenic carbonates (21), demonstrating congruence between estimates of ancient pCO₂ levels based on paleobotany and nonbiological proxies.

Figure 2.

Reconstructed atmospheric CO₂ variations during the Late Cretaceous–Early Tertiary dervied from the SI of fossil leaf cuticles calibrated by using inverse regression and stomatal ratios (see Table 1). Values are means ± 1 SE. The KTB estimate (○), derived from fossil ferns, represents a minimum value. The vertical bar indicates the CO₂ range predicted from geochemical modeling of the long-term carbon cycle (17).

Immediately above the KTB, the SI of fossil fronds of aff. Stenochlaena have extremely low SIs in comparison to fronds of modern S. palustris (Table 1), and those of three other modern nonepiphytic Stenochlaena spp. (SI = 28–32, n = 3 spp.). These values are beyond the range of the calibration dataset (Fig. 1; Table 1), suggesting the ferns grew under an atmospheric pCO₂ level of at least ≈2,300 ppm. One potential complicator of our estimate is reduction of solar illumination by stratospheric sulfate aerosols decades to centuries after the KTB impact event, which would cause reductions in SI similar to those caused by increased atmospheric pCO₂. However, measurement of helium isotopes from the KTB claystone in marine rocks indicates that the claystone was deposited over a period of at least 10 ± 2 thousand years (kyr) (±1 σ) (22), more than sufficient time for removal of dust and sulfate aerosols from of the atmosphere. Therefore, if the KTB clay in both terrestrial and marine sections was formed by the same set of geologic processes, then the low fern SI is consistent with a high pCO₂ environment, rather than changes in irradiance, resulting from impact-derived tropospheric debris, because the entire KTB claystone layer was deposited over at least 10 kyr (22), a time of sufficient duration to allow any debris to settle out of the atmosphere. The assumption that the low SI values reflect a high paleo-CO₂ level must be considered against the caveat that, despite the abundance of Stenochlaena spp. leaf megafossils immediately above the KTB within the Raton Basin, extensive field and laboratory investigations have not yet located specimens from other localities with cuticles suitably preserved for SI determinations. Moreover, our estimate of highly elevated pCO₂ just after the extinction event is based on fern SI, whereas the background pCO₂ is based on Ginkgo, a less than ideal situation created by sample availability. Therefore this result must be taken as provisional.

Underlying Processes.

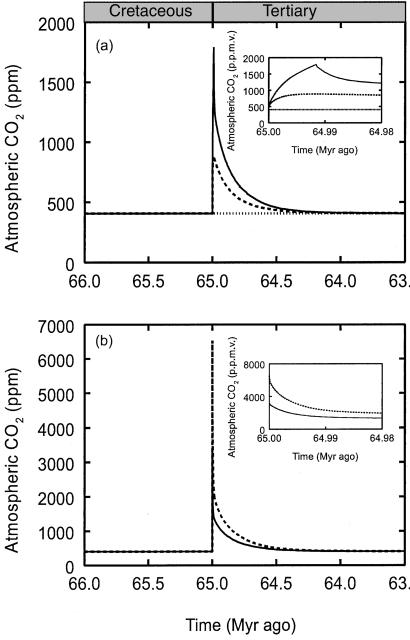
Proceeding on the basis that our KTB pCO₂ estimate is secure, we investigated the likely underlying mechanism(s) responsible in a series of numerical experiments with a global biogeochemical carbon cycle model emphasizing the roles of ocean chemistry and chemical weathering of carbonate and silicate rocks (11). We determined the relative contribution of the two phenomena likely to have been involved in the observed post-KTB pCO₂ increase: (i) an increase in volcanic CO₂ outgassing from the eruption of the Deccan Traps; and (ii) carbonate vaporization by a bolide impact. Both assessments were made assuming collapse in marine biological primary production, as indicated by loss of the planktonic-to-benthic stable carbon isotope gradient (reviewed in ref. 23) (the so-called “Strangelove ocean”). By itself, the loss of an oceanic biological pump to efficiently deliver CO₂ to the deep ocean leads to a marked, but transient, pCO₂ increase from 400 to 900 ppm (Fig. 3a) that would account for ≈25% of the post-KTB pCO₂ rise.

Figure 3.

Simulated effects of a collapse in oceanic productivity (so-called Strangelove ocean), CO₂ outgassing during the eruption of the Deccan Traps and an extraterrestrial bolide impact on atmospheric pCO₂ changes across the KTB. (a) Effects of volcanic CO₂ emissions over a period of 10 kyr (solid line), and 2 Myr (finely divided line), and the effect of a Strangelove ocean (broken line) on atmospheric pCO₂. (b) The atmospheric pCO₂ response arising from an instantaneous injection of 6,500 (solid line) or 13,000 Gt CO₂ (broken line) from a bolide impact. (Insets) The atmospheric pCO₂ response in each case for the first 20 kyr of each simulation.

Volcanic CO₂ emissions were simulated by taking an upper limit for the total CO₂ emission from the Deccan traps of 5 × 10¹⁷ mol (≈6,000 Gt) (3) and varying the rate of injection into the ocean-atmosphere system between 10 kyr (unrealistically assumes the KTB claystone layer is entirely of volcanic origin) and 2 Myr (the span of K-Ar dates for the Deccan Traps basalts) as upper and lower durations, respectively. Simulated enhanced volcanic CO₂ emissions over a period of 2 Myr had no discernable effect on atmosphere pCO₂ because the additional volcanic input is a small fraction of the background rate (Fig. 3a). When the emissions occur in a more extreme case, with a 6,000-Gt pulse of CO₂ being injected into the atmosphere over 10 kyr, pCO₂ rises by 1,400 ppm with a Strangelove ocean (Fig. 3a). These results are consistent with earlier carbon cycle model simulations of mantle degassing during the emplacement of the Deccan Trap basalts (24). However, there is little dating evidence to support a short 10-kyr duration for the eruption of the entire Deccan Traps and best estimates place it at 1–2 Myr (25). If this is the case, as seems likely, the direct effects of the Deccan Traps eruptions on atmospheric pCO₂ were small (23) (Fig. 3a). Use of an alternative formulation for weathering sensitivity to climate (19) damps the atmospheric response to Deccan volcanism even further.

The potential for a bolide impact at the KTB to influence atmospheric pCO₂ levels depends on the mass of CO₂ injected into the atmosphere. Our sensitivity analyses indicated that a direct injection of at least ≈6,400 Gt CO₂ into the atmosphere is required to increase pCO₂ levels sufficiently so that they are still 2,000 ppm some 10 kyr after the KTB (Fig. 3b). If the fossil ferns above the claystone layer record an atmospheric CO₂ level over 10 kyr after the impact, or if pCO₂ values >2,300 ppm, then a correspondingly larger mass of CO₂ is implicated. A further simulation (results not shown), for example, indicates that 13,000 Gt CO₂ would be required to drive atmospheric pCO₂ sufficiently high (6,000 ppm) such that pCO₂ levels of ≈2,300 ppm still existed 20 kyr after the impact. Even larger amounts are required if an alternative weathering feedback is invoked (19). Injections of these magnitudes lead to very short-lived high atmospheric CO₂ values, but with a draw-down resulting from the induction of ocean chemistry feedbacks over the ensuing 0.5 Myr (Fig. 3b).

Our estimated total mass of between 6,400 and 13,000 Gt of CO₂ evacuated from the carbonate terrace by the KT impact event lies at the lower end of the range derived from early numerical modeling of a projectile impacting on a 3-km thick limestone bed (7). However, it is significantly greater than the range of 350 to 3,500 Gt CO₂ derived from more recent model studies of the Chicxulub impact. These later geophysical modeling studies derive lower values than earlier studies by considering the effects of modeling in two and three dimensions, providing more precise characterization of target rock, using higher vaporization pressures for calcium carbonate, and varying impact angle (26–28). The discrepancy between our high estimated mass of impact-derived CO₂ relative to that of recent geophysical models could mean that our combined paleobotanical/geochemical analysis omits at least one important process or contains at least one incorrect assumption. However, it could also mean that geophysical models of the bolide impact grossly underestimate the amount of CO₂ released to the atmosphere at the KTB because they fail to incorporate processes such as shear heating of target rock by an oblique impact, which could increase CO₂ production by up to an order of magnitude (29).

Climate model and radiative transfer calculations (30) indicate that a rise in atmospheric pCO₂ to 2,300 ppm within 10 kyr of the KTB (Table 1) would have increased climate forcing by +12 W⋅m⁻², leading to an average global warming of ≈7.5°C (range of uncertainty = 4.5^oC to 13.5^oC) (30). As is well documented from the paleoclimatic record (31), warming would have been significantly greater than the global mean at high latitudes and significantly less at low latitudes. This pattern is consistent with oxygen isotope evidence for warming of mid to high latitude ocean surface waters by 10–12°C within a few thousand years after the impact event (reviewed in ref. 32) and with foliar physiognomic evidence for similar warming of midlatitude terrestrial climates during the earliest Paleocene (33). Such marked warming during the earliest Paleocene would have strongly stressed ecosystems already affected by cold temperatures and the blockage of sunlight during “impact winter” and contributed to the well-documented mass extinction at the KTB (1, 7). Although oceanic warming appears to be diminished or lacking at low-latitudes (34), interpretation of the low-latitude record is problematic because of significant diagenetic alteration (35) and unrecognized depositional hiatuses (36).

Abbreviations

Myr

million years

KTB

Cretaceous-Tertiary boundary

SI

stomatal index

kyr

thousand years