A framework for sustainability science: A renovated IPAT identity

Abstract

Learning actors' leverage for change along the journey to sustainability requires quantifying the component forces of environmental impact and integrating them. Population, income, consumers' behavior, and producers' efficiency jointly force impact. Here, we renovate the “IPAT Identity” to identify actors with the forces. Forcing impact I are P for population, A for income as gross domestic product (GDP) per capita, C for intensity of use as a good per GDP, and T for efficiency ratios as impact per good. In the “ImPACT Identity,” parents modify P, workers modify A, consumers modify C, and producers modify T. Because annual percentage changes in component forces add to a change in national impact, actors' leverage is reflected transparently in consistent units of annual percentage changes that can be compared from force to force. Examples from energy and food, farming and manufacturing, and steel and water show that declining C, called dematerialization, can temper the sustainability challenge of growth (P × A), and that innovation or efficient technology that lowers T can counter rising consumption (P × A × C). Income elasticity can accommodate connections between income and other forces. From rates of change of forces, the identity can forecast impacts. Alternatively, by identifying the necessary change in forces to cause a projected impact, ImPACT can assay the likelihood and practicability of environmental targets and timetables. An annual 2–3% progress in consumption and technology over many decades and sectors provides a benchmark for sustainability.

In this paper, we renovate a method widely used for analyzing, projecting, and thus guiding the use of resources with less impact. The method builds on the “IPAT Identity” that Commoner, Ehrlich, and Holdren introduced (1–4). In IPAT, the forces of population (P), affluence (A), and technology (T) cause an impact (I). During the past three decades, the meaning of P has endured, but changing definitions and dimensions of I, A, and T plus connections among the forces have confused discussion. Technology has been cast as both villain and hero and has been a mere residual left over. For all of the talk of IPAT, only a few analysts (5) bothered to estimate quantities for the forces and widen knowledge through the identity.

Moreover, during the last decade, industrial ecologists, systematically seeking leverage to lessen environmental harm, have taken a keen interest in a term not in IPAT. Industrial ecologists call it “intensity of use,” calculated as annual uses per gross domestic product (GDP) of goods from fuel and iron to timber and land (6). For example, energy and carbon per GDP have become popular indicators of performance with regard to global warming.

Here, we shall illustrate how dimensionally correct identities transparently connect environmental impact to intensity of use plus other forces driving impact. The identities connect environmental impacts with iron inflexibility to the driving forces, revealing the leverage of actors. Illustrations of impact range from water consumed and land tilled to greenhouse gases emitted. The driving forces range from population and GDP to food per GDP and crop per hectare. Our illustrations begin a codification, arranging, and systematizing of the identities to identify actors with leverage on forces for sustainability and, conversely, how much achieving an environmental goal will cost in changed forces.

Dimensions Make an Iron Framework from Forces to Impact

To every quantity, a dimension or unit attaches. “One thousand coal” means nothing until we attach “tons.” If the objective were anticipating greenhouse warming, the tons would require conversion to degrees Celsius by multiplication. The multipliers would be carbon dioxide tons per ton of coal burned and degrees warming per carbon dioxide ton. A further objective of relating population and power generation to warming would require more ratios such as kilowatt-hours per person and coal per kilowatt. The multiplication and change of dimensions must proceed until the dimensions on the driving side of the identity correspond to those on the resulting side. Dimensions provide an ironclad audit of forces proposed for an index of impact, and the simplicity guarantees wide applicability.

Commoner (1) demonstrated a system of dimensions by an amusing example:

I (bottles) = P (capita) × A (gallons of beer per capita) × T (bottles per gallon).

Although dimensionally correct, measuring affluence as gallons of beer per capita surprises. Beer is really taste, not affluence. Bottles per gallon scarcely indicate technology. Bottles of inert silica scarcely seem to be a poisonous environmental impact. If roadside litter rather than poison was intended as the environmental impact, then

I (bottles per mile) = P (capita) × A₁ (miles driven per capita) × A₂ (gallons of beer per mile driven) × T₁ (bottles used per gallon beer) × T₂ (bottles out the window per bottle used).

This identity extends population, affluence, and technology to a clear impact in dimensionally correct terms. It shows the forces putting bottles along the road so that environmentalists might condemn them. Control birth, drive less, drink less beer per mile, empty larger bottles, and shun defenestration.

Actors Drive Forces

We first codify the identity, connecting force to impact with standard words and symbols for forces (Table 1). In addition to defining symbols for an impact and the forces causing it, we name actors who can lever the forces and illustrate with carbon emission. A capital letter refers to a force such as population P and names its annual percentage change with a lowercase p.

• I and i. The identity begins with the environmental impact on the left side, whose dimensions must be identical to the product of the dimensions on the right side and is illustrated by emission.

• P and p. Population, which parents affect.

• A and a. Gross Domestic or World Product per person (GDP/capita). Produced by workers, A gives the income or economic muscle for the population to use. To reflect the symbol, we might call A affluence. Because affluence means rich or opulent, we instead usually call A income because it extends from poverty to riches.

• C and c. Intensity of use, such as energy per GDP. Consumers lever C as they decide to employ more or less of their economic muscle on the product that will eventually impact the environment. We define dematerialization, or resource sparing by consumer behavior, as a declining C and so negative c.

• T_i and t_i. The ratio of environmental impact to goods demanded by people and produced. Engineers and industry can affect this force by inventing, perfecting, and employing technology. For brevity, we call these actors “producers.” In the first column of the table with energy consumption per GDP as the intensity of use C and emission as the impact I, dimensions require T to be emission per energy. More than one T_i would be required if, e.g., the forcing of global warming had been chosen for the impact; then T₁ would be carbon emission per energy, and T₂ would be the climate forcing per carbon emitted. In the end, the dimensions on the left must match those of I. We define a declining T as efficiency, getting more consumable goods per environmental impact.

Table 1.

Symbols for environmental impacts and the actors and forces that affect them, exemplified by energy emission

Category	Symbol	Actors	Dimension
Impact	I	All	Emission
Population	P	Parents	Capita
Affluence	A	Workers	GDP/capita
Intensity of use	C	Consumers	Energy/GDP
Efficiency	T	Producers	Emission/energy
Consumption/capita	A × C		Energy/capita
Consumer challenge	P × A × T		GDP × (Emission/Energy)
Technology challenge	P × A × C		Energy
Sustainability challenge	P × A		GDP
Sustainability levers	C × T		Emission/GDP

The combination A × C is per capita consumption or, in the example, per capita energy use. Other forces combine to challenge the actors whose force and hence lever is unnamed. For example, P × A × T challenges consumers. Consumers must meet their challenge by using their lever C of less energy per GDP. Similarly, given P × A × C emission, mitigation depends solely on producers using their lever to lower the ratio of emission to energy, which makes P × A × C the producers' challenge.

Sustainable consumption and production are responding to wants and needs for a better life with minimum impact. So, the combined forces P × A, with dimension GDP, challenge consumers and producers to use their levers C × T, emission per GDP. Sustainability levers seem an apt name for C × T, emission per GDP. C × T accepts the drive for a better life embodied in the forces of population and income and challenges consumers' lifestyle and producers' skill to lessen impact and so to sustain a good life.

These definitions assembled into the framework called ImPACT can organize the accretion of definitions and dimensions that IPAT has collected since it emerged a generation ago. A goal is finding which actor has leverage for lessening environmental impact. Hence, recasting the identity to separate consumption per person into A × C and the sustainability levers of energy per GDP into C × T has a virtue. It separates economic muscle A from the C consumers choose and from the T producers lever. It separates the effects of lifestyles from technologies to lower impact per economic output, which must both be understood on the journey to sustainability (7). It separates the consumers' choice C from the producers' accomplishment T. For a government, ImPACT separates success in slowing P and lifting A from success in encouraging conservation in C and regulating pollution in T.

ImPACT simply shows changing environmental impact means changing four multiplying forces: the number of people, the economic muscle of each, the fraction of economic activity devoted to a good, and the impact of making the good. Consumers can lessen impact by using lever C, and producers can lessen impact by innovating with lever T. Dematerialization is declining C, and efficiency is declining T.

Countering One Another, Forces Temper Impacts

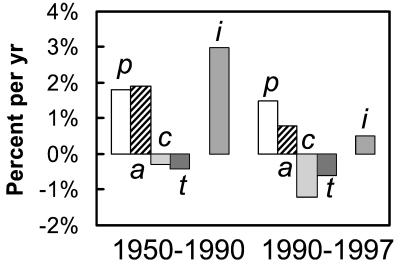
We exemplified the dimensions of the identity with the impact of carbon emission, which fits like a glove the formulation ImPACT and its cast of four actors. In this so-called Kaya identity, population P, workers' economic muscle A, consumers' use C of that muscle for energy consumption, and finally the producers' T emission of gas per unit of energy drive the impact I of gas emission. Hoffert et al. (8) used the identity, where the change per yr i is carbon emitted, c is energy per GDP, and t is emission per energy. For the world 1950–1990, they estimated that intensity of use declining 0.3 and efficiency improving 0.4% per yr moderated the increase in emission i to about 3% per yr (Fig. 1). For the 1990s, we estimated that slowing income growth, falling intensity of use, and greater efficiency limited i to 0.5% per yr.

Figure 1.

The changes of population (p), income (a), intensity of use of energy (c), and carbon emission per energy (t) altering global carbon emission (impact, i) (data sources: first period, ref. 8; second period, www.eia.doe.gov/oiaf/ieo/pdf/append_a.pdf; gross world production from World Bank).

The declining c, which was faster in the second period than in the first, is dematerialization. The declining t, which was also faster in the second period, is improving efficiency. These examples illustrate that the declining C called dematerialization can moderate the challenge of burgeoning consumption P × A × C. They also show the innovation called efficiency that lowers T can counter rising consumption P × A × C. The combined declines of C × T might be called decarbonization and striving to meet the sustainability challenge. Forces counter one another, and so temper impacts in the face of rising P × A.

Multiple Ratios Balance Dimensions of an Impact

More than one force may come between consumption and a clear environmental impact. Consider the impact of meat consumption on the expanse of cropland, which some single out as driving agricultural expansion. In the U.S., growing animal feed (corn, oats, barley, and sorghum) occupies one-third of the cropland. The familiar population p and income a begin the tally of changing forces driving cropland change i. Here, meat consumption per GDP becomes changing intensity of use c. Because the feed ratios for beef, pork, and poultry differ, the choice of meat and efficiency of feeding animals changes the amount of feed necessary to produce the chosen diet, requiring the t₁. Because crop yields vary among crops and over the years, the final determinant t₂ is the change of cropland area to produce a ton of feed grain. Analyzing these forces that change the cropland growing feed shows how meat on the table integrates them into cropland area (15).

Annually on average during 1967–1992, U.S. population rose 1.0%, and income rose 1.5%, lifting GDP just over 2.5%. But, surprising environmentalists and cattlemen alike, consumers lowered their annual meat consumption per GDP, the intensity of use C, by 1.5%. At the same time quantity changed, the quality also changed. The portion of pork remained steady, but the portion of beef fell and poultry rose. Because the ratio of feed to meat is lower for poultry than beef, this change lowered the average ratio. This change might be ascribed to consumers' dietary choice and a C₂ inserted in the equation. Instead, we ascribed it to producers' efficient husbandry providing more meat per feed. We inserted a T₁, implying that producers provided more meat with less feed. This situation is analogous to producers of energy lowering T emission of carbon gas per unit of energy by shifting from coal to gas fuel. The calculated feed to produce a unit of meat fell at an annual rate t₁ of 0.9%.

Among the forces, the land required to produce a ton of feed changed most. Farmers raised yields of feed grain, decreasing the land needed per ton of feed by 2.4% annually. When the changes are added, c + t₁ + t₂ outweigh the challenge of people and their incomes, p + a. In an example illustrating the need for more than one T to balance the dimensions of forces and impact and the tempering of impact by both consumers and producers, the calculations for ImPACT show cropland for grain-fed animals to produce meat for Americans shrank 2.2% annually.

Forces Change Both Slowly and Swiftly

Trends of forces rather than averages spanning periods reveal the transient nature of rapid change. The mention above of “iron” inflexibility and dimensions makes remarking on the fluctuating rates of steel production appropriate. In the U.S. during the 20th century, epochs such as World War I, the Great Depression, and World War II scarcely affected the course of p, which grew rather steadily at 1–2% per yr. However, such periods meant big fluctuations in a and the intensity of use c of steel. The change in income a calculated from 9-yr averages ranged from a boom of 8% per yr to a depression of −3%. To focus on trends, we generally smooth the data over a few years. Because such rapid changes could not persist for a century, the annual change a calculated from the difference 1900–1998 was only 1.8% per yr. While the intensity of use c rollercoasted from a rise of 20% per yr to a fall of 12%, the difference between 1900–1998 was a slight dematerialization of 0.5% per yr. (Nine-year averages from various U.S. Census Bureau reports and from U.S. Geologic Survey http://minerals.usgs.gov/pubs/of01-006/ironandsteel.pdf). Even without T to connect consumption to a clear environmental impact, the trend in steel consumption exemplifies the steadiness of P compared with the variability of income A and intensity of use C. To extend this steel consumption P × A × C to an impact of, say, ore mined requires T, mining per steel production, which the recycling of scrap could lower and thus temper the impact.

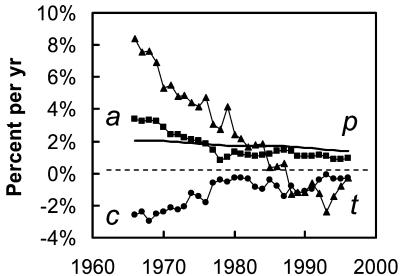
In another farm technology, the rapid rise in the use of nitrogen fertilizer after World War II tumbled from an explosive 11% rise of global use in the 1960s to little change in the 1990s (Fig. 2). The growth of population slowed steadily, and with some fluctuation, the rise of income also slowed. The C crop per GDP regularly fell. The preeminent force leveling fertilizer use, however, was the rapid deceleration of fertilizer per crop production. By using the T lever, farmers learned to produce more grain without tandem additions of fertilizer.

Figure 2.

The forces that slowed the rise of global use of nitrogen fertilizer. The annual changes of population (p), income (a), intensity of use of crops (c), and fertilizer per crop (t) calculated from 9-year running averages (source: ref. 9).

Sometimes, as in steel production, the variability of a and c means their eye-popping changes are passing specters but not enduring threats to the environment. In many cases, as in nitrogen fertilizer, the rapid rise of a new product slows, alleviating the fear of a rise that seems to be exponential at first but soon shows itself to be logistic.

Forces Connect with Each Other

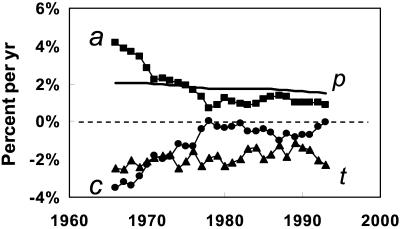
Multiplying the forces P × A × C × T together implies that they are independent. They are not (10). Although income surely affects adaptation to an impacted environment, we concentrate on connections among forces and the impact I itself. In a cross section of nations in 1989, a connection between A and C × T was evident in the smaller emission of CO₂ per income and population in rich than in poor countries (5). In another example, plotting the courses of the forces driving the expanse of cropland reveals connections among the forces (Fig. 3). The mirroring of changing income by changing intensity of use reveals by far the closest connection among these forces. As an example, we examine the connection between income and intensity of use, remembering that other connections exist.

Figure 3.

The mirroring of global income by the intensity of consumption of food. The changes of population (p), income (a), intensity of consumption of food (c), and land per crop (t) (source: ref. 11).

Economists connect food consumption to income with an income elasticity b. Per capita consumption A × C is proportional to A^b_, and so a + c = b × a. Engels' law that the proportion of family budgets spent on food declines as income rises means b < 1, making the demand for food inelastic. If elasticity b = 0.3, then annually raising income 1% raises per capita food demand 0.3%. A comparison of per capita nutrients with per capita GDP quickly shows that for the same periods and nations, elasticity ranges from low for calories and vegetal protein to moderate for animal protein (data from http://www.fao.org). Further, the moderate elasticity for animal protein declines with growing income. A general income elasticity can be estimated from a food production index (http://apps.fao.org/). The index weights food supply by the market value of the constituents of the food basket. Estimated for the globe during 1961–1997, the income elasticity of the food index per capita is 0.3.

If we know the income elasticity b of per capita consumption a + c, we also know the elasticity of per GDP consumption c is (b − 1). If b = 0.3, then the elasticity of c is −0.7. Whenever the elasticity b of consumption per person is less than 1, the elasticity of intensity of use c will inevitably be a negative (b − 1). Put another way, let the estimated income elasticity of changing per capita consumption be 0.3; then, a 1% annual increase in a of income will cause a 0.3% increase in a + c of per capita consumption, and thus, a 0.7% fall in c intensity of use. Such a coupling of dematerialization with rising income plus reasonable rates of change of population, income, and yield project shrinking global cropland (11).

Developing as well as developed nations dematerialize. During the last quarter of the 20th century in six developing nations with income rising faster than 2% per yr, food per GDP dematerialized at 1.5–2.0% per yr (11). At the same time, in five of these developing nations, food per capita rose.

Because declining intensity of use, i.e., negative c, is dematerialization, raising income inescapably dematerializes whenever income elasticity of consumption per person is less than 1. Conversely, lowering income materializes whenever elasticity of consumption per person is less than 1 and so does not lessen impact in proportion to the declining income.

Dematerialization as income rises brings to mind the so-called environmental Kuznets curve. In an example, a curve of intensity of use C first rises as income A grows but then falls, tracing an inverted U of first materialization and then dematerialization (6). If C is independent of A, no Kuznets curve will be traced. On the other hand, if C is proportional to A^(b−1), ln(C) will rise when b is greater than 1 and dematerialize when b is less than 1. Thus, the changing slope of the inverted U can be regarded as a change from income elasticity to inelasticity as income rises.

A graph of sulfur dioxide concentration in the air increasing and then falling as income grows also exemplifies a Kuznets curve (12). Like the Kuznets curve for dematerialization, this graph also requires connections among income and the other forces causing impact. Let population in an area be related to income with an elasticity b_P, C with an elasticity (b − 1), and technology with an elasticity b_T. Then, the change in ln(I) or pollutant concentration with ln(A) or income will be [bP + 1 + (b − 1) + b_T]. If the three elasticities are zero because the forces are independent of income, ln(I) will rise in proportion to income. This result would trace the rise but not the fall of the Kuznets curve. On the other hand, relations with income represented by the three could decrease population in the area, raise consumption little, and improve technology as income rises. Then, a beneficial combination could cause the Kuznets curve's decline at high income. Again, Kuznets curves can be regarded as evidence of connections with changing elasticities between income and other forces.

Sectors Act Differently

Sectors of an economy may act differently to change national impact. Because water with land and air compose the environmental trinity, dematerialization in the form of dewatering surely lessens environmental impact. In a panel of data across states and through 1960–1995, Rock (13) found significant dewatering per rising income or per production in industry. These exceeded the dewatering in public supply, which, in turn, exceeded an insignificant dewatering in agriculture.

During the period 1970–1995, U.S. population, income, and water use per GDP changed fairly steadily (Table 2). During that quarter century, population grew about 1% per yr and income grew about 1.5%. Because use grew only 0.2%, water use per GDP fell at 2.3% per yr. Which sectors exerted the most leverage to achieve this impressive meeting of the sustainability challenge? With production indices in agriculture and manufacturing and water use per sector, we can delve deeper, comparing industrial and agricultural actors and both consumers and producers. Intensity of use C is agricultural or manufacturing production per all of the economic activity encompassed by GDP. The negative c in Table 2 for agriculture indicates agriculture grew more slowly than other sectors, whereas the positive c indicates manufacturing grew more swiftly. The negative t in agriculture shows agricultural withdrawal of water for irrigation grew more slowly than agriculture as a whole. The 5.1% per yr decline of water use per manufacturing shows dramatically increased efficiency by these producers.

Table 2.

Changes per year of four forces driving changes in water use in the U.S. agricultural and manufacturing sectors, 1970/95

Sector	i	p	a	c	t
National	0.2%	1.0%	1.5%	−2.3%
Agr	0.1%	1.0%	1.5%	−0.7%	−1.7%
Mfg	−1.9%	1.0%	1.5%	0.6%	−5.0%

In all lines, i, p, and a are the national changes of water withdrawal, population, and GDP per capita. In line National, −2.3% is the change in water withdrawal per GDP, c + t. In lines Agr and Mfg, c is the changing index of agriculture or manufacturing per GDP. The t is changing water withdrawn for irrigation per all agricultural production or changing industrial water use—except thermoelectric power—per manufacturing (data sources: World Bank for GDP, U.S. Geological Survey for water withdrawal, and Statistical Abstract of the U.S. for indices). 

A sector's effect on national impact depends on the size of the sector as well as its changing efficiency. So, how much do changes in sectors affect national impact? We answer by letting C_i × T_i be the intensity of impact or sustainability levers of the i^th sector, the volume of water withdrawn by a sector divided by the national GDP.

The water withdrawals reported by the U.S. Geological Survey were grouped into three sectors: public supply, which comprised 10% of withdrawals in 1995; rural (rural domestic and livestock plus irrigation), which comprised 36%; and industrial (thermoelectric power plus other industrial use), which comprised 54%. During the period 1970–1995, public contributed 0.1%, rural contributed 0.8%, and industrial contributed 1.4% to the national 2.3% per yr decline of C × T. This decline countered most of the 2.5% rise of P × A, the sustainability challenge.

Farla and Blok (14) separated The Netherlands economy into sectors from health and business services through manufacturing to greenhouses. Their analysis showed that dematerializations within sectors rather than a shift among sectors produced the national dematerialization of energy consumption lagging economic output. So, ImPACT can dissect forces within the national total. Further, the leverage of the actors in a single sector for changing a national impact can be estimated. Where data permit, the categories of actors could, of course, be separated into male and female or age cohorts, such as children and seniors, as well as sectors of the economy.

Projections Can Be Robust

Learning historical rates of change of the forces invites projections. We put our faith in extracting stable patterns from history. To be projected, they must be logical enough for us to reason about their changes but simple enough to grasp, and they must be so sturdy that they are not blown this way and that by prices, interest rates, preferences, and other fluctuations that set models adrift. The steady slowing of p makes a predictable foundation. Although income fluctuates, its long course is an increase a of 1–2% per yr. Short-run fluctuations are countered for many staples by income inelasticity, stabilizing a + c. So, from a specification of a rate of innovation t, ImPACT transparently and simply projects an impact, such as the expansion of cropland.

Alternatively, by identifying how forces must change to reach a goal, ImPACT can assay the practicability of a target and timetable. Anticipating change during, say, the 20 years between 1990–2010 of the Kyoto agreement takes a robust method. Could analysis by ImPACT have provided some foresight about the targets adopted with high aspirations in 1997 in Kyoto?

Comparison of the aspirations with recent American and French experience tests prospects. The “1980s” lines of Table 3 show the increase in i plus the accompanying changes in p, a, c, and t from 1980–1990, a decade that the Kyoto negotiators could have had in mind. In both nations, population grew slowly but income grew rapidly. Also, both nations lowered their intensity of use c of energy, leaving per capita use nearly unchanged and implying an income elasticity near zero. Efficiency t of carbon emission per energy improved slightly in the U.S. and improved dramatically in France. The national emissions in the U.S. increased a slow 0.5% per yr in the U.S. and fell 2.8% in France.

Table 3.

Changes in two nations

Nation	i	p	a	c	t
U.S.
1980s actual	0.5	0.9	2.2	−2.4	−0.2
Kyoto required	−1.4	0.8	1.7	−1.2	−2.7
1990s actual	1.3	1.0	2.1	−1.5	−0.3
Relax required	−1.8	0.8	1.7	−1.2	−3.1
France
1980s actual	−2.8	0.5	1.8	−1.9	−3.2
Kyoto required	−0.8	0.4	1.7	−1.2	−1.7
1990s actual	0.7	0.4	1.2	0.0	−0.9
Relax required	−1.1	0.4	1.7	−1.2	−2.0

Changes in percent per year of population p, income a, intensity of use of energy c, and technology t altering greenhouse gas emissions i for two nations. The Kyoto targets would have been achieved over 1997–2010 and Relaxed targets over 2001–2010 (data source: www.eia.doe.gov/oiaf/ieo/pdf/append_a.pdf). 

The “Kyoto required” lines in Table 3 show the annual 1.4% decline of national emission necessary for the U.S. to meet its Kyoto target of 93% of 1990 emissions between 1997–2010. For France, a 0.8% rate of decline was required to attain 92% of 1990 emissions in the same period. To allocate this decline among the four forces, we have inserted reasonable rates for p and a. We calculated c from an income elasticity b of 0.3, and t as the residuum. Comparing experience to the t tests practicability. To meet the 1997 Kyoto Protocol, the U.S. would nearly have had to match the French improvement of t emission per energy during the 1980s, and France would have had to continue its remarkable improvement, won largely by producers installing more than 40 GW of nuclear generating capacity.

The lines “1990s actual” in Table 3 show the actual changes for 1990–2000. Moderate population growth continued, and income grew, especially in the USA, although the intensity of use c declined in the U.S., implying an elasticity b of about 0.3; c did not decline in France, implying an elasticity of fully 1 there. Efficiency measured as emission per energy improved in both nations, but more slowly than the French performance of the 1980s and more slowly in either nation than needed to hit their Kyoto targets.

Later, in Bonn and Marrakech, the targets were relaxed. The final “Relax required” lines show the prospects of reducing emissions during 2001–2010 to 98% of the 1990 emissions. Despite the relaxation, reasonable values of population and income changes plus an income elasticity b of 0.3 require even more rapid improvements in technology t during 2001–2010. Reaching either the Kyoto or relaxed targets requires unlikely behavior. The U.S. would need to apply its sustainability levers to lower c + t from the yearly declines of 1.8% in the 1990s to 4.3%, and France would need to move the 0.9% decline of the 1990s to 3.2%. ImPACT quickly and transparently shows the changes necessary to reach environmental goals and tests practicability.

Discussion

After illustrating ImPACT's analysis of diverse forces and impacts, we discuss its relevance to sustainable production and consumption, to environmental indicators, to the prevalence of dematerialization, and to foresight.

Sustainable production and consumption are responding to the needs for a better life with minimum impact on the environment. ImPACT gives sustainability a concrete form, such as less emission, and names the actors who can achieve such a goal. Although the goal is unexceptionable, progressing from discussion to action requires assigning responsibilities to those with leverage. ImPACT assigns responsibility for P to parents, for A to workers, for C to consumers, and for T to producers. Institutions (including regulations and markets), domestic and international tranquility, capacity, and even style will affect the actors, but ImPACT assigns responsibility to the ultimate actors. Because the desired sustainability requires a better life for the living, parents rather than death must gradually slow the growth of P. Because sustainability includes a better life, humanity's steady ambition for income must be accepted. So, without forgetting that parents might do more and that unemployment might keep workers from raising A, we call the remaining, more malleable and variable combined forces C × T the sustainability lever. Encouraging consumers to be temperate and producers to lower the impact of their production can work the lever.

Navigating toward the goal of sustainability requires the compass of an environmental indicator that integrates changing forces. Unfortunately when an integrated indicator is proposed, questions of the weight to give each of the combined forces bedevil the candidate who might otherwise guide the common journey of all of the actors to sustainability. Fortunately the iron rule that the dimensions on the right of ImPACT balance the dimensions of a genuine environmental impact on the left resolves questions of weight. By settling questions of weight, the iron rule makes ImPACT a reliable and revealing indicator that encompasses the causes of environmental quality and measures progress toward sustainability.

Provisos, of course, accompany ImPACT. Although it bears the advantages of clear genealogy plus a pronounceable acronym, ImPACT carries other baggage, too. Although we have carefully given A the dimensions of GDP per person, the parameter was first named A for affluence. Affluence connotes riches. Despite our clear dimensions for A, the reader must guard against any connotation that, say, an Indian's rise from an A of $241 in 1985 to $312 in 1994 is flowing riches. Similarly, a high value of T or impact per good may well reflect low technology such as a smoking power plant or scanty crop yield, whereas a low T reflects high efficiency. While using the acronym and showing the descent from IPAT, one must remember the dimensions of A and T in ImPACT.

A second proviso concerns connections among forces. Nations with rapid income growth tend to have slower growth of population, and rising A provides economic muscle to lower T. The benefit of an environmental Kuznets curve requires connections of P, C, and T to A. It requires these connections lower P × C × T faster than high incomes rise. Above, the mirroring of income in food consumption gave us the opportunity to move from naming the connections to analyzing them. The familiar concept of income elasticity represents the dependence of per capita consumption or intensity of use upon income. At the same time that elasticity seems to simplify projection into merely projecting income, it turns attention to the estimation and projection of elasticity. The comparison of two nations and two decades with regard to energy and GDP showed how variable income elasticity is, in part, because the prices that we ignored do change. Nevertheless, in the search for sustainable consumption, the parameter c locates the consumers' effect on impact, and in turn, elasticity quantifies its dependence on income.

Defining dematerialization as a declining C and, thus, as a negative c makes consumers responsible for lowering consumption of a material per income. This definition clarifies and separates the responsibility of consumers to use fewer goods per income from the responsibility of producers to impact the environment less per goods.

Dematerialization is prevalent globally and in developed and developing nations, as negative values for c in Table 4 show. Its prevalence begins with the elasticity b < 1 or inelasticity that characterizes necessities. Then c's elasticity of (b − 1) and rising incomes guarantee dematerialization. Broadly, dematerialization arises from substitution and saturation. Cans, which now contain 97% of American beer, soon replaced the bottles whose rise Commoner targeted. Had he called bottles consumption rather than technology, the falling consumption of bottles would have dramatized dematerialization by substitution. In another example, if forest area disturbed were the impact, replacing wood railway ties with concrete would dematerialize wood per GDP.

Table 4.

Prevalence of dematerialization

Impact	Place	Years	c	t
CO2 emission	Global	50/90	−0.3	−0.4
CO2 emission	Global	91/99	−1.2	−0.6
CO2 emission	France	1980s	−1.9	−3.2
CO2 emission	France	1990s	0	−0.9
N fertilizer	Global	1960s	−2.6	8.4
N fertilizer	Global	1990s	−0.3	−0.3
Land for feed	U.S.	67/92	−1.5	−3.3
Cropland	Global	1970s	−1.3	−1.5
Cropland	Global	1990s	−0.1	−2.3
Cropland	India	1970s	−1.1	−1.7
Cropland	India	1990s	−3.4	−2.6
Water	U.S. Agr	70/95	−0.7	−1.7
Water	U.S. Mfg	70/95	0.6	−5.1

The prevalence of dematerialization indicated by falling c and of improving efficiency shown by falling t percent per year. The t for land for feed for meat is t₁ + t₂. The sustainability levers change c + t. 

The saturation that inelasticity and Engels' law reflect is less dramatic. Rising income increases the consumption of necessities but does it more and more slowly as people are saturated, for example, with food, water, and energy services such as auto travel and home heating, regardless of how rich they are. Because necessities are major items in steady demand and rising income is widespread, dematerialization prevails. Although these characteristics of staples will generally bring the good news of dematerialization as income rises, the poverty that lowers per capita consumption will materialize. Although they are not staples, new products such as CDs and PCs boom and also reach a saturation level along a logistic path or even decline. Thus, dematerialization soon dims the hope of unending business fortune and tempers the fear of impact from seemingly exponential growth.

Foreseeing whether producers can meet their challenge requires anticipating what rising p + a + c they must counter with a t of improved efficiency. Over the long run, global population grows steadily but at a rate now declining from 2% toward 1% per yr and perhaps lower. With joyous ups and scary downs, income per capita seems to average a growth of 1–2% per yr. Given the connection between income and the consumption of a staple, intensity of use commonly declines a fraction, say, −0.3, of the rising income. So, without extra help from consumers, producers must annually counter p + a + c = 1.7% (i.e., 1 + 1 − 0.3 = 1.7%) if population and income each grow 1%. If income grows faster at 2%, then producers must counter 2.4%. In percent per yr, the 3.2% decrease in carbon emission per energy in France in the 1980s combining with a 1.9% decrease in intensity of use countered a 2.3% increase in GDP to lower emissions 2.8% (Table 3). In the U.S., the combined forces of rising yield and changing consumption falling 3.3% per yr countered rising GDP to shrink cropland for feed (Table 4). Globally and in India during the 1990s, rising yield lowered t faster than 2% per yr. Countering the rise of environmental impact all alone obviously challenges producers severely, not least as they fully exploit past inventions or approach physical limits on efficiency. Present low efficiencies exemplified by smoking power plants and average crop yields far below those achieved by master farmers, however, show much may still be done. The continued improved efficiencies shown by negative t in all figures are encouraging. Thus, examples show the producers' task is feasible.

If consumers join and help producers work the sustainability lever to lower c + t, they must match or exceed only the p + a of 2–3% per yr. If consumers' dematerialization corresponded to (b − 1) of −0.6 rather than −0.3, improving efficiency need equal or exceed 1.4 or 1.8 in the hypothetical examples of growth above. Of the 13 examples of c + t in Table 4 from the 1960s to 1990s and France to India, 8 improved faster than 2% per yr, showing that the sustainability challenge is not impossible.

From historical rates of change of the four forces and common sense about their limits, ImPACT can foresee impacts. Also, by identifying the change in forces necessary for a projected impact such as the goal of reducing carbon emission, ImPACT can assay practicability and thus help set targets. ImPACT's logic combines with simplicity to make its projections inescapable and understood. An annual 2–3% progress in consumption and technology over many decades and sectors seems a robust, understandable, and workable benchmark for sustainability.

Abbreviation

GDP

gross domestic product